Probabilistic Principal Component Analysis with Expectation Maximization (PPCA-EM) Facilitates Volume Classification and Estimates the Missing Data

Abstract

We have developed a new method for classifying 3D reconstructions with missing data obtained by electron microscopy techniques. The method is based on principal component analysis (PCA) combined with expectation maximization. The missing data, together with the principal components, are treated as hidden variables that are estimated by maximizing a likelihood function. PCA in 3D is similar to PCA for 2D image analysis. A lower dimensional subspace of significant features is selected, into which the data are projected, and if desired, subsequently classified. In addition, our new algorithm estimates the missing data for each individual volume within the lower dimensional subspace. Application to both a large model data set and cryo-electron microscopy experimental data demonstrates the good performance of the algorithm and illustrates its potential for studying macromolecular assemblies with continuous conformational variations.

1. Introduction

Electron tomography can be used to determine the 3D structures of individual subcellular components and to reconstruct complete specimen areas containing many macromolecules (Hoppe et al. 1968, 1976a, b, c). While the technique is ideally suited for the analysis of heterogeneous samples, the low signal-to-noise ratio found in electron tomographic reconstructions of individual objects limits its efficacy.

Averaging techniques have been extensively used for more than four decades to increase the signal-to-noise ratio for 2D image analysis (Markham et al. 1963, 1964; Saxton and Frank 1977; Frank et al. 1978). Major progress was achieved through the introduction of correspondence analysis with associated classification tools (Bretaudiere et al. 1981; van Heel and Frank 1981; Frank and van Heel 1982; Bretaudiere and Frank 1986). This enabled the objective classification of the data into sets of images showing identical particles before averaging, which results in average images with substantially higher resolution and increased signal-to-noise ratio.

Several single particle 3D reconstruction methods incorporate some form of 2D averaging techniques in their algorithms, which results implicitly in 3D averaging. The first method developed was the random conical reconstruction technique, in which one micrograph at high specimen tilt, showing many single particles, is recorded, followed by a second micrograph of the same specimen area without tilt (Radermacher et al. 1986, 1987, 1988). The images extracted from the 0°-micrograph are used for alignment and classification of the particles, and reconstructions are calculated from the corresponding tilt images. The orthogonal tilt reconstruction technique is based on a similar principle. Images are collected at ±45° and one of the tilts is used for alignment and classification, and the other for computing the 3D reconstructions (Leschziner and Nogales 2006). An alternative method used for single particle reconstruction is angular reconstitution (van Heel 1987) where the reconstruction is calculated entirely from micrographs without tilt and the orientation of the particles is calculated by common line methods (Crowther et al. 1970).

Most 3D averaging methods, with either explicit or implicit averaging, work reliably when applied to sets of identical aligned particles. If multiple copies of identical objects are present in a tomogram, averaging of subtomograms can increase the signal-to-noise ratio of the final 3D structures (Knauer et al. 1983; Oettl et al. 1983; Grünewald et al. 2003; Förster & Hegerl 2007). When data are heterogeneous, a classification step is necessary before averaging. For tomographic data, the classification can only be applied to 3D volumes or subvolumes. On the other hand, the random conical reconstruction technique allows for a classification into sets of particles with identical conformation and orientation by applying one of the many methods developed for 2D classification and averaging to the 0°-images. The classification results are imposed onto the tilt images, and then reconstructions are calculated separately for each class. While heterogeneous particles are separated in the resulting 3D reconstructions, identical particles in different orientations are also separated into different classes. Identical 3D structures (originally in different orientations) can be aligned and averaged. However, even after 3D alignment of volumes calculated using any 3D electron microscopy technique, visual classification can be inaccurate. Missing data can result in structural distortions that might lead to misclassifications (Fig. 1). Thus, mathematical methods that can classify volumes irrespective of missing data need to be employed.

Figure 1.

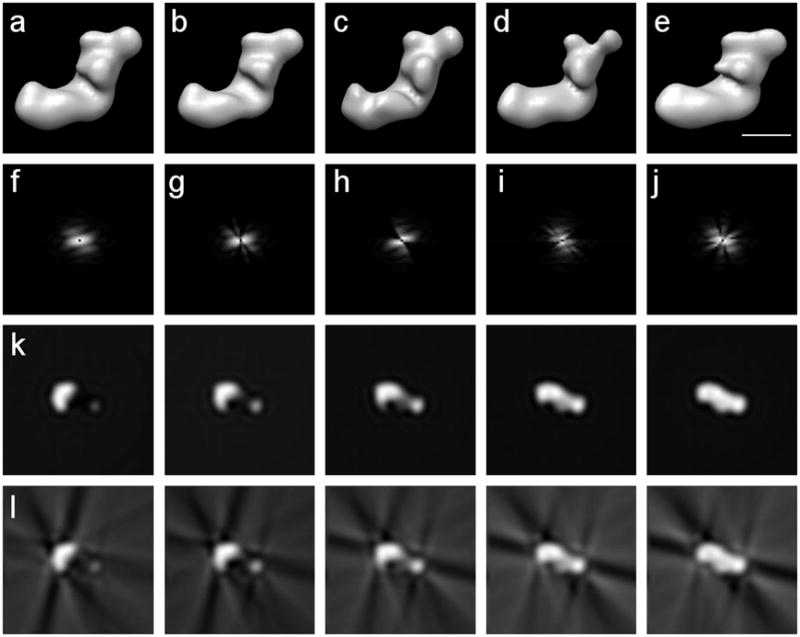
Reconstructions from complete and incomplete sets of noise-free projections of complex I from Y. lipolytica forming a single-axis tilt series around the y-axis; volume size 64×64×64 voxels; voxel size 9Å; low-pass filtered to 36Å. (a) Reconstruction from a complete set. (b)-(e) Reconstructions with 30% missing data using four different subsets of projections. (f)-(j) Power spectra of the central slices of the Fourier transforms of (a)-(e) respectively. (k) Five consecutive x-z slices around the center of the complete reconstruction in (a). (l) Five consecutive x-z slices around the center of the reconstruction with missing data in (b). Clearly visible are the artifacts caused by the missing data. Scale bar 100Å.

3D classification of volumes with missing data has been used for more than a decade (Walz et al. 1997; Winkler and Taylor 1999; Winkler 2007). Only recently have these methods been extended to classify volumes with missing data in different orientations (Bartesaghi et al. 2008; Förster et al. 2008; Scheres et al. 2009). The core of the classification scheme in Bartesaghi et al. (2008) is a hierarchical ascendant classification based on pairwise distances between volumes. The calculation of the distances is restricted to the Fourier areas common to each pair of volumes, which minimizes the influence of the missing data. An algorithm based on principal component analysis, presented later, eliminates the influence of the missing data by excluding it from the calculation of the cross-correlation matrix (Förster et al. 2008). Here, the correlation coefficients are renormalized depending on the amount of overlapping data in each pair of volumes. Both algorithms allow for the recovery of missing data by calculating 3D class averages provided that the data exist in at least one class member.

We present here a robust feature extraction method for the application to 3D reconstructions with missing data, PPCA-EM, based on Probabilistic Principal Component Analysis using Expectation Maximization (Roweis 1997; Tipping and Bishop 1999; Yu et al. 2008). The algorithm extracts the main features of the structure independently of the existence and specific geometry of the missing data as it estimates the latter for each individual volume. In the end, the algorithm represents the data set in a lower dimensional subspace. Once the dimensionality has been reduced, the data can be classified by any standard algorithm, including Diday's method of moving centers (Diday 1971), k-means (MacQueen 1967), fuzzy c-means (Dunn 1973; Bezdek 1981; Carazo et al. 1990) and hierarchical ascendant classification (Johnson 1967).

PPCA-EM has two major advantages over earlier approaches. First, the algorithm finds an approximate principal subspace and the approximate principal component projections regardless of the missing data. Second, the algorithm estimates the missing data for each individual volume. Therefore, the missing data can be estimated even if a data set exhibits only continuous variations without relying on class averages.

2. Background

Principal component analysis (PCA) is a multivariate statistical technique that reduces the dimensionality of the data while maintaining the maximum variance. Let the observation vector t ∈ ℝ^d represent a 2D image or a 3D volume, rearranged as a one-dimensional vector so that each component in t corresponds to a pixel or voxel, with d being the number of pixels or voxels. In a set of well aligned images, the components of t vary when the represented structures vary or when noise corrupts the data.

A set of n observation vectors, {t_i,i=1,2,…,n}, forms a scattered cloud in a d-dimensional space. PCA searches for the directions with the highest variance, (e.g., Lebart 1984). The classical method to derive the principal components is eigendecomposition (Pearson 1901) or singular value decomposition (Golub and Loan 1996) of the covariance matrix of the data.

The covariance matrix is defined as Σ = E[(t−μ)(t−μ)^T] ∈ ℝ^d×d, where E denotes the expectation with respect to the probability distribution of t; the superscript “T”, the transpose operator; and μ = E[t] ∈ ℝ^d, the mean of t. In practice, the covariance matrix is estimated using the scatter matrix, $\mathbf{S}={\sum }_{i=1}^n({\mathbf{t}}_i-\widehat{\mathbf{\mu }}){({\mathbf{t}}_i-\widehat{\mathbf{\mu }})}^{\text{T}}/n$, where the sample mean, $\widehat{\mathbf{\mu }}={\sum }_{i=1}^n{\mathbf{t}}_i/n$ is an estimation of the true mean.

By definition, the eigenvectors ω_j ∈ ℝ^d and the eigenvalues λ_j ∈ ℝ of the scatter matrix satisfy

$$\mathbf{S}{\mathbf{\omega }}_j={\lambda }_j{\mathbf{\omega }}_j,j=1,2,\mathrm{\dots },q^{\prime },$$

where q′ is the rank of S and q′ ≤ min(d,n). The values of λ_j describe the variance of the observations in the direction of the corresponding eigenvectors ω_j and are arranged in descending order, λ₁ ≥ λ₂ ≥ … λ_q′ ≥ 0. Thus the corresponding eigenvectors, ω₁, ω₂,…,ω_q′ , are sorted in descending order of significance. Each eigenvector is normalized so that ${\mathbf{\omega }}_i^{\text{T}}{\mathbf{\omega }}_j={\delta }_{ij}$, where δ_ij is the Kronecker delta (which is 1 for i = j and 0 otherwise).

The original observations t_i can be projected into the subspace defined by the q most significant eigenvectors ω_j, j = 1,2,…q (where q ≤ q′):

$${\mathbf{x}}_i={({\mathbf{\omega }}_1,{\mathbf{\omega }}_2,\dots ,{\mathbf{\omega }}_q)}^{\text{T}}({\mathbf{t}}_i-\mathbf{\mu })\in {ℝ}^q.$$

The x_i approximately represent the t_i in a q-dimensional space while retaining the variance of the data set as much as possible.

The relationships between x_i and t_i can be formulated in a linear form,

$${\mathbf{t}}_i=\mathbf{W}{\mathbf{x}}_i+\mathbf{\mu }+{\mathbf{\epsilon }}_i,$$ (1)

where W = (ω₁, ω₂,…,ω_q) and the ε_i are the residuals: the difference between the approximation and the observed data. Tipping & Bishop (1999) proposed a probabilistic model for the variables in Equation 1. In their model, the latent variables x_i, are assumed to have a normal distribution,

$${\mathbf{x}}_i\sim N(0,\mathbf{I}),$$ (2)

where I denotes the identity matrix. The residuals, ε_i, are assumed to be independent and normally distributed with a mean of zero and an isotropic variance of σ²,

$${\mathbf{\epsilon }}_i\sim N(0,{\sigma }^2\mathbf{I}).$$ (3)

These probabilistic assumptions are consistent with other eigendecomposition methods: PCA is a special case in the limit when σ² →0 (Roweis 1997).

The introduction of a probabilistic model facilitates the use of the expectation maximization (EM) algorithm (Dempster et al. 1977) to estimate the latent variables. We first present the PPCA-EM algorithm for complete data sets. This framework was established by Tipping & Bishop (1999) using an iterated, two-step process.

In the expectation (E) step, the hidden (unknown) variables are estimated from the observations and the current values of the parameters. Statistical moments of the latent variables, 〈x_i〉 and $\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{T}}\rangle$, are estimated using p(x_i | t_i, W, σ²), the conditional probability density of x_i given the observations t_i and the current values of W and σ², (Little and Rubin 1987). Following the probability assumptions made in Equations 2 and 3, one obtains,

$$\langle {\mathbf{x}}_i\rangle ={({\mathbf{W}}^{\text{T}}\mathbf{W}+{\sigma }^2\mathbf{I})}^{-1}{\mathbf{W}}^{\text{T}}({\mathbf{t}}_i-\mathbf{\mu }),$$ (4)

$$\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{T}}\rangle ={\sigma }^2{({\mathbf{W}}^{\text{T}}\mathbf{W}+{\sigma }^2\mathbf{I})}^{-1}+\langle {\mathbf{x}}_i\rangle {\langle {\mathbf{x}}_i\rangle }^{\text{T}},$$

where the superscript “−1” denotes matrix inversion. Equation 4 is used to update the value of the x_i.

In the maximization (M) step, new estimates of the parameters, W and σ², are computed by maximizing the conditional expectation of the log-likelihood, 〈ℓ〉, with respect to the conditional probability density of the unknown variables x_i given the known variables t_i, p(x_i ∣ t_i, W, σ²). The log-likelihood is defined in terms of the joint probability of the observed variables and the latent variables,

$$\mathit{\ell }=\sum _{i=1}^{n}lnp({\mathbf{t}}_i,{\mathbf{x}}_i),$$ (5)

where the joint probability density

$$p({\mathbf{t}}_i,{\mathbf{x}}_i)={(2\pi {\sigma }^2)}^{-d/2}\exp \left\{-\frac{{\Vert {\mathbf{t}}_i-\mathbf{W}{\mathbf{x}}_i-\mathbf{\mu }\Vert }^2}{2{\sigma }^2}\right\}{(2\pi )}^{-q/2}\exp \left\{-\frac{{\Vert {\mathbf{x}}_i\Vert }^2}{2}\right\}$$

can be computed from Equation 1 combined with the probabilistic assumptions in Equations 2 and 3. The conditional expectation of the log-likelihood (Eq. 5) then becomes

$$\langle \mathit{\ell }\rangle =-\sum _{i=1}^n\{\frac{d}{2}\ln {\sigma }^2+\frac{1}{2}\text{tr}\left(\langle {\mathbf{x}}_{\text{i}}{\mathbf{x}}_i^{\text{T}}\rangle \right)+\frac{1}{2{\sigma }^2}{\Vert {\mathbf{t}}_i-\mathbf{\mu }\Vert }^2-\frac{1}{{\sigma }^2}{\langle {\mathbf{x}}_i\rangle }^{\text{T}}{\mathbf{W}}^{\text{T}}({\mathbf{t}}_i-\mathbf{\mu })+\frac{1}{2{\sigma }^2}\text{tr}\left({\mathbf{W}}^{\text{T}}\mathbf{W}\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{T}}\rangle \right)\}.$$ (6)

Maximizing the conditional expectation defined in Equation 6 with respect to W and σ² yields a new estimate for W,

$$\mathbf{W}=\left[\sum _{i=1}^n({\mathbf{t}}_i-\mathbf{\mu }){\langle {\mathbf{x}}_i\rangle }^{\text{T}}\right]{\left[\sum _{i=1}^n\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{T}}\rangle \right]}^{-1};$$ (7)

and using the above quantity for σ²,

$${\sigma }^{\text{2}}=\frac{1}{nd}\sum _{i=1}^n\left\{{\Vert {\mathbf{t}}_i-\mathbf{\mu }\Vert }^2-2{\langle {\mathbf{x}}_i\rangle }^{\text{T}}{\mathbf{W}}^{\text{T}}\left({\mathbf{t}}_i-\mathbf{\mu }\right)+\text{tr}\left(\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{T}}\rangle {\mathbf{W}}^{\text{T}}\mathbf{W}\right)\right\}.$$ (8)

In Equation 7, we assume min(n, d) ≥ q so that the matrix inversion can be carried out.

The E-step and M-step are iterated using the most recent estimates of 〈x_i〉 and $\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{T}}\rangle$ (for i = 1,2…,n), and of W and σ² until no major change occurs in the estimation. It has been shown analytically that this procedure converges to the maximum-likelihood estimation (Dempster et al. 1977). The limiting values of Equations 4, 7 and 8 correspond to the final estimates of the latent variables x_i which are the estimates of the q principal components of t_i; the matrix W which spans the estimated eigenspace; and σ², the variance of the residuals.

3. Methods

3.1 PPCA-EM algorithm

Probabilistic principal component analysis using expectation maximization (PPCA-EM) is readily adapted to observations with missing data (Tipping and Bishop 1999; Roweis 1997). We have extended the technique to encompass 3D reconstructions from electron micrographs with missing data, either originating from tomographic tilt series (single-axis, dual-axis or conical), random conical tilting, or any other technique with incomplete angular coverage(Yu et al. 2008). Different tilting schemes result in different geometries of missing data: single-axis tilting has a missing wedge; dual-axis tilting has a missing pyramid; while conical and random conical tilting have a missing cone that after angular refinement may assume an irregular shape (Radermacher 1980; Radermacher and Hoppe 1980). However, the presence of the coefficients in the Fourier transform of 3D reconstructions can be traced based on the projection-slice-theorem, which states that the 2D Fourier transform of a projection is a central section through the 3D Fourier transform of the object. This is most straightforward in a polar coordinate system, since each radial line is either completely determined or completely missing. Each radial line can easily be indexed, and therefore no special geometrical restrictions to the shape of the missing data need to be considered. Our 3D reconstruction algorithm using Radon transforms maintains a counter of the actual number of radial lines averaged in each direction (Radermacher 1994, 1997). This counter is currently used to properly calculate the average of each radial line in the reconstruction.

We have further extended the PPCA-EM algorithm to complex space to facilitate the application to 3D reconstructions in different forms. Hence t_i ∈ ℂ^d, for all i = 1,2,…,n. In addition, for each t_i we can store the counter from the reconstruction algorithm in a vector ρ_i ∈ ℝ^d, where either ρ_i,j ≥ 1 if t_i,j is present; or ρ_i,j = 0 if t_i,j is missing. These vectors can be used as an index for every component of t_i, indicating the presence or absence of the component. In addition to its use as a Boolean indicator, in PPCA-EM, the value can be used for a more accurate calculation of the weighted mean in Equation 11.

The PPCA-EM algorithm can be extended to incomplete data sets with the above information. The relationship between the observations t_i and the latent variables x_i in Equation 1 then becomes

$$\left(\begin{array}{c}{\mathbf{t}}_i^{(p)}\\ {\mathbf{t}}_i^{(m)}\end{array}\right)=\left(\begin{array}{c}{\mathbf{W}}_i^{(p)}\\ {\mathbf{W}}_i^{(m)}\end{array}\right){\mathbf{x}}_i+\left(\begin{array}{c}{\mathbf{\mu }}_i^{(p)}\\ {\mathbf{\mu }}_i^{(m)}\end{array}\right)+{\mathbf{\epsilon }}_i,$$ (9)

where the indices of t_i have been permutated so that ${\mathbf{t}}_i^{(p)}\in {ℂ}^{d_i^{\left(p\right)}}$ denotes the present data in the ith observation, and ${\mathbf{t}}_i^{(m)}\in {ℂ}^{d_i^{\left(m\right)}}$, the missing data, with $d_i^{(p)}+d_i^{(m)}=d$ for all i = 1,2,…n. The superscript indicates either present (p) or missing (m) data. In general, each volume has different subsets of present and missing data, and consequently requires a different permutation of its indices. The jth component of t_i is in ${\mathbf{t}}_i^{(p)}$ if and only if ρ_i,j ≥ 1, otherwise it is in ${\mathbf{t}}_i^{(m)}$. Likewise, the transform matrix W separates by rows into two parts ${\mathbf{W}}_i^{(p)}$ and ${\mathbf{W}}_i^{(m)}$, and the means μ_i into ${\mathbf{\mu }}_i^{(p)}$ and ${\mathbf{\mu }}_i^{(m)}$ for each volume, for i = 1,2,…n, in accordance with the above permutation.

The model (Eq. 9) is simplified by introducing the centered variable y_i = t_i − μ,

$$\left(\begin{array}{c}{\mathbf{y}}_i^{(p)}\\ {\mathbf{y}}_i^{(m)}\end{array}\right)=\left(\begin{array}{c}{\mathbf{W}}_i^{(p)}\\ {\mathbf{W}}_i^{(m)}\end{array}\right){\mathbf{x}}_i+{\mathbf{\epsilon }}_i.$$ (10)

Here, μ is estimated using the sample mean μ̂ properly weighted to account for the missing data. Each component μ̂_j is calculated as

$${\widehat{\mu }}_j=\frac{{\sum }_{i=1}^n{t}_{i,j}{\rho }_{i,j}}{{\sum }_{i=1}^n{\rho }_{i,j}}.$$ (11)

The missing components have 0 weights and do not contribute to the mean.

Based on the probabilistic assumptions (Eqs. 2 and 3) and the linearity of the Gaussian distribution, the model (Eq. 10) yields the conditional probability density y_i|x_i ∼ N(Wx_i, σ²I) and the marginal probability density y_i ∼ N(0, WW^H + σ²I). Here the superscript “H” denotes the Hermitian conjugate, which is the transpose of the complex conjugate, since the algorithm is valid for either real or complex data.

The expectation maximization algorithm can be used to estimate the latent variables x_i, the model parameter W and σ², and the missing data ${\mathbf{y}}_i^{(m)}$, which are treated as additional hidden variables. Specifically, for each i = 1,2,…n, the values of x_i and ${\mathbf{y}}_i^{(m)}$ can be estimated by their statistical mean, 〈x_i〉 and $\langle {\mathbf{y}}_i^{(m)}\rangle$, taken with respect to the conditional probability density $p\left({\mathbf{x}}_i,{\mathbf{y}}_i^{(m)}|{\mathbf{y}}_i^{(p)},\mathbf{W},{\sigma }^2\right)$. In this context, the iterative, two-step process described in Section 2 can be extended as follows.

In the E-step, the first-and second-order statistical moments of x_i and ${\mathbf{y}}_i^{(m)}$ are directly evaluated using $p\left({\mathbf{x}}_i,{\mathbf{y}}_i^{(m)}|{\mathbf{y}}_i^{(p)},\mathbf{W},{\sigma }^2\right)$. Whence, for i = 1,2,…n,

$$\langle {\mathbf{x}}_i\rangle ={\left({\mathbf{W}}_i^{(p)\text{H}}{\mathbf{W}}_i^{(p)}+{\sigma }^2\mathbf{I}\right)}^{-1}{\mathbf{W}}_i^{(p)\text{H}}{\mathbf{y}}_i^{(p)},$$ (12)

$$\langle {\mathbf{y}}_i^{(m)}\rangle ={\mathbf{W}}_i^{(m)}{\left({\mathbf{W}}_i^{(p)\text{H}}{\mathbf{W}}_i^{(p)}+{\sigma }^2\mathbf{I}\right)}^{-1}{\mathbf{W}}_i^{(p)\text{H}}{\mathbf{y}}_i^{(p)}={\mathbf{W}}_i^{(m)}\langle {\mathbf{x}}_i\rangle ,$$ (13)

$$\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{H}}\rangle ={\sigma }^2{\left({\mathbf{W}}_i^{(p)\text{H}}{\mathbf{W}}_i^{(p)}+{\sigma }^2\mathbf{I}\right)}^{-1}+\langle {\mathbf{x}}_i\rangle {\langle {\mathbf{x}}_i\rangle }^{\text{H}},$$

$$\langle {\mathbf{y}}_i^{(m)}{\mathbf{y}}_i^{(m)\text{H}}\rangle ={\sigma }^2\left(\mathbf{I}+{\mathbf{W}}_i^{(m)}{\left({\mathbf{W}}_i^{(p)\text{H}}{\mathbf{W}}_i^{(p)}+{\sigma }^2\mathbf{I}\right)}^{-1}{\mathbf{W}}_i^{(m)\text{H}}\right)+\langle {\mathbf{y}}_i^{(m)}\rangle {\langle {\mathbf{y}}_i^{(m)}\rangle }^{\text{H}},$$

$$\langle {\mathbf{y}}_i^{(m)}{\mathbf{x}}_i^{\text{H}}\rangle =-{\sigma }^2{\mathbf{W}}_i^{(m)}{\left({\mathbf{W}}_i^{(p)\text{H}}{\mathbf{W}}_i^{(p)}+{\sigma }^2\mathbf{I}\right)}^{-1}+\langle {\mathbf{y}}_i^{(m)}\rangle {\langle {\mathbf{x}}_i\rangle }^{\text{H}}.$$

Note that these moments depend explicitly only upon the current values of ${\mathbf{W}}_i^{(p)}$, ${\mathbf{W}}_i^{(m)}$, σ² and the present data ${\mathbf{y}}_i^{(p)}$. Instead of the entire volumes, only the present data ${\mathbf{y}}_i^{(p)}$ are used to estimate the latent variables x_i, which eliminates any artifacts caused by the missing data (Eq. 12). The missing data ${\mathbf{y}}_i^{(m)}$ are estimated at the same time from the model given the value of the latent variables x_i and the corresponding rows in the transform matrix ${\mathbf{W}}_i^{(m)}$ (Eq. 13).

In the M-step, the log-likelihood is again defined by Equation 5, and the conditional expectation of the log-likelihood with respect to $p\left({\mathbf{x}}_i,{\mathbf{y}}_i^{(m)}|{\mathbf{y}}_i^{(p)},\mathbf{W},{\sigma }^2\right)$ is $\langle \mathit{\ell }\rangle =-\sum _{i=1}^n\left\{\frac{d}{2}ln{\sigma }^2+\frac{1}{2}\text{tr}\left(\langle {\mathbf{x}}_{\text{i}}{\mathbf{x}}_i^{\text{H}}\rangle \right)+\frac{1}{2{\sigma }^2}{\mathbf{y}}_i^{\left(p\right)\text{H}}{\mathbf{y}}_i^{\left(p\right)}-\frac{1}{{\sigma }^2}{\langle {\mathbf{x}}_i\rangle }^{\text{H}}{\mathbf{W}}_i^{\left(p\right)\text{H}}{\mathbf{y}}_i^{\left(p\right)}-\frac{1}{{\sigma }^2}\text{tr}\left({\mathbf{W}}_i^{\left(m\right)\text{H}}\langle {\mathbf{y}}_i^{\left(m\right)}{\mathbf{x}}_i^{\text{H}}\rangle \right)+\frac{1}{2{\sigma }^2}\text{tr}\left({\mathbf{W}}^{\text{H}}\mathbf{W}\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{H}}\rangle \right)+\frac{1}{2{\sigma }^2}\text{tr}\left(\langle {\mathbf{y}}_i^{\left(m\right)}{\mathbf{y}}_i^{\left(m\right)\text{H}}\rangle \right)\right\}.$

Maximizing 〈ℓ〉 with respect to each element w_jk of W yields two different solutions depending if w_jk belongs to ${\mathbf{W}}_i^{(p)}$ or ${\mathbf{W}}_i^{(m)}$, which usually differs for each i = 1,2,…n. We create a set of composite matrices, G_i ∈ℂ^d×q for each i = 1,2,…n. Each element g_i,jk of G_i is either an element of ${\mathbf{y}}_i^{(p)}{\langle {\mathbf{x}}_i\rangle }^{\text{H}}\in {ℂ}^{d_i^{\left(p\right)}\times q}$ if the jth component of the ith observation is present, or an element of $\langle {\mathbf{y}}_i^{(m)}{\mathbf{x}}_i^{\text{H}}\rangle \in {ℂ}^{d_i^{\left(m\right)}\times q}$ if the jth component of the ith observation is missing. Hence,

$$g_{i,jk}=\{\begin{array}{c}{y}_{i,j\prime }^{(p)}{\langle {\mathbf{x}}_i\rangle }_k^{\text{C}},\text{if}{\rho }_{i,j}\ge 1,\\ {\langle {\mathbf{y}}_i^{(m)}{\mathbf{x}}_i^{\text{H}}\rangle }_{j″k},\text{if}{\rho }_{i,j}=0,\end{array}$$ (14)

where the superscript “C” denotes the complex conjugate. Here, j′ is the index in ${\mathbf{y}}_i^{(p)}$ that corresponds to the jth component of y_i and j″ is the index in ${\mathbf{y}}_i^{(m)}$ that corresponds to the jth component of y_i. The indices j′ and j″ can be obtained using the same permutations as in Equation 9. Introducing G_i enables a concise formulation for the new estimate of W,

$$\mathbf{W}=\left[\sum _{i=1}^n{\mathbf{G}}_i\right]{\left[\sum _{i=1}^n\langle {\mathbf{x}}_i{\mathbf{x}}_i^{\text{H}}\rangle \right]}^{-1}.$$ (15)

Under the assumption that σ² → 0, Equations 12 and 13 in the E-step simplify to

$$\langle {\mathbf{x}}_i\rangle ={\left({\mathbf{W}}_i^{(p)\text{H}}{\mathbf{W}}_i^{(p)}\right)}^{-1}{\mathbf{W}}_i^{(p)\text{H}}{\mathbf{y}}_i^{(p)},$$ (16)

$$\langle {\mathbf{y}}_i^{(m)}\rangle ={\mathbf{W}}_i^{(m)}{\left({\mathbf{W}}_i^{(p)\text{H}}{\mathbf{W}}_i^{(p)}\right)}^{-1}{\mathbf{W}}_i^{(p)\text{H}}{\mathbf{y}}_i^{(p)}={\mathbf{W}}_i^{(m)}\langle {\mathbf{x}}_i\rangle .$$ (17)

Likewise, the new estimate of W (Eq. 15) in the M-step simplifies to

$$\mathbf{W}=\left[\sum _{i=1}^n\langle {\mathbf{y}}_i\rangle {\langle {\mathbf{x}}_i\rangle }^{\text{H}}\right]{\left[\sum _{i=1}^n\langle {\mathbf{x}}_i\rangle {\langle {\mathbf{x}}_i\rangle }^{\text{H}}\right]}^{-1},$$ (18)

where 〈y_i〉 is constructed similarly as G_i (Eq. 14),

$${\langle {\mathbf{y}}_i\rangle }_j=\{\begin{array}{ll}{y}_{i,j\prime }^{(p)},\hfill & \text{if}{\rho }_{i,j}\ge 1,\hfill \\ {\langle {\mathbf{y}}_i^{(m)}\rangle }_{j″},\hfill & \text{if}{\rho }_{i,j}=0,\hfill \end{array}$$ (19)

where j′ and j″ are the same as in Equation 14. Note that during the E-step, the most recent estimates of W are entered into the right-hand sides of Equations 16 and 17. Likewise, during the M-step, the most recent estimates of 〈x_i〉 and $\langle {\mathbf{y}}_i^{(m)}\rangle$ are entered into the right-hand side of Equation 18.

Equations 16, 17 and 18 are iterated until a predefined convergence criterion is met or a maximum number of iterations is reached. As a convergence criterion we used the condition that the normalized change of the square error falls below a critical value. We defined the square error in the kth iteration as $e_k={\sum }_{i=1}^n{\Vert \langle {\mathbf{y}}_i\rangle -\mathbf{W}\langle {\mathbf{x}}_i\rangle \Vert }^2$, and the normalized change of the square error as

$${\Delta }_k=\left(e_{k-1}-e_k\right)/e_k.$$ (20)

The current version of the PPCA-EM algorithm was implemented in Python 2.5, using the numpy package, a Python interface for the LAPACK subroutine library (Numpy 2009).

3.2 Performance Measure

Three statistical tests were carried out to investigate the performance of the PPCA-EM algorithm: First, Fisher's Least Significant Difference (LSD) test to measure the separation between known classes; second, k-means to demonstrate how our algorithm facilitates clustering or classification; and finally, discrepancy comparisons to evaluate the estimation of the missing data.

Fisher's LSD test is a widely used statistical inference method to measure the separation between multiple classes, which is an extension of Student's t-test to multiple classes, (Ott and Longnecker 2003). Here we grouped the x_i's, representing the volumes, according to the known classes, and measured the separation between groups by calculating

$$D(i,j)=\frac{\left|{\overline{\mathbf{x}}}_i-{\overline{\mathbf{x}}}_j\right|}{\sqrt{{\displaystyle \frac{\sum _{k=1}^m\sum _{\text{all}l\text{in}\text{class}k}{\Vert {\mathbf{x}}_l‐{\overline{\mathbf{x}}}_k\Vert }^2}{n-m}\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}}},i,j=1,2,\dots m,$$

where m is the number of classes in the data set, n is the number of total volumes, n_i is the number of members in ith class and x̅_i is the mean of the ith class. The minimum LSD score,

$$\widehat{D}=\underset{i\ne j}{\min }D(i,j),$$

which indicates the least separation between two classes, was used as the performance score of the algorithm. The difference D̂ was compared to a critical value, D_c, obtained from Student's t-distribution at α = 0.005, with n − m degrees of freedom. The class separation was considered successful when the difference between the class means was statistically significant at α = 0.005, i.e., D̂ > D_c. For each experimental condition, the success rate was defined as the ratio of the number of successful trials over the total number of trials, expressed as a percentage.

The k-means algorithm, one of the widely used classification/clustering algorithms, was used to demonstrate how our PPCA-EM algorithm facilitates classification and clustering. PCA is typically followed by a classification algorithm applied to the representation of the data in the principal component subspace. Likewise, classification techniques can be applied to the results of PPCA-EM. The combination of the k-means algorithm and the known classes of the data set allows for easy identification of any misclassified reconstructions. A paucity of misclassified reconstructions provides an additional indicator of an appropriate extraction of the main features of the data.

The accuracy of the estimation of the missing data was evaluated by calculating the normalized distance between the complete 3D Fourier volumes reconstructed from all projections and the volumes with the missing data estimated. As a distance measure we used the Fourier discrepancy, based on the real space discrepancy (Herman et al. 1973; Colsher 1977),

$$\delta =\frac{1}{n}\sum _{i=1}^n\sqrt{\frac{\sum _{j=1}^d{\left({\tilde{t}}_{i,j}-t_{i,j}^o\right)}^2}{\sum _{j=1}^d{\left(t_{i,j}^o-{\overline{t}}_i\right)}^2}}$$ (21)

Here, $t_{i,j}^o$ is the jth component of the ith complete volume, t̅_i is the mean of the ith volume, and t̃_i,j = 〈y_i〉_i + μ̂_j (Eqs. 19 and 11) is the jth component of the ith volume with the missing data estimated.

4. Test Data

4.1 Model Data

We applied the PPCA-EM algorithm to a synthetic problem based on a binary version of a 3D reconstruction of complex I from Yarrowia lipolytica (Radermacher et al. 2006; Clason et al. 2007). We chose a model derived from a 3D reconstruction of complex I with the motivation that the results obtained here may advance the understanding of the variations we observed earlier. Using a binary version of the structure ensured that the starting volume was complete and had no missing data. The test data set consisted of a set of 3D volumes containing four classes obtained by applying the skew transform

$$\left(\begin{array}{c}x\prime \\ y\prime \\ z\prime \end{array}\right)=\left(\begin{array}{ccc}1& a& b\\ 0& 1& c\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$$ (22)

to the binary volume. Here (x, y, z) denote the coordinates of the voxel in the original volume; (x′, y′, z′), the coordinates of the voxel in the skewed volume; and a,b,c, the parameters that define the skew operation. Specifically, we used a = 0,b = 0, c = 0 for class 1, a = 0.25,b = 0.1,c = 0.1 for class 2, a = 0.1,b = 0.25,c = 0.1 for class 3 and a = 0.1,b = 0.1,c = 0.25 for class 4. These four structures were then resized to 64×64×64 voxels resulting in a voxel size of 9Å (Fig. 2).

Figure 2.

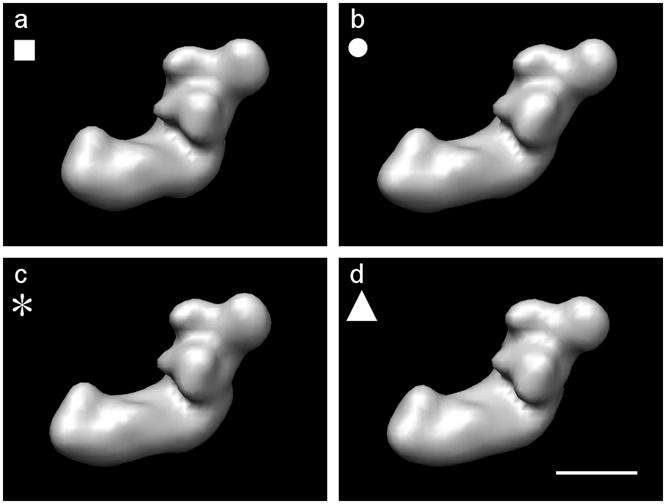
The four starting models derived from a binary volume of complex I from Y. lipolytica, calculated by shearing using Eq. 22, low-pass filtered to 36Å. (a) Original volume a = 0,b = 0.c = 0 (class 1). (b) Volume sheared by a = 0.25,b = 0.1,c = 0.1 (class 2). (c) Volume sheared by a = 0.1,b = 0.25,c = 0.1 (class 3). (d) Volume sheared by a = 0.1,b = 0.1,c = 0.25 (class 4). The symbols (■, ●, *, ▲) are used to identify the classes in subsequent Figures 6 and 7. Even though the parameters have the same values in three of the transformations, the visibility of the differences changes depending on the viewing direction. A skew along either the x-axis or the y-axis is more obvious, since we are viewing along the z-direction. Scale bar 100Å.

Single-axis tilt projections were calculated with 2° angular interval and low-pass filtered to 36Å resolution. Gaussian noise was generated, low-pass filtered to the same resolution as the signal and added to every projection separately before calculating each of the reconstructions. The signal-to-noise ratio was measured as the ratio between the standard deviation of the signal and the standard deviation of the noise out to 36Å resolution. From these projections, multiple 3D reconstructions with missing data were calculated using randomly selected subsets of the projections. We used the 3D Radon inversion algorithm as the reconstruction algorithm (Radermacher 1994, 1997). The angular increments for the 3D Radon transforms were the same as for the single axis tilt series. Therefore, the summation of the 2D Radon transforms of the projections into 3D Radon transforms corresponded to a simple stacking of each 2D transform into the corresponding angular slice of the 3D transform. No averaging occurred, and the signal-to-noise ratio in the 3D transforms is the same as the signal-to-noise ratio in the 2D Radon transform of the projections. 3D polar Fourier transforms were calculated by a 1D Fourier transform of each radial line in the 3D Radon transforms (Deans 1983).

One hundred experimental conditions were created by using all possible combinations of the following three parameters: signal-to-noise ratio (2.0, 1.5, 1.0 and 0.5 at 36Å resolution; corresponding to 0.81, 0.58, 0.41 and 0.19 at full resolution (18Å), respectively) (see supplementary Fig. s1); percentage of missing data (10%, 15%, 20%, 25% and 30%) and total number of volumes in a data set (20, 40, 60, 80 and 100), equally distributed over the four classes. Each combination was repeated 27 times varying the noise and the random selection of missing data. A total of 2700 data sets were created to test the algorithm.

The algorithm was applied to the 3D polar Fourier transforms weighted with $\sqrt{\mathit{\text{r}}\ast }$ to partially compensate for the uneven sampling in polar coordinates. Working in Fourier space, we can easily restrict the resolution by limiting the radius of the Fourier transforms, which also reduces the dimensions of t_i, d. When a discrete polar Fourier transform is applied using a 2° sampling interval, 267300 Fourier components are needed to represent the structure to full resolution of 18Å (32 Fourier pixels). The resolution limit of 36Å (16 Fourier pixels) reduces the dimensions of t_i to 137700.

The PPCA-EM algorithm was applied using a convergence criterion (Eq. 20) of Δ_k ≤ 10⁻⁶. For each data set, eight feature vectors ω_i, i = 1,…8 (Eq. 1) were determined together with the latent variables x_i (Eq. 10) which are the coordinates of the original volumes in the 8 dimensional subspaces. The missing data in each volume were additionally estimated based on the 8 feature vectors (Eq. 17).

4.2 Experimental Data

The algorithm was applied to cryo-electron microscopy data of Saccharomyces cerevisiae phosphofructokinase (PFK, EC 2.7.1.11, 835 kDa, 21S). PFK is a glycolytic enzyme that catalyses the phosphorylation of fructose-6-phosphate (F6P) in the presence of ATP and its activity is tightly regulated by many allosteric effectors (Sols 1981). In the presence of 3 mM F6P the enzyme is in the active state, while in the presence of 1 mM ATP and 3 mM MgCl₂ the enzyme is in the inactive state. The octameric structure of S. cerevisiae PFK has been solved by a combination of Random Conical Tilt cryo-electron microscopy (Ruiz et al. 2001) and 3D reference based alignment of cryo-electron microscopy images without tilt in both states to better than 13Å resolution (Ruiz et al. 2003; Barcena et al. 2007).

The octameric enzyme in both states can be described as a dimer of tetramers, a top tetramer and a bottom tetramer. The F6P and the ATP states differ mainly in the rotation angle between the top and the bottom tetramers (75° rotation for PFK in the F6P-state and 46° rotation for PFK in the ATP-state). These differences, easily visualized in 3D (Fig. 3e-h), can only be observed in very specific 2D projections (Fig. 3a-d). In addition, even though each of the two tetramers in a given state contains 2α and 2β subunits, the tetramers do not possess identical conformations. Pseudo-symmetric PFK structures can be obtained by applying a rotation of 180° around the short axis of the molecule followed by a 75° rotation for the F6P-state or followed by a 46° rotation for the ATP-state. These symmetry operations bring the bottom tetramers to the positions previously occupied by the top tetramers. Both, ATP and F6P induce different structural changes to the top and bottom tetramers in the octamer thus introducing a slight asymmetry that is not visible in 2D projections of the enzyme and it is barely recognizable in 3D structures. The variations observed are mainly concentrated on the catalytic surface defined by the N-terminal domains of the α and β subunits, which exhibit different small relative shifts. These differences have been hypothesized as being part of the functional mechanism of PFK (Barcena et al. 2007).

Figure 3.

Experimental data of PFK in different states. (a)-(d) sample cryo-electron microscopy images each used to reconstruct the structures below in (e)-(h) respectively. (e) PFK in presence of F6P, where the bottom tetramer is in the F6P-bound state. (f) PFK in presence of ATP, where the bottom tetramer is in the ATP-bound state. (g) PFK in presence of F6P, where the top tetramer is in the F6P-bound state. (h) PFK in presence of ATP, where the top tetramer is in the ATP-bound state. The symbols (◆, ●, ▲, ■) are used to identify the classes in subsequent Figure 9. Scale bar 100Å.

The cryo-electron microscopy data set of the F6P bound state contained 16700 aligned projections extracted from 0°-micrographs and the cryo-electron microscopy data set of the ATP bound state contained 14500 aligned projections extracted from 0°-micrographs. Since PFK is an elongated molecule, the projections show PFK mainly rotating around its long axis. Thus, the data sets represent approximately a single axis tilt series with random tilt angles. For this analysis the projections were interpolated down to a pixel size of 7.2 Å. We have used the projections of PFK in the F6P and ATP states with the angular parameters obtained in the original reconstruction, which gives two states showing large conformational changes. By rotating the projections using the symmetry operations described above (180/75 for the F6P state and 180/46 for the ATP state), we were able to calculate PFK volumes in pseudo-symmetric states, in order to test the performance of the algorithm for detecting small conformational changes. 25 different subsets of only 100 randomly selected projections were used to calculate 25 reconstructions for each state. In addition to the missing data occuring in each reconstruction, randomly selected angular sections were removed from the 3D Radon/Fourier transforms, to insure that the volumes had at least 40% missing data in random directions. All reconstructions were aligned to each other prior to any multivariate statistical analysis.

The resulting data set contained 100 volumes, each reconstructed from 100 projections of vitrified PFK and exhibiting at least 40% missing data in their Fourier transforms. Test calculations were carried out in the same order as for the model data: standard PCA applied to the data-set set without missing data. Standard PCA and PCA-EM to the data set with missing data.

5. Results and Discussion

The PPCA-EM algorithm was applied to all 2700 model data sets. The results were calculated from the 27 experiments created for each of the 100 conditions defined by the multiple combination of SNR, percentage of missing data and number of volumes (Fig. 4).

Figure 4.

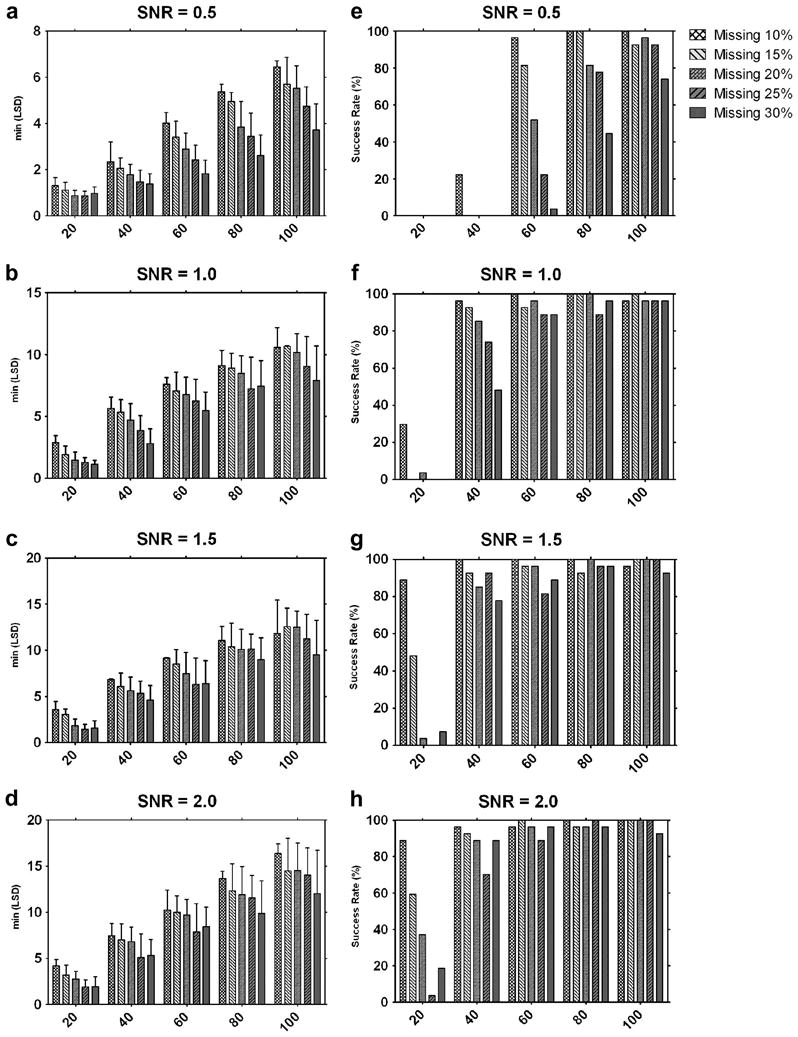
Results of the 2700 tests for 100 different combinations of the three parameters: signal-to-noise ratio, percentage of missing data, number of volumes in a data set. Left column (a)-(d): Each bar represents the mean of the 27 minimum LSD scores for each condition. Test combinations of missing data and number of volumes are represented in graphs for the different SNR used. Error bars show standard deviations. Right column (e)-(h): Each bar represents the success rates of the 27 experiments for each condition at different SNR.

A comparison of all the experiments shows the influence of the different parameters on the performance of the algorithm, measured by the minimum LSD scores (Fig. 4a-d). And the success rates at different SNR are shown in Figure 4e-h. For example, at a SNR of 0.5, with 30% percent missing data, and a data set of only 20 volumes, there was no single success in all 27 experiments (Fig. 4e). On the contrary, at a SNR of 2.0, with 10% percent data missing, and a data set of 100 volumes all 27 trials were successful (Fig. 4h).

Some rare success experiments were observed during the extensive testing of the algorithm. For instance, there was one successful experiment at SNR 1.0, with 20% missing data, and a data set of only 20 volumes (Fig. 4f). Close analysis of this data set showed that the area of missing data in this set of volumes had a substantial overlap, thus minimizing the influence of the missing data on the separation between classes. The statistical nature of the experiments causes other fluctuations visible in both SNR=1.5 and SNR=2.0 cases (Fig. 4g and 4h). An increase in performance is observed when the missing data increases from 25% to 30% in the cases of 20, 40, and 60 volumes, but not in the cases of 80 and 100 volumes. These are common statistical fluctuations that occur when only few data points are sampled (here less than 60) and that disappear when the number of samples increases.

Based on the test calculations, the minimum conditions required to obtain a certain reliability of the results can be estimated. A success rate above 70% can be observed for a SNR of 1 if the number of volumes is larger than 40 and the missing data are less than 25% (Fig. 4f). For a data set of 60 or more volumes, the success rate at a SNR of 1 was always above 70% for all percentages of missing data tested (Fig. 4f). When the data set contained 100 volumes, a 70% success rate was achieved for all modeled conditions, including those with a SNR of 0.5.

The three parameters that affect the results of PPCA-EM can be adjusted in various ways to improve the conditions for applying the algorithm. An increase in success rate can be achieved by increasing the number of volumes, by decreasing the percentage of the missing data, or by increasing the SNR for a given data set. The best method to improve the performance of the algorithm depends on the microscopy technique used for data collection. When electron tomography is used as reconstruction technique, an increase in the number of volumes can be easily achieved by collecting an additional tomography series, which usually contains a large number of subtomograms of the macromolecular structure of interest. In addition, the amount of missing data can be reduced by tilting to a higher angle, by collecting double-tilt series, or by using the conical tilt geometry (Radermacher 1980; Radermacher and Hoppe 1980), see Figure 5 and Table 1. Reconstructions from single-axis tilt series with ±60° angular range have 33.3% missing data. The performance of the PPCA-EM algorithm when applied to this data set can be approximately evaluated based on our tests under the condition of 30% missing data. A dual-axis tilt series also with ±60° angular range dramatically decreases the amounts of missing data to 16%, and our tests with 15% missing data provide a good reference for this condition. If the SNR is the limitation, it may be possible to increase the SNR by lowering the resolution while preserving sufficient detail for structural differentiation. When the random conical reconstruction technique is used, the easiest parameter to optimize is the SNR of the reconstructed volumes by collecting additional tilt pairs. Often the percentage of missing data can be reduced simply by using a higher tilt angle (Fig. 5 and Tab. 1). A large reduction in the percentage of missing data from 13.4% to 6.0% is achieved by increasing the tilt angle from 60° to 70°, which can be easily reached with modern specimen holders.

Figure 5.

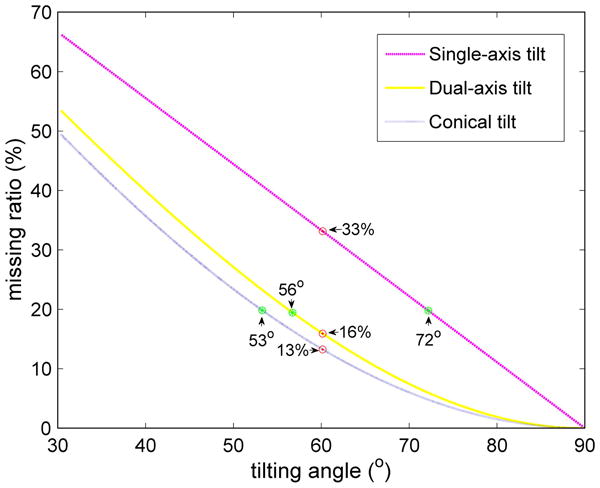
Graph representing the percentage of missing data for different tilting geometries. The x-axis indicates the maximum tilt angle for single-axis and dual-axis tilting, or the fixed tilt angle for conical tilting. Marked are the percentages of missing data for a tilt angle of 60° (red dots) and the tilt angles for 20% missing data (green stars) for each different geometry.

Table 1.

Tilt geometries and percentage of missing data. (a) The percentage of missing data for different tilt geometries and tilt angles. (b) The tilt angles for different tilt geometries and the percentage of missing data. * For conical/random conical (RC) the angular value represents the fixed tilt angle.

a
	single-axis	dual-axis	conical/RC
±30°	66.7%	53.9%	50.0%
±45°	50.0%	33.4%	29.3%
±60°	33.3%	16.0%	13.4%
±70°	22.2%	7.5%	6.0%
±80°	11.1%	1.9%	1.5%
b
	single-axis	dual-axis	conical/RC
10%	∓81°	∓67°	64°
15%	∓77°	∓61°	58°
20%	∓72°	∓56°	53°
25%	∓68°	∓52°	49°
30%	∓63°	∓48°	44°

The performance of the algorithm is illustrated in more detail for one of the data sets containing 100 volumes with a SNR of 0.5 and 30% missing data (Figs. 6, 7 and 8)¹. Plots of the data in the subspace defined by the first three principal components are shown in Figure 6, in which symbols of the same shape and color identify the synthetic original classes. The scatter plots are represented using only the real part of the principal components, which most clearly show the separation of the data. The results of standard PCA when no data are missing demonstrate that PCA is able to capture the main features of the structures and shows an obvious separation into four classes (Fig. 6a). Figure 6b shows the results of standard PCA when the missing data are replaced with 0. The missing data dominate the analysis and no class separation can be detected. Even when eight principal components are visualized pairwise in all possible combinations, no class separation can be detected (results not shown). When the PPCA-EM is applied to the same data set with missing data (Fig. 6c), the correct clustering is achieved, however the volumes belonging to classes 3 and 4, localized at the two opposite ends of a single elongated cloud, are still loosely connected.

Figure 6.

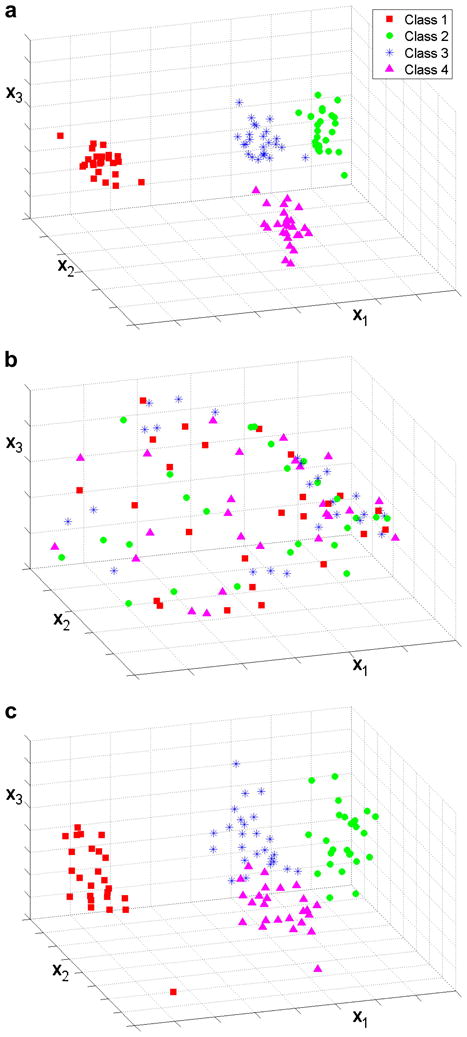
Scatter plots of the real part of the first three principal components, x₁, x₂ and x₃, for a data set with 100 volumes and SNR of 0.5. Symbols correspond to the true classes of each volume. (a) Data set with no missing data, standard PCA. The four classes are clearly separated. (b) 30% missing data, standard PCA. The results are dominated by the missing data. (c) 30% missing data, PPCA-EM. Classes 1 and 2 are well separated. Classes 3 and 4 are loosely connected but easily separable.

Figure 7.

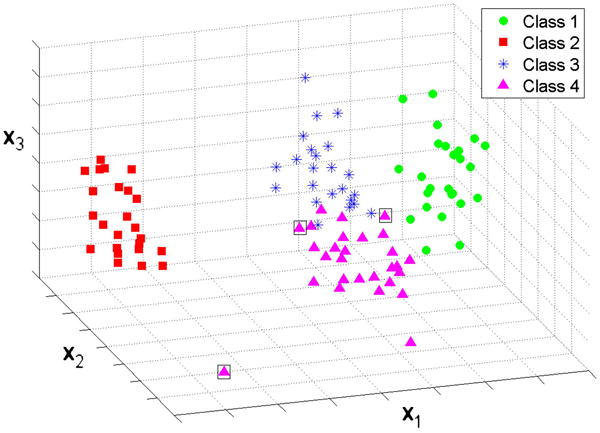
Classification results of the k-means algorithm applied to the results of PPCA-EM shown in Figure 6c. Only three misclassifications occur, enclosed in boxes. Here, the symbols correspond to the classes identified by the k-means algorithm.

Figure 8.

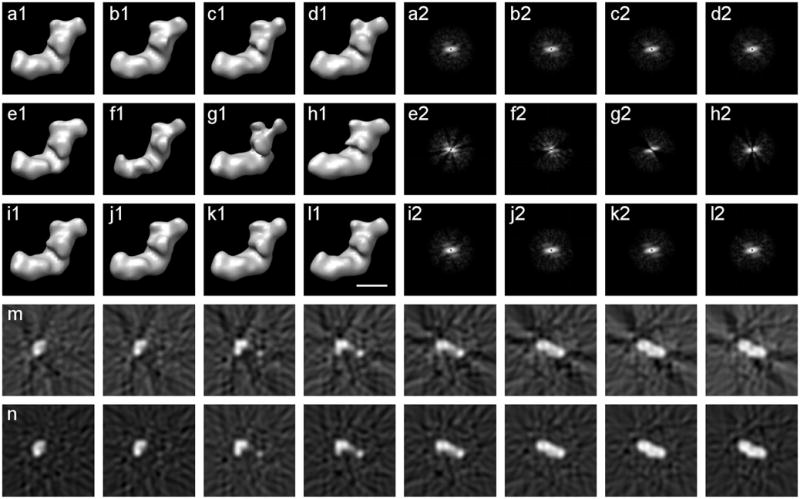
Reconstructions of class 1 with complete, incomplete, and estimated data, SNR=0.5. (a1)-(d1) Four reconstructions without missing data, any differences are caused by variation in noise. (a2)-(d2) Power spectra of the central slices of the Fourier transforms of (a1)-(d1) respectively. (e1)-(h1) Four reconstructions with 30% missing data. (e2)-(h2) Power spectra of the central slices of the Fourier transforms of (e1)-(h1) respectively. (i1)-(l1) Four reconstructions with estimated missing data from PPCA-EM. Each reconstruction closely resembles the corresponding complete reconstruction in (a1)-(d1). (i2)-(l2) Power spectra of the central slices of the Fourier transforms of (i1)-(l1) respectively, notice the filled-in estimated missing data. (m) Eight consecutive x-z slices around the center of the incomplete reconstruction in (e1). (n) Eight consecutive x-z slices around the center of the reconstruction with estimated missing data in (i1). Notice how the artifacts caused by the missing data are reduced by PPCA-EM. Scale bar 100Å.

When k-means clustering with k=4 was applied (Fig. 7), using the same coordinates as in Figure 6, the majority of the volumes were classified correctly into the original classes. Only 3 volumes out of 100 were misclassified (indicated by boxes in Figure 7). Note that no special attempt was made at this point to optimize the classification algorithm.

The PPCA-EM algorithm estimates not only the principal components but also the missing data for each single volume. The reconstructions with the estimated data (Fig. 8i1-l1) closely resemble the corresponding reconstructions without missing data (Fig. 8a1-d1). When the power spectra of the corresponding volumes are compared (Fig. 8i2-l2, a2-d2), the estimation appears better at lower resolution. However, a comparison of these power spectra with the power spectrum of a noise-free reconstruction (e.g., Fig. 1f) shows that the higher resolution spectrum contains mostly noise.

We compared three different methods for estimating the missing data by calculating Fourier discrepancies (Eq. 21) for the 100 volumes in the data set for each method (Tab. 2). The first method substitutes the missing data with the weighted mean of the total data set; the second method substitutes the missing data with the weighted mean of the class to which the volume belongs; and the third method uses the estimate from the PPCA-EM algorithm. The overall weighted mean is the worst estimation of the missing data, while the best estimation is obtained by PPCA-EM. The PPCA-EM algorithm aims at estimating the data including the variations originating from the noise, while the estimation from class averages implicitly includes a noise reduction. If a good classification can be obtained, the weighted class mean is a reasonable method for estimating the missing data. With a continuous distribution of the data, and no clear classification, the estimation by PPCA-EM is superior.

Table 2.

The Fourier discrepancy values for the three possible methods for estimating missing data.

	Fourier Discrepancy
Total mean	0.7301∓0.0010
Class mean	0.6015∓0.0002
PPCA-EM	0.5865∓0.0003

The application of the PPCA-EM algorithm to the cryo-electron microscopy PFK data set demonstrates the effectiveness of the algorithm applied to experimental data. The scatter plots of the volumes projected onto the first principal components are illustrated in Figure 9, in which the symbols are shaped and colored according to the different states of PFK. Without missing data, standard PCA is able to resolve the volumes into four well separated clusters (Fig. 9a). Thus, here PCA can capture the features that enable accurate volume classification, and can elucidate both the large and small variations in the data set. However, with at least 40% missing data, standard PCA neither captures the features nor separates the classes clearly (Fig. 9b). The PPCA-EM algorithm, when applied to the same data set with at least 40% missing data, is able to reproduce the correct clusters in the subspace of the largest principal components (Fig. 9c). Data clustering for both PCA and PPCA-EM was checked by examining 2D scatter plots of the volumes projected onto different combinations of the real and imaginary parts, and also the amplitudes of the largest principal components. Interestingly, for the PFK data the best separation was observed when the volumes were projected on the space defined by the real part versus the imaginary part of the first principal component. It should be noted that for the case of the model data of complex I, the best separation was observed in the 3D space defined by real parts of the first 3 principal components. Thus, once the principal components of a data set are obtained, the data should be analyzed in different 2D or 3D spaces, where the imaginary parts of the principal components are treated as additional principal components.

Figure 9.

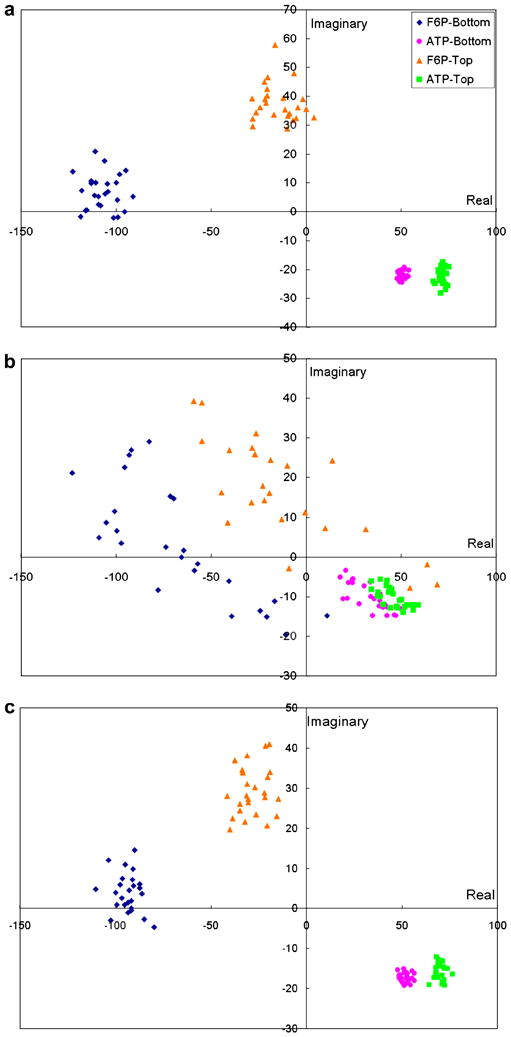
Scatter plots of the PFK volumes projected onto the first principal component, real part vs. imaginary part. Polar Fourier volumes reconstructed with 100 projections were used. Symbols correspond to different states of PFK. (a) No missing data, standard PCA. (b) 40% missing data, standard PCA. (c) 40% missing data, PPCA-EM.

Our PPCA-EM algorithm performs well on data with real noise as demonstrated by the results obtained with the experimental data set. Even though the Gaussian noise, assumed in the algorithm, is an approximation of the noise present in electron micrographs, the PPCA-EM algorithm is able to perform a principal component analysis on electron microscopy volumes with missing data. This is not surprising given the fact that standard PCA, where a Gaussian noise assumption is implied, has been highly successful as a multivariate statistical analysis method in the analysis of 2D electron microscopy images.

Currently, there are four algorithms available in electron microscopy that can analyze 3D volumes with missing data in different orientations. Förster's algorithm uses constrained cross-correlation to reduce the dimensionality of the volumes (Förster et al. 2008). Bartesaghi's algorithm is able to determine the translational and rotational alignments, and assign each volume to a class using a pairwise distance constrained in the commonly present part of the volumes (Bartesaghi et al. 2008). Neither algorithms estimate missing data for individual volumes. Scheres' algorithm, reported after the first submission of this paper, aligns, classifies and estimates missing data for 3D volumes based on expectation maximization (Scheres et al. 2009). None of the three algorithms estimate feature vectors. Our PPCA-EM algorithm extracts feature vectors, reduces the dimensionality of the data, and estimates the missing data for individual volumes. A specific classification algorithm is not included, leaving a wide choice of classification techniques. The technique best suited for a specific data set can be selected. When the data set exhibits continuous variations, these will be visible in the scatter plots produced in feature subspaces, and will not be obscured by a possibly artificial classification. Since our algorithm estimates missing data for individual volumes, averaging of subpopulation is not required.

In summary, we have derived the explicit formulations for the extension of the probabilistic principal component analysis to the application to 3D reconstructions with missing data. Extensive testing of the algorithm both with model and real data has demonstrated its high performance and illustrated its limitations. Most of these limitations can be overcome by increasing the information in the data set in a microscopy technique dependent fashion. The application to real data has shown that our algorithm can detect slight conformational differences that are not visible in 2D projections and barely visible in 3D. In addition to the separation of heterogeneous reconstructions, our algorithm estimates correctly the missing data for each single volume without requiring class averages. The importance of this feature will become prominent as more and more biological systems are studied that do not show well defined states but continuous variations.