Electron Tunneling Pathways and Role of Adenine in Repair of Cyclobutane Pyrimidine Dimer by DNA Photolyase

Abstract

Electron tunneling pathways in enzymes are critical to their catalytic efficiency. Through electron tunneling, photolyase, a photoenzyme, splits UV-induced cyclobutane pyrimidine dimer into two normal bases. Here, we report our systematic characterization and analyses of photo-initiated three electron transfer processes and cyclobutane ring splitting by following the entire dynamical evolution during enzymatic repair with femtosecond resolution. We observed the complete dynamics of the reactants, all intermediates and final products, and determined their reaction time scales. Using (deoxy)uracil and thymine as dimer substrates, we unambiguously determined the electron tunneling pathways for the forward electron transfer to initiate repair and for the final electron return to restore the active cofactor and complete the catalytic photocycle. Significantly, we found that the adenine moiety of the unusual bent flavin cofactor is essential to mediating all electron-transfer dynamics through a super-exchange mechanism, leading to a delicate balance of time scales. The cyclobutane ring splitting takes tens of picoseconds while electron-transfer dynamics all occur on a longer time scale. The active-site structural integrity, unique electron tunneling pathways and the critical role of adenine assure the synergy of these elementary steps in this complex photorepair machinery to achieve maximum repair efficiency which is close to unity. Finally, we used the Marcus electron-transfer theory to evaluate all three electron transfer processes and thus obtained their reaction driving forces (free energies), reorganization energies, and electronic coupling constants, concluding the forward and futile back electron transfer in the normal region and that the final electron return of the catalytic cycle is in the inverted region.

Introduction

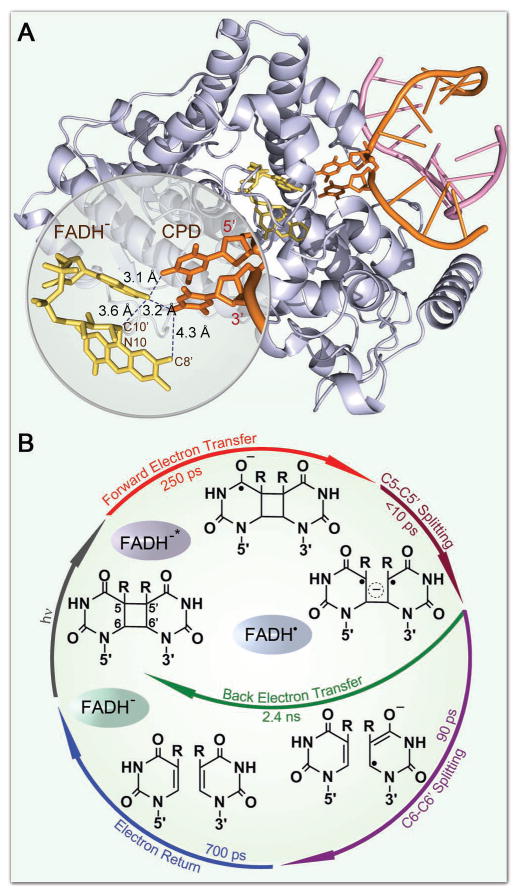
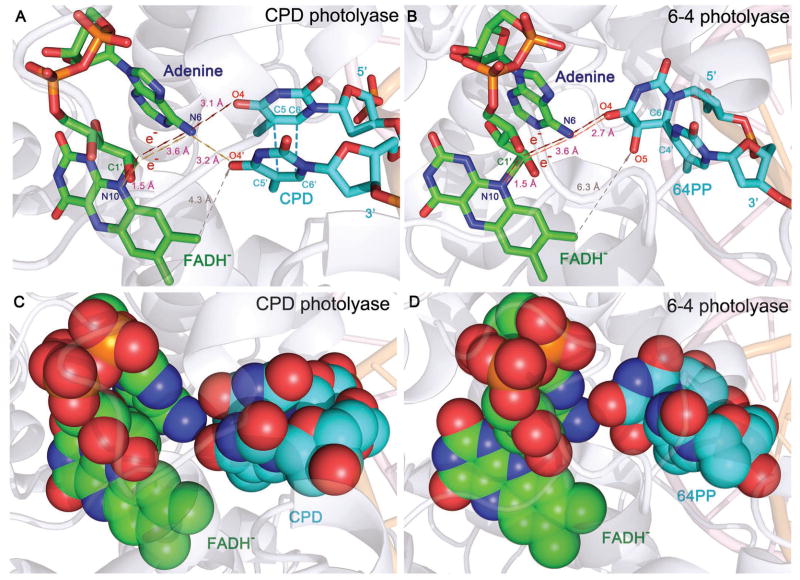
Cyclobutane pyrimidine dimer (CPD), induced by irradiation of ultraviolet (UV) light, leads to DNA mutagenesis and possible skin cancer.^1–4 Photolyase, which contains an active cofactor flavin adenine dinucleotide in fully reduced form (FADH⁻) as the catalytic cofactor, repairs CPD through an electron transfer (ET) mechanism upon excitation by blue light.^5–8 The structure of the A. nidulans photolyase with thymine dimer (T<>T) complex after in situ repair is shown in Figure 1A.⁹ With femtosecond (fs)-resolved spectroscopy, we recently followed the entire repair dynamics from the reactants, to intermediates, and finally to products and thus resolved the complete repair photocycle by photolyase (Figure 1B).^8,10 Briefly, the excited FADH⁻ donates one electron to CPD in 250 picoseconds (ps). The cyclobutane pyrimidine ring in anionic CPD breaks sequentially in less than 10 ps and in 90 ps, respectively, and the electron from the repaired anionic thymine (T⁻) returns to FADH^• in 700 ps, finishing the photocycle and restoring the damaged DNA and the catalytic cofactor. The futile back ET, parallel to the ring splitting, occurs very slowly in 2.4 nanoseconds (ns), favoring the repair channel. However, a key question remains unresolved: How the electron tunnels between excited FADH⁻ and T<>T in the forward ET and between FADH^• and T⁻ in the electron return following splitting of the cyclobutane ring. Two main tunneling schemes have been proposed based on theoretical calculations.^11–14 One model suggests that the electron tunnels through the intervening adenine moiety at a longer distance of about 8 Å with the unusual U-shape configuration of the cofactor.^11,12 The other model concludes that the electron would directly travel through space at a “shorter” distance of 4.3 Å (Fig. 1A).^13,14 Thus, to experimentally determine the electron transfer pathway and the tunneling directionality, we carefully designed an experimental approach that would allow us to examine the ET dynamics and determine the electron tunneling routes.

Figure 1.

X-ray structure of enzyme-substrate complex and the molecular mechanism and photocycle of CPD repair. (A) A complex structure of A. nidulans photolyase (light-blue ribbon) containing the catalytic cofactor FADH⁻ (yellow stick) and duplex DNA (orange and pink ribbons) with a repaired CPD lesion (orange stick). A close-up view shows the relative positions of the catalytic cofactor FADH⁻ and the repaired substrate with various distances for two potential tunneling pathways. The adenine moiety of FADH⁻ was in van der Waals contact with both 5′ and 3′ sides of CPD. (B) The complete photocycle of T<>T repair by photolyase with all resolved elementary steps and their reaction times, elucidating the molecular mechanism at the most fundamental level.

Our study provides new insights into protein electron transfer at a short distance (<10 Å)^15–19 in contrast to the numerous long-range protein ETs that have been carried out in the past two decades.^20–32 Some long-distance ET reactions use certain protein residues as electron donating/accepting intermediates, especially aromatic residues of tryptophan and tyrosine, to complete an electron hopping process.^19–21 Most ETs employ protein matrix to facilitate electron tunneling via a super-exchange mechanism.^22–32 The electron tunneling pathways in proteins usually consist of covalent bonds, hydrogen bonds, and spatial protein architectures with secondary structures of α-helices and β-sheets. These ETs typically occur at long distances and their ET rates are much faster than those by simply tunneling through space (vacuum type) or in aqueous solution. For photolyase studied here, the ET is at a short distance within 10 Å with two possible tunneling pathways: one is “shorter” but with no molecular mediation and therefore would correspond to tunneling in space and the other has a longer distance with an intervening molecule in the pathway. Here, we have addressed the question of which route the electron takes and how this step affects the repair function.

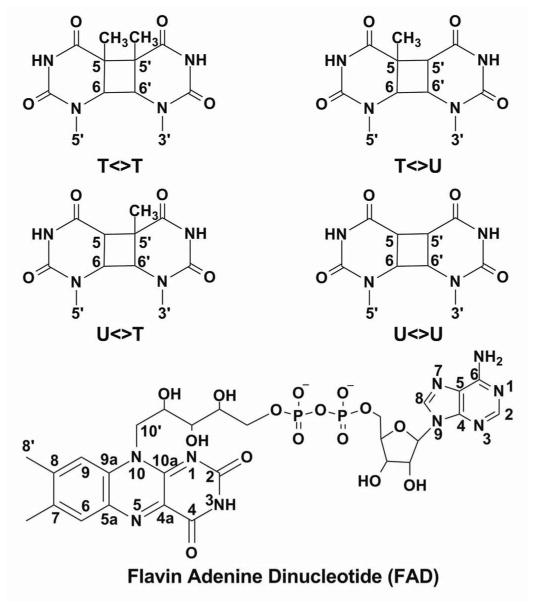
To answer this question, we used a series of (deoxy)uracil-modified dimers (scheme 1) (T<>T, U<>T, T<>U and U<>U) and performed a complete series of fs-resolved studies from visible to UV light region. A brief report of these extensive studies has been given in ref. 10 and here we give a full account of the detailed analyses of ET pathways in repair of CPD by photolyase. With more than 13 probe wavelengths from visible to UV light, we were able to resolve the dynamics of forward ET, back ET without repair, bond splitting, and electron return following the ring splitting in all CPD substrates as well as with the determination of the enzyme/substrate binding constants and total repair quantum yields. Using the semi-classical Marcus ET theory, we evaluate the driving forces, reorganization energies and electronic coupling constants of these electron tunneling processes. These results elucidate the electron tunneling pathways and the role of intervening adenine in these pathways, and provide the molecular basis for the high repair efficiency of photolyase.

Scheme 1.

Chemical Structures of Various Damaged Substrates and Flavin Adenine Dinucleotide

Materials and Methods

Sample Preparation

The purification of E. coli CPD photolyase with depletion of the antenna cofactor has been reported previously.^33,34 For all fs-resolved experiments with UV detection, 100 μM of enzyme (or 50 μM in experiments with the probe wavelengths at shorter than 300 nm) was used in a reaction buffer containing 100 mM NaCl, 50 mM Tris-HCl, pH 7.5, 20 mM dithiothreitol, 1 mM EDTA, and 50% (v/v) glycerol. For all measurements in the visible-light region, a higher enzyme concentration of 300 μM was used.

We prepared various CPD substrates (T<>T, T<>U, U<>T and U<>U) as described previously.^10,35 The final concentration of all CPD substrates used in fs-resolved experiments was 18 mM. The ratio of the substrate to photolyase was at least 60:1 and thus the samples could be used for several hours for fs-resolved measurements without any noticeable change of the repair dynamics.

Enzyme Activities

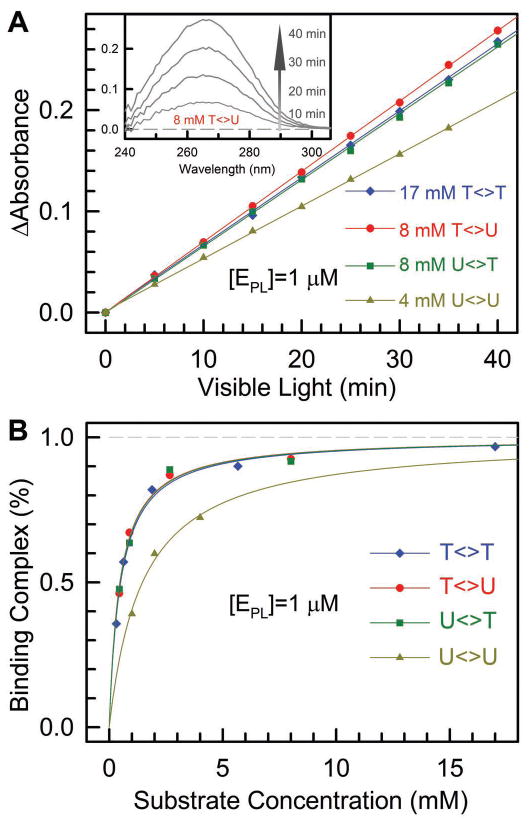
We quantitatively measured the enzyme activities of various substrate (T<>U, U<>T, U<>U and T<>T) repair by photolyase. First, we determined the dissociation constants (or binding constants) of photolyase-CPD complexes (E·S). We prepared several sets of mixtures in cuvettes with 1 μM concentration photolyase with excess T<>T, T<>U, U<>T, or U<>U substrates. Then, the cuvettes were irradiated at room temperature with 360-nm light (UVP lamp) at a distance of 6 cm. The inset in Figure 2A shows a typical repair process with the absorbance increasing with time as a result of formation of the T and U bases. Figure 2A shows typical steady-state repair measurements for the four substrates. For each substrate repair, we plotted the absorbance changes against time with different substrate concentrations. Given [S]≫[E], a small amount of substrate repair over the time course of our reaction does not change the substrate concentration measurably. Thus, the resulting slopes (m) will be directly proportional to the binding complex concentrations, [E·S]. For any two concentrations of the substrate, we can solve their binding complex concentrations (and the dissociation constant) as follows.

Figure 2.

Determination of dissociation constants and repair quantum yields of various CPD substrates. (A) The relative repair quantum yields of T<>U, U<>T and U<>U to T<>T by photolyase by monitoring the formation of thymine/uracil bases using 266-nm absorption changes (inset) with 365-nm irradiation of the enzyme-substrate solution. With dissociation constants and known repair quantum yield of T<>T repair of 0.82, the repair quantum yields of T<>U, U<>T and U<>U were obtained. (B) The dissociation constants of photolyase-CPD complexes were obtained by measuring the binding complexes relative to substrate concentrations and then fit using eq. (3).

$$K_d=\frac{({[E]}_1-{[ES]}_1){[S]}_1}{{[ES]}_1}=\frac{({[E]}_2-{[ES]}_2){[S]}_2}{{[ES]}_2},$$ (1)

$$\frac{{[ES]}_1}{{[ES]}_2}=\frac{m_1}{m_2}$$ (2)

To be more accurate, after solving for enzyme-substate concentrations, we plotted the binding complex percentage ([ES]/[E]) against substrate concentration and using the following equation fit the dissociation constant, K_d.

$$\frac{1}{[ES]/[E]}-1=\frac{K_d}{[S]}$$ (3)

Figure 2B shows the fitting results for four substrates and the derived four dissociation constants are 5.0×10⁻⁴, 4.7×10⁻⁴, 4.8×10⁻⁴ and 1.5×10⁻³ M for T<>T, T<>U, U<>T and U<>U, respectively. The first three substrates have similar dissociation constants (~5×10⁻⁴ M) and for U<>U, the dissociation constant is the largest by a factor of 3.

By knowing the dissociation constants and under the same reaction conditions, then we can obtain the repair quantum yields. From Figure 2A, by comparing the slopes of T<>U, U<>T, and U<>U with the T<>T repair and taking account of the binding complex concentrations, and the known repair quantum yield of T<>T which is 0.82,³⁶ we obtained the repair quantum yields of 0.88, 0.86 and 0.84 for T<>U, U<>T and U<>U, respectively. We did not observe any absorption change at 266 nm in control experiments with only substrates (T<>U, U<>T and U<>U) at the same concentrations under the same irradiation conditions. Note that the obtained repair quantum yields for T<>U, U<>T and U<>U are larger than those reported in earlier studies.³⁶ We believe that the new values here are more accurate because of the careful determination of dissociation (or binding) constants and also consistent with the measured various reaction rates of individual steps in the overall repair reaction as shown below.

Femtosecond Absorption Spectroscopy

We used the transient-absorption method for all the fs-resolved experiments. The experimental layout has been detailed elsewhere.^17,24 Briefly, for all measurements, the pump pulse at 400 nm in 1 kHz was generated by the doubling of 800 nm in a 0.2 mm thick β-barium borate crystal (BBO, type I). The pump pulse energy was typically attenuated to 140–200 nJ/pulse before being focused into the sample cell. All desired probe wavelengths, from visible to ultraviolet, were generated from optical parametric amplifiers (OPA-800C and TOPAS, Spectra-Physics). The instrument response time is about 250 fs and all experiments were done at the magic angle (54.7°). Samples were kept fast stirring during irradiation to maintain the fresh complex concentration as well as to avoid heating and photobleaching. All enzyme reactions in fs-resolved measurements were carried out under anaerobic conditions at room temperature.

Results and Discussion

Electron Injection, Adenine Mediation and Tunneling Pathway

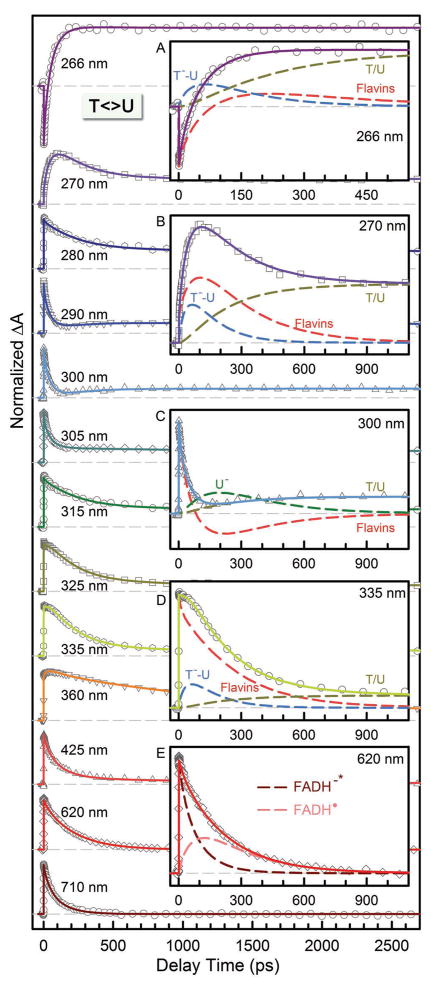
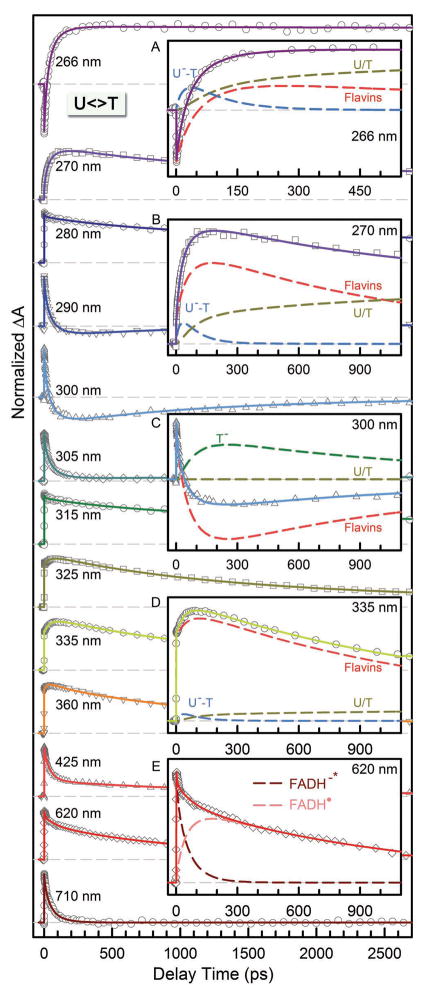
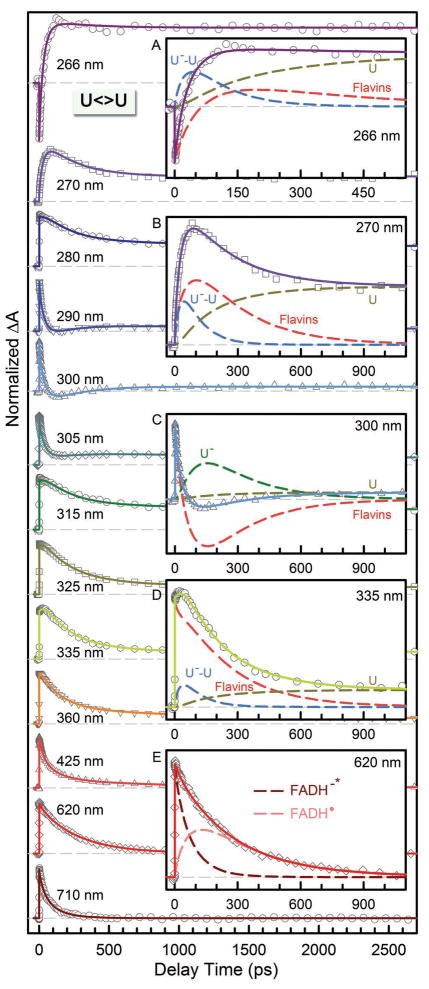
Figures 3–5 show femtosecond-resolved absorption dynamics of T<>U, U<>T and U<>U repair by photolyase with thirteen detection wavelengths from visible 710 nm to UV 266 nm to map out the complete dynamic evolution of the repair. In our earlier report,¹⁰ we showed the evidence of ET pathways in five transients at 710, 620, 335, 300 and 270 nm. Here, the complete set of detections covers the entire dynamic evolution of the reactants, intermediates and final products, and ensures our systematic and accurate data analyses. Specifically, in the visible region from 710 to 425 nm, we detected only flavin species. At 710 nm, only excited state FADH^−* has absorption⁸ and thus the transients directly reflect the electron injection dynamics from excited cofactor to CPD substrates. These dynamics were observed to follow a stretched-single-exponential decay, Ae^−(t/τ)β, in 75, 57, and 66 ps (τ) with the stretched parameters of 0.87, 0.89 and 0.92 (β) for T<>U, U<>T and U<>U, respectively. It should be emphasized that the time constants obtained here are accurate with an error bar of at most 5% with the high single-to-noise ratio and multiple measurements. In our earlier studies of T<>T repair,^8,10 we observed a decay of 170 ps with β=0.71. As pointed out elsewhere,^8,10,37–39 the stretched-exponential dynamic behavior results from the modulation of ET reactions by active-site solvation. The active-site solvation occurs in a few picoseconds to sub-nanoseconds. Thus, the longer ET dynamics has a smaller parameter β and shows more stretched behavior, indicating more coupling between active-site motions and electron tunneling.

Figure 3.

Femtosecond-resolved transient absorption dynamics of T<>U repair by photolyase at probe wavelengths from 710 to 266 nm. The transients probed at 266, 270, 300, 335 and 620 nm are deconvoluted in insets A–E, respectively. All transients were fitted by considering flavin-related species (dashed red in insets A–D and dashed pink and dark red in inset E), substrate intermediates of T⁻-U (dashed blue) and U⁻ (dashed dark green), and thymine/uracil products (dashed dark yellow).

Figure 5.

Femtosecond-resolved transient absorption dynamics of U<>T repair by photolyase at probe wavelengths from 710 to 266 nm. The transients probed at 266, 270, 300, 335 and 620 nm are deconvoluted in insets A–E, respectively. All transients were fitted by considering flavin-related species (dashed red in insets A–D and dashed pink and dark red in inset E), substrate intermediates of U⁻-T (dashed blue) and T⁻ (dashed dark green), and uracil/thymine products (dashed dark yellow).

Using $\langle \tau \rangle =\frac{\tau }{\beta }\mathrm{\Gamma }(\frac{1}{\beta })$ to derive the average times³⁷ and then taking the FADH^−* lifetime (1.3 ns)⁸ contributions into account, we obtained the average time scales of 212, 80, 60 and 69 ps and final ET times of 250, 85, 63, and 73 ps (Table 1) for T<>T, T<>U, U<>T and U<>U, respectively. Thus, the ET dynamics (rates) from the excited FADH⁻ to four CPD substrates vary in a decreasing order of 5′-U<>T-3′ > U<>U > T<>U > T<>T. This observation is significant and indicates that the electron tunnels toward ending at the 5′ side, not the 3′ side, of the dimers. U<>T and T<>U have the similar reduction potentials, but the ET time lengthens by more than 35% from 63 ps of U<>T to 85 ps of T<>U, i.e., the rate decreases to 74%. Theoretical studies showed the similar binding configurations¹¹ for U<>T and T<>U and thus the observed differences in ET rates should not come from the electronic couplings because of the similar donor-acceptor separation. Also, such changes of ET rates, if caused by the electronic coupling, could lead to a distance increase of 0.3–0.4 Å, which was not observed in the simulations¹¹ and is also unlikely in structural and electrostatic interactions.^9,40

Table 1.

Results of Reaction Times, Efficiencies of the Elementary Steps and Overall Repair Quantum Yields of Various Damaged Substrates^a

Substrate	QY	β	<τFET>b	BFETc	<τBET>	<τsp>	Bspc	<τER>
T<>T	0.82	0.71	250	0.85	2400	90	0.96	700
T<>U	0.88	0.87	85	0.94	1175	75	0.94	185
U<>T	0.86	0.89	63	0.95	315	35	0.90	1220
U<>U	0.84	0.92	73	0.95	260	35	0.88	210

^aAll times are in unit of picosecond. Here β is the stretched parameter and QY is the overall repair quantum yield of damaged substrates calculated by QY=B_FET × B_SP or by direct measurement.

^b<τ_FET> is calculated from ${[{(\frac{\tau }{\beta }\mathrm{\Gamma }(\frac{1}{\beta }))}^{-1}-\frac{1}{{\tau }_l}]}^{-1}$. τ is the observed timescale of FADH^−* decay at 710 nm and τ_l is 1.3 ns determined in the absence of substrate.

^cB_FET and B_sp are efficiencies of the forward ET and the ring splitting and calculated by B_FET = 〈τ_FET〉⁻¹/(〈τ_FET〉⁻¹ + τ₁⁻¹) and B_sp = 〈τ_sp〉⁻¹/(〈τ_sp〉⁻¹ + 〈τ_BET〉⁻¹), respectively.

The uracil base has a reduction potential more positive than thymine by ~0.11 V.⁴¹ Although the electronic interactions between T and U in the covalent CPD species delocalize the CPD states and result in similar redox properties of U<>T and T<>U, the U moiety without a methyl group at the C5 position at the 5′ side should have a larger electron affinity than the T moiety. Thus, if the adenine moiety of FADH⁻ is involved in electron tunneling, our results would indicate that the local configuration and orientation favors the electron tunneling to the 5′ side, rather than the 3′ side (Fig. 1A), although the distances from the adenine to the two sides are nearly equal,⁹ 3.1 and 3.2 Å, respectively. The larger ET rate of U<>T vs. T<>U also excludes the electron tunneling pathway directly from the o-xylene ring of the flavin to the 3′ side of the dimer¹³ (Fig. 1A). Thus, we conclude that the electron tunnels through the adenine moiety and this conclusion will also be separately obtained from the ring splitting dynamics as shown below.

Given that the reduction potentials of adenine and FADH⁻ is −2.52 V⁴¹ and +0.08 V⁴² vs. NHE, respectively, and assuming the S₁←S₀ transition of FADH⁻ near the end of absorption at 480–500 nm (2.58–2.48 eV), the intramolecular electron hopping from the isoalloxazine ring to adenine in FADH^−* is unfavorable due to the free energy ΔG~+(0.02–0.12) eV. In the absence of substrate, we did not observe any fast decay of FADH^−* and the excited-state dynamics is in nanoseconds.^8,10 Even if the ET occurred without substrate from FADH^−* to adenine, the ET time would be longer than 1.3 ns.⁸ Thus, we can rule out the possibility of direct two-step electron hopping between the isoalloxazine ring and the substrates bridged by adenine in a total of 63–85 ps. If the two-step hopping did occur, the first-step hopping from the isoalloxazine ring to adenine should happen at least in 63–85 ps, assuming the second-step hopping from the adenine moiety to substrates is instantaneous with a short separation distance of 3.1 Å. With the substrates, even though the redox properties of FADH^−* could be affected, it is unlikely that the first-step ET reaction from the isoalloxazine ring to adenine, if occurred, would drastically speed up from nanoseconds to tens of picoseconds upon binding of substrates. Thus, we conclude that the electron tunneling from the isoalloxazine ring to substrates must be mediated by adenine through a super-exchange mechanism.

We can estimate the ET times for the two proposed ET pathways. Both tunneling routes are a hybrid of structural and chemical configurations. We first need to determine the initial location of the tunneling electron in FADH^−*. Some calculations concluded that the electron density in the HOMO molecular orbital of the ground state and in LUMO of the excited state is mainly localized at the pyrimidine and pyrazine rings in FADH^−11,12,43 and that only a minor change of the electron distribution occurs upon excitation, which leads to a small variation of dipole moments of the two states, as observed to be about 1–2 D in recent experiments.^38,44 Other calculations concluded that the electron in LUMO is localized at the o-xylene ring,^13,14 resulting in a huge change of dipole moments of the two states in more than 10 D, which is contrary to experimental observations.^38,44 Thus, the electron tunneling starts at the side of the pyrimidine and pyrazine rings and here we assume the N10 (scheme 1) position in FADH^−* as the initial starting point for the calculation of two potential ET pathways. The first route is from N10 to C10′ through a covalent bond in 1.5 Å, then from C10′ passing through the adenine in 3.6 Å and finally reaching the 5′ side of the dimer in 3.1 Å (scheme 1 and Fig. 1A). The total tunneling length is 8.2 Å. The second pathway is from N10 to C8′ through four covalent bonds in 5.7 Å and then to the 3′ side of the dimer in 4.3 Å (scheme 1 and Fig. 1A). The total tunneling length in this second route could be 10 Å, although the distance between the isoalloxazine ring and the 3′ side of the dimer is the shortest at 4.3 Å. Thus, using the empirical ET formula below,^25,45 we can estimate the ET times for the two hybrid tunneling pathways.

$$logk=13-A-3.1\frac{{(\mathrm{\Delta }G+\lambda )}^2}{\lambda },A=\beta (r-r_0)loge=0.434\beta (r-r_0)$$ (4)

where k is the ET rate in s⁻¹, A is related to the electronic coupling term, ΔG is the total free energy of the reaction in eV, λ is the reorganization energy in eV, β here is the empirical ET parameter in Å⁻¹ and r is the separation distance in Å. r₀ is the van der Waals distance at 3.0 Å for calculating ET rates at long tunneling distances.

For different tunneling configurations, the β parameters are different.^25,27,46 For tunneling through covalent bonds, here we could use A=0.434βr with β=0.71 Å⁻¹ assuming r₀=0;^25,27 we subtract the van der Walls distance of 3.0 Å (r₀ in eq. 4) from the second tunneling segments for both hybrid pathways. In this way, we could get a total minimum A term in eq. (4) for the entire hybrid pathways. For tunneling in proteins mediated by different structures, β=1.0–1.4 Å⁻¹, while for tunneling directly through space, β=2.9–4.0 Å⁻¹. Thus, for the first hybrid pathway, we obtain A=2.07–2.71 and for the second hybrid route, A=3.39–4.02. For the T<>T dimer, the free energy ΔG is −0.44 eV and the reorganization energy λ is 1.21 eV (see below). Thus, we obtained ET times of 389 ps-1.7 ns for the first pathway and of 8.1–34.7 ns for the second route. The measured ET time for T<>T is 250 ps, closer to the estimated value of 389 ps through the first hybrid tunneling pathway. Thus, the electron tunnels through the covalent bond N10-C10′ at 1.5 Å and then from C10′ to the 5′ side of the dimer in 6.7 Å mediated by adenine nearly in the middle pathway. Using the measured ET time of 250 ps, we obtained β=0.83 Å⁻¹ for the tunneling from C10′ to the 5′-side dimer due to the mediation by the adenine moiety. Thus, from the C10′ position to the 5′-side dimer, the nature of tunneling is more likely toward the covalent bond tunneling (β=0.71 Å⁻¹) by 3.6 Å from C10′ to adenine (N6 atom in scheme 1) and 3.1 Å from adenine to the 5′-side dimer. Such a hybrid tunneling pathway mediated by the adenine moiety is also observed in 6-4 photoproduct repair by 6-4 photolyase.⁴⁷ In that system, the first pathway to the 5′ side of the 6-4 photoproduct through adenine is nearly the same as in the dimer repair, but the separation between C8′ to the nearest 3′ side of the 6-4 photoproduct in the second route increases to 6.3 Å.⁴⁸ However, the forward ET has a similar dynamics of 280 ps due to the first unique hybrid tunneling pathway through the adenine moiety in the unusual U-shape configuration of FADH⁻ at the active site.⁴⁷ Thus, the adenine moiety plays a critical role in mediating electron tunneling in repair of damaged DNA through a super-exchange mechanism.

With the measured forward ET dynamics, we can determine the electronic coupling constant (J) and related free energy for different substrates. We can rewrite eq. (4) in a semi-classical ET expression.^25,45

$$k_{ET}=\sqrt{\frac{4{\pi }^3}{h^2\lambda k_{B}T}}{J}^2\times {10}^{-\frac{3.1{(\mathrm{\Delta }G+\lambda )}^2}{\lambda }}$$ (5)

where h and k_B are Planck and Boltzmann constants, respectively, and T is temperature in Kelvin. For the four different substrates, the coupling constant (J) and the reorganization energy (λ) can be considered as constants. Knowing the redox potential T<>T/T<>T⁻ to be −1.96 V vs. NHE,^49–51 the free energy ΔG is calculated to be −0.44 eV using E_0-0=2.48 eV for forward ET between FADH^−* and T<>T (Table 2). Interestingly, both reduction potentials of T and T<>T are ~0.11 V more negative than U and U<>U in organic solvents, respectively.^41,51 Thus, the free energy of forward ET between FADH^−* and U<>U is around −0.55 eV. Considering the reported reorganization energy of λ to be 1.2–1.4 eV in flavoprotein ETs^52–54 as a fitting reference value and taking into account a larger J and a slightly smaller λ in the forward ET than in the electron return (see below), we obtain the free energy for ET with U<>U to be −0.59 eV, λ=1.21 eV and J=3.0 meV. The coupling constant of 3.0 meV is in a good agreement with the theoretical calculation which assumed electron tunneling through adenine instead of space.¹¹ Using the obtained λ and J values, we calculate free energy (ΔG) of −0.61 eV for U<>T and −0.57 eV for T<>U (Table 2). The difference of 40 meV for U<>T and T<>U probably results from the preferred electron tunneling directionality to the 5′ side rather than 3′ side of the dimer, assuming the same electronic coupling constants for both ETs. It should be pointed out here that the values of λ and J for the forward ET could be slightly smaller, but with the constraints of the back ET with a slightly larger λ and smaller J and the consideration of both forward and back ET together, the obtained λ and J are indeed around 1.2 eV and 3.0 meV. We also recently used the Sumi-Marcus theory (2D) to analyze the data and obtained the slightly smaller result (1.07 eV). The larger λ is mainly from the larger λ_i (vibrational distortion energy), due to the significant structural change of FADH⁻ to FADH.

Table 2.

The Derived Free Energies of all Elementary Steps in Repair of Various Substrates^a

Substrate	GFETb	ΔGBET	ΔG‡spc	ΔGER
T<>T	−0.44	−0.22	0.174	−2.26
T<>U	−0.57	−0.29	0.170	−2.10
U<>T	−0.61	−0.42	0.152	−2.32
U<>U	−0.59	−0.44	0.152	−2.12

^aAll free energies are in unit of eV. The reduction potentials of several involved species are E(FADH^•/FADH⁻)=+0.08 V vs. NHE in the presence of substrate binding to photolyase, E(T/T⁻) =−2.18 V, E(U/U⁻)= −2.07 V and E(T<>T/T<>T⁻)= −1.96 V.

^bThe 2.48 eV for the S₁←S₀ transition at 500 nm is used in calculation of ΔG_FET.

^cThe pre-exponential factor A in calculation of ΔG^‡_sp from k=Aexp(−ΔG^‡_sp/(k_BT)) is assumed to be 10¹³ s⁻¹.

Sequential Ring Splitting, Back Electron Transfer and High Quantum Efficiency

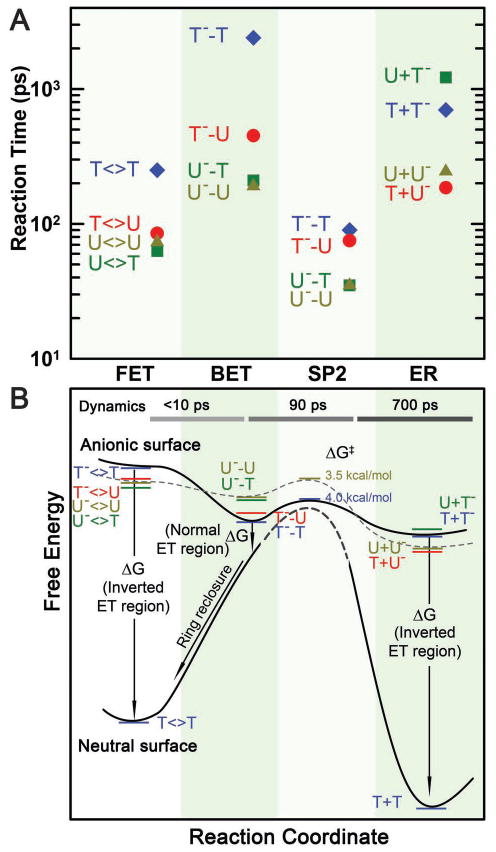
With understanding of the forward ET dynamics probed at 710 nm, we tuned the probe wavelength to 625 nm to detect the flavin intermediate FADH^• and to 425 nm to detect the flavin product FADH⁻ (Figures 3–5). To detect the substrate-related intermediates and products, we extended the probe wavelengths to UV region from 360 to 266 nm and observed a series of striking features of transients. All these transients can be fit systematically only with the sequential model shown in Fig. 1B and the deconvoluted transients probed at 266, 270, 300, 335 and 620 nm are shown in A–E insets in Figs. 3–5. The final results are listed in Table 1 and the resulting reaction times of all elementary steps are also shown in Figure 6A.

Figure 6.

Reaction times and free energy diagrams of the elementary steps in splitting of CPD substrates. (A) Reaction times of each elementary step observed in repair of various substrates (T<>T, T<>U, U<>U and U<>T), including the forward ET, the C6-C6′ bond splitting, futile back ET and final electron return to complete the photocycle. Note the order in reaction times of three ET processes for four different substrates and also the faster bond splitting than the back ET and electron return. (B) The free energy profiles along the reaction coordinate after the forward ET in repair of CPD substrates with the time scales of the dynamics shown at the top. On the anionic surface, the solid curve represents the splitting of T<>T⁻ while the dashed curve for U<>U⁻. On the neutral surface, the bond-breaking activation barrier (dashed curve) is very high according to theoretical calculations. Note the different regions, normal or inverted, of three ET processes and the ring reclosure after the futile back ET.

After charge separation, the anionic CPD could follow two routes: repair of the dimer by breaking of two C-C bonds and back ET to the original ground state without repair. Experimentally, we did not observe any signals of T⁻<>U, U⁻<>U, U⁻<>T at all wavelengths, indicating that the C5-C5′ bond breaks instantaneously, leading to the trace accumulation of CPD anions. Our fitting results give an upper limit of less than 10 ps for the C5-C5′ bond breaking, otherwise we should have observed noticeable signals of CPD anions in the UV region. Thus, the splitting of the C5-C5′ bond has little activation barrier (Fig. 6B) and occurs ultrafast, consistent with extensive theoretical calculations.^55–63 In contrast, the back ET without any bond breaking has a driving force about −2.0 eV^42,51 and should occur within hundreds of ps in the Marcus inverted region, comparable with 6-4 photoproduct repair.⁴⁷ Thus, the back ET from intact CPD anions could not compete with the C5-C5′ bond breaking, leading to the complete evolution along the first bond splitting.

At wavelengths shorter than 360 nm, we observed the anionic intermediates of T⁻-U, U⁻-U and U⁻-T (insets A, B and D of Figs. 3–5). Following the C5-C5′ bond breaking within a few picoseconds, the dynamics of T⁻-U, U⁻-U and U⁻-T decay in 64, 31 and 30 ps, representing the total dynamics (rates) of both the C6-C6′ bond breakage of anionic CPD intermediates and futile back ET after the C5-C5′ splitting. Given the splitting branching of T⁻-U, U⁻-U and U⁻-T as 0.94, 0.88 and 0.90 (Table 1), respectively, the T⁻-U takes the similar bond splitting time of 75 ps as T⁻-T in 90 ps, but the C6-C6′ bond in U⁻-U and U⁻-T splits on a much faster time scale of 35 ps. These splitting times are much longer than our recent theoretical values (less than 1 ps) of the C-C bond splitting in a CPD model system in bulk water.⁶¹ Clearly, the second C6-C6′ bond breaking has a longer time with T and a shorter time with U at the 5′ side. Thus, after the C5-C5′ bond breakage, the excess electron mainly remains at the 5′ side because the T moiety at the 5′ side with a methyl group at the C5 position can significantly stabilize the anionic radical and thus has a longer time of the C6-C6′ splitting. This observation also supports the electron tunneling toward the 5′ side of the dimer, which also must pass through the adenine moiety.

According to the transition-state theory, we estimated the activation energy of ~0.174 eV (4.02 kcal/mol) for T⁻-T bond breaking, ~0.170 eV (3.93 kcal/mol) for T⁻-U bond splitting, and ~0.152 eV (3.51 kcal/mol) for U⁻-T and U⁻-U bond cleavage (Fig. 6B). Thus, the stabilization in T⁻-T by the methyl group(s) at the C5 (and C5′) position leads to ~0.022 eV (0.51 kcal/mol) more for the activation of the bond splitting than U⁻-U. On the other hand, before the C6-C6′ splitting, the futile back ET results in the neutral intermediates to reclose the ring by formation of the C5-C5′ bond again and return to the original ground state (Fig. 6B). The splitting of C6-C6′ bond in the neutral ground state after the back ET is probably insignificant. The splitting of the CPD lesion on the neutral surface (Fig. 6B) is unlikely and the recent theoretical studies have shown that a free energy of larger than 1.7 eV is required to lengthen and break the C5-C5′ bond.^61,64 Thus, the free energy for back ET after the C5-C5′ breaking must be around −0.34 eV (−1.96 eV+1.7 eV−0.08 eV) (Fig. 6B). Assuming the reorganization energy to be the similar as the forward ET, 1.21 eV, the back ET thus switches to the Marcus normal region (Fig. 6B). From the measured quantum yields (Table 1), we obtained the back ET time scales of 1175, 315 and 260 ps for T⁻-U, U⁻-T and U⁻-U, respectively, much shorter than that for T⁻-T in 2.4 ns. Thus, the back ET dynamics change in a decreasing order of 5′-U⁻-U-3′ > U⁻-T > T⁻-U > T⁻-T (Fig. 6A). Using the same λ and J values of 1.21 eV and 3 meV, respectively, we obtained the free energy of back ET to be −0.22 eV for T-T⁻, −0.29 eV for T⁻-U, −0.42 eV for U⁻-T, and −0.44 eV for U⁻-U (Table 2).

Although thymine has a reduction potential more negative than uracil by 0.11 V, which would lead to a larger driving force and a faster back ET, it seems that the methyl group at C5/C5′ position significantly stabilizes the anion intermediate, resulting in the less driving force and strategic slowdown of the back ET. With T at the 5′ side, the stabilization energy is about 0.15 eV by comparison of T⁻-U vs. U⁻-U, while T at the 3′ side the stabilization energy is about 0.02 eV from U⁻-T vs. U⁻-U, indicating that the electron is mainly localized at the 5′ side with a partial distribution on the 3′ side and the methyl group at the C5′ position has some stabilization effect. Our recent high-level calculation^61,63 showed that the electron is delocalized between the two bases and even solvated by neighboring water molecules. As shown above, the methyl group also stabilizes the transition-state free energy ΔG^‡ of T⁻-T by 0.022 eV, compared with U⁻-U, to slow down the C6-C6′ breaking. Thus, the methyl group(s) at the C5 (C5′) position slows down both rates of the bond splitting and futile back ET. However, the free energy due to the stabilization by the methyl groups in T⁻-T is 0.22 eV higher than in U⁻-U, well exceeding its lower reduction potential, leading to a much longer back ET time (2.4 ns), and strongly favoring the splitting channel for a high repair quantum yield.

The total repair quantum yield is the product of two-step yields: forward ET branching and complete splitting branching. As shown in Table 1, the forward ET with T<>T has the longest time scale of 250 ps and thus has the smallest first-step branching of 0.85. However, due to the longest back ET time of 2.4 ns even with the longest C6-C6′ bond splitting time of 90 ps, the second-step splitting branching is highest, 0.96, among all four substrates. Thus, the highest second-step splitting branching compensates for the lowest first-step forward ET branching, still leading to a high total quantum yield of 0.82. Similarly, for the three uracil-substituted substrates, the forward ET is faster and results in a larger first-step branching of 0.94–0.95, but the splitting branching becomes relatively smaller, 0.88–0.94, due to the faster back ET process. However, the total quantum yields are similar in the range of 0.84–0.88. Thus, for all four CPD substrates, the total quantum yields are optimized and all lie in the range of 0.82–0.88, a very high repair efficiency of close to 1 for the complex repair photomachinery.

Electron Return, Catalytic Restoration and Repair Photocycle

After a sequential breakage of both C-C bonds, the cyclobutane ring is repaired but the electron must return semiquinone FADH^• to complete the photocycle and restore the catalytic state of FADH⁻. In UV region, we did observe the signal of T⁻ and U⁻ intermediates around 300 nm (inset C of Figs. 3–5) and the products of T and U in various substrates (insets A–D of Figs. 3–5). The (T+U)⁻ and (U+U)⁻ have faster return dynamics of 185 and 210 ps than (T+T)⁻ with 700 ps, while (U+T)⁻ has the longest electron return time of 1220 ps. The electron-return dynamics are much slower than the ring splitting and thus both processes are decoupled. From the four measured electron-return times, the U at the 3′ side has faster charge recombination and the T at the 3′ side has slower electron-return dynamics. After the cyclobutane ring splits, the electron mostly stays at the 3′ side. From the X-ray structure,^9,40,65 several water molecules, polar/charged residues, and the highly reducing FADH^• are all around the 3′ side, which probably stabilizes and solvates the electron.

Thus, the electron-return dynamics for the four substrates vary in a decreasing order of 5′-T+U⁻-3′ > U+U⁻ > T+T⁻ > U+T⁻ (Fig. 6A). Again, the direct electron hopping from T⁻/U⁻ to the adenine moiety is unlikely due to the positive free energy of +0.3/+0.4 eV⁴¹ (Table 2). However, the back electron tunneling from T⁻ at the 3′ side passing the adenine-mediated pathway again to final FADH^• has a large driving force of −2.26 eV^41,42 (Table 2) and such tunneling is feasible in hundreds of ps and is probably in the Marcus inverted region. Using eqs. (4) and (5) for the electron-return dynamics of T+T⁻ and U+U⁻ (ΔG around −2.15 eV) and by consideration of a smaller J and a larger λ in the electron return than in the forward ET, we obtained the electronic coupling and reorganization energy of 2.6 meV and 1.37 eV for return tunneling, and the free energy of −2.12 eV for U+U⁻. The reorganization energy is slightly larger than that of the forward ET (1.21 eV) because the electron return is in the Marcus inverted region (Fig. 6B) and the donor-acceptor pairs of both reactions are different, FADH^−*/T<>T for the forward ET and T⁻/FADH^• for the electron return. The smaller coupling value, compared with the forward ET (3.0 meV), indicates that electron tunneling favors the 5′ side over the 3′ side as observed. Also, the excess driving force of T⁻ (the more negative reduction potential) over U⁻ slows down the tunneling rate. Using the obtained J and λ values, we obtained a smaller free energy of −2.10 eV for T+U⁻ and a larger free energy of −2.32 eV for U+T⁻ (Table 2). Comparing T+U⁻ with U+U⁻ and T+T⁻ with U+T⁻, the U at the 5′ side slows down the electron return due to the strong electron affinity of U to hinder the electron tunneling back to FADH^•, effectively, leading to more negative free energies, but in the inverted ET region.

The electron return within nanoseconds is necessary and essential to complete the photocycle for further DNA repair by photolyase. In addition, a long stay of the extra electron in repaired DNA is harmful and could induce other new damage.^66,67 All these dynamics of the elementary steps involved in photorepair machinery appear to be well optimized by evolution. To recapitulate, as shown in Fig. 1B for the complete photocycle and in Fig. 6 for all reaction dynamics and molecular mechanism, we completely mapped out the entire evolution of catalytic repair process. Photolyase uses a photon and an electron to repair damaged DNA with no net change in the redox state of the flavin cofactor through a cyclic ET mechanism. Four elementary steps of forward ET, back ET, two C-C bond splitting, and electron return all occur ultrafast and in synergy to maximize the repair quantum yield.

We note that a recent report⁶⁸ using the T<>T substrate and a 500-ps time resolution is in agreement with our earlier studies⁸ with this substrate by detection of the flavin radical intermediate in the visible-light region and with an earlier paper⁶⁹ that claimed the detection of the repaired product thymine (T) at 266 nm. Here, for the first time by using high time resolution, wide probe wavelengths and multiple substrates, and by careful analyses of the coupling of ET dynamics with active-site solvation,^8,10,38,70 we have mapped out all elementary steps of the repair photocycle by photolyase and provided experimental rational for its high repair efficiency.

Conclusions

We reported here our systematic characterization and analyses of three electron transfer processes and cyclobutane ring splitting involved in repair of damaged DNA by photolyase. With femtosecond resolution and (deoxy)uracil-substituted substrates of cyclobutane pyrimidine dimers at the 5′ and 3′ sides of DNA, we completely mapped out the entire dynamic evolution of repair processes for four different T<>T, T<>U, U<>T and U<>U combinations. We resolved all the dynamics of four elementary reactions of the forward ET with one electron injection from the cofactor into the substrate, sequential cyclobutane ring splitting of two single carbon-carbon bonds, futile back ET after the first carbon-carbon splitting to return to the original ground state by reclosure of the ring, and final electron return after the repair to the cofactor to restore the catalytic active sate and complete the photocycle. These dynamics significantly depend on the locations of T and U at the 5′ or 3′ side of DNA and thus provide unique and strong evidence for determination of the electron tunneling pathways for the forward ET and final electron return. As shown in Figure 7 for both CPD photolyase and 6-4 photolyase, the forward ET ends on the 5′ side of DNA with a hybrid of tunneling configurations. The electron passes through the critical intervening adenine moiety of the unusual bent configuration of the cofactor flavin through a super-exchange mechanism. All atoms in the adenine-mediated pathway are in van der Waals contact with their neighboring ones, but the through-space tunneling pathway obviously has a vacuum-type gap, regardless of the distances, in both photolyases. For CPD photolyase, the electron return after the repair starts at the 3′ side, shifting from the 5′ side during splitting, and follows the reverse direction through the mediated adenine (Fig. 7). Both electron tunneling pathways have unique, high directionality.

Figure 7.

Active-site structures of enzyme-substrate complexes. (A) The relative positions of active cofactor FADH⁻ and repaired substrate at CPD photolyase (A. nidulans). The red and golden arrows represent two electron tunneling pathways of the forward ET and electron return after repair, respectively. The gray arrows show the unfavorable through-space electron tunneling pathway. (B) The relative positions of FADH⁻ and substrate 6-4 photoproduct of 6-4 photolyase (A. thaliana). Similarly, the red and dark-red arrows show the tunneling pathways of the forward and futile back ET between flavin and 6-4 photoproduct, similar to CPD photolyase. The through-space tunneling distance is 6.3 Å in gray arrows. (C) and (D), the space-filled representation of the structures in (A) and (B). The adenine-mediated tunneling pathways are completely filled with atom contacts while the through-space tunneling routes have gaps in the pathways, which decrease ET rates due to the weak electronic coupling.

We determined all time scales of the four elementary steps. The forward ET occurs in tens to hundreds of picoseconds. The cyclobutane ring splitting in a sequential way is ultrafast within tens of picoseconds. The futile back ET to the original ground state without repair takes hundreds of picoseconds to nanoseconds. After repair, the electron takes the similar time scales to restore the initial catalytic active state of the cofactor flavin. Using the Marcus ET theory, we obtained all ET free energies, reorganization energies and electronic coupling constants for three ET processes. The forward and back ET is in the normal region and the electron return is in the inverted region. For the hybrid tunneling pathways mediated by the adenine moiety, the reorganization energies and electronic coupling constants are relatively large, 1.21–1.37 eV and 2.6–3.0 meV, respectively. Clearly, through evolution, the active-site configuration and electrostatics must have enabled the enzyme to split the cyclobutane ring as fast as possible to exceed all other competing and potentially harmful processes. The unique bent configuration of the flavin cofactor assures the critical adenine position to mediate all three ET processes in hundreds of picoseconds to nanoseconds, slower than the ring splitting, in a delicate balance of time scales. These ET times are not too slow to decrease the efficiency of the forward ET and not too fast to increase the futile back ET channel. Such structural integrity, unique electron tunneling pathways and the critical role of adenine ensure a high repair quantum yield in a synergistic way to optimize the forward ET, futile back ET and ring splitting in this complex photorepair machinery, and finally achieve a high repair efficiency close to unity.

Figure 4.

Femtosecond-resolved transient absorption dynamics of U<>U repair by photolyase at probe wavelengths from 710 to 266 nm. The transients probed at 266, 270, 300, 335 and 620 nm are deconvoluted in insets A–E, respectively. All transients were fitted by considering flavin-related species (dashed red in insets A–D and dashed pink and dark red in inset E), substrate intermediates of U⁻-U (dashed blue) and U⁻ (dashed dark green), and uracil products (dashed dark yellow).