Sparse OCT: Optimizing compressed sensing in spectral domain optical coherence tomography

Abstract

We applied compressed sensing (CS) to spectral domain optical coherence tomography (SD-OCT). Namely, CS was applied to the spectral data in reconstructing A-mode images. This would eliminate the need for a large amount of spectral data for image reconstruction and processing. We tested the CS method by randomly undersampling k-space SD-OCT signal. OCT images are reconstructed by solving an optimization problem that minimizes the l1 norm to enforce sparsity, subject to data consistency constraints. Variable density random sampling and uniform density random sampling were studied and compared, which shows the former undersampling scheme can achieve accurate signal recovery using less data.

1. INTRODUCTION

Compressed sensing (CS) theory stipulates that exact signal reconstruct can be obtained from highly undersampled data, given that the signal has a sparse representation [1]. After CS first demonstrated its feasibility in MRI [2], it has been adopted by various imaging modalities including optical imaging modalities, such as optical holography [3], diffuse optical tomography [4], and optical coherence tomography (OCT) [5, 6].

As a high-resolution high-speed cross-sectional imaging technique, OCT has been used widely in medical diagnostics and imaging [7–12]. In recent years, Fourier domain OCT (FD OCT) has supplanted conventional time domain OCT (TD OCT) in many applications [13–16], due to a better sensitivity and imaging speed compared to TD OCT. Particularly, spectral domain OCT (SD OCT), one type of FD OCT, uses an array detector such as a CCD or CMOS camera to sample the interference spectrum called interferogram. The measured interferogram, and the object, the axial profile of a sample, are simply a Fourier pair, which makes the image construction straightforward. However, according to Nyquist theorem, to achieve a larger imaging depth with a given axial resolution, it requires more sampling points, i.e., more pixels in the array detector to capture the spectral interferogram, which limits the imaging speed. Moreover, the massive data acquired becomes a heavy burden for data processing and storage. In this study, we explored the potential of using compressed sensing in SD OCT (CS SD OCT), to reduce the amount of spectral data acquisition required for high-resolution image reconstruction. In this study, we use an OCT system described in detail in [5].

2. SD OCT AND CS

In SD OCT, measurements are taken in Fourier domain. Denoting the sample as a vector x and denoting k-space measurements as a vector y, we can relate x and y using Fourier transformation (F):

$$\mathbf{y}=\mathbf{Fx}$$ (1)

Conventional FD OCT reconstruction relies on inverse Fourier transformation, as shown in Eq. (2).

$$\mathbf{x}={\mathbf{F}}^{-\mathbf{1}}\mathbf{y}$$ (2)

Under conventional reconstruction, the total number of samples in Fourier domain is determined by the spectral range of the spectrometer and the imaging depth required.

CS takes a significantly different approach from conventional reconstruction. According to the CS theory, measuring a small number of random linear combinations of an object x can lead to accurate object reconstruction. In applying CS, one has to make sure that the following three conditions hold:

Sparsity

Assume an object x∈R^N and there exists an orthonormal basis (ψ_i : i=1,…N) for R^N. x can be projected to the basis and represented by transform coefficients θ_i= x·ψ_i. Here · indicates inner product. The presentation of x in R^N can be considered as sparse if θ_i satisfies the following inequality [15]:

$${\left|\right|\theta \left|\right|}_p={\left(\sum _i{\left|{\theta }_i\right|}^p\right)}^{1/p}\le R$$ (3)

In Eq. (3), 0<p<2 and R>0. In practice, p usually takes the value of 1. As a result, algorithms for CS promote sparsity by minimizing l₁ norm of an image in a given presentation. More concretely, x can be considered as sparse when it has only a few non-zero coefficients in the representation domain Ψ.

Incoherence

CS requires an undersampling scheme that results in noise like aliasing artifact. As to CS OCT, Fourier domain (Φ) and pixel domain (Ψ) are concerned when the image is sparse in pixel domain. Fortunately, the incoherence between these two domains has been elaboratively studied in literature [2, 5].

Non-linear reconstruction

In order to recover x from randomly undersampled measurements, CS solves the following constrained optimization problem:

$$\mathit{minimize}{\left|\right|\mathbf{Wx}\left|\right|}_1,\text{s}.\text{t}.{\left|\right|{\mathbf{F}}_{\mathbf{u}}\mathbf{x}-{\mathbf{y}}_{\mathbf{u}}\left|\right|}_2<\epsilon$$ (4)

In Eq. (4), F_u is the operator for incomplete Fourier measurement; ε controls the data consistency; the objective function of this optimization problem is the ℓ1 norm of the image in Ψ, which essentially promotes sparsity. In this study, we solved Eq.(4) iteratively, using non-linear conjugate gradients (CG) and backtracking line-search [2, 5].

3. UNIFORM AND VARIABLE DENSITY RANDOM SAMPLING

Incoherent random undersampling was achieved by applying a random mask to the array detector that continuously samples the spectrum. A more practical and realistic implementation would involve randomly acquiring only a certain fraction of the pixels within the array. The mask determines whether a pixel of the array will be selected or not, depending on a certain probability distribution function. The design of the mask will affect the accuracy of CS reconstruction and the algorithm’s efficiency. The most straightforward incoherent undersampling scheme is a uniform density random sampling (UDRS), in which every pixel has the same probability of being sampled or dropped out. However, UDRS clearly is not an optimized sampling scheme, because the spectrum of the OCT light source is not constant. The source spectrum is almost zero at some pixels and those pixels do not contribute much to the A-scan reconstructed. As a result, it is rational to take a variable density random sampling (VDRS), which samples less where the source’s spectral intensity is small and samples more where the source’s spectral intensity is large.

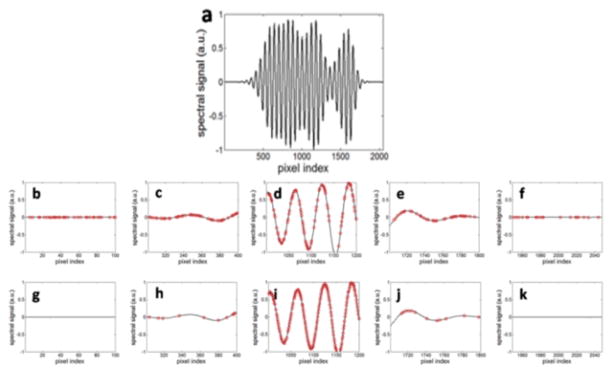
UDRS and VDRS are illustrated in Fig. 1. The interferometric spectrum obtained when a mirror is used as an object is shown in Fig. 1(a). Seen from Fig. 1(a), the source spectrum is maximized at the center of the CCD array and is almost zero at left and right ends of the array. We designed masks for UDRS and VDRS to sample 50% of the pixels. UDRS samples pixels in the whole array detector with the same probability, as shown in Fig 1(b) – (f) which clearly exhibits the drawback of UDRS. A lot of data points are sampled when the spectral intensity is almost zero, as shown in Fig. 1(b) and (f). On the other hand, we generate a mask for VDRS and the probability of selecting a pixel is proportional to the source spectral intensity at that pixel, as shown in Fig. 1(g) – (k). VDRS does not sample any data points in Fig. 1(g) and (f), because the spectral intensity is almost zero at the edge of the array detector. Moreover, VDRS samples almost every data point in Fig 1(i), because the source has largest spectral intensity in the center of the camera.

Fig. 1.

(a) Interference spectrum of high resolution OCT; (b)–(f), sections of interference spectrum sampled using UDRS at different parts of the detector; (g)–(k), sections of interference spectrum sampled using UDRS at different parts of the detector

To show that VDRS will allow CS reconstruction using less data, we reconstructed OCT A-scans using CS approach based on UDRS shown in Fig.1(b) – (f), and VDRS shown in Fig. 1(g) – (k). We use signal to noise ratio (SNR) to evaluate the performance of different sampling schemes. SNR is defined as SNR=10log₁₀(x_max²/σ²), in which x_max and σ are the peak value and standard deviation of OCT signal, respectively. The noise in the reconstructed image contains real noise which is due to the random nature of physical parameters. The measured “noise” also includes noise like aliasing that originates from random undersampling. Such aliasing gets completely removed after an ideal CS reconstruction. However, a practical CS reconstruction algorithm maximizes sparsity under the constraint of data consistency. Therefore, noise due to aliasing cannot be completely removed, and SNR can be used as a way to measure and to evaluate a sampling scheme. A large SNR indicates a good “mask” and vice versa. SNRs obtained under UDRS and VDRS at different undersampling rate are summarized in Fig 2, which shows that VDRS outperforms UDRS. To achieve a given SNR, VDRS requires less sampling rate than UDRS.

Fig. 2.

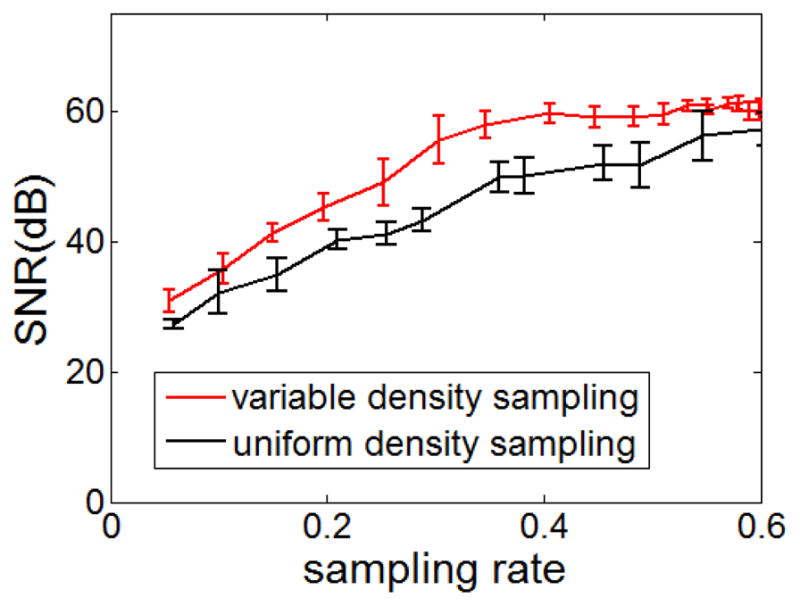
SNRs obtained using VDRS and UDRS, at different under sampling rate

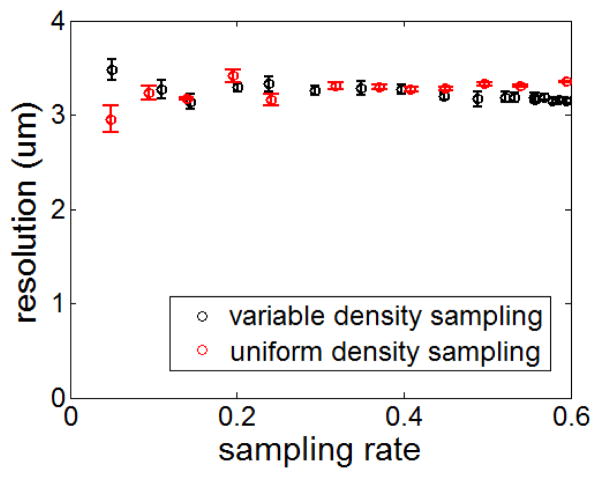
We also studied the performance of UDRS and VDRS in term of image resolution. We measured the FWHM resolution of OCT signal obtained from spectral data shown in Fig. 1(a) by CS reconstruction based on UDRS and VDRS. Results are shown in Fig. 3. Note that the axial resolution obtained from a conventional reconstruction using complete spectral data is measured to be 3.2μm. Seen from Fig. 3, both UDRS and VDRS can achieve an axial resolution close to the conventional reconstruction, and the resolution is well preserved even at extremely low sampling rate

Fig. 3.

spatial resolution obtained using different sampling schemes.

Our preliminary result suggests that VDRS allows CS reconstruction using less data, and will potentially result in a significantly reduced data acquisition time. However, the probability distribution function that we used to generate the VDRS mask is not necessarily optimized. Therefore, in the future study, we will study various ways to achieve random undersampling and compare their performance.

4. CONCLUSION AND DISCUSSION

In this work we applied compressed sensing techniques in SD OCT. Variable density random sampling and uniform density random sampling are compared. We demonstrated and verified the effectiveness of CS in phase sensitive OCT, which shows that CS has great potential in OCT’s application as a sensor to capture fast dynamic processes.