Quantitative MRI measurement of lung density must account for the change in T₂* with lung inflation

Abstract

PURPOSE

To evaluate lung water density at three different levels of lung inflation in normal lungs using a fast gradient echo sequence developed for rapid imaging.

MATERIALS AND METHODS

Ten healthy volunteers were imaged with a fast gradient echo sequence that collects 12 images alternating between 2 closely-space echoes in a single 9-second breath-hold. Data were fit to a single exponential to determine lung water density and T₂*. Data were evaluated in a single imaging slice at total lung capacity (TLC), functional residual capacity (FRC) and residual volume (RV). ANOVA for repeated measures was used to statistically evaluate changes in T₂* and lung water density across lung volumes, imaging plane, and spatial locations in the lung.

RESULTS

In normal subjects (n=10), T₂* (and [lung density/water density]) was 1.2±0.1 msec (0.10±0.02), 1.8±0.2 msec (0.25±0.04), and 2.0±0.2 msec (0.27±0.03) at TLC, FRC, and RV, respectively. Results also show that there is a considerable inter-subject variability in the values of T₂*.

CONCLUSION

Data show that T₂* in the lung is very short, and varies considerably with lung volume. Thus, if quantitative assessment of lung density within a breathhold is to be measured accurately then it is necessary to also determine T₂*.

INTRODUCTION

Quantitative determination of lung density content is potentially useful in the monitoring and study of pulmonary interstitial edema, and also for evaluating lung physiology under a variety of conditions. Many imaging modalities have been utilized for measuring lung density such as PET (1–3), CT (4), and MRI (5–10). For example, in a study using MRI techniques, Hopkins et al. (11), showed a density gradient in the normal lung due to the effects of gravity and found correcting for these gradients was important when considering the effects of gravity on pulmonary perfusion. A subsequent study investigating the effects of prone positioning on the distribution of pulmonary perfusion (12) also included quantitative density characterization and corrected for these deformation effects. MRI, with its intrinsic sensitivity to water proton density, provides a promising approach for measuring lung water especially since there are no concerns regarding ionizing radiation as there are in some other imaging modalities such as PET and CT.

The lung is a difficult organ to image using MRI, since the overall density is low and subsequently MR signal is low. Several studies have examined the response of MR relaxation times (T₂, CPMG T₂, and Hahn T₂) to estimate lung water in animal models (13,14). Despite the short T₂ decay of the lung, these techniques were shown to be sensitive enough to estimate lung water. However, due to long imaging times (~ 4 min), it is impractical to employ similar techniques in rapidly repeated physiological human studies such as recovery following head-down tilt (15,16) or if lung water density is needed at lung volumes other than functional residual capacity that require imaging to be completed within a breathhold. As a result, rapid imaging techniques such as gradient echo imaging (T₂*) are required unless one is willing to accept the cumulative effects (longitudinal variation) of free breathing imaging (5).

Due to the multitude of air-tissue interfaces in the lung, magnetic susceptibility effects are high. As a consequence of these high magnetic susceptibility effects, T₂* of the lung is extremely short and has been reported in the vicinity of ~1.4 msec (6,10) in normal lungs. As a result, gradient echo imaging of the lung suffers from significant signal loss as the MR signal decays rapidly. Consequently, for an accurate determination of lung water content one must back-extrapolate the signal from lung to an echo time of zero, which presupposes that the T₂* is accurately known. However, because the lung expands and contracts (density varies approximately 3–4 fold as the lung is inflated from residual volume to total lung capacity), altering the geometry of the air-tissue interfaces (17), one would expect T₂* to be dependent on the lung volume at which imaging is performed (6) and between different regions of the lung with different degrees of inflation (10). Further, T₂* itself may vary between individuals and with disease and thus could be exploited to provide additional information on lung pathologies in which detailed aspects of lung structure might change, such as emphysema and pulmonary fibrosis.

Our goal was to implement an imaging sequence specifically for rapid, quantitative, lung water imaging. A fast gradient echo pulse sequence was adapted to collect 12 images alternating between 2 closely-spaced echoes (6 images acquired at an echo time ~1.0 msec and 6 images at an echo time of 1.8 msec) in a single 9-second breath-hold. The resulting data are fit with a single exponential decay function to determine lung water density and T₂*. We show that such an implementation is practical within the constraints of reasonable breath-hold time for the imaging, that both lung water density and T₂* vary in a systematic way with lung volume, and that in order to accurately measure lung water content, the effects of changes in T₂* with the lung volume must be taken into account necessitating the use of more than one echo time. However individual variability is enough that T₂* should be individually measured in all subjects to minimize error.

METHODS

Pulse Sequence And Acquisition

To obtain T₂* and lung water measurements a gradient echo (GRE) sequence was developed that rapidly acquires multiple single echo images within a single breath-hold. A single slice in the right lung was scanned with our multi-echo fast gradient echo (mGRE) sequence on a 1.5T GE HDx EXCITE twinspeed scanner with the body coil. The mGRE sequence consists of a small flip angle slice selective excitation followed immediately by the collection of a single full line of Fourier data. The sequence begins by collecting 10 disdaqs (discarded data acquisitions), and then steps through multiple phase encoding steps at a fixed echo time (TE) and repetition time (TR) until k-space is filled for a single 2D image. The sequence then repeats by filling k-space acquired at a second echo time while keeping TR constant.

For a single 9 second breath-hold scan, the cycle described above is repeated such that 12 images were acquired alternating between a long (TE2) and a short echo time (TE1). 6 images (even images: 2,4,6,…,12) were acquired with an echo time (TE1) being set to TE[min], the shortest time permitted by sequence parameters (~ 1.0 msec). The remaining 6 images (odd images: 1,3,5,…,11) were acquired with an user selectable echo time (TE2) based on signal to noise ratio (SNR) considerations. Sequence parameters were TR = 10 msec, flip angle = 10 deg, slice thickness = 15 mm, FOV = 48 cm, receiver bandwidth = 125 kHz, and a full acquisition matrix of 64 × 64.

Optimizing the use of this pulse sequence to determine accurate and precise measurement of T₂* and lung water density required that a number factors be considered, which were: assuring steady state conditions of signal, examining the effects of low SNR when selecting the range of echo times, and making optimal choices in echo times while allowing for data collection during a single breath-hold.

Assuring Steady State Conditions

Due to the low flip angle of the excitation pulse, the second rf pulse in our sequence transforms the magnetization into longitudinal and transverse components. For this study, no attempt was made to spoil the transverse magnetization in our mGRE sequence (18). However, with the TR being sufficiently long (TR = 10 msec, T₂* ~ 1.4 msec) it is likely that there will be little coherent transverse magnetization in the lung carried over from one excitation to the next. Therefore, the approach to steady state is an approach to incoherent steady-state. For our mGRE sequence, we chose to empirically determine the time at which the signal reaches steady state and to exclude data that might be biased from the mean signal and lead to an inaccurate estimate of T₂* (see Results).

To determine the time it takes for the signal to reach steady-state, a single slice in the right lung was scanned in both the coronal and sagittal plane for a single subject using a preliminary mGRE sequence. Twelve sets of data were acquired within a 9 second breath-hold scan for a fixed echo time (set to TE[min] ~ 1 msec). The scan was then repeated 5 times at residual volume (RV), functional residual capacity (FRC), and total lung capacity (TLC). A region of interest (ROI) was drawn manually to encompass the entire lung in each image for each scan using AMIRA (TGS systems). A mean signal intensity within the lung ROI was determined in images 1 through 12 in each scan and averaged across repetitions. The number of images required for the relative signal to reach steady state (defined as the mean signal of the lung being no more than the average of the final 4 acquisitions plus one-half of the SD) was determined (see Results).

Low SNR Considerations – Range Of Echo Times

For a GRE acquisition, the signal within the lung is regulated by the proton density and the T₂* of the tissue. For the lung, where proton density is extremely low and the signal decays rapidly (a short T₂*), ensuring an adequate SNR by appropriate selection of the imaging echo time is critical. MR image data is typically presented after calculating the magnitude of the complex data. In the presence of noise, both the real and the imaginary components of the complex data are Gaussian-distributed where the real component has a non-zero mean. After calculating the magnitude, image data can be described by a Rician distribution (19,20). For high SNR conditions (SNR ≥ 2) (19), the Rician distribution can be approximated by a Gaussian distribution and multiple measures of the signal will converge to the mean signal. However, for low SNR conditions (SNR < 2) the image intensity will be biased due to the noise and will lead to an overestimation of the mean signal and thus inaccurate estimates of T₂*. Since it is not possible to correct this error in post processing, it is necessary to acquire data with a SNR greater than 2 to minimize signal bias due to low SNR which will lead to an inaccurate measurement of T₂*. In practice, this was accomplished by setting an upper limit on the echo time (TE[max]) so as not to degrade the SNR too much.

Based on preliminary imaging studies we performed, the SNR of the lung when imaging with an echo time of 1.0 msec (TE[min]) at 1.5T was approximately 22, 17, and 6 at RV, FRC, and TLC, respectively. The SNR was calculated as the mean signal within a ROI drawn manually to encompass the entire lung divided by the standard deviation of the signal for a ROI of similar area placed in the background of the image. Hatabu and colleagues previously estimated the T₂* of the lung to be approximately 1.4 msec (6). Using those values and ensuring that SNR never falls below a value of 2, the longest permissible echo time (TE[max]) that was appropriate for imaging at RV, FRC, and TLC was 3.4 msec, 2.6 msec, and 1.8 msec, respectively.

Optimizing Choice Of Echo Times

Under low SNR conditions, the precision of determining the signal at a particular echo time can be improved by taking multiple measures. Within the constraints of the current application, we have the ability to collect up to 8 measurements for the fit (see Pulse Sequence and Acquisition above). Based on the assumption that the signal in the lung is unbiased (SNR > 2) and can be appropriately modeled by a single exponential, Monte Carlo simulations were implemented to determine the optimum distribution of echo times to accurately determine the decay of the signal, T₂*, and the back-extrapolated value of lung water density. These simulations ranged from having 8 equally spaced echo times between TE[min] determined by the scanner specifications and TE[max] determined by the SNR criteria (see above) at one extreme, to having 4 echo times at TE[min] and 4 at TE[max]. Between those extreme cases we considered several other distributions of echo time. Runs of 1,000,000 sets for each condition that included realistic values for the noise seen in our preliminary data collections were performed for each selection of TE ( 1.0 msec > TE > 1.8 msec) and using typical assumed values of lung water content (SNR = 5 at TE[min] for TLC) and T₂* (1.4 msec) with the intent of minimizing the mean-squared error in both values.

Monte Carlo results determined that the best scenario was to collect multiple measures at two echo times, at the minimum possible TE[min] (~1.0 msec), and where the second echo time was located where the mean signal is greater than 2 (the minimum that met our SNR criterion, see above). In this circumstance, mean-square errors for both lung water density and T₂* were simultaneously minimized.

Single Exponential Decay

The above discussion has assumed that T₂* decay of the signal from the lung can be accurately described by a single exponential. To confirm this assumption, additional data were collected at a fixed TE2 across all lung volumes. A fixed TE2 was selected to be 1.8 msec, such that at TLC (where density is minimum) the SNR in the lung was greater than 2 (Table 1). For the case of a single exponential, both datasets should converge to similar results.

Table 1.

Lung volume, echo times, average fractional lung water density, average T₂^*, and SNR at TE2 for each scan.

Lung	TE1	TE2	Fractional Lung	Water Density	T2* (msec)		SNR at
Volume	(msec)	(msec)	Coronal	Sagittal	Coronal	Sagittal	TE2
RV	1.0	3.4a	0.28±0.04*	0.28±0.03*	2.02±0.21*	1.72±0.10*	5.9±1.5
RV	1.0	1.8b	0.27±0.03	0.27±0.02	1.95±0.17	1.76±0.17	13.3±3.1
FRC	1.0	2.6a	0.25±0.04#	0.23±0.03#	1.67±0.21#	1.50±0.08	5.9±1.2
FRC	1.0	1.8b	0.25±0.04	0.22±0.02	1.78±0.24	1.57±0.08	10.0±1.7
TLC	1.0	1.8a,b	0.10±0.01+	0.10±0.03+	1.19±0.21+ 1.37±0.08+
3.4±0.9

^aLongest permissible echo time (TE[max]) that was appropriate for imaging at RV, FRC, and TLC.

^bFixed echo time across all lung volumes.

^*Significantly different between RV and FRC, at P < 0.003.

^#Significantly different between FRC and TLC, at P < 0.0001.

⁺Significantly different between RV and TLC, at P < 0.0001.

MRI Acquisition

Imaging was conducted in 10 healthy volunteers (6 males, 4 females) recruited from the UCSD general population and who provided written informed consent approved by the Human Research Protection Program at the University of California, San Diego. A single sagittal and a single coronal slice were acquired in the right lung at RV with TE2 = 1.8 msec, RV with TE2 = 3.4 msec, FRC with TE2 = 1.8 msec, FRC with TE2 = 2.6 msec, and TLC with TE2 = 1.8 msec (Table 1). All measurements were repeated in three independent breath-hold mGRE scans of 9 secs while keeping prescan gain, power, and shim values constant. These five sets of data were acquired in each scan plane as described in Table 1. Thus, a total of 360 images were acquired in 30 independent breath-hold scans for each subject (total scan time ~ 30 minutes). Long echo times (TE2) were based on SNR considerations (see above). The coronal slice was positioned to encompass the posterior one third of the descending aorta and the sagittal slice was positioned where the lung has its greatest anterior/posterior dimension.

Each scan included simultaneous imaging of a gadolinium-doped water phantom for absolute calibration (Berlex Imaging, Magnetvist, 469 mg/ml gadopentetate dimeglumine, 1:5,500 dilution) allowing each measure of lung water density to be expressed as a fraction of water. The phantom was created by emptying the contents of two 1L saline bags and refilling each bag with the same dilution (single batch) of gadolinium-doped water. One 1L bag was placed on the chest just over the right lung, and the other 1L bag was placed under the right arm.

Calculation Of T₂* And Fractional Lung Water Density

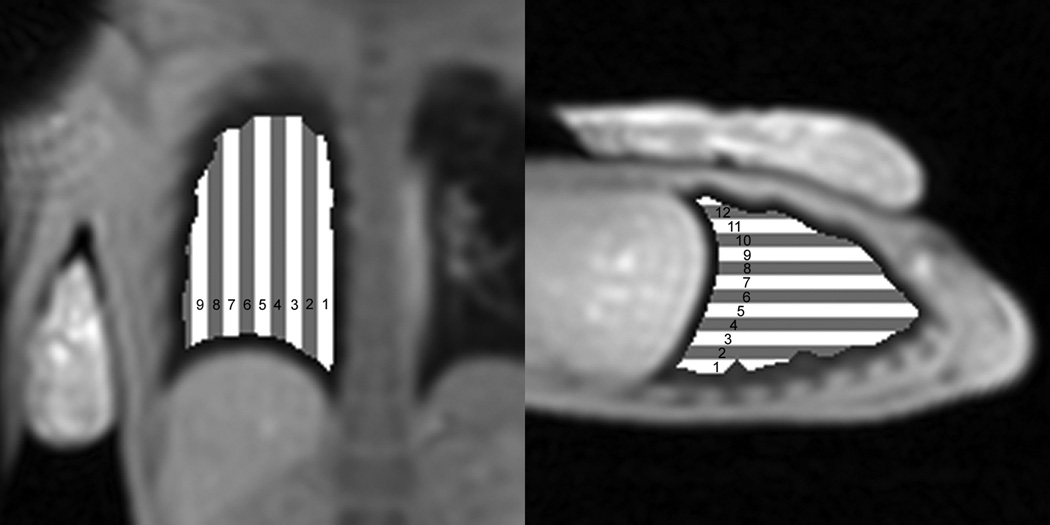
Two volumes of interest (VOIs) were drawn manually for each scan using AMIRA (TGS systems) in which one VOI encompassed the entire lung (avoiding partial volume effects at the chest wall and medastinum) and the other VOI encompassed the phantom within the imaging slice. The lung VOI was then separated into smaller ROIs with a width of 4 voxels (0.9475 cm) and a height determined by the extent of the lung VOI. The first ROI in the lung VOI is located in the most posterior section of the right lung for the sagittal slice and the most medial margin of the right lung in the coronal slice (Figure 1).

Figure 1.

Relative location of lung ROIs within lung VOI for coronal (left image) and sagittal (right image) imaging plane. ROIs start at the most medial margin in the coronal imaging plane and the most posterior position of the lung in the sagittal plane.

After discarding images 1 through 4 to ensure magnetization reached steady state (see below), the mean signal intensity within each lung ROI was determined in images 5 through 12 in each scan, ${\overline{\mathrm{I}}}_{\mathrm{j}}^{\mathrm{k}}$, where j is the image at each echo time (t₅ = TE2, t₆ = TE1, t₇ = TE2, …, t₁₂ = TE1) and k is the ROI location. The signal of the lung at an echo time of zero (I₀) and T₂* were calculated for each ROI by fitting the mean signal in the lung obtained from 8 images to, ${\overline{I}}_j^k=I_0\text{exp}\left(-t_j/T_2^{*}\right)$.

Assuming that the signal within the doped-water phantom was a good representation of the signal within the lung without any partial volume effects (i.e. 100% water), an absolute measure of lung water density can be obtained. However, it is impractical to create a phantom that mimics the decay constants of the lung. Since the decay constants of the phantom (T₁ = 1.1 sec, T₂ = 1.2 sec) were much longer than in the lung, this will result in a coherent build-up of signal in the phantom towards steady-state. The complicated dependence of the coherent steady-state signal makes it difficult to determine an analytic form of the signal. Since the decay constants of the phantom are static, we chose to empirically determine a “correction factor” (c_p) permitting us to use the mean phantom signal as a reference for absolute calibration.

To determine c_p, the phantom was independently scanned using our mGRE sequence with the sequence parameters stated above. An additional set of data was acquired with the TR being sufficiently long (TR = 6 sec) to avoid coherent steady state. Results showed that T₂ decay effects were negligible (~ 0.5%), the mean signal of the phantom reaches steady state by image 2 in the acquisition, and a correction factor of 1.78 (c_p= mean phantom signal at TR = 6 sec / mean phantom signal at TR = 10 msec).

Fractional lung water density was calculated for each ROI as the ratio, I₀/(c_p•I_p), where I_p is the mean signal of the phantom at TE1 and TR = 10 msec. Average T₂* and fractional lung density were calculated for each lung volume, scan plane, choice of TE2, and ROI. Each scan was inspected to ensure that the lung volume was static through the duration of the breath-hold as shown by a stationary diaphragm, and data were excluded that did not meet these criteria.

Statistical Analysis

ANOVA (Statview, 5.0 SAS Institute, Cary, NC) for repeated measures was used to statistically evaluate changes in the major dependent variables over three repeated measures: 1) lung volume (3 levels: RV, FRC, and TLC), 2) imaging plane (2 levels: sagittal, coronal), 3) TE2 (2 levels: fixed, max) and 4) spatial location within lung (9 levels for coronal, and 13 levels for sagittal). Dependent variables for this analysis were T₂* in units of msec, and fractional lung water density (dimensionless). Where overall significance occurred, post hoc testing was conducted using Student’s t-tests. All data are presented as means, SD, and the null-hypothesis (no effect) was rejected for P < 0.05 (2 tailed).

RESULTS

Steady-State Condition

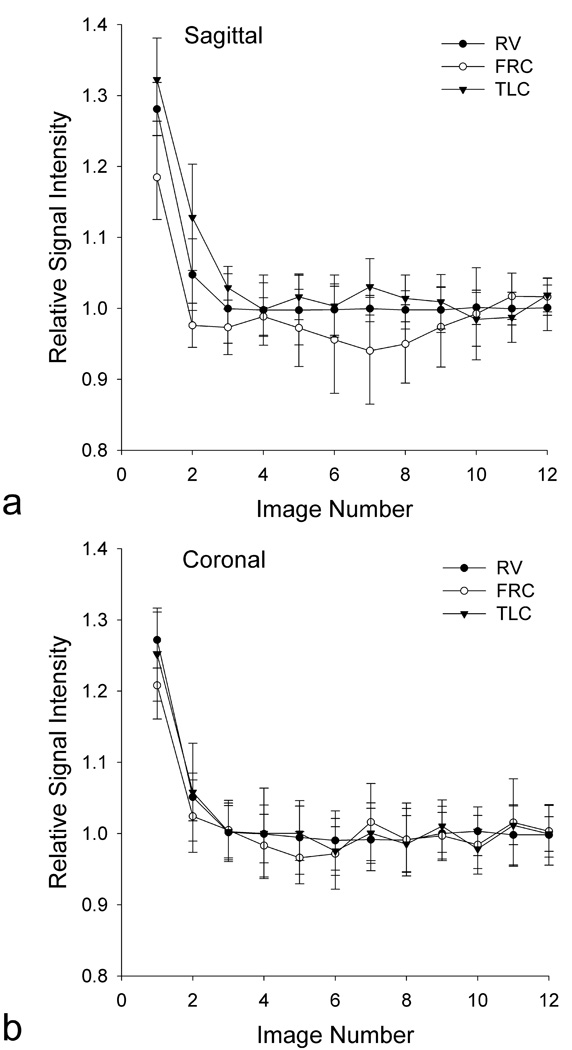
Data from the steady-state test shown in Figure 2 demonstrate that the mean signal within the lung at all the volumes studied fails to reach steady state (defined as the mean signal of the entire lung within the slice being no more than the average of the final 4 acquisitions plus one-half of the SD) for the first two to three images with image 4 meeting this criterion. Based on this observation we chose to discard the first four images from our acquisition scheme and so T₂* and fractional lung water density analysis was limited to the final 8 images.

Figure 2.

Average signal of the lung from 12 successive images divided by the average of the last 4 images, showing the approach to steady-state for a single subject. Error bars show the SD over the 5 repetitions at each image number divided by the average of the last 4 images. Results are shown for the (a) sagittal and (b) coronal imaging plane at RV, FRC, and TLC. The signal of the lung does not reach steady state until image 4 in both imaging planes and at all 3 lung volumes.

SNR Considerations

SNR values for the whole lung in the sagittal plane were inspected to ensure that data collected at TE2 had a SNR greater than 2. SNR values (mean signal ROI / standard deviation of a ROI of an equal area placed in the background) at TE[max] were 5.9, 5.9, and 3.4 at RV, FRC, and TLC, respectively (Table 1). If the SNR approaches a value of two at TE[max], T₂* could be overestimated by as much as 35%. However, at TLC where the density is minimum, this could lead to an error of ±0.01 in the measurement of fractional lung density, which is of minimal physiological significance.

Verification Of Single Exponential Behavior

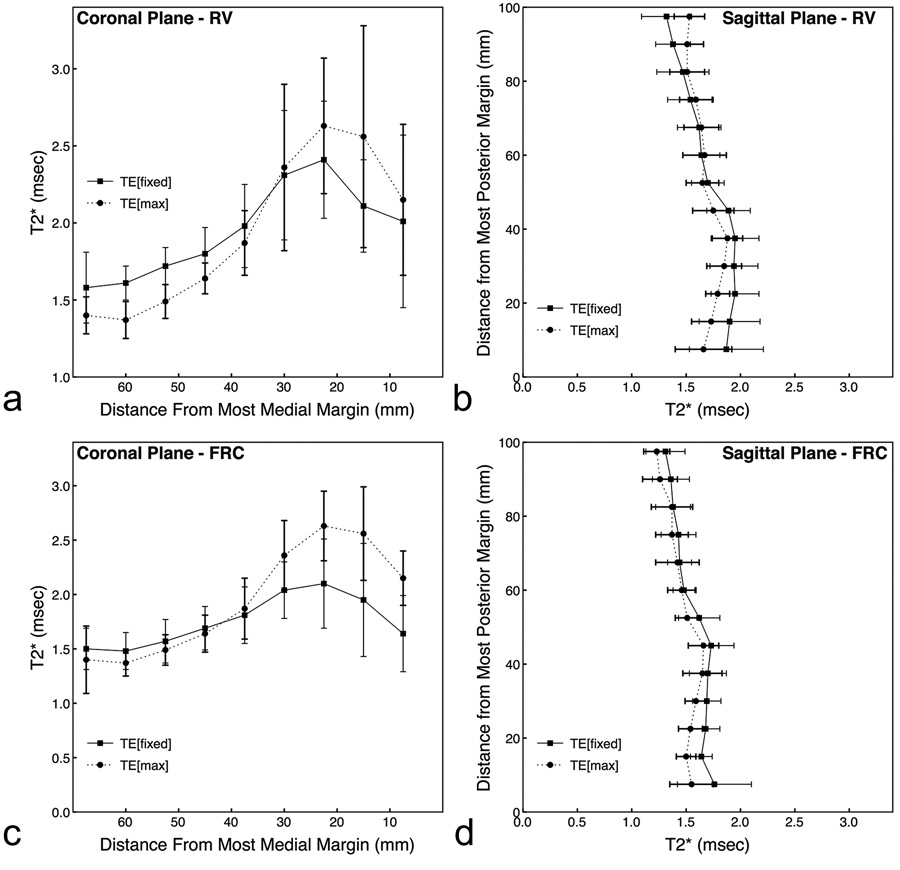
T₂* values across the lung for data acquired at RV and FRC with different TE2 values are shown in Figure 3. If lung water can be accurately described as a single exponential, the T₂* for each region in the lung at each lung volume should provide similar results for both datasets. There was no significant main effect of TE2 (TE[fixed] vs TE[max]) for data acquired at sagittal RV (P = 0.36), coronal RV (P = 0.90) and coronal FRC (P = 0.11) for T₂* averaged over all lung ROIs. These results support the above statement. However, there was a significant effect for sagittal FRC (P = 0.0002) where T₂* at TE[fixed] was 1.56±0.23 msec, and at TE[max] was 1.45±0.19 msec. There was also a significant lung region (ROI) by echo time interaction for sagittal FRC (P=0.007), coronal FRC (P=0.04), sagittal RV (P<0.0001), and coronal RV (P<0.0001). These statistically significant interactions were expected since signal from both lung tissue and large vessels contribute to the average signal, especially for ROIs located in close proximity to the medial margin of the lung. However, with the contribution of signal from the large vessels, the differences in T₂* does not greatly alter estimates of fractional lung density. For example, at sagittal FRC, the observed difference would lead to a ~ 5% error in the calculation of fractional lung density, which is of minimal physiological significance.

Figure 3.

Effects of using different TE values on estimates of T₂*. Spatial results are from data acquired at RV (a,b: scans 1 and 4 in Table 1), and FRC (c,d: scans 2 and 5 in Table 1) in the coronal (a,c) and sagittal (b,d) imaging planes at either a fixed TE2 (square–solid line) or TE[max] (circle–dotted line). There was no significant main effect for TE2 (TE[fixed] vs TE[max]) for data acquired at sagittal RV (P = 0.36), coronal RV (P = 0.90) and coronal FRC (P = 0.11) for T₂* averaged over all lung ROIs. There was a significant effect main effect for TE2 for sagittal FRC (P = 0.0002). There was also a significant lung region (ROI) by echo time interaction for RV and FRC in both planes (P< 0.04).

M₀ And T₂*: Effect Of Lung Volume And Scan Plane

T₂* and fractional lung water density values of the whole lung were also compared between lung volumes and scan plane from data acquired at RV, FRC, and TLC for a maximum TE2 (1.8 msec at RV, 2.4 msec at FRC, and 3.4 msec at TLC) (Table 1). To ensure the validity of the data, as expected, fractional lung water density (Table 1) changed significantly with lung volume (P <0.0001) with minimum values seen at TLC (full inspiration), and maximum values at RV (full expiration). Lung density was maximum at RV (0.28 ± 0.04) and minimum at TLC (0.10 ± 0.03). These changes were significantly different between all lung volumes (P < 0.0001) but not significantly different between image planes (P < 0.32).

In parallel with the changes in lung density there was a similar, although less pronounced change in T₂* of the whole lung, which fell as lung volume increased (Table 1). As was the case for lung density there were significant differences between lung volumes (P<0.0001) but also between scan planes (P<0.0177). There was also a significant scan plane by lung volume interaction such T₂* decreased more with increasing lung volume in the coronal than in the sagittal plane (P<0.0001). The difference in T₂* between the coronal and sagittal planes was likely a simple consequence of the position of the lung slice with lung density increasing as the imaging plane is moved to dependent regions. Despite the fact that the T₂* decreased more in the coronal imaging plane than in the sagittal (lung volume and plane interaction), the average lung density at different lung volumes did not change with scan plane (Table 1).

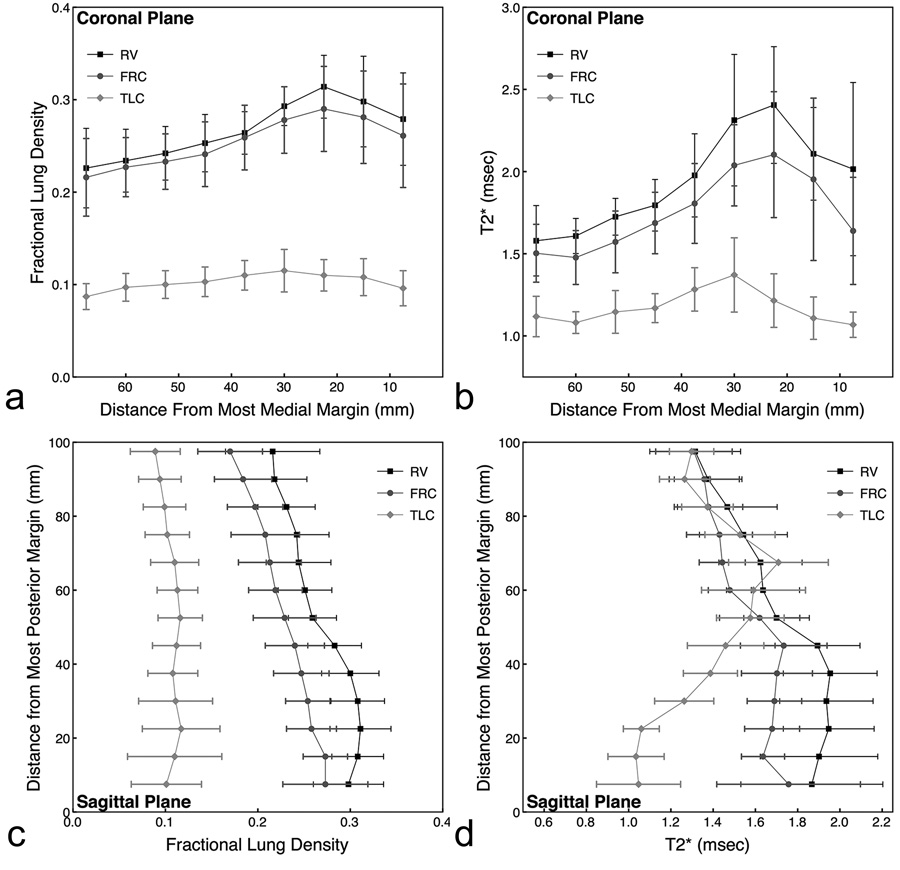
At RV and FRC in the coronal plane, fractional lung density and T₂* gradually rose with distance from the most medial margin of the lung through locations where large vessel are present (Figure 4a and 4b). Lateral to the large vessels, both values decreased. Fractional lung density and T₂* exhibited similar trends, and the overall values also decreased with increasing lung volume. At TLC, both fractional lung density and T₂* were fairly uniform across the slice. This was expected since the large vessels were moved anterior of the imaging slice with an increase in lung volume to TLC and thus did not contribute to the results.

Figure 4.

Effects of lung volume and scan plane on (a,c) fractional lung water density and (b,d) T₂*. The results are from data acquired at RV, FRC, and TLC for a maximum TE2 (3.4 msec at RV, 2.4 msec at FRC, and 1.8 msec at TLC). There was a significant main effect for lung volume at P <0.0001.

At RV and FRC in the sagittal imaging plane, fractional lung density increased from nondependent to dependent regions of the lung (Figure 4c and 4d). Similar to the results observed in the coronal imaging plane, fractional lung density remained uniform across the lung at TLC. T₂* in the sagittal imaging plane decreased as lung volume increased, but this only occurred in the dependent (posterior) regions of the lung. Across all lung volumes, T₂* had similar values in nondependent regions of the lung despite differences in fractional water density.

DISCUSSION

Fractional lung water density decreased with increasing lung volume (Table 1). That lung density fell with increasing lung volume is, of course, expected, as lung expansion occurs largely through inspiration of air while tissue and blood volumes within the lung remain essentially constant. There is a small effect of the lower intrathoracic pressure at TLC increasing blood volume slightly (~ 7% for the whole lung, corresponding to ~1% in the imaging slice) (21) but this is secondary to overall simple air inflation. Whole lung and spatial fractional lung density results support current research that states the lung density increases in dependent regions of the lung (“slinky effect”) (11,12), and that the density of the lung is relatively uniform at TLC (see Figures 4a & 4c).

T₂* decreased significantly as lung volume increased (Table 1), but remained within the previously reported range (0.89 msec < T₂* < 2.18 msec) (6,10). The exact mechanism that results in changes in T₂* cannot be discerned from these data. Clearly it is related to lung volume, however not in a linear fashion as the differences in T₂* between lung volumes are not in proportion to the differences in density (Figure 4c and 4d). Whatever the exact mechanism, the large change in T₂* with lung volume shows that if quantitative lung density is to be measured, then imaging at a single echo time and assuming a fixed value for T₂* is not accurate, and images with at least two echo times must be collected within a single breath-hold to account for the effect of differing T₂*.

Our results show that there is a profound effect of lung density on T₂* that must be taken into consideration when imaging at different lung volumes if quantitative lung density is to be accurately calculated. However, the results also show that there is a considerable inter-subject variability in the values of T₂* as evidenced by the error bars in Figure 4b and 4d. In order to assess the effect of individual variability of T₂* on calculated lung density we compared our calculated values of fractional lung water density (that take into consideration of the individual values of T₂*) with values calculated using the signal obtained at TE[min] (TE ~ 1 msec) and assuming the average values of T₂* obtained at each lung volume (mean values in Table 1). The intent of this analysis was to provide an estimate of the likely error in the lung density that remains using grouped mean values for T₂* to calculate lung density even when the average effect of lung volume on T₂* is taken into account.

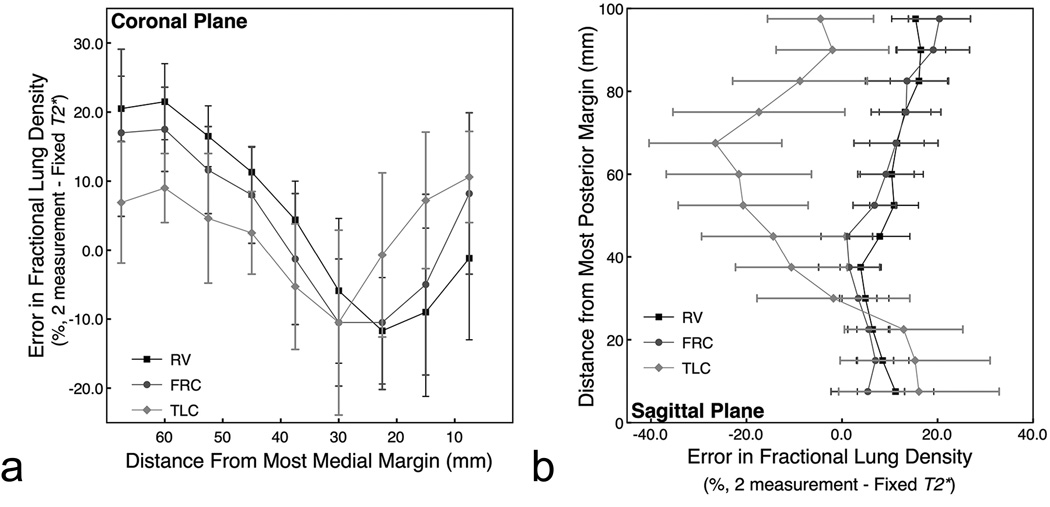
These results are plotted in Figure 5 as the error from fractional lung water density calculated using our two echo time approach. There was up to a 21.5% ± 13.3% (coronal plane) and a 19.8% ± 26.5% (sagittal plane) error in lung density. The implications of this are that even if the effect of lung volume on T₂* is taken into account, there is still a considerable inter-subject variability in T₂* that results in unacceptable errors in calculated lung density unless T₂* is measured in every subject.

Figure 5.

Percent difference in fractional lung water density across subjects between two methods of calculating fractional lung water density. The first method calculates lung water density by back-extrapolating the signal to and echo time of zero based on images acquired at two echo times and calculates T₂* on a subject by subject basis (2 measurement). The second method also back-extrapolates the signal to an echo time of zero, but the fit is based on a fixed T₂* and an image acquired at a single short echo time (Fixed T₂*). There is up to a 21.5% ± 13.3% (a: coronal) and a 19.8% ± 26.5% (b: sagittal) error in lung density calculated assuming mean values of T₂* across subjects due to a considerable inter-subject variability in T₂*.

In conclusion, the results from this study clearly show that not only is T₂* in the lung very short (which was already well appreciated)(6,10), but that it varies considerably with lung volume, and that there is considerable inter-subject variability. Thus, if quantitative assessment of lung density is to be measured accurately then it is necessary to also determine T₂* in every subject. Our implementation of a multi-image gradient echo sequence in which repeated measures at two values of TE are used, both of which meet the criterion of having adequate signal to noise ratio permits highly reproducible determinations of lung density to be acquired in a single 9-second breath-hold. Even though the calculation of T₂* can be altered by the contribution of signal from the large vessels (~ 5% error), the proposed technique can be easily applied on a subject-by-subject basis in a very short period of time, and thus offer significant advantages. Additionally, individual values of T₂* are also obtained which may have the potential to shed light on underlying lung pathologies in future studies.

The major finding of this study is that measures of lung density can be obtained in a breath-hold provided you acquire data with 2 echoes that take into account the observed changes in T₂* based on lung volume.