Density, frequency and the expressive phonology of children with phonological delay

Abstract

The effect of word-level variables on expressive phonology has not been widely studied, although the properties of words likely bear on the emergence of sound structure (Stoel-Gammon, 2011). Eight preschoolers, diagnosed with phonological delay, were assigned to treatment to experimentally induce gains in expressive phonology. Erred sounds were taught using stimulus words that varied orthogonally in neighborhood density and word frequency as the independent variables. Generalization was the dependent variable, defined as production accuracy of treated and untreated (erred) sounds. Blocked comparisons showed that dense neighborhoods triggered greater generalization, but frequency did not have a clear differential effect. Orthogonal comparisons revealed graded effects, with frequent words from dense neighborhoods being optimal for generalization. The results contrast with prior literature, which has reported a sparse neighborhood advantage for children with phonological delay. There is a suggestion that children with phonological delay require greater than usual cue redundancy and convergence to prompt expressive phonological learning.

INTRODUCTION

Contemporary research has convincingly demonstrated that statistical regularities in the input are available to, and used by, children as a possible bootstrap to language acquisition (e.g. Garlock, Walley & Metsala, 2001; Jusczyk, Luce & Charles-Luce, 1994; Saffran, Aslin & Newport, 1996). Reliable input cues have been isolated at the level of the word and also at the level of the sounds that make up the word. Thus, dual sources of information, deriving from LEXICAL (word) and SUBLEXICAL (phonological) structure, contribute to the language acquisition process.

In terms of lexical structure, two widely studied variables are neighborhood density and word frequency. DENSITY estimates the phonetic similarity of word forms based on one-phoneme substitutions, deletions or additions (Luce, 1986), whereas FREQUENCY estimates the occurrence of a given word in the language. In terms of sublexical structure, the variable that has received most attention is PHONOTACTIC PROBABILITY, which is defined as the likelihood of occurrence of a given sound and/or sound sequence in the language (Vitevitch & Luce, 2004). To date, research has largely focused on these lexical and sublexical variables in the context of children’s acquisition and recognition of new words, with primary evidence coming from spoken word perception (e.g. Metsala, 1997; Storkel, 2001; Swingley & Aslin, 2000). This line of inquiry has generally supported frequent patterns (words or sounds) and dense neighborhoods as most influential to children’s word learning.

In an invited review recently published in JCL, Stoel-Gammon (2011) brings to the forefront an alternate, but complementary perspective. Specifically, she argues that the same regularities that assist children in word learning also assist their acquisition of expressive phonology. She reasons that, if word learning capitalizes on cues at dual levels of structure, then it is likely that the effects are bidirectional : words and sounds converge to enable word learning and, likewise, phonological learning. Studies of the effects of statistical regularities on expressive phonology are emerging (Beckman & Edwards, 2000; Munson, 2001), but preliminary results suggest that children’s sensitivity to cues for production might not match those for perception (Stoel-Gammon, 2011). While asymmetries between production and perception have long been recognized in language acquisition (Gerken, 1994), Stoel-Gammon (2011) offers a possible reconciliation within this contemporary context. She notes that, although children might perceptually attune to, and discriminate statistical regularities associated with lexical and sublexical structure, they might not have specified and/or organized that same information to the level or degree needed to support accurate production. The apparent asymmetries and the paucity of research prompted Stoel-Gammon’s (2011) call for further study of statistical variables relative to expressive phonology. The present article responds to this call by evaluating density and frequency in phonological learning by children with phonological delay (PD) enrolled in clinical treatment. Density and frequency were examined for insight to the ways that lexical variables impact sublexical learning, thereby honing in on word-to-sound influences. Children with PD were of interest given methodological and theoretical advantages inherent to their study. Clinical treatment afforded the experimental manipulation and served as the platform for inducing change in the phonologies of the children. By way of background and motivation, we begin with an overview of the characteristics of children with PD, and then turn to the two studies that have examined density and frequency relative to expressive phonology in this clinical population. The review intentionally narrows in on the effects of statistical regularities for the purpose of phonological learning, as exemplified by gains in accuracy of production and as induced through explicit training.

Children with phonological delay

Children with PD constitute a subgroup of preschoolers who present with severely reduced phonemic inventories relative to the ambient language and to children of the same age, in the absence of overt causes and with few other apparent developmental lags (Gierut, 2008b). Because these children are highly unintelligible, they warrant clinical treatment to induce phonological learning. They are likely to be first identified as preschoolers (Shriberg, Kwiatkowski & Gruber, 1994), so it is possible to engage them in phonological and learning tasks that would otherwise tax the skills or attention of a younger child. Treatment itself is designed as an experiment, where instructional stimuli or methods serve as independent variables, and gains in expressive phonology serve as dependent variables. Because treatment accelerates learning, it provides an opportunity to glimpse phonological gains on a longitudinal but compressed timescale, which might otherwise be protracted.

While the causal factors behind PD are unknown, it has long been hypothesized that a possible source of children’s errors in production lies in the nature of their underlying lexical representations of words (Stoel-Gammon, 2011). This follows directly from linguistic accounts of typical phonological acquisition, which posit that learning the sound system of a language requires change (Dinnsen, 1984), elaboration (Rice & Avery, 1995), and/or reorganization (Gnanadesikan, 1996) of phonological properties associated with lexical representations. Other psycholinguistic models (Walley, 1993) have advanced similar proposals about sublexical change in children’s representations (although these are not without controversy; e.g. Dollaghan, 1994). One claim of the psycholinguistic models is that phonological elaboration of lexical representations is motivated by dense neighborhoods comprised of frequent words, such that phonetically similar forms necessitate phonemic distinctiveness. The relevance is that when the clinical, linguistic and psycholinguistic hypotheses are taken together, the ideas may be arranged as a series of propositions, which generate testable predictions for children with PD. Specifically, (i) the locus of PD may lie in the nature of children’s lexical representations; (ii) the sublexical structure of representations may be vulnerable given children’s restricted phonemic inventories; (iii) word-level variables prompt sublexical change in expressive phonology; (iv) density and frequency are two specific word-level variables that motivate sublexical change; and (v) dense neighborhoods composed of frequent words provide a ripe context for sublexical change. If true, then experimental manipulations of word-level variables in the treatment of PD are expected to result in differential phonological learning, such that frequent words from dense neighborhoods are predicted as optimal for growth of the expressive phonology.

Density, frequency and phonological treatment

To our knowledge, there are two studies that considered word-level variables in the design of phonological treatment for purposes of documenting acquisition of the expressive phonology by children with PD (Gierut, Morrisette & Champion, 1999; Morrisette & Gierut, 2002). In one study (Gierut et al., 1999), twelve children were enrolled in a single-subject alternating treatments manipulation to assess gains in production of the treated sound. In the complementary study (Morrisette & Gierut, 2002), eight children participated in a multiple baseline manipulation to assess system-wide gains in the expressive phonology. In both experiments, children were taught sounds in stimulus words that systematically varied in density or frequency value based on adult lexical counts (Nusbaum, Pisoni & Davis, 1984). Stimuli were blocked to yield either dense versus sparse or frequent versus infrequent conditions. Within a condition, stimuli were further balanced for the complementary variable. That is, when blocked by density, half the treated words were frequent items and half infrequent items. Likewise, when blocked by frequency, half the treated words were from dense and half sparse neighborhoods. This ensured that there was just one independent variable (density or frequency), with the alternate property being controlled. Generalization to treated and untreated erred sounds was measured, with results converging across studies. Namely, words from sparse neighborhoods promoted greater generalization accuracy than dense, and frequent words induced greater generalization accuracy than infrequent. The best-of-the-best conditions for phonological learning were thus sparse neighborhoods or frequent words.

While this work demonstrated that word-level variables affect phonological learning by children with PD, it was not without caveat. On the side of frequency, the findings were in sync with typical phonological acquisition (Stoel-Gammon, 2011), but on the side of density, they were not. In PD, sparse neighborhoods were optimal for production, but in typical development, it was the reverse, with dense neighborhoods being most beneficial for expressive phonology. There are at least two possible reasons for the observed asymmetry associated with density. One possibility is that children with PD do not, or cannot, capitalize on dense structure to the same extent, or in the same way, as in typical development (Storkel, 2004b; Storkel & Hoover, 2010b). Another possibility is that the density asymmetry was entwined with the methodology. Recall that density was manipulated independent of frequency in prior treatment studies (Gierut et al., 1999; Morrisette & Gierut, 2002). While the latter is a conventional research tack, every word does have both a density and a frequency value, such that, in naturalistic circumstances, the two properties co-occur and also co-vary. Also, it is now well established that density is positively correlated with phonotactic probability (Vitevitch & Luce, 2004), which was left free to vary in the aforementioned studies. Both points must now be taken into account if it is to be determined which cues affect expressive phonology, and how these may or may not converge for children with PD.

The purpose of this study was to reassess the effects of density and frequency by orthogonally manipulating the stimulus words of treatment, with further control of other properties. The goals were twofold: to sort out possible population differences from methodological nuances associated with density, and to fill apparent gaps in the literature on statistical regularities and the expressive phonology.

METHODS

The children

Eight children were recruited by public announcement to area schools, daycare facilities, and early childhood programs. To participate, children had to be identified as having PD, characterized by a reduced consonantal inventory relative to English and to expected phonological development. This was established by performance at least one standard deviation below the normative mean reported for age- and gender-matched peers on the Goldman-Fristoe Test of Articulation–2 (Goldman & Fristoe, 2000), with a minimum of six sounds produced in error across contexts on this measure. Children also had to be within three and six years of age because this is an approximate time frame for accelerated speech sound normalization (Shriberg et al., 1994). Inclusionary criteria further required that children perform within typical limits on a battery of diagnostic tests (Gierut, 2008b: 42), which evaluated hearing acuity, oral-motor structure and function, non-verbal intelligence, working memory, expressive and receptive vocabulary, and language. Exclusionary criteria included literacy, bilingualism and concurrent enrollment in treatment for speech and/or language disorders. In all, three boys and five girls met these criteria ; their mean age was 4;0 (years; months) (range 3;0–5; 5), shown in Table 1.

TABLE 1.

Participant and experimental characteristics

Participant characteristics				Experimental characteristics
Gender	Age (years; months)	GFTA-2	Phonemes excluded	Neighborhood structure	Word frequency	Baselines	Treated sound
M	3;5	73	f v θ ð s z ʃ ʧ ʤ l r h	Dense	Frequent	3	s
F	4;8	61	ŋ θ ð ʃ ʧ ʤ l r	Dense	Frequent	4	r
F	3;0	70	f v θ ð l w j	Dense	Infrequent	2	f
F	4;7	72	ŋ k g θ ð l r	Dense	Infrequent	3	r
F	3;0	53	ŋ p t k g f v θ ð s z ʃ ʧ ʤ l r	Sparse	Frequent	2	f
M	5;5	52	ŋ k g θ ð ʃ ʧ l r	Sparse	Frequent	3	l
M	3;11	69	ŋ v θ ð ʃ ʧ ʤ l r j h	Sparse	Infrequent	2	l
F	4;0	74	f v θ D s z ʃ ʧ ʤ r	Sparse	Infrequent	3	s

NOTE: GFTA-2=Goldman-Fristoe Test of Articulation–2 (Goldman & Fristoe, 2000) standard score.

Expressive phonological samples and analyses

Descriptions of the expressive phonologies of the children were developed. Production data were elicited using the Phonological Knowledge Protocol (PKP; Gierut, 2008b). This is a conventional structured probe that samples each English sound in each relevant word position in multiple exemplars. It provides for representative sampling of the statistical patterns of English by including, for example, words from dense/sparse neighborhoods, and frequent/infrequent words (Gierut, 2008b: 70–92 for statistics). It further provides for elicitation of minimal pairs and morphophonemic alternations as evidence of the phonemic status of sounds in a child’s expressive phonology.

PKP data were collected using a spontaneous picture-naming task. A child’s responses were digitally recorded by the experimenter, and subsequently transcribed by independent trained listeners using narrow notation of the IPA. Transcribers had no contact with the children or families, and were blinded to the experiment. Phonetically transcribed responses were entered into an archival database by a separate team of research assistants who were also blinded to the experiment. Archival entries were used to compute percentages of accurate production and to develop standard phonological analyses (Dinnsen, 1984). Phonological analyses established each child’s phonetic and phonemic inventories, distribution of sounds and rule-governed alternations.

The phonemic inventory was central to this study because it delineated which sounds were used by a child to differentiate meaning, and which were not. Sounds that were present in the phonemic inventory did not warrant treatment because they were already functional (i.e. contrastive) in a child’s expressive phonology. By comparison, sounds excluded from the phonemic inventory were non-contrastive and produced with near 0% accuracy on the PKP (Gierut & O’Connor, 2002). These warranted treatment to bring a child’s expressive phonology on track with typical development and in line with the English language.

Linguistically, sounds excluded from the phonemic inventory reflect phonotactic constraints on the grammar (Dinnsen, 1984: 12). There are three general types of phonotactic constraints: INVENTORY CONSTRAINTS, which ban specific sounds from occurring (e.g. velar fricatives are prohibited in English); POSITIONAL CONSTRAINTS, which ban specific sounds from occurring in particular contexts (e.g. velar nasals occur word-finally, but are prohibited word-initially in English); and SEQUENCE CONSTRAINTS, which ban certain sequences of sounds (e.g. consecutive sonorant– sonorant consonants such as /mr-/ are prohibited onsets of English). In this study, inventory constraints informed the independent variable because sounds excluded from the phonemic inventory were the focus of treatment for all children. Likewise, inventory constraints were measured as the dependent variable to establish which sounds excluded from the inventory evidenced gains in accuracy of production. On average, children of the study excluded ten sounds from the phonemic inventory (range 7–16; Table 1).

Experimental design

A single-subject, staggered, multiple-baseline (MBL) across-subjects design was used. Single-subject designs are based on the premise that a child serves as his or her own control (McReynolds & Kearns, 1983). By their very nature, single-subject designs take into account potential individual differences associated with internal or external factors, e.g. age, severity of PD, attention or family dynamics. The MBL is one particular singlesubject design that is implemented as a period of no treatment followed by treatment for each child. In a staggered application of the MBL, children are enrolled in treatment sequentially, rather than concurrently. In an across-subjects application of the MBL, each child serves as one leg of a given experimental condition, such that effects are culled from multiple children, rather than multiple behaviors. Legs of the MBL further provide for replication as a reflection of the generalizability of treatment effects. For phonological treatment, generalizability is typically achieved by demonstrating that the effects of treatment are not sound-specific.

As applied in this study, the no-treatment or baseline phase of the MBL ensured stability of a child’s performance prior to the instatement of treatment, namely, that sounds excluded from the phonemic inventory showed little fluctuation in production accuracy (± 10% variation, following McReynolds & Kearns, 1983). To assess stability of performance over time, each child was given more than one baseline (Table 1). To assess stability across legs of the MBL, the number of baselines was increased by one as successive children enrolled. Based on principles of single-subject design, baseline stability helps to establish a causal relationship between experimental treatment and change in performance. The ongoing stability of time-lagged baselines further demonstrates that change in performance is not attributable to maturation. If maturation were at work, then children next to enroll would be expected to evidence gains in the absence of treatment because the extended period of baseline monitoring would have afforded them the time to mature.

As applied herein, the treatment phase of the MBL supplied the independent variable, namely, treatment of a sound excluded from a child’s phonemic inventory using stimulus words that orthogonally varied in density and frequency. Four children were taught a sound in words from dense neighborhoods, and four others in words from sparse neighborhoods. Within and across conditions, frequency was further varied, such that two of four children were treated on frequent, and two others on infrequent words. Hereafter, we refer to the conditions as Dense–Freq, Dense–Infreq, Sparse–Freq and Sparse–Infreq. Through these manipulations, it was possible to examine the blocked effects of dense/sparse neighborhoods and frequent/infrequent words as in prior studies, in addition to the combined effects of density and frequency in keeping with the central aim of this study.

The dependent variable was generalization, operationalized as the percentage accuracy of production of sounds excluded from a child’s baseline phonemic inventory as measured on the PKP. Generalization data were collected longitudinally, with samples obtained at baseline, at the completion of each treatment step (outlined below), and immediately following completion of treatment. Generalization data were also collected throughout treatment on a variable ratio schedule averaging two sessions. On average, 13 PKP samples (range: 8–16) were obtained from each child. Consistent with the enrollment procedures above, each PKP sample was digitally recorded and phonetically transcribed, with transcriptions entered into the archival database. The data were used to compute separate percentages of accuracy for each sound excluded from a given child’s phonemic inventory at each sampling point in time. Thus, accuracy was documented for every sound excluded from the phonemic inventory of a child at approximately thirteen points in time, corresponding to the thirteen PKP samples that were administered on average. The full set of longitudinal data was then evaluated in data analysis.

Because accuracy data were derived from descriptive phonetic transcriptions, it was necessary to document reliability. Transcription reliability was established for 10% of the longitudinal PKP data collected from each child. Independent transcriptions from two judges were compared point-to-point, with mean agreement being 92% based on 2,317 consonants transcribed.

Treated stimuli

The overarching goal of treatment was the elimination of inventory constraints as the unified linguistic characterization of all children’s error patterns. Each child was taught one sound excluded from his or her phonemic inventory. The treated sound was pseudo-randomly assigned to accommodate individual differences in children’s inventories while also providing for replication. Half the children were taught a fricative, and half a liquid, balanced by condition. The treated fricative was either /f/ or /s/, and the liquid was either /l/ or /r/; these are shown in Table 1 by condition and by child. The treated sound was taught in the initial position of eight treated words that conformed to the density/frequency characteristics of a child’s experimental assignment; the treated words are shown in the ‘Appendix’. Treated words were picturable, of suitable content for a child, and non-overlapping with PKP items so as to keep treated stimuli distinct from generalization stimuli. Several considerations went into the selection of the treated sounds and treated words, as detailed below.

Treated sounds

The sound /f/, /s/, /l/ or /r/ was selected for treatment for five reasons. First, these sounds were taught in the two previous studies of density and frequency in treatment of PD (Gierut et al., 1999; Morrisette & Gierut, 2002). To maintain consistency with the literature and in the interest of replication and comparison, they were again chosen here. Second, these sounds are vulnerable to developmental errors of production (Smit, Hand, Freilinger, Bernthal & Bird, 1990). Third, treatment studies typically demonstrate the generalizability of effects by manipulating an error pattern that is common to all participants, but uniquely instantiated by individual children (e.g. Rvachew & Nowak, 2001; Tyler, Edwards, & Saxman, 1987). The consequence is that children are taught different sounds, which are tailored to their phonological needs, but which fall under the larger umbrella of a commonly shared error pattern. Single-subject design explicitly provides for individual variation in the treated sound because each participant serves as his or her own control. In the present study, we adopted the same tack. Inventory constraints constituted the common pattern to be remediated in treatment, with the treated sound being specific to the expressive phonology of an individual child. Fourth, the use of different treated sounds has the further effect of bolstering the ecological and clinical validity of the findings. Because treated sounds varied, the impact of density and frequency on the elimination of inventory constraints could be established more broadly. Last, and most critical, the selection of treated sounds was constrained by the planned manipulations of density and frequency relative to the actual (but asymmetric) distribution of words in the English language. Recall that each treated sound was taught using eight stimulus words that conformed to a child’s experimental assignment, while also being picturable, appropriate and non-overlapping with items of the PKP. Given this, some sounds with the potential for treatment had to be set aside outright because there were simply too few words in the English language to yield an adequate set of eight stimuli. To illustrate, there are seven word-initial /z/ forms that occur in dense neighborhoods of English (Nusbaum et al., 1984), one of which is sampled on the PKP, leaving just six (not eight) possible stimuli for treatment. Similarly, there are no word-initial /z/ forms that occur frequently in English (Nusbaum et al., 1984), thereby further precluding /z/ as a possible treated sound. By comparison, the selection of /f/, /s/, /l/ or /r/ guaranteed roughly forty word-initial items for each sound and each category, dense/sparse and frequent/infrequent. This provided an adequate pool from which to select treated words.

Treated words

Treated words were selected based on density and frequency values, as retrieved from the Hoosier Mental Lexicon (Nusbaum et al., 1984). This is an online database that supplies the density of 20,000 words of the Merriam-Webster Dictionary, with corresponding frequencies from Kučera and Francis (1967). An adult corpus was used for consistency with the two prior treatment studies involving the manipulation of density and frequency in PD (Gierut et al., 1999; Morrisette & Gierut, 2002), which the present study aimed to extend and replicate. Some have suggested that child corpora may provide a more accurate reference (Dollaghan, 1994). Yet others argue that adult corpora may be extended to the study of children for reasons associated with the normalization of standard distributions (Kelly & Martin, 1994), correlations showing the equivalence of corpora (Storkel & Hoover, 2010a) and behavioral demonstrations of similar effects across corpora (Gierut & Dale, 2007). This debate notwithstanding, an adult corpus was used herein for ease of translation and uniformity across studies of PD, and to enable future comparisons between the performance of children and adults as a means of examining developmental continuity.

To initiate stimulus selection, conventional operational definitions based on the raw values of density and frequency (Luce, 1986) were applied, such that words from dense neighborhoods were to have ten or more similarity neighbors, and frequent words were to have a raw count of 100 or more occurrences per million. In this study, treated words from dense neighborhoods had a mean of twenty-one neighbors, whereas those from sparse neighborhoods had a mean of four neighbors. Treated words that were classified as frequent had a mean of 293 occurrences and infrequent, twenty-one occurrences. In all, four sets of treated words were identified in accord with the crossing of density and frequency by experimental condition.

Because density and frequency are correlated with other properties of word structure, it was necessary to consider and control for alternate (and potentially confounding) variables in stimulus selection. Specifically, for density, there is an established negative correlation with word length (Pisoni, Nusbaum, Luce & Slowiaczek, 1985): dense neighborhoods are largely comprised of short words. Indeed, in this study, the treated words from dense neighborhoods averaged 3.2 segments, whereas those in sparse neighborhoods averaged 4.5 segments in length. This reflected the expected negative correlation between density and length (r(64)=−0.78, p<0.001), but it also resulted in a statistically significant difference in length between the dense/sparse stimulus sets (t(62)=−8.33, p<0.001). Typically, laboratory studies handle such correlations by holding length constant in stimulus selection; however, this may not be feasible, ecologically valid or necessarily desirable when naturalistic stimuli are used and when children are involved as participants (see Storkel, 2004a, for review). Such was the case in the present study. Accordingly, the recommended alternative (p. 1465) is to transform raw density values using z-score conversion and/or median transformation for length. Transformed density values are computed relative to all words that are of the same length in a given corpus (i.e. the Hoosier Mental Lexicon). In this way, length is taken into account to minimize potential confounds. Importantly, transformed density values appear to be better predictors of the behavioral patterns to emerge from experimental manipulations of density (p. 1466).

We followed this standard by applying both the procedure for density z-score conversion and density median transformation as outlined by Storkel (2004a: 1458–60). Particular attention was given to the data provided about the Hoosier Mental Lexicon. Specifically, Storkel (Table 2, p. 1459) reported the mean and standard deviation for neighborhood density by word length for all words of the Hoosier Mental Lexicon; these values were used in computation of density z-scores. Likewise, Storkel (Table 2, p. 1459) reported the median and interquartile range for neighborhood density by word length for all words of the Hoosier Mental Lexicon; these values were used in computation of density median transformations.

TABLE 2.

Summary of blocked and orthogonal results based on the criterion cut-off of 10 % mean generalization accuracy in coding yes/no generalization (Elbert et al., 1984), the rank procedure for replicated AB design (Marascuilo & Serlin, 1988), and effect size for single-subject design (Beeson & Robey, 2006)

Condition	Criterion cut-off		Rank procedure		Effect size
	M % accuracy	Coding	n/N1	p	d
Blocked
Dense	34%	Yes	7/8	0.03	13.11
Sparse	11%	Yes	5/7	0.16	4.25
Frequent	22%	Yes	7/8	0.03	9.01
Infrequent	28%	Yes	5/7	0.16	8.35
Orthogonal
Dense–Freq	30%	Yes	5/5	0.03	14.83
Dense–Infreq	41%	Yes	2/32		11.39
Sparse–Freq	4%	No	2/32		3.19
Sparse–Infreq	17%	Yes	3/42		5.311

¹n=Number of factors evidencing positive gain; N=Number of possible factors examined for positive gain (i.e. number of subject × treated and untreated sounds from the same and different manner classes; see Morrisette & Gierut, 2002: 150).

²Inadequate power due to the number of factors evidencing positive gain by children enrolled in these conditions.

With referent values in place, density z-scores were calculated herein using the equation: (Obtained raw density value – M)/SD (Storkel, 2004a: 1458). That is, for each treated word in each condition, the obtained raw density value was subtracted from the mean density value reported by Storkel (Table 2, p. 1459) for all words of the Hoosier Mental Lexicon that were of the same length. This value was then divided by the standard deviation, also reported by Storkel (Table 2, p. 1459) for all words of the Hoosier Mental Lexicon that were of the same length. To illustrate, funny was a treated word associated with the dense condition (see ‘Appendix’). It consists of four segments, and has a raw density value of eleven. The mean density of all four-segment words in the Hoosier Mental Lexicon is 6.87 (SD=4.53) (Table 2, p. 1459). Thus, the density z-score of funny was 0.91 (i.e. (11–6.87)/4.53). By comparison, lazy was a treated word associated with the sparse condition (see ‘Appendix’). It too consists of four segments, but has a raw density value of seven. Its density z-score was 0.03 (i.e. (7–6.87)/4.53). This procedure was followed to derive the mean density z-scores for treated words used in the dense/sparse conditions. The average density z-score for the dense condition was 0.83, and the sparse condition −0.09, resulting in a statistically significant difference in density by condition (t(62)=4.52, p<0.001). Importantly, there was no correlation between the density z-scores and word length (r(64)=−0.17, p=0.18).

Density median transformation scores were also computed, using the equation: (Obtained raw density value – Mdn)/1/2 IQR) (Storkel, 2004a: 1458). Procedures were much the same as above, with median transformation scores generated for each treated word used in the dense/sparse conditions. Values reported by Storkel (Table 2, p. 1459) again supplied the median and inter-quartile range for density based on all words of the Hoosier Mental Lexicon by length. The resulting mean density median transformation for treated words of the dense condition was 1.17, and for treated words of the sparse condition 0.18. Density median transformation values were statistically significant by condition (t(62)=3.72, p<0.001), with no correlation between the transformed density values and length (r(64)=−0.14, p=0.28).

Together, the density conversions provided the needed experimental safeguard to demonstrate that the treated stimuli were distinct in density by condition, even when length was taken into account. This established that density, not length, was a primary independent variable. (For completeness, the length of the treated words sorted by frequency was not statistically different (t(62)=−0.14, p=0.89). Average length of frequent versus infrequent treated words was 3.8 versus 3.9 segments, 2.8 versus 2.9 biphones and 1.4 versus 1.5 syllables, respectively.)

Besides length, density is positively correlated with phonotactic probability (Vitevitch & Luce, 2004): words in dense neighborhoods are largely comprised of common sounds and sound sequences. Thus, it was necessary to establish that treated words from dense/sparse neighborhoods did not differ in phonotactic probability as a spurious variable. We followed standard procedures recommended in the literature (Storkel, 2004a), computing the sums of segment and biphone frequencies for each stimulus word using a publicly available calculator (Vitevitch & Luce, 2004), with z-score conversion for length. Resulting values were binarily coded using the rubric that positive phonotactic values reflect common sound sequences, and negative values rare sound sequences. Chi-square analyses revealed no differences in commonality or rarity of the phonotactic patterns associated with treated stimuli from dense versus sparse neighborhoods. This held for sum of segment frequencies (χ² (1, N=64)=1.82, p=0.18) and sum of biphone frequencies (χ² (1, N=64)=0.58, p=0.45). The proportion of common:rare words was 1.2:1, yielding a nearly equivalent distribution of phonotactic probability by density. Density, not phonotactic probability, was thus retained as a primary independent variable.

Frequency is likewise correlated with other statistical cues. Specifically, there is a negative correlation between frequency and age-of-word-acquisition (AoA; Gilhooly & Watson, 1981). AoA is a reliable and behaviorally valid subjective estimate of when a given set of words was first acquired, as determined by child (Walley & Metsala, 1992) or adult judges (Gilhooly & Logie, 1980). The observed correlation is that high-frequency words tend to be earlier acquired, although the directionality of the effect remains a point of debate (Gilhooly & Watson, 1981). Once again, it was necessary to eliminate AoA as a potential confound, rendering frequency as a primary independent variable. This was accomplished by retrieving the AoA values of stimulus words in reference to the normative counts of Gilhooly and Logie (1980) and Bird, Franklin and Howard (2001). Resulting AoA values were binarily coded, with words acquired before age six defined as early acquired in keeping with the inclusionary criteria for participation in this study. Chi-square analyses revealed no difference in the AoA values of frequent versus infrequent stimuli (χ² (1, N=44)=0, p=1.0). Overall, the ratio of early:late AoA words was 1.1:1, with near equal distribution of AoA by frequency. As above, frequency, not AoA, was established as a primary independent variable.

Imageability was a related consideration because it is negatively correlated with AoA (Bird et al., 2001): earlier acquired words tend to be highly imageable, keeping in mind too that the treated words used in this study were to be picturable. Above, we demonstrated that treated words were equivalent in AoA. It might be expected then that they would be comparable in imageability, given the reported correlation. Nonetheless, this needed to be confirmed. Subjective imageability ratings were retrieved from Bird et al. (2001) for the treated words. Mean imageability ratings of treated words were 255 versus 213 for dense versus sparse neighborhoods, respectively, and 230 versus 259 for frequent versus infrequent stimuli, respectively. There was no significant difference in the imageability ratings of treated words sorted by density (t(28)=0.47, p=0.64), or sorted by frequency (t(28)=−0.29, p=0.78).

Beyond these controls, developmental phonological characteristics of the treated words were taken into account, given the interest in expressive phonology. The classification scheme of Shriberg and colleagues (1994) was used to code each sound of each treated word by its expected developmental order of emergence. This scheme sorts sounds into early-8 /m n p b d w j h/, mid-8 /ŋ k g t f v ʧ ʤ/ and late-8 /θ ð s z ʃ ʒ r l/ sets. The distribution of early-, mid- and late-8 segments and clusters in treated words from dense neighborhoods was 8, 17, 31 and 7, respectively; thus, treated words in dense neighborhoods were largely composed of late-8 sounds. For sparse neighborhoods, the distribution of early-, mid- and late-8 segments and clusters was 12, 17, 45 and 15, respectively; again, treated words in sparse neighborhoods were largely composed of late-8 sounds. Chi-square analyses showed no significant difference in the segmental and cluster composition of treated words based on the expected developmental order of emergence when sorted by density (χ² (3, N=152)=1.9, p=0.59). Likewise, there was no significant difference in the segmental composition of treated words based on developmental order when sorted by frequency (χ² (3, N=152)= 0.19, p=0.98). As before, treated words sorted by frequency consisted mostly of late-8 sounds. These analyses ensured that the segmental make-up of treated words was comparable on developmental phonological grounds.

Two final phonological considerations were taken into account in treated word selection. To the extent possible, treated stimulus sets were comprised of unique words that were not also neighbors (minimal pairs) of each other: 94% of treated stimuli (60 of 64 words) were non-overlapping in phonological form. The intent was to constrain a child’s exposure to the neighborhood structure of the treated words per se, without further enhancement of that structure in the form of minimal pair contrasts. Also, to the extent possible, treated stimuli did not form neighbors (minimal pairs) with PKP words: 98% of relevant PKP words (423 of 431 words) were non-overlapping in phonological form with treated words. The intent was to minimize the possible inflation of generalization effects by keeping the treated stimuli distinct from those used to measure generalization.

It must be recognized that any number of added factors might have been taken into account in stimulus selection, e.g. featural distinction, stress and grammatical or semantic class. Following Magnuson and colleagues (2007), these were left free to vary. Our objective was to capture the range of variation in English, while at the same time block for the primary variables of interest. In this regard, density and frequency were the key properties varied within a stimulus set as independent variables, while word length, phonotactic probability, AoA, imageability, developmental order of segmental emergence and minimal pairs were controlled across stimulus sets.

Treatment procedures

Children were provided treatment three times weekly in individual sessions, each one hour in duration. Treatment followed a conventional protocol (Gierut, 2008a) consisting of two steps. The first was imitation of the treated sound in treated words. During imitation, a child viewed a picture of the treated word displayed on a computer monitor; the clinician said the depicted word; the child repeated that word. Each treated word was presented as a discrete trial, and feedback about accuracy of production was provided on a continuous schedule. Accuracy of production was assessed for the treated sound in the treated word-initial position; accurate production of the word form was not also required, in keeping with conventional principles of phonological treatment (Hodson & Paden, 1991: 119). In cases of inaccurate production of the treated sound, instructions about articulatory placement were provided, and an additional model was presented. Imitation continued until a child achieved 75% accuracy of production of the treated sound in the treated words over two consecutive sessions or until seven total sessions were completed, whichever occurred first. Following this, treatment shifted to spontaneous naming. The child again viewed the picture of the treated word on a computer monitor, but was to independently name that item with accurate production of the treated sound. Feedback and instruction were provided in the same manner outlined for imitation. This continued until a child achieved 90% accuracy of production over three consecutive sessions or until twelve total sessions were completed, whichever occurred first.

In all, children were afforded a maximum of nineteen treatment sessions (i.e. nineteen hours of training). They had the further opportunity to complete the protocol more rapidly, if they achieved performance levels of 75% and 90% accuracy of production over consecutive imitation and spontaneous sessions, respectively. Thus, time- and/or performance-based criteria determined time in treatment for a given child. In this study, those assigned to the dense conditions tended to follow time-based advancement through the protocol, whereas those assigned to the sparse conditions tended to follow performance-based advancement. Overall, the average number of sessions provided to any given child was fifteen, and the average by condition was nineteen for Dense–Freq, nineteen for Dense–Infreq, seven for Sparse–Freq and fourteen for Sparse–Infreq. Across conditions, there was no statistically significant difference in the number of sessions provided in each step of treatment (χ² (3, N=117)=1.12, p=0.77). Overall, mean accuracy of the treated sound at completion of treatment was 94%. Mean accuracy by condition was 93% for Dense–Freq, 85% for Dense–Infreq, 99% for Sparse–Freq and 96% for Sparse–Infreq. It must be underscored that performance during treatment showed only that children learned what was taught. The critical question was how children then transferred what had been learned to the expressive phonology. Treatment thus served as the conduit from which children were left free to generalize in keeping with the dependent variable.

Data analysis

Four sets of analyses of longitudinal generalization data were completed. Recall that, for each child, at each PKP sampling point in time, percentages of production accuracy were computed for each sound excluded from the phonemic inventory. This included the treated sound as sampled across contexts and words, as well as other untreated (erred) sounds. Any sound that evidenced any gain at any sampling point in time was entered into analysis, and the full set of longitudinal data associated with that sound was evaluated. Approximately 11,356 productions were examined for generalization, with each child contributing at least 1,420 productions over time.

The first two evaluations were complementary in establishing which experimental conditions induced generalization from qualitative and quantitative vantages, respectively. The analyses were identical to prior studies of density/frequency in treatment of PD (Morrisette & Gierut, 2002), and for comparison purposes, were again applied herein. Qualitatively, a dichotomous yes/no coding of generalization was applied to each experimental condition. The coding of yes/no generalization was based on the accepted criterion cut-off of 10% or greater mean generalization accuracy relative to baseline performance for children of a given condition (Elbert, Dinnsen & Powell, 1984). This analysis offered preliminary insight to the experimental conditions affiliated with generalization. The quantitative analysis followed, using the rank procedure for replicated AB multiple baseline design to establish generalization as a statistically reliable effect (Morrisette & Gierut, 2002: 150). Briefly, the procedure makes use of the combined Sign test (Marascuilo & Serlin, 1988), organizing sounds that generalized into three sets or ‘factors’ for each child by condition. The three factors were the treated sound, sounds from the same manner class as the treated (within-class generalization) and sounds from different manner classes than the treated (across-class generalization). The number of factors varied depending on which sounds generalized, e.g. if a given child showed no generalization to the treated sound, then that factor was not instantiated (see Table 2). Mean baseline performance and longitudinal generalization accuracy were computed and ranked for each factor, with the difference between ranks totaled by experimental condition. A binomial distribution, where p=0.05, was then applied to determine whether the resulting generalization was statistically reliable.

The third evaluation stands apart in its calculation of effect size for single-subject experimental design. This is a relatively new addition to the single-subject literature that has been introduced as a way of quantifying treatment efficacy, with an eye toward meta-analyses of small-n studies (Beeson & Robey, 2006). Effect size captures the magnitude of generalization for a given treatment condition, with values compared across conditions to identify which is relatively most efficacious. In this study, standard mean difference (d; Beeson & Robey, 2006) was computed. Mean accuracy of baseline data was calculated, along with mean accuracy of longitudinal generalization data. The difference between means was obtained and divided by the standard deviation of the baseline, corrected for continuity (Gierut & Morrisette, 2011b), to achieve the effect size, d. While benchmarks for interpretation of d have been established for between-group designs, it is inappropriate to extend these to small-n studies (Beeson & Robey, 2006). Standards for what constitutes a small, medium or large effect must be developed empirically, but before this can be established, reports of effect size in single-subject studies must accumulate. To our knowledge, there are only four studies enrolling clinical populations in some form of linguistic treatment that have cited effect sizes, with d values in the range of 2.0 to 18.0 (Beeson & Robey, 2006; Gierut & Morrisette, 2011a; 2011b). Data from the present study added to this base as a secondary contribution.

The three aforementioned analyses (i.e. criterion cut-off, rank procedure, effect size) were applied to the generalization data in comparisons blocked by density (dense vs. sparse neighborhoods) and by frequency (frequent vs. infrequent words), as well as in the orthogonal comparison of density × frequency. Together, the results revealed the TRIGGERS of generalization, namely, which type of treated words prompted generalization in the expressive phonology of children with PD.

For the fourth analysis, attention shifted from an evaluation of percentage accuracies to a descriptive characterization of the lexical properties of the PKP words that actually generalized. While certain words might trigger generalization, it was reasonable to also ask which words were the TARGETS of generalization or the recipients of that change (Morrisette, 2000). Consider, for example, that treatment in the Dense–Freq condition might only result in generalization to other frequent words in dense neighborhoods. To address this, the density and frequency values of PKP words that showed improvement in production accuracy from baseline to posttreatment were retrieved from the Hoosier Mental Lexicon (Nusbaum et al., 1984). Chi-square analyses were computed to determine whether there were differences in which words generalized based on neighborhood or frequency characteristics. The collective set of analyses thus identified both the triggers and targets of generalization.

RESULTS

The results emphasize the experimental manipulation of density and frequency as triggers of phonological generalization in treatment, in keeping with the central purpose of the study. The presentation is organized to summarize blocked, then orthogonal comparisons of density and frequency, as summarized in Table 2. This is followed by a description of the targets of generalization, with a summary of the density/frequency characteristics of PKP words that generalized as a consequence of treatment.

Triggers of phonological generalization

In the blocked comparison of density, both dense and sparse treatment conditions induced generalization based on the 10% criterion cut-off. This is shown in Table 2, which reports the mean percentage accuracy by condition and then codes that as yes/no generalization based on the 10% criterion cut-off (Elbert et al., 1984). The rank procedure confirmed that generalization associated with words from dense neighborhoods was statistically reliable, where p=0.03, whereas that associated with sparse neighborhoods was not. Comparisons of effect size further established that the magnitude of generalization that derived from teaching words from dense neighborhoods was three times greater than sparse neighborhoods (d=13.11 vs. 4.25, respectively). Thus, when frequency was removed from consideration, treatment of words from dense neighborhoods induced greater phonological generalization, with convergence across analyses.

In the blocked comparison of frequency, Table 2 again shows that the 10% mean generalization cut-off was achieved in treatment of both frequent and infrequent words. The rank procedure confirmed that frequent words resulted in statistically reliable effects, but the same did not hold for infrequent words. In terms of effect size, treatment of frequent words resulted in a slightly greater magnitude of gain than infrequent words (d=9.01 vs. 8.35, respectively). Thus, frequent words had a modest advantage over infrequent for phonological generalization, when density was removed from consideration.

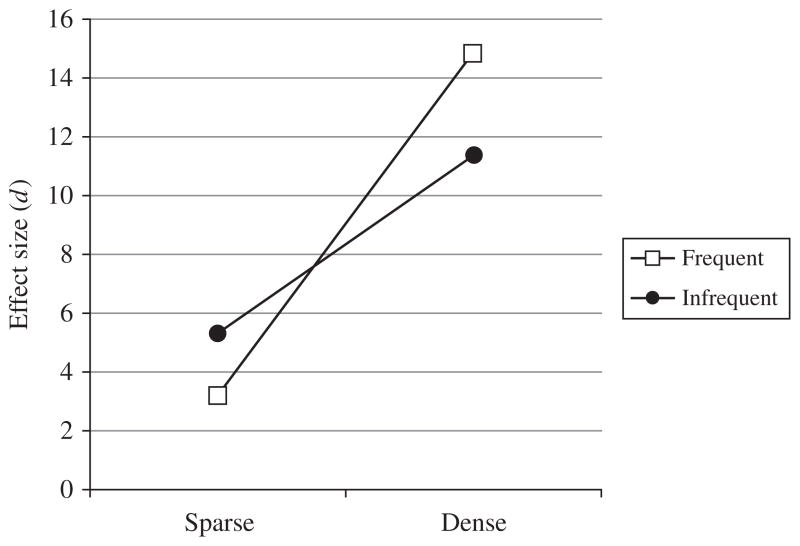
Orthogonal comparisons rendered a more detailed picture of the interface of density and frequency relative to generalization. Table 2 shows that children achieved the 10% criterion cut-off in three of four experimental conditions: Dense–Freq, Dense–Infreq and Sparse–Infreq. Of these, only the Dense–Freq condition resulted in reliable effects based on the rank procedure because children of this condition generalized to treated and untreated sounds from treated and untreated manner classes (see ‘Data analysis’ above for a description of the rank procedure and variance in the number of factors). Effect sizes associated with the four experimental conditions are plotted in Figure 1, from which three observations may be gleaned. First, treatment of words from dense neighborhoods, whether frequent or infrequent, consistently resulted in a greater effect size than sparse neighborhoods (see also Table 2). Second, the relative effect sizes were graded, such that Dense–Freq>Dense–Infreq> Sparse–Infreq>Sparse–Freq in magnitude of generalization. The optimal trigger of phonological generalization thus appeared to be treatment of frequent words from dense neighborhoods. A final observation hints at a possible interaction between density and frequency. That is, frequency reversed in direction of generalization effects, depending on neighborhood density. Notice in Figure 1 that the Dense–Freq condition outranked the Dense–Infreq (d=14.83 vs. 11.39, respectively), whereas it was just the reverse for the Sparse–Infreq condition relative to the Sparse–Freq (d=5.31 vs. 3.19, respectively). This suggests that the influence of a word’s frequency may shift depending on its residence in a neighborhood.

Fig. 1.

Effect size associated with phonological generalization resulting from the orthogonal manipulation of density and frequency in treatment.

Targets of phonological generalization

Chi-square analysis showed no significant difference in the density of PKP words that showed improved production accuracy as a result of treating words from dense versus sparse neighborhoods (χ² (1, N=303)=1.58, p=0.21). PKP words that generalized were almost equally split across dense and sparse neighborhoods, on the order of 1.2:1. Likewise, there was no significant difference in the frequency of PKP words that generalized as a result of treating frequent versus infrequent words (χ² (1, N=303)=2.83, p=0.09). Again, PKP words that generalized included frequent and infrequent items, on the order of 1:1.9. These results suggest that improvements in the expressive phonology of children with PD took place across a variety of words with ranging properties of density/frequency.

DISCUSSION

This study set out to reassess how density and frequency affect acquisition of the expressive phonology by children with PD enrolled in treatment. The main finding was a differential effect of density on phonological learning. Dense neighborhoods were consistently affiliated with greater gains in the phonologies of children with PD as a consequence of treatment. The effect held independent of frequency, and was confirmed through converging analytic perspectives. By comparison, there was not a clear differential effect of frequency: frequent and infrequent words led to near equivalent phonological gains. Moreover, the way that frequency contributed to generalization appeared to depend on its pairing with density, indicative of a potential interaction between variables. The results hinted of graded generalization effects, such that the Dense–Freq condition was most efficacious as a trigger of phonological learning. While the Dense–Freq condition might have triggered the greatest learning, improvements in production accuracy were not limited to just those same kinds of words; rather, accuracy extended to untreated words with varied lexical characteristics, including dense/sparse and frequent/infrequent items. This suggests that the Dense–Freq condition infused system-wide change that fanned across sounds of the phonology, and also words of the lexicon. Taken together, the main findings speak to at least four outstanding issues that frame the discussion. These are (i) the utility of statistical cues for children with PD; (ii) the function of density in shaping phonemic contrasts; (iii) an asymmetry in words that are triggers versus targets of phonological learning; and (iv) a possible interaction of density and frequency in phonological learning.

Population trait or methodology?

Recall that a motivation for the present study was the finding that children with PD benefit from sparse neighborhoods in phonological learning (Gierut et al., 1999; Morrisette & Gierut, 2002). This stood apart from typical development, giving rise to the hypothesis that a sparse neighborhood advantage may be a diagnostic hallmark of PD (Storkel, 2004b; Storkel & Hoover, 2010b). In light of our findings, this hypothesis was not supported: children capitalized on words from dense neighborhoods to promote expansion of the phonemic inventory, consistent with typical phonological acquisition (Stoel-Gammon, 2011). Consequently, density might not be the parameter that uniquely distinguishes PD from typical development.

Instead, it is likely that methodological differences account for the disparity in density effects across studies of PD. The difference can be traced to the independent versus concurrent manipulation of density relative to frequency. In the present study, density and frequency were fully crossed in the experimental conditions, whereas previously, density was held constant but frequency was balanced across conditions. An implication is that the function of a given statistical variable may wax and wane depending on the other cues that might be operating concurrently. Here, density was bolstered by orthogonal manipulations, whereas frequency appeared to play less of a differential role in generalization. This observation is of interest because other developmental studies, also involving orthogonal manipulations of density and frequency, have reported similar effects (Garlock et al., 2001; Krull, Choi, Kirk, Prusick & French, 2010). In each case, when density moved to the forefront, the effects of frequency receded (see also Gierut & Morrisette, 2011a, for similar findings in the orthogonal variation of frequency and AoA). This has led to a suggestion that the relationship between statistical variables may be multiplicative, not additive (Krull et al., 2010). In future research, it will be important to develop this point further by examining the combined contributions of input variables to the expressive phonology. Work along these lines is beginning, with emphasis on the disambiguation of correlated variables, namely, density and phonotactic probability (Storkel & Hoover, 2010b), or frequency and AoA (Gierut & Morrisette, 2011a). By building this line of study, it may be possible to determine if there are precedents, weightings, and/or trade-offs among statistical regularities relative to the expressive phonology.

There is also another possible explanation for the waxing and waning of density and frequency that warrants consideration. In particular, the prominence of behavioral effects may vary depending on the reference norms that are used. Consider that in this, and other developmental studies which co-varied density and frequency (Garlock et al., 2001), an adult lexical corpus was consulted in stimulus development. Yet there are likely differences in the size and structure of a child’s lexicon relative to the adult (Walley, 1993). For a child, neighborhoods appear to be denser (Coady & Aslin, 2003), and words of the lexicon are shorter (Charles-Luce & Luce, 1990) and more frequent (Storkel & Hoover, 2010b). Moreover, differential effects have been reported in connection with the use of different corpora, child versus adult and reception versus expression (Goodman, Dale & Li, 2008; Krull et al., 2010; but see Gierut & Dale, 2007, for consistency of effects across corpora in PD). In future research, it will be necessary to test the application of different lexical corpora against acquisition of the expressive phonology. This may be accomplished by direct replication, or by confirmation that the coding of experimental stimuli as dense/sparse or frequent/infrequent is the same across corpora (Storkel & Lee, 2011). Applications of child corpora in particular may have further methodological advantages in that known relationships between statistical variables might be easier to control. For example, because children’s neighborhoods are denser but words are generally shorter, it may be possible to identify ample stimuli of the same length that vary in density in a child-based corpus. This would eliminate the need to use transformed values in stimulus selection (Storkel, 2004a), which may have the undesired consequence of inflating behavioral effects. Research along these lines would address two limitations of the present study, namely, the use of an adult corpus in stimulus selection and transformed density values in the operational definition of the independent variables. As a possible broader outcome, the results to emerge from such research may help settle debates about the suitability of different corpora in developmental research (cf. Charles-Luce & Luce, 1990; 1995; Dollaghan, 1994).

The present findings also have possible applied consequences for the design of instructional programs for PD, but it will necessary to proceed with caution in the translation of research to practice. Clinically, teaching erred sounds in words from dense neighborhoods is likely to be effective in promoting the expressive phonology, particularly when the treated words are also frequently occurring. However, it must be underscored that this recommendation is relevant only to children whose primary deficit is a severely reduced phonemic inventory, who are enrolled in instructional programs to eliminate inventory constraints. In future research, it will be necessary to demonstrate the effects of dense neighborhoods for children who exhibit other phonotactic errors associated with positional or sequence constraints. An intriguing possibility is that the words that are optimal for generalization may vary depending on the nature of the phonotactic error being treated. This, in turn, may reveal the unique function of statistical regularities in the acquisition of expressive phonology.

Density and expressive phonology

A second point of discussion is to consider how words from dense neighborhoods gave rise to the greatest system-wide phonological generalization. To evaluate this, we return to the hypothesis that the representation of words is a possible source of PD. If true, then it is possible that dense structure served multiple functions, all of which converged to magnify sublexical structure in treatment. Consider that, because treatment was phonological in nature, it might have cast a ‘floodlight’ on the sound system. In turn, dense neighborhoods might have drawn a child’s attention to the phonological structure of the treated words, with that structure being revealed in several ways.

Specifically, because words from dense neighborhoods have many phonetically similar counterparts, these too would have been activated in treatment. Consequently, the same phonological details would have been realized again and again. A treated word like rope, for example, activates neighbors road, robe, hope and soap, among others. Notice the shared points of overlap involving the body (/ro/) and rime (/op/), respectively. One possibility is that resemblances in segmental and syllabic structure were reinforced in treatment of words from dense neighborhoods.

Another way that dense neighborhoods might have brought sublexical structure to the forefront was through the occurrence of minimal pairs. Dense neighborhoods essentially define lexical pockets of minimal pairs, which themselves are revealing of phonemic distinctions. As such, treated words from dense neighborhoods might have ‘spotlighted’ (Peters & Strömqvist, 1996) the range of phonemic contrasts exemplified in a given neighborhood. Thus, neighbor activation may have reinforced overlapping phonological structure while, at the same time, highlighted unique points of difference among minimally distinct forms in dense neighborhoods. It is also the case that minimal pairs are central to the differentiation of meaning in language, and meaning, in turn, is the foundation of the lexicon. Possibly, exposure to words from dense neighborhoods strengthened the critical association between form and meaning.

Other aspects of dense neighborhoods might have been conducive to the process of generalization itself. In particular, treated words from dense neighborhoods were all members of the same cohort, where cohort is defined as words that begin with the same initial consonant (Norris, 1994). It is relevant that words of a cohort are not necessarily in the same neighborhood (Magnuson et al., 2007). For example, sun and sat are in the same cohort, but sun has as its neighbors bun or fun, whereas sat has as its neighbors bat or fat. Given this, treatment may have revealed two sides of lexical organization associated with cohort and neighborhood structure, respectively. Some have suggested that when children are exposed to a broader problem space such as this, it enables the generalization process (Gerken, 2006). Thus, treatment directed toward production of words from dense neighborhoods with shared cohorts may have facilitated greater generalization in children with PD.

Ultimately, the input provided to a child in treatment might have converged to guide the discovery of basic phonological constructs. This idea would be consistent with MacWhinney’s (1987) claim that functional cues make abstract linguistic structure known. Perhaps, through treatment of words from dense neighborhoods, a child inferred certain underlying properties of phonological systems, such as what is a phone, phoneme, minimal pair or well-formed syllable. It might have been precisely this convergence of more than one cue that tripped phonological generalization. An implication that emerges is that statistical regularities in the input must be made especially redundant in order for children with PD to extract crucial sublexical details and advance the expressive phonology.

Future studies that examine multiple cues in tandem are again needed to test this hypothesis. Through this sort of work, it may be possible to delineate whether cue redundancy is necessitated in the case of PD, and to establish which and how many cues must converge as primary evidence in treatment. Research along these lines would have the added benefit of addressing another limitation of the present study, namely, the small sample size. Replications through enrollment of increased numbers of children with PD, who present with varied error patterns being taught sounds that vary in developmental order of emergence, would confirm the robustness of the density effects. A likely outcome would be the characterization of individual differences relative to the effects of statistical variables on expressive phonology.

Triggers versus targets of phonological gains

The results of this study bring up a distinction between the properties of words that trigger phonological learning as opposed to the properties of words that are the targets, or recipients, of improved production accuracy. At first glance, it might be expected that the types of words to induce generalization would be the same as those that undergo generalization in 1:1 correspondence. For example, if words from dense neighborhoods were taught, then it might be expected that untreated words, also from dense neighborhoods, would show improved production accuracy. This, however, was not borne out in the present study, nor has it been found in the literature on PD (Morrisette, 2000), typical phonological development (Leonard, Newhoff & Mesalam, 1980) or fully developed linguistic systems generally (Labov, 1994). Rather, the primary way that phonological innovations are introduced in child or adult grammars is through LEXICAL DIFFUSION (Chen & Wang, 1975); that is, sound change takes place gradually on a word-by-word basis.

While many have tried to find the driving force behind lexical diffusion, this line of research has not met uniform success. Some have considered statistical factors in diffusion (Bybee, 2001), whereas others have entertained sociolinguistic (Labov, 1994) or perceptual/articulatory (Janson, 1983) factors. Still others have suggested that diffusion might be cyclic (Morrisette, 2004), with change defined by alternations in the value of word-level variables (e.g. change high-frequency words, then change low-frequency words, then return to change more high-frequency words, and so on). Despite efforts, there has been no clear resolve in identifying or predicting precisely which words undergo diffusion when new sounds are introduced to the phonemic inventory.

This notwithstanding, the present results are wholly consistent with lexical diffusion. Treated words from dense neighborhoods triggered phonological gain, but the targets of change cross-cut organizational properties of the lexicon to encompass all kinds of words. Of importance, broad lexical change went hand-in-hand with broad phonological change in the composition of children’s phonemic inventories. This dual benefit to lexical and sublexical structure underscores the bidirectional influences between phonology and the lexicon that Stoel-Gammon (2011) emphasized.

For the future, it might be appropriate to consider the other side of the coin, namely, circumstances under which the process of lexical diffusion stalls. It may be that, for children with PD, certain word types resist improved production accuracy even in the face of long-term intervention. Words that resist change might align based on their statistical properties, such that certain word-level variables might be found to block or inhibit phonological generalization.

Interactions of density and frequency

As a final point of discussion, we consider a possible interaction between density and frequency, similar to that reported in other developmental work involving orthogonal evaluations of these two variables (Krull et al., 2010). As shown in Figure 1, there was a possible interaction given the graded generalization by condition, such that the impact of frequency seemed to vary based on the value of density: Dense–Freq>Dense–Infreq, but Sparse–Infreq>Sparse–Freq. The advantages of density for phonological learning have already been discussed, and the importance of frequency relative to density was shown to be consistent with the literature (Stoel- Gammon, 2011). Of interest here is the finding that the Sparse–Infreq condition was relatively more effective than the Sparse–Freq condition in promoting generalization. Based on the literature (Stoel-Gammon, 2011), neither sparse neighborhoods nor infrequent words are expected to impact the expressive phonology in a major way. There are, however, two possibilities that might describe the results; namely, treated words associated with the sparse conditions may have acted like nonwords or lexical islands (Garlock et al., 2001).

With regard to nonwords, in the Sparse–Infreq condition, children might have viewed the treated stimuli as novel forms because they had few resemblents and rarely occurred. It has been reported that lexical novelty attracts children’s attention (Storkel & Hoover, 2010b), that nonwords activate sublexical structure (Vitevitch & Luce, 2004) and that children with PD experience greater generalization following exposure to nonwords (Gierut, Morrisette & Ziemer, 2010). Together, these are possible reasons why positive gains may have occurred in the Sparse–Infreq condition.

With regard to lexical islands, in the Sparse–Freq condition, children might have had little motivation to change the expressive phonology. These treated words occurred often in the input, but there were few other competitors in the similarity neighborhood. Consequently, a child would have had little difficulty differentiating treated words from other phonetically similar words because the forms were already distinct. This may be a reason why the Sparse–Freq condition was least effective in triggering generalization.

While intriguing, these accounts of an apparent interaction should be viewed with caution. Keep in mind that the presumed interaction between density and frequency was identified based on graded effect size values, and not relative to interpretive standards associated with small, medium or large effects. As noted, benchmarks for interpretation of effect size in single-subject design have yet to be established empirically, necessitating first the accumulation of effect size data; the present findings contribute in this regard. Once benchmarks are eventually in place, it is possible that the graded effect sizes reported herein may fall into a single interpretive category, blurring the potential interaction. Still, it must be recognized that even the smallest effect size differences between treatments can have significant real-world consequences for the functional outcome of children with PD, thereby highlighting a distinction between experimentally and clinically significant gains in expressive phonology (Bain & Dollaghan, 1991).

Nevertheless, future studies may be interested in the contributions of nonwords and lexical islands to the expressive phonology for independent reasons. For nonwords, it will be important to disentangle the effects of novelty from those of statistical regularity (Saffran & Thiessen, 2003) and to further disentangle novelty in phonological form from novelty in meaning (Gierut et al., 2010). To our knowledge, there have been no evaluations of lexical islands in treatment and thus their effect on the expressive phonology remains unknown.

CONCLUSION

This study capitalized on Stoel-Gammon’s (2011) observation that regularities in word-level variables affect children’s acquisition of expressive phonology. The approach adopted was novel in its inclusion of children with PD, experimental manipulation of treatment to induce change in the expressive phonology, and orthogonal variation of density and frequency. Results showed that children with PD made the greatest gains in expressive phonology following treatment of frequent words from dense neighborhoods. This finding aligned with typical phonological development, but stood apart from prior studies of PD that found a sparse neighborhood advantage. Differences were reconciled by considering the effects of multiple converging cues on phonological generalization, with the hypothesis that children with PD might warrant greater than usual cue redundancy to extract sublexical information. The findings also documented the most-to-least influential cues for growth of the expressive phonology and an asymmetry between triggers and targets of phonological learning as exemplified by the process of lexical diffusion. New directions for research were offered to further tease apart the complexities of statistical regularities relative to expressive phonology, with emphasis on the concurrent manipulation of more than one variable. Through continued work, it should be possible to delineate how lexical and sublexical structure contributes to phonological learning in particular, and language learning in general, by garnering complementary evidence from expression and reception.

APPENDIX

Dense
Frequent		Infrequent
same	race	fairy	rake
saw	reach	fan	rat
serve	real	fast	reef
set	red	fence	rich
side	rest	fist	rope
size	right	foal	round
soon	road	fog	rug
sound	role	funny	rush
Sparse
Frequent		Infrequent
family	labor	launch	circus
field	language	lazy	saddle
figure	level	lemon	sailor
final	little	lens	siren
first	living	lion	soccer
foreign	local	lizard	sofa
forward	longer	llama	soldier
further	lost	lumber	supper