Impact of diagnostic misclassification on estimation of genetic correlations using genome-wide genotypes

Abstract

Disorders that share genetic risk factors often are placed in closely related diagnostic categories and treated similarly. Until recently, evidence for shared genetic etiology derived from classical research strategies – coaggregation in family and twin studies. Accumulating sufficient numbers of families was often problematic. However, in the era of genome-wide genotyping, we can now directly estimate the degree of sharing of genetic risk factors between disorders. This strategy is practical even for very rare disorders, where it is infeasible to ascertain informative families. Importantly, the estimates of genetic correlations from genome-wide genotypes are derived using such distant relatives that contamination by shared environmental factors seems unlikely. However, any method that seeks to quantify the shared etiology of disorders assumes they can be distinguished diagnostically from one another without error. Here we investigate the impact of misdiagnosis on estimates of genetic correlation both from traditional family data and from genome-wide genotypes of case–control samples from unrelated individuals. Our analyses show similar results for levels of misdiagnosis in both types of data. In both scenarios, genetic variances and heritabilities tend to be slightly underestimated but genetic correlations are overestimated, sometimes substantially so. For example, two genetically distinct but equally heritable disorders each with prevalence 1%, can generate false-positive estimates of genetic correlations of >0.2 in the presence of 10% reciprocal misdiagnosis. Strategies for minimizing the effects of misdiagnosis in cross-disorder genetic studies are discussed.

Introduction

Medical nosologies often seek to make their classifications based on an understanding of the etiological relationship between disorders. That is, as we classify syndromes into disorders and diseases and place them into individual diagnostic categories, a recurrent question is the degree of etiological overlap between them. Because of the consistent importance of familial/genetic factors, traditional genetic strategies, including family and twin studies, have often been used to examine this question, for example,¹ in twin and family studies, the approach utilized has been an examination of familial coaggregation – the tendency for disorder A to occur in excess in the relatives of probands with disorder B and vice versa. Such data can be used to estimate the genetic correlation between the two disorders. Evidence that two disorders strongly co-aggregate in families and/or have a high genetic correlation would then suggest that they are closely etiologically related and should be classified within a single super-ordinate category or even as subtypes of one disorder.

However, such an approach assumes that the disorders can be distinguished diagnostically from one another without error. For many biomedical disorders, this assumption may not be true. For example, a recent careful 10-year longitudinal study of 450 first admissions with psychosis based on research interviews showed that over the 10-year period, 15% of subjects initially diagnosed with bipolar disorder were re-diagnosed with schizophrenia, whereas 4% of schizophrenia diagnoses were re-classified as bipolar disorder.² In a much larger sample, using the hospital records from the Danish Psychiatric Central Register of all psychiatric inpatient admissions in Denmark between 1970 and 2006, the diagnostic course of all 18 820 first-time admissions with either schizophrenia, bipolar disorder or schizoaffective disorder was examined.³ This study produced results broadly similar to the smaller study in that for first-time admissions for bipolar disorder (n=3801) and schizophrenia (n=12 141), 15% and 6%, respectively, had later admissions of one or more of the other disorders (including schizoaffective disorder).

The genomics era now provides us with new opportunities to explore the shared genetic etiology between disorders. Genome-wide association studies (GWAS) measure genetic polymorphisms (eg, single nucleotide polymorphisms, SNPs) at several hundred thousand positions in the genome. New methods show how these data can be used to estimate the proportion of variation in liability to disease that is associated with SNPs,⁴ and these estimates represent a lower limit of the heritability. These methods use very distant relationships between individuals, so estimates are unlikely to be confounded with common environmental effects, which can be difficult to disentangle from the genetic component of familiality in family studies. The methodology can be extended to estimation of the genetic correlation between different disorders that is tagged by SNPs. Evidence for a genetic correlation between disorders estimated directly by interrogation of the genome could have an important impact on the design of future genetic and functional studies.

Over 20 years ago, one of us (KSK) developed a model to predict the observed pattern of familial co-aggregation between two disorders that would be expected solely on diagnostic mis-classification.⁵ We extend this earlier work in two ways to understand how estimates of genetic correlation derived from GWAS data may be influenced by diagnostic misclassification. Firstly, Kendler⁵ showed the impact of diagnostic misclassification on recurrence risks to relatives, but did not quantify the impact on the estimates of genetic parameters because to do this requires a critical assumption that common environment does not impact on familiality. Here, we accept that critical assumption (which for some disorders can be justified) and quantify the impact of diagnostic misclassification on estimates of the genetic parameters of heritability and genetic correlation calculated from family studies, considering scenarios where the true genetic parameters take on a range of values including a non-zero genetic correlation. Quantifying the impact of misdiagnosis on genetic parameters from family data provides important benchmarking for our second approach in which we consider the impact of misclassification on the estimation of genetic variance and covariance parameters estimable from genome-wide SNP data.

Methods

Estimation of genetic parameters from family data

Following Kendler,⁵ we consider two disorders A and B whose genetic epidemiology can be defined by 6 parameters K_TA, K_TB, λ_TA, λ_TB, M_TA, M_TB and r_gT: where K_TA, K_TB are the lifetime risks of the disorders, λ_TA and λ_TB are the recurrence risks to first-degree relatives of having the same disorder, M_TA is the misclassification rate of disorder A as disorder B and M_TB is the misclassification rate of disorder A as disorder B. r_gT is the genetic correlation between the disorders (note in Kendler⁵ this was always zero and so was not specifically considered). We use the subscript T to emphasize that these parameters refer to the true classification of the disorders.

From these parameters, we can calculate other parameters for the true disorders: the heritabilities of the disorders on the liability scale, h²_TA and h²_TB (see Appendix), under the critical assumption that all familiality represented in the recurrence risk is of additive genetic origin, and the lifetime risk of the disorders in first-degree relatives K_TA/TA, K_TB/TB, K_TA/TB, K_TB/TA. The subscripts refer to true disorder of proband/true disorder of first-degree relative. However, the true disorders are not observed, only the diagnosed disorders are observed; we use the symbol D in the subscript to denote parameters of the diagnosed disorders. We can calculate the lifetime risk of individuals with true disorder A and also diagnosed as having disorder A as

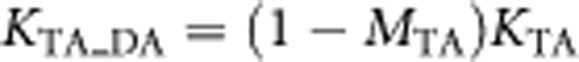and likewise for other combinations.

K_{TA_DB}=M_TA K_TA, K_{TB_DB}=(1−M_TB) K_TB and K_{TB_DA}=M_TB K_TB. From these, we can calculate the lifetime probabilities of being diagnosed with disorder A or B as

The diagnosis misclassification rate, the proportion of those diagnosed as having disorder A, but truly having disorder B, is M_DA=K_{TB_DA}/K_DA, and similarly M_DB=K_{TA_DB}/K_DB.

Genetic parameters estimated from observable data are based on lifetime risks of the diagnosed disorders in probands and their relatives. With real data, these genetic parameters (heritabilities, genetic correlation, common environmental components) are estimated using maximum likelihood techniques, which optimize the information from different types of relatives, and simultaneously account for confounders such as age or sex. However, in the absence of such confounders and with only one type of relative, genetic parameters can be estimated using the classic equations derived by Falconer⁶ and Reich, James and Morris⁷ from the lifetime risks of the diagnosed disorders in probands and their relatives, that is, K_DA and K_DB and K_DA/DA, K_DB/DB, K_DA/DB and K_DB/DA; as before, the diagnosis before the slash (/) is of the proband, and after the slash is of the relatives. Calculation of these lifetime risks depends on the flow of information from diagnosed disorder of the proband, to true disorder of proband, to the true disorder of relative, to the diagnosed disorder of relative. A number of steps are needed to calculate these risks.

Similar expressions, can be derived for K_DB/DB, K_DA/DB and K_DB/DA as shown by Kendler.⁵ From these risks, we can calculate the heritabilities on the liability scale that would be estimated from the observed diagnostic classifications, h²_DA and h²_DB and the genetic correlation between them r_gD (see Appendix). Even in the absence of misdiagnosis, the validity of these estimates depends on the critical assumption that common environment does not have a role in familiality. Comparison of the true genetic parameters and the parameters estimated from the diagnostic classification reflects the impact of the misdiagnosis between disorders.

Estimation of genetic parameters from genome-wide genotypes

Genome-wide genotypes can be used to estimate the proportion of variance in case–control status explained by the genotyped variants.⁴ A linear model can be used to describe the relationship between case–control status and random additive genetic effects

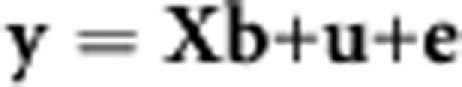where y is a vector of 0,1, where 0 represent controls and 1 cases. b is a vector of fixed effects or covariates (such as sex or ancestry principal components), X is an incidence matrix linking cases/controls to the fixed effects appropriate to them. u is a vector of additive genetic effects on the 0, 1 disease scale and e is a vector of random error terms. The variance of y is V(y)=Aσ_u²+Iσ_e², where σ_u² and σ_e² are the variances of the genetic and error effects, I is the identity matrix and A is a matrix of additive genetic similarity⁸ relationships calculated from genome-wide genotypes so that element i,j of A is the additive genetic relationship between individual i and individual j, and the cases and controls have been selected so that the coefficient of relationship between any pair is small so that individuals are unrelated in the classical sense. The variances are estimated by (restricted) maximum likelihood and the ratio of estimates σ_u²/(σ_u²+σ_e²) is the proportion of variance in case–control status explained by the genome-wide genotypes and so is heritability on this scale. In the absence of fixed effects other than the mean, σ_u²+σ_e²=P(1−P), the binomial variance of case–control status, where P is the proportion of cases in the sample. Bivariate models can be applied to case and control sets from two different disorders (A and B), estimating the additive genetic variances accounted for by the genotypes σ_uA² and σ_uB², the additive genetic covariance between σ_uA,_uB and the genetic correlation can be calculated as σ_uA,uB/(σ_uAσ_uB).

Our interest is on the impact of misdiagnosis of cases on the estimated genetic parameters. As before, we use the subscripts TA and TB to refer to parameters of the true disorders A and B, and subscripts DA and DB to denote the parameters of the diagnosed disorders. If we assume that the numbers of cases and controls for true disorder A are N_caseTA and N_controlA, and similarly for disorder B there are N_caseTB cases and N_controlB controls. As before, M_TA is the proportion of true A cases that are misdiagnosed as having disorder B and M_TB is the proportion of true B cases that are misdiagnosed as having disorder A. We can calculate the number of cases that have diagnosis A or B,

We can calculate the genetic variance and covariances that will be attributed to the diagnosed disorders as a function of the variances and covariances of the true disorders. The proportional allocation of true variance/covariance components to diagnosed variance/covariance components is represented in the schematic in Supplementary Figure 1, so that

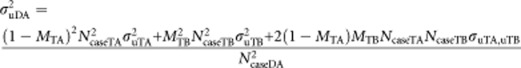The proportions of variance in case–control status explained by the SNPs on the observed scale is then

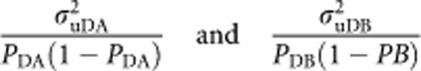where

The genetic correlation estimated for the diagnosed disorders is

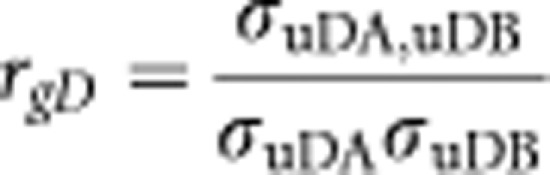Lee et al⁴ provided a post-hoc transformation to convert the estimates on the cases–control observed scale to the population liability scale. We do not need to add this complication here, and in fact the correlation estimates on the observed scale are good estimates of the correlation on the liability scale (unpublished simulation results). We can use these relationships to investigate the impact of misdiagnosis rates on estimates of the proportion of variance explained by SNPs. In real life, we do not know the true diagnosis of individuals, so we demonstrate the validity of these expressions using estimates from real genome-wide data in which misclassification is artificially imposed.

Application to genome-wide genotype data

We checked the validity of our derivations using the genome-wide genotype data from the Wellcome Trust Case Control Consortium (WTCCC)⁹ considering two disorders with (to our knowledge) no excess of familial co-occurrence and hence expected zero genetic correlation between disorders, namely Crohn's disease and type I diabetes. The WTCCC data sets included two control samples. Here we allocate the 1958 birth cohort as the control sample for the Crohn's disease cases and the National Blood Service sample as the control set for type I diabetes. A bivariate analysis of these case–control sets had been undertaken by Lee et al,⁴ Supplementary Table 10) demonstrating a negligible genetic correlation. Since our interest is to investigate the impact of imposed misdiagnosis rates on parameter estimates, we will refer to Crohn's disease as disorder A and type I diabetes as disorder B, in order to emphasize that our estimates result from artificially imposed misclassification between the disorders. Stringent quality control measures were applied to the case–control data; this stringency is necessary as small errors for each SNP can be accumulated to bias estimates of variance explained by SNPs,⁴ but in doing so may remove some real signal. SNPs with minor allele frequencies <0.01 or missing rates >0.001 were excluded as were SNPs, whose P-values were <0.05 for the Hardy–Weinberg equilibrium test and for missingness-difference between cases and controls. A two-locus QC test¹⁰ was also applied to help in identifying artefacts reflecting batch effects. Sex chromosomes were excluded from the analysis. To keep only distantly related individuals, both individuals from a pair with an estimated similarity relationship >0.05 were excluded (which excludes relationships approximately closer than second-cousins), considering all pairs of individuals across all case and control sets. After this QC process, there were 1557 cases and 1384 controls for disorder A, and 1675 cases and 1195 controls for disorder B and a total of 155 121 SNPs. We estimated the genetic and environmental variances and covariances in a bivariate model using an average information-REML that directly uses the variance covariance matrix of all observations¹¹ and is suitable for SNP-based covariance structure among unrelated individuals. These estimates are those of the ‘true' disorders. We then repeated the analyses (i) after allocating 10% of disorder A cases as disorder B cases and (ii) after allocating 10% of disorder A cases as disorder B cases and vice versa. We repeated these random allocation 100 times and compared the mean estimates from these ‘diagnosed' disorders to their expectations based on the estimates from the ‘true' disorders.

Results

Estimation of genetic parameters from family data

To investigate the impact of misdiagnosis on estimation of genetic parameters, we consider three examples based on psychiatric disorders presented and justified by Kendler.⁵ These examples focus on real scenarios, while at the same time consider different combinations of the key parameters of the two disorders, namely lifetime risk and recurrence risk to relatives. Kendler⁵ implicitly assumed that the true genetic correlation between disorders was zero, thereby assuming that co-occurrence of disorders within families resulted from misdiagnosis. Here we relax that assumption and also consider scenarios where the true genetic correlation is greater than zero.

Example 1: Schizophrenia (disorder A) and bipolar disorder (disorder B)

We assume that the true lifetime risk of both schizophrenia and bipolar disorder is 1%, that is, K_TA=K_TB=0.01 and recurrence risk to relatives for both disorders of 8.0, that is, λ_TA=λ_TB=8.0. These parameters equate to a heritability of liability of h²_TA=h²_TB=0.76. We consider different combinations of misdiagnosis rates of the true disorders M_TA, M_TB and consider the genetic correlation between the true disorders to be R_gt=0, 0.25, 0.5. Results are presented in Table 1; those for R_gt=0 directly correspond to Table 3 of Kendler.⁵ When there is no misdiagnosis between disorders M_TA=M_TB=0, the genetic parameters estimated from the diagnosed disorders are the same as the true genetic parameters, as expected. When the misdiagnosis rate is balanced, that is, M_TA=M_TB≠0 then the lifetime risk of the diagnosed disorders are the same as the lifetime risk of the true disorders, but as expected this breaks down when the misdiagnosis rate between the disorders is unbalanced. As the misdiagnosis rates increase, the estimates of the heritabilities based on the diagnosed disorders decrease and the estimates of the genetic correlation increase. As noted by Kendler,⁵ misdiagnosis has a more important impact on the recurrence risks associated with the co-occurrence of disorders within families than on the recurrence risks for the same disorder. Hence, misdiagnosis has a greater impact on the estimates of genetic correlation than on estimates of heritabilities. For example, a 10% misdiagnosis rate of true bipolar disorder being diagnosed as schizophrenia would result in estimates of heritabilities of 0.71 and 0.74, respectively, for schizophrenia and bipolar disorder compared with the true values of 0.76, but would generate an estimate of the genetic correlation as 0.20 when the true value is zero. As might be expected, the impact of misdiagnosis on estimates of genetic parameters from diagnosed disorders compared with the genetic parameters for the true disorders decreases as the true genetic correlation increases. Our methods allow us also to consider estimates of genetic parameters estimated from diagnoses of second-degree relatives. Misclassification between diagnoses generates lower estimates of heritabilities and genetic correlations from recurrence risks of second-degree relatives than those estimated from first-degree relatives (results not shown). In real-life, sampling errors on recurrence risks to relatives are usually high, and so it is unlikely that examination of inconsistency of estimates based on recurrence risks from first- and second-degree relatives would be conclusive.

Table 1. Impact of misclassification between schizophrenia (disorder A) and bipolar disorder (disorder B) on estimation of genetic parameters from recurrence risks in first-degree relatives.

				rgT=0			rgT=0.25			rgT=0.5
MTA	MTB	KDA	KD	h2DA	h2DB	rgD	h2DA	h2DB	rgD	h2DA	h2DB	rgD
0	0	1.00	1.00	76	76	0	76	76	25	76	76	50
5	5	1.00	1.00	72	72	21	73	73	39	74	74	59
10	10	1.00	1.00	68	68	37	69	69	51	71	71	67
15	15	1.00	1.00	65	65	50	66	66	61	69	69	74
20	20	1.00	1.00	62	62	62	64	64	70	67	67	80
30	30	1.00	1.00	56	56	82	59	59	86	63	63	91
40	40	1.00	1.00	52	52	95	56	56	96	61	61	98
50	50	1.00	1.00	51	51	100	55	55	100	60	60	100
0	5	1.05	0.95	74	75	11	74	75	32	75	75	54
0	10	1.10	0.90	71	74	20	72	74	38	74	74	58
0	15	1.15	0.85	69	73	28	71	73	44	73	73	62
0	20	1.20	0.80	67	71	34	69	71	48	72	71	65
0	30	1.30	0.70	65	69	45	67	69	57	71	69	70

Parameters follow those used in Table 3 of Kendler.⁵ All values are expressed as percentages. The true disease prevalences are assumed to be 1% for both schizophrenia and bipolar disorder, K_TA=K_TB=1%. True recurrence risks to first-degree relatives are λ_TA=λ_TB=8.0. These parameters equate to true heritabilities on the liability scale of h_TA²=h_TB²=0.76. M_TA is the proportion of true schizophrenia cases misclassified as bipolar disorder and M_TB is the proportion of true bipolar disorder cases misclassified as schizophrenia. The true genetic correlation between the disorders is r_gT=0, 0.25,0.5. The estimated parameters based on diagnosed prevalences and recurrences risks have subscript D.

Example 2: Schizophrenia (disorder A) and brief psychotic disorder (disorder B)

We consider two disorders of approximately equal lifetime risk, K_TA=K_TB,=0.01, but quite different evidence of familiality so that λ_TA,= 8.0, λ_TB=2.0. These parameters equate to a heritability of liability of h²_TA=0.76 and h²_TB=0.21. We consider different combinations of misdiagnosis rates of the true disorders M_TA, M_TB and consider genetic correlation between the true disorders to be R_gT=0, 0.25, 0.5. Results are presented in Table 2; when R_gT=0 the scenarios correspond to Table 5 of Kendler.⁵ Misclassification of diagnosis has less impact on the estimate of heritability for brief psychotic disorder, because the absolute values are lower, but still generates non-negligible inflation of the estimates of the genetic correlations.

Table 2. Impact of misclassification between schizophrenia (disorder A) and brief psychotic disorder (disorder B) on estimation of genetic parameters from recurrence risks in first-degree relatives.

				rgT=0			rgT=0.25			rgT=0.5
MTA	MTB	KDA	KD	h2DA	h2DB	rgD	h2DA	h2DB	rgD	h2DA	h2DB	rgD
0	0	1.00	1.00	76	21	0	76	21	25	76	21	50
5	5	1.00	1.00	72	20	25	72	21	44	73	21	63
10	10	1.00	1.00	68	19	45	69	20	59	69	22	73
15	15	1.00	1.00	64	19	62	65	21	72	66	23	82
20	20	1.00	1.00	60	20	75	61	22	81	62	25	88
30	30	1.00	1.00	51	23	91	53	26	93	55	29	96
0	5	1.05	0.95	73	21	3	74	21	27	74	21	51
0	10	1.10	0.90	71	21	6	71	21	29	72	21	52
0	15	1.15	0.85	68	20	9	69	20	31	70	20	54
0	20	1.20	0.80	66	20	12	67	20	33	68	20	55
0	30	1.30	0.70	62	19	17	63	19	37	65	19	57
5	0	0.95	1.05	75	20	22	75	21	41	75	22	61
10	0	0.90	1.10	74	20	38	74	21	54	74	22	70
15	0	0.85	1.15	73	20	52	73	22	64	73	24	77
20	0	0.80	1.20	71	20	63	71	22	72	71	25	82
30	0	0.70	1.30	69	22	77	69	25	83	69	28	89

Parameters for the disorders follow those used in Table 5 of Kendler.⁵ All values are expressed as percentages. The true disease prevalences are assumed to be 1% for both schizophrenia and brief psychotic disorder, K_TA=K_TB=1%. True recurrence risks to first-degree relatives are λ_TA,=8.0, λ_TB=2.0. These parameters equate to true heritabilities on the liability scale of h²_TA=0.76 and h²_TB=0.21. M_TA is the proportion of true schizophrenia cases misclassified as brief psychotic disorder and M_TB is the proportion of true brief psychotic disorder cases misclassified as schizophrenia. The true genetic correlation between the disorders is r_gT=0, 0.25,0.5. The estimated parameters based on diagnosed prevalences and recurrences risks have subscript D.

Example 3: Schizophrenia (disorder A) and delusional disorder (disorder B)

We consider two disorders that differ 10-fold in lifetime risk, K_TA=0.01 and K_TB=0.001, and also differ in evidence of familiality so that λ_TA,=8.0, λ_TB=2.0. These parameters equate to a heritability of liability of h²_TA=0.76 and h²_TB=0.13. We consider different combinations of misdiagnosis rates of the true disorders M_TA, M_TB and consider genetic correlation between the true disorders to be r_gT=0, 0.25, 0.5. Results are presented in Table 3, and when r_gT=0 the scenarios correspond to Table 6 of Kendler.⁵ Misclassification of diagnosis has very little impact on the estimates of heritability for either disorder. However, misdiagnosis of the more common disorder (schizophrenia) to the less common disorder of only 1% generates an estimated genetic correlation of 0.39. Misdiagnosis from the less common disorder to the more common disorder has a negligible impact on the estimates of the genetic correlation.

Table 3. Impact of misclassification between schizophrenia (disorder A)and delusional disorder (disorder B) on estimation of genetic parameters from recurrence risks in first-degree relatives.

				rgT=0			rgT=0.25			rgT=0.5
MTA	MTB	KDA	KD	h2DA	h2DB	rgD	h2DA	h2DB	rgD	h2DA	h2DB	rgD
0	0	1.00	0.10	76	13	0	76	13	25	76	13	50
1	1	0.99	0.11	76	12	39	76	13	54	76	14	70
2	2	0.98	0.12	76	12	63	76	13	72	76	15	82
3	3	0.97	0.13	75	13	77	75	15	83	75	16	89
5	5	0.96	0.15	75	16	91	75	18	93	75	20	95
1	10	1.00	0.10	75	12	42	76	12	57	76	13	72
2	20	1.00	0.10	75	12	71	75	13	78	75	15	85
3	30	1.00	0.10	74	14	87	74	16	90	74	18	93
0	10	1.01	0.09	76	13	1	76	13	25	76	13	50
0	20	1.02	0.08	75	12	1	75	12	26	75	12	51
0	50	1.05	0.05	73	12	3	74	12	27	74	12	51
1	0	0.99	0.11	76	12	39	76	13	54	76	14	70
2	0	0.98	0.12	76	12	62	76	13	72	76	15	81
5	0	0.95	0.15	75	16	90	75	18	92	75	20	94

Parameters follow those used in Table 6 of Kendler.⁵ All values are expressed as percentages. The true disease prevalences are assumed to be 1% for schizophrenia and 0.1% delusional disorder, K_TA=1% and K_TB=0.1%. True recurrence risks to first-degree relatives are λ_TA,= 8.0, λ_TB=2.0. These parameters equate to true heritabilities on the liability scale of h²_TA=0.76 and h²_TB=0.13. M_TA is the proportion of true schizophrenia cases misclassified as delusional disorder and M_TB is the proportion of true delusional disorder cases misclassified as schizophrenia. The true genetic correlation between the disorders is r_gT=0, 0.25,0.5. The estimated parameters based on diagnosed prevalences and recurrences risks have subscript D.

Estimation of genetic parameters from genome-wide genotypes

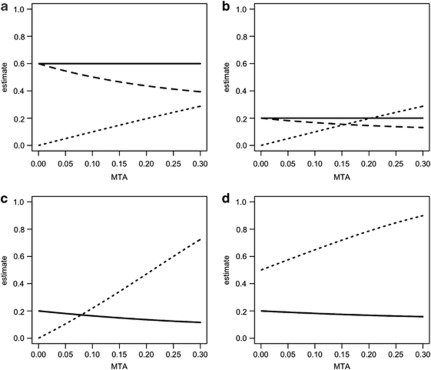
Using the stringently cleaned genome-wide genotypes from the WTCCC, the proportion of variance in case–control status explained by SNPs was 0.391 (SE 0.089) for disorder A and 0.470 (SE 0.093) for disorder B, with a non-significant genetic correlation of 0.023 (SE 0.155). The estimates of proportion of variance explained reported here are lower than (but not significantly different from) those reported in Supplementary Table S10 of Lee et al;⁴ here we applied more stringent QC and included 10 ancestry principle components, thus avoiding artifactual influences, at the expense of the loss of real signal. We use these observed ‘true' parameters to calculate the expected genetic parameters under the two misdiagnosis models. The calculated genetic parameters agreed well with those estimated from the data given for sampling variation (Table 4). Misclassification of a true disorder to the other diagnostic class decreases the estimates of the proportion of variance explained by SNPs even though the total variance in case–control status is little changed, P_T(1−P_T) vs P_D(1−P_D). Misclassification of diagnoses can generate a substantial genetic correlation between the diagnosed disorders when the true genetic correlation is zero. We considered a range of values for the true variances and covariances explained by SNPs and a range of values for the misclassification rates and used the derived equations to examine the impact on the parameters that would be estimated from the diagnosed disorders. The conclusions drawn from these examples paralleled the conclusions drawn when estimating genetic parameters from family data. For example, in Figure 1 we compare four scenarios in which we assume that the true number of cases and controls for each disorder are equal. In Figure 1a, 60% of the variance in true case–control status is explained by genome-wide SNPs for both disorders, disorder A can be misdiagnosed as disorder B but not vice versa; the true genetic correlation between disorders is zero. The estimate of the proportion of variance explained for trait A is not affected by the misdiagnosis, because all diagnosed A cases are truly A. In contrast, the estimate of the variance explained by SNPs for disorder B decreases with an increasing contamination of diagnosis by disorder A cases. For example, for a 10% misdiagnosis rate, the estimate of variance explained by SNPs decreases from 0.60 to 0.50 and this is accompanied by an estimate of the genetic correlation of 0.10. Figure 1b repeats the analysis but now considers two disorders with a lower genetic contribution to their etiology so that only 0.2 of the variance in true case–control status is explained by SNPs. In this case, the reduction in variance explained by SNPs for disorder B under 10% misdiagnosis from disorder A is small (from 0.20 to 0.17), but this is still accompanied by the same inflated estimate of the genetic correlation of 0.10. Figure 1c repeats Figure 1b, but includes reciprocal misdiagnosis between the two disorders. Now the variance explained by SNPs is biased downwards a little for both disorders (from 0.20 to 0.16, when the misdiagnosis rates are 10%), but the impact on the genetic correlation is more pronounced (estimated to be 0.22 when M_TA=M_TB=0.1). Figure 1d repeats Figure 1c except that now the true genetic correlation between the disorders is 0.5. Now we see that the impact of misdiagnosis is less pronounced: the estimates of variance explained by SNPs are less biased (0.18) and the estimated genetic correlation is proportionally less inflated (the slope of the relationship with M_TA is reduced compared with Figure 1c) and the correlation is estimated to be 0.65 at a reciprocal misdiagnosis rate of 10%.

Table 4. The impact of misdiagnosis in estimating genetic parameter from genome-wide genotypes.

							Proportion of variance explained by SNPs
MTA	MTB	‘True' (T) or diagnosed (D) disorders	Estimated from data or calculateda	σuA2	σuB2	σ2uA,uB	Disorder A	Disorder B	rg
0	0	T	Estimated	0.096	0.112	0.002	0.391 (0.089)	0.470 (0.093)	0.023 (0.155)
0.1	0	D	Estimated	0.096	0.092	0.013	0.387 (0.029)	0.393 (0.023)	0.139 (0.055)
		D	Calculated	0.096	0.095	0.010	0.385	0.396	0.109
0.1	0.1	D	Estimated	0.075	0.093	0.024	0.304 (0.034)	0.388 (0.035)	0.296 (0.092)
		D	Calculated	0.079	0.093	0.021	0.316	0.383	0.244

^aCalculated using equations in text based on the estimates from the true disorders and misclassification rates.

M_TA proportion of disorder A cases labelled as disorder B cases; M_TB proportion of disorder B cases labelled as disorder A cases. Values in parentheses are the standard errors for the parameters estimated when M_TA=M_TB=0, but otherwise are the standard deviations over 100 replicates.

Figure 1.

Illustrations of the impact of misdiagnosis rate of true disorder A cases as disorder B (M_TA) on parameters estimated by genome-wide SNPs: Proportion of variance in case–control status explained by SNPs for disorder A (solid line), disorder B (dashed line) and the genetic correlation between disorders A and B explained by SNPs (dotted line). (a) Proportion of variance that can be explained by SNPs for true disorders A and B=0.6, true genetic correlation 0, no misdiagnosis of true disorder B cases as disorder A, M_TB=0. (b) As (a) but proportion of variance that can be explained by SNPs for true disorders A and B=0.2. (c) As (b) but M_TB=M_TA. (d) As (c) but true genetic correlation between disorders is 0.5. Note: the dashed line does not show when the values are the same as for the solid line.

Discussion

The era of genome-wide genotyping will allow direct estimation of a shared genetic etiology between disorders in a more direct and widely available way than has hitherto been possible. Until now evidence for a shared genetic etiology could only be achieved through co-occurrence of disorders in related individuals (ie, in family, twin or adoptee samples). The use of genome-wide genotypes from case–control studies to estimate genetic correlations averts two potential problems associated with estimating genetic correlations from family data. First, estimates could be obtained even for very rare disorders where it would be infeasible to collect adequate numbers of co-occurrences within related individuals. Second, the estimates of genetic correlations from genome-wide genotypes are derived using such distant relatives that contamination by shared environmental factors seems unlikely.

The current study was motivated by a desire to understand the impact of misclassification on the estimates of genetic parameters obtained by analysis of genome-wide genotypes. One of the reasons to be concerned about this problem is that the drive to increase sample size to obtain power to detect alleles of small effect has sometimes meant reduced attention and resources given to diagnostic evaluations. Thus, in striving for the samples needed to detect risk alleles for complex disorders we may be increasing the chances of diagnostic misclassifications adding ‘noise' to the system. For example, a case–control study of 5000 cases and 5000 controls has the power equivalent to that of a study of only 3200 cases and 3200 controls, or 64% of the sample size, when 20% of the case sample has been misdiagnosed (assuming no true pleiotropy between the disorders at the risk locus), see online Supplementary information.

Our analyses found that the proportion of variance explained by SNPs is underestimated in the presence of diagnostic misclassification compared with the variance explained by SNPs of the true disorder. However, under most realistic misclassification rates, this underestimation is likely to be modest and well with the sampling error of the estimate. By contrast, misclassification can generate substantial estimates of genetic correlation and the impact is greatest when there is no genetic correlation between the true disorders (Tables 1, 2 and 3, Figure 1). This latter point is obvious if we consider the most extreme example, where the true genetic correlation between the disorders is 1. In this case, the disorders are genetically the same, but environmental or stochastic process generates different phenotypes, then (of course) misclassification has no impact on the estimation of the genetic parameters. To benchmark these results using genotype data, we considered the impact of diagnostic misclassification on the estimation of genetic parameters from family data. To do this, we extended the derivations of Kendler,⁵ who considered the impact of diagnostic misclassification on the recurrence risks to relatives. Our extension makes the crucial assumption that the recurrence risks to relatives reflect only additive genetic rather than common environmental causes of familiality. We show that diagnostic misclassification has similar impact on the genetic parameters estimated from family data as it does from genome-wide genotypes.

We can conclude that variance explained by SNPs for a disorder is a lower limit of the heritability. It is a lower limit, firstly because the SNPs do not represent all of the variance in the genome, but even if they did, diagnostic misclassification will tend to lead to underestimates. In contrast, in the absence of diagnostic misclassification, the genetic correlation between disorders estimated from genome-wide genotypes is an unbiased estimate of the true genetic correlation, if we can assume that the genetic correlation is the same across the risk allele frequency spectrum (as less common and rare risk alleles are under-represented on genome-wide genotyping platforms). However, in the presence of diagnostic misclassification, the estimated genetic correlation will provide an upper bound on the true genetic correlation; only quantification of the misclassification rates can provide some insight into the extent of the upward bias of the genetic correlation. However, substantial reciprocal misdiagnosis rates would be needed for a substantial estimate of the genetic correlation (>0.2) to be achieved when the true genetic correlation is zero.

The conundrum then is how to estimate the magnitude of diagnostic misclassification and determine its biasing effects on observed genetic correlations. For example, it is reasonable to expect that studies which personalize diagnostic assessments using a standardized research protocol would produce lower misclassification rates than those observed using diagnoses recorded for clinical purposes as are typically done in data from national registries. For example, Lichtenstein et al (2007)¹² used the National Swedish records to estimate the heritabilities of schizophrenia and bipolar disorder and the genetic correlation between them. To overcome problems from misclassification the authors undertook additional analyses and individuals required two hospital admissions to qualify as having a disorder. Their estimated genetic correlation between schizophrenia and bipolar disorder was 0.60; misclassification rates of 20% or more would be needed for this to reflect a true null genetic correlation.

Investigators will need to consider methods to reduce a priori misclassification in the design of a study or, alternatively, to detect it post-hoc at the data-analytical stage. For example, for many disorders, clinical manifestations are less specific early in the disease course but become more typical with time. This might suggest that data collection projects exclude subjects in the first several years after first presentation to reduce risk of misclassification. Alternatively, if the hypothesis that diagnostic error rates decline with length of illness is true, then if a genetic correlation was observed between two such disorders that arises in part through misclassification, the correlation should decline if subjects diagnosed early in the course of illness are excluded from analysis. For a number of medical disorders, subjects can present with classical clinical presentations or with mixed features. In psychiatry, the diagnosis of ‘schizo-affective disorder' typically has clinical features both of schizophrenia and mood disorders.¹³ In gastroenterology, non-specific inflammatory bowel disease patients typically have symptoms both of ulcerative colitis and Crohn's disease.¹⁴ Such cases likely have a higher chance of misclassification and their a priori exclusion should reduce the chances of a misclassification-driven genetic correlation. Alternatively, their exclusion at the data analysis stage should reduce the observed genetic correlation.

Limitations

These results should be interpreted in the context of several potential conceptual and/or methodological limitations. First, we do not consider the problem of misdiagnosis between having a disorder and having no disorder at all. The impact of this diagnostic problem should reduce estimates of genetic variance for a disorder and co-variance with a related disorder. Second, we have not considered the realistic scenario that misclassification rates would vary in a systematic way between collection sites in a multicenter collaborative project. Between-site differences might include the average age of the cases, the quality of diagnostic information (eg, with large potential differences between samples ascertained at in- vs out-patient facilities). Third, we have assumed that the joint distribution of the liabilities of the two disorders can be approximately represented by a bivariate normal distribution.

Appendix

The derivations of Falconer⁶ and Reich, James and Morris⁷ show that we can calculate heritability on the liability scale (h²) from the lifetime risk of disease (K) and the recurrence risk to relatives λ_R. Then the lifetime probability of disease in the relatives is K_R=λ_RK. Under the liability threshold model, those with phenotypic liability, Z ∼ N(0,1), greater than the threshold t are diseased such that distribution p(Z > t)=Φ(t)=K and Φ(t_R)=K_R. i is the mean liability of the diseased group in the population, calculated as i=y/K, where y is the height of the normal curve at threshold t. a_R is the coefficient of relationship between the relatives and probands, for example, if relatives are children of probands a_R =0.5.

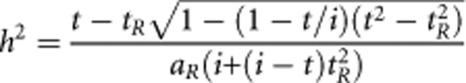Similarly, the genetic correlation between two disorders 1 and 2 is calculated as

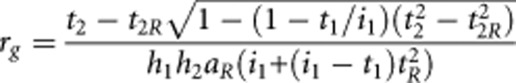where the proband has disorder 1 and the relative has disorder 2. The disorders have lifetime risks of K₁ and K₂ and the lifetime risk of disorder 2 in relatives of disorder 1 probands is K_2R.

The authors declare no conflict of interest.