An evaluation of different meta-analysis approaches in the presence of allelic heterogeneity

Abstract

Meta-analysis has proven a useful tool in genetic association studies. Allelic heterogeneity can arise from ethnic background differences across populations being meta-analyzed (for example, in search of common frequency variants through genome-wide association studies), and through the presence of multiple low frequency and rare associated variants in the same functional unit of interest (for example, within a gene or a regulatory region). The latter challenge will be increasingly relevant in whole-genome and whole-exome sequencing studies investigating association with complex traits. Here, we evaluate the performance of different approaches to meta-analysis in the presence of allelic heterogeneity. We simulate allelic heterogeneity scenarios in three populations and examine the performance of current approaches to the analysis of these data. We show that current approaches can detect only a small fraction of common frequency causal variants. We also find that for low-frequency variants with large effects (odds ratios 2–3), single-point tests have high power, but also high false-positive rates. P-value based meta-analysis of summary results from allele-matching locus-wide tests outperforms collapsing approaches. We conclude that current strategies for the combination of genetic association data in the presence of allelic heterogeneity are insufficiently powered.

Introduction

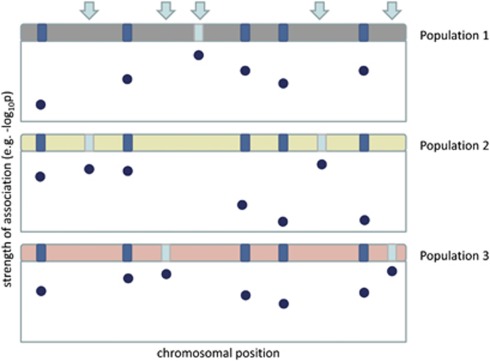
The combination of genetic association studies in a meta-analysis framework can increase power to make novel discoveries. Large-scale meta-analyses across multiple data sets have become the mainstream approach to genome-wide association scans (GWAS). These studies have been successful in identifying common (minor allele frequency (MAF) ≥0.05) genetic variants that underlie a variety of phenotypes and diseases, and have so far mostly focused on similar-ancestry populations, primarily of European descent. As more GWAS across diverse populations of Asian and African ancestry start to accrue, examples of allelic heterogeneity at established common disease loci begin to emerge,^{1, 2, 3, 4} and the need to develop powerful strategies for meta-analyzing genetically different populations becomes prominent.^{5, 6} Although large sample sizes can help guard against false-negative and false-positive results, a major potential caveat is that allelic heterogeneity across populations (Figure 1) could lead to the dramatic dilution of power to detect true positive signals.⁷ In this work, we evaluate the power of existing methods for the meta-analysis of data across populations.

Figure 1.

Schematic overview of allelic heterogeneity in a chromosomal region implicated in disease across three populations. Variants are represented by dark and light blue boxes. Causal variants are population-specific (shown in light blue and indicated by arrows, N=5) and the strongest signal of association is found for a different variant in each population (the y axis describes the strength of association).

Allelic heterogeneity is also poised to be a major concern in whole-genome and whole-exome sequencing studies investigating the association of low-frequency and rare variants with complex traits.^{8, 9, 10, 11} It is expected that multiple different causal variants of low frequency will be found to reside within the same functional units, and that different alleles will be carried by different individuals across studies. Locus-wide approaches to detect association and thus increase power have been proposed, but it is not yet clear whether existing meta-analysis approaches will be useful in combining data across data sets to increase power.

Whether trying to identify common variants of small effect sizes or low-frequency/rare variants with modest effect sizes, large samples are required and those are likely to be achieved by synthesizing data across multiple populations. Here we outline and evaluate different strategies for the meta-analysis of genetic association data in the presence of allelic heterogeneity. Based on simulated data, we provide insights into strategies for analyzing common variant signals across data sets and resequencing studies that aim to identify low-frequency variant associations in the presence of allelic heterogeneity.

Materials and methods

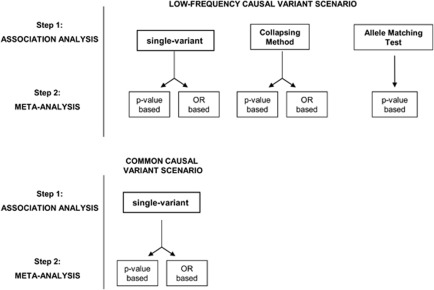
Case–control data across three populations were simulated under two distinct allelic heterogeneity scenarios, (a) common causal variants with small effect sizes (odds ratio (OR) 1. 1–1.2) and (b) low-frequency causal variants with larger effect sizes (OR 2–3; Table 1). For each replicate of simulated data, an association analysis was performed in each of the three populations followed by meta-analysis (Figure 2). For each of the two distinct allelic heterogeneity scenarios, we simulated 1400 replicates of genotypic and phenotypic data for a case–control study of 2000 cases and 2000 controls, for three different populations. To mimic allelic heterogeneity, populations were set to have different causal variants associated with disease. Causal alleles were set to be population-specific, that is, they were not present in the other two populations. When we repeated the simulations allowing causal variants to be present, but not associated with the phenotype, in all three populations, our results remained the same qualitatively (data not shown). All replicates where there was a shared causal allele among populations were excluded from the meta-analysis, yielding 1025 replicates for the common variant scenario and 1163 replicates for the low-frequency scenario. In population 1, there is one causal variant, whereas populations 2 and 3 each have two causal variants that are not in strong linkage disequilibrium (LD) with one another. For each scenario, the frequency and OR of the causal alleles are provided in Table 1.

Table 1. Allele frequency and OR of the simulated common frequency (MAF ≥0.05) and low-frequency (MAF <0.05) causal variants per population.

	Common variant allele frequency	OR	Rare variant allele frequency	OR
Population 1	0.30	1.10	0.04	2.0
Population 2	0.15	1.15	0.01	2.0
	0.20	1.15	0.01	2.5
Population 3	0.40	1.10	0.02	2.0
	0.15	1.20	0.01	3.0

Abbreviations: MAF, minor allele frequency; OR, odds ratio.

Figure 2.

Flowchart providing an overview of the analyses carried out.

Genotypic data were simulated using the hapsim R package and were based on pilot study data from the 1000 Genomes Project¹² (August 2009 Release, 68 CEU samples) for an arbitrary 150 kb region from chromosome 1 with a genome-average recombination rate of approximately 1 Mb/cM. We filtered out variants with quality scores below 10, which resulted in a region consisting of 110 variants. First, a population of 40 000 haplotypes was simulated such that the allele frequencies and pair-wise LD mimic those of the specified region from the 1000 Genomes Project data.¹³ This approach produces realistic resequencing data that include variants with MAFs below 0.01; in our region there were variants with MAF as low as 0.0079. The causal allele(s) were chosen randomly from among those with a MAF near the setting for the simulation, and when there were two causal alleles the choice for the second allele was restricted such that it was not in strong LD with the first causal variant (r² <0.4). Individuals were formed by randomly pairing the haplotypes from the haplotype population.

Case–control status was generated by using a multiplicative model for the genotype relative risks (RRs) to compute the probability of disease given the genotype at the causal variant and its RR.¹⁴ This probability was then used to generate a Bernoulli random variable that ascertains an individual as a case when its value is 1, and a control otherwise. For this reason, it was necessary to oversample (say, 5N) the number of individuals N to ensure that the desired number of cases was attained.

The association study was performed for each population separately, using three different approaches: (a) classical single-variant analysis for each variant in the region, (b) a collapsing method¹¹ and (c) an allele-matching association test¹⁴ For the single-variant analysis a χ²-test of association was carried out at each variant, resulting in a P-value and OR for independent association of each variant to phenotype. The latter two methods were locus-based tests, so that only a single test was performed. There are various versions of the collapsing method, and all combine information across multiple variant sites into a univariate test for disease association with an accumulation of rare variants.^{11, 15} In the version we considered, phenotype is modeled as a function of the indicator variable of rare variants that carry at least one minor allele:

where Y_i is the case–control status for individual i, r_i denotes the number of rare variants that carry at least one copy of the minor allele, I(r_i)=1{ r_i > 0 } is the indicator variable for the presence of at least one minor allele at any rare variant for subject i, and β is the expected increase when an individual carries at least one minor allele at any rare variant compared with one that has a complete absence of rare minor alleles. Analysis of deviance is used to compare the maximized likelihoods of the null (β=0) and unconstrained β models in the construction of likelihood ratio tests of disease association for an accumulation of rare variants.

The allele-matching association test considered is the kernel-based association test (KBAT),¹⁴ which tests for a joint association of multiple variants (correlated or independent) with a categorical phenotype, without any assumptions on the directions of individual variant effects. First, similarity scores y_l(ij) between individuals i and j in group l (eg, 1=cases, 2=controls) are determined by using a kernel, such as the Allele Match kernel, which is the count of shared alleles between the genotypes of two individuals. Let g_i be the genotype score at a specific variant, which is conveniently defined as the number of reference alleles at the variant, as knowledge of the risk allele is irrelevant. At a given variant, for individuals i≠j in group l with respective genotypes g_l(i) and g_l(j), the similarity score y_l(ij) takes on values 4 (identical genotypes), 2 (one homozygous, other heterozygous) and 0 (otherwise). By defining the kernel in this way, there is no need to have knowledge of the risk allele at each variant. The similarity scores y_l(ij) between individuals i and j in group l are modeled using a one-way ANOVA model at each variant:

Where μ is the general effect for pairs of individuals, α_l is the group-specific treatment effect, and to test for disease association the null hypothesis is H₀:α₁=α₂. The single-variant test statistic at marker k is the ratio of the between group sum of squares SSB_k and the within group sum of squares SSW_k, and the K-marker KBAT test statistic is

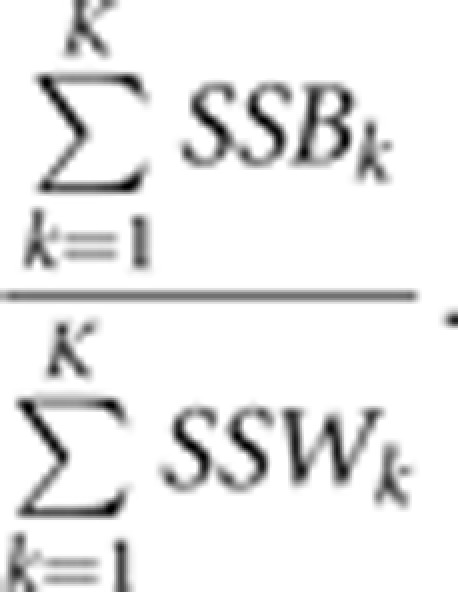Clearly the similarity scores y_l(ij) are not independent normal random variables, so that neither the single-variant test statistics nor the KBAT test statistic may be approximated by an F-distribution. Thus, permutation is required to obtain the P-value for each locus. For comparison purposes with the collapsing method, we only include variants with MAF <0.05 in the KBAT.

After completing the association analyses, sets of results were obtained for each of the three analyzed populations: 110 single-variant P-values and corresponding ORs, one for each tested variant; collapsing method P-value and OR; and KBAT P-value (and test-statistic, but no OR). We then carried out a meta-analysis across the three populations using two different approaches: (i) OR based (fixed and random effects) and (ii) P-value based (Fisher's product method). Methods of fixed effect meta-analysis are based on the mathematical assumption that every study in the meta-analysis shares a common (or ‘fixed') true effect size, and differences in the observed effect sizes are only due to the random error within in each study. Under this assumption, if every study were infinitely large, the results of every study would be identical. This is the same as assuming there is no heterogeneity among the studies. A random effects meta-analysis makes the assumption that individual studies are sampled from populations that may have similar, but not identical, true effect sizes. Differences in observed effect sizes arise from random error as in fixed effects, as well as true variation in effect size. Conclusions arising from the random effects analysis could be generalized to a range of populations, whereas those from the fixed effects are restricted to populations that are identical to those used in the analysis. Both approaches are of interest in testing whether sufficiently strong effects in a single population could still emerge as signals upon meta-analysis. Because of the unavailability of an OR from the KBAT, we only applied a P-value-based meta-analysis for this method. We used a combination of in-house scripts and the software GWAMA¹⁶ to conduct meta-analyses.

In each replicate, there were five causal loci. For the single-point method, we report identified loci as the proportion of replicates that detect association with at least one causal variant. For the collapsing and allele-matching methods, a nominal significance threshold was kept at 0.05. In single-variant analysis, 110 variant markers were tested and the threshold for variant-specific analysis was set to 0.00045 (0.05/110).

Results

In the setting of common causal variants with small effect sizes, the detection of causal variants or loci was unsatisfactory based on single-variant tests, and power of the meta-analysis approaches to detect at least one causal variant ranged from 5. 5 to 15.7% (Table 2). The P-value-based meta-analysis approach was slightly more successful than the fixed effects OR-based approach (15.7% vs 11.0%), with the random effects OR-based approach performing worst (5.5%). It is noteworthy that the meta-analysis of common variants with small effects in the presence of allelic heterogeneity does not detect association with any of the causal variants in 84.3% of the replicates, even in the appreciable sample size of 6000 cases and 6000 controls. Conversely, none of the replicates identified all five causal variants across the three studied populations (Table 2).

Table 2. Single-point meta-analysis results summary.

Meta-analysis type	Power (%)	False-positive rate (%)	1 Causal variant found	2 Causal variants found	3 Causal variants found	4 Causal variants found	5 Causal variants found
MAF ≥0.05
P-value based	15.71	14.41	12.49	2.54	0.59	0.10	0
OR based (fixed effects)	11.02	15.51	7.02	2.93	0.88	0.20	0
OR based (random effects)	5.46	10.05	3.71	1.46	0.29	0	0
MAF <0.05
P-value based	100	71.97	19.26	42.65	30.78	6.96	0.34
OR based (fixed effects)	98.28	51.76	57.95	31.99	7.14	1.20	0
OR based (random effects)	6.45	13.93	5.76	0.69	0	0	0

Abbreviations: MAF, minor allele frequency; OR, odds ratio.

In the low-frequency causal variant scenario, we found that the meta-analysis of single-point association results had greatest power to detect at least one of the causal alleles, with the P-value meta-analysis having 100% power, followed by the fixed effects of OR-based meta-analysis with 98% power (Table 2). However, these meta-analyses also gave rise to a very high false-positive rate, with the P-value-based and fixed effects OR-based approaches identifying at least one false positive association in 72% and 51.8% of the replicates, respectively. Only 4 out of 1163 replicates correctly detected association at all five causal variants through the P-value-based meta-analysis, whereas none of the replicates achieved this in the OR-based meta-analysis approaches (Table 2).

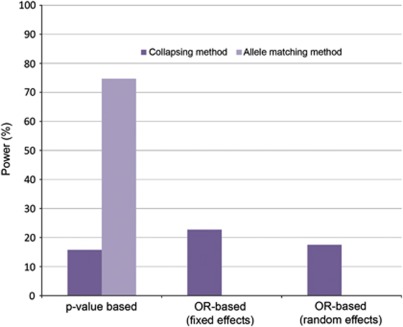
The locus-wide collapsing tests examining low-frequency and rare variants (MAF <0.05) in aggregate demonstrated lower power to detect association. Here, the P-value-based meta-analysis method performed worst with 15.7% power, whereas the OR-based fixed effects approach performed best with 22.7% power. The allele-matching method demonstrated clear power advantages, with 74.7% power to detect association at the locus level, despite the underlying allelic heterogeneity (Figure 3).

Figure 3.

Locus-wide meta-analysis results summary.

Discussion

Our findings demonstrate the low sensitivity of current approaches to detect common causal variants in the presence of allelic heterogeneity when meta-analyzing across genetically heterogeneous populations. The field of statistical genetics is active in developing and testing new approaches to overcome these issues and to enable powerful trans-ethnic mapping.¹⁷

We found the choice of methodological approach to detecting low-frequency variants in the era of whole-exome and whole-genome sequencing to greatly affect association study power. However, the power of individual locus-wide methods critically depends on the allelic architecture of disease. For example, in these simulations there were only one or two low frequency causal variants in each population, and the collapsing method has been designed to perform optimally in the presence of an accumulation of multiple rare variants. Single-point approaches to the meta-analysis of low-frequency variants performed poorly with respect to false-positive rate and, within the power constraints of our study, almost never detected all causal alleles. It appears that given a large enough sample size, allele-matching methods provide good power to detect association at the locus level in the presence of allelic heterogeneity. As the currently sparse set of next-generation sequencing empirical data for complex traits begins to grow, the need for powerful meta-analysis methods that account for heterogeneity increases. The development of such approaches will allow the next set of large-scale meta-analyses to take place, and will therefore pave the way for successful novel locus discovery.

The authors declare no conflict of interest.