Supernovae, an accelerating universe and the cosmological constant

Abstract

Observations of supernova explosions halfway back to the Big Bang give plausible evidence that the expansion of the universe has been accelerating since that epoch, approximately 8 billion years ago and suggest that energy associated with the vacuum itself may be responsible for the acceleration.

For 40 years, astronomers have hoped to measure changes in the expansion rate of the universe as a way to measure the mass density of the universe and the geometry of space and to predict the future of cosmic expansion. In 1998, two groups reported plausible evidence based on supernova explosions that the expansion of the universe is not slowing down, as predicted by the simplest models, but actually accelerating. If these results are confirmed, it will require a major change in our picture for the universe. We will be forced to add another constituent to our best model for the universe, a form of vacuum energy that drives the expansion, which makes the large-scale geometry Euclidean, and which contains most of the energy density in the universe (1). This paper aims to sketch the background to this discovery, to show some of the evidence for cosmic acceleration, and to equip an interested, but skeptical, reader with the right kinds of questions to ask of astrophysical colleagues.

Astronomers have known since Hubble’s observations in 1929 that the universe is expanding (2). This was promptly incorporated into a dynamical picture of the universe based on general relativity, which describes how the presence of matter, or other energy forms in the universe, affect the curvature of space and the expansion of the universe. A decade before the discovery of cosmic expansion, Einstein introduced a “cosmological constant” into his equations, to make the universe static, in accord with the astronomical wisdom of the day. When the astronomical evidence changed, he quickly abandoned the cosmological constant and much later referred to it as his “greatest blunder” (3). Since 1929, it has been the burning ambition of observers of the expanding universe to determine the energy content and the curvature from astronomical measurements. In 1998, we may have achieved that long-sought-after goal.

The observational problem is to discover objects that can be seen at large redshifts, so the cosmological effects are large enough to measure, and that are well enough understood so that their apparent brightness can be trusted to give a reliable measure of their distance. The long, winding path of observational cosmology is littered with the wreckage of past attempts to do this with galaxies, whose properties evolve over time much too rapidly to serve as “standard candles” for this work. But type Ia supernovae (SN Ia) can be seen to redshift 1, and their intrinsic scatter in brightness is small enough so that the cosmological effects on the observed brightness as a function of redshift can be measured. At a redshift of 0.5, the difference in apparent magnitude between a universe that is flat, decelerating, and just barely closed by matter, Ω_m = 1, and a universe that is hyperbolic and empty, Ω_m = 0, is ≈25% in the flux of a supernova. The scatter in SN Ia brightness for a single object, after correcting for the light curve shape (as described below), is only ≈15%, so a relatively small number of supernovae can produce a significant measurement of the cosmology. The result is surprising evidence for an accelerating, but geometrically flat, universe.

The Brightest Supernovae

Supernovae were named and classified by the astrophysicist Fritz Zwicky in the 1930s. They are powerful stellar explosions in which a single star becomes as bright as 10⁹ stars like the sun. The modern taxonomy of supernovae (4) separates them into two types, type I (SN I) and type II (SN II) depending on whether they show hydrogen lines in their spectra at maximum light. A more physical description, based on models for the explosions and circumstantial evidence based on the locations where supernovae of various types are found, attributes the hydrogen-free type Ia supernovae to the thermonuclear detonation of white dwarf stars and the type II (as well as SN Ib and Ic) to the core collapse of massive stars. The SN Ia are thought to leave no stellar remnant while the SN II and their cousins are responsible for the formation of neutron stars and stellar-mass black holes. Despite their very different origins and mechanisms, the intrinsic luminosity of both types is comparable. The combined rates of supernovae are on the order of a few per century in a galaxy like ours. Tycho’s supernova of 1572, in our own Milky Way, was probably a SN Ia, while SN 1987A in the Large Magellanic Cloud was a variant of the SN II class.

For cosmology, the key property that makes SN Ia useful is that they are the brightest class of supernova and have the smallest spread in intrinsic luminosity. Theoretically, a narrow range of luminosities for SN Ia might stem from the upper mass limit for the white dwarfs that explode to form them: 1.4 solar masses is the Chandrasekhar limit for electron degeneracy support of a cold mass of carbon and oxygen that comprises a white dwarf. Though a carbon-oxygen white dwarf at the Chandrasekhar limit is stable, it may explode if a binary companion adds to its mass. When a thermonuclear burning wave destroys such a star, by burning approximately 0.5 solar mass of it to iron-peak elements, the resulting “standard bomb” may make a good beacon to judge cosmic distances.

In the 1960s and 1970s, the measurements of supernova light curves were crude by modern standards because they were made with photographic plates, and it was plausible that all of the observed variation in SN Ia luminosities came from the difficult problem of measuring the supernova light on the background of a distant galaxy with a nonlinear detector (Fig. 1). In that innocent time, imaginative theorists (for example, see refs. 5 and 6) sketched how supernova observations might be used to determine whether the universe was decelerating, as would be expected if gravity’s effect had been accumulating over the time of cosmic expansion, by looking at the redshifts and fluxes for distant supernovae.

Figure 1.

SN 1994D, a nearby supernova imaged with the Hubble Space Telescope.

Search for the ‘Standard Bomb’

The advent of charge-coupled device (CCD) silicon detector arrays made it possible to find supernovae that are far enough away for deceleration to produce a measurable deviation from the inverse square law seen by Hubble. The observational problem was to find these faint and distant supernovae near the peak of their light curves. This challenge was met by a Danish-led group (7) who anticipated most of the techniques used later. They made monthly observations at the Danish 1.5-m telescope in Chile to catch fresh supernova explosions and used a CCD to gather their data and a computer to subtract a reference image from each night’s picture to find the new events. They coordinated follow-up observations to get spectra (to show the events were really SN Ia and to get the redshift) and to measure the light curve of the supernova’s rise and fall. However, in 2 years of searching, because their small telescope was slow to reach faint magnitudes and their CCD had a small field of view, they only snared one good event, SN 1998U, which was a SN Ia at a redshift of 0.3, and then retired from the field.

The widespread application of CCDs and a diligent attention to studying all of the bright supernovae soon made it clear that there were real differences in intrinsic brightness among SN Ia. In 1991 alone, the observed range in brightness, from SN 1991bg to SN 1991T, was approximately a factor of 3. Left untreated, this scatter could wreak havoc with attempts to judge cosmic acceleration. Determining the relation between distance and redshift through a standard candle only works well when the distance can be inferred precisely from the flux. While some brave souls forged ahead with further attempts to find distant supernovae by extending the methods of the Danes to bigger, faster telescopes and more capable detectors provided at the U.S. National Optical Astronomy Observatories (8), a group of astronomers at the University of Chile’s Cerro Calán observatory and their partners at the Cerro Tololo Interamerican Observatory (CTIO) began the Calán/Tololo supernova search (9) to strengthen our understanding of SN Ia as distance indicators.

Although the Calán/Tololo search was carried out photographically, this was very effective in searching wide areas of the sky for nearby supernovae. Because the astronomers could be certain that each month’s search would have a good probability of turning up one or more SN Ia, they were able to schedule follow-up observations with the CTIO telescopes to obtain good CCD observations of their discoveries. Following the clues derived earlier from a few objects (10), the Calán/Tololo measurements showed that, although there was a real variation in the luminosity of SN Ia, it was closely correlated with the shape of the supernova’s light curve. Intrinsically luminous supernovae rise slowly and decline slowly, while their fainter siblings rise and decline more quickly (11). More SN Ia light curves were added to the database (12, 13) and a more sophisticated way to use all the information in the light curve to estimate the distance, the Multicolor Light Curve Shape method (MLCS), was created (12, 13). As a result of these efforts, the scatter in luminosity for SN Ia was pushed downward from approximately 40% to less than 15%, which makes SN Ia the best standard candles in astronomy and suitable tools for the fine discrimination needed to discriminate one history of the universe from another.

Meanwhile, the Supernova Cosmology Project (SCP) continued to search for high redshift supernovae. By 1997, the SCP had a preliminary result (14). Based on seven supernovae discovered in 1994 and 1995, the Calán/Tololo low redshift sample, and a variant of the luminosity-light curve relation, they concluded that the evidence favored a high matter density universe, Ω_m = 0.88 ± 0.6. They argued that the supernova data at that point placed the strongest constraint on the possible value of the cosmological constant, with their best estimate being Ω_Λ = 0.05.

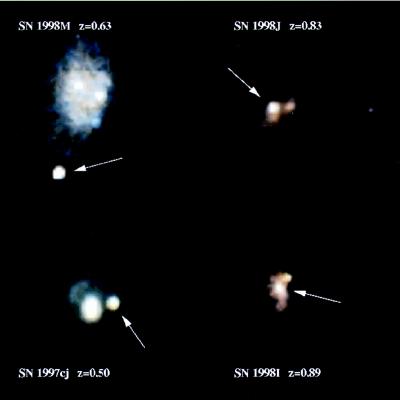
Another group, the High-Z Supernova Team (of which I am a member) introduced a number of new developments, including custom filters, which help minimize the effect of redshift on interpreting the observed fluxes, and ways to use observations in two colors to estimate the absorbing effects of interstellar dust on the supernova light by measuring the reddening it produces. The High-Z team found its first supernova, SN 1995K, in 1995 (15) and now has detected more than 70 events. Fig. 2 illustrates some of the high redshift supernovae discovered by the High-Z Team that have been observed with the Hubble Space Telescope (HST). The supernovae are, in general, found and studied from ground-based observatories, but the HST provides much better separation of the supernova from the background galaxy, which leads to more precise measurements of the supernova’s light curve.

Figure 2.

High redshift supernovae observed with the Hubble Space Telescope.

Cosmic Acceleration

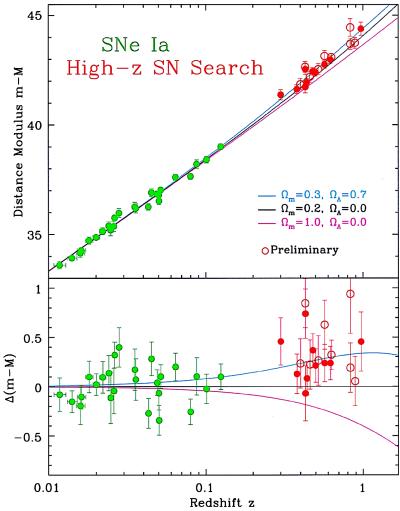
In 1998, both teams reported new results (15–20). As illustrated in Fig. 3, the Hubble diagram for SN Ia now extends to sufficiently high redshift and has enough supernovae with small enough error bars so that the expected effects of cosmic deceleration should be detectable. If the universe had been decelerating—–in the way it would if it contained the closure density of matter, that is, if Ω_m = 1—then the light emitted at redshift z = 0.5 by a SN Ia would not have traveled as far, compared with a situation where the universe had been coasting at a constant rate—characteristic of an empty universe, where Ω_m = 0. For a universe with Ω_m = 1, the flux from the distant supernova therefore would be ≈25% brighter. But the distant supernovae are not brighter than expected in a coasting universe, they are dimmer. For this to happen, the universe must be accelerating while the light from the supernova is in transit to our observatories.

Figure 3.

The Hubble diagram for SN Ia. The lines show the predictions for cosmologies with varying amounts of Ω_m and Ω_Λ. The observed points all lie above the line for a universe with zero Λ. The lower panel, with the slope caused by the inverse square law taken out, shows the difference between the predictions more clearly and shows why a model with Ω_Λ > 0 is favored.

Cosmic acceleration is not a new idea (21) and an energy component to the universe that might have an accelerating effect was proposed by Einstein in 1917. Since then, the cosmological constant has been like a pair of your grandfather’s spats—occasionally tried on for costume events—but these new results suggest that they are not just coming back into fashion, they are now de rigeur.

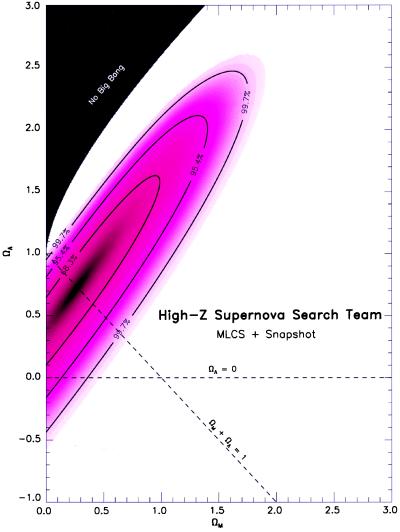
The supernova results define an allowed region in the Ω_m, Ω_Λ plane, as shown in Fig. 4. The constraint is approximately described by Ω_m − Ω_Λ = constant, which gives a surprisingly tight limit on the expansion time, which for a plausible Hubble constant of 65 km sec⁻¹⋅Mpc⁻¹ is 14 ± 1 Gyr. Although a matter-dominated universe with Ω_m = 1 appears to be ruled out by the data, and on the face of it Ω_Λ >0 is favored by the supernova observations, there is still a remote possibility that the present observations can be produced in a universe where the cosmological constant is 0. However, as both teams build up the data and improve their understanding of possible systematic effects, that faint hope for a simpler universe could be snuffed out.

Figure 4.

The Ω_m, Ω_Λ plane. Using the supernova data, a likelihood analysis shows the probability that any chosen pair of Ω_m, Ω_Λ values fits the observations. The allowed region is large and follows the direction of Ω_m − Ω_Λ = a constant. Ω_m = 1 is far from the allowed region. Many pairs of geometrically flat solutions with Ω_m + Ω_Λ = 1 are possible. Ω_Λ = 0 is not very probable in this analysis.

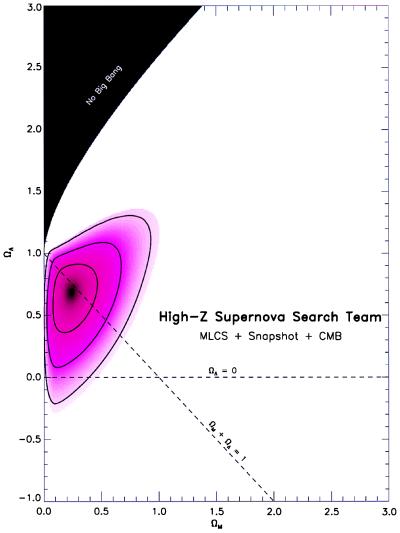
An interesting exercise is to combine the supernova data with measurements of the fluctuations in the cosmic microwave background (CMB). Present-day observations suggest there is a characteristic angular scale to the CMB roughness around the 1^o scale that can be linked through robust theory to the linear scale of fluctuations at the time when the universe became transparent. This translates into a constraint on Ω_m + Ω_Λ, which many theorists have noticed is orthogonal to the supernova constraint. By combining the two types of measurements, it has been shown that the best solution for the High-Z sample (shown in Fig. 5) has Ω_m = 0.3 and Ω_Λ = 0.7 (19). This is a plausible pair of values. The matter density has been estimated by several routes (which have nothing to do with supernovae or the CMB) to be in the vicinity of Ω_m = 0.3, while a universe in which Ω_m + Ω_Λ = 1 gives the universe the geometry of flat space and often is cited as a prediction of the simplest models of inflationary cosmology. The CMB results will continue to improve as the results flow in from a large number of ground- and balloon-based experiments. Decisive results from the Microwave Anisotropy Probe satellite are expected in 2002.

Figure 5.

Ω_m, Ω_Λ plane for the combination of supernova constraints and measurements of the CMB.

Problems with the SN Ruler?

It is still early days in the use of high redshift supernovae for cosmology. Could there be some problem with the use of SN Ia that has not yet come to light? Could there be some other reason, which has nothing to do with cosmology, that makes the objects found at a redshift z = 0.5 approximately 25% fainter than the SN Ia we see nearby? While both teams have tried hard to identify and rule out systematic problems, both are using a slender (and common) database of local supernovae to correct the observed fluxes for the effects of the supernova redshift and spectral details as observed through fixed filters. These “k-corrections” conceivably could produce some problems for particular supernova ages and redshifts, but because the supernovae are sampled over a significant range of redshifts and through a variety of filters, it is hard to see exactly how this technical detail would produce the observed effect. Still, it will be well worth the trouble to gather detailed observations of nearby supernovae as they are discovered to improve our knowledge of supernova spectra.

It is not hard to imagine other possibilities that could lead to problems based on the supernovae themselves: the distant supernovae are explosions that took place 8 billion years ago. They are younger objects than nearby SN Ia. This could affect the properties of the stars that led to SN Ia long ago compared with the present and also could affect the chemical composition of the white dwarfs that explode, both near and far. Because the present-day understanding of SN Ia is incomplete, we don’t know exactly how changes in the stellar population or the composition would affect the luminosity (22). However, the evidence from nearby samples with different star-forming histories, in spiral and elliptical galaxies, is that the light curve shape methods account for the systematic difference between SN Ia in old and young stellar populations.

Even more sinister could be the effects of cosmic dust, which could absorb light from distant supernovae, and lead to their apparent faintness. However the interstellar dust in our own galaxy absorbs more blue light than red, so it leaves a distinct reddening signature that the two-filter observations should detect. The High-Z Team corrects for both the nearby and distant supernovae in the same way by using these color measurements, which should eliminate the effects of interstellar dust from Fig. 3. The Supernova Cosmology Project argues that the dust effect is small and similar in the high and low redshift samples, so no net correction is needed. It is possible to imagine special dust that is not noticed nearby and that has the right size distribution to absorb all wavelengths equally (23). Such “gray dust” would have to be smoothly distributed, because we do not see the increased scatter that patchy dust thick enough to produce the observed dimming, would introduce. If this material exists, there is a powerful test that could discriminate between a cosmology that is dominated by Ω_Λ and one in which specially constructed dust produces the dimming at redshift 0.5. Since a cosmological constant is a constant energy density, while the density of matter has been declining as (1+z)³, by looking back to z = 1, we could observe the era (not so long ago) when matter was the most important constituent of the universe and the universe was decelerating. At those redshifts, the relation between redshift and flux would bend back toward brighter fluxes, while the effects of gray dust presumably would grow, or at least remain constant. To make accurate measurements of this effect will require discovering and making good measurements of redshift 1 supernovae whose light is redshifted into the infrared. The Next Generation Space Telescope may play an important role in this decisive test.

Finally, I note that a constant energy density is not the only possibility. More elaborate physical models in which the energy density changes with time also have been proposed (24), and they can be constrained by using the supernovae and other observations. But in any case, it seems as if supernova observations finally have made it possible to carry out the program outlined by Sandage (25, 26) to determine the acceleration and the geometry of the universe by observing the distances and redshifts of standard candles.