Scaling the universe: Gravitational lenses and the Hubble constant

Abstract

Gravitational lenses, besides being interesting in their own right, have been demonstrated to be suitable as “gravitational standard rulers” for the measurement of the rate of expansion of the Universe (H_o), as well as to constrain the values of the cosmological parameters such as Ω_o and Λ_o that control the evolution of the volume of the Universe with cosmic time.

It is the grand endeavor of astronomy at the close of the 20th century to chart the cosmos, from planets around stars in our own solar neighborhood to the farthest reaches (in both the spatial and temporal sense) of our observable Universe. Just as the radius of our Earth sets the scale for terrestrial distances, the scale for cosmological distances is set by the expansion rate of the scale factor of the Universe, as parameterized by Hubble’s constant H_o. The Hubble constant determines the relationship between the observable Doppler shift seen in the spectra of distant galaxies and quasars and the physical distance to that object (see Box).

One of the key projects in modern astronomy is the quantification of the so-called “distance ladder”, the interlocked set of primary distance measurements to known astronomical objects and calibrated secondary distance measures that can be applied to observations. Ever since the time of Edwin Hubble himself, the determination of the distance ladder, of which the Hubble constant is the ultimate and perhaps most important rung, has been a long-standing goal of observational astronomers. A particularly promising method for measuring the scale of the Universe is provided by naturally occurring gravitational lenses—a chance superposition of a massive galaxy along the line of sight toward a distant astronomical beacon such as a bright galaxy or quasar that gravitationally bends light rays, often forming multiple distinct images of the background object.

Gravitational Lensing

The phenomenon of gravitational lensing is closely related to the gravitational deflection of light rays passing close to a massive body like the Sun. It was realized by Zwicky (1, 2) that distant galaxies would serve as gravitational telescopes for even more distant background galaxies. Although a massive object is not a lens in the traditional sense of bringing parallel rays to a focus, it can form multiple (albeit distorted) images of background objects. Depending on the nature of the source being lensed, one may observe a set of discrete compact images, arcs, or even a complete ring (3).

If the surface mass density of the lensing object is greater than a critical value, then multiple images can be formed of a compact background source of light. Galaxies of sizes and masses comparable to or larger than our own Milky Way galaxy will typically exceed this critical density, and thus may act as lenses. The most common configuration of images is a double, such as the archetypical lens B0957 + 561. Furthermore, deflecting mass distributions with significant ellipticity will enable production of image configurations with more than two components (for example, “quad” lenses such as MG 0414 + 045 and CLASS B1608 + 656; Fig. 1). The time delay between any two images is proportional to H_o⁻¹ (but only weakly dependent on other cosmological factors such as Ω₀ and Ω_tot). Measurement of the time delay can thus yield the Hubble constant. (A cosmological primer is published as supplemental data on the PNAS web site, www.pnas.org.)

The scale of the Universe with respect to current scales is represented by the redshift z, where—due to the Hubble expansion the wavelength λ of the light from a distant object— it appears to us to be stretched to an observed wavelength λ(1 + z), and for moderate redshifts (z ≪ 1), the inferred Hubble (Doppler) velocity is approximately v = c × z/H₀. Thus, the Hubble constant H₀ provides the conversion between recession velocity and distance v = H₀ × r (where H₀ is in units of km⋅s⁻¹⋅Mpc⁻¹). Thus, redshift is the primary cosmological distance indicator. Note that the inverse of Hubble constant has the units of time, and the Hubble time t₀ = H₀⁻¹ gives us a scale for the expansion age of the Universe (best estimates of the current age being ≈9–15 Gyr). There are a number of parameters that go into the cosmological model that relate the distances, redshifts, and times at which that observed phenomena (which are seen by the light they emit or absorb) are seen to occur (for a complete cosmological primer, see refs. 36 and 37). The Hubble constant H₀ is merely a measure of the current expansion rate, and thus a measure of its current rate of change, q0, tells us whether the expansion is accelerating or decelerating. Whether the expansion is accelerating or decelerating depends on the mean density of matter and energy in the Universe, as mutual gravitation (a high density) is fighting against the momentum of the expansion. This is exactly analogous to the relationship between the mass of a body like the Earth or Moon, and the escape velocity from its surface (11 km⋅s⁻¹ for the Earth) such that the orbit of a projectile launched with greater than the escape velocity will be open and the projectile will travel forever, lost from the Earth’s gravity. Likewise, a rapidly expanding Universe (a larger value of H₀) with a lower mass-energy density means that the universal expansion will continue forever. We define the density parameter Ω₀ as the fraction of the mass-energy density in the Universe as a fraction of the critical value that will asymptotically bring the expansion to a halt in the infinite. Furthermore, this Ω can be related to the topology of the Universe, which is determined by Ω_tot, the sum of the mass-energy densities in matter Ω₀ and in any possible cosmological constant Ω_Λ. A popular suite of cosmological models has a globally flat Universe Ω_tot = 1, with a subcritical matter density Ω₀ < 1 and the remainder taken up in vacuum energy Ω_Λ = 1 − Ω₀ > 0. [Technically, this missing energy Ω_tot − Ω₀ could be in the form of matter with an arbitrary equation of state. This has been recently considered in the context of inflationary cosmological models (38)].

Figure 1.

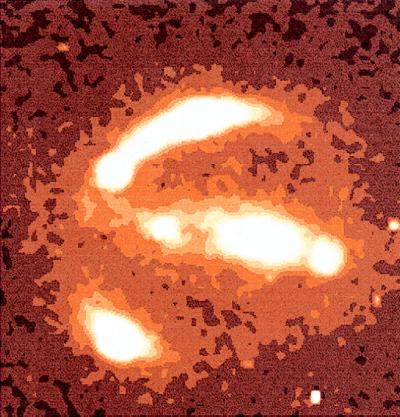
A selection of four VLA radio images of gravitational lens systems from the MG, JVAS, and CLASS surveys. The data was obtained during the CLASS observations, and consists of 30-second “snapshots”, thus demonstrating the superb sensitivity of the Very Large Array. CLASS VLA radio images of (non-CLASS and CLASS) gravitational lenses: Upper Left, B0957 + 561; Upper Right, MG0414 + 055; Lower Left, CLASS B1608 + 656; Lower Right, CLASS B1933 + 507. Images courtesy of CLASS.

Fighting Gravity: Scaling the Distance Ladder

Most methods for calibrating the redshift–distance relation, which is primarily controlled by the Hubble constant at low redshifts, rely on a series of primary and secondary distance indicators (4). Most of the popular methods are yielding H_o in the range 50–70 km⋅s⁻¹⋅Mpc⁻¹ (5). At moderate (z > 0.1) cosmological distances, where the individual galaxy physical velocities (typically a few hundred km⋅s⁻¹) are small compared with the apparent Hubble expansion velocity; only a few distance indicators have been found to be reliable, and then only with a number of assumptions in the calibration. For example, bright type I-a supernovae have been used to measure H_o (6). It has long been recognized that “direct” methods such as gravitational lensing and the Sunyaev-Zeldovich effect, which has measured H_o = 54 ± 14 km⋅s⁻¹⋅Mpc⁻¹ (7), could be used as one-step distance measures and thus provide an independent check on the more traditional methods of finding the Hubble constant.

The possible use of gravitational lenses to determine H_o was the subject of a remarkably prescient 1964 paper by Refsdal (8), and the then-newly discovered quasars suggested as possible targets. Quasar emissions are particularly amenable to gravitational lensing studies. These bright objects can be seen out to large redshifts and nearly always exhibit measurable variations in brightness at both optical and radio wavelengths. The essential features of gravitational lensing as applied to compact emission regions of active galactic nuclei are (i) the formation of multiple images at angular positions determined by the source–lens–observer geometry (including the cosmology) and the mass distribution in the lens; (ii) relative magnifications that are dependent on the geometry and lensing mass but are achromatic; and (iii) path lengths for rays along the image trajectories that are in general different by a predictable delay, which depends on mass and geometry in a different manner than the image positions and magnifications. In principle, observations of the relative delays between variations in the images could be used to solve for the mass distribution and H_o independently.

The task of measuring the optical and radio light-curves is a daunting one. The typical variations in the radio flux density are ≈5% of the total, and thus calibration errors must be controlled to this level or better. The statistical uncertainty in light-curve measurements is not the limiting factor, however, in the determination of H_o for most lens systems. In practice, the mass model itself must be solved for, using some of the constraints provided by the image positions and brightnesses. Furthermore, in many of the known lenses (for example, 0957 + 651, 1608 + 656) a single deflector (even with ellipsoidal mass distributions) does not reproduce the lensing geometry, and thus more complicated models with two or more deflectors are required. These extra parameters translate into fewer free parameters to constrain the time delay, and in the worst cases, leave too few constraints for the measured time delay to constrain H_o separately from the mass. This is evident in the case of B0957 + 561, which has an exquisitely determined time delay (9), but because the lens consists of a galaxy with an associated compact group of galaxies, the limits on H_o depend strongly on the underconstrained mass model.

Gravitational Lens Surveys

Progress in using gravitational lenses to determine H_o will rely on finding a core sample of 10 or so lens systems with relatively simple mass models (that is, single galaxies) and/or with well-constrained lensing potentials (that is, with more than two images or with Einstein rings). For example, in the visible light band, quasars provide ideal background objects for lensing surveys, as they are plentiful (hundreds per square degree on the sky), and they have a steep luminosity function and thus the amplification bias due to gravitational lensing leads to a relatively large probability (≈0.5–1%) of any given bright quasar being lensed. However, there are also significant drawbacks to optical surveys, including dust obscuration and microlensing, as well as the sheer difficulty of identification of the lenses (10). The new generation of CCD-based large optical surveys, such as the Sloan Digital Sky Survey (SDSS) (11), should be able to overcome these problems.

Radio wavelength surveys have proved thus far, in spite of lower lensing rates (≈0.1–0.3%), to be the most effective harvesters of lenses for cosmological studies. The parent samples have been identified from moderate-wavelength (λ = 6 cm) single-dish surveys such as the GB6 catalogue (12), and the workhorse for the imaging survey has been the Very Large Array (VLA), an interferometric array of 27 radio antennas located in New Mexico. The first such VLA survey was the MIT–Green Bank (MG) survey (13). This pioneering survey yielded a number of lens systems, including the first “Einstein ring” where the extended radio emission was imaged into a complete circular ring. The MG survey uses no spectral preselection and thus should yield an accurate accounting for lenses of all configurations, including arcs and rings. However, the morphology of radio galaxies is often complex in appearance and can confuse the identification of that small fraction of lensing-distorted objects. Therefore, the Jodrell–VLA Astrometric Survey (JVAS) (14–16) targeted flat-spectrum radio sources, which were more likely to consist of multiple compact images if lensed. Finally, the Cosmic Lens All-Sky Survey (CLASS) (17), of which the author is a primary investigator, extended the JVAS to fainter radio sources, keeping the spectral selection intact. Over 15,000 radio sources have been observed in the combined JVAS–CLASS sample, with 16 confirmed lenses (as of January 1999). Meanwhile, several smaller-scale radio surveys have begun covering the southern sky.

In the end, both optical and radio monitoring of the lenses prove complementary, allowing a consistency check on the derived lensing parameters.

Current Status of the Field

All of the lens surveys described in the preceding section are ongoing, and new lenses continue to be discovered regularly. However, as of early 1999, there are still relatively few gravitational lens systems that have been monitored for variability and have produced a reasonably robust determination of the Hubble constant.

B0957 + 561.

The first gravitational lens, discovered in 1979, is B0957 + 561 (18). This system has two images of the background quasar separated by 6.1 arc-seconds (Fig. 1, Upper Left), but the lens consists of a galaxy at z = 0.36, and together with a compact group of galaxies (19) makes the mass model complex, and moreover underconstrained by the observations. However, the relatively large image separation means that the time delays are correspondingly large and thus easily determined accurately. Optical measurements have given the most accurate delay of Δt = 417 ± 3 days (95%) (9), which yields a value of H_o = 63 ± 13 km⋅s⁻¹⋅Mpc⁻¹ (95%). However, a recent analysis of the modeling of the galaxy and cluster mass distribution shows a substantially larger dispersion in the allowable values of H_o (20), and thus more observational constraints are needed to narrow the model uncertainties.

B0218 + 357. This gravitational lens system, which was discovered as part of JVAS (14–16), consists of two compact radio components, separated by 0.335 arc-seconds, and an Einstein ring. Recent monitoring with the VLA has yielded a time delay of 10.5 ± 0.4 days, which, when combined with a preliminary lens model, gives H_o = 69 (+13/−19) km⋅s⁻¹⋅Mpc⁻¹ (95%) (21). Improved models should increase the precision of the determination.

PG 1115 + 080. PG 1115 + 080, the second lens system to be discovered, consists of four optical images of a z = 1.722 quasi-stellar object (QSO) (22). This system is radio quiet, but diligent optical monitoring has yielded a time delay (23) that, when combined with modeling based on HST NICMOS images, gives Hubble constant determinations in the range H_o = 59 ± 14 km·s⁻¹ Mpc⁻¹ (24, 25). Again, it is clear that the mass model of the lens is the limiting factor, and further constraints will be necessary to yield an accurate Hubble constant measurement.

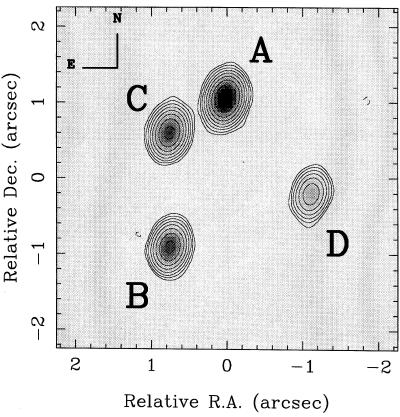
CLASS B1608+656. This system (Fig. 2) has four compact [<10 milli(arc-second)] radio components, as well as an infrared Einstein ring (17, 26). The image geometry and flux ratios are not well fit by a single-lens model, and HST images show the lensing galaxy to have two brightness centers, consistent with it being a binary galaxy lens. Extensive VLA monitoring of this source (Fig. 3) was carried out in 1997 and 1998, yielding measurable delays between the primary image and the other three images, and an estimate of the Hubble constant of H_o = 59 ± 4 ± 15 km⋅s⁻¹⋅Mpc⁻¹ (90%) (27) (where the two error bars represent statistical uncertainty from the time delay and the larger uncertainty due to the model). The current best-fit model, with two deflectors at the same redshift, is shown in Fig. 4.

Figure 2.

(Left) CLASS B1608 + 656 VLA image at 8.46 GHz. (Right) CLASS B1608 + 656 HST WFPC2 image. Note the Einstein ring due to lensing of extended background galaxy emission, as well as the binary nature of the lensing galaxy. Images courtesy of CLASS.

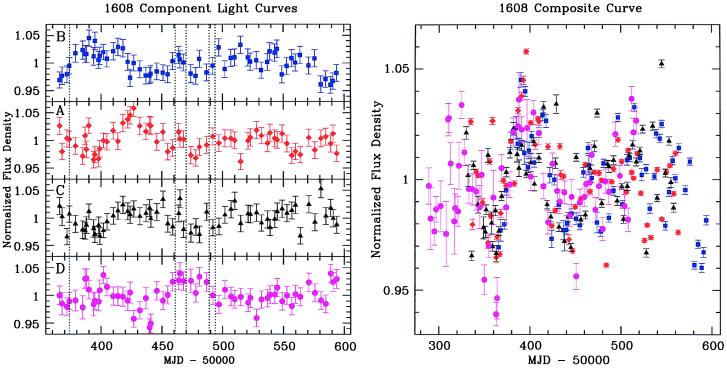
Figure 3.

(Left) CLASS B1608 + 656 VLA monitoring data for individual components A–D. (Right) CLASS B1608 + 656 VLA monitoring data, shifted by best-fit relative magnifications and time delays of each component, and stacked. The three independent delays BC, BA, and BD all are consistent with the best-fit mass model and Hubble constant, and thus in principle, modeling of the extended ring emission can further constrain the gravitational potential, reducing the large model uncertainty. Image courtesy of Chris Fassnacht (NRAO).

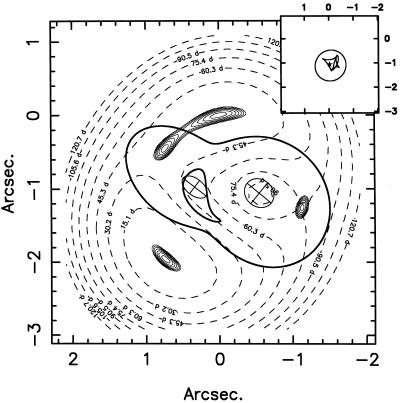
Figure 4.

The lensing model for CLASS B1608 + 656, showing the image positions (light solid contours), locations and ellipticities of the lens components (ellipses), lens isopotential contours (dark solid contours), and surfaces of constant time delay (dashed contours, with delays labeled). Note that as in all quad systems, the observed images correspond to minima or saddle-points in the Fermat potential, while the unobserved fifth image that appears at a maximum of the time delay is highly demagnified. The Inset at the upper right shows the source-plane configuration along with the outer critical curves (the transition from one to three total images) and the inner caustics (from three to five images). The star marks the inferred location of the background radio source, which lies just inside the inner caustic. Image courtesy of Leon Koopmans (Groningen).

Cosmology with Lenses

In addition to measuring the Hubble constant, the distribution of lensing in a well selected sample of distant astronomical sources provides a critical constraint on the overall geometry of the Universe. For example, the probability of lensing for the parent sample depends on the run of volume with distance. In particular, the rate at which the expansion rate evolves with time can alter the relative sample volumes at different redshifts. It has long been a goal to constrain the allowable energy content of the Universe by counts of lenses (28).

Cosmological studies of lensing have gained new importance with the recent reports of a possible measurement of an acceleration (a negative deceleration parameter) of the Universal expansion (29, 30). Data from optical and radio lensing surveys constrain the fraction of the closure density that can be in the form of a cosmological constant Λ to be Ω_Λ < 0.62 (90%) (31) for globally flat cosmologies. Thus, the lensing constraints are now approaching the sensitivity level needed to confirm or reject the best-fit values obtained from the supernovae and other data, and should be able to do so in the near future.

Future Prospects and New Twists

The field of gravitational lensing, although certainly mature in a theoretical sense, is still growing observationally as new and more powerful telescopes and computational tools come on-line. With the completion of northern CLASS in 1999, the focus at radio wavelengths will shift to the southern sky. In addition, large digital optical surveys such as SDSS will make large optical lens surveys practical, and the growing sophistication of infrared imaging technology will help alleviate the effects of dust obscuration on the optical observations.

We will certainly discover new gravitational lenses in the coming decade. In addition to building a broad picture of the lensing distribution in a survey sample, we may also hope to find one or more “Golden Lenses” that will unambiguously yield an accurate determination of the Hubble constant. So far, our known lenses have fallen short of this ideal, yet it is probably only a matter of time and perseverance before a suitable candidate is found.

I finish by noting that the strong lensing regime, where multiple images or Einstein rings are formed primarily by galaxy-mass deflectors, is not the only case in which gravitational lensing is known or important. For example, microlensing of distant stars in our galaxy and its nearby companions (32) is providing important new constraints on galactic structure and the nature of dark matter (33). Also, lensing by massive (≈10¹⁵ solar-mass) clusters of galaxies has been used as a cosmic telescope to magnify faint background galaxies (34). A number of programs are being carried out to search for the “weak lensing” distortions of the galaxy shapes by large-scale structures in the Universe, which can potentially place further constraints on the overall matter density parameter Ω₀ (35).