Abstract
The “combined-stimulation advantage” refers to an improvement in speech recognition when cochlear-implant or vocoded stimulation is supplemented by low-frequency acoustic information. Previous studies have been interpreted as evidence for “super-additive” or “synergistic” effects in the combination of low-frequency and electric or vocoded speech information by human listeners. However, this conclusion was based on predictions of performance obtained using a suboptimal high-threshold model of information combination. The present study shows that a different model, based on Gaussian signal detection theory, can predict surprisingly large combined-stimulation advantages, even when performance with either information source alone is close to chance, without involving any synergistic interaction. A reanalysis of published data using this model reveals that previous results, which have been interpreted as evidence for super-additive effects in perception of combined speech stimuli, are actually consistent with a more parsimonious explanation, according to which the combined-stimulation advantage reflects an optimal combination of two independent sources of information. The present results do not rule out the possible existence of synergistic effects in combined stimulation; however, they emphasize the possibility that the combined-stimulation advantages observed in some studies can be explained simply by non-interactive combination of two information sources.
INTRODUCTION
The combination of acoustic and electric stimulation, as a way to enhance speech-recognition performance in cochlear-implant (CI) users, has generated considerable interest in recent years (e.g., von Ilberg et al., 1999; Gantz and Turner, 2003; Ching et al., 2004; Gantz and Turner, 2004; Gantz et al., 2004; Turner et al., 2004; Kong et al., 2005; Gantz et al., 2006; Gfeller et al., 2006; Dorman et al., 2008; Büchner et al., 2009; Cullington and Zeng, 2009). One form of electro-acoustic stimulation (EAS) involves electric stimulation of the basal part of the cochlea using a short-electrode array, and acoustic stimulation of the more apical region of the cochlea, which corresponds to relatively low-frequency regions of residual acoustic hearing. Alternatively, electric stimulation using a long-electrode array in one ear can be combined with acoustic stimulation of the opposite ear that retains some residual hearing (Ching et al., 2004; Kong et al., 2005; Mok et al., 2006).
Several studies have demonstrated that EAS can produce significantly—and sometimes, considerably—higher speech-recognition performance than either electric or acoustic stimulation alone, especially in noise backgrounds (e.g., Gantz and Turner, 2003; Ching et al., 2004; Gantz and Turner, 2004; Gantz et al., 2004; Turner et al., 2004; Kong et al., 2005; Gantz et al., 2006; Gfeller et al., 2006; Dorman et al., 2008; Büchner et al., 2009; Cullington and Zeng, 2009). This effect is commonly referred to as the “combined-stimulation advantage.” In addition to studies of the EAS advantage in CI users, several studies have examined the potential benefits of combined stimulation in normal-hearing listeners, using simulations of EAS. In these simulations, envelope-vocoder processing is used to simulate CI processing, while lowpass filtering is used to simulate residual low-frequency hearing. Consistent with the results of CI studies, several simulated-EAS studies have demonstrated significant benefits of combined (i.e., lowpass-filtered and vocoded) stimulation, especially in noisy backgrounds (Turner et al., 2004; Dorman et al., 2005; Qin and Oxenham, 2006; Kong and Carlyon, 2007; Li and Loizou, 2008; Chen and Loizou, 2010).
While the combined-stimulation advantage is now well established, its underlying mechanisms are still debated. Possible explanations for the effect can be divided into two main categories. According to the first type of explanation, listeners do better with combined stimulation than with vocoded (or electric) signals alone because unprocessed low-frequency signals contain cues that facilitate or enhance the processing of cues pertaining to a target voice in the presence of a competing voice or background noise. In particular, it has been suggested that fundamental-frequency (F0) information conveyed by low-numbered harmonics can help listeners track the target voice (e.g., Turner et al., 2004; Qin and Oxenham, 2006; Brown and Bacon, 2009). From a more general standpoint, it has been suggested that low-frequency signals provide listeners with cues, which they can use to disambiguate target- and masker-related information in a mixture of vocoded (or electric) signals; in effect, the low-frequency cues “tell” the listener when to “glimpse” at the mixture to selectively extract relevant information concerning specifically the target (e.g., Li and Loizou, 2008; Brown and Bacon, 2009). These explanations appear to imply a form of synergy in the combination of low-frequency and vocoded signals, whereby listeners extract more information from the vocoded mixture of target and masker when low-frequency cues are present, than they do in the absence of such cues. We refer to this as the “super-additivity” hypothesis.
A second type of explanation for the fact that listeners do better with both vocoded and low-frequency signals than they do with either type of signal alone is, simply, that they then have access to two sources of information, instead of just one. Several authors have noted that important phonetic cues are present at low frequencies, and that these cues can usefully supplement the limited cues present in higher-frequency vocoded (or electric) signals (e.g., Turner et al., 2004; Qin and Oxenham, 2006; Kong and Carlyon, 2007; Li and Loizou, 2008; Brown and Bacon, 2010). Thus, to the extent that low-frequency signals do not interfere with the perceptual processing of information in vocoded (or electric) signals, and they are not ignored by listeners, performance should be higher with both signals present than with either signal in isolation, without necessarily having to posit the existence of synergistic interactions between low-frequency and vocoded (or electric) signals. We refer to this type of explanation as the “simple additivity” hypothesis.
The extent to which the combined-stimulation advantages that have been measured in previous studies can be quantitatively accounted for in terms of simple additivity is not entirely clear. Kong and Carlyon (2007) were the first to address this question rigorously, using a theoretically principled approach. Specifically, these authors tested whether percent-correct (PC) scores for the recognition of words presented in combined (lowpass-filtered + vocoder) stimulation were significantly higher than predicted by a model that assumes no interaction in the combination of information across the unprocessed and vocoded signals; we describe and discuss this model in Sec. 2. They found that for two of the signal-to-noise ratios (SNRs) tested in their study (+5 and +10 dB), performance was indeed higher than predicted by their model. Taken at face value, this finding suggests that, at least for these two conditions, the results cannot be accounted for by the simple-additivity hypothesis. However, it is important to note that the probability-summation model, used by Kong and Carlyon (2007) to predict performance in the combined-stimulation case, is suboptimal, meaning that it is possible in principle for an observer to achieve higher performance than predicted by this model, even without assuming any kind of synergistic interactions (see Braida, 1991). Therefore, the possibility remains that the large combined-stimulation benefits observed by Kong and Carlyon (2007) can actually be accounted for without assuming synergistic interactions in the perceptual combination of low-frequency and vocoded information. In fact, Kong and Carlyon (2007) did not rule out this second possibility; they acknowledged that adding low-frequency acoustic signals to vocoded (or electric) signals may improve recognition performance simply by providing additional low-frequency phonetic information.
To our knowledge, only two other published studies have compared listeners’ performance in combined-stimulation conditions with model predictions (Kong and Braida, 2011; Seldran et al., 2011). Kong and Braida (2011) measured identification performance for consonants and vowels in quiet in normal-hearing listeners and CI users in non-combined stimulation conditions (i.e., hearing aid alone and CI alone for the CI users, and lowpass-filtered speech alone or vocoded speech alone for the normal-hearing listeners) and combined-stimulation conditions (i.e., hearing aid plus CI for the CI users and lowpass-filtered plus vocoded speech for the normal hearing listeners). They then compared the magnitude of the combined-stimulation advantage measured in the two groups with predictions obtained using a signal-detection-theory (SDT) model of bimodal integration (Braida, 1991; Ronan et al., 2004), in which speech sounds are represented by vectors in a multidimensional feature space, and are assigned multivariate Gaussian probability density functions. Kong and Braida (2011) found that the performance of the normal-hearing listeners and of the CI users was usually lower than expected based on the optimal (i.e., maximum-likelihood) version of this model, but that it could be accounted for by the model if different (sub-optimal) decision rules were assumed. In the other recent study (Seldran et al., 2011), the authors measured the performance of normal-hearing listeners in a task involving the recognition of words presented in quiet or in a cafeteria-noise background at different SNRs in three listening conditions: lowpass-filtered speech alone, vocoded speech alone, and lowpass-filtered plus vocoded speech simultaneously. They then compared the performance of the listeners in the combined-stimulation conditions with the predictions of the probability-summation model and of two optimal-observer models based on Gaussian-SDT assumptions (Green and Swets, 1966). They found that the performance of the listeners was consistently under-predicted by the probability-summation model, but that it could be accounted for by either of the two Gaussian-SDT models. It is important to note that these Gaussian-SDT models did not involve any constructive interaction in the processing of low-frequency and vocoded (or electric) signals.
Our goal in the present study was threefold. First, we sought to clarify the assumptions, and the limitations, of the probability-summation rule as a model of perceptual integration in the context of studies of the combined-stimulation advantage. Second, we sought to clarify the assumptions, and the limitations, of optimal Gaussian-SDT models, and to explain why these models can account for large combined-stimulation advantages (i.e., large differences in PC scores between combined and non-combined conditions) without involving any synergistic interaction in the perceptual-integration process. Third, we sought to examine whether, and how well, these models could account quantitatively for the combined-stimulation advantages that have been measured in previous studies. Although there are many published studies on the combined stimulation advantage, here, for illustration purposes, we focus on two representative examples (Qin and Oxenham, 2006; Kong and Carlyon, 2007).
ASSUMPTIONS AND LIMITATIONS OF THE PROBABILITY-SUMMATION MODEL
The probability-summation rule can be written formally as
| (1) |
In this equation and the following ones, PC denotes the predicted probability of a correct response with combined stimulation, PL denotes the proportion of correct responses measured for lowpass-filtered stimuli alone, and PV denotes the proportion of correct responses measured for vocoded (or electric) stimuli alone. Equation 1 can be rewritten as
| (2) |
Equation 2 can be easily identified with the basic law of probability that gives the probability of occurrence of either or both of two independent and not mutually exclusive events, A and B
| (3) |
Here, the A and B events correspond to the correct identification of the lowpass signal, and to the correct identification of the vocoded (or electric) signal. In words, Eq. 3 asserts that the probability of correctly identifying the lowpass signal or the vocoded signal (or both) equals the probability of correctly identifying the lowpass signal, plus the probability of correctly identifying the vocoder signal, minus the probability of correctly identifying both signals.
The probability-summation model has been used in various contexts (for reviews of the origins and limitations of this model, see Treisman, 1998; Wickens, 2002; Macmillan and Creelman, 2005). In particular, it has been applied to predict the detection of simple events (e.g., signal versus no signal) at the output of two or more sensory channels (e.g., Pirenne, 1943; Green and Swets, 1966; Pelli, 1985). Fletcher (1953) used it to predict the probability of a correct response in experiments involving the recognition of simultaneously presented bands of speech, based on the measured proportions of correct responses for each band in isolation. Boothroyd and Nittrouer also used and extended this model to analyze temporal context effects in the identification of phonemes (Boothroyd and Nittrouer, 1988; Nittrouer and Boothroyd, 1990). However, the rationale for applying the probability-summation model in the context of EAS studies is not straightforward.
From Eqs. 1, 2, 3, the application of the probability-summation model requires important assumptions. The first assumption is that the lowpass and vocoded signals (L and V signals, respectively) are identified separately and independently, in such a way that the correct or incorrect identification of the L signal does not influence the identification of the V signal, and vice versa. In other words, there is no interaction in the processing of the L and V signals. This assumption is justified, since the goal is to obtain predictions of performance for the combined case under the null hypothesis of no interaction between the L and V channels.
The second assumption implied by the probability-summation rule is that a correct response is produced whenever at least one of the two channels produces a correct output, i.e., whenever the L signal or the V signal is correctly identified. This second assumption is not so easily justified.1 For example, suppose that in the combined-stimulation condition of a simulated-EAS experiment the vowel /i/ was presented and the vocoded signal was identified as /i/ (i.e., the correct answer), but the simultaneous lowpass signal was identified as /u/ (i.e., an incorrect answer).2 The probability-summation model assumes that whenever the signals identified at the outputs of the A and V channels are in conflict, the listener invariably selects the correct answer. Thus, this model predicts that the listener will always give the correct answer, /i/, in this situation. However, it is not clear why, and how, the listener should always be able to guess correctly which of the two conflicting responses is correct. More plausibly, the listener will sometimes choose the incorrect answer. This will result in lower performance than predicted by the probability-summation rule. From this point of view, it appears that predictions obtained using the probability-summation model may be overly optimistic, and that a more realistic version of this model would only reinforce the conclusion of super-additive effects in human listeners. However, there is a more fundamental problem with the probability-summation model. Even if it is assumed that, when faced with conflicting responses from the L and V channels, the listener always knows the correct answer, the decision rule implied by this model is suboptimal. This means that it is possible—at least in principle—for an observer to achieve a higher level of performance by using a different decision rule. In fact, as we demonstrate in Sec. 3, Gaussian SDT models can achieve considerably higher performance than predicted by the probability-summation model. This conclusion has significant implications for the interpretation of the results of EAS and vocoder-simulated EAS experiments.
GAUSSIAN-SDT MODELS OF CUE-COMBINATION
The probability-summation model falls in the category of post-labeling models (Braida, 1991). Models of this type assume that listeners first identify speech items (phonemes, syllables, or words) within each channel, then combine the resulting identification decisions in some way, e.g., by selecting one of the two answers with a certain probability. In contrast, pre-labeling models posit that listeners combine information across channels before they make a decision as to which item was presented (Braida, 1991; Uchanski and Braida, 1998; Müsch and Buus, 2001; Ronan et al., 2004). In general, post-labeling decision strategies are suboptimal (e.g., Green and Swets, 1966; Wickens, 2002), although the extent to which their performance falls short of the upper bound defined by maximum-likelihood decision strategies can vary, depending on the specifics of the situation being modeled (e.g., Pelli, 1985). Pre-labeling models can achieve optimality if the decision variable(s) formed by combining information across channels are related monotonically to the likelihoods of the different hypotheses (in this case, different speech items), and the decision rule invariably selects as a response the stimulus alternative that is the most likely a posteriori (Green and Swets, 1966; van Trees, 1968).
In the context of speech-recognition experiments, in which the listener’s task is to identify a speech item (e.g., a word) drawn from a set of m items—which is generally known in the psychophysics literature as an m-alternative forced-choice (mAFC) task—the maximum-likelihood decision rule is to choose the response alternative corresponding to the item indexed by k (k = 1, …, m), such that
| (4) |
where denotes the likelihood that item i (i = 1,…, m) was presented, given the received signal (Green and Birdsall, 1958; van Trees, 1968). In other words, the observer should always choose the response corresponding to the most likely item, given the received signal. If the m items are all equally likely, this decision rule is equivalent to the maximum-a posteriori decision rule, which maximizes the long-term average proportion of correct responses (van Trees, 1968).
Following previous investigators (e.g., Green and Birdsall, 1958; Müsch and Buus, 2001), we assume that the observer only has access to a noisy representation, x, of the transmitted signal, hj (j = 1,…, m), and that it can compute a quantity, yi (i = 1,…, m) which is directly proportional to the likelihood of signal i,. Note that we use the convention of denoting vectors by boldface characters. The representation of the received signal as a vector is quite general. For example, the vectors x and hj may be thought of as sampled time waveforms or as arrays of phonetic-feature activation values (e.g., Braida, 1991).3 The noise in the received signal may be of internal or external origin. This includes background noise, neural noise, as well as random variations in speech signals due to within- and across-speaker variability (Green and Swets, 1966; Uchanski and Braida, 1998). For simplicity, and justified by the central limit theorem (Green and Swets, 1966), it is assumed that the noise is additive and Gaussian with a constant variance. Moreover, consistent with the standard Gaussian-SDT model for the mAFC task (see Green and Dai, 1991), the variables, yi, i = 1,…, m, are assumed to have an expected value of zero for all i ≠ j, and an expected value greater-than-zero for i = j.
With these simplifying assumptions, it can be shown (e.g., van Trees, 1968) that the probability of a correct response, P, equals
| (5) |
where φ(.) denotes the standard normal probability density function, (.) denotes the cumulative standard normal function, and d′ equals the ratio of the mean to standard deviation of yi = j. Equation 5 can be inverted numerically to obtain an estimate of d′ based on a measured proportion of correct response in an experiment.
This model can be extended to the case where the observer receives two signals, for example, a low-frequency unprocessed signal and a vocoded (or electric) signal. In this situation, the observer is assumed to compute, for each i = 1,…, m, a pair of decision variables, yi,L and yi,V, where the superscripts L and V refer to the low-frequency and vocoded signals, respectively. To arrive at a decision, the observer must then combine yi,L with yi,V. The number of ways in which two variables can be combined is infinite. Here, we focus on the maximum-likelihood decision rule. Given the assumptions stated above, it can be shown (Green and Swets, 1966) that an optimal decision rule involves choosing response k such that
| (6) |
where
| (7) |
The variables ωL and ωV may be thought of as relative weights, which the observer assigns to the (noisy) observations of the low-frequency and vocoded signals. Intuitively, it is clear that the observer will achieve a higher correct-recognition score if the weights are adjusted based on the relative reliability of the two signals, with greater weight given to the more reliable signal and less weight to the less reliable signal. Mathematically, the reliability of a signal is directly related to the magnitude of the signal, and inversely related to the variance of the noise. Here, these magnitudes and variances correspond, respectively, to the expected values and variances of yj,L (for the low-frequency part) and yj,V (for the vocoded part). To maximize the probability of a correct decision, the weights should be adjusted as follows (Green and Swets, 1966):
| (8) |
and
| (9) |
where E[.] and V[.] are the mathematical expectation and variance operators.
To prevent the weights from becoming arbitrarily large, we add the constraints that the weights must be between 0 and 1, and that their sum must equal 1. This leads to a re-formulation of the linear-combination model as
| (10) |
with
| (11) |
where
| (12) |
and
| (13) |
Since zi is directly proportional to yi, the decision rules defined by Eqs. 6, 7, 8, 9, 10, 11, 12, 13 are equivalent.4 Therefore, the index of sensitivity for these two rules is the same. This index can be computed as
| (14) |
with
| (15) |
and
| (16) |
where σ2 is the total variance of the noise resulting from the combination of information across the low-frequency and vocoded signals, and denotes the variance of any additional noise, hereafter referred to as “late” noise. This late noise is assumed to be present in combined and non-combined stimulation conditions, and its magnitude is assumed to be constant. One example of a possible source of late noise is inattention.
Two specific cases must be considered. If σ2, and the contribution of the late noise is negligible, d′ is approximately equal to , where and can be estimated based on the PCs measured in unimodal (i.e., low-frequency signal alone and vocoded signal alone) conditions using Eq. 5. This case can be referred to as the “independent-noises” model. Denoting the estimates of sensitivity as and , the predicted proportion of correct responses for this case is
| (17) |
By contrast, if σ2, so that the late noise is the only significant source of noise limiting performance, which we refer to as the “late-noise” model, the predicted proportion of correct responses is
| (18) |
It is important to note that, like the probability-summation model, these two Gaussian-SDT models do not assume any synergistic interaction in the processing of the low-frequency and vocoded signals. This can be seen by noting that Eqs. 12 or 13 contain no interaction term involving a product of and . These models involve no mechanism whereby sensitivity to the vocoded signal is enhanced by the addition of the low-frequency signal (or vice versa). Therefore, the predictions obtained using these models provide an indication of the performance that can be achieved in combined-stimulation conditions without any constructive interaction in the processing of the low-frequency and vocoded signals.
The two Gaussian-SDT models outlined above were briefly described in Seldran et al. (2011), and they present some similarities with Braida’s (1991) pre-labeling model of bimodal identification (see also Ronan et al., 2004). In particular, these models are all based on the assumption that the observer combines Gaussian observations before choosing a response. This contrasts with post-labeling models, and with the probability-summation model, in which the observer is assumed to make separate identification judgments about the stimulus in each channel, and then to combine these judgments (i.e., discrete random variables) to determine a response. Braida’s (1991) pre-labeling model is more sophisticated than the two Gaussian-SDT models described above, in that it takes into account the relative locations of the stimulus and response centers in the multi-dimensional feature space (for details, see Braida, 1991; Ronan et al., 2004). These two types of Gaussian-SDT models both have advantages and limitations. One advantage of Braida’s (1991) pre-labeling model is that it can be used to obtain phoneme-specific predictions of recognition performance, whereas the two Gaussian-SDT models described above only yield overall PC predictions. One advantage of the Gaussian-SDT models, however, is that they are somewhat simpler, and have fewer free parameters, than Braida’s (1991) pre-labeling model; their predictions only depend on the parameter, m, whereas for Braida’s (1991) pre-labeling model, different predictions are obtained depending on the locations of the response centers relative to the stimulus centers in the multi-dimensional feature space (Braida, 1991; Ronan, 2004). However, the independent-noise model described above shares one important feature with Braida’s (1991) optimal pre-labeling model (i.e., the version of the model in which all of the response centers coincide with the stimulus centers), in that these two models both predict that the sensitivity for the combined case equals the Pythagorean sum of the sensitivities measured in the two unimodal conditions.
REVISITING SUPER-ADDITIVE EFFECTS IN COMBINED STIMULATION
Proof of principle
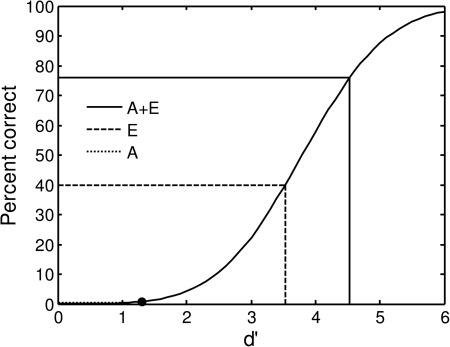
In this section we demonstrate that the Gaussian-SDT models described in Sec. 3 can account in principle for large benefits of combined stimulation, even when performance with either of the constituent signals (lowpass-filtered or vocoded) is close to chance. Consider the curve relating PC to d′, which is shown in Fig. 1. This curve corresponds to the psychometric function predicted using Eq. 13, with m set to 8000. This number was based on the work by Müsch and Buus (2001). They reanalyzed Kryter’s (1962) data on speech intelligibility as a function of set-size, and found that setting m to 8000 led to more accurate predictions of performance for open-set speech-recognition experiments, and experiments involving more than a few hundred potential items (e.g., words), than setting m to the actual number of potential stimuli or response alternatives. A similar effect was observed by Green and Birdsall (1958), who suggested that when the stimulus set is large and its contents are not known in advance to the listener, performance is determined not by the number of stimulus alternatives but by the number of response alternatives, which in this case may equal the size of the listener’s active vocabulary. Müsch and Buus (2001) estimated the size of this vocabulary at about 8000 words.
Figure 1.
Illustration of the ability of the Gaussian-SDT model to predict a large combined-stimulation advantage, even when one of the two information sources yields close-to-chance performance when presented on its own. The solid curve shows the relationship between d′ and PC for the mAFC identification task with m = 8000, as predicted by the maximum-likelihood Gaussian-SDT model [Eq. 7]. The dashed and solid lines illustrate the connection between d’ for acoustic stimulation alone (A), electric stimulation alone (E), and combined stimulation (A + E), to the corresponding PC points on the psychometric function. The horizontal short-dotted line close to the x-axis indicates the PC corresponding to d′ = 1 for the A condition; this PC was very close to zero, or to the chance rate (1/8000). For the E condition, PC equals 40%, which corresponds to a d’ of approximately 3.5. The late noise model described in the text predicts that d′ for the A + E condition equals the sum of these two d′s, i.e., 4.5. This corresponds to a PC of approximately 75%. The filled circle marks the point on the psychometric function corresponding to a 0.5 probability of observing zero correct responses out of 75 trials in this observer; this corresponds to a d′ of about 1.3.
The filled circle marks the point on the psychometric function corresponding to a 0.5 probability of observing zero correct responses out of 75 trials—the average number of words per condition per listener in Kong and Carlyon’s (2007) study—assuming no over-dispersion. (In the presence of over-dispersion, the filled circle would correspond to an even higher d′.) Note that the d′ corresponding to this point equals 1.3. This means that if a listener who behaves according to this model had a d′ of 1.3, there would be an approximate 1-in-2 chance of observing a PC of zero in this listener, for the considered condition. Let us assume that in the lowpass-only condition the listener had an even lower d′, 1, and that in the vocoded condition the same listener achieved 40% correct. As indicated by the dashed line, this corresponds to a d′ of about 3.5. The notion that a PC of zero can correspond to a d′ larger than zero can be understood in light of Kong and Carlyon’s (2007) remark that although a lowpass-filtered or vocoded speech signal “may not be sufficient to identify any whole words, this does not mean that it conveys no phonetic information at all.”
According to the late-noise model, d′ for the combined condition should be equal to 1 + 3.5 = 4.5. The solid line shows that the PC corresponding to this d′ of 4.5 is close to 75%. In other words, this late-noise model predicts that when lowpass-filtered stimuli, which yield essentially 0% correct when presented on their own, are combined with vocoded stimuli (as in simulated EAS studies) or with electric stimuli (as in real EAS studies), which yield 40% correct when presented on their own, the listener should be able to achieve about 75% correct. Note that this model assumes no interaction in the extraction of information from the lowpass and vocoded stimuli, i.e., the model has no “super-additive” mechanism. However, if these results were analyzed using the probability-summation model, they would lead to the conclusion that super-additivity occurred because, in this example, the probability-summation rule predicts that PC in the combined case should be no more than 40%.
Application to two published datasets
In this section, we apply the models described above to published data by Kong and Carlyon (2007) and Qin and Oxenham (2006). Background information and methodological details can be found in those articles.
Sentence identification
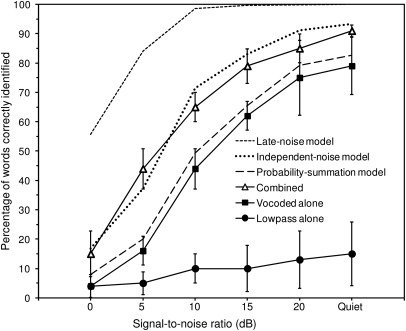
Figure 2 replots the data from Kong and Carlyon’s (2007) Fig. 1, overlaid with the predictions of the probability-summation, late-noise, and independent-noise models. The predictions of the latter two models were computed with the parameter m set to 8000 (see Sec. 4A for the justification of this choice). The within-subject standard errors that were displayed in the original figure have been multiplied by 1.96, so that the error bars in Fig. 2 show the 95% confidence intervals (within subjects). Two points are noteworthy. The first is that listeners’ performance in the combined-stimulation condition is remarkably well predicted by the independent-noise model, with predictions often falling with the 95% confidence intervals of the data points.
Figure 2.
Measured and predicted performance in a combined-stimulation experiment involving the identification of words for sentences presented in quiet and in background noise. The data are from Kong and Carlyon (2007), Fig. 1. As indicated in the key, the data for different stimulation modes (lowpass-alone, vocoded alone, and combined) are shown using different symbols connected by solid lines, using the same code as in Kong and Carlyon’s Fig. 1. Model predictions are shown using dashed and dotted lines with no symbols. As in Kong and Carlyon’s Fig. 1, the long-dashed lines correspond to the predictions of the probability-summation model. The predictions of the two other models tested in this study, the late-noise model and the independent-noise model, are shown using short-dashed and dotted lines, respectively. The labels underneath the x-axis indicate the different SNRs tested by Kong and Carlyon (2007), and the quiet condition. The error bars show 95% confidence intervals around the mean PCs; these confidence intervals were computed based on the error bars shown in Kong and Carlyon’s (2007) Fig. 1, which were obtained after partialing out across-subject variability as explained in that article.
The second point is that the predictions of the late-noise model (shown by the short-dashed line at the top) are consistently and substantially higher than the mean PCs measured in the combined-stimulation conditions in the human listeners. Thus, human listeners’ ability to combine the information contained in lowpass and vocoded speech signals is substantially lower than predicted by a model in which the only source of performance-limiting noise occurs after the combination of information provided by the lowpass and vocoded stimuli. This is perhaps not entirely surprising, since most of the conditions tested by Kong and Carlyon (2007) involved an external interferer, i.e., a significant source of noise located before the combination of information across channels. However, one might have expected the late-noise model to correctly predict listeners’ performance in the quiet condition; instead, the prediction of this model was higher than the listeners’ performance even for that condition. This suggests that even in quiet listening conditions, human listeners’ performance is significantly limited by other sources of noise than late (i.e., post-combination) noise.
Double-vowel identification
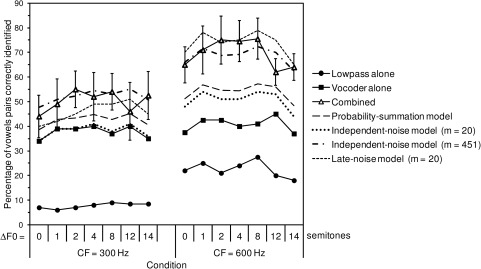
Figure 3 shows proportions of correct responses measured by Qin and Oxenham (2006) in an experiment involving the identification of pairs of concurrently presented vowels. Two lowpass-filter cutoff frequencies (CFs) of the acoustic stimulation (300 and 600 Hz), and seven F0 separations (ΔF0, ranging from 0–14 semitones), were tested in this experiment. The data for lowpass-filtered, vocoded, and combined (lowpass-filtered + vocoded) stimuli are shown as symbols connected by solid lines, using the same coding scheme as in Fig. 2. The predictions of the probability-summation, independent-noise, and late-noise models are superimposed on the data. For this experiment, the parameter, m, in the latter two models was set to 20, which is the number of different vowel pairs presented to the listeners, and the number of response alternatives.
Figure 3.
Measured and predicted performance in a combined-stimulation experiment involving the identification of pairs of concurrent vowels. The data are from Qin and Oxenham (2006), Fig. 2. The labels underneath the x-axis refer to different conditions, involving combinations of seven F0 separations (ranging from 0–14 semitones), and two lowpass-filter CFs (300 and 600 Hz). Data corresponding to different presentation modes (lowpass-filtered, vocoded, and combined) are indicated by symbols, and the predictions of the different models (independent-noise, late-noise, and probability summation) are indicated by different lines styles, as in Fig. 2. The error bars show 95% confidence intervals around mean PCs for the combined conditions; these confidence intervals were determined by multiplying the size of the standard-error bars reported by Qin and Oxenham by 1.96. For the independent-noise and late-noise models, predictions were generated with the parameter, m, set to 20, which is the number of vowel pairs that listeners had to identify in this experiment. In addition, simulations were run to find the value of m that minimized the squared error between the data and the predictions of the independent-noise model. This value was found to be equal to 451, and the “predictions” that were obtained using this value are also shown (dashed-dotted lines).
As for the Kong and Carlyon (2007) data, the predictions of the probability-summation model (dotted line) generally fall below the mean PCs of the listeners in combined-stimulation conditions (triangles). For the 600-Hz CF conditions (shown on the right), the predictions of the probability-summation model fall systematically below the lower limit of the 95% confidence intervals around the mean PCs across listeners. The discrepancy between data and predictions is less pronounced for the 300-Hz CF conditions (shown on the left); for these conditions, the predictions of the model fall within the limits of the 95% confidence intervals around the data for four out of the seven ΔF0 conditions tested. On the whole, however, the probability-summation model does not provide a satisfactory account of these data.
The independent-noises model under-estimated listeners’ performance in most of the combined-stimulation conditions of this experiment. As for the probability-summation model, the discrepancy is more pronounced for the 600-Hz CF condition, where performance in lowpass-alone conditions was generally higher than for the 300-Hz CF conditions. Thus, for these data, the independent-noises model with m equal to the number of alternatives (i.e., 20) cannot fully account for the large improvements in vowel-identification performance that were measured by Qin and Oxenham (2006) when lowpass-filtered signals were added to vocoded signals. However, it is important to note that the predictions of the independent-noises model can be brought in line with the data if m is allowed to exceed 20. The dashed-dotted lines in Fig. 3 show the predictions of the independent-noises model with m set to 451, which is the value that was found to minimize the squared error between the data and the model predictions. As can be seen, with this m value, the model predictions fall within the 95% confidence intervals of the data, with only one exception (for the 600-Hz CF, 12-semitones condition). It is worth emphasizing that, although in this example, m was allowed to vary to yield the best possible fit, it was not allowed to differ across conditions; thus, the finding that the same m value of 451 was found to fit the data of both the 300-Hz CF and the 600-Hz CF conditions well is not trivial. However, it is also important to note that this m value is ad hoc, and is substantially larger than the number of response alternatives in the considered experiment. One interpretation of this outcome is that the level of uncertainty of the listeners in this experiment may have been higher than expected based on the number of possible stimuli, i.e., the listeners entertained more than one template for each response alternative (see Pelli, 1985). Another possible interpretation is that the listeners did not, in fact, entertain more templates than there were response alternatives, so that the only possible setting for m is 20, which implies that the independent-noises model cannot account for the data of Qin and Oxenham (2006). If the latter interpretation is correct, this would raise the question of why the model is able to account for some data sets—namely, the data of Kong and Carlyon (2007)—but not others. At present, we can only speculate as to why this may be the case.
Possible reasons include differences in the nature of the task (open-set vs closed-set) or in the test materials (words in sentence context vs concurrent vowels). For example, human listeners’ perceptual and decision processes in experiments involving relatively small stimulus sets may not conform as well to the simplifying assumptions and asymptotic approximations of SDT models (i.e., Gaussian distributions, statistically independent observations, and orthogonal templates) as those underlying recognition performance with open (or large) stimulus sets. This might explain why the independent-noises model was less successful for Qin and Oxenham’s (2006) data than for Kong and Carlyon’s (2007) data.
Finally, with only two exceptions (corresponding to the 2-semitone ΔF0 condition for the 300-Hz CF and to the 12-semitone condition for the 600-Hz CF), the predictions of the late-noise model always fall within the bounds of the 95% confidence intervals around the listeners’ mean PCs. We do not have an explanation for why the late-noise model correctly predicts listeners’ performance in Qin and Oxenham’s (2006) experiment while it over-predicts listeners’ performance in Kong and Carlyon’s (2007) experiment. We simply note that Qin and Oxenham’s and Kong and Carlyon’s experiments involved very different stimuli (concurrently presented steady-state vowels for the former, sentences presented in backward-speech masker for the latter) and tasks (closed-set identification for the former, open-set speech recognition for the latter). Taken at face value, our finding that the Kong and Carlyon data were better fitted by the independent-noises model suggests that this model might provide a more accurate representation of the processes underlying human listeners’ performance in open-set speech-recognition tasks with an energetic masker, whereas the late-noise model might be more adequate for explaining human listeners’ performance in double-vowel experiments. Ultimately, it could be that a model including both pre- and post-combination noises is needed to account for the effects of combined-stimulation on performance in different tasks, using different stimuli. The predictions of the independent-noises model and late-noise model tested in this study provide lower and upper bounds, respectively, on the predictions that would be obtained using an independent- plus late-noise model.
LIMITATIONS AND PERSPECTIVES
The examples described above demonstrate that it is possible to account for combined-stimulation advantages that are as large as, or larger than, those that have been measured in earlier studies, using relatively simple decision-theoretic models that do not involve interactions in the combination of lowpass and vocoded speech cues. These findings are encouraging and suggest that these models could be used in future studies of the combined-stimulation advantage. However, it is important to acknowledge that these models entail several simplifying assumptions. In the remainder of this section, we examine some of these assumptions and suggest ways in which the models might be refined in future work.
Nature and number of speech templates
A fundamental assumption of the two Gaussian-SDT models described in this article is that, when recognizing speech, listeners systematically compare internal representations of incoming acoustic signals with internal “templates” stored in long-term memory. This assumption is quite common in the context of speech-recognition models; indeed, it is difficult to conceive of a speech-recognition system that does not involve some form of comparison with stored representations of phonemes, syllables, entire words, or features. However, at present, the nature and the number of speech templates stored in the human brain and activated during an open- or closed-set speech-recognition task are still subject to debate. In modeling Kong and Carlyon’s (2007) data, we assumed that the templates corresponded to entire words rather than to syllables or phonemes. This choice seemed natural, since Kong and Carlyon (2007) measured the percentage of correctly repeated keywords, rather than the number of correctly repeated syllables or phonemes. Had these authors used another measure of performance, such as the percentage of correctly repeated syllables, the same models could have been used, at least in principle.
However, it is important to note that the nature of the basic “speech items” that are assumed in the model may have important implications concerning both the interpretation of the number of items (m), and assumptions concerning the statistical independence of these items; we return to this important issue of statistical independence in Sec. 5B.
In addition, we assumed that the parameter, m, which in this context represented the average size of listeners active vocabulary, was as estimated by Müsch and Buus (2001). These authors found that the results of open-set speech-recognition experiments involving isolated words (Kryter, 1962) or words in sentence context (Warren et al., 1995) were well described when an active-vocabulary size of 8000 was assumed. The same number was found to also describe the data of Kong and Carlyon (2007) well in the current study. However, we cannot rule out the possibility that this outcome was coincidental. Moreover, this finding does not imply that the same m value will generally provide a good fit for other data sets, especially if the data were obtained using a different type of speech material.5
That the same m value cannot correctly predict combined-stimulation advantages measured using different types of speech material or conditions is already evident in the present study: the results of Qin and Oxenham’s (2006) study involving vowels were found to be most accurately predicted with an m value of 451, rather than 8000. In addition, there is some evidence that an m value of 8000 does not always yield the best fit even for open-set speech-recognition data. In a recent study, Seldran et al. (2011) found that the performance of their listeners in a task involving the recognition of isolated disyllabic French words under simulated combined-stimulation conditions was better fitted by the independent-noises model when the value of m was about 2 orders of magnitude larger than 8000.
What might explain the fact that values of m considerably larger than the number of response alternatives (Qin and Oxenham, 2006), or any plausible estimate of the size of listeners’ active vocabulary (Seldran et al., 2011), are needed to account for the large combined-stimulation advantages that were observed in these studies? One possible answer is that the independent-noises model with no interaction simply cannot provide a plausible account for these data. Alternatively, it is conceivable that the value of m, which represents the number of candidate templates being entertained by the listener and, therefore, the listener’s degree of “uncertainty” (Pelli, 1985), is smaller in the combined-stimulation condition—reflecting less uncertainty—than in the lowpass-alone and vocoded-alone conditions. To understand why this reduction in uncertainty might happen, consider that, when provided with vocoded-alone stimuli, the listener may not have access to important voicing cues which, when available (as in the combined-stimulation case) considerably reduce the space of candidate phonemes, syllables, or words, that the listener has to search through. Conversely, when presented with lowpass-alone stimuli, the listener does not have access to high-frequency envelope cues that signal the presence of fricatives and would, if available, constrain the space of candidate phonemes, syllables, and words for the current stimulus.
The question may be raised as to whether assuming a reduced uncertainty in combined-stimulation conditions, compared to non-combined conditions, is equivalent to assuming the existence of significant interactions in the combination of lowpass and vocoded information. Providing a clear answer to this question requires formulating models of the combined-stimulation advantage that involve interactions in the cue-combination process. For example, the decision-theoretic models described above could be modified so that is larger in the presence of low-frequency information (i.e., in the combined-stimulation condition) than in the absence of such information. However, this implies adding an extra degree of freedom in the model, and it makes it possible to predict an arbitrarily large combined-stimulation advantage, simply by assuming an arbitrarily large increase in the value of when low-frequency information is added. An important goal for future studies, therefore, is to formulate principled models of the combined-stimulation advantage that involve synergistic combination of low-frequency and vocoded (or electric) sources of information, and to demonstrate that these models can provide a (statistically) significantly better account of experimental data, even after their higher number of degrees of freedom is taken into account.
Equal a priori probabilities and lack of contextual influences
The maximum-likelihood decision rule for the mAFC task (Green and Birdsall, 1958; Müsch and Buus, 2001; Pelli et al., 2006), on which Eqs. 12, 14, and 15 are based, hinges on the simplifying assumption that the speech items are all equally likely a priori.
If this assumption is not met, the proportion of correct responses obtained using this decision rule will fall short of the proportion of correct responses obtained using the maximum-a posteriori rule, which takes into account differences in the a priori probabilities of speech items. It is well known that some phonemes, syllables, and words in the English language, or in any other spoken language, occur with a greater frequency than others. Thus, in open-set speech recognition tasks, the a priori probabilities of different phonemes, syllables, and words are likely to reflect, at least in part, the a priori probabilities of phonemes, syllables, and words in the considered language. To the extent that human listeners have, and use, knowledge of these a priori probabilities, more accurate predictions of speech-recognition performance might be obtained using models that take these probabilities into account, especially in open-set speech recognition tests.
Another simplifying assumption, which is commonly made in macroscopic models of speech-recognition performance, is that the probability of correctly identifying a word, syllable, or phoneme is independent of the context. It is well known that, in syntactically and semantically lawful sentences, this is not the case; for example, the choice of last keyword in a sentence is usually constrained by the words that precede it. Although the two Gaussian SDT models considered in this article do not explicitly model contextual dependencies in the speech-recognition process, they do nonetheless provide a mechanism for taking into account the influence of linguistic redundancy on speech-recognition performance via the parameter m. The value of this parameter reflects the degree of the listener’s uncertainty concerning the identity of the signal (e.g., word). Even when the actual degree of uncertainty varies within the course of a sentence due to linguistic redundancy effects, the average degree of uncertainty may be approximately constant, for a given speech corpus. This may explain why the independent-noises model was found to be reasonably successful in predicting PC in the combined-stimulation conditions of Kong and Carlyon’s (2007) experiment, even though the experiment measured PC for words presented in the context of sentences with a relatively high degree of linguistic redundancy in them. It will be important to test these assumptions in future studies.
Orthogonality of speech templates
Another assumption of the decision-theoretic models considered in this article is that the templates to which incoming signals are being matched by the observer are mutually orthogonal, i.e., uncorrelated. This simplifying assumption is often made in decision-theoretic models of mAFC tasks (e.g., Green and Birdsall, 1958; Müsch and Buus, 2001; Pelli et al., 2006), and it is supported by the results of a reanalysis of speech-recognition data obtained using monosyllabic words for various set sizes and various SNRs (Green and Birdsall, 1958). However, it must be acknowledged that this assumption is, at best, a convenient approximation. Studies of confusion matrices in speech-recognition experiments demonstrate that some speech items are more likely to be confused with each other than with other, more dissimilar-sounding items (Miller and Nicely, 1954). This suggests that speech templates are partly correlated.
Although taking into account such internal correlations does not appear to be crucially important for developing reasonably successful macroscopic models of speech-recognition performance, i.e., models that seek to predict overall recognition performance (e.g., Green and Birdsall, 1958; Müsch and Buus, 2001), it is obviously important when developing models that can also predict confusion patterns. Moreover, even if the goal is to predict overall PC, taking into account any available knowledge concerning patterns of confusions may yield more accurate predictions. From this point of view, the models described in this article may be viewed as simplifications of more sophisticated predictive models of speech-recognition performance in combined-stimulation (or multi-band) conditions based on performance in non-combined (or single-band) conditions, such as those proposed by Braida and colleagues (Braida, 1991; Ronan et al., 2004; Kong and Braida, 2011).
CONCLUSIONS
-
(1)
Evidence for super-additive effects in the perceptual processing of combined speech stimuli based on predictions obtained using the probability-summation model should be interpreted with caution, because this model is largely suboptimal. PC performance measured in combined-stimulation conditions can be higher than predicted by the probability-summation rule, even if the two sources of information (acoustic and electric, or vocoded) are combined additively.
-
(2)
Gaussian-SDT models, which implement optimal (maximum-likelihood) decision rules, can account for considerably larger benefits of combined stimulation than predicted by the probability-summation model, without the need to posit the existence of constructive interactions between the two channels of information. These models can account for the seemingly surprising finding that lowpass-filtered speech stimuli, which produce chance performance when presented on their own, can nonetheless significantly enhance performance when combined with vocoded or electric stimuli (e.g., Kong et al., 2005; Kong and Carlyon, 2007). Therefore, such findings should not be interpreted automatically as evidence for synergistic interactions.
-
(3)
For the particular data sets analyzed in this study, although synergistic effects are not ruled out, Gaussian-SDT models of cue combination were found to account for human listeners’ performance in combined-stimulation conditions. Although a more extensive reanalysis of published data sets is needed to determine whether this conclusion holds more generally, the present results suggest that, at the very least, Gaussian-SDT models of non-interactive information combination provide a good starting point for principled analyses (or re-analyses) of data obtained in EAS or simulated EAS studies.
ACKNOWLEDGMENTS
This work was supported by NIH R01 DC05216. The authors are grateful to Dr. R. P. Carlyon, Dr. L. Demany, Dr. Y. Y. Kong, and to one anonymous reviewer, for helpful suggestions on an earlier version of the manuscript.
Footnotes
In the context of detection experiments, the assumption that a correct response occurs whenever the signal is detected in at least one of the sensory channels is a logical consequence of the high-threshold postulate (see Macmillan and Creelman, 2005; Wickens, 2002). According to this postulate, the presentation of noise can never trigger a “detect” state. The high-threshold observer is aware of this fact. Thus, whenever at least one sensory channel is in the detect state, the high-threshold observer always responds “signal,” and this always leads to a correct response. However, as the example in the main text illustrates, it is less clear how the high- threshold postulate applies in the context of a forced-choice identification task involving more than two possible stimulus-response alternatives—which is usually the case in EAS experiments.
This outcome is likely because the vowels /i/ and /u/ have similar first-formant frequencies (around 350–450 Hz), but very different second-formant frequencies (around 1100 Hz for /u/ versus 2300–2800 Hz for /i/) (Hillenbrand et al., 1995); thus, these two vowels are likely to be confused when listening to a lowpass-filtered version of the speech signal, but less likely to be confused when listening to a highpass-filtered vocoded version of the speech signal.
A model of how speech signals are encoded and decoded in the human auditory system remains elusive, and is beyond the scope of this study.
In decision theory, two decision rules are considered to be equivalent if they always lead to the same decision.
One might expect the combined-stimulation advantage to be influenced by the degree of linguistic redundancy (or “context”) of the speech material (e.g., Brown and Bacon, 2009). To the extent that low redundancy corresponds to a higher m value (i.e., more uncertainty) than high redundancy, the SDT models outlined above could predict larger effects of combined stimulation for low-redundancy than for high-redundancy speech material, simply because in these models the steepness of the psychometric function increases as m increases. Contrary to this prediction, Brown and Bacon (2009) found a larger benefit when they supplemented vocoded speech with an informative low-frequency pure-tone carrier for high-context than for low-context sentences. This suggests that other factors, which are not well captured by the simple SDT models described above, can influence the magnitude of combined stimulation advantages in human listeners.
References
- Boothroyd, A., and Nittrouer, S. (1988). “Mathematical treatment of context effects in phoneme and word recognition,” J. Acoust. Soc. Am. 84, 101–114. 10.1121/1.396976 [DOI] [PubMed] [Google Scholar]
- Braida, L. D. (1991). “Crossmodal integration in the identification of consonant segments,” Q. J. Exp. Psychol. A 43, 647–677. 10.1080/14640749108400991 [DOI] [PubMed] [Google Scholar]
- Brown, C. A., and Bacon, S. P. (2009). “Low-frequency speech cues and simulated electric-acoustic hearing,” J. Acoust. Soc. Am. 125, 1658–1665. 10.1121/1.3068441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown, C. A., and Bacon, S. P. (2010). “Fundamental frequency and speech intelligibility in background noise,” Hear. Res. 266, 52–59. 10.1016/j.heares.2009.08.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Büchner, A., Schüssler, M., Battmer, R. D., Stover, T., Lesinski-Schiedat, A., and Lenarz, T. (2009). “Impact of low-frequency hearing,” Audiol. Neuro-Otol. 14(11), 8–13. 10.1159/000206490 [DOI] [PubMed] [Google Scholar]
- Chen, F., and Loizou, P. C. (2010). “Contribution of consonant landmarks to speech recognition in simulated acoustic-electric hearing,” Ear Hear. 31, 259–267. 10.1097/AUD.0b013e3181c7db17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ching, T. Y., Incerti, P., and Hill, M. (2004). “Binaural benefits for adults who use hearing aids and cochlear implants in opposite ears,” Ear Hear. 25, 9–21. 10.1097/01.AUD.0000111261.84611.C8 [DOI] [PubMed] [Google Scholar]
- Cullington, H. E., and Zeng, F. G. (2009). “Bimodal hearing benefit for speech recognition with competing voice in cochlear implant subject with normal hearing in contralateral ear,” Ear Hear. 31, 70–73. 10.1097/AUD.0b013e3181bc7722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorman, M. F., Gifford, R. H., Spahr, A. J., and McKarns, S. A. (2008). “The benefits of combining acoustic and electric stimulation for the recognition of speech, voice and melodies,” Audiol. Neuro-Otol. 13, 105–112. 10.1159/000111782 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorman, M. F., Spahr, A. J., Loizou, P. C., Dana, C. J., and Schmidt, J. S. (2005). “Acoustic simulations of combined electric and acoustic hearing (EAS),” Ear Hear. 26, 371–380. 10.1097/00003446-200508000-00001 [DOI] [PubMed] [Google Scholar]
- Fletcher, H. (1953). Speech and Hearing in Communication (Van Nostrand, New York: ), 461 p. [Google Scholar]
- Gantz, B. J., and Turner, C. (2004). “Combining acoustic and electrical speech processing: Iowa/Nucleus hybrid implant,” Acta Oto-Laryngol. 124, 344–347. 10.1080/00016480410016423 [DOI] [PubMed] [Google Scholar]
- Gantz, B. J., Turner, C., and Gfeller, K. (2004). “Expanding cochlear implant technology: Combined electrical and acoustical speech processing,” Cochlear Implants International 5(1), 8–14. 10.1002/cii.147 [DOI] [PubMed] [Google Scholar]
- Gantz, B. J., Turner, C., and Gfeller, K. E. (2006). “Acoustic plus electric speech processing: preliminary results of a multicenter clinical trial of the Iowa/Nucleus Hybrid implant,” Audiol. Neuro-Otol. 11(1), 63–68. 10.1159/000095616 [DOI] [PubMed] [Google Scholar]
- Gantz, B. J., and Turner, C. W. (2003). “Combining acoustic and electrical hearing,” Laryngoscope 113, 1726–1730. 10.1097/00005537-200310000-00012 [DOI] [PubMed] [Google Scholar]
- Gfeller, K. E., Olszewski, C., Turner, C., Gantz, B., and Oleson, J. (2006). “Music perception with cochlear implants and residual hearing,” Audiol. Neuro-Otol. 11(1), 12–15. 10.1159/000095608 [DOI] [PubMed] [Google Scholar]
- Green, D. M., and Birdsall, T. G. (1958). “The effect of vocabulary size on articulation score,” Technical Memorandum No. 81 and Technical Note AFCRC-TR-57-58, University of Michigan, Electronic Defense Group.
- Green, D. M., and Dai, H. P. (1991). “Probability of being correct with 1 of M orthogonal signals,” Percept. Psychophys. 49, 100–101. 10.3758/BF03211621 [DOI] [PubMed] [Google Scholar]
- Green, D. M., and Swets, J. A. (1966). Signal Detection Theory and Psychophysics (Krieger, New York: ), 479 p. [Google Scholar]
- Hillenbrand, J., Getty, L. A., Clark, M. J., and Wheeler, K. (1995). “Acoustic characteristics of American English vowels,” J. Acoust. Soc. Am. 97, 3099–3111. 10.1121/1.411872 [DOI] [PubMed] [Google Scholar]
- Kong, Y. Y., and Braida, L. D. (2011). “Cross-frequency integration for consonant and vowel identification in bimodal hearing,” J. Speech Lang. Hear. Res. 54, 959–980. 10.1044/1092-4388(2010/10-0197) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong, Y. Y., and Carlyon, R. P. (2007). “Improved speech recognition in noise in simulated binaurally combined acoustic and electric stimulation,” J. Acoust. Soc. Am. 121, 3717–3727. 10.1121/1.2717408 [DOI] [PubMed] [Google Scholar]
- Kong, Y. Y., Stickney, G. S., and Zeng, F. G. (2005). “Speech and melody recognition in binaurally combined acoustic and electric hearing,” J. Acoust. Soc. Am. 117, 1351–1361. 10.1121/1.1857526 [DOI] [PubMed] [Google Scholar]
- Kryter, K. D. (1962). “Methods for the calculation and use of the articulation index,” J. Acoust. Soc. Am. 34, 1689–1697. 10.1121/1.1909094 [DOI] [Google Scholar]
- Li, N., and Loizou, P. C. (2008). “A glimpsing account for the benefit of simulated combined acoustic and electric hearing,” J. Acoust. Soc. Am. 123, 2287–2294. 10.1121/1.2839013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macmillan, N. A., and Creelman, C. D. (2005). Detection Theory: A User’s Guide (Erlbaum, Mahwah, NJ: ), 492 p. [Google Scholar]
- Miller, G. A., and Nicely, P. E. (1954). “An analysis of perceptual confusion among some English consonants,” J. Acoust. Soc. Am. 27, 338–352. 10.1121/1.1907526 [DOI] [Google Scholar]
- Mok, M., Grayden, D., Dowell, R. C., and Lawrence, D. (2006). “Speech perception for adults who use hearing aids in conjunction with cochlear implants in opposite ears,” J. Speech Lang. Hear. Res. 49, 338–351. 10.1044/1092-4388(2006/027) [DOI] [PubMed] [Google Scholar]
- Müsch, H., and Buus, S. (2001). “Using statistical decision theory to predict speech intelligibility. I. Model structure,” J. Acoust. Soc. Am. 109, 2896–2909. 10.1121/1.1371971 [DOI] [PubMed] [Google Scholar]
- Nittrouer, S., and Boothroyd, A. (1990). “Context effects in phoneme and word recognition by young children and older adults,” J. Acoust. Soc. Am. 87, 2705–2715. 10.1121/1.399061 [DOI] [PubMed] [Google Scholar]
- Pelli, D. G. (1985). “Uncertainty explains many aspects of visual contrast detection and discrimination,” J. Opt. Soc. Am. A 2, 1508–1532. 10.1364/JOSAA.2.001508 [DOI] [PubMed] [Google Scholar]
- Pelli, D. G., Burns, C. W., Farell, B., and Moore-Page, D. C. (2006). “Feature detection and letter identification,” Vision Res. 46, 4646–4674. 10.1016/j.visres.2006.04.023 [DOI] [PubMed] [Google Scholar]
- Pirenne, M. H. (1943). “Binocular and uniocular threshold of vision,” Nature 152, 698–699. 10.1038/152698a0 [DOI] [Google Scholar]
- Qin, M. K., and Oxenham, A. J. (2006). “Effects of introducing unprocessed low-frequency information on the reception of envelope-vocoder processed speech,” J. Acoust. Soc. Am. 119, 2417–2426. 10.1121/1.2178719 [DOI] [PubMed] [Google Scholar]
- Ronan, D., Dix, A. K., Shah, P., and Braida, L. D. (2004). “Integration across frequency bands for consonant identification,” J. Acoust. Soc. Am. 116, 1749–1762. 10.1121/1.1777858 [DOI] [PubMed] [Google Scholar]
- Seldran, F., Micheyl, C., Truy, E., Berger-Vachon, C., Thai-Van, and H., Gallego, S. (2011). “A model-based analysis of the combined-stimulation advantage,” Hear. Res. 282, 252–264. 10.1016/j.heares.2011.06.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treisman, M. (1998). “Combining information: probability summation and probability averaging in detection and discrimination,” Psychol. Methods 3, 252–265. 10.1037/1082-989X.3.2.252 [DOI] [Google Scholar]
- Turner, C. W., Gantz, B. J., Vidal, C., Behrens, A., and Henry, B. A. (2004). “Speech recognition in noise for cochlear implant listeners: benefits of residual acoustic hearing,” J. Acoust. Soc. Am. 115, 1729–1735. 10.1121/1.1687425 [DOI] [PubMed] [Google Scholar]
- Uchanski, R. M., and Braida, L. D. (1998). “Effects of token variability on our ability to distinguish between vowels,” Percept. Psychophys. 60, 533–543. 10.3758/BF03206044 [DOI] [PubMed] [Google Scholar]
- van Trees, H. L. (1968). Detection, Estimation, and Modulation Theory. Part I (Wiley, New York: ), 696 p. [Google Scholar]
- von Ilberg, C., Kiefer, J., Tillein, J., Pfenningdorff, T., Hartmann, R., Stürzebecher, E., and Klinke, R. (1999). “Electric-acoustic stimulation of the auditory system. New technology for severe hearing loss,” J. Otorhinolaryngol. Relat. Spec. 61, 334–340. 10.1159/000027695 [DOI] [PubMed] [Google Scholar]
- Warren, R. M., Riener, K. R., Bashford, J. J. A., and Brubaker, B. S. (1995). “Spectral redundancy: Intelligibility of sentences heard through narrow spectral slits,” Percept. Psychophys. 57, 175–182. 10.3758/BF03206503 [DOI] [PubMed] [Google Scholar]
- Wickens, T. (2002). Elementary Signal Detection Theory (Oxford University Press, Oxford: ), 262 p. [Google Scholar]