Further evidence that fundamental-frequency difference limens measure pitch discrimination

Abstract

Difference limens for complex tones (DLCs) that differ in F0 are widely regarded as a measure of periodicity-pitch discrimination. However, because F0 changes are inevitably accompanied by changes in the frequencies of the harmonics, DLCs may actually reflect the discriminability of individual components. To test this hypothesis, DLCs were measured for complex tones, the component frequencies of which were shifted coherently upward or downward by ΔF = 0%, 25%, 37.5%, or 50% of the F0, yielding fully harmonic (ΔF = 0%), strongly inharmonic (ΔF = 25%, 37.5%), or odd-harmonic (ΔF = 50%) tones. If DLCs truly reflect periodicity-pitch discriminability, they should be larger (worse) for inharmonic tones than for harmonic and odd harmonic tones because inharmonic tones have a weaker pitch. Consistent with this prediction, the results of two experiments showed a non-monotonic dependence of DLCs on ΔF, with larger DLCs for ΔF’s of ±25% or ±37.5% than for ΔF’s of 0 or ±50% of F0. These findings are consistent with models of pitch perception that involve harmonic templates or with an autocorrelation-based model provided that more than just the highest peak in the summary autocorrelogram is taken into account.

INTRODUCTION

The sounds produced by most musical instruments, and many speech or animal-communication sounds, are harmonic, meaning that their component frequencies are all integer multiples of a common low frequency, which is traditionally referred to as the fundamental frequency (F0). These harmonic sounds evoke a pitch corresponding to their F0; this is variously referred to as “residue pitch” (de Boer, 1956a; Schouten et al., 1962), “periodicity pitch” (Terhardt, 1970), or “virtual pitch” (Terhardt, 1979).

A traditional approach for determining how accurately listeners can perceive the pitch of complex tones involves measuring thresholds for the discrimination of small changes in F0 between two successive harmonic tones (e.g., Moore and Glasberg, 1988; Houtsma and Smurzynszki, 1990; Shackleton and Carlyon, 1994; Demany and Semal, 2002; Micheyl and Oxenham, 2004; Moore and Moore, 2003a; Hopkins and Moore, 2007; Oxenham et al., 2009). Experiments of this type are traditionally referred to as “F0-discrimination experiments,” and the thresholds that are measured in such experiments are usually referred to as F0-discrimination thresholds or difference limens for F0 (DLF0s). These thresholds are commonly regarded as a measure of listeners’ ability to discriminate F0 or, subjectively, residue pitch. However, when the complex tones being compared are composed of the same harmonic ranks, listeners need not compare F0 or residue pitch to perform the task; they can instead directly compare the frequencies of corresponding harmonics in the tone complexes. Consistent with this hypothesis, Faulkner (1985) found that difference limens for pairs of complex tones (DLCs) that contained the same harmonics were generally smaller than DLCs for pairs of tones that did not each contain the same set of harmonics.

Two studies have questioned this conclusion. In the first, Moore and Glasberg (1990) measured DLCs for complex tones that contained corresponding low-rank harmonics—making it possible for listeners to discriminate shifts in the frequencies of individual partials—but different upper-rank harmonics, so that the tones differed in timbre. The results revealed that the DLCs for such tones were larger than the DLCs for tones that contained only corresponding harmonics and thus had a more similar timbre. Moore and Glasberg (1990) interpreted this finding as evidence that timbre differences interfere with the ability to perceive pitch differences, even with corresponding harmonics, thus providing an alternative interpretation for Faulkner’s (1985) results. In addition, Moore and Glasberg (1990) measured DLCs for complex tones that were made inharmonic by shifting the frequencies of odd and even harmonics by 15% of their nominal F0, in opposite directions, which produced inharmonic complex tones with an irregular spectral spacing. They found that the DLCs for such inharmonic tones were larger than the DLCs for harmonic tones. They interpreted this outcome as further evidence that DLCs reflect residue-pitch discrimination and are larger when residue pitch is weak or ambiguous as is usually the case for inharmonic tones. Based on these findings, Moore and Glasberg (1990) concluded that DLCs for complex tones with common harmonics depend on residue pitch comparisons rather than on comparisons of the pitches of the partials.

A more recent study by Micheyl et al. (2010) provided further evidence that DLCs reflect the discriminability of residue pitch rather than that of individual partials. Their results showed significantly larger DLCs for inharmonic complex tones produced by shifting the frequencies of all of the components of a harmonic complex tone upward by a constant amount (ΔF) in Hertz, which maintained the regular spectral spacing of the components on a linear frequency scale, than for harmonic complex tones. Because the perceptual grouping, or “fusion,” of spectral components appears to depend more on regular spectral spacing than on harmonicity per se (Roberts and Brunstrom, 1998, 2001, 2003; Brunstrom and Roberts, 2000), the results of Micheyl et al. (2010) cannot be explained simply by weak fusion of the inharmonic tone components, compared to the harmonic stimuli.

The current study extends the study of Micheyl et al. (2010) in two ways. A first limitation of their study stems from the fact that it did not test frequency shifts larger than 25% of the F0. If the conclusion that DLCs reflect residue-pitch discrimination is correct, DLCs should decrease as ΔF is increased from 25% to 50% of the F0. This is because, when ΔF equals 50% of the F0, the stimulus becomes periodic again with a fundamental period equal to twice the original F0 period. Spectrally, the stimulus corresponds to an odd-harmonics series with a missing F0 equal to one half of the frequency separation between consecutive components. Introspectively, complex tones consisting of odd-numbered harmonics elicit a more salient pitch than inharmonic complex tones produced by applying a frequency shift of 25% (Roberts and Brunstrom, 2001). Thus if DLCs reflect residue-pitch discrimination rather than comparisons of individual component frequencies, they should vary nonmonotonically with ΔF, first increasing as ΔF increases from 0% to 25% of the F0, then decreasing as ΔF increases from 25% to 50%.

A second limitation of the study of Micheyl et al. (2010) is that the frequency shifts were always positive. As a result, the frequency ratios between consecutive components in the frequency-shifted tones were always smaller, on average, than the frequency ratios between consecutive components in the harmonic tones.1 Smaller frequency ratios between consecutive components imply that on a logarithmic frequency scale, consecutive frequency components are separated by a smaller distance on average in inharmonic conditions than in harmonic conditions. The finding of Micheyl et al. (2010) of larger DLCs for inharmonic than for harmonic tones may have been due to this effect rather than to inharmonic tones having a less salient pitch. To investigate this possibility, the current study tested negative ΔF’s (−25%, −37.5%, and −50%) in addition to positive ΔF’s.

A final goal of this study was to examine whether the dependence of DLCs on ΔF can be explained by an autocorrelation model of pitch discrimination. “Place” models of pitch perception that involve harmonic templates (e.g., Goldstein, 1973; Wightman, 1973; Cohen et al., 1995; Cedolin and Delgutte, 2005) and temporal models involving “periodic templates” (e.g., Cariani, 2004; Bidelman and Heinz, 2011) can, at least in principle, account for better discriminability of harmonic complex tones than for inharmonic complex tones. This is because harmonic (or periodic) templates cannot match place (or temporal) responses patterns to inharmonic tones as well as they match response patterns to harmonic tones. However, it was not clear whether two frequently used metrics of pitch discriminability or salience, based on the autocorrelation function—namely, the Euclidean distance (ED) (Meddis and Hewitt, 1991a,b; Meddis and O’Mard, 1997; Bernstein and Oxenham, 2005) and the first highest peak corresponding to a non-zero lag (Cariani and Delgutte, 1996a,b; Patterson et al., 1996; Patterson et al., 2000; Yost, 1996a, 1997; Yost et al., 1996)—could also account for differences in discrimination thresholds between harmonic and inharmonic tones. To address this question, we computed “summary autocorrelation functions” (SACFs) (Meddis and O’Mard, 1997) for complex tones having the same spectral and temporal characteristics as those used in this study and examined whether the psychophysical data could be accounted for using the ED or the first highest peak in the SACFs.

EXPERIMENT 1: MAIN EXPERIMENT

Methods

Listeners

Ten listeners (6 female, 4 male; ages 18–30 yr, mean= 22.5 yr) participated in this experiment. The listeners had 5–12 yr (mean = 9.6 yr) of experience playing one or two musical instruments. All had normal hearing, defined as pure-tone thresholds of 15 dB HL or less at octave frequencies between 500 and 8000 Hz. The listeners first participated in a familiarization test during which they performed six runs of the tracking procedure, described in the following text, using harmonic complex tones. During testing, listeners were seated in a double-walled sound-attenuating booth (IAC). Participants provided written informed consent prior to inclusion in the study and were paid for their participation.

Stimuli

The stimuli were harmonic and inharmonic complex tones. The harmonic tones contained harmonics with ranks between N and N+5. The lowest harmonic number, N, was equal to 2 in one of the two observation intervals of a trial and to 3 in the other interval. The F0s of the two harmonic tones presented on a trial were equal to F0_high = F0_ref(1 + ΔF0/100)^1/2 for the higher-F0 tone, and F0_low = F0_ref(1 + ΔF0/100)^−1/2 for the lower-F0 tone, where F0_ref is the “reference” F0 (in Hz), which was defined as the geometric mean of the two F0s presented on a trial, and ΔF0 is the difference between the two F0s and is expressed as a percentage of the lower F0. On each trial, F0_ref was drawn at random from a 20%-wide uniform probability distribution centered on 400 Hz. This across-trial “roving” of F0 was introduced to discourage listeners from forming a representation of the standard in long-term memory and then comparing incoming tones against this fixed representation rather than against each other. As explained in the next section (Sec. 2A3), the percentage F0 difference between the two complexes, ΔF0, was varied adaptively during the course of a block of trials.

The frequency-shifted tones were produced by shifting the component frequencies of the harmonic tones upward or downward by the same amount in Hz. Depending on the condition being tested, the frequency shift, ΔF, was equal to plus or minus (±) 25%, 37.5%, 50% of the F0 of the harmonic tone prior to the application of any frequency shift. The 37.5% shift was introduced following Brunstorm and Roberts (2000; see also Roberts and Brunstrom, 2001). These authors found that, like the 25% shift, the 37.5% shift resulted in stimuli having an ambiguous pitch, but in addition, for the 37.5% shift, there is an emerging pitch component one octave below the F0. As shown in Sec. 5, this emerging sub-octave component is apparent in SACFs of simulated auditory-nerve-fiber responses.

The tones were 400 ms in duration each, including 20-ms on and off (raised-cosine) ramps. The starting phases of the harmonics were drawn independently in each presentation from a uniform distribution with 0–360° support. The tones had a level of 50 dB SPL per component, corresponding to an overall level of 57.8 dB SPL. The tones were presented in pink noise with a spectrum level of 20 dB SPL at 800 Hz. This level was selected based on previous findings, which indicate that it should be sufficiently high to mask any potential distortion products generated by the complex tones (e.g., Oxenham et al., 2009). The noise started 400 ms before the first tone on a trial and ended 400 ms after the offset of the second tone on each trial.

Procedure

The DLCs for the harmonic and inharmonic tones were measured using a two-interval, two-alternative forced-choice (2I-2AFC) paradigm and a transformed two-down, one-up procedure that tracked the 70.7%-correct point on the psychometric function (Levitt, 1971). On each trial, two tones were presented that differed in F0 (where, here and in the remainder of the text, the term “F0” refers to the F0 of the complex prior to frequency shifting). The higher-F0 tone was played either first or second with equal probability. The task of the listener was to indicate which of the two observation intervals contained the higher-F0 tone. The two observation intervals were marked on the computer screen. Listeners gave their responses by pressing “1” or “2” on a computer keyboard. At the beginning of an adaptive “run” (block of trials), the F0-difference (ΔF0) between the two tones was set to 4% of the F0. This difference was increased following each incorrect response and decreased following two consecutive correct responses. Until the first reversal in the direction of the change in the tracking variable from “up” to “down,” ΔF0 was increased and decreased by a factor of 4. This factor was reduced to 2 after the second up-to-down reversal, and to $\sqrt{2}$ after the third up-to-down reversal. The adaptive procedure stopped after a total of four reversals with the smallest step size. Threshold was computed as the geometric mean of the ΔF0 values at the last four reversals.

As in the main experiment of Micheyl et al. (2010) two adaptive tracks were randomly interleaved on each run. On one track, the lowest harmonic number (N) was 2 for the lower-F0 complex and 3 for the higher-F0 complex; thus, the frequency of the lowest harmonic and the F0 changed in the same direction between the two observation intervals. For the other track, it was the opposite. These two types of tracks are referred to as “consistent” and “inconsistent” tracks, respectively. Had these two track types not been interleaved, the listeners would have been able to perform the task correctly, and consistently, based on changes in the frequency of the lowest (or highest) harmonic or on changes in the spectral center of gravity (subjectively, the timbre) of the stimuli. For example, if all trials had been of the “consistent” type, listeners would have scored a correct response by pressing the button corresponding to the interval containing the tone with the brighter timbre. If all trials had been of the “inconsistent” type, listeners would have scored a correct response by pressing the button corresponding to the interval containing the tone with the duller timbre. The random interleaving of “consistent” and “inconsistent” tracks was to prevent the listeners from doing this; because the change in timbre did not provide a reliable cue, listeners could not perform consistently above chance by relying solely on this cue.

Listeners were instructed that they should focus on pitch and try to ignore changes in other aspects of the sound, such as timbre, as much as possible. Feedback was provided after each trial in the form of a message (“correct” or “false”) displayed on the computer screen. Thresholds were computed separately for the two tracks based on the ΔF0 values on the last four turn-points of the adaptive staircase procedure within each track. Therefore two threshold estimates were obtained for each adaptive run, one for each track.

All but one listener completed six runs of the interleaved-tracking procedure per frequency-shift condition. The other listener completed only two runs per condition. However, because the two thresholds measured in this listener were consistent with each other and fell in the range of the thresholds measured in other listeners, they were included in the analysis.

Apparatus

A Madsen Conera^TM Diagnostic Audiometer (GN Otometrics, A/S) was used for pure-tone audiometry. During the experiments proper, stimulus presentation and response collection were controlled using the AFC software package (Stefan Ewert, Universität Oldenburg) under matlab (The MathWorks, Inc.). The stimuli were generated digitally and played out via a soundcard (LynxStudio L22) with 24-bit resolution and a sampling frequency of 32 kHz. They were presented monaurally to the listener via Sennheiser HD 580 headphones.

Data analysis

Statistical analyses involved repeated-measures analyses of variance (ANOVA) followed by planned (a priori) pairwise comparisons using Student’s paired t-tests. Thresholds were log-transformed prior to averaging and statistical analyses. The thresholds and threshold ratios, shown in the figures or reported in the text in the following text, were computed using geometric means. Standard deviations and standard errors were computed on the log-transformed thresholds.

Results

DLCs for “consistent” and “inconsistent” tracks

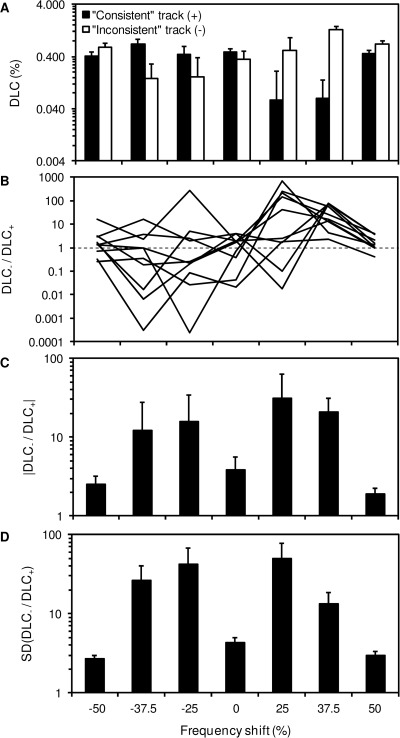
The mean DLCs across all listeners are shown in Fig. 1A for each frequency-shift condition. The DLCs for “consistent” tracks are shown separately from DLCs for “inconsistent” tracks. Larger discrepancies between the two types of tracks are apparent for frequency shifts of ±25% or ±37.5% than for frequency shifts of 0% and ±50%. However, a statistical analysis of these data revealed that these mean DLCs only differed significantly between consistent and inconsistent tracks for the +37.5% frequency shift [t(9) = −7.77, P < 0.0005; for the other conditions: |t(9)| < 1.92, P > 0.087]. In this condition, the DLCs measured on inconsistent tracks were larger than the DLCs measured on consistent tracks.

Figure 1.

DLCs and DLC ratios measured for “consistent” and “inconsistent” tracks as a function of frequency shift in Experiment 1. (A) Geometric-mean DLCs across all listeners, for “consistent” tracks (filled bars), and “inconsistent” tracks (empty bars). (B) Individual DLC ratios. These ratios were obtained by dividing the geometric-mean DLCs across “inconsistent” tracks (denoted DLC₋), in a given listener and a given frequency-shift condition, by the geometric-mean DLC across corresponding “consistent” tracks (denoted DLC₊), for the same listener and condition. Ratios larger than 1 indicate larger DLCs on “inconsistent” tracks than on “consistent” tracks. (C) Geometric-mean of the deviations of the DLC ratios from 1. These values were obtained by computing the mean of the absolute values of the log-transformed DLC ratios across all runs for a given frequency-shift condition in a given listener, then, taking the mean across listeners, and finally, transforming back to the linear domain by applying the antilog function. (D) Geometric-mean SD of DLC ratios. These values were obtained by computing the SD of the log-transformed DLC ratios across runs in a given listener, squaring the results, computing the mean across runs, and finally, transforming back to the linear domain by applying the antilog function. Error bars show +1 geometric standard error of the geometric mean across listeners.

The reason why the apparent differences in mean DLCs between consistent and inconsistent tracks were not statistically significant for the other frequency-shift conditions can be understood by considering individual data, which are shown in Fig. 1B. This figure shows individual DLC ratios, which were obtained by dividing the mean DLC across all inconsistent tracks (DLC₋) by the mean DLCs across all consistent tracks (DLC₊), separately for each listener and each frequency-shift condition. The different lines correspond to different listeners. Ratios greater than 1 indicate larger DLCs on inconsistent than on consistent tracks, whereas values less than 1 indicate the converse. Note that except for the +37.5% and +50% frequency-shift conditions, in which all or most listeners had DLC ratios above 1, DLCs ratios were distributed below and above 1. The magnitude of the deviation from 1 of the DLC ratios was computed as the antilog of the absolute value of the difference between the log-transformed DLCs measured on consistent and inconsistent tracks. This magnitude is shown in Fig. 1C and provides a measure of the difference in DLCs between the two types of tracks, irrespective of the sign. As can be see in Fig. 1C, the average magnitude was consistently larger for the ±25% and ±37.5% frequency-shift conditions than for the 0% and ±50% frequency-shift conditions [paired t-test comparing the mean of the absolute values of the differences in the log-transformed DLCs between consistent and inconsistent tracks, averaged across the 0% and± 50% on the one hand and across the ±25% and ±37.5% on the other hand; t(9) = 6.62, P < 0.0005]. This indicates that the DLCs measured on consistent tracks and the DLCs measured on inconsistent tracks in a given listener were significantly more different from each other in the ±25% and± 37.5% frequency-shift conditions than in the 0 and ±50% frequency-shift conditions.

Variability in the DLC ratios was observed, not only across listeners, but also across runs within a given listener. This is illustrated in Fig. 1D, where the histogram bars show the geometric mean, across listeners, of the across-run geometric standard deviation (SD) of the DLC ratios—a measure of the across-run variability of the DLC ratios.2 This quantity was larger, on average, for the ±25% and ±37.5% frequency-shift conditions than for the 0% and ±50% frequency-shift conditions [paired t-test comparing the SDs of the log-transformed DLC ratios across the following two sets of conditions: 0% and ±50% on the one hand, and ±25% and ±37.5% on the other hand; t(9) = 3.62, P < 0.006].

The observed variability in DLC ratios across listeners and runs suggests that listeners used inconsistent response strategies. For instance, it may be that listeners’ judgments were more influenced by timbre than by pitch on some runs than on others. Based on informal reports from the listeners, the fact that the DLCs measured on consistent tracks were sometimes larger than the DLCs measured on inconsistent tracks, whereas the opposite pattern should have been observed if the listeners tended to confuse higher pitch with brighter timbre, appears to be due to listeners “over-compensating” for a perceived tendency to follow the “wrong” cue.

Overall, the results shown in Fig. 1 are consistent with the finding of Micheyl et al. (2010) that “raw” DLCs measured separately on consistent and inconsistent tracks are influenced by other factors than F0 or residue pitch, which co-vary with changes in the lowest harmonic number. The results also extend the findings of Micheyl et al. (2010) by showing that similar patterns are observed for both positive and negative frequency-shifted complexes.

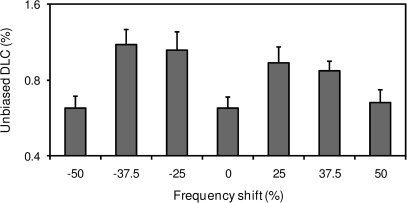
Unbiased DLCs

Figure 2 shows “unbiased DLCs,” which were computed by combining the DLCs measured on consistent and inconsistent tracks (from the same run) according to the following equation (see Micheyl et al., 2010 for an explanation of the basis of this equation),

$${\mathrm{DLC}}_{\mathrm{u}}=100[\sqrt{(1+\frac{{\mathrm{DLC}}_{+}}{100})(1+\frac{{\mathrm{DLC}}_{-}}{100})}-1].$$ (1)

In this equation, DLC₊ and DLC₋ denote the DLCs (in % of F0) measured on consistent and inconsistent tracks, respectively, and DLC_u is the “unbiased” DLC (also in % of F0). Modeling listeners’ decisions in Experiment 1 as based on a linear combination of the difference in F0 and the difference in the lowest-component frequency (both expressed in octaves), unbiased DLCs provide a measure of listeners’ ability to discriminate F0-related changes, uncontaminated by response biases related to changes in the frequency of the lowest component across the two observation intervals of each trial (see Micheyl et al., 2010 for details). Unbiased DLCs were computed separately for each pair of “raw” DLCs corresponding to “consistent” and “inconsistent” tracks within the same run and the log-transformed unbiased DLCs were averaged within and across listeners to produce Fig. 2.

Figure 2.

Geometric-mean unbiased DLCs across all listeners. See text for details concerning the computation of these values. Error bars show +1 geometric standard error of the geometric mean across listeners.

A repeated-measures analysis of variance (ANOVA) on the log-transformed unbiased DLCs showed a significant main effect of frequency shift [F(6, 54) = 6.91, P < 0.0005]. Planned comparisons revealed that the unbiased DLCs obtained in the ±25% and ±37.5% frequency-shift conditions were significantly larger on average than both the unbiased DLCs obtained in the 0% frequency-shift condition [paired t-tests comparing the 0% and −37.5% frequency-shift conditions: t(9) = 3.97, P = 0.003; for 0% versus −25%: t(9) = 3.01, P = 0.015; for 0% versus +25%: t(9) = 4.69, P = 0.001; for 0% versus +37.5% t(9) = 6.01, P < 0.0005] and the unbiased DLCs obtained in the ±50% frequency-shift conditions [t(9) = 5.40, P < 0.0005 for −50% versus −37.5%; t(9) = 3.19, P = 0.011 for −50% versus −25%; t(9) = 2.76, P = 0.022 for +50% versus +25%; and t(9) = 3.21, P = 0.011 for +50% versus +37.5%]. No statistically significant difference in unbiased DLCs was observed when comparing the 0% and ±50% frequency-shift conditions [for 0% versus −50%: t(9) = 0.002, P = 0.998; for 0% versus +50%: t(9) = 0.725, P = 0.487].

Discussion

The pattern of results obtained in this experiment is broadly consistent with the hypothesis that when discriminating complex tones, listeners compare residue pitches rather than the frequencies or pitches of individual partials. In this context, the finding of larger unbiased DLCs in the ±25% and ±37.5% frequency-shift conditions than in the 0% frequency-shift condition can be understood by considering that inharmonic tones evoke a more ambiguous, less well-defined pitch than harmonic complexes. The large discrepancies in raw DLCs between consistent and inconsistent tracks, which are apparent in these frequency-shift conditions, presumably reflect the fact that the weak and ambiguous pitch of the stimuli led the listeners to rely more heavily on other cues, such as changes in the frequency of the lowest harmonic or changes in the spectral center of gravity of the complex—which were presumably perceived as timbre changes. Because the direction of changes in the frequency of the lowest harmonic number only provided a valid cue on trials corresponding to consistent tracks, and the two tracks were randomly intermingled, this could explain why DLCs measured on consistent tracks were often smaller than DLCs measured on inconsistent tracks. Based on our informal discussions with the listeners and on personal introspection, we believe that the opposite effect—smaller DLCs on inconsistent tracks than on consistent tracks—resulted from listeners being aware of their tendency to rely on the wrong cue and to then try to correct for this tendency by giving a response opposite to that suggested by the direction of the timbre change. In this context, the large across- and within-listener variability in both the direction and the magnitude of the differences in DLCs between consistent and inconsistent tracks, which is apparent in Fig. 1, may reflect differences in listening or response strategies across listeners or across runs within a given listener. Moreover, the fact that the variability was larger in the ±25% and ±37.5% frequency-shift conditions than in the 0%-shift condition is consistent with the interpretation that in the latter condition, the pitch was less ambiguous, making it possible for listeners to rely more on changes in pitch than on changes in timbre. The finding that the unbiased DLCs decreased as magnitude of the frequency shift increased from 25% or 37.5% to 50% was expected, given that a 50% shift yields an odd-harmonic complex, which evokes a more salient and less ambiguous pitch than an inharmonic complex in which all components are shifted by 25% or 37.5% of the F0 (Brunstrom and Roberts, 2000; Roberts and Brunstrom, 2001).

The finding of larger unbiased DLCs in the +25% frequency-shift condition than in the 0%-shift condition is consistent with the results of a previous study (Micheyl et al., 2010). One difference between the results of the current study and those of the previous study is that in the previous study, the raw DLCs measured on consistent tracks were generally, and consistently, smaller than the raw DLCs measured on inconsistent tracks—in contrast to the across-listener and across-run variability in the sign of the DLC differences in the current study. We do not have a clear-cut explanation for the origin of this difference at present. One possible explanation relates to inter-individual differences in listening (or response) strategies: The participants who were recruited in the current study were perhaps more inclined toward correcting for their tendency to follow timbre changes, which they could infer based on the visual feedback that they received after each trial or based on their own introspection. Feedback does not seem to be a critical factor, however: Micheyl et al. (2010) tested all listeners both with and without feedback and found that feedback had no major influence on the results. Alternatively, or in addition, it is possible that the use of different test conditions, with a larger number of frequency-shift conditions in the current study than in the previous study, contributed to promoting the use of different listening (or response) strategies.

The finding that negative frequency shifts were at least as effective as positive frequency shifts in elevating unbiased DLCs makes it very unlikely that the finding of elevated unbiased DLCs in positive frequency-shift conditions (compared to the 0% frequency-shift condition) in the current study, and the previous study by Micheyl et al. (2010) merely reflects smaller relative frequency spacing between components for the inharmonic complexes than for the harmonic complexes. Although smaller frequency ratios between consecutive components may lead to greater peripheral interactions between components, this effect cannot explain why in the current study, negative frequency shifts, which led to larger frequency ratios between components than for the unshifted complexes, were as effective as positive shifts in elevating DLCs.

Consistent with Moore and Glasberg (1990) and Micheyl et al. (2010), the present results are difficult to reconcile with the hypothesis that in experiments that involve complex tones with corresponding spectral components, listeners compare representations of the frequencies of individual components (Faulkner, 1985). Interactions between components passing through relatively broad auditory filters can result in less accurate representations of the frequencies of individual components when other components are present, and these interactions may be more detrimental when the components are inharmonic than when they are harmonic. However, in the current study, as in the study of Micheyl et al. (2010) and in some of the conditions tested by Moore and Glasberg (1990), the complex-tone components were well resolved peripherally. This makes it unlikely that the frequencies of these components were significantly more or less accurately encoded in the auditory nerve, depending on whether they were harmonically or inharmonically related to the frequencies of the other components present in the complex. We cannot rule out the possibility that cross-frequency interactions generated at higher levels of processing within the auditory system affect neural representations of the frequencies of individual components, depending on whether these components are harmonic or inharmonic; however, we are not aware of published data that would indicate the existence of such harmonicity-dependent neural representations of individual partials in complex tones.

EXPERIMENT 2: SINGLE-TRACK PROCEDURE

Rationale

Although the pattern of variation of unbiased DLCs as a function of ΔF in Experiment 1 is consistent with the hypothesis that unbiased DLCs reflect residue-pitch discrimination, the computation of unbiased DLCs rests on various assumptions concerning the sensory and decision processes leading from a stimulus to a response in this type of experiment; these assumptions are described in detail in the Appendix A of Micheyl et al. (2010). Some of these assumptions refer to unobservable variables corresponding to internal states of the listener that cannot be measured directly. Therefore it would be reassuring if the qualitative pattern of results obtained in Experiment 1 and illustrated in Fig. 2 could be confirmed using an approach that does not involve the calculation of unbiased DLCs. Micheyl et al. (2010) found that DLCs measured using a single-track procedure—in which consistent and inconsistent trials were randomly intermingled but in which the results of these two types of trials were not treated separately—showed the same effect of inharmonicity as the unbiased DLCs measured in the same listeners using an interleaved-tracking procedure. However, Micheyl et al. (2010) tested only one ΔF condition (+25% of F0) with the single-track procedure, and it remains unclear whether their finding holds for other ΔF’s. Accordingly, Experiment 2 extended the control experiment of Micheyl et al. (2010) by measuring DLCs using a single-track procedure in a subset of the listeners from Experiment 1 for all of the frequency-shift conditions tested in that experiment.

Methods

Six of the listeners from Experiment 1 also participated in the current experiment. All six listeners completed three runs in each of the frequency-shift conditions. The stimuli were similar to those used in Experiment 1. As in that experiment, the frequency of the lowest component changed in a random direction (not related systematically to the direction of changes in F0) across observation intervals. The only difference between Experiment 1 and the current experiment was in the tracking procedure. Instead of tracking ΔF0 (the F0 difference between the two tones, prior to the application of any frequency shift) separately for consistent and inconsistent trials, here, a single track (i.e., a single ΔF0 variable) was used. The variable was updated, i.e., increased, decreased, or left unchanged, according to the two-down one-up adaptive-tracking rule, following each trial, regardless of whether the trial was of the consistent or inconsistent type. At the end of a run, the values of the tracking variable corresponding to the last four reversals in the direction of the adaptive staircase were averaged to obtain the DLC for that run.

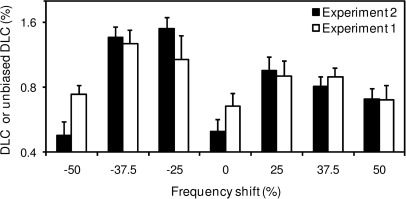
Results

The results of this experiment are shown in Fig. 3 (solid bars). To facilitate comparisons between these DLCs and the unbiased DLCs measured in Experiment 1, the unbiased DLCs of the six listeners who participated in the current experiment were averaged and plotted in Fig. 3 (empty bars). In general, the pattern of the results in the two experiments was very similar. The only condition in which a significant difference between the direct DLCs (Experiment 2) and unbiased DLCs (Experiment 1) was observed was the 0%-shift condition [t(5) = 2.84, P = 0.036; for all other conditions: ∣t(5)∣ < 2.27, P > 0.05]. Importantly, the DLCs and the unbiased DLCs showed a qualitatively similar pattern of variation as a function of ΔF, being significantly larger on average in the ±25% and ±37.5% frequency-shift conditions than in the 0% and ±50% frequency-shift conditions [t(5) = 3.30, P = 0.022 for DLCs; t(5) = 4.06, P = 0.010 for unbiased DLCs].

Figure 3.

Geometric-mean DLCs measured in Experiment 2 and geometric-mean unbiased DLCs measured in the same listeners in Experiment 1. The former are shown by solid bars; the latter are shown using empty bars. Error bars show +1 geometric standard error of the geometric mean across listeners.

Discussion

The results of this experiment indicate that the non-monotonic dependence of DLCs on ΔF, which was observed in Experiment 1, was not simply a result of the dual-tracking procedure or of the computation of unbiased DLCs; the nonmonotic pattern for both positive and negative frequency shifts can be replicated using a simpler measurement procedure, in which the outcomes of consistent and inconsistent trials are not tracked separately.

Although a single-track adaptive procedure is more straightforward to implement than a dual-track procedure, the latter offers the advantage that it provides an indication of the extent to which a listener’s responses were influenced by changes in timbre, or any other aspect of the sensation that co-varies with the frequency of the lowest component in the complex, but is unrelated to residue pitch. This information may help experimenters identify listeners who are more or less able to ignore irrelevant timbre when judging pitch.

EXPERIMENT 3: SPECTRALLY SHAPED COMPLEXES

Rationale

Consistent with the stimuli used by Glabserg and Moore (1990) and Micheyl et al. (2010), the unshifted harmonic complex tones in Experiments 1 and 2 consisted of equal-amplitude components. For such stimuli, it is possible that listeners rely on shifts in the frequency of the lowest component or on shifts in the spectral centroid of the complex (Moore and Moore, 2003a,b; Dai, 2010). To alleviate this concern, experimenters often use bandpass-filtered complex tones with relatively shallow slopes (e.g., Carlyon and Shackleton, 1994; Moore and Moore, 2003a; Micheyl and Oxenham, 2004). In such experiments, the two complex tones presented on a trial usually go through the same filter, so that they have identical spectral envelopes, and the lowest-harmonic number is not roved. It is important to note that this stimulus design does not rule out the possibility that listeners compare the frequencies, or pitches, of individual components; however, it makes potential spectral edge cues (Kohlrausch and Houtsma, 1992) or cues related to the spectral center of gravity (von Bismark, 1974), less salient.

The goal of the current experiment was to test whether significantly larger DLCs are observed for inharmonic complex tones than for harmonic complex tones when the tones are bandpass-filtered. We reasoned that if the DLCs measured with bandpass-filtered complexes reflect residue-pitch comparisons rather than comparisons of individual harmonics, they should be significantly larger for inharmonic complexes tones produced using frequency shifts of ±25% and ±37.5% than for (unshifted) harmonic complex tones. However, if listeners rely instead on comparisons of individual component frequencies, DLCs should not depend on whether the components are harmonic or inharmonic.

Methods

The main difference between this experiment and the previous two experiments is that the spectral components of the complex tones were selectively attenuated to simulate the operation of a bandpass filter with shallow slopes (−7.3 dB/octave). Specifically, the attenuation was applied to components with frequencies lower or higher than our specified corner frequencies. The corner frequencies were set to correspond approximately with the fourth and seventh harmonics in the first condition and the fifth and eighth harmonics in the second condition. Because the F0s of the two complex tones (prior to any frequency shifting) differed across the two observation intervals, the frequencies of the components also differed. However, it was important that the spectral envelope of the stimuli, and therefore, the characteristics of the “filter,” did not change across observation intervals, so as not to provide listeners with a spectral- envelope cue. Therefore the lower corner frequency was automatically set by the program on each trial in such a way that it always equaled the geometric mean of the frequencies of the fourth or fifth harmonic of the two complex tones on the current trial. Similarly, the upper corner frequency was set to the geometric mean of the frequencies of the seventh or eighth harmonic of the two complex tones presented on the current trial. This ensured that the lower corner frequency of the filter always fell in the center (on a logarithmic scale) of the frequencies of the corresponding components of the two tones. The number of components in the complexes was increased, from 6 in the previous two experiments to 16 in the current experiment, so that there would be enough components to fill the 6-dB passband of the filter.

As in Experiment 1, an adaptive procedure with two interleaved tracks was used in the current experiment. However, unlike for Experiment 1, in the current experiment, the rank of the lowest component was not allowed to vary across the two observation intervals within a trial.

Instead the rank differed only across trials corresponding to different tracks. In one track, the rank of the lowest component corresponded to the second harmonic (with the filter corner frequency set to the fourth harmonic); in the other track, it corresponded to the third harmonic (with the filter corner frequency set to the fifth harmonic). Using this procedure, we could obtain data for two lowest-component rank conditions simultaneously. Eight of the listeners from Experiment 1, including the six listeners who participated in Experiment 2, also participated in the current experiment.

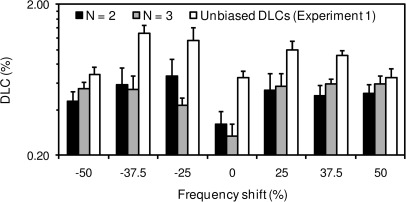
Results

The mean DLCs for this experiment are shown in Fig. 4. The DLCs measured on tracks corresponding to N = 2 and N = 3 are shown as solid and gray bars, respectively. No significant effect of N was observed [F(1, 7) = 0.105, P = 0.755], but DLCs varied significantly across frequency shifts [F(6, 42) = 42.81, P = 0.003]. Planned paired comparisons between DLCs measured in different frequency-shift conditions showed significant differences between the 0%-shift condition and each of the non-zero frequency-shift conditions [8.71< F(1, 7) < 93.99, 0.0005 < P < 0.021]; DLCs were smaller for the 0%-shift condition than for any of the non-zero conditions. No other significant difference was found between the different non-zero frequency-shift conditions.

Figure 4.

Geometric-mean DLCs measured in Experiment 3 and geometric-mean unbiased DLCs measured in the same listeners in Experiment 1. The solid bars correspond to the N = 2 condition of Experiment 3. The gray bars correspond to the N = 3 condition of Experiment 3. The empty bars correspond to unbiased DLCs in Experiment 1. Error bars show +1 geometric standard error of the geometric mean across listeners.

The empty bars in Fig. 4 show the mean unbiased DLCs that were measured in Experiment 1 for the same eight listeners who took part in the current experiment. These unbiased DLCs were generally larger than those measured in the current experiment [planned contrast analysis comparing the mean of the DLCs across the two N conditions in the current experiment with the unbiased DLCs measured in Experiment 1: F(1, 7) = 99.10, P < 0.0005]. This was the case for all frequency-shift conditions considered one at a time [12.95< F(1, 7) < 40.87, 0.0005 < P < 0.009] except for the +50% frequency condition [F(1, 7) = 2.14, P = 0.187].

Discussion

The finding of significantly lower DLCs in the 0%-shift condition than in the ±25% and ±37.5% frequency-shift conditions is consistent with the results of the previous two experiments and suggests that the listeners were not just comparing the frequencies of corresponding individual harmonics across the two observation intervals but that their judgments were influenced by residue pitch. This finding has implications for the interpretation of the results obtained in previous studies of pitch perception using bandpass-filtered complex tones with shallow slopes. Specifically, it suggests that this stimulus design is effective in preventing listeners from basing their responses on shifts in the frequency of the lowest (or highest) component in the complex (Dai, 2010) or on shifts in the spectral centroid (Moore and Moore, 2003a). Indeed if the DLCs measured in this experiment solely reflected the use of these types of cues, they should have been independent of ΔF.

One difference between the results of this experiment and the results of the previous two experiments relates to the lack of significant difference between the DLCs measured in the odd-harmonic (±50% frequency-shift) conditions and the DLCs measured in the inharmonic (±25% and ±37.5%) frequency-shift conditions. We can only offer a tentative explanation concerning the origin of this difference that is related to the fact that the spectral characteristics of the stimuli differed between the current experiment and the previous two experiments. In particular, in Experiments 1 and 2, the stimuli each contained six components (corresponding to harmonics 2 to 7 or 3 to 8). By contrast, in the current experiment, the stimuli had a trapezoidal spectral envelope, with corner frequencies corresponding either to the 4th and 7th harmonics or to the 5th and 8th harmonic, so that only four components (instead of six) were contained in the stimulus passband. Data in the literature indicate that the pitch salience of complex tones increases with the number of components (Goldstein et al., 1978; Houtsma and Smurzynski, 1990; Laguitton et al., 1998). Although, for strictly harmonic complex tones, four resolved harmonics may suffice to evoke a salient pitch, it is conceivable that the pitch of odd-harmonic stimuli remains ambiguous with only four components present in the passband. This may explain why the DLCs for odd-harmonic stimuli in the current experiment were not significantly lower than the DLCs for inharmonic stimuli.

IMPLICATIONS FOR PITCH-PERCEPTION MODELS

Spectral template-matching models

The finding of larger DLCs for inharmonic tones than for harmonic tones can be accounted for, in principle, by pitch-perception models that use harmonic or periodic templates to estimate pitch (e.g., Goldstein, 1973; Wightman, 1973; Gerson and Goldstein, 1978; Goldstein et al., 1978; Terhardt et al., 1982; Srulovicz and Goldstein, 1983; Cohen et al., 1995; Cedolin and Delgutte, 2005). Because harmonic templates cannot match an inharmonic input perfectly, models of this type produce less precise—or multiple—matches for inharmonic inputs than for harmonic ones. This is reflected in smaller or broader peaks in the representations that are used to determine residue pitch in these models, e.g., the “transformed peripheral activity pattern” in Wightman’s (1973) “pattern-transformation model” or the “likelihood function” in Goldstein’s (1973) “optimal processor.” For example, Wightman’s pattern-transformation model predicts a decrease in pitch strength as the magnitude of the frequency shift (ΔF) increases over a range of about 20% for a 200-Hz F0 stimulus [see Fig. 4 in Wightman (1973)]. Although Wightman (1973) did not report discrimination-threshold predictions using his model, it is likely that a shift in the estimated pitch, i.e., a horizontal shift in the position of the dominant peak in the transformed peripheral activity pattern, is less easily discriminated if the peak is small and broad than if it is tall and sharp. A similar idea underlies predictions of pitch accuracy in Goldstein’s (1973) model and its more recent extensions (e.g., Gerson and Goldstein, 1978; Srulovicz and Goldstein, 1983). Thus harmonic template-matching models can account, at least qualitatively, for the finding of larger pitch-discrimination thresholds for inharmonic tones than for harmonic tones.

Harmonic-template-matching models can also account, in principle, for the finding of small DLCs for shifts equal to ±50% of the F0 (Experiments 1 and 2). Although a template containing all harmonics may not match the odd-harmonic stimuli quite as well as a template that contains solely odd harmonics, this can be remedied by including templates for incomplete harmonic series into the model, as was done by Gerson and Goldstein (1978). While the suggestion that the auditory system may contain templates for odd-harmonic series may seem contrived, it is important to note that inasmuch as templates arise through repeated exposure to natural harmonic sounds, these templates are likely to include a variety of spectral shapes. For instance, the sounds produced by some musical instruments, such as the clarinet, are dominated by energy at the odd harmonics. Including templates with a wide variety of spectral shapes may be necessary for spectral template-based models to successfully mimic human listeners’ ability to perceive the pitch of natural stimuli, which can have widely different spectral envelopes.

Temporal autocorrelation model

An alternative approach to modeling pitch perception, which has gained popularity during the last two decades, relies on the computation of the autocorrelation function—specifically, the SACF (Meddis and Hewitt, 1991a,b; Meddis and O’Mard, 1997). The SACF is obtained by summing the autocorrelation functions of the outputs of frequency-selective auditory filters with different characteristic frequencies (CFs; e.g., Meddis and Hewitt, 1991a,b; Cariani and Delgutte, 1996a,b; Meddis and O’Mard, 1997). One advantageous feature of the SACF is that the F0 can be determined directly, based on the location of the first salient peak corresponding to a non-zero lag (e.g., de Cheveigné, 2005). Moreover, it has been suggested that the height of the first SACF peak is directly related to perceived pitch strength or pitch salience (Cariani and Delgutte, 1996a,b; Patterson et al., 1996; Patterson et al., 2000; Yost, 1996a, 1997; Yost et al., 1996). Because stimuli that evoke a salient pitch, such as complex tones with well-resolved harmonics, usually yield smaller discrimination thresholds than stimuli that elicit a weak pitch, such as amplitude-modulated noise (Burns and Viemeister, 1976; Shackleton and Carlyon, 1994), the height of the first SACF peak should also correlate with pitch discriminability. Previous studies using iterated ripple noise (IRN) have found that it does (Yost, 1996a,b; Patterson et al., 2000) with the possible exception of long-duration (1 s or longer) stimuli (Yost, 2009). Alternatively, it has been suggested that pitch discriminability depends on differences between the SACFs evoked by the two stimuli being discriminated across the entire range of lags, as measured by the ED (e.g., Meddis and Hewitt, 1991a,b; Meddis and O’Mard, 1997; Bernstein and Oxenham, 2005).

To determine whether the height of the first peak in the SACF, the ED, or some other aspect of the SACF, could account for the non-monotonic variation in unbiased DLCs across frequency-shift conditions observed in Experiment 1, we computed SACFs for pairs of harmonic and frequency-shifted complex-tone signals generated in the same way as those used in the experiment. The details of the model that were used to compute these SACFs are provided in the Appendix. In short, the model included two stages: first, a simulation of peripheral processing including cochlear filtering and compression, auditory-nerve rate-level functions, and frequency-dependent phase locking; second, the computation of the autocorrelation functions of simulated instantaneous spike-rate functions across virtual fibers corresponding to different CFs, followed by CF-dependent weighting to simulate CF-dependent limitations on periodicity encoding in the central auditory system (Cariani, 2004), and finally, summation of the weighted autocorrelation functions across channels.

The resulting SACFs are shown in Fig. 5. Each panel in this figure corresponds to one of the frequency-shift conditions tested in Experiment 1, ranging from +50% at the top to −50% at the bottom. In each panel, two SACFs are shown, corresponding to the lower- and higher-F0 complexes. For these simulations, the lower and higher F0s differed by 0.4% of the lower F0 with a geometric mean equal to 400 Hz. The ΔF0 value of 0.4% of F0 corresponds approximately to the mean DLC measured in the 0%-shift condition of Experiment 1 (Fig. 1). Moreover, to illustrate the influence of the within-trial roving of the lowest harmonic number, which was used in this experiment, the lower- and higher-F0 stimuli that were used for these simulations contained harmonics (before frequency shifting) 2 to 8 and 3 to 9, respectively.

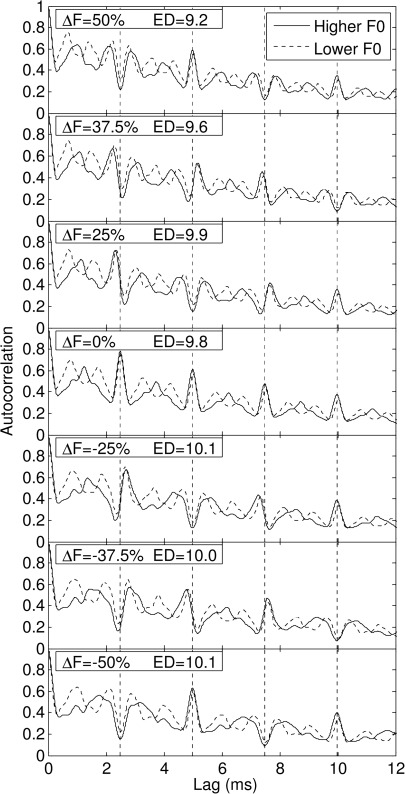
Figure 5.

SACFs for stimuli similar to those used in experiment 1. Each panel corresponds to one of the frequency shifts used in the experiment (the ΔF value is indicated in the upper-left corner)and shows two SACFs: One corresponding to the lower-F0 complex (dashed line) and one corresponding to the higher-F0 complex (solid line). For these simulations, the two F0s (where F0 refers to the F0 prior to the application of coherent frequency shifting) were separated by 0.4% of the lower F0 and geometrically centered on 400 Hz. The computed ED between the two SACFs is explicitly indicated within each panel. The vertical dashed lines indicate the lags corresponding to the F0 of the lower complex and sub-harmonics thereof.

Three observations are worth pointing out. First, in all frequency-shift conditions, relatively large differences between the two SACFs were observed, as reflected in ED values substantially larger than zero; note that the ED is indicated within each panel. These salient SACF differences, which were observed even when the F0 difference between the two tones was set to zero, primarily reflect the difference in spectral content between the stimuli—due to the fact that one stimulus was generated using harmonics 2-8 while the other was generated using harmonics 3-9. While the unbiased DLCs varied non-monotonically as a function of ΔF in Experiment 1, the ED increased monotonically as ΔF decreased from +50% to −50%. Based on these observations, we conclude that the ED does not correctly predict pitch discriminability. Second, for the 0%-shift condition (middle panel), the highest SACF peak (other than the peak corresponding to a lag of zero) occurred at a lag corresponding to the F0—the lag corresponding to the F0 of the lower-F0 complex is indicated by the first vertical dashed line. This is consistent with the hypothesis that the highest SACF peak corresponding to a non-zero lag indicates the perceived pitch (Yost, 1996a,b; Patterson et al., 2000). However, for the other ΔF conditions, the highest SACF peak (other than the zero-lag peak) did not always coincide with the expected perceived pitch as estimated based on the results of previous psychophysical studies of pitch perception for frequency-shifted tones (de Boer, 1956b; Schouten et al., 1962; Patterson, 1973; Patterson and Wightman, 1976; Moore and Moore, 2003b; Micheyl et al., 2010). Nonetheless, it may be possible to reconcile these simulation results with the present and previous results by considering that pitch perception depends on a combination of information across multiple SACF peaks. In particular, the presence of a salient, relatively sharp, and unambiguous peak corresponding to F0/2 in both the 0% and ±50% ΔF conditions compared to smaller and broader corresponding peaks in the ±25% and ±37.5% conditions, suggests a possible explanation for our finding that unbiased DLCs were significantly smaller in the harmonic than in the inharmonic conditions.

Additional work is needed to clarify how information distributed across multiple SACF peaks should be combined to correctly predict the ensemble of psychophysical data available to date, including those collected in the current study.

SUMMARY AND CONCLUSIONS

The findings of this study may be summarized as follows.

• (1)The results of both Experiments 1 and 2 lend further support to the conclusions of earlier studies (Moore and Glasberg, 1990; Micheyl et al., 2010) according to which, when discriminating harmonic complex tones with different F0s, listeners actually discriminate residue pitch rather than the frequencies or pitches of individual partials. Importantly, this was the case even though the stimuli in this study always contained several corresponding frequency components, allowing listeners to base their judgments on local frequency shifts. This outcome is inconsistent with the view that when comparing complex tones that contain corresponding harmonics, listeners always compare the frequencies or pitches of individual partials (Faulkner, 1985).
• (2)The results of Experiment 3 indicate that the conclusion that listeners compare complex pitch (i.e., residue, periodicity, or virtual pitch) rather than the pitches or frequencies of individual partials, extends to situations in which the lowest harmonic number is not roved and in which the tones are bandpass filtered using relatively shallow slopes to limit listeners’ ability to take advantage of spectral-envelope cues. This finding provides further assurance that the DLCs that have been measured in previous studies of pitch perception, using bandpass-filtered complex tones without any roving of the lowest-harmonic number or of the spectral envelope (e.g., Carlyon and Shackleton, 1994; Micheyl and Oxenham, 2004), actually reflect the discriminability of residue pitch.
• (3)Simulations using a temporal autocorrelation model of pitch perception suggest that larger unbiased DLCs for complex tones shifted by ±25% and ±37.5% of F0 than for harmonic or odd-harmonic complex tones may be explained by assuming that pitch perception depends on a combination of information across multiple SACF peaks (as in, e.g., Cariani, 2004; Cedolin and Delgutte, 2005; Bidelman and Heinz, 2011) rather than on the highest SACF peak corresponding to a non-zero lag or the ED. However, it is important to acknowledge, first, that additional work is needed to more precisely specify the decision rule that, when applied to SACFs, can correctly predict the perceived pitch and pitch discriminability for inharmonic complex tones and, second, that “spectral” models of pitch perception involving harmonic templates (e.g., Goldstein, 1973; Wightman, 1973; Terhardt, 1974) can also account, in principle, for the finding of poorer discriminability for harmonic or odd-harmonic tones than for inharmonic tones.

APPENDIX: AUTOCORRELATION MODEL

The peripheral auditory model that we used to simulate auditory-nerve-fiber responses to harmonic and inharmonic complex tones involved the following steps. First, middle-ear filtering was simulated by attenuating the amplitudes of the spectral components according to the middle- ear transfer function described in Glasberg and Moore (2006). Second, additive synthesis was used to produce stimulus waveforms (for the simulations, the sampling frequency was set to 100 kHz), and cochlear filtering was simulated by passing each resulting waveform through a bank of gammatone filters (Patterson et al., 1995) with CFs spaced equally on the ERBN scale (Glasberg and Moore, 1990) from 5 to 35 ERBN, i.e., 163 to 9675 Hz. Third, cochlear compression was simulated by passing the envelope of each gammatone filter output through a compressive nonlinearity described by the following equation (Sachs et al., 1989).

$$d(t)=e(t){(1+\frac{e(t)}{{10}^{c/20}})}^{-1/3},$$ (A1)

where d(t) is the magnitude of basilar-membrane displacement, e(t) is the Hilbert envelope of the considered gammatone-filter output, and c is the “compression threshold,” which refers to the point at which the slope of the function relating input level to basilar-membrane displacement decreases (for details, see Sachs et al., 1989); following Sachs et al. (1989), c was set to 30 dB SPL.

Fourth, the time-varying mean spike rate was determined using the following transformation (Sachs et al., 1989)

$$\overline{r}(t)=\frac{{\overline{r}}_{\text{max}}{[d(t)/{10}^{\theta /20}]}^{1.77}}{1+{[d(t)/{10}^{\theta /20}]}^{1.77}}+r_s,$$ (A2)

where θ is the assumed threshold of the simulated auditory-nerve fiber (in dB SPL), ${\overline{r}}_{\text{max}}$ is the maximum mean rate (i.e., the “saturation” rate, in spike/s), and r_s is the spontaneous rate (also in spike/s). The simulations presented in this article were obtained with θ set to 20 dB SPL, which corresponds to a “low threshold” fiber (Liberman, 1978), and with r_s set to 10 spike/s. While we acknowledge that this spontaneous rate, which was chosen to maximize the peak-to- trough ratios in the SACF, is atypically low for low-threshold fibers, simulations performed using higher values for this parameter led to qualitatively similar conclusions. Similarly, changes in the value of the threshold parameter, θ, did not markedly affect the conclusions. Note that the time-varying “mean spike rate” described in Eq. A2 follows the envelope but not the temporal fine structure of the input; the fine-structure is introduced in the following equation.

Fifth, the instantaneous spike rate was determined using the equation (Colburn, 1973),

$$r(t)=\frac{\overline{r}(t)}{I_0(g(\overline{f}))}{e}^{g(\overline{f})\mathit{cos}\left(\mathit{arg}[\stackrel{⌢}{x}(t)]\right)}.$$ (A3)

In this equation, I₀ is the zeroth-order modified Bessel function of the first kind; g is a parameter related monotonically to the synchronization index or “vector strength” (see following text); $\hat{x}(t)$ is the analytic signal of the gammatone-filter output; the function $\arg [\hat{x}(t)]$ gives the instantaneous phase, and the $\mathit{cos}\left(\mathit{arg}[\hat{x}(t)]\right)$ gives the carrier (or temporal fine structure); finally, $\overline{f}$ is the geometric-mean instantaneous frequency (in Hz) of the gammatone-filter output, which was computed as,

$$\overline{f}=\exp (1/T{\int }_T\mathit{ln}\left((\partial \mathit{arg}[\hat{x}(t)]/\partial t2\pi )\right)\mathit{dt}),$$ (A4)

where T denotes the time interval over which the gammatone filter output was taken (in s). Equation A4 makes use of the fact that the instantaneous frequency equals the derivative of the instantaneous phase with respect to time. In practice, negative instantaneous frequencies, which occasionally occurred during zero crossings of the gammatone filter output, had to be removed. The time interval, T, was chosen so that the gammatone-filter output was in the steady state (i.e., transients were not included). The duration of the interval was set to twice the lag corresponding to the lowest F0 for which the ACF was computed.

The frequency-dependent parameter, $g(\overline{f})$, in Eq. A3 is related to the frequency-dependent synchronization index, $s(\overline{f})$, by (Colburn, 1973)

$$g(\overline{f})=\frac{I_1(s(\overline{f}))}{I_0(s(\overline{f}))}.$$ (A5)

The dependence of the synchronization index on frequency is not known for humans. Here, the dependence of the synchronization index on input frequency was modeled as

$$s(\overline{f})=s_0{\left|\frac{1}{1+\sqrt{-1}\frac{\overline{f}}{{\overline{f}}_c}}\right|}^6.$$ (A6)

The two vertical bars on the right-hand side of Eq. A6 denote the absolute-value operator, which was used to compute the magnitude of the complex quantity between the bars. The variable, s₀, which denotes the maximum synchronization index, was set to 0.8; this value corresponds approximately to the mean synchronization index measured in auditory-nerve fibers of cats and other mammals in response to low-frequency pure-tones (e.g., Johnson, 1980). Equation A6 represents the transfer function of a low-pass filter obtained by cascading six first-order low-pass filters with a cutoff frequency, ${\overline{f}}_c$, of 4800 Hz. These parameters were chosen so that s(t) would roll off at roughly 100 dB/decade above about 2500 Hz (Heinz et al., 2001).3

The output of the above-described peripheral auditory model consisted of an ensemble of time-dependent instantaneous spike rates, r_i(t), where the index, i (1,…, n), refers to the ith peripheral auditory “channel” in the ensemble of n channels. The un-normalized ACF of each half-wave-rectified filter output was computed using the following equation,

$$c_i\left[l\right]=\sum _{k=0}^{m-1}p[k]p[k+l],$$ (A7)

where l indexes the “lag” (or time shift), m equals the length of the ACF window (expressed as a number of samples), and

$$p[j]=r(j{\Delta }_t){\Delta }_t$$ (A8)

is the probability of a spike occurring in a time interval of length Δ_t (s) centered on the jth sample. The value of Δ_t was equal to the sampling period, i.e., the inverse of the sampling frequency; r is the time-dependent instantaneous spiking rate computed using Eq. A3.

Following previous investigators (e.g., Cariani, 2004; Bernstein and Oxenham, 2005; Bidelman and Heinz, 2011), the unnormalized ACF from each channel was multiplied point-wise by a weight vector, which is sometimes referred to as a “lag window,”

$$w_i\left[l\right]=e^{-l/{\tau }_i},l=1,\dots ,m.$$ (A9)

The channel-dependent time constant, τ_i, was obtained using the following equation,

$$\mathit{ln}({\tau }_i)=\beta \mathit{ln}{(f_{\mathit{ci}})}^{\alpha },$$ (A10)

where f_ci denotes the CF of channel i. The values of the constants, α, and β, were set in such a way that the mean-squared-error between the time constants produced using Eq. A10, and the time constants used by Cariani (2004) for CFs comprised between 100 and 1320 Hz was minimized. The resulting time constants ranged from 4.3 ms for the highest CF included in the model (9675 Hz) to 24.4 ms for the lowest CF (165 Hz). Finally, the “summary ACF” (SACF) was computed as the average of the ACFs across all channels.