Abstract
Purpose: To improve image quality and accuracy in dedicated breast computed tomography (BCT) by removing the x-ray scatter signal included in the BCT projections.
Methods: The previously characterized magnitude and distribution of x-ray scatter in BCT results in both cupping artifacts and reduction of contrast and accuracy in the reconstructions. In this study, an image processing method is proposed that estimates and subtracts the low-frequency x-ray scatter signal included in each BCT projection postacquisition and prereconstruction. The estimation of this signal is performed using simple additional hardware, one additional BCT projection acquisition with negligible radiation dose, and simple image processing software algorithms. The high frequency quantum noise due to the scatter signal is reduced using a noise filter postreconstruction. The dosimetric consequences and validity of the assumptions of this algorithm were determined using Monte Carlo simulations. The feasibility of this method was determined by imaging a breast phantom on a BCT clinical prototype and comparing the corrected reconstructions to the unprocessed reconstructions and to reconstructions obtained from fan-beam acquisitions as a reference standard. One-dimensional profiles of the reconstructions and objective image quality metrics were used to determine the impact of the algorithm.
Results: The proposed additional acquisition results in negligible additional radiation dose to the imaged breast (∼0.4% of the standard BCT acquisition). The processed phantom reconstruction showed substantially reduced cupping artifacts, increased contrast between adipose and glandular tissue equivalents, higher voxel value accuracy, and no discernible blurring of high frequency features.
Conclusions: The proposed scatter correction method for dedicated breast CT is feasible and can result in highly improved image quality. Further optimization and testing, especially with patient images, is necessary to characterize its impact on clinical performance.
Keywords: breast CT, scatter correction, Monte Carlo, beam stop array, x-ray, mammography, image processing
INTRODUCTION
Although mammography is currently the most common breast imaging technique currently in use, it is not without limitations. Chief among them is its two-dimensional nature, which results in tissue superposition, causing both the possibility for normal tissue to obscure a lesion and for normal tissue overlap to mimic a suspicious lesion. These two effects result in a decrease of sensitivity and specificity for detection and diagnosis of breast cancer, especially in dense breasts.1, 2 To improve on the clinical performance of breast cancer imaging, one of the new technologies being developed is dedicated breast computed tomography (BCT),3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 which has the potential to increase both sensitivity and specificity for detection and diagnosis of breast cancer due to its elimination of the tissue superposition phenomenon. Although promising, the clinical performance advantage of BCT is still being investigated.
BCT is a cone beam CT technique that has been optimized for breast cancer imaging. This involves a geometric setup that results in only the imaged breast being directly irradiated by the x-ray beam, a decrease in the x-ray energy used to acquire the images so as to increase the soft-tissue contrast, and the use of flat panel imagers with small pixel sizes to increase the spatial resolution of the reconstructed images, among other modifications.
However, as is the case with other cone beam CT imaging techniques, BCT suffers from the inclusion of a substantial x-ray scatter signal in the BCT projections. Due to the magnitude and distribution of the scatter signal, which has been previously characterized,16, 17 the BCT reconstructions include cupping artifacts (a reduction in the voxel values toward the center of the breasts) and a reduction in voxel value accuracy and contrast.18
Many scatter reduction methods have been suggested, both specifically for BCT and for other cone beam CT applications. These include the use of an antiscatter grid,19, 20, 21 the use of bow-tie filters,19 extrapolation of the signal under the projections of the collimator leaves,22 assuming either a constant SPR (Ref. 23) or shift-invariant scatter point spread functions,24, 25 performing Monte Carlo (MC) simulations of each acquisition,26 using primary signal modulation27, 28 or using a beam stop array or strip.29, 30, 31, 32, 33, 34 For the beam stop array or strip methods, several acquisition protocols and array geometries have been proposed in an effort to minimize or completely eliminate the need to acquire additional projections, which involve both additional scan time and radiation dose. These methods include interprojection interpolation of the scatter estimate,29, 30 movement of the beam stop array during the scan,31, 32, 33 and positioning of the array so as to take advantage of data redundancies.34 Finally, some analytical model-based algorithms have been proposed showing promising results.35, 36
Here, a novel method for x-ray scatter reduction for BCT imaging is proposed that is inspired by the beam stop array method, but it is fundamentally distinct, involving negligible additional dose and having the potential to be more accurate. Due to its lack of assumptions related to BCT imaging, the proposed method has the potential to be applicable for other cone beam CT and radiographic applications, although this possibility would need to be further investigated. To determine the feasibility and the potential for image quality and accuracy improvement in BCT, both Monte Carlo simulations and phantom testing were performed.
METHODS AND MATERIALS
Scatter reduction method
The fraction of the total x-ray signal that is due to scattered x-rays at any location in a BCT projection, denoted scatter fraction (SF), can be of the order of 50%.16 However, the scatter contribution from a single pencil beam illuminating the breast is very low. It is the combination through convolution of scatter point spread functions with the whole primary x-ray field that results in a substantial scatter signal. Therefore, sampling of the breast attenuation via a limited number of pencil beams throughout the field of view should result in a minimal x-ray scatter signal, yielding information, at discrete image locations, of the primary-only signal. The difference between the primary-only signals at these sampled locations and the total image signals at the same locations from a full field acquisition is therefore an estimate of the scatter signal present in the full field projections. Since it is known that the scatter signal in a BCT projection includes only low spatial frequencies, interpolation or approximation of the scatter signal throughout the whole projection from the estimated discretely sampled points is possible and should yield an adequate estimate of the true x-ray scatter signal. Once this scatter estimate is obtained, it can be subtracted from the acquired BCT projections to obtain an estimate of the primary-only signal in the BCT projections. These projections can now be used to reconstruct the corrected, scatter-free, BCT image.
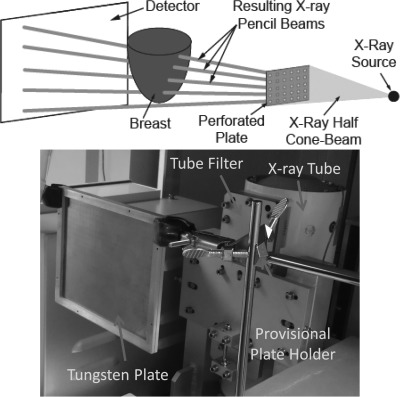
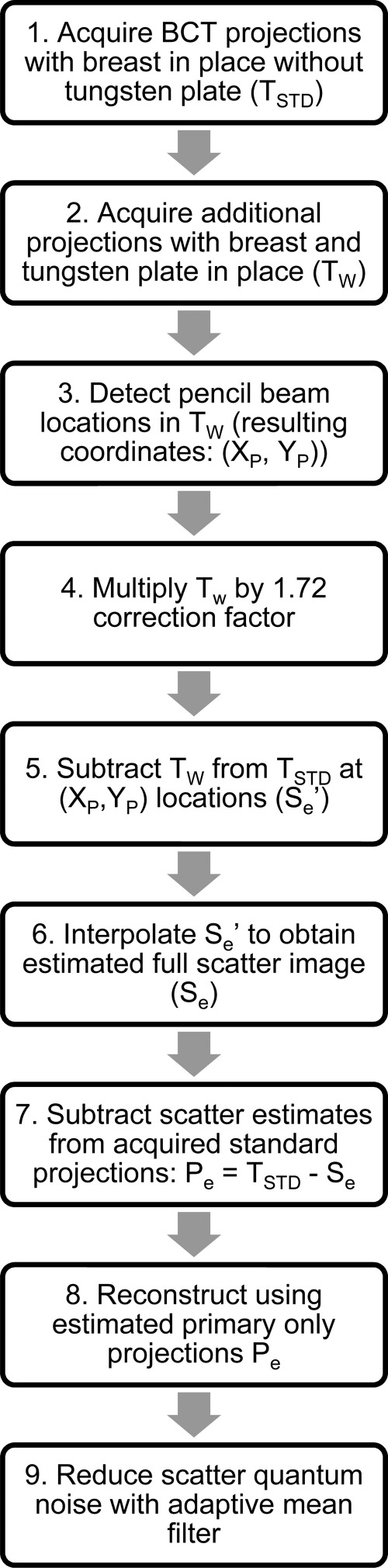
To implement this method, it is necessary to acquire an additional set of BCT projections of the imaged breast immediately after acquiring the set of standard BCT projections. For this additional set, however, the x-ray beam needs to be limited to a discrete number of pencil beams. For this, a thin perforated tungsten plate, thick enough to attenuate all x-rays except for those that travel through the perforations, is placed between the x-ray source and the imaged breast (Fig. 1). The x-ray spectrum used by the BCT clinical prototype (Koning Corp., West Henrietta, NY) installed at our institution37 uses a single x-ray spectrum for all acquisitions, with a fixed tube voltage of 49 kVp and a tungsten target and aluminum filter resulting in a first half value layer of 1.39 mm Al.37 For this spectrum, it was determined that the thinnest commercially available tungsten sheet (0.254 mm) was thick enough to attenuate >99% of the x-ray beam. A plate of this thickness, big enough for its projection to cover the entire detector when placed 20 cm from the x-ray source, was perforated with an array of holes of 0.3556 mm diameter, each separated, center-to-center, by 6.67 mm in both directions. The hole diameter chosen was the smallest sized hole that could be machined in a tungsten plate. The hole separation, considering the magnification factor due to the system setup (source to imager distance = 92.3 cm, source to plate distance = 20 cm, magnification = 92.3/20 = 4.62x) resulted in a sampling distance at the detector of approximately 3 cm. These parameter selections were deemed suitable for this initial study, considering the competing requirements of maximizing sampling rate while minimizing total x-ray field size to minimize scatter at the detector and dose to the imaged breast. This setup resulted in an array of approximately 100 pencil beams illuminating the imaged breast and detector. Therefore, the primary-only signal would be sampled at 100 different points throughout the image. The implementation of the entire algorithm is detailed in Fig. 2.
Figure 1.
(Top) Schematic of the setup for the acquisition of the additional BCT projections with the perforated tungsten plate in place. (Bottom) Photograph of the perforated tungsten plate placed in the BCT system between the x-ray tube and the position of the breast being imaged. A portion of the plate holder, currently a static holder that is manually inserted and extracted from the field of view, can also be seen.
Figure 2.
Flow chart of the proposed scatter correction method.
Due to the finite focal spot size (nominal size of 0.3 mm)38 and the unfocused nature of the perforations on the tungsten plate, the placement of the tungsten plate results in a reduction of the intensity of the incident x-ray pencil beams compared to the intensity of the beam at the corresponding locations with the plate absent. Although the thinness of the tungsten plate was aimed to minimize this, acquisition of a BCT projection with no object in place with and without the plate in place resulted in a reduction in signal at the pencil beam locations of a factor of approximately 1.72. Therefore, in step 4 of the algorithm (Fig. 2), the pencil beam signal is first multiplied by this correction factor. The implementation of this proposed method in different BCT systems that may use a different spectrum from that used in this study’s BCT system may result in the need for the use of a tungsten plate of a different thickness to ensure the appropriate attenuation of the x-ray field. This variation in plate thickness may also result in a variation in this correction factor.
It should be noted that since the pencil beam locations are found automatically and independently in each projection (step 3 in Fig. 2) (“Find Maxima” function, IMAGEJ, National Institutes of Health, Bethesda, MD), repeatability in the positioning of the tungsten plate between acquisitions is not required.
The interpolation of the scatter-only signal estimate is performed using an inverse distance weighting interpolation algorithm,39 followed by Gaussian smoothing to reduce the impact of noise on the interpolation.
X-ray scatter quantum noise reduction
As has been previously discussed,40 any algorithm that involves the subtraction of the low-frequency scatter signal postacquisition results in an increase in the relative image noise due to the remaining quantum noise from the x-ray scatter signal that is not subtracted out. Therefore, to ameliorate this effect, the use of a noise reduction filter postreconstruction, the adaptive mean filter,41 is included in the proposed algorithm. Although many edge-preserving noise filters have been proposed in the past,40, 41, 42, 43 an exhaustive comparison of each is beyond the scope of the present study.
Monte Carlo simulations
Using a previously developed and validated Monte Carlo simulation37, 44 based on the GEANT4 toolkit,45, 46 the acquisition of a BCT projection of a semi-ellipsoidal breast using the available clinical prototype with and without the tungsten plate in place was simulated. To simulate a high scatter condition, the breast was simulated as a homogeneous breast of average composition (20% glandular density47) having a diameter at the chest wall of 18 cm and a chest wall to nipple distance of 18 cm. The x-ray source was simulated as a 0.3 mm square source that emits x-rays isotropically toward the detector with a previously estimated energy distribution resulting from an aluminum-filtered x-ray tube set at a tube voltage of 49 kVp.37 The average glandular dose from the standard acquisition and the acquisition with the tungsten plate in place was obtained and compared. In addition, to verify the validity of the primary-only estimate at the pencil beam locations, the resulting scatter fractions at these locations were obtained.
Phantom testing
To test the proposed algorithm, a breast phantom consisting of a latex glove full of water (representative of breast glandular tissue37, 48, 49) was inserted in a cylinder of olive oil (representative of breast adipose tissue37, 48, 49) and placed on the BCT system. Various small solid cylindrical targets (CIRS, Inc., Norfolk, VA) were inserted inside each of the glove fingers. These targets included one representative of a homogeneous mixture of 40% glandular/60% adipose tissue, one representative of adipose tissue with a set of six microcalcifications each 400 μm in diameter, and one representative of 100% adipose tissue. To again simulate a high scatter condition, the breast phantom was approximately 16 cm in diameter and 16 cm in height. The BCT system used for the acquisitions uses a fixed exposure time per projection of 8 ms, while the tube current used for each acquisition is user-selectable, however, and for this study was set to 200 mA, which was the value recommended by the system’s automatic exposure control. With the breast phantom in place, both the standard BCT projections and the special BCT projections with the tungsten plate in place were acquired. The acquired standard BCT projections were processed using the proposed method and reconstructed using the BCT system’s native FDK reconstruction.50
To obtain a best-case scenario and independent almost-scatter-free acquisition of the breast phantom, a third acquisition was performed after placing a lead sheet on the x-ray tube as close as possible to the output window so that only a fan-beam is emitted. The resulting slit, approximately 1 mm thick, resulted in a fan beam that was estimated at 12 mm thick at the isocenter. The resulting reconstruction from this fan beam acquisition was used as a reference standard for evaluation of the capabilities of the proposed method.
To determine the effectiveness of the proposed method, one-dimensional profiles through homogeneous areas of the phantom, as well as areas including some of the included signals were obtained. In addition, the signal difference of the means and the contrast-to-noise ratio (CNR) between regions of interest (ROI) of 100% adipose and 100% glandular were calculated. Histograms of the reconstructions with and without the proposed method and of the fan beam image were also obtained and compared. Finally, the representation of a microcalcification was analyzed to determine if the noise reduction filter results in any unacceptable blurring of the reconstructed image.
RESULTS
Monte Carlo simulations
As expected, due to the severely limited x-ray field used by the BCT projections with the tungsten plate in place, the glandular dose to the simulated breast during acquisition of the pencil beam projections was 0.44% of the glandular dose during acquisition of the standard BCT projections. This confirms that the additional acquisitions necessary for the proposed method result in negligible additional radiation dose.
The mean scatter fraction at the pencil beam locations in the BCT projection with the tungsten plate within the area occupied by the projection of the breast was 0.68% (range: 0.44%–2.15%). This confirms that the assumption that the pencil beam signal consists entirely of primary signal is valid. As mentioned previously, the simulation was performed for a high scatter condition; therefore, these scatter fraction estimates can be taken as an upper limit on the error introduced by this assumption.
Phantom testing
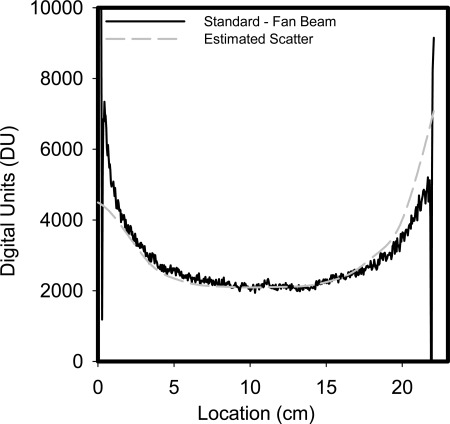
Under the assumption that the difference between the fan beam projections and the unprocessed standard projections are due to scatter only, then Fig. 3 shows horizontal profiles of the measured scatter in one of the BCT projections and the corresponding scatter estimate resulting from the proposed method. It is apparent that the method estimates the scatter signal adequately, with some divergence at the edges of the phantom, where the signal in the projections varies rapidly. Some mismatch between the fan beam projection and the unprocessed standard projection can also be seen (large variations in measured scatter about 2–3 pixels wide at each side of the phantom), possibly due to some motion of the phantom while the lead blocker was being placed for the acquisition of the fan beam image.
Figure 3.
Horizontal profiles of the measured scatter (subtraction of fan beam projection image from the unprocessed standard projection image) and of the scatter estimated by the proposed method at the corresponding location. The profiles correspond approximately to the vertical location shown in the reconstructions in Fig. 4. A good estimate of the scatter signal can be seen, with some divergence close to the edges of the phantom.
Figure 4 shows a slice of the phantom reconstructions of the BCT fan beam, unprocessed standard and processed acquisitions at approximately the same vertical location shown in the horizontal profiles in Fig. 3. As can be seen, the fan beam slice exhibits a very homogeneous signal for both the adipose tissue equivalent background and the glandular equivalent signals. The reconstruction of the processed projections shows substantial reduction in the cupping artifact seen in the standard BCT projection and improvement in the contrast between the signals and the background.
Figure 4.
Reconstructed slices of the breast phantom: (i) fan-beam acquisition; (ii) unprocessed standard acquisition; (iii) processed acquisition. The streak artifacts seen in the images (diagonally from bottom left to top right of the phantom) are due to the handle of the cylindrical phantom, which is not visible due to the window/level settings used. The window width and level (W/L) for these images are: (i) 330/-145, (ii) 270/-275, and (iii) 330/-135.
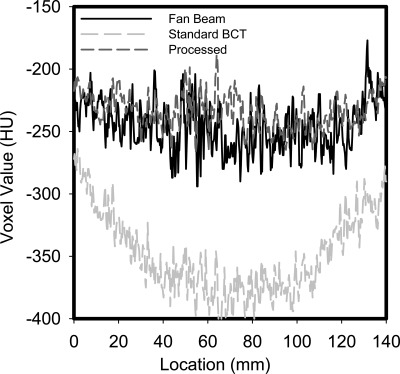
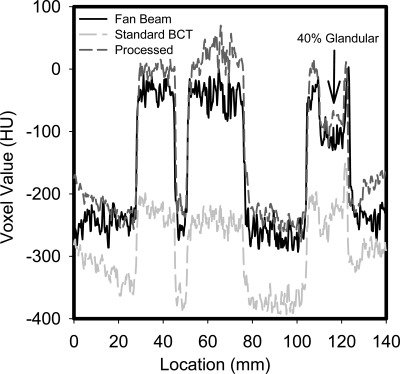
Profiles through homogeneous areas and areas with signals in the reconstructions are shown in Figs. 56, respectively. As can be seen in Fig. 5, the cupping present in the original BCT reconstruction is substantial, and it is greatly reduced by the proposed method. In addition, the values of the voxels (Hounsfield units) in the processed reconstruction are very similar to those in the fan beam reconstruction. From the profile that includes the 100% and 40% glandular targets in an adipose background (Fig. 6), it can be clearly seen that the loss of signal difference in the standard reconstruction is greatly recovered in the processed reconstruction. From this profile, it can be seen that the proposed method results in a higher voxel value for the 100% glandular inserts than that in the fan beam reconstruction.
Figure 5.
Profile through a homogeneous (adipose-equivalent) area of the reconstructions of the fan beam, unprocessed standard, and processed acquisitions. The considerable cupping artifact present in the standard image, and its substantial correction in the processed reconstruction can be clearly seen.
Figure 6.
Profile through an area in the reconstructions containing an adipose-equivalent background (lowest voxel value), 100% glandular-equivalent signals (highest voxel values), and a 40% glandular/60% adipose-equivalent signal (arrow). The improved contrast and accuracy of the processed reconstruction compared to the standard one is apparent.
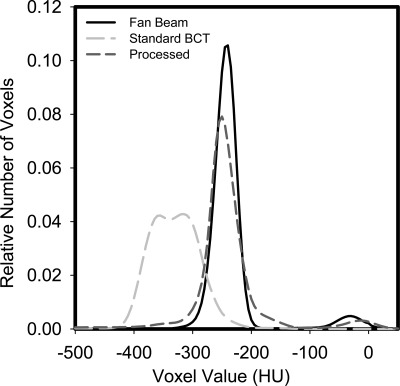
The probability density functions of the fan beam and original and processed BCT reconstructions can be seen in Fig. 7. The clear separation of the adipose tissue equivalent background and the glandular tissue equivalent voxels is apparent in the fan beam and processed reconstructions, while this separation is lost in the original BCT reconstructions.
Figure 7.
Probability density functions of the fan beam, unprocessed standard, and processed reconstructions. The improved separation of the adipose and glandular signals in the processed reconstruction is clear.
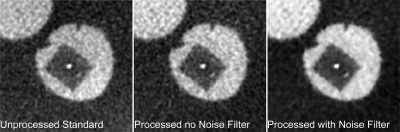
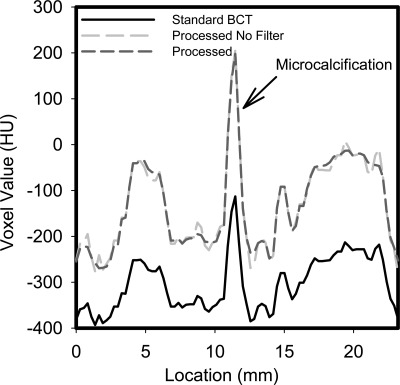
The ROI that includes a microcalcification, and the corresponding profile, shown in Figs. 89, respectively, show that the adaptive mean noise filter has very little impact on the small detailed features in the image while improving the image quality metrics listed in Table TABLE I..
Figure 8.
Portion of reconstruction that includes a 400 μm diameter microcalcification in the unprocessed standard reconstruction and the scatter processed reconstruction with and without the final step in the proposed method, the noise filtering. It can be seen that there is no distinguishable loss in detail of the microcalcification, while the image noise is reduced.
Figure 9.
Profile through the microcalcification shown in Fig. 8, showing the increase in signal due to the proposed process and the negligible loss of resolution due to the application of the noise filter.
TABLE I.
Image quality metrics.
| Mean of signal (HU) | ||||
|---|---|---|---|---|
| 100% adipose | 100% glandular | Signal difference (HU) | CNR | |
| Fan beam | −254 | −39 | 215 | 13.7 |
| Standard BCT | −359 | −243 | 117 | 10.2 |
| Processed before noise filter | −236 | 8 | 244 | 11.8 |
| Processed after noise filter | −237 | 6 | 243 | 23.8 |
DISCUSSION
As seen from the results, the proposed method has resulted in images that substantially reduce the cupping artifact present in the original BCT acquisition and have similar characteristics to the fan beam images. In the profile that includes the water (glandular-equivalent) signals in Fig. 6 and from the ROI metrics in Table TABLE I., it can be seen that the corrected reconstruction results in a somewhat higher voxel value for water than the fan beam image. Although this may be due to over-correction of the scatter signal, it is also noteworthy that the voxel values for water in the corrected reconstructions are closer to 0 HU (the known true voxel value for water) than the fan beam. Therefore, it is possible that the difference in the value of water is due to the fan beam acquisition including some residual scatter signal, rather than an over-correction by the proposed method. A more detailed investigation involving thinner fan beams and their impact on the reconstructed water voxel value would be necessary to better determine the accuracy of the used reference standard.
Based on the Monte Carlo simulation results and the phantom testing, the proposed method appears to be able to substantially reduce the impact of the inclusion of the x-ray scatter signal in BCT imaging while resulting in negligible additional radiation dose to the imaged breast. Although the feasibility of the method has been shown, its reliability and flexibility when applied to real patients’ breasts of different sizes and shapes need to be studied. It is entirely possible that although for the current testing no assumptions were made on the shape or composition of the imaged object (one of the inherent strengths of this method), once more irregular shapes, such as the pendant human breast, are imaged a more robust interpolation algorithm may be required. This may be especially true given the divergence found between the estimated and measured scatter signal close to the edges of the phantom in the horizontal profiles in Fig. 3. In addition, although the limited testing performed has shown feasibility of the proposed method, its true diagnostic impact would have to be evaluated on a large patient case set with outcomes related to clinical performance as the appropriate metric.
As mentioned in Sec. 2, further investigation of the varied edge-preserving noise filters previously proposed needs to be performed to determine the one that results in the best image quality for this application. It is important to note that the aim of the filter in this method is not to reduce the impact of all quantum noise but that that is contributed by the scatter signal.
Although the proposed method has been shown to result in negligible additional radiation dose to the imaged breast, it does result in an increase in the acquisition time. Since an entire additional set of BCT projections needs to be acquired, the total scan time is at least doubled. However, since the tungsten plate has to be positioned in between scans, the minimum total scan time increase, even with an automated and fast positioner, is somewhat larger. In the BCT system used for this study, acquisition of a BCT projection set can only start with the x-ray tube-detector gantry located at the same “home” position, so currently an entire 10 s revolution needs to be performed while the tungsten plate is positioned before the next projection set is acquired. This results in a total scan time of 30 s, which includes a 10 s gap in the middle when the plate is being positioned and no acquisition is taking place. The system could be modified to start acquiring the second projection set at any gantry angle once the tungsten plate is in place, so this total scan time could be reduced. However, the impact that any motion of the breast between the standard and additional acquisition may have on the correction remains to be investigated. As mentioned in the Introduction, some beam stop array methods have been proposed for general CBCT involving interpolation or leveraging data redundancy resulting in negligible or no additional scanning time and dose.29, 30, 31, 32, 33, 34 The efficacy of some of these algorithms, especially those involving interpolation or estimation of the primary signal, in a high spatial resolution modality such as breast CT would need to be evaluated.
In addition, the optimal size and separation of the perforations on the tungsten plate, as well as the optimal distance between the plate and the x-ray source remains to be investigated. For this, a balance needs to be achieved between maximizing sampling rate for an adequate interpolation for the scatter estimation while minimizing the total x-ray field size to minimize both the dose to the breast and the inclusion of scatter in the pencil beam signals.
Finally, due to the relatively low energy x-ray spectrum used in BCT compared to whole body CT, a substantial amount of beam hardening occurs as the x-ray beam travels through the breast. This beam hardening can introduce loss of contrast and additional cupping51 that would not be corrected by the proposed method. To avoid this issue, a reconstruction algorithm that incorporates the polychromatic nature of the x-ray beam and therefore takes beam hardening into account needs to be used. Development of such a reconstruction algorithm for BCT, based on work performed for breast tomosynthesis reconstruction, is being pursued.52
CONCLUSIONS
An x-ray scatter correction method involving both additional hardware and software processing postacquisition has been proposed for dedicated breast CT imaging. Its potential for improving image quality and accuracy has been shown, while additional optimization and more extensive testing, especially on patients, need to be performed. Since the only assumption that is necessary for the correct behavior of this algorithm is the low-frequency characteristic of the x-ray scatter signal, a phenomenon that is true for most, if not all, x-ray based imaging, it is feasible that the proposed algorithm may have the potential to be applicable in other imaging modalities, most notably other cone beam CT applications.
ACKNOWLEDGMENTS
The project described was supported by Grants Numbers P50CA128301 and R01CA163746 from the National Cancer Institute and the Georgia Research Alliance (Cancer Research Award). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute, the National Institutes of Health, or the Georgia Research Alliance.
References
- Kerlikowske K., Grady D., Barclay J., Sickles E. A., and Ernster V., “Effect of age, breast density, and family history on the sensitivity of first screening mammography,” JAMA 276, 33–38 (1996). 10.1001/jama.1996.03540010035027 [DOI] [PubMed] [Google Scholar]
- Kolb T. M., Lichy J., and Newhouse J. H., “Comparison of the performance of screening mammography, physical examination, and breast US and evaluation of factors that influence them: An analysis of 27,825 patient evaluations,” Radiology 225, 165–175 (2002). 10.1148/radiol.2251011667 [DOI] [PubMed] [Google Scholar]
- Boone J. M., Nelson T. R., Lindfors K. K., and Seibert J. A., “Dedicated breast CT: Radiation dose and image quality evaluation,” Radiology 221, 657–667 (2001). 10.1148/radiol.2213010334 [DOI] [PubMed] [Google Scholar]
- Chen B. and Ning R., “Cone-beam volume CT breast imaging: Feasibility study,” Med. Phys. 29, 755–770 (2002). 10.1118/1.1461843 [DOI] [PubMed] [Google Scholar]
- Ning R., Conover D. L., Chen B., Schiffhauer L., Cullinan J., Ning Y., and Robinson A. E., “Flat-panel-detector-based cone-beam volume CT breast imaging: Phantom and specimen study,” Proc. SPIE 4682, 218–227 (2002). 10.1117/12.465562 [DOI] [Google Scholar]
- Boone J. M., Shah N., and Nelson T. R., “A comprehensive analysis of DgN(CT) coefficients for pendant-geometry cone-beam breast computed tomography,” Med. Phys. 31, 226–235 (2004). 10.1118/1.1636571 [DOI] [PubMed] [Google Scholar]
- Ning R., Yu Y., Conover D. L., Lu X., He H., Chen Z., Schiffhauer L., and Cullinan J., “Preliminary system characterization of flat-panel-detector-based cone-beam CT for breast imaging,” Proc. SPIE 5368, 292–303 (2004). 10.1117/12.536231 [DOI] [Google Scholar]
- Boone J. M., “Breast CT: Its prospect for breast cancer screening and diagnosis,” in Advances in Breast Imaging: Physics, Technology and Clinical Applications, Categorical Course in Diagnostic Radiology Physics, edited by Karellas A. and Giger M. L. (Radiological Society of North America (RSNA), Oak Brook, IL, 2004), pp. 165–177. [Google Scholar]
- Boone J. M., Kwan A. L. C., Yang K., Burkett G. W., Lindfors K. K., and Nelson T. R., “Computed tomography for imaging the breast,” J. Mammary Gland Biol. Neoplasia 11, 103–111 (2006). 10.1007/s10911-006-9017-1 [DOI] [PubMed] [Google Scholar]
- Gong X., Glick S. J., Liu B., Vedula A. A., and Thacker S., “A computer simulation study comparing lesion detection accuracy with digital mammography, breast tomosynthesis, and cone-beam CT breast imaging,” Med. Phys. 33, 1041–1052 (2006). 10.1118/1.2174127 [DOI] [PubMed] [Google Scholar]
- Altunbas M. C., Shaw C. C., Chen L., Lai C., Liu X., Han T., and Wang T., “A post-reconstruction method to correct cupping artifacts in cone beam breast computed tomography,” Med. Phys. 34, 3109–3118 (2007). 10.1118/1.2748106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glick S. J., Thacker S., Gong X., and Liu B., “Evaluating the impact of x-ray spectral shape on image quality in flat-panel CT breast imaging,” Med. Phys. 34, 5–24 (2007). 10.1118/1.2388574 [DOI] [PubMed] [Google Scholar]
- Ning R., Conover D., Yu Y., Zhang Y., Cai W., Betancourt-Benitez R., and Lu X., “A novel cone beam breast CT scanner: System evaluation,” Proc. SPIE 6510, 651030–651039 (2007). 10.1117/12.710340 [DOI] [Google Scholar]
- Sechopoulos I., Vedantham S., Suryanarayanan S., D’Orsi C. J., and Karellas A., “Monte Carlo and phantom study of the radiation dose to the body from dedicated CT of the breast,” Radiology 247, 98–105 (2008). 10.1148/radiol.2471071080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindfors K. K., Boone J. M., Nelson T. R., Yang K., Kwan A. L. C., and Miller D. F., “Dedicated breast CT: Initial clinical experience,” Radiology 246, 725–733 (2008). 10.1148/radiol.2463070410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwan A. L. C., Boone J. M., and Shah N., “Evaluation of x-ray scatter properties in a dedicated cone-beam breast CT scanner,” Med. Phys. 32, 2967–2975 (2005). 10.1118/1.1954908 [DOI] [PubMed] [Google Scholar]
- Liu B., Glick S. J., and Groiselle C., “Characterization of scatter radiation in cone beam CT mammography,” Proc. SPIE 5745, 818–827 (2005). 10.1117/12.595396 [DOI] [Google Scholar]
- Bhagtani R. and Schmidt T. G., “Simulated scatter performance of an inverse-geometry dedicated breast CT system,” Med. Phys. 36, 788–796 (2009). 10.1118/1.3077165 [DOI] [PubMed] [Google Scholar]
- Tang X., Ning R., Yu R., and Conover D. L., “Investigation into the influence of x-ray scatter on the imaging performance of an x-ray flat-panel imager-based cone-beam volume CT,” Proc. SPIE 4320, 851–860 (2001). 10.1117/12.430868 [DOI] [Google Scholar]
- Endo M., Tsunoo T., Nakamori N., and Yoshida K., “Effect of scattered radiation on image noise in cone beam CT,” Med. Phys. 28, 469–474 (2001). 10.1118/1.1357457 [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Moseley D. J., Bakhtiar B., Richard S., and Jaffray D. A., “The influence of antiscatter grids on soft-tissue detectability in cone-beam computed tomography with flat-panel detectors,” Med. Phys. 31, 3506–3520 (2004). 10.1118/1.1819789 [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Daly M. J., Bakhtiar B., Moseley D. J., Richard S., Keller H., and Jaffray D. A., “A simple, direct method for x-ray scatter estimation and correction in digital radiography and cone-beam CT,” Med. Phys. 33, 187–197 (2006). 10.1118/1.2148916 [DOI] [PubMed] [Google Scholar]
- Rinkel J., Gerfault L., Esteve F., and Dinten J.-M., “A new method for x-ray scatter correction: First assessment on a cone-beam CT experimental setup,” Phys. Med. Biol. 52, 4633–4652 (2007). 10.1088/0031-9155/52/15/018 [DOI] [PubMed] [Google Scholar]
- Spies L., Ebert M., Groh B. A., Hesse B. M., and Bortfeld T., “Correction of scatter in megavoltage cone-beam CT,” Phys. Med. Biol. 46, 821–833 (2001). 10.1088/0031-9155/46/3/316 [DOI] [PubMed] [Google Scholar]
- Li H., Mohan R., and Zhu X. R., “Scatter kernel estimation with an edge-spread function method for cone-beam computed tomography imaging,” Phys. Med. Biol. 53, 6729–6748 (2008). 10.1088/0031-9155/53/23/006 [DOI] [PubMed] [Google Scholar]
- Zbijewski W. and Beekman F. J., “Efficient Monte Carlo based scatter artifact reduction in cone-beam micro-CT,” IEEE Trans. Med. Imaging 25, 817–827 (2006). 10.1109/TMI.2006.872328 [DOI] [PubMed] [Google Scholar]
- Zhu L., Bennett N. R., and Fahrig R., “Scatter correction method for x-ray CT using primary modulation: Theory and preliminary results,” IEEE Trans. Med. Imaging 25, 1573–1587 (2006). 10.1109/TMI.2006.884636 [DOI] [PubMed] [Google Scholar]
- Zhu L., StarLack J., Bennett N. R., Li T., Xing L., and Fahrig R., “Improved scatter correction for x-ray conebeam CT using primary modulation,” Proc. SPIE 6510, 65101U–65108U (2007). 10.1117/12.713678 [DOI] [Google Scholar]
- Ning R., Tang X., and Conover D. L., “X-ray scatter suppression algorithm for cone-beam volume CT,” Proc. SPIE 4682, 774–781 (2002). 10.1117/12.465628 [DOI] [Google Scholar]
- Ning R., Tang X., and Conover D., “X-ray scatter correction algorithm for cone beam CT imaging,” Med. Phys. 31, 1195–1202 (2004). 10.1118/1.1711475 [DOI] [PubMed] [Google Scholar]
- Zhu L., Strobel N., and Fahrig R., “X-ray scatter correction for cone-beam CT using moving blocker array,” Proc. SPIE 5745, 251–258 (2005). 10.1117/12.594699 [DOI] [Google Scholar]
- Liu X., Shaw C. C., Wang T., Chen L., Altunbas M. C., and Kappadath S. C., “An accurate scatter measurement and correction technique for cone beam breast CT imaging using scanning sampled measurement (SSM) technique,” Proc. SPIE 6142, 614234–614237 (2006). 10.1117/12.656655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J.-Y., Ren L., Liu Q., Kim J., Wen N., Guan H., Movsas B., and Chetty I. J., “Combining scatter reduction and correction to improve image quality in cone-beam computed tomography (CBCT),” Med. Phys. 37, 5634–5644 (2010). 10.1118/1.3497272 [DOI] [PubMed] [Google Scholar]
- Niu T. and Zhu L., “Scatter correction for full-fan volumetric CT using a stationary beam blocker in a single full scan,” Med. Phys. 38, 6027–6038 (2011). 10.1118/1.3651619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiegert J., Bertram M., Rose G., and Aach T., “Model based scatter correction for cone-beam computed tomography,” Proc. SPIE 5745, 271–282 (2005). 10.1117/12.594520 [DOI] [Google Scholar]
- Kyriakou Y., Riedel T., and Kalender W. A., “Combining deterministic and Monte Carlo calculations for fast estimation of scatter intensities in CT,” Phys. Med. Biol. 51, 4567–4586 (2006). 10.1088/0031-9155/51/18/008 [DOI] [PubMed] [Google Scholar]
- Sechopoulos I., Feng S. S. J., and D’Orsi C. J., “Dosimetric characterization of a dedicated breast computed tomography clinical prototype,” Med. Phys. 37, 4110–4120 (2010). 10.1118/1.3457331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Connell A., Conover D. L., Zhang Y., Seifert P., Logan-Young W., Lin C.-F. L., Sahler L., and Ning R., “Cone-beam CT for breast imaging: Radiation dose, breast coverage, and image quality,” Am. J. Roentgenol. 195, 496–509 (2010). 10.2214/AJR.08.1017 [DOI] [PubMed] [Google Scholar]
- Shepard D., “A two-dimensional interpolation function for irregularly-spaced data,” in Proceedings of the 1968 23rd ACM National Conference (ACM, New York, NY, 1968), pp. 517–524.
- Zhu L., Wang J., and Xing L., “Noise suppression in scatter correction for cone-beam CT,” Med. Phys. 36, 741–752 (2009). 10.1118/1.3063001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez R. C. and Woods R. E., Digital Image Processing, 2nd ed. (Prentice Hall, Upper Saddle River, NJ, 2002). [Google Scholar]
- Weickert J., Anisotropic Diffusion in Image Processing (Teubner-Verlag, Stuttgart, Germany, 1998). [Google Scholar]
- Zhong J., Ning R., and Conover D., “Image denoising based on multiscale singularity detection for cone beam CT breast imaging,” IEEE Trans. Med. Imaging 23, 696–703 (2004). 10.1109/TMI.2004.826944 [DOI] [PubMed] [Google Scholar]
- Sechopoulos I., Vedantham S., Suryanarayanan S., and Karellas A., “SU-FF-I-12: Validation of GEANT4’s predictions on x-ray scatter and glandular dose in pendant-geometry cone-beam breast CT,” Med. Phys. 33, 1999–1999 (2006). 10.1118/1.2240250 [DOI] [Google Scholar]
- Agostinelli S. et al. , “GEANT4—A simulation toolkit,” Nucl. Instrum. Methods Phys. Res. A 506, 250–303 (2003). 10.1016/S0168-9002(03)01368-8 [DOI] [Google Scholar]
- Allison J. et al. , “GEANT4 developments and applications,” IEEE Trans. Nucl. Sci. 53, 270–278 (2006). 10.1109/TNS.2006.869826 [DOI] [Google Scholar]
- Yaffe M. J., Boone J. M., Packard N., Alonzo-Proulx O., Huang S. Y., Peressotti C. L., Al-Mayah A., and Brock K., “The myth of the 50–50 breast,” Med. Phys. 36, 5437–5443 (2009). 10.1118/1.3250863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito M., “Dual-energy approach to contrast-enhanced mammography using the balanced filter method: Spectral optimization and preliminary phantom measurement,” Med. Phys. 34, 4236–4246 (2007). 10.1118/1.2790841 [DOI] [PubMed] [Google Scholar]
- Feng S. S. J. and Sechopoulos I., “Clinical Digital Breast Tomosynthesis System: Dosimetric Characterization,” Radiology 263, 35–42 (2012). 10.1148/radiol.11111789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A. 1, 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- Shikhaliev P. M., “Beam hardening artefacts in computed tomography with photon counting, charge integrating and energy weighting detectors: A simulation study,” Phys. Med. Biol. 50, 5813–5827 (2005). 10.1088/0031-9155/50/24/004 [DOI] [PubMed] [Google Scholar]
- Chung J., Nagy J. G., and Sechopoulos I., “Numerical algorithms for polyenergetic digital breast tomosynthesis reconstruction,” SIAM J. Imaging Sci. 3, 133–152 (2010). 10.1137/090749633 [DOI] [Google Scholar]