The Matching Law: A Tutorial for Practitioners

Abstract

The application of the matching law has historically been limited to use as a quantitative measurement tool in the experimental analysis of behavior to describe temporally extended patterns of behavior-environment relations. In recent years, however, applications of the matching law have been translated to clinical settings and populations to gain a better understanding of how naturally-occurring events affect socially important behaviors. This tutorial provides a brief background of the conceptual foundations of matching, an overview of the various matching equations that have been used in research, and a description of how to interpret the data derived from these equations in the context of numerous examples of matching analyses conducted with socially important behavior. An appendix of resources is provided to direct readers to primary sources, as well as useful articles and books on the topic.

Behavior analysts have been interested in the environmental determinants of why behaviors are allocated to particular choice alternatives for some time. Behaviorally speaking, choice is regarded as the distribution of behavior to reinforcement alternatives (see Fisher & Mazur, 1997). In this sense, a “choice” is nothing more than the emission of a particular response in lieu of others. Every instance of operant responding represents the choice to engage in that given behavior at that moment in time, whether due to positive or negative reinforcement (Herrnstein, 1970).

As behavior analysts observe the relative distribution of behavior to reinforcement alternatives, preference may be derived by the proportion of responses allocated to each. Within this conceptual framework, more responding to one alternative indicates a relative preference for that alternative. By simply recording how a client distributes their responses, we can identify preference. For example, one can—with some degree of accuracy—simply observe the behavior of children on a playground to infer their preferences with respect to games, play pals, jungle gym activities, and so on. If we aggregate responses (behaviors emitted on the playground) over time, we can compare these aggregated responses to other possible responses in the environment to determine relative preference. In more colloquial examples, consider how a teacher makes decisions as to what examples to use with her students or how a child chooses which care-giver to approach to request attention. In both cases, history of reinforcement can help explain the present choice. A teacher may use one teaching example over another because, in the past, it evoked more student interest, resulted in better student scores, was easier to explain, etc. Likewise, a child may approach a particular caregiver because that caregiver provides more enthusiastic attention, delivers higher rates of attention, responds to requests more quickly, etc. Each of these examples highlight the importance of understanding the broader, temporally extended, pattern of decision making within the context of reinforcer dimensions associated with each choice alternative (see Neef, Shade, & Miller, 1994).

What Is the Matching Law?

Since the early 1960s (Herrnstein, 1961), behavior analysts have theorized that choice (i.e., relative preference) may be understood—and accurately predicted—by examining relative rates of reinforcement associated with each option (e.g., pecking one of two keys, choosing one worksheet over another, emitting appropriate or problem behavior). In this conceptual framework, relatively dense sources of reinforcement will feature relatively higher rates of behavior (i.e., organisms demonstrate preference for the most reinforcing events/settings). Put simply, behavior matches reinforcement. Herrnstein (1961) formally conceptualized the matching law during a study assessing pigeons' preference for sources of reinforcement. In this study, pigeons could peck one of two response keys in an operant chamber, each of which was on a variable interval (VI) reinforcement schedule. Within this preparation, these two VI schedules were concurrently available and independent of one another; that is, pecking on one key did not affect the schedule of reinforcement on the other. When Herrnstein plotted the relative rates of behavior against relative rates of reinforcement, he found a positive relation between the two resembling a nearly perfect correlation (i.e., a one unit increase in reinforcement was associated with a one unit increase in behavior). This nearly perfect correlation of matching is depicted in Figure 1. Figure 1 illustrates that as reinforcer deliveries increase along the x-axis, proportional increases in behavior are depicted along the y-axis. This correlation is visually apparent in each data point, as each data point represents a perfect correspondence between relative rates of reinforcement and behavior. The line represents the strength of this correlation. In Figure 1, the best fit line features a slope of 1 and each x-axis value (relative rates of reinforcement) perfectly predict y-axis values (relative rates of behaviors) with strict correspondence to the matching law (i.e., all data points fall directly on the line). This observation that relative rates of behavior may be predicted by relative rates of reinforcements resulted in Herrnstein's formulation of the matching law, which states that:

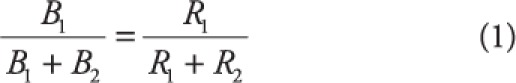where B denotes rate of responses (e.g., responses per minute) at either alternative (denoted by subscripts 1 and 2) and R denotes rate of reinforcement (e.g., reinforcers per minute) at said alternatives. For example, if response B₁ resulted in twice as many reinforcer deliveries relative to B₂ (i.e., R₁ is double the size of R₂), the matching law predicts twice as many B₁ responses. Note that proportions of time spent engaging in behaviors or consuming reinforcers may be used in lieu of rate (see Baum & Rachlin, 1969), such that time spent engaging in behaviors matches reinforcement. When investigating time/duration-based measures of matching, B may be replaced with T (time spent engaging in the response), and durations of reinforcer delivery may use as R in Equation 1.

Figure 1.

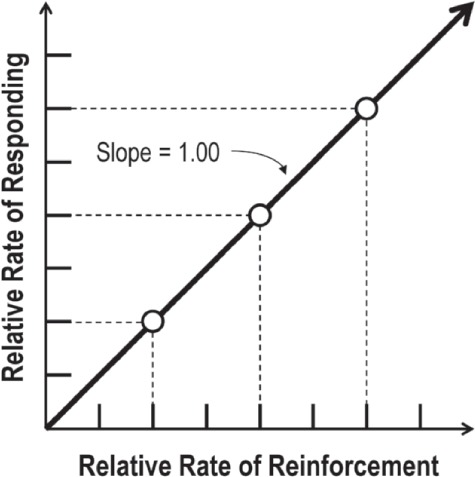
Hypothetical plot of the relative rate of responding changing in perfect proportion to relative rates of reinforcement, that is, “matching.” The left side of Equation 1 captures relative rate of responding (y-axis), whereas relative reinforcement rate is captured by the right side of Equation 1 (x-axis).

How does matching occur in the “real world” where people are not in operant chambers with responses limited to two keys? In one example, Borrero et al. (2010) hypothesized and experimentally demonstrated that an account of matching could be found in the distribution of problem and appropriate behaviors emitted by children with developmental disabilities. These researchers proposed that children distribute either appropriate or inappropriate behaviors as a function of relative rates of reinforcement. Borrero and colleagues conceptualized problem behavior as B₁ and appropriate behaviors as B₂, while experimentally manipulating rates of reinforcement for each response. According to the matching law, relative rates of problem and appropriate behavior should “match” the relative amount of reinforcement associated with each response class.

Suppose that, using the same procedures employed by Borrero et al. (2010), you review a client's data set obtained from mand training sessions. To complete your analysis, you determine that a particular target mand (i.e., a mand you are training) shares the same function as aggression (for this example, we will use attention). Coding your data in this manner results in rates of aggression and appropriate manding as B₁ and B₂, respectively, with R₁ and R₂ representing attention delivered contingent upon aggression and mands. If you were to plot your data in a typical matching plot where relative behavior (B₁/[B₁ + B₂]) is plotted on the y-axis as a function of relative reinforcement (R₁/[R₁ + R₂]) on the x-axis, we would expect the data points to fall along a diagonal line with a slope of 1 (assuming perfect matching wherein one unit change in reinforcement results in one unit change of behavior). Thus, in Figure 2, theoretically “perfect” matching is denoted by the dashed diagonal line. As the hypothetical data in Figure 2 indicate, your client's data fall almost perfectly along this line, suggesting that behavior did indeed conform to the matching law. That is, relative rates of behavior were predicted by relative rates of reinforcement for each response type.

Figure 2.

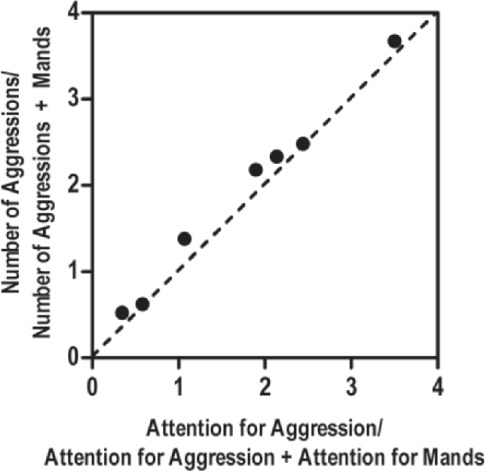
A hypothetical matching law plot of a client's aggressive behavior and manding. The dashed diagonal line depicts perfect matching. The left side of Equation 1 captures relative rate of responding (y-axis), whereas relative reinforcement rate is captured by the right side of Equation 1 (x-axis).

The Generalized Matching Equation

As one might expect, however, researchers are not always successful in identifying or producing “perfect” matching. Many times, the slope of the line through the data points does not correspond to a perfect proportional change in behavior as a function of reinforcement (i.e., the slope does not equal 1). In other cases, there may be a slope of 1, but the line is shifted upward or downward such that the line does not originate (i.e., the y-intercept) from the origin of the graph (i.e., does not pass through coordinate 0,0), meaning that some preexisting bias is impacting responding. For example, if a right-handed child is expected to sort picture cards from piles on either the right or left side of a table, the child may demonstrate a bias for the right given her handedness. To account for such deviations, Baum (1974) proposed the generalized matching equation (GME), which is algebraically equivalent to Equation 1, with the addition of logarithmic transformations and free parameters s and b. The logarithmic transformation of the ratios ensures that the resulting regression line is straight, rather than curvilinear. Having linear regression lines permits an analysis that is more easily interpretable (see Baum, 1974; Shull, 1990). The GME states that:

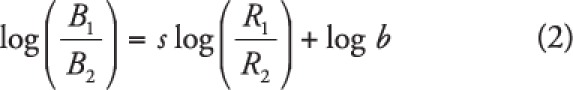where s represents the slope of the best fit line, and b represents the y-intercept. That s and b are free parameters implies that they are not known until linear regression has been applied to the data set (see Reed, 2009). Parameter b (bias) represents how much preference the organism has for either behavior that cannot be accounted for by reinforcement alone. Because the best-fit line allows the behavior analyst to model operant responding at any relative rate of reinforcement, we can examine what responding would look like when there are exactly equal rates of reinforcement for B₁ and B₂. In other words, when there is no difference in the amount of reinforcement that is produced on each alternative, one would expect to see equal responding across each alternative, all else being equal. Figure 3 depicts the log ratios of reinforcement and behavior along the x- and y-axis, respectively. In the top left panel of Figure 3, the log transformation (with a base of 10) of the ratio 1/1 equals zero. Thus, the behavior analyst can examine behavior when log (R₁/R₂) equals zero (that is, reinforcement rate is equal across the responses) to determine the value of the y-intercept—this would occur at the zero value on the x-axis. If the y-intercept (b) is greater than zero, there is a bias for B₁ that is unrelated to reinforcement rate; this is because B₁ is in the numerator of the ratio, and if B₁ is greater than B₂, the log ratio would be positive. An example of positive bias is depicted in the top middle panel of Figure 3, where the y-intercept is above coordinates 0,0. Likewise, if the y-intercept is negative, there is a bias for B₂ (see top right panel of Figure 3). Deviations in bias (away from zero) can result from a host of factors, such as physical characteristics of the organism or environment that unintentionally affect the ability to respond (Baum, 1974; e.g., handedness, color bias, quality of caregivers' attention).

Figure 3.

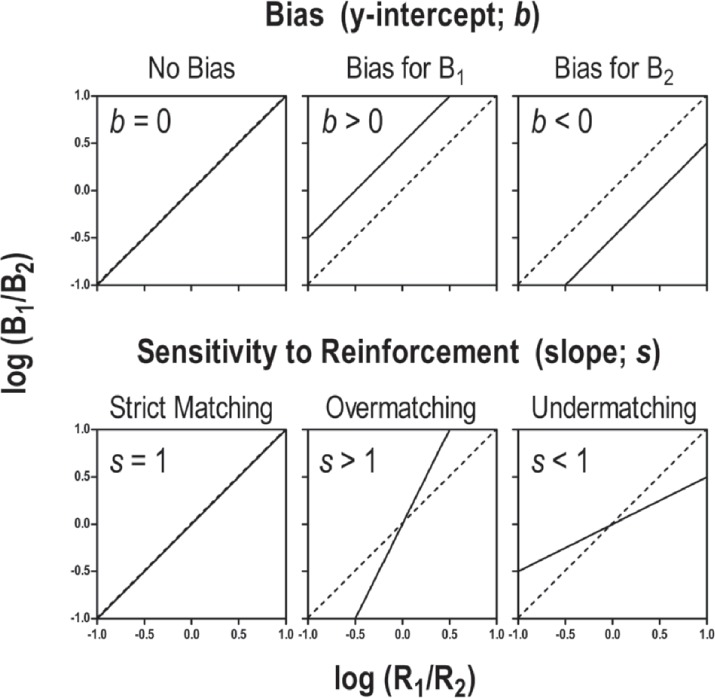
The top panel depicts possible variations in bias using the GME, whereas the bottom panel depicts possible variations in sensitivity to reinforcement. The left side of Equation 2 captures relative rate of responding (y-axis), whereas relative reinforcement rate is captured by the right side of Equation 2 (x-axis).

Of particular interest to practitioners may be the differential effects that reinforcer dimensions may have in producing the biased responding described in the previous paragraph. In one demonstration of this concept in education, Neef, Mace, Shea, and Shade (1992) offered the choice between two stacks of math problems to students receiving special education services (emotional disturbance and behavior disorders). In particular, the researchers arranged concurrent VI schedules across the two stacks in equal- and unequal-quality reinforcement phases. During equal-quality phases, the two stacks of math problems concurrently featured the same reinforcers (nickels or program money used as conditioned reinforcers in the classroom's token economy). Results suggested that students responded across the two stacks in accordance with the matching law (i.e., relative rates of math problem completion were predicted by the programmed rates of reinforcement on each stack). In the alternate unequal-quality phase, one stack featured nickels while the other featured program money. In this unequal-quality phase, all three students allocated relatively more responding to the stack featuring the nickel reinforcers than what was predicted by the relative reinforcement rates. Thus, these students exhibited a bias for the nickels that could not be explained by rate of reinforcement alone. In a follow-up study, Neef et al. (1994) conducted analyses of students' academic response distributions across two stacks of math problems under differing reinforcer dimension comparisons. Dimensions consisted of (a) rate (i.e., the concurrent VI schedule in place for each stack of math problems), (b) quality (i.e., relative preference for reinforcers available for each stack of math problems), (c) delay (i.e., time between point delivery and exchange for backup reinforcer), and (d) effort (i.e., difficulty of the math problems). Using highly controlled comparisons wherein target dimensions varied during a session across the math problem stacks while holding other dimensions equal, Neef et al. demonstrated that students have idiosyncratic biases for reinforcer dimensions. For example, some students may differentially prefer sooner rewards over higher-quality ones, whereas other students may prefer less effortful contingencies that result in delayed access to rewards over more effortful contingencies that result in immediate ones. These data highlight the notion that practitioners can engineer the environment to favor appropriate responses by arranging contingencies that make it less effortful for the learner to obtain high rates of immediately available, high quality rewards for the desired behavior, relative to those associated with undesirable behaviors.

Understanding idiosyncratic preferences for reinforcers in applied setting via matching analyses suggests the bias parameter may have utility in quantifying the degree to which reinforcers are substitutable (i.e., serve similar functions and maintain responding at similar levels) in treatment scenarios. If a matching law analysis indicates no bias for two responses associated with differing dimensions of reinforcement, these reinforcers may be considered substitutable. However, if a bias is detected via reinforcer parameter manipulations, the practitioner can isolate the preferred dimension and program reinforcers accordingly; this approach may be useful in contexts that prohibit the ability to arrange all appetitive dimensions of reinforcement (e.g., specific classroom demands associated with the target response do not permit frequent rates of reinforcer delivery, but may permit more immediate or higher quality reinforcers). For example, Reed and Martens (2008) used procedures similar to those described by Neef et al. (1992, 1994) with students receiving standard educational services (i.e., not special education), to demonstrate the utility of matching to academic performance. In Experiment 1 of Reed and Martens' study, the difficulty of the problems in each stack was matched to students' current instructional level (i.e., in a previous assessment, the students demonstrated the ability to complete these problems accurately and fluently). Under this “symmetrical” arrangement, students' responding was in accord with the GME (Equation 2) with little to no bias for either stack (assessed quantitatively using the b parameter from Equation 2). In Experiment 2, one stack of math problems featured difficult (i.e., accurate but nonfluent) problems, whereas the other stack remained at the students' instructional levels. Under this “asymmetrical” arrangement, substantial increases in bias (b) were observed toward the math problems that were at the students' instructional level (i.e., the “easy” problems). These results suggest that, when educating students on material outside of their present instructional level—that is, outside of content in which they are accurate and fluent—students will prefer to engage in activities that are less effortful even when reinforcement favors the more effortful response. From an education standpoint, this is concerning. And as such, simply providing relatively more reinforcement for the more effortful task may not be enough to increase preference for the task. More importantly, such arrangements could result in the student choosing to engage in off-task behaviors—that are presumably less effortful and more reinforcing—that may be undesirable and problematic in classroom contexts (e.g., talking to their neighbor, attending to nonacademic stimuli). We return to this discussion and provide some solutions (grounded in matching theory) for such scenarios in the Additional Implications for Practice section later in this article.

In the GME, s, or sensitivity to reinforcement, represents the amount of change in behavior associated with each change in reinforcement. When s is close to 1, a unit change in relative rates of reinforcement features an equal unit change in relative rates of behavior. An example of strict matching is illustrated in the bottom left panel of Figure 3. In this case, increases in relative rates of reinforcement (along the x-axis) are identical to increases in relative rates of behavior (along the y-axis). For example, if the rate of reinforcement on one response alternative doubled, we would expect to see exactly twice as much responding on that alternative. If s is greater than 1, the organism is considered to be overmatching (i.e., the organism is emitting relatively more responses than what is necessary to obtain reinforcement; specifically, the organism is disproportionally emitting more responses toward the richer reinforcement alternative). As the bottom middle panel of Figure 3 depicts, overmatching is observed when the relative rates of behavior increase more quickly along the y-axis than the change in relative rates of behavior increase along the x-axis (i.e., the slope is greater than 1). For example, if the rate of reinforcement on one response alternative doubles, we may see more than twice as much responding (e.g., 3 times as much) on that alternative. Undermatching implies that fewer responses are emitted based on the available reinforcers for one alternative, and thus s is less than 1 (see bottom right panel of Figure 3). In this case, as relative rates of reinforcement increase along the y-axis, the increase in behavior is less than predicted, such that the slope is less than 1. Undermatching is also indicative of responding disproportionally more toward the leaner reinforcement alternative. Extreme undermatching (s close to 0) is considered to be representative of indifference or insensitivity to reinforcement. Matters of sensitivity to reinforcement are important to consider in clinical or educational settings. If clients demonstrate overmatching, they are not contacting programmed reinforcers associated with the behavior on the relatively leaner schedule of reinforcement. For example, a client receives attention from Staff Member A 3 times as often as she does from Staff Member B. If the client spends 90% of her time near Staff Member A—that is, demonstrating high sensitivity to reinforcement or overmatching—she will miss out on many of the pleasant interactions Staff Member B could provide. Likewise, if the client does not change her interactions between Staff Members as they begin to alter their patterns of attending, the client's sensitivity to reinforcement would be low (i.e., behavior is not changing as a function of reinforcement), representing undermatching.

A final consideration when understanding behavior-environment relations using the GME is the degree to which this theoretical model of matching accounts for variation in the data. That is, the GME is useful for describing various deviations from perfect matching, implying that the data do indeed vary. Because the GME relies on regression to fit the line to the data points (for a more detailed discussion on linear regression, see Motulsky & Christopoulos, 2004), the regression analysis can provide a quantitative account of how well the GME describes the data pattern. This account is termed variance accounted for (and is typically denoted as R², VAC, or VAF in journal articles) because it informs the analyst to the percentage/proportion of variance in the data that is explained by the GME. If the GME perfectly describes the data (even with deviations in matching with respect to sensitivity to reinforcement or bias), one could reliably predict every data point with 100% accuracy. In this case, the percentage of variance accounted for by the GME would be 100% (or 1.0, as a proportion). This is rarely the case in matching law studies, but analysts typically hope to observe R² as close to 1.0 as possible.

Having explained the GME (Equation 2), we will return to the hypothetical client data and reexamine matching with respect to sensitivity to reinforcement and bias using the GME (Equation 2). As Figure 4 illustrates, the slope of the line (sensitivity to reinforcement, or s) was .87. That is, when there is a one-unit change increase in reinforcement for aggression, there is slightly less than a one-unit change (.87) in aggression. In other words, the client exhibits undermatching. Moreover, with a y-intercept (bias, or b) of -.009, there was virtually no bias. That is, if we model responding when reinforcement rates for aggression and appropriate mands are equal, the relative ratio of behaviors is approximately equal; the preference for behavior appears to be based on reinforcement rates alone, and not because of any particular characteristic of response form or quality of attention for each response form. Finally, examining the R² value of the best-fit line, it is evident that the GME provides an excellent account of the behavior pattern, with 98% of the variance being accounted for by Equation 2. In other words, the GME can explain 98% of the variance in relative rates of behavior, given the known relative rates of reinforcement.

Figure 4.

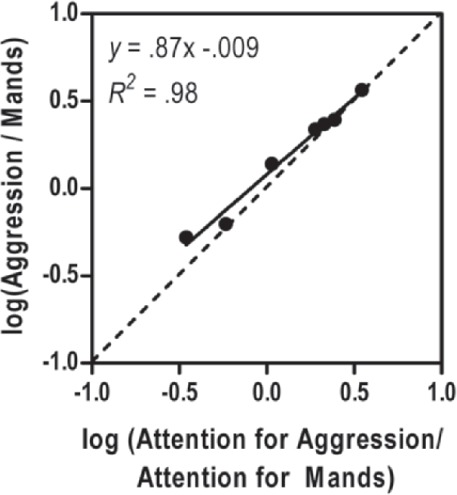
A generalized matching law plot and parameters of a hypothetical client's aggression/manding data set. The solid line depicts the best-fit line, whereas the dashed diagonal line depicts perfect matching. The left side of Equation 2 captures relative rate of responding (y-axis), whereas relative reinforcement rate is captured by the right side of Equation 2 (x-axis).

Herrnstein's Hyperbola

Behavior analysts cannot always—if ever—accurately identify all of the sources of reinforcement that may govern organisms' choice. Both the “real world” and tightly controlled experimental settings consist of countless reinforcement alternatives for any organism at any given time (McDowell, 1988). Put another way, it may be shortsighted to simply assume that choice is limited to two options, as is dictated by Equations 1 and 2, and in cases where only one target behavior is concerned, a single-alternative matching theory is necessary.

To account for a single-alternative conceptualization of choice, Herrnstein (1970) proposed a modification to the matching law to account for all possible responses and sources of reinforcement (B_e and R_e, respectively), such that:

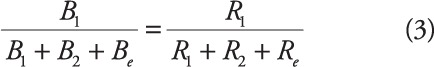Further derivation of this form of matching collapses the sum of all rates of responses (sum of all Bs) to parameter k, and collapses R₂ into R_e. To understand what these terms describe, consider a situation in which a practitioner is interested in on-task behavior and attention associated with on-task behavior, while noting that many different topographies of off-task behavior may occur (e.g., talking to a neighbor, staring out the window). In this situation, all of these possible off-task responses are also associated with some kind of reinforcement, although it may not be specifically captured by the measurement system the practitioner has chosen to employ in her observations. An estimate of the sum of all on- and off-task behaviors constitute k, with R_e serving as an estimate for the sum of all reinforcers associated with the off-task responses (i.e., those not specifically captured in the measurement system). In short, deriving these fitted parameters (k and R_e) accounts for the assumption that only one response and source of reinforcement are identifiable with the measurement system in place, with the recognition that other responses and sources of reinforcement are present but may not be captured by this measurement system:

Using simple algebra and multiplying both sides by k to isolate B₁, we are left with Herrnstein's (1970) single-alternative matching equation:

where B₁ represents the rate of the target response (in the above example, on-task behavior), R₁ represents the rate of reinforcement associated with B₁ (e.g., attention for on-task behavior), and k and R_e represent free parameters that are derived by fitting a hyperbola. A hyperbola is an open curve that, in the case of matching, curves upward away from the origin and continues infinitely, decelerating until it appears to be a flat horizontal line nearly parallel to the x-axis, which is the asymptote to the data points. That is, k and R_e are not known to the researcher until a nonlinear best-fit line is produced. When matching data are plotted and Equation 5 is used to analyze the data, the best-fit line is a negatively accelerated hyperbolic curve (see Figure 5). In a negatively accelerated curve, changes in x-values initially result in large changes in y-values, but as x-values continue to increase, the proportional change in the y-values decrease. In other words, the hyperbolic curve starts accelerating steeply (i.e., more closely resembling a vertical line) but then decelerates less until there is little change in the y-values relative to the increasing x-values (i.e., more closely resembling a horizontal line).

Figure 5.

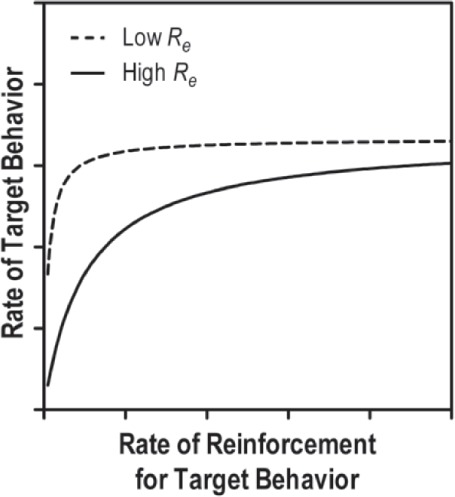
A hypothetical single-alternative matching law plot depicting hyperbolas derived from low (dashed) and high (solid) R_e values.

In Herrnstein's single-alternative equation (i.e., the quantitative law of effect; 1970), reinforcement rates are the x-values, with rates of the target behavior comprising the y-values. The parameter k represents a constant property of behavior (e.g., the effort associated with the response, the speed at which the response can be emitted) that governs the maximum amount of behavior that can be emitted during an observation period. Thus, in the hyperbolic function that this equation describes, k represents the y-asymptote of the hyperbolic curve (that is, where the top of the curve flattens out). Because Equation 5 represents a negatively accelerated function, there comes a point in which higher rates of behavior are simply impossible to achieve due to physical constraints of the environment or the biological/physiological characteristics of the organism. For example, no matter how much reinforcement you provide, an elementary-aged student cannot possibly be on-task every second of the school day. In sum, as reinforcement rates increase, rates of the target behavior will ultimately stop increasing as it reaches its ceiling of potential. The free parameter k quantifies this ceiling.

Finally, R_e represents the estimated rate of extraneous reinforcement that is reducing the organism's rate of the target behavior. With regard to the role of R_e in the hyperbola, this parameter influences the shape of the hyperbola's curvature. The relation between R_e and rates of the target behavior are depicted in Figure 5 where the rate of reinforcement for the target behavior is plotted along the x-axis, with the rate of the target behavior plotted along the y-axis. As Figure 5 illustrates, higher rates of extraneous reinforcement reduce the degree to which the organism's target behavior is sensitive to reinforcement. That is, the line becomes more flat at small values on the y-axis, compared to the data pattern indicating a low R_e, suggesting that less target behavior is emitted when more extraneous reinforcement is delivered in the environment.

Noncontingent reinforcement, a likely characteristic of highly enriched environments, should effectively decrease motivation to respond thereby expediting the point at which behavior reaches its maximum. Having more extraneous reinforcement thus weakens the reinforcing properties associated with the target behavior. For example, consider a situation in which a student is motivated by teacher attention. The teacher may program praise for appropriate attention bids, but also provides high rates of attention in the form of reprimands, redirections, instructions, etc. When the number of extraneous reinforcers (R_e; e.g., reprimands, redirections, instructions) is high, the student will exhibit lower rates of appropriate behaviors. From a graphical and statistical perspective, lower R_e values result in a curve that has a steeper initial slope, while higher R_e values result in a lower initial slope.

The single-alternative matching equation has been used to document numerous instances of matching in the natural environment (see McDowell, 1988). In one example, McDowell (1988) demonstrated that Equation 5 accounted for a young boy's rate of self-injurious behavior, with reprimands serving as the presumed maintaining consequence. The percentage of variance accounted for by Equation 5 was 99.7, suggesting that the matching law almost perfectly described this child's behavior, which is noteworthy given that these data were taken when no schedules of reinforcement were programmed by the researchers (i.e., data were collected during naturally occurring caregiver-child interactions). In another example of single-alternative matching in natural environments, Martens and Houk (1989) demonstrated that the disruptive behavior of an adolescent girl with intellectual disabilities was described by single-alternative matching, with percentage of variance accounted for by Equation 5 averaging 63%. In both cases, these data document the importance of understanding the relation between observed and extraneous reinforcers on the emission of socially important behaviors.

Additional Implications for Practice

Understanding the interplay between competing sources of reinforcers via the matching law enables behavior analysts to increase select behaviors, while subsequently decreasing others. One of the most widely used behavior change tactics to meet such goals in practice is differential reinforcement (see Petscher, Rey, & Bailey, 2009), which, strictly speaking, consists of limiting or withholding reinforcers for one behavior and delivering them contingent upon another. Due to this approach of simultaneously increasing one response and decreasing another, this procedure is frequently used for both skill acquisition (e.g., Vladescu & Kodak, 2010) and behavior reduction (e.g., Machalicek, O'Reilly, Beretvas, Sigafoos, & Lancioni, 2007). Note, however, that differential reinforcement does not necessarily require the extinction of a problem behavior while a functionally equivalent appropriate behavior is reinforced. In many cases, a behavior analyst may be interested in differentially reinforcing one response more than another, even though neither is necessarily more “appropriate” than another. For example, Athens and Vollmer (2010) used a differential reinforcement of alternative behavior without extinction procedure to evaluate the effects of manipulating various dimensions of reinforcement (e.g., duration, quality, delay) on behavior of seven children with ADHD or autism. After a functional assessment was conducted to determine the functions of the problem behaviors, the experimenters manipulated the (a) duration of reinforcement (e.g., 5–45 s), (b) quality of reinforcement (e.g., high, low), (c) delay to reinforcement (e.g., 0–60 s), and (d) combination of the above (e.g., 5-s reinforcer access [duration] to a low quality reinforcer, following a 10-s delay) on both problem behavior and appropriate behavior. In these arrangements, relatively more reinforcement was delivered contingent on the appropriate behavior as compared to the problem behavior. Within a matching law framework, we may conceptualize appropriate behavior and problem behavior as B₁ and B₂ and the relative reinforcement rates as R₁ and R₂, respectively. As one would expect, there was little to no difference between rates of both behaviors when the relative reinforcement rates for both behaviors were equal. When reinforcement favored the appropriate behavior, however, the children engaged in relatively more appropriate behavior as compared to problem behavior. Although this effect was observed when only a single dimension of reinforcement was manipulated for both behaviors, the effect was more pronounced when a combination of the dimensions were changed (i.e., when the deck was stacked more heavily in favor of appropriate behavior). Put simply, the children matched their behavior to what was relatively more reinforcing.

In addition to providing a theoretical framework to treatment selections, the matching law has also been used as an analytical tool to document behavior change in the presence of certain independent variables. For example, Murray and Kollins (2000) hypothesized that because the matching law quantitatively describes how sensitive individuals' behaviors are to reinforcement, the parameters derived by matching analyses may be useful in documenting the efficacy of treatments specifically aimed at increasing sensitivity to reinforcement. In particular, Murray and Kollins presented a mathematics task to two boys diagnosed with ADHD. During these sessions, math problem completion was reinforced on various VI schedules. With a baseline rate of responding documented, the researchers conducted identical sessions in the presence of either meth-ylphenidate (a drug commonly prescribed to individuals with ADHD to reduce signs and symptoms commonly associated with ADHD) or a placebo. Using the single-alternative matching equation (because there was only one set of math problems to complete), the researchers documented higher k values and more variance accounted for when participants were provided methylphenidate. These results offer some preliminary within-subject evidence that this drug may help behavior become more sensitive to reinforcement contingencies for children with ADHD. Note, however, that other within- (see Neef, Bicard, Endo, Coury, & Aman, 2005) and between-subjects (see Neef, Marckel, et al., 2005) comparisons have found that children with ADHD prefer immediate rewards in concurrent operants arrangements, regardless of whether they are on medication. More research is thus necessary to understand the role of medication in sensitivity to reward in children with ADHD.

Conclusion

In sum, the matching law has proven to be a robust analytical tool in the description of behavior-environment interactions. The implicit implications of the matching law regarding the power of switching contingencies from favoring one response alternative (e.g., problem behavior) to another (e.g., desired behaviors) offer hope in the treatment of problem behaviors, as well as in the acquisition of socially important skills. As an analytical tool, the matching law provides a concise quantitative description of an organism's pattern of behavior over large time spans (see Critchfield & Reed, 2009), which permits the behavior analyst to more thoroughly understand and predict the organism's interactions with the environment. Such understanding may ultimately give rise to more efficient and effective behavior change solutions. The reader is encouraged to explore the resources provided in the Appendix to learn more about the matching law and its utility.

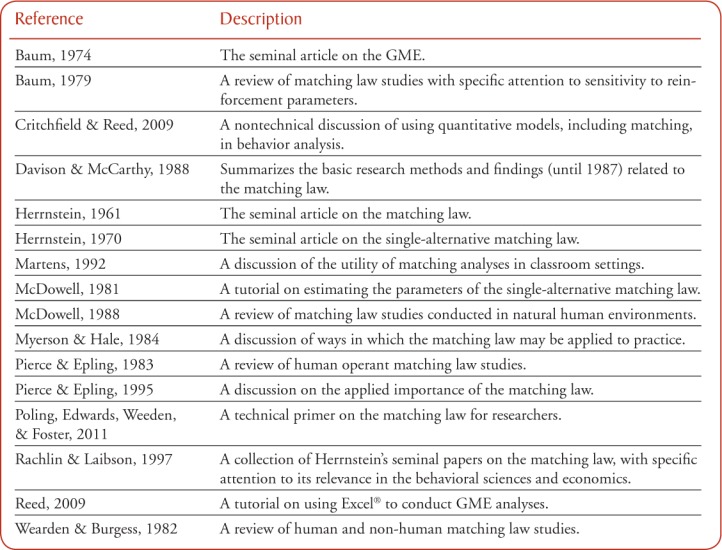
Appendix.

Additional Resources on the Matching Law