Probabilistic Modeling of Selective Stimulation of the Human Sciatic Nerve with a Flat Interface Nerve Electrode

Abstract

Ankle control is critical to both standing balance and efficient walking. This hypothesis presented in this paper is that a Flat Interface Nerve Electrode (FINE) placed around the sciatic nerve with a fixed number of contacts at predetermined locations and without a priori knowledge of the nerve’s underlying neuroanatomy can selectively control each ankle motion. Models of the human sciatic nerve surrounded by a FINE of varying size were created and used to calculate the probability of selective activation of axons within any arbitrarily designated, contiguous group of fascicles. Simulations support the hypothesis and suggest that currently available implantable technology cannot selectively recruit each target plantar flexor individually but can restore plantar flexion or dorsiflexion from a site on the sciatic nerve without spillover to antagonists. Successful activation of individual ankle muscles in 90% of the population can be achieved by utilizing bipolar stimulation and/or by using a cuff with at least 20 contacts.

1. Introduction

As neural interfaces become increasingly complex the use of computer simulations to guide the development of practical neural prostheses becomes increasingly important. The value of computer simulations for guiding the design of a neural prosthesis has been realized by multiple researchers (Schiefer et al. 2008; Woock et al. 2010; Yoo et al. 2004). For example, in (Schiefer et al. 2008) an 8-contact flat interface nerve electrode (FINE) selectively recruited knee extensor or hip flexor muscles to levels that were expected to restore the sit-to-stand transition and facilitate gate. The results from the computer simulations were statistically and positively correlated with those from a series of intraoperative experiments (Schiefer et al. 2010).

The success of the pre-clinical computer modeling for the design of a FINE for selective activation of axons within the human femoral nerve has galvanized a similar approach to design a neural interface for the human sciatic nerve (SN). With respect to the SN, selective stimulation is important because various phases of gait require specific ankle motions – dorsiflexion (DF) or plantar flexion (PF) – without the accompaniment of excessive foot inversion (FI) or eversion (FE) or toe flexion (TF) or extension (TE). Proper ankle control is critical to both standing balance and efficient walking. A neural interface to control the SN could have broad applications.

There are an estimated 5.5 to 6.0 million individuals with a history of stroke and 250,000 to 450,000 individuals living with a spinal cord injury (SCI) in the United States (CDC 2007; Nobunaga et al. 1999). An additional 250,000 to 350,000 Americans are estimated to have multiple sclerosis and as many as 800,000 are living with cerebral palsy (National Institute of Neurological Disorders and Stroke 2010). All of these conditions can result in lack of coordinated motor control ranging in degree from minor to complete paralysis.

A common problem within these populations is foot-drop: a condition in which an individual is unable to partially or fully dorsiflex the foot. As a result, foot-floor clearance is compromised as the foot drags during swing phases of gait. In addition to foot-drop, these populations can have diminished or absent plantar flexion, which reduces propulsive force during gait and impairs control of tibial advancement during stance. Both of these deficits could be corrected by stimulating the appropriate axons within the sciatic nerve (SN).

Surface electrodes can restore dorsiflexion by activating the tibialis anterior, but frequently recruit the peroneus longus, which everts and plantar flexes the foot (O’Keeffe and Lyons 2002; Taylor et al. 1999). Intramuscular electrodes can also produce reciprocal, but energetically inefficient stepping in individuals paralyzed by spinal cord injury (Kobetic et al. 1999; Sharma et al. 1998). Locating the electrode close to the nerve facilitates full recruitment of the target muscle(s), which increases the force or moment developed. Implantable neuroprostheses for foot-drop have attempted to balance the secondary inversion of the dorsiflexors with additional channels of stimulation to the evertors through a single multicontact nerve cuff on the common peroneal nerve (Hansen et al. 2002; Hoffer et al. 1996; Sinkjaer et al. 1995). To date, no implanted walking system has provided both balanced dorsiflexion and active plantar flexion, although animal and acute human feasibility studies suggest it is possible.

In cat studies, selective and graded muscle contractions have been reported with spiral nerve cuff electrodes placed around (Grill and Mortimer 1996; Sweeney et al. 1990; Tarler and Mortimer 2003, 2004, 2007; Veraart et al. 1993) or a penetrating electrode array placed in the SN (Branner and Normann 2000; Branner et al. 2004; Branner et al. 2001; McDonnall et al. 2004a, 2004b). Similar results have been found with the intrafascicular electrodes (Badia et al. 2011; Boretius et al. 2010; Nannini and Horch 1991; Yoshida and Horch 1993). Other animal experiments have shown that the FINE can selectively restore individual functions controlled by the SN (Leventhal and Durand 2003; Tarler and Mortimer 2003; Tyler and Durand 2002). However, nerve morphology differs markedly between animals and humans. For example, the rat SN contains less than 5 fascicles and the cat SN contains 5 to 10 fascicles whereas the human SN contains 25 to 70, depending on the location along the nerve (Badia et al. 2010; Gustafson et al. 2011; Sladjana et al. 2008).

The hypothesis of this study is that a FINE around the SN with a fixed number of contacts at predetermined locations and without a priori knowledge of the nerve’s underlying neuroanatomy can selectively control each ankle motion though individual muscle recruitment. Through the use of finite element method (FEM) models, recently developed linear approximations to non-linear axonal models, and biomechanical models, this simulation study investigated multiple electrode configurations utilizing monopolar and bipolar stimulation. Nerve simulations were based on actual geometry and fascicular distribution within the distal SN derived from quantitative anatomical studies (Gustafson et al. 2011). Similar techniques have been used in other studies (Butson et al. 2011; Deurloo et al. 1998; Grinberg et al. 2008; Lertmanorat et al. 2006; Leventhal and Durand 2003; Schiefer et al. 2008; Veltink et al. 1989; Wodlinger and Durand 2009). While the subject of this study is the SN, the modeling techniques are generalized and the results are broadly applicable to any nerve with a similar distribution of fascicles and number of innervated muscles.

2. Methods

2.1. FEM Development

Anatomically correct FEM models of the distal human SN just proximal to the bifurcation into the tibial and common peroneal nerves were created from a histological cross section. The nerve contained 27 fascicles. A digitized cross sectional image of the distal SN was imported into MATLAB (Mathworks, Natick, MA). Borders of the epineurium and endoneurium were traced. Traced fascicles were converted into round fascicles while preserving each fascicle’s cross sectional area. The perineurium of each fascicle was added at a thickness of 3% of the fascicular diameter (Grinberg et al. 2008). The nerve was reshaped to multiple dimensions to account for varying FINE geometries. Although fascicles have been demonstrated to change shape in animal trials (Tyler and Durand 2003), they were assumed only to move and retain their shape in this study. When required to move to accommodate the dimensions of the FINE, fascicles were algorithmically shifted inward as has been described previously (Schiefer et al. 2008). The coordinates of the neural tissues were used to construct a 3D FEM model in Maxwell 3D V12 (Ansoft, Pittsburgh, PA).

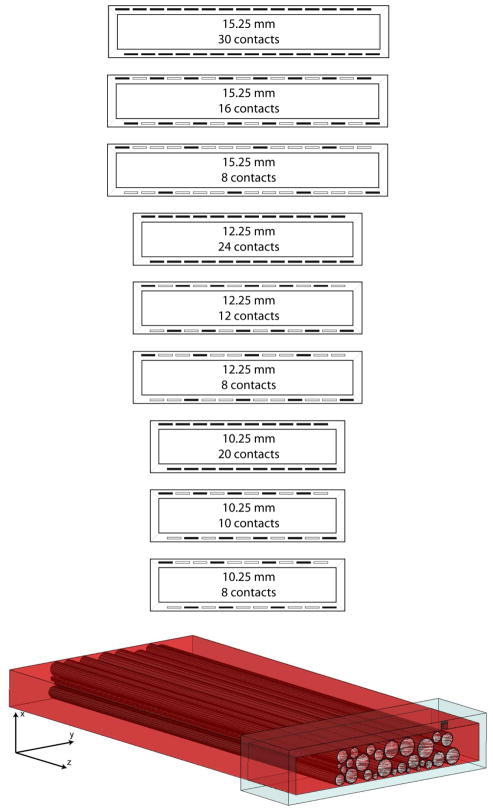
Fascicles and the epineurium were extruded to create a semi-infinite 3D FEM model. The conductivity of the perineurium, epineurium, and saline were isotropic and set at 2, 83, and 2000 mS/m, respectively, whereas the conductivity of the endoneurium was set at 83 mS/m in the transverse directions and 571 mS/m along the extruded direction (Choi et al. 2001). FINEs were modeled, centered about the nerve, with opening widths of 10.25, 12.25, and 15.25 mm, opening heights of 2, 2.25, 2.5, 2.75, and 3 mm, and containing 8, 10, 12, 16, 20, 24, or 30 stimulating contacts (Fig. 1A). Each permutation of opening height and width were modeled except for 2 × 10.25 mm, which did not contain enough cross sectional area to fit all fascicles without compression. Simulated platinum stimulating surfaces were 0.5 × 0.5 mm and spaced 1.0 mm on-center (Schiefer et al. 2008; Tyler and Durand 2003). The maximum number of contacts within the cuff were governed by the width of the cuff and ranged from 20 contacts in the 10.25 mm cuff to 30 contacts in the 15.25 mm cuff. One FEM was created for each active contact within the cuff. Contacts on the upper inner surface of the cuff were offset from those on the bottom surface, which maximized the space throughout the cuff that could be selectively activated. This design was found to be optimal in computer simulations of the femoral nerve (Schiefer et al. 2008) and shown to be effective during intraoperative cuff evaluations (Schiefer et al. 2010). To simulate the intraoperative environment, any space between the cuff and the nerve was modeled as saline. To reduce simulation time, models were symmetrically split along the z-plane and a symmetry boundary condition was applied (Fig. 1B).

Fig. 1.

(top) The distribution of contacts within the different modeled FINEs. The opening height of the cuff was varied from 2–3 mm. The opening width of the cuff was varied from 10.25–15.25 mm. The number of contacts in the cuff was varied from 8–30. Dark rectangles in the cuff indicate the location of contacts. (bottom) The 3D FEM model derived from a human sciatic nerve histological cross section. The model contains a plane of symmetry so all objects were split across the z-axis. This included splitting the cuff, the contact seen in the upper right corner of the cuff, all neural tissue, and the saline environment (not shown).

2.2. Simulating Axonal Response

The electrical potentials induced by a 1 mA cathodic input current at a single contact were calculated with Maxwell. The potentials were exported to MATLAB, where the voltages along axons were interpolated using a 3D cubic spline. Within each fascicle, 100 axons with varying diameters were randomly and uniformly distributed using a published distribution (Garven et al. 1962). The offset of the central Node of Ranvier, defined as the node closest to the center of the stimulating electrode, was randomly varied between 0 mm (the node was directly aligned with the electrode on the z-plane) and half of the axon’s intermodal length. A linear approximation (Peterson et al. 2011) to the MRG double cable axon model (McIntyre et al. 2002; Richardson et al. 2000) was used to determine if an axon propagated an action potential in response to the applied electric field for varied pulse durations. The approximated double cable axon model included persistent and fast sodium, slow potassium, and leakage currents. Simulations were run at 50 pulse widths (PWs) from 0.005 to 0.25 ms and 99 pulse amplitudes (PAs) from 0.10 to 5.0 mA for monopolar stimulation. For bipolar stimulation, both contacts were considered to be independent and could operate at any of 20 pulse widths and 20 pulse amplitudes within the same ranges. For bipolar simulations, one contact acted as a cathode while one of the nearest neighboring contacts, either an adjacent contact or a contact on the opposite surface of the FINE, was assigned as either an anode or a cathode.

2.3. Probabilistic Population Response

Results from the axonal simulations were analyzed to determine which contacts produced the greatest selectivity. As in previous modeling and intraoperative studies, selectivity was defined as the percentage of axons activated within all fascicles innervating a target while limiting the percentage of activated axons not innervating the target to no more than 10% (Choi et al. 2001; K. H. Polasek et al. 2009).

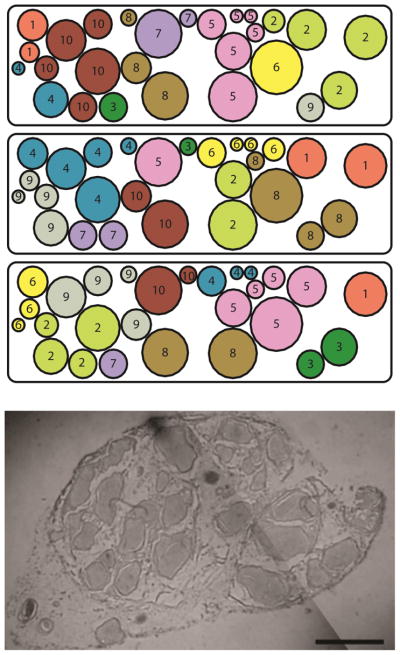
Unlike the femoral modeling study, information mapping specific fascicles to their respective muscles was not available for the sciatic cross section necessitating adoption of a Monte Carlo approach. Fascicles within the nerve model were clustered into “groups” (Fig. 2). Each group represented a possible target: one or more muscles contributing to a specific function. Based on distal innervation patterns, the number of possible target groups was varied from 9 to 15, accounting for synergies that reduce the number of independent muscles innervated by the distal SN from the maximum of 25. Allowing the intrinsic foot muscles responsible for abduction and adduction of the toes to be grouped into an “other” category (O), the remaining muscles are responsible for knee flexion (KF), PF, DF, FI, FE, TF, and TE. Also, sensory (S) groups exist within the nerve and were included in the model.

Fig. 2.

An example of fascicle clustering. The number of clusters in the nerve was varied from 9 to 15. Once the number of clusters in the nerve was assigned, 100 iterations were created. Here, 3 of the 100 random iterations of the 10-cluster model are shown. The models are based on the histological cross section of the sciatic nerve shown (bar=2mm; image courtesy Dr. Kenneth Gustafson).

The number of possible target groups within the nerve was varied from 9 representing the ideal scenario where all muscles responsible for a specific function map to a single location within the nerve, to 15 representing the non-ideal scenario where muscles with unrelated functions map to locations within the nerve that separate synergistic functions. For each model, 100 unique grouping iterations were created. That is, for models in which the fascicles were assigned to 9 groups, 100 unique iterations were analyzed wherein each iteration contained a unique set of fascicular assignments, producing a total of 900 observations. The percentage of unique variations in which a required minimum selectivity (discussed below) was obtained was then determined and reported as a probability. To be conservative, 90% of the fascicular clusters were required to have axonal activations that achieved the minimum required selectivity. Data were analyzed using a logistic regression. Responses were considered significantly different at the α=0.05 level.

2.4. Required Minimum Selectivity

Multiple steps were taken to determine the minimum selectivity required to restore a lost function. First, an OpenSim (Delp et al. 2007) biomechanical model of the lower limb was used to assess the magnitude of PF, DF, FI, FE, TF, and TE moment generated by each of 12 muscles innervated by the SN: soleus (Sol), medial and lateral gastrocnemius (MG, LG), tibialis posterior (TP), tibialis anterior (TA), peroneus longus (PL), peroneus brevis (PB), peroneus tertius (PT), flexor hallucis longus (FHL), extensor hallucis longus (EHL), flexor digitorum longus (FDL), and extensor digitorum longus (EDL). These moments were reduced by 50% to account for disuse atrophy (Acosta 2002). Based on able-bodied moments about the ankle acquired during walking (Fatone et al. 2009), the percentage of the reduced-strength maximum moment required to restore PF or DF during gait was determined. Knowing the percent of muscle activation required, the percent of axons innervating the muscle that had to be stimulated was calculated based on the non-linear relationship described by (Enoka and Fuglevand 2001). Specifically, the force generated by a motor unit can be described as

$$y_i=y_1{e}^{\frac{ln\left(\frac{y_n}{y_1}\right)•i}{n}}$$ (1)

in which y_i is the force or innervation number of motor unit i, y₁ is the force or innervation number of the smallest motor unit, y_n is the force or the innervation number of the largest motor unit, and n is the total number of motor units. Application of this equation resulted in the non-linear relationship wherein the small population of large motor units contributed to the majority of force generated by a muscle and the large population of small motor units contributed a relatively small percentage to the total force generated by the muscle. Muscle-specific parameters were collected from the literature (Botterman and Cope 1988; Boyd 1968; Enoka and Fuglevand 2001; Feiereisen et al. 1997; Gordon et al. 1990; Holmback et al. 2003; Ito et al. 2003; Kernell et al. 1983; Macefield et al. 1996; Moss 1992; Ohira et al. 2000; Powers and Binder 1991; Ward et al. 2009; Winter 2009).

To model all permutations of FINE height, width, and stimulating contact, a total of 350 FEMs of the human SN were created. The output of each FEM was analyzed under 700 unique scenarios (100 iterations × 7 group sizes) to determine the probability of selectively stimulating any given cluster of fascicles within the model. With each fascicle containing 100 axons subjected to each permutation of PW and PA in monopolar and bipolar mode, 1.33×10¹² axon simulations were analyzed. FEM simulations required approximately 30 minutes per model. Axonal simulations were run on 15 computers in parallel and required approximately 900 wall hours (13,500 computer hours) to complete.

3. Results

3.1. Required Minimum Selectivity

The anticipated achievable moments that were acquired from OpenSim are detailed in Table 1 after accounting for muscle atrophy. Based on able-bodied moments observed during walking (Fatone et al. 2009), the percentage of the reduced-strength maximum moment required to restore PF or DF during gait was determined. Simultaneously, the Sol, MG, and LG needed to be activated to 89% and the PL to 48% to restore 1.2 Nm/kg PF. It was also determined that the TA needed to be activated to 67% to restore 0.11 Nm/kg DF during gait with reduced muscle strength. Additionally, the PB needed to be activated to 38% to balance FI created by the TA.

TABLE 1.

Opensim-Derived Moments [Nm/Kg]

Muscle	DF (+)	FI (+)	TF (+)
	PF (−)	FE (−)	TE (−)
Sol	−0.81	0.05	0.00
MG	−0.36	0.01	0.00
LG	−0.16	0.01	0.00
TP	−0.04	0.16	0.00
TA	0.17	0.04	0.00
PL	−0.04	−0.13	0.00
PB	−0.01	−0.07	0.00
EHL	0.04	0.00	−0.01
EDL	0.08	−0.03	−0.02
FHL	−0.03	0.03	0.02
FDL	−0.01	0.03	0.02

Moments are normalized to a 75 kg subject and reduced by 50% to account for muscle weakness. PT was considered to be a relatively weak muscle and removed from the list.

Using these required activation levels from the validated OpenSim model and eq. (1), the percentage of axons that needed to be activated was estimated to be 38%, 40%, 37%, and 14% for the Sol, MG, LG, and PL, respectively. The percentage of axons that needed to be activated for the TA and PB was estimated to be 24% and 11%, respectively. This was under the condition that no spillover to antagonistic muscles occurred and under the assumption that larger diameter axons were recruited before smaller diameter axons. Allowing for up to 10% spillover, these values increased to as high as 57% axonal activation, which was rounded up to 60% to be conservative. Thus, models were analyzed to determine the probability that at least 60% of the axons in any given fascicular group were selectively activated.

3.2. Probabilistic Population Response

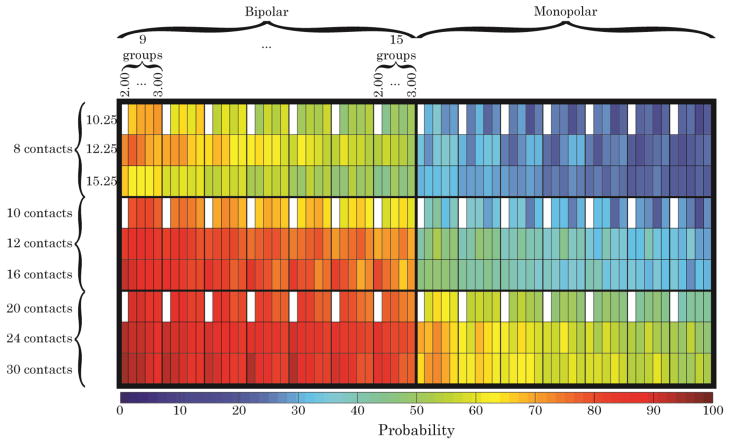
The probability that 60% of the axons within any given cluster of fascicles were activated is shown (Fig. 3). Simulations suggested that at least 16 contacts operated in a bipolar mode were required to achieve the 60% activation level in at least 90% of the population when the nerve contained nine distinct populations of fascicles that needed to be selectively activated. This increased to at least 24 contacts when the nerve contained 10–11 groups of fascicles and to 30 contacts when 12–13 clusters of fascicles needed to be selectively stimulated. Bipolar stimulation produced greater selectivity than monopolar stimulation and, therefore, increased the probability that 60% of the axons within a fascicular group would be activated. Across all group sizes, the greatest increase in selectivity when using bipolar stimulation was attained for the 16-contact FINE, for which the probability that 60% of the axons within a target fascicular group was activated increased by 42±4%. Cuffs with either fewer or more than 16 contacts did not exhibit comparable increases in probability. Cuff dimensions and the number of fascicular groups within the nerve had a smaller effect on the increase in selectivity when using bipolar stimulation.

Fig. 3.

The probability of activating at least 60% of the axons within any given group of fascicles in the sciatic nerve models. Each major row is divided into three sub-rows, corresponding to the three FINE widths simulated. The top major row shows results for an evenly-spaced 8-contact FINE. The middle major row illustrates the “half complement” of contacts within the cuff. The bottom major row illustrates the full complement of contacts in the cuff. The left major column illustrates the effects of adding a second source of stimulation, either cathodic or anodic. Each major column is divided into seven sub-columns. The left-most sub-column illustrates results from when the model’s fascicles were divided into 9 clusters, representing a best case scenario. The right-most sub-column illustrates results from when the model’s fascicles were divided into 15 clusters, representing a worst case scenario. Each sub-column is further divided into five sub-columns, corresponding to the five FINE heights simulated. White boxes indicate models that could not be created due to lack of fascicular space within the cuff.

The implantable stimulators that we use in our studies do not operate in a bipolar mode. Further, currently available implantable FINEs have 8 independent contacts. The data were analyzed to determine the recruitment level that could be achieved using an 8-channel FINE delivering monopolar stimulation. It was found that if 9 fascicular groups needed to be selectively stimulated, there was a 50% probability of activating at least 40% of the axons in each group (Fig. 4, Fig. 5).

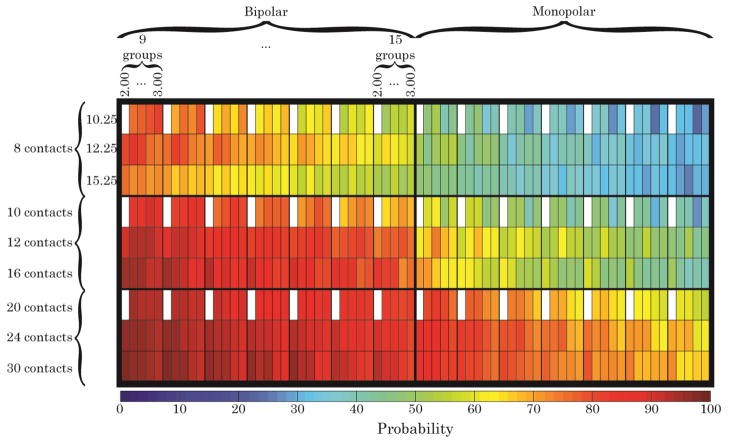
Fig. 4.

The probability of activating at least 40% of the axons within any given group of fascicles in the sciatic nerve models. A 40% activation level is still expected to produce a sufficient moment for PF and DF, provided there is no spillover to an antagonist. Simulations suggest that there is an approximately 50% probability that an 8-contact FINE operated in monopolar mode could selectively activate 40% of the axons in any fascicular group when there are 9 unique groups within the cross section.

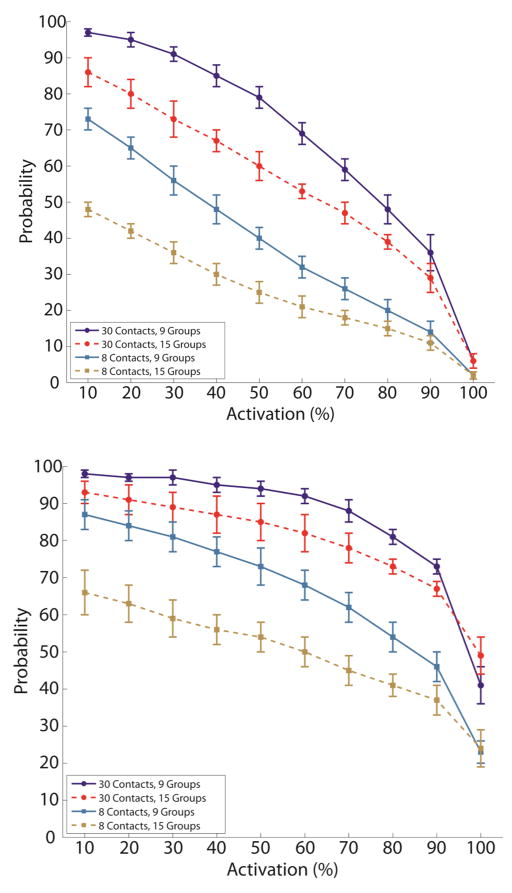
Fig. 5.

The probability, ranging from 0 to 100%, of activating a given percentage of the axons within a cluster of fascicles decreases as the as the percent required to be activated increased, as the number of contacts available decreased, and as the number of fascicle clusters increased. This was true for monopolar (top) and bipolar (bottom) stimulation. The probability of selective activation was greater with bipolar stimulation.

The relationship between axon activation level and probability was inversely proportional (Fig. 5). The probability of activating a fixed percentage of axons also decreased as the number of fascicle groups increased and as the number of contacts decreased (Fig. 5, Fig. 6). As the axon activation level approached 100%, the probability of achieving this level approached 0 (4%±2%) when limited to monopolar stimulation. However, if the cuff was operated in bipolar mode, the probability of achieving 100% axon activation was 35%±10%.

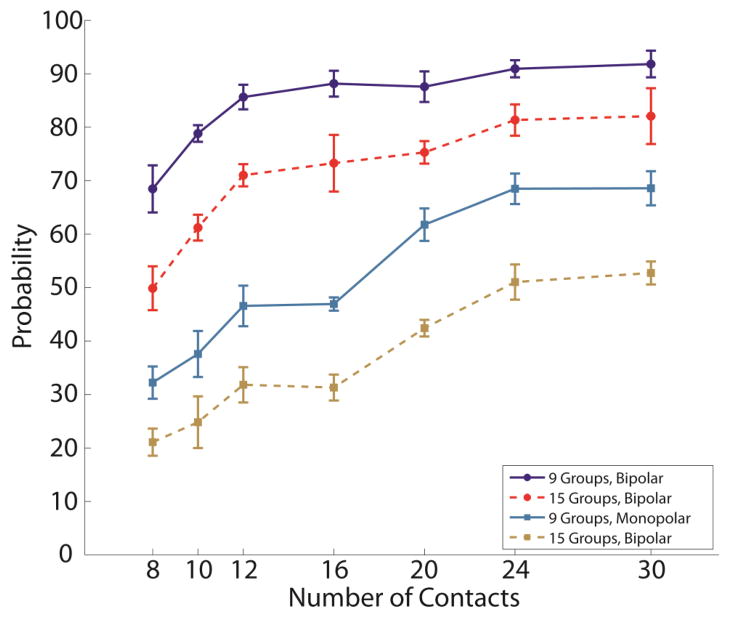
Fig. 6.

The probability of activating 60% of the axons in a target group of fascicles increases as the number of contacts available in the FINE increases. The probability also increases if bipolar stimulation can be used. The probability of activating 60% of the axons in a target fascicular group increased as the number of fascicular groups decreased.

The standardized estimates using a logistic regression were as follows: number of active contacts (0.42), number of contacts in the cuff (0.32), number of fascicular groups (−0.12), height (−0.02), and width (−0.04). This suggests there was a strong positive effect on probability by increasing the number of active contacts and the number of contacts within the cuff, there was a smaller negative effect on probability by increasing the number of fascicular groups, and there was a very small negative effect on probability when increasing either the height or width of the cuff. All parameters were found to be statistically significant (p<0.0001).

3.3. Trends in Stimulus Parameters

In bipolar simulations anodic stimulus partly cancelled the cathodic stimulus, allowing for greater recruitment of a target population without undesired spillover. In approximately 95% of bipolar simulations in which all contacts were available, the PW and PA that maximized selectivity were ≤ 185 μs and 4.5 mA, respectively. In bipolar simulations with 8 contacts, the PW and PA that maximized selectivity were ≤ 240 μs and 4.0 mA, respectively. By contrast, in approximately 95% of monopolar simulations the PW and PA that maximized selectivity were ≤ 25 μs and 1.5 mA, respectively.

Dual cathode stimulation was chosen to maximize selectivity in less than 1% of simulations. Cathode-anode stimulation maximized selectivity in 81% to 97% of simulations when 8 to all contacts were available, respectively. In the remainder of simulations, ranging from 3% for those with all contacts to 18% for those with 8 contacts, no stimulus was found to be selective. These values were larger for monopolar simulations, ranging from 6% for those with all contacts to 28% for those with 8 contacts.

4. Discussion

The probability of a successful outcome was greatest when bipolar stimulation was employed. In fact, bipolar stimulation with an 8-contact FINE was comparable to monopolar stimulation with 20 to 30 contacts (Fig. 6). In agreement with other studies (Choi et al. 2001; Schiefer et al. 2008), for a given cuff dimension, a FINE with more contacts was more likely than a cuff with fewer contacts to selectively recruit a sufficient percentage of axons in any given fascicular group.

The requirement that 60% of the axons were activated in any fascicular group was conservative. If spillover to antagonists can be minimized, the percentage of axons that need to be selectively stimulated is estimated to approach 40% to restore PF and 30% to restore DF. Simulations suggested that the probability of selectively recruiting 40% of the axons within any given fascicular group with a bipolar 8-contact FINE is 80%, which may be acceptable.

The required number of contacts to selectively activate 60% of the axons in at least 90% of the fascicular groups increased from 20 when fascicles were divided into 9 distinct groups to 30 when the fascicles were divided into 12 distinct groups. This represented a 50% increase in the number of required contacts but a 33% increase in the number of fascicle groups. The reason for the greater increase in the number of required contacts is explained when considering the frequency at which a single fascicle comprises a group. When there were fewer fascicular groups in the nerve, the likelihood that any one group contained only one or a small number of fascicles was lower than when the nerve contained many fascicular groups. As the likelihood of needing to stimulate a single, isolated fascicle increases, the number of contacts required to shape the stimulus field also increases.

The implantable stimulators currently available to us are limited to 16 monopolar channels and currently available FINEs contain 8 channels. Under these limitations, simulations suggest that there is an approximately 50% probability of activating at least 40% of the axons within any given fascicular group (9-group model). Therefore, selective recruitment to the conservative 60% level is unlikely with an 8-contact FINE operated with monopolar stimulation if PF needs to be isolated from DF, FI, FE, TF, and TE. However, based on Eq. 1 and the OpenSim simulations, activating 40% of the axons in a fascicular group corresponds to approximately 85% of the total muscle force that can be generated. This would translate to approximately 95% of the PF needed during the propulsive phases of gait and would be sufficient to produce the DF force needed during swing-through to prevent foot-drop. Activation at these levels also is expected to be sufficient for individuals who exhibit less than the 50% muscle atrophy accounted for in these models. It should be noted that when fitting the curve described by eq. (1) to estimate the required activation level of axons, human data were not available for all parameters. When human parameters couldn’t be found, data from cats were utilized. Because all curves fell within a tight range on the normalized scales, it was assumed that this approach was reasonable.

The combination of the required 60% activation level, the 90% successful outcome probability, and the 50% reduction in muscle strength likely makes the overall interpretation of the results conservative. To satisfy the 90% probability requirement, an 8-contact monopolar FINE is not expected to selectively activate more than 10% of the axons in any fascicular group if there are more than 8 fascicular groups within the nerve. However, this cuff satisfied the 90% probability requirement and recruited at least 20% of the axons in any fascicular group when there were only 5 fascicular groups (data not shown), which would be sufficient to restore at least 65% of the required moment for PF and 90% of that required for DF but may result in simultaneous recruitment of FI, FE, TF, or TE. Five fascicular groups correspond to a scenario when there was a group of fascicles responsible for PF and a group responsible for DF surrounded by undesired groups.

When considering optimality, there are many ways in which to view the data. The probability of producing any specific axonal activation increased as the number of contacts within the FINE increased. While a FINE with 30 contacts maximizes likelihood of successfully isolating individual muscles to the specified levels of recruitment, it is not necessarily optimal. Simultaneous activation of N muscles that contribute to the same function with <N contacts would take advantage of functional synergies. Based on the histology obtained by (Gustafson et al. 2011), there is a high probability that fascicles containing axons innervating agonists are grouped together at this level of the sciatic nerve, which is similar to what was found in the human femoral nerve just proximal to a major branch point (Gustafson et al. 2009; Schiefer et al. 2008). At a minimum, the Compton-Cruveilhier septum – the division between the fascicles forming the tibial and common peronal nerves – is expected to exist inside the sciatic nerve trunk at this level and would naturally divide PFs from DFs (Sladjana et al. 2008).

Contact-for-contact, the 8-contact FINE maximized the probability of selectively recruiting 60% of the axons in any fascicular group normalized by the number of contacts within the cuff. The percent increase in probability obtained by increasing the number of contacts from 8 to 30 was less than the percent increase in the number of contacts. However, as discussed, the 8-contact FINE is likely insufficient. Perhaps the closest to optimal was the 10 channel FINE capable of operating in a bipolar mode. Using this design, there was an approximately 70% chance of selectively recruiting at least 60% of the axons in any given fascicular group and an approximately 80% chance of selectively recruiting the requisite 40%. Further, when comparing monopolar to bipolar stimulation, a FINE with 10 contacts showed the greatest increase in the probability of success..

For a given number of contacts, FINEs with smaller opening heights or widths were more likely to selectively recruit axons. However the low standardized estimates for the cuff dimensions suggests that the dimensions of the cuff were not as important as the other three factors: the number of active contacts, total number of contacts, and number of groups that had to be selectively stimulated. Practically, the cuff must not be too small to occlude blood flow nor too large to allow for current shunting around the nerve. Should the cuff occlude blood flow, axonal degeneration would likely follow, and in extreme cases, denervation could occur. Should the cuff be too large, stimulating current could be shunted around the nerve. A shunting volume between the nerve and the cuff would reduce the efficacy of the cuff, as was observed in the femoral nerve modeling and intraoperative studies. Therefore, multiple sizes of the cuff should be manufactured to ensure an intimate but non-occlusive fit around the nerve.

The logistic regression indicated that as the number of fascicular groups increased, the likelihood of selectively activating 60% of the axons in any given fascicular group decreased. Interestingly, this trend reversed when the minimum selectivity increased to 100%, that is, selective activation of all axons within a given fascicular group. In this scenario, although the overall probability of success was small, the chances of activating all of the axons within a group were highest when the group consisted of a single fascicle and the probability of a group having a single fascicle was greatest when the nerve was divided into the greatest number of fascicular clusters.

Blood vessels were not modeled in this study. If a blood vessel were to be enclosed within the volume of the cuff, it may affect the selective stimulation of a target population of axons, depending on the size of the vessel and its position relative to the axons and contact(s) used. As with the effect of a neighboring fascicle, the largest effect on selectivity would most likely occur if the blood vessel were positioned between the contact and the target population (Grinberg et al. 2008). The effect would be further exacerbated if the target population were confined to a single fascicle. However, the likelihood that a target population is contained within a single fascicle increases as the total number of fascicular groups within the nerve increases. Therefore, while a blood vessel may reduce the selectivity for a specific target, its impact will be decreased as the number of stimulating contacts and target groups increases. Nonetheless, it would be prudent to avoid placing a blood vessel within the cuff not only to avoid any reductions in selectivity that might accompany it, but also to reduce the volume devoted to non-neural tissue and to reduce the chances of blood flow occlusion.

For a fixed number of contacts, a bipolar stimulator is expected to produce greater selectivity than a monopolar stimulator. In fact, simulations suggest that a bipolar stimulator can produce greater selectivity than a monopolar stimulator with twice as many leads. A system with fewer leads will tend to simplify the implantation of the system by reducing the number of leads that must be routed subcutaneously and the number of connections that must be made from the stimulator implanted in the abdomen to the cuff implanted on the distal sciatic nerve. Further, as the number of channels increases, so too does the rigidity of the leads, which may cause tissue insult, particularly as the leads cross joints. Therefore, in addition to the improvement in selectivity, there is a practical benefit to using a bipolar stimulator, at least until the time when sparse-lead multiplexed systems or “leadless” systems are available. Thus, it is essential to determine whether adding more independent stimulus channels or operating in the bipolar regime would be more cost effective and efficient for achieving the desired level of selectivity. Either option would require our custom implantable stimulators to be redesigned. Several commercially available implantable stimulators are capable of providing sufficient independent and simultaneous channels, and therefore offer an alternative stimulus source. In the meantime, more distal sites on the tibial and common peroneal nerves where spillover to antagonists is less of a concern are likely to provide the best results for selective activation of the ankle musculature.

Using Monte Carlo simulations to create unique cross sections was not practical because of the number of parameters being investigated. That is, with 350 unique combinations of varied parameters per cross section, thousands of FEMs would have to be run. The approach taken analyzed the same cross section in thousands of ways by varying which fascicles were assigned to various functional groups. This approach is expected to account for variation observed in the general population. Thus, a primary assumption was that the cross section used for the models was representative of the population. If the cross section had far fewer or far more fascicles than what is observed on average, or if this cross section’s distribution of fascicular diameters is skewed from the true distribution, the probabilities may no longer apply to the general population. This is unlikely, however, because the cross section was representative of those collected during an unrelated anatomical study of the SN (Gustafson et al. 2011). Across all models, each contact was chosen in both monopolar and bipolar scenario but no contact was consistently chosen more or less frequently than any other contact. This suggested that the algorithm that assigned the fascicles to functional groups effectively created groups at all locations within the nerve and did not favor clusters at any one location. As such, the Monte Carlo-inspired technique described in this study should prove useful in future modeling studies. In fact, because the model was generalized, the results should hold true for any nerve with a similar number of fascicles that are divided up into a similar number of groups. The only changes that would need to be made to apply these results to a similar nerve would be to obtain moment data specific to the joint of interest and determine the appropriate axon activation level required to produce those moments.

The conductance values assigned in the FEM models were obtained from (Choi et al. 2001). The perineurial conductance, 2 mS/m, was derived from frog and carried an underlying assumption that the perineurial thickness was 100 μm (Weerasuriya et al. 1984). The conductance value used falls within the rage reported in literature: 0.6–10 mS/m (Choi et al. 2001; Deurloo et al. 2001, 2003; Koole et al. 1997; Perez-Orive and Durand 2000; Veltink et al. 1989). Models have shown that decreased perineurial conductance increases axonal thresholds, but that population recruitment trends remain unaffected (Grinberg et al. 2008). Choi et al. assumed the epineurial conductance was equivalent to the transverse conductance of the endoneurium due to the structural similarity of the two tissues. Because both of these tissues are believed to be isotropic, a change in their conductance is only expected to change the amplitude of depolorarization, leaving the spread of current, and, more importantly, the second spatial difference of the voltage along axons unaffected. Thus, while the outcomes are not expected to change with differing perineurial and epineurial conductances, the stimulus amplitude to achieve the outcome may. However, the endoneurial conductance, derived from cat dorsal column, was anisotropic (Ranck and Bement 1965). If the in vivo endoneural conductance differs from that used in the models, then the spread of current, the second spatial difference in the voltage along the axons, and the trends observed in the models may not transfer to humans unless the ratio in transverse:longitudinal conductance remains approximately 15%.

Although one group of fascicles within every simulation was designated as sensory fibers, as would be expected for those axons traveling to the sural nerve, the direct effect of stimulating sensory fibers within other fascicle groups was not modeled. It is likely that an extraneural cuff will stimulate larger diameter, myelinated sensory fibers such as those associated with muscle spindles (type Ia), Golgi tendon organs (type Ib), and mechanoreceptors (type II). While activation of sensory fibers is not expected to alter selectivity, their activation could alter the system’s dynamics. The most obvious example would be eliciting a reflex that changes the position of the limb. However, it is likely that clinically deployed neuroprostheses do activate these axons but neither adverse nor profound effects on the efficacy of these systems have been attributed to type I axon activation. The sensate population may perceive pressure due to activation of type II sensory axons, but they are not expected to experience pain, because pain fibers are small in diameter, unmyelinated, and difficult to activate (K. Polasek 2007).

5. Conclusion

Simulations suggest that currently available implantable FINEs and stimulators will not produce sufficient selective activation to restore PF but could produce sufficient selective activation to restore DF in 90% of the population. To improve the likelihood that a single cuff implanted on the SN could restore both of these functions without spillover to FI, FE, TF, or TE, either more channels must be added to the FINE or the stimulator will need to operate in a bipolar mode.