Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Jun 1.
Published in final edited form as: J Electromyogr Kinesiol. 2012 Feb 12;22(3):494–500. doi: 10.1016/j.jelekin.2012.01.011

Influence of Amplitude Cancellation on the Accuracy of Determining the Onset of Muscle Activity from the Surface Electromyogram

Mark Jesunathadas a, Sameer S Aidoor a, Kevin G Keenan b, Dario Farina c, Roger M Enoka a
PMCID: PMC3357456  NIHMSID: NIHMS352904  PMID: 22330887

Abstract

The purpose of the study was to quantify the influence of amplitude cancellation on the accuracy of detecting the onset of muscle activity based on an analysis of simulated surface electromyographic (EMG) signals. EMG activity of a generic lower limb muscle was simulated during the stance phase of human gait. Surface EMG signals were generated with and without amplitude cancellation by summing simulated motor unit potentials either before (cancellation EMG) or after (no-cancellation EMG) the potentials had been rectified. The two sets of EMG signals were compared at forces of 30 and 80% of maximum voluntary contraction (MVC) and with various low-pass filter cut-off frequencies. Onset time was determined both visually and by an algorithm that identified when the mean amplitude of the signal within a sliding window exceeded a specified standard deviation (SD) above the baseline mean. Onset error was greater for the no-cancellation conditions when determined automatically and by visual inspection. However, the differences in onset error between the two cancellation conditions appear to be clinically insignificant. Therefore, amplitude cancellation does not appear to limit the ability to detect the onset of muscle activity from the surface EMG.

Keywords: EMG onset, Amplitude cancellation, Computer simulation

1. Introduction

Much effort has been devoted to determine accurate and reliable methods to detect the onset of muscle activity from electromyographic (EMG) recordings, as the measurement can be important for determining the pattern of muscle activation in both experimental and clinical research (Chang et al. 2006; Dorel et al. 2008; Babyar et al. 2007; Cordo and Nashner 1982; Dimitrova et al. 2004; Graupe et al. 1982; Micera et al. 1998; Nieuwboer et al. 2004; Zardoshti-Kermani et al. 1995). Numerous methods have been proposed to process and automatically analyze EMG signals that minimize errors in detecting the onset of muscle activity (Micera et al. 1998; Di Fabio 1987; Hodges and Bui 1996; Lee et al. 2007; Li and Caldwell 1999; Merlo et al. 2003; Staude et al. 2001; Studenski eat al. 1991; Türker 1993; Van Boxtel et al. 1993).

Despite recent advances in EMG onset detection algorithms (Lev Vaisman et al. 2010; Solnik et al. 2010), it remains unclear if estimates of the onset of muscle activity from the surface EMG are confounded by the reduction in signal amplitude due to the overlap of opposing phases of motor unit action potentials (Day and Hulliger 2001; Keenan et al. 2005). Such amplitude cancellation results in an unavoidable loss of information in the surface EMG signal and varies with the force of the contraction (Day and Hulliger 2001; Keenan et al. 2005; 2006). The attenuation of EMG amplitude presumably influences the ability to detect the onset of muscle activity. This effect may differ depending on whether the onset of an EMG signal is determined by visual inspection or with a computer algorithm, which defines when the signal amplitude within a specific duration is greater than a specified value above the baseline mean.

The purpose of this study was to quantify the influence of amplitude cancellation on the accuracy of detecting the onset of muscle activity based on an analysis of simulated surface EMG signals. The primary hypothesis was that amplitude cancellation would impair the ability to detect the onset of simulated EMG signals. Furthermore, we hypothesized that amplitude cancellation would influence the parameters of the computer algorithm and low-pass filter frequency that produced the least amount of onset error.

2. Methods

Simulated surface EMG signals were generated using an adapted version of a model of motor unit recruitment and rate coding (Day and Hulliger 2001; Keenan et al. 2005; Fuglevand et al. 1993). The model was modified to simulate the isometric force properties of a generic lower limb muscle during 540 ms of the stance phase of human walking (Ishikawa et al. 2005). Surface EMG signals with and without amplitude cancellation were generated at different force levels and with different signal characteristics. EMG onset was estimated visually and with different computer algorithms for both the cancellation and no-cancellation EMG signals. The actual EMG onset time for each force level was determined as the average over 20 trials from EMG signals simulated without amplitude cancellation and without white Gaussian noise added to the signal. Each of the 20 trials involved a random distribution of the motor unit territories in the muscle, which simulates the variability that would occur across subjects, while keeping the activation pattern the same. The error in detecting EMG onset at each force level corresponded to the difference between the onset times identified in each condition and the actual EMG onset time.

2.1. Model parameters

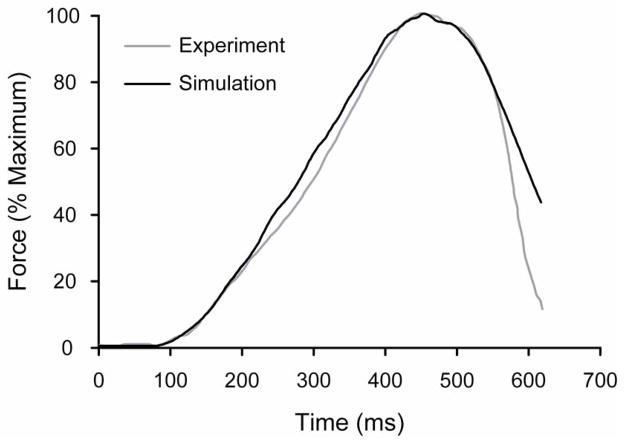
The model was implemented in MATLAB® version 6b (The Mathworks, Natick MA). The parameters of the model were similar to those described previously (Keenan et al. 2005; Fuglevand et al. 1993), but were modified so that the properties of the simulated motor unit pool resembled those of a generic lower limb muscle. The accuracy of the model was determined by visually comparing the simulated force profile with the experimentally observed force profile measured in the Achilles tendon during the stance phase of human walking (Ishikawa et al. 2005) (Figure 1). The simulated motor unit pool comprised 350 motor units, with an exponential distribution of recruitment thresholds, twitch forces, and twitch contraction times (Fuglevand et al. 1993). Motor unit recruitment and discharge rates were determined by an excitation function that acted on the entire motor unit pool. Minimal discharge rates were set at 8 pulses per second (pps) for all motor units, whereas maximal discharge rates decreased linearly from 35 pps for motor unit 1 to 25 pps for motor unit 350.

Figure 1.

Figure 1

Open in a new tab

Experimental (gray) and simulated (black) Achilles-tendon force traces during the stance phase of human walking. Force data are expressed as a percent of maximal force so that the experimental and simulated force traces could be compared. The simulated force trace was generated to achieve the maximal force that the model muscle could produce.

The simulated muscle was modeled as an anisotropic, non-homogeneous, cylindrical volume conductor with surrounding layers of subcutaneous tissue and skin. It was modeled to have a circular cross-sectional area with muscle fiber lengths and diameters, innervation numbers, and motor unit territories similar to those used previously (Keenan et al. 2005). Motor unit action potentials were generated for each active motor unit and were either summed and then rectified (cancellation condition) or rectified and then summed (no-cancellation condition). The surface EMG was generated based on a bipolar electrode configuration with an inter-electrode distance of 10 mm and with circular electrodes that were 4 mm in diameter (Keenan et al. 2005). The simulation was run 20 times for each condition so that the variability in the model parameters could influence the variability in the surface EMG signals.

2.2. Simulated conditions

To evaluate the influence of amplitude cancellation in combination with different signal conditions, simulated surface EMG signals were generated with and without amplitude cancellation at different forces and low-pass filter cut-off frequencies. Previous investigations have shown that the amount of amplitude cancellation can be greater at larger forces (Keenan et al. 2005). Therefore, the simulated EMG signals were generated at forces equivalent to 30 and 80% MVC force so that it was possible to determine the influence of different amounts of amplitude cancellation on the ability to detect the EMG onset time. The EMG signals in both cancellation conditions were low-pass filtered with cut-off frequencies of 100, 350, and 500 Hz, which corresponds to the low-pass filter cut-off frequencies used to condition EMG signals for onset detection (Micera et al. 1998, Hodges and Bui 1996; Merlo et al. 2003). White Gaussian noise was added to the EMG signals so that the signal-to-noise ratio (SNR) for the cancellation EMG at each force level was 15 dB (Bonato et al. 1998; Guia Rosa et al. 2008). The same level of noise was added to the EMG signals in both cancellation conditions (cancellation and no-cancellation) to match experimental settings in which the level of noise within a signal is due primarily to external factors (Türker et al. 1993). This meant that the no-cancellation signals had greater SNRs.

2.3. EMG onset detection

Surface EMG signals were generated at each force without amplitude cancellation and additive white noise to identify the actual EMG onset time at each force in the simulated surface recordings. The time at which the EMG signals first had a value greater than zero was set as the EMG onset time. These EMG signals were generated over 20 trials at each force, and the average EMG onset time at each force was set as the actual EMG onset time.

The EMG onset times for both cancellation conditions were estimated by visual inspection and with computer algorithms similar to those used previously (Di Fabio 1987; Hodges and Bui 1996). The computer algorithms utilized a sliding window with durations of 10, 25, and 50 ms that were advanced in 0.2 ms steps starting from the beginning of the signal. If the mean value within the sliding window was greater than either 1, 2, or 3 SDs of the baseline noise, then the middle sample within the window was taken as the EMG onset time. The middle sample of the window was used to reduce the incidence of onset times that were delayed from the actual onset time and to minimize the presumed influence of the slope of the EMG trace on the estimate of onset time (Hodges and Bui 1996).

The error in the EMG onset time as estimated with these computer algorithms was quantified at each force level for four conditions: amplitude cancellation, low-pass filter cut-off frequency, sliding window, and SD threshold. Positive and negative onset errors indicated that EMG onset time was estimated to occur either after or before the actual onset time, respectively.

To test the influence of amplitude cancellation on visually determined EMG onset times, two individuals with experience in analyzing EMG signals determined the onset of the simulated surface EMG signals by visual inspection. Each individual visually determined the onset of nine EMG signals at each force level for two conditions: amplitude cancellation and low-pass filter cut-off frequency. The two individuals visually examined the same EMG signals at each force three times, but separated their analysis of EMG signals by at least two days. The time resolution available to the two investigators to view the surface EMG signals ranged between 1 s and 0.2 ms. Furthermore, a cursor that identified the time and amplitude coordinates of the each EMG data point was used by the investigators to assist in estimating EMG onset time.

2.4. Statistical analysis

To quantify the amount of amplitude cancellation in the EMG signals, the root-mean-square (RMS) values were determined across all signal conditions for each force level over the first 250 ms of the EMG signals. Paired t-tests were used to compare the RMS values between the cancellation and no-cancellation EMG signals at each force level. Repeated-measures ANOVA (Huynh – Feldt correction) was used to compare the EMG onset errors obtained from the estimation of EMG onset times using the computer algorithms. There were five factors in this within-subjects comparison (amplitude cancellation, target force, low-pass filter cut-off frequency, sliding window duration, and SD threshold). Repeated-measures ANOVA (Huynh – Feldt correction) was also used to compare the EMG onset errors obtained with the visual-inspection method of onset detection. There were three factors in this within-subjects comparison (amplitude cancellation, target force, and low-pass filter cut-off frequency) and one between-subjects factor (investigator).

Post-hoc analysis with paired-samples t-tests were used when appropriate to compare the onset errors of signals in the cancellation and no-cancellation condition at each force, low-pass filter frequency, sliding window, and SD threshold. Bonferroni-corrected multiple-comparisons analysis was used to identify differences in EMG onset errors between each force, low-pass filter frequency, sliding window, and SD threshold for the cancellation and no-cancellation signals. Statistics were performed in SPSS versions 17.0, and a P value less than 0.05 was considered significant for the ANOVA analysis; whereas a P values less than 0.025 or 0.017 were considered significant when post-hoc analysis consisted of two (force level) or three comparisons (low-pass filter cut-off frequency, sliding window duration, SD threshold), respectively. All values in text are reported as mean ± standard deviation.

3. Results

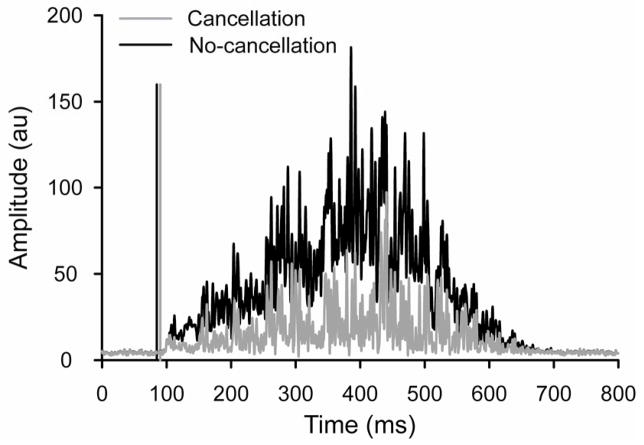
The surface EMG signals generated with amplitude cancellation had significantly lower RMS values than those with no amplitude cancellation at all forces (P < 0.001). The standard deviations of actual EMG onset times at 30% and 80% MVC force were 0.25 and 0.14 ms, respectively. Figure 2 shows representative examples of EMG signals generated with and without amplitude cancellation at 30% MVC force.

Figure 2.

Figure 2

Open in a new tab

Representative example of simulated surface EMG signals for the cancellation (gray) and no-cancellation (black) conditions at a target force of 30% MVC and a low-pass filter set at 500 Hz. The computer algorithm used to detect EMG onset comprised a sliding window of 50 ms and a threshold of 2 SD above baseline noise. The vertical lines indicate the average onset times for selected signals.

3.1. Computer-based EMG onset

The EMG onset error for the signals with and without amplitude cancellation was negative when averaged across all other EMG signal conditions and computer algorithms indicating that onset was estimated to occur before the actual EMG onset time. Contrary to expectations, the average error in EMG onset time from the simulated surface EMG signals with amplitude cancellation (−8.56 ± 12.9 ms) was significantly less (P < 0.001; Huynh-Feldt correction) than the error in the signals without amplitude cancellation (−9.80 ± 12.7 ms) across all other signal conditions (force and low-pass filter cut-off frequencies) and computer algorithms (sliding windows and SD thresholds). Furthermore, the pattern of onset error differed for the EMG signals in the cancellation and no-cancellation conditions as indicated by significant 2-way interactions between the cancellation conditions and all the other parameters (force, low-pass filter cut-off frequencies, sliding windows, and SD thresholds; P < 0.001 – Huynh-Feldt correction).

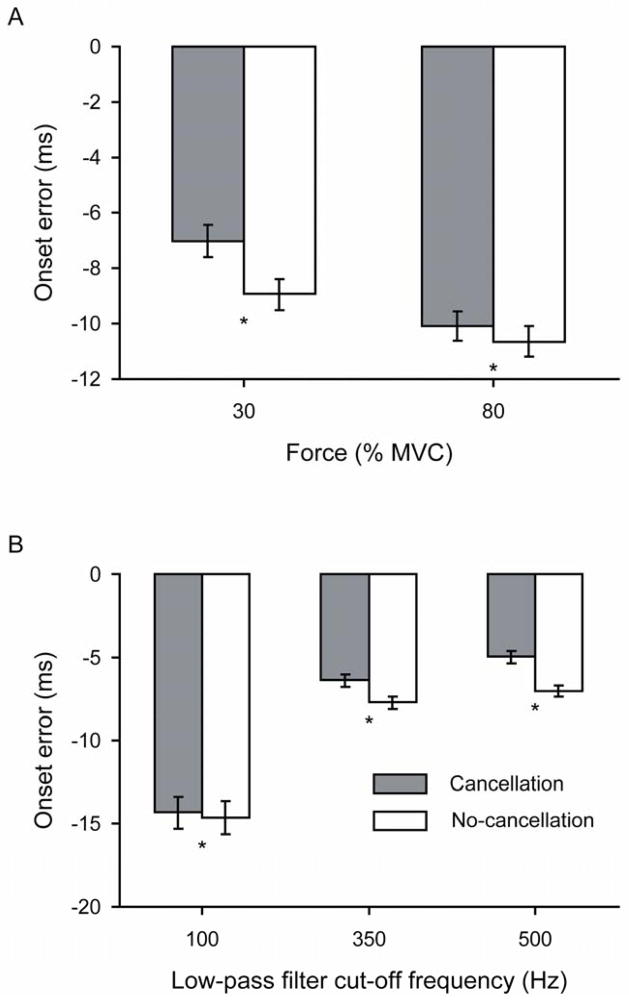
The onset error varied with the target contraction force (P = 0.002), and was −7.99 ± 12.9 ms at 30% and −10.4 ± 12.6 ms at 80% MVC force when averaged across the two cancellation conditions. Post-hoc analysis indicated that EMG onset error for the no-cancellation conditions was significantly greater than for the cancellation conditions at each target force (P≤0.001; Figure 3A).

Figure 3.

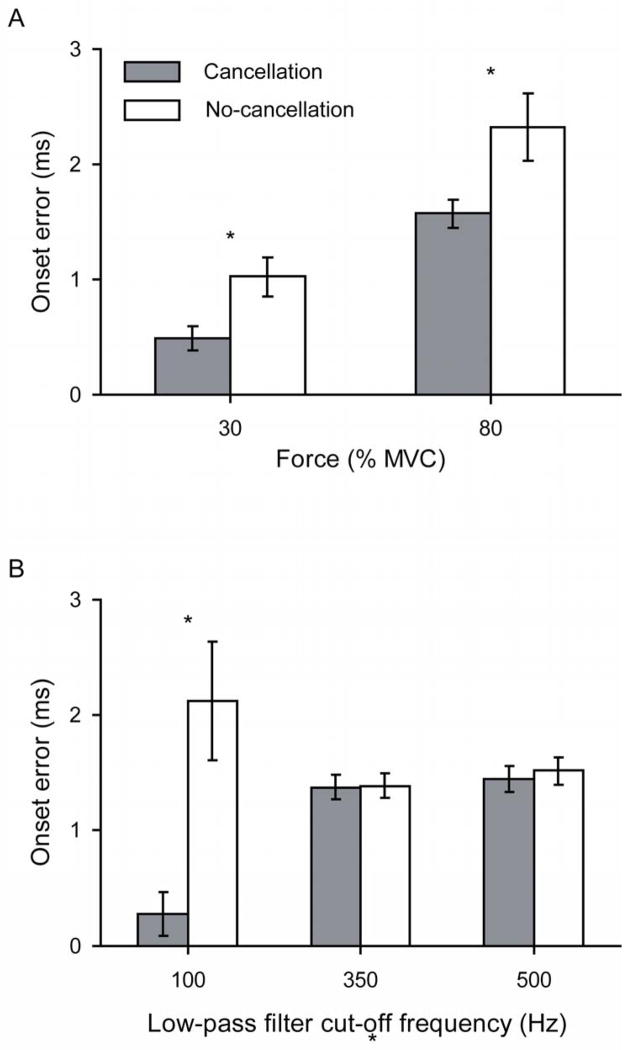
Figure 3

Open in a new tab

Onset errors estimated with the computer algorithm for the simulated cancellation and no-cancellation EMG signals. The errors were averaged across all other conditions for each independent variable. A) Target forces of 30% and 80% MVC and B) Low-pass filter cut-off frequencies of 100, 350, and 500 Hz. * P < 0.025 and P < 0.017 between the cancellation and no-cancellation conditions for A and B, respectively.

The influence of the low-pass filter cut-off frequency on the onset error differed between the cancellation and no-cancellation signals (P < 0.001 – Huynh-Feldt correction). Post-hoc analysis revealed that the onset error was greater for the no-cancellation conditions at each low-pass filter cut-off frequency (P < 0.001). The onset errors ranged from −14.6 ± 18.7 ms at 100 Hz to −7.01 ± 6.68 ms at 500 Hz, and from −14.3 ± 18.8 ms to −4.97 ± 6.91 ms for the no-cancellation and cancellation conditions, respectively. The low-pass filter cut-off frequency at which the average onset error was minimal was 500 Hz for both cancellation conditions (Figure 3B).

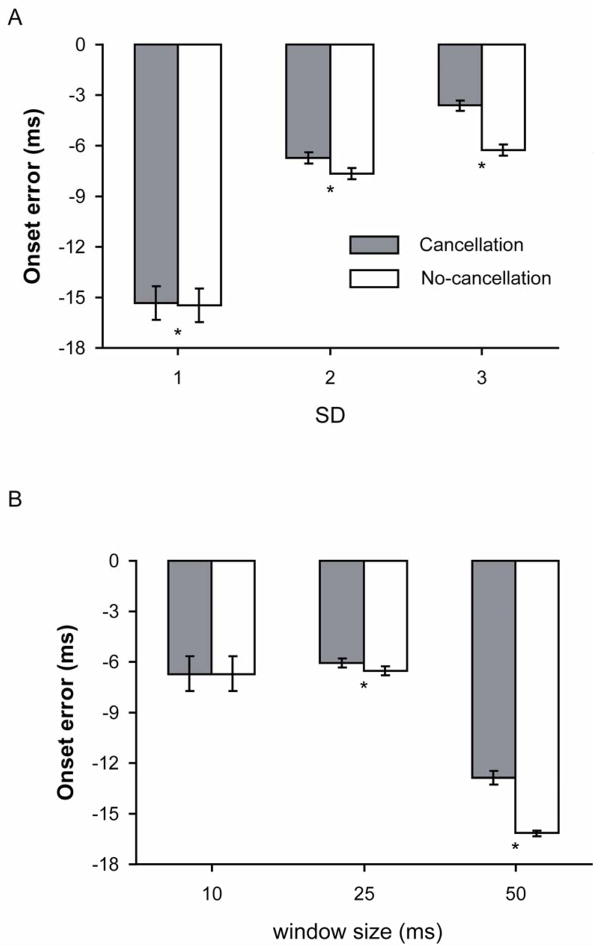
The accuracy of detecting the EMG onset time varied across the SD thresholds (P < 0.001 – Huynh-Feldt correction). Post-hoc analysis revealed that the onset error at each SD threshold was greater for the no-cancellation conditions (P < 0.001). The onset error across all SD thresholds ranged from −15.3 ± 18.8 ms for 1 SD through −3.63 ± 6.19 ms for 3 SD for the cancellation conditions and from −15.5 ± 18.7 ms to −6.25 ± 6.18 ms for the no-cancellation conditions (Figure 4A). Also, the error was least when the threshold was set at 3 SD for both cancellation conditions.

Figure 4.

Figure 4

Open in a new tab

Onset errors for the cancellation and no-cancellation EMG signals when using a computer algorithm with A) threshold levels of 1, 2, and 3 SD above baseline noise and B) sliding windows with widths of 10, 25, and 50 ms, averaged across all other conditions. * P < 0.017 between the cancellation and no-cancellation conditions.

Onset error was influenced by the duration of the sliding window (P < 0.001 – Huynh-Feldt correction). Post-hoc analysis showed that the onset error was significantly greater for the no-cancellation conditions compared with the cancellation conditions for sliding-window durations of 25 and 50 ms (P < 0.001), but the onset error did not differ for the cancellation compared with the no-cancellation conditions when a sliding window of 10 ms was used in the computer algorithms (P = 0.033). A sliding window of 50 ms resulted in the greatest onset error for both cancellation conditions and resulted in the greatest difference in onset error between the cancellation (−12.9 ± 7.51 ms) and no-cancellation (−16.2 ± 3.12 ms) conditions. The sliding window duration that resulted in the least onset error was 25 ms for both the cancellation (-6.08 ± 5.43 ms) and no-cancellation (−6.53 ± 4.77 ms) conditions (Figure 4B).

There were combinations of signal conditions and computer algorithms that produced onset errors of less than 1.0 ms for the cancellation and no-cancellation conditions. These parameters always included window durations of 10 ms and thresholds of 2 or 3 SDs above baseline noise. The combination of parameters that minimized the onset error was identical for both EMG cancellation conditions.

3.2. Visual onset determination

Two investigators visually determined the onset of muscle activity from the same signals. The average coefficient of variation for onset times across days was low for both investigators. The greatest coefficient of variation across days was 0.30 ± 0.185%, which was achieved by investigator 1 at 80% MVC force across the no-cancellation signals. The average onset error across all conditions differed for the two investigators: 0.364 ± 2.11 ms for investigator 1 and 2.15 ± 1.55 ms for investigator 2 (P < 0.001). However, the data were averaged across investigators.

In contrast to the computer-based methods, visual inspection typically estimated the EMG onset time to occur after the actual EMG onset time. Contrary to expectations, the onset error was greater for the no-cancellation conditions (1.67 ± 1.88 ms) than for the cancellation conditions (1.03 ± 0.991 ms) based on visual inspection of the EMG signals (P < 0.001).

The onset error varied with the force of the contraction (P < 0.001) and the influence of amplitude cancellation on the onset error differed across target forces (P < 0.001). Post-hoc analysis indicated that onset error at each target force was greater for the no-cancellation than the cancellation conditions (P≤0.006). The greatest amount of error occurred at 80% MVC for both the cancellation (1.57 ± 0.880 ms) and no-cancellation conditions (2.32 ± 2.18 ms) (Figure 5A).

Figure 5.

Figure 5

Open in a new tab

Onset errors estimated from visual inspection of the simulated EMG signals in the cancellation and no-cancellation conditions that were generated at A) forces of 30% and 80% MVC and B) low-pass filter cut-off frequencies of 100, 350, and 500 Hz, averaged across all other conditions. * P < 0.017 between the cancellation and no-cancellation conditions.

Low-pass filtering the EMG signals significantly altered the onset error obtained by visual inspection (P < 0.001), and led to different patterns of onset error for the cancellation and no-cancellation conditions (P < 0.001). For example, the least amount of error occurred in the EMG signals when low-pass filtered with a cut-off frequency of 100 Hz for the cancellation conditions (0.277 ± 1.10 ms) and 350 Hz for the no-cancellation conditions (1.38 ± 0.636 ms). Post-hoc analysis indicated that the onset error was significantly less for the cancellation compared with the no-cancellation EMG signals only at a low-pass filter cut-off frequency of 100 Hz (P < 0.001; Figure 5B).

Similar to the results for the computer-based methods, onset errors of less than 1.0 ms for both cancellation conditions were observed with the visual-inspection method. However, the particular signal conditions that minimized onset error differed for the two cancellation conditions.

4. Discussion

The results of the current study indicate that the presence of amplitude cancellation in the surface EMG influences the ability of both computer algorithms and visual examination of the recording to detect the onset of muscle activity. Contrary to the hypothesis, amplitude cancellation did not limit the ability to detect the onset of muscle activity using either computer algorithms or visual inspection.

4.1. Computer-based methods

Although we hypothesized that amplitude cancellation would increase the error in detecting the onset of muscle activity from the surface EMG, onset error was greater for signals with no amplitude cancellation and for stronger contractions. Furthermore, the greatest difference in onset error between the cancellation and no-cancellation conditions occurred at the lower force (30% MVC force), in which the amount of amplitude cancellation was less than at 80% MVC force. These finding suggest that the initial slope of signals largely influences the ability to detect the onset of EMG signals and that the increase in observed onset error may increase non-linearly and approach a plateau at larger initial slopes.

Signals without amplitude cancellation had SNRs that were greater than those with amplitude cancellation, which resulted in a large slope at the beginning of an EMG signal (Figure 2). Although larger slopes have been associated with greater accuracy in determining the onset of the surface EMG signal, the large slope likely increased the early onset detection for the no-cancellation EMG signals (Merlo et al. 2003; Staude et al.1996; 2001). Although the use of the middle of the sliding window was expected to reduce the incidence of delayed EMG onset times and result in more accurate onset time estimates (Hodges and Bui 1996), it often resulted in early detection of EMG onset for the signals without amplitude cancellation. Thus, the SNR and slope of signal should be considered when determining when the onset is defined within a sliding window. For example, it seems that the onset should be defined later in the window for signals with large SNRs and initial slopes.

Low-pass filtering of surface EMG signals is commonly used to assist in identifying the onset of the signal because it attenuates abrupt changes in the surface EMG and reduces the probability of a computer algorithm incorrectly specifying the onset of the surface EMG activity (Cordo and Nashner 1982; Hodges and Bui 1996; Morey-Klapsing et al. 2004; Staude et al. 1996; 2001). The influence of the low-pass filter cut-off frequency, however, is not monotonic. For example, Hodges and Bui (1996) showed that excessive smoothing (such as a cut-off frequency of 10 Hz) or not enough smoothing (such as a cut-off frequency of 500 Hz) both lead to large errors in detecting the onset of an EMG signal, which led Hodges and Bui (1996) to recommend a low-pass filter with a cut-off frequency of 50 Hz. In contrast to the results of Hodges and Bui (1996), low-pass filtering at 500 Hz led to the least amount of error for both cancellation conditions in the current study. The contrasting results are likely due to differences in the temporal and amplitude features of the signals between the two studies. For example, the EMG traces shown in Hodges and Bui (1996) indicate that the amplitude of the experimentally recorded EMG signals, in which the actual onset was not known, returned briefly to baseline soon after the contraction began (~250 ms), whereas the no-cancellation signals in the current study did not return to baseline until the contraction ended (540 ms). Furthermore, onset was defined as the middle of the sliding window in the current study and as the initial sample in Hodges and Bui (1996). This finding seems to indicate that the choice of low-pass filter cut-off frequency depends not only on the temporal and amplitude characteristics of the signal, but also on the specific parameters used in the detection algorithm.

The ability of the computer algorithm to detect the onset of the surface EMG in both cancellation conditions depended on the SD threshold used by the computer algorithm. Although the error was statistically greater for the no-cancellation conditions for each SD threshold used, a threshold of 3 SD led to the least amount of error in both cancellation conditions. Furthermore, the 3-SD threshold led to the greatest difference in onset error between the two cancellation conditions. Nonetheless, the results indicate there is no single SD threshold that is optimal and the value depends on the other parameters of the computer algorithm and signal conditioning.

Previous studies have reported that moderate window durations (25 ms) are preferable for detecting the EMG onset time (Hodges and Bui 1996). The results of the current study confirm these findings. EMG signals in both cancellation conditions required, on average, a moderate window duration (25 ms) to minimize the error in detecting the onset of the EMG signals. However, the onset error was still greater for the no-cancellation conditions, except when the window duration was 10 ms. The combination of the initial slopes of the EMG signals and the choice of defining the middle sample of the sliding window as the point of onset detection may have also influenced these results. Because the mean value within the sliding window likely reached the prescribed threshold in the no-cancellation signals before the cancellation signals, use of the last point rather than the middle sample of the window to define EMG onset may have reduced the early onset estimates for the non-cancellation signals.

The results from the computer-based analysis of EMG onset indicate that amplitude cancellation resulted in statistically less error in detecting the onset of muscle activity from the surface EMG. However, the differences in onset error between the signal conditions were often less than 1 ms, which is of little practical or clinical consequence. Furthermore, minimization of onset error for both the cancellation and no-cancellation conditions with the same parameters and low-pass filter cut-off frequencies may have been the consequence of a better match between these parameters and the temporal and amplitude characteristics of the cancellation signals than no-cancellation signals.

4.2. Visual onset determination

Contrary to expectations, errors in detecting EMG onset by visual determination were greater for the no-cancellation conditions than for the cancellation conditions. This was due to the difficulty in identifying the onset of the EMG signals in the cancellation condition because of the noise in the signal, and the two experts typically erred on the side of assigning the onset to be earlier and thus closer to the actual EMG onset time. Nonetheless, the results from the visual-inspection method indicate that signals generated at moderate forces, low levels of noise, and sufficient smoothing can minimize errors in onset determination.

Similar to the results from the computer-based detection of EMG onset time, the greatest error occurred at the largest target force for both the cancellation and no-cancellation conditions. This finding seems to indicate that investigators were more conservative in assigning an onset time to a signal when the beginning slope of the signal was large. Consistent with this interpretation, the difference in onset time between the cancellation and no-cancellation condition was greatest for the 80% MVC force, in which the difference in amplitude between the signals was greatest.

Onset error was greater for the no-cancellation than cancellation signals for each low-pass filter cut-off frequency. In contrast to the results of the computer algorithm, the low-pass filter cut-off frequency that resulted in the least amount of onset error differed between the cancellation and no-cancellation conditions and was lower than the cut-off frequency that minimized onset error for the computer algorithm (500 Hz). The finding indicates that the higher frequency content in the EMG signals increases the difficulty for visually determining the onset of muscle activity, especially for signals with amplitude cancellation.

4.3. Limitations

The current model aimed to estimate the influence of amplitude cancellation on a generic lower limb muscle attaching to the Achilles tendon. Although attempts were made to model the physiological characteristics of lower leg muscles, the pennation angle of the muscle fibers was not included in the model. Previous research indicates that the orientation of the electrodes relative to the muscle fibers can also influence the amplitude and frequency characteristics of the EMG signal (Farina et al. 2004). Pennation angle is positively related to the amplitude of the EMG signal (Hodges et al. 2003; Manal et al. 2008), however, an increase in the angle between muscle fibers and the surface electrodes during a contraction may reduce EMG amplitude and alter the frequency characteristics of the signal compared with that detected for a parallel arrangement between electrodes and muscle fibers (Camic et al. 2011; Vigreux et al. 1979). Furthermore, the muscle fibers and surface electrodes are not always in parallel planes, as was the case for the current model. In some pennated muscles, for example the tibialis anterior, muscle fibers traverse a plane that is at an angle to the plane of skin and subcutaneous tissue. Although Keenan et al. (2005) reported a similar pattern of amplitude cancellation for the simulated EMG signal to that observed by Day and Hulliger (2001) for the cat soleus muscle, the details of the influence of muscle fiber pennation angle on amplitude cancellation have not been examined systematically. Presumably, pennation angle will influence the combination of parameters that minimize the error in detecting the onset of the EMG signal.

4.4. Conclusions and recommendations

Amplitude cancellation resulted in less error in detecting the onset of muscle activity in simulated surface EMG signals when estimated with computer algorithms and by visual inspection. Thus, it seems that amplitude cancellation may not limit the ability of computer algorithms to detect the onset of EMG signals in signals with moderate to high forces and with high SNRs. Furthermore, both computer algorithms and visual inspection can closely approximate the onset of muscle activity from the surface EMG with or without the presence of amplitude cancellation. However, the choice of algorithm and filtering technique should be based on the amplitude and temporal characteristics of the signals.

Although the aim of the current study was to investigate the influence of amplitude cancellation on the ability to detect EMG onset time, the results partially validate previous work on the factors that influence the estimation of EMG onset time (Micera et al. 1998; Di Fabio 1987; Hodges and Bui 1996; Lee et al. 2007; Li and Caldwell 1999; Merlo et al. 2003; Staude et al. 2001; Studenski eat al. 1991; Türker 1993; Van Boxtel et al. 1993). The findings confirm that estimates of onset times from experimental EMG signals (i.e., those with amplitude cancellation) are influenced by the methods used to condition the signal. Furthermore, onset error can be minimized in experimental EMG recordings by using visual inspection to estimate onset time when the contraction force is moderate or high. Thus, the performance of computer algorithms should be validated with estimates obtained by visual inspection.

Acknowledgments

This work was supported by National Institutes of Health Grant AG09000 (National Institute of Aging) to Roger M. Enoka. The authors thank Jamie Justice, Elysia Sheu, and Thorsten Rudroff for their technical assistance.

Biographies

graphic file with name nihms352904b1.gifMark Jesunathadas completed received a B.S. in mechanical engineering at the California State Polytechnic University Pomona in 2003 and a Ph.D. in integrative physiology from the University of Colorado in Boulder in 2009. He is currently a postdoctoral research associate at Arizona State University in Tempe in the Department of Biological and Health Systems Engineering. His research focuses on the neural mechanisms involved in grasping and dexterous object manipulation.

graphic file with name nihms352904b2.gifSameer Aidoor received a B.E. degree in Electronics Engineering from the University of Mumbai, India, in 2003, and a M.S. degree in Electrical Engineering with certification in Embedded Systems Design from the University of Colorado at Boulder in 2006. His previous work includes mathematical modeling of physiological systems, simulation of the muscle EMG, and research on the influence of amplitude cancellation in surface EMG, as a research assistant in the Neurophysiology of Movement Laboratory at the University of Colorado at Boulder. He currently works on firmware engineering for next-generation hard disk drive processors and studying hardware interactions in real-time embedded systems.

graphic file with name nihms352904b3.gifKevin G. Keenan received his B.S. (1990) and M.S. (1998) degrees in Kinesiology from the University of Michigan. He subsequently worked as the Head Strength and Conditioning Coach at Providence College prior to receiving his Ph.D. in Integrative Physiology from the University of Colorado-Boulder (2005) and completing post-doctoral training (2005–2008) at Cornell University in the Sibley School of Mechanical and Aerospace Engineering. He is currently an Assistant Professor in the Department of Kinesiology at the University of Wisconsin-Milwaukee. His research interests focus on understanding the interplay between motor function, physical activity, and health using high-density surface EMG arrays, long-term (>6 hrs) surface EMG recordings, indwelling EMG recordings, and computational modeling.

graphic file with name nihms352904b4.gifDario Farina obtained the MSc degree in Electronics Engineering from Politecnico di Torino, Torino, Italy, in 1998, and the PhD degrees in Automatic Control and Computer Science and in Electronics and Communications Engineering from the Ecole Centrale de Nantes, Nantes, France, and Politecnico di Torino, respectively, in 2002. In 2002–2004 he has been Research Assistant Professor at Politecnico di Torino and in 2004–2008 Associate Professor in Biomedical Engineering at Aalborg University, Aalborg, Denmark. From 2008 to 2010 he has been a Full Professor in Motor Control and Biomedical Signal Processing and Head of the Research Group on Neural Engineering and Neurophysiology of Movement at Aalborg University. In 2010 he has been appointed Full Professor and Founding Chair of the Department of Neurorehabilitation Engineering at the University Medical Center Göttingen, Georg-August University, Germany, within the Bernstein Center for Computational Neuroscience. He is also the Chair for NeuroInformatics of the Bernstein Focus Neurotechnology Göttingen. Since 2010 he is the Vice-President of the International Society of Electrophysiology and Kinesiology (ISEK). He is the recipient of the 2010 IEEE Engineering in Medicine and Biology Society Early Career Achievement Award for his contributions to biomedical signal processing and to electrophysiology. He is an Associate Editor of IEEE Transactions on Biomedical Engineering and of Medical & Biological Engineering & Computing and member of the Editorial Boards of the Journal of Electromyography and Kinesiology and of the Journal of Neuroscience Methods. His research focuses on biomedical signal processing, modeling, neurorehabilitation technology, and neural control of movement. Within these areas, he has (co)-authored approximately 250 papers in peer-reviewed Journals and over 300 among conference papers/abstracts, book chapters and encyclopedia contributions.

graphic file with name nihms352904b5.gifRoger M. Enoka completed undergraduate training in physical education at the University of Otago in New Zealand prior to obtaining an MS degree in biomechanics and a PhD degree in kinesiology from the University of Washington in Seattle. He has held faculty positions in the Department of Exercise and Sport Sciences and the Department of Physiology at the University of Arizona and in the Department of Biomedical Engineering at the Cleveland Clinic Foundation. He is currently a professor in the Department of Integrative Physiology at the University of Colorado in Boulder. His research focuses on the neuromuscular mechanisms that mediate the acute adjustments and chronic adaptations experienced by the neuromuscular system of humans.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Babyar SR, McCloskey KH, Reding M. Surface electromyography of lumbar paraspinal muscles during seated passive tilting of patients with lateropulsion following stroke. Neurorehabil Neural Repair. 2007;21(2):127–1236. doi: 10.1177/1545968306291857. [DOI] [PubMed] [Google Scholar]
  • 2.Bonato P, D’Alessio T, Knaflitz M. A statistical method for the measurement of muscle activation intervals from surface myoelectric signal during gait. IEEE Trans Biomed Eng. 1998;45(3):287–299. doi: 10.1109/10.661154. [DOI] [PubMed] [Google Scholar]
  • 3.Chang C, Kubo M, Buzzi U, Ulrich B. Early changes in muscle activation patterns of toddlers during walking. Infant Behav Dev. 2006;29(2):175–188. doi: 10.1016/j.infbeh.2005.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Camic CL, Housh TJ, Hendrix CR, Zuniga JM, Bergstrom HC, Schmidt RJ, Johnson GO. The influence of the muscle fiber pennation angle and innervations zone on the identification of neuromuscular fatigue during cycle ergometry. J Electromyogr Kinesiol. 2011;21(1):33–40. doi: 10.1016/j.jelekin.2010.09.010. [DOI] [PubMed] [Google Scholar]
  • 5.Cordo PJ, Nashner LM. Properties of postural adjustments associated with rapid arm movements. J Neurophysiol. 1982;47(2):287–302. doi: 10.1152/jn.1982.47.2.287. [DOI] [PubMed] [Google Scholar]
  • 6.Day SJ, Hulliger M. Experimental simulation of cat electromyogram: evidence for algebraic summation of motor-unit action-potential trains. J Neurophysiol. 2001;86(5):2144–2158. doi: 10.1152/jn.2001.86.5.2144. [DOI] [PubMed] [Google Scholar]
  • 7.Di Fabio RP. Reliability of computerized surface electromyography for determining the onset of muscle activity. Phys Ther. 1987;67(1):43–48. doi: 10.1093/ptj/67.1.43. [DOI] [PubMed] [Google Scholar]
  • 8.Dimitrova D, Horak FB, Nutt JG. Postural muscle responses to multidirectional translations in patients with Parkinson’s disease. J Neurophysiol. 2004;91(1):489–501. doi: 10.1152/jn.00094.2003. [DOI] [PubMed] [Google Scholar]
  • 9.Dorel S, Couturier A, Hug F. Intra-session repeatability of lower limb muscles activation pattern during pedaling. J Electromyogr Kinesiol. 2008;18(5):857–865. doi: 10.1016/j.jelekin.2007.03.002. [DOI] [PubMed] [Google Scholar]
  • 10.Farina D, Merletti R, Enoka RM. The extraction of neural strategies from the surface EMG. J Appl Physiol. 2004;96(4):1486–1495. doi: 10.1152/japplphysiol.01070.2003. [DOI] [PubMed] [Google Scholar]
  • 11.Fuglevand AJ, Winter DA, Patla AE. Models of recruitment and rate coding organization in motor-unit pools. J Neurophysiol. 1993;70(6):2470–2488. doi: 10.1152/jn.1993.70.6.2470. [DOI] [PubMed] [Google Scholar]
  • 12.Graupe D, Salahi J, Kohn KH. Multifunctional prosthesis and orthosis control via microcomputer identification of temporal pattern differences in single-site myoelectric signals. J Biomed Eng. 1982;4(1):17–22. doi: 10.1016/0141-5425(82)90021-8. [DOI] [PubMed] [Google Scholar]
  • 13.Guia Rosa I, Garcia MAC, Nogueira de Souza M. A novel electromyographic signal simulator for muscle contraction studies. Comput Methods Programs Biomed. 2008;89(3):269–274. doi: 10.1016/j.cmpb.2007.10.009. [DOI] [PubMed] [Google Scholar]
  • 14.Hodges PW, Pengel LH, Herbert RD, Gandevia SC. Measurement of muscle contraction with ultrasound imaging. Muscle Nerve. 2003;27(6):682–692. doi: 10.1002/mus.10375. [DOI] [PubMed] [Google Scholar]
  • 15.Hodges PW, Bui BHl. A comparison of computer-based methods for the determination of onset of muscle contraction using electromyography. Electroencephalogr Clin Neurophysiol. 1996;101(6):511–519. doi: 10.1016/s0013-4694(96)95190-5. [DOI] [PubMed] [Google Scholar]
  • 16.Ishikawa M, Komi PV, Grey MJ, Lepola V, Brüggemann GP. Muscle-tendon interaction and elastic energy usage in human walking. J Appl Physiol. 2005;99(2):603–608. doi: 10.1152/japplphysiol.00189.2005. [DOI] [PubMed] [Google Scholar]
  • 17.Keenan KG, Farina D, Maluf KS, Merletti R, Enoka RM. Influence of amplitude cancellation on the simulated surface electromyogram. J Appl Physiol. 2005;98(1):120–131. doi: 10.1152/japplphysiol.00894.2004. [DOI] [PubMed] [Google Scholar]
  • 18.Keenan KG, Farina D, Merletti R, Enoka RM. Amplitude cancellation reduces the size of motor unit potentials averaged from the surface EMG. J Appl Physiol. 2006;100(6):1928–1937. doi: 10.1152/japplphysiol.01282.2005. [DOI] [PubMed] [Google Scholar]
  • 19.Lee AS, Cholewicki J, Reeves NP. The effect of background muscle activity on computerized detection of sEMG onset and offset. J Biomech. 2007;40(15):3521–3526. doi: 10.1016/j.jbiomech.2007.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Li L, Caldwell GE. Coefficient of cross correlation and the time domain correspondence. J Electromyogr Kinesiol. 1999;9(6):385–389. doi: 10.1016/s1050-6411(99)00012-7. [DOI] [PubMed] [Google Scholar]
  • 21.Manal K, Roberts DP, Buchanan TS. Can pennation angles be predicted from EMGs for the primary ankle plantar and dorsiflexors during isometric contractions? J Biomech. 2008;7(41):2492–2497. doi: 10.1016/j.jbiomech.2008.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Merlo A, Farina D, Merletti R. A fast and reliable technique for muscle activity detection from surface EMG signals. IEEE Trans Biomed Eng. 2003;50(3):316–323. doi: 10.1109/TBME.2003.808829. [DOI] [PubMed] [Google Scholar]
  • 23.Micera S, Sabatini AM, Dario P. An algorithm for detecting the onset of muscle contraction by EMG signal processing. Med Eng Phys. 1998;20(3):211–215. doi: 10.1016/s1350-4533(98)00017-4. [DOI] [PubMed] [Google Scholar]
  • 24.Morey-Klapsing G, Arampatzis A, Brüggemann GP. Choosing EMG parameters: comparison of different onset determination algorithms and EMG integrals in a joint stability study. Clin Biomech. 2004;19(2):196–201. doi: 10.1016/j.clinbiomech.2003.10.010. [DOI] [PubMed] [Google Scholar]
  • 25.Nieuwboer A, Dom R, De Weerdt W, Desloover K, Janssens L, Stijn V. Electromyographic profiles of freezing episodes in patients with Parkinson’s disease. Brain. 2004;127(Pt 7):1650–1660. doi: 10.1093/brain/awh189. [DOI] [PubMed] [Google Scholar]
  • 26.Solnik S, Rider P, Steinweg K, De Vita P, Hortobágyi T. Teager-Kaiser energy operator signal conditioning improves EMG onset detection. Eur J Appl Phyiol. 2010;110(3):489–498. doi: 10.1007/s00421-010-1521-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Staude G, Flachenecker C, Daumer M, Wolf W. Onset detection in surface electromyographic signals: a systematic comparison of methods. EURASIP J Appl Signal Processing. 2001;2001(1):67–81. [Google Scholar]
  • 28.Staude GH, Wolf WM, Appel U, Dengler R. Methods for onset detection of voluntary motor responses in tremor patients. IEEE Trans Biomed Eng. 1996;43(2):177–188. doi: 10.1109/10.481987. [DOI] [PubMed] [Google Scholar]
  • 29.Studenski S, Duncan PW, Chandler J. Postural responses and effector factors in persons with unexplained falls: results and methodologic issues. J Am Geriatr Soc. 1991;39(3):229–234. doi: 10.1111/j.1532-5415.1991.tb01642.x. [DOI] [PubMed] [Google Scholar]
  • 30.Türker K. Electromyography: some methodological problems and issues. Phys Ther. 1993;73(10):698–701. doi: 10.1093/ptj/73.10.698. [DOI] [PubMed] [Google Scholar]
  • 31.Van Boxtel GJM, Geraats LHD, Van Den Berg-Lenssen MMC, Brunia CHM. Detection of EMG onset in ERP research. Pyschophysiology. 1993;30(4):405–412. doi: 10.1111/j.1469-8986.1993.tb02062.x. [DOI] [PubMed] [Google Scholar]
  • 32.Vigreux B, Cnockaert JC, Pertuzon E. Factors influencing quantified surface EMGs. Eur J Appl Physiol Occup Physiol. 1979;41(2):119–129. doi: 10.1007/BF00421659. [DOI] [PubMed] [Google Scholar]
  • 33.Zardoshti-Kermani M, Wheeler BC, Badie K, Hashemi RM. EMG feature evaluation for movement control of upper extremity prosthesis. IEEE Trans Rehabil Eng. 1995;3(4):324–333. [Google Scholar]

RESOURCES