Helioseismology: Probing the interior of a star

Abstract

Helioseismology offers, for the first time, an opportunity to probe in detail the deep interior of a star (our Sun). The results will have a profound impact on our understanding not only of the solar interior, but also neutrino physics, stellar evolution theory, and stellar population studies in astrophysics.

In 1962, Leighton, Noyes and Simon (1) discovered patches of the Sun’s surface moving up and down, with a velocity of the order of 15 cm⋅s⁻¹ (in a background noise of 330 m⋅s⁻¹!), with periods near 5 minutes. Termed the “5-minute oscillation,” the motions were originally believed to be local in character and somehow related to turbulent convection in the solar atmosphere. A few years later, Ulrich (2) and, independently, Leibacher and Stein (3) suggested that the phenomenon is global and that the observed oscillations are the manifestation at the solar surface of resonant sound waves (pressure modes, or p-modes) traveling in the solar interior. There are ≈10 million resonant p-modes in the Sun, with periods ranging from minutes to hours. Like sound waves trapped in an organ pipe, the p-modes are effectively trapped in a spherical-shell cavity defined by the surface and an inner turning radius that depends on the physical characteristics of the mode itself and the interior. Linear theory can be used to describe the oscillations because their amplitudes are small. Spherical harmonics, characterized by their degree l and azimuthal order m, describe the angular component of the mode eigenfunctions.

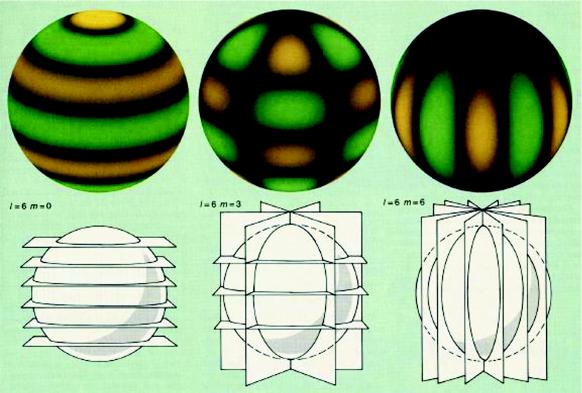
The properties of spherical harmonics used to describe nonradial oscillations in the Sun are illustrated in Fig. 1. In addition, the radial order n is related to the number of nodes in the radial eigenfunction. In general low-l modes penetrate more deeply inside the Sun: that is, have deeper inner turning radii than higher l-valued p-modes. It is this property that gives p-modes remarkable diagnostic power for probing layers of different depth in the solar interior.

Figure 1.

Spherical harmonics for l = 6, m = 0, m = 3, and m = 6, respectively, from left to right (Courtesy J. W. Leibacher, National Solar Observatory).

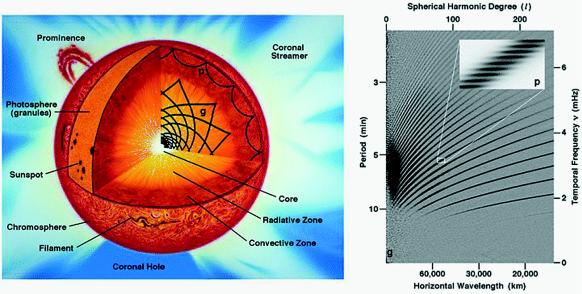
The cut-away illustration of the solar interior (Fig. 2 Left) shows the region in which p-modes propagate. Linearized theory predicts (2, 4) a characteristic pattern of the dependence of the eigenfrequencies on horizontal wavelength. The right-hand side diagram in Fig. 2, which plots the frequencies versus horizontal wavelength for observed p-modes, displays the characteristic ridges in which most of the power in the observed p-mode oscillations is concentrated. The first diagrams of this kind confirmed the global character of the solar p-mode oscillations (5), and helioseismology was born.

Figure 2.

(Left) Cut-away of the solar interior showing the location of the convection zone. The regions where p-modes and g-modes propagate are indicated. (Right) Plot of p-mode frequencies vs. horizontal wavelength as observed in the Sun (Courtesy J. W. Leibacher, National Solar Observatory).

The science of helioseismology is thus the study of the solar interior using p-modes as probes of its interior structure. Because p-mode frequencies are Doppler-shifted by motions in the line of sight, they also can be used to study the internal dynamics of the Sun, such as internal rotation and convection.

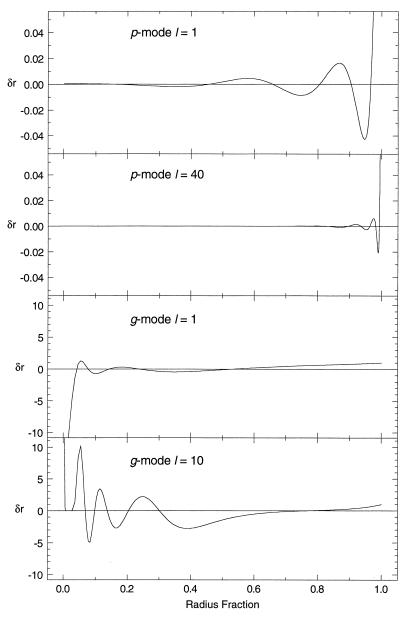
Stellar oscillation theory also predicts the existence of buoyancy driven modes (gravity modes, or g-modes) that have been observed in other astrophysical contexts. It is unclear at this point whether g-modes are excited in the Sun. They are exponentially damped in convective regions; hence, their amplitudes at the top of the solar convective envelope are expected to be much smaller than in the radiative core. The regions of the Sun in which g-modes can propagate with large amplitudes are illustrated in Fig. 2. Fig. 3 is a plot of amplitudes of the radial eigenfunctions of p-modes and g-modes. Note that, in contrast to p-modes, which have maximum amplitudes in the outer parts of the Sun, g-modes exhibit their largest amplitudes in the solar core. If observable, g-modes would be sensitive probes of the solar core, where the p-modes are least sensitive.

Figure 3.

Amplitudes of radial eigenfunctions for a typical p-mode (Upper) and g-mode (Lower).

There are many facets to helioseismology. The results described in the next sections are primarily selected to emphasize the contribution of helioseismology to the study of stellar evolution and related applications to astrophysics and physics. The interpretation of a wealth of ground-based data, most recently provided by the Global Oscillation Network Group (GONG) project, a network of observing stations distributed around the globe to observe the Sun continuously, and the SOHO space mission, have led to many advances. A list of the most important accomplishments of seismology would include the following: the testing of the physical assumptions of stellar evolution theory; the determination of the depth of the solar convection zone; the reconstruction by inversion of the internal rotation profile in the outer half of the solar radius; the detailed probing of the superadiabatic transition layer near the solar surface; the realization of the important role played by the diffusion of helium in the interior of the Sun and the seismic determination of the helium abundance in the convection zone; the determination of the age of the Sun by seismic means; the setting of a strong constraint on varying-G cosmologies; and, finally, the demonstration that the solar neutrino discrepancy is likely to reveal fundamental new knowledge about neutrinos and their interaction with matter.

Depth of Convection Zone

The first important result regarding the internal structure of the Sun was the determination of the depth of the surface convection zone (6). It is possible, using an inversion of the solar p-mode, to derive the dependence of the speed of sound on depth throughout most of the solar interior. There is a discontinuity in the sound speed slope at the bottom boundary of the solar convective envelope, where the temperature gradient changes from adiabatic to radiative. This transition has been located precisely at the radius fraction 0.713 ± 0.003 (6, 7). The importance of knowing the depth of the convection zone goes beyond merely understanding the extent of convective mixing in the solar envelope. Combined with the wealth of information available about the Sun—that is, its mass, surface chemical composition, radius, and luminosity—knowledge of the convection zone depth constrains physical models of the deep interior as well.

The Solar Tachocline

Helioseismology provides a unique opportunity to study the rotation of the Sun. Because rotation breaks the spherical symmetry of the model, the azimuthal eigenvalue m is no longer degenerate, and the frequency of the p-mode is split into a (2l + 1) term multiplet. Inversions of the intermediate and low-l p-modes rotational splitting due to the Doppler effect reveal information about the rotational state of the solar interior. They show that the bulk of the convection zone rotates differentially in much the same way as the solar surface and that there is an abrupt transition in the rotation rate at the base of the convection zone, where the rotation becomes effectively independent of latitude. This relatively thin transition region is called the tachocline. As it has become amenable to detailed study, the solar tachocline has attracted considerable interest (7, 8). This is because, in the tachocline region, circulation currents may be responsible for the mixing into the interior of light elements such as lithium, which burns in the interior >2.4 million K. This tachocline is also believed to be where the solar dynamo that controls solar activity is anchored. Its complex structure is the result of a number of competing physical effects: convective overshoot, the downward diffusion of helium and heavy elements, and turbulence induced by rotational shear and other rotationally induced material flows. The tachocline structure thus provides an invaluable snapshot of the state of the solar interior at one moment during solar evolution.

Superadiabatic Transition Layer

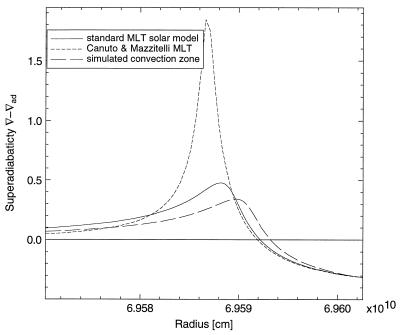
The transition between deep convection, where the temperature gradient is nearly adiabatic, and the shallow outer layers of the Sun, where radiative losses dominate, is difficult to model. This layer is thin and highly turbulent. Its superadiabatic radiative temperature gradient dominates the energy transfer (Fig. 4). This layer is usually described by the mixing length theory (9). As it is now possible (just) to compute three-dimensional simulations of stellar convection that are physically realistic, there is a renewed effort to model this region in greater detail (10, 11).

Figure 4.

Models of the superadiabatic gradient in the Sun. Here, ∇ stands for the logarithmic temperature-pressure gradient (dlogT/dlogP). MLT stands for mixing length theory. The Canuto-Mazzitelli (15) theory is an improved mixing length theory.

The superadiabatic layer, as it is known, effectively determines the radius of the Sun. Once we are able to model this layer, we will then be able to calculate the radii of Sun-like stars more accurately than the current determinations based on the mixing length theory. Helioseismology is critical to this developing field, providing the only means to test the numerical simulations of convection.

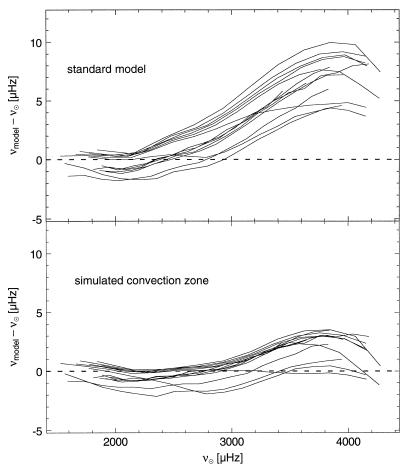
It is now well established that calculated p-mode frequencies depend sensitively on the treatment of the surface boundary conditions (12), particularly at the high frequency end. The difference between observed and calculated p-mode frequencies in an up-to-date standard solar model (13) in which the surface boundary conditions are based on the mixing length theory of convection is shown in Fig. 5 Upper. The lower panel shows the effect of improving the surface boundary conditions by adapting a simulated convection zone to a solar model (14). The opportunity offered by helioseismology to understand the physics of the superadiabatic transition layer in stars with surface convection zones will have far-reaching implications for stellar evolution theory and its many applications to astronomy. Coupled with progress in low temperature opacities, understanding the radiative hydrodynamics of cool star envelopes will remove the main uncertainty in the calculation of stellar radii (usually characterized as the “mixing length uncertainty”), resulting in greatly enhanced confidence in the determination of star cluster ages and the chronology of the galaxy. Similarly, the position of the red giant branch in the color-magnitude diagram as a function of age and chemical composition is a major tool in stellar population studies and in the population synthesis of distant systems, which badly needs calibration, based on sound physical modeling.

Figure 5.

Frequency difference diagrams (calculated minus observed) for solar p-modes with degree l in the range from 0 to 100. The upper panel shows a standard model constructed with the mixing length theory of convection, and the lower panel shows the same interior model with a more realistic simulated convection zone.

The Solar Helium Abundance

The helium abundance of the Sun is an important piece of information in discussions of galactic nucleosynthesis. The helium abundance of the Sun cannot be determined accurately spectroscopically because solar helium lines are chromospheric and are formed out of thermodynamic equilibrium. Until now, stellar evolution theory has provided the best way of evaluating the solar helium abundance; since the solar heavy element content is known, the luminosity of the standard solar model is primarily dependent on the adopted helium abundance. Indeed, tweaking the initial helium content is the usual way of matching a solar model to the observed solar luminosity.

Now seismic inversions of the Sun provide an independent, precise method of determining the helium abundance in the solar convection zone (16). The solar helium content by mass has recently been evaluated as Y = 0.248 ± 0.002 (17). This result is to be compared with Y(initial) of ≈0.275 from stellar evolution. It is consistent with the conclusion that helium diffusion must take place in the solar interior.

Seismic Age of the Sun

The age of the Sun is an important parameter in calculating a standard solar model. In the case of evolutionary models, it is defined as the time it has taken the Sun to evolve from the zero-age main sequence (zams), where nuclear reactions just begin to dominate gravitation as the primary energy source, to the present day. The age of the Sun is normally matched to the age of the oldest meteorites, T(meteor). The radioactive clocks of the meteorites are expected to be set to zero during the last high temperature event in the primordial solar system nebula, which occurs in the pre-main sequence phase. In fact, the time of formation of the meteorites, the time of the existence of the accretion disk, and the time of the emergence of the central star from the optically thick circumstellar cloud all occur within 10 million years of each other. Observations of disks around T Tauri stars show that the disk dissipates before the central star reaches the zero-age main sequence.

Based on pre-main sequence evolution calculations and accounting for mass loss, one can estimate the time between the start of the meteoritic clocks and the zams to be T(to zams) = 40 ∓ 10 million years. The age of the Sun is then calculated from T(sun) = T(meteor) − T(to zams) (18). From an estimate of the age of the oldest meteorites being 4.57 ± 0.4 billion years, the age of the Sun is 4.53 ± 0.4 billion years (19, 20). The error associated with the T(to zams) does not significantly affect the overall determination.

The seismic age of the Sun depends sensitively on the inclusion of helium and heavy element diffusion in the models. Only then is it possible to obtain simultaneously best agreement with the p-mode frequencies and agreement with the observed surface heavy element content and the meteoritic age of the Sun. At the present time, the best seismic age for the Sun is estimated at 4.5 ± 0.10 billion years (13), consistent with the meteoritic age.

Constraint on Varying-G Cosmology

One of the unexpected results from the high quality helioseismological data now available has been the setting of a strong limit on the variation of the universal gravitational constant G during the lifetime of the Sun. The limit is ≈(1/G)dG/dt < 1.6 × 10⁻¹² per year. This limit is stronger by almost one order of magnitude than constraints on the current maximum time variation derived from radar ranging and the measurements of binary pulsar timing (21).

Solar Neutrinos and Neutrino Physics

Helioseismology now reveals close agreement between the observed p-mode frequencies and the prediction of a standard solar model that includes the effects of helium and heavy element diffusion. Nonstandard models can generally also be ruled out by seismology (13). The same conclusion has been reached by using an equivalent inversion approach, which shows that the run of sound speed agrees best with observation (within 0.2%) in standard solar models that also include diffusion (22). Helioseismology thus supports the conclusion that the solution to the solar neutrino problem, that is, the discrepancy between the observed neutrino flux from the Sun and the standard solar model, will not be found in stellar physics but will require instead improvements in neutrino physics.

Future Directions

Helioseismology is now entering a more mature stage. Research efforts will increasingly focus on the investigation of the solar internal dynamics and the detailed study of magnetic field structures. Can the success of helioseismology be duplicated for stars?