Skip to main content
NCBI home page
Ambio logoLink to Ambio
. 2011 Oct 4;41(2):151–160. doi: 10.1007/s13280-011-0182-0

Does Divergence of Nutrient Load Measurements Matter for Successful Mitigation of Marine Eutrophication?

Ing-Marie Gren 1,✉, Georgia Destouni 2
PMCID: PMC3357834  PMID: 22396095

Abstract

Successful implementation of an international nutrient abatement agreement, such as the Baltic Sea Action Plan (BSAP), requires consistent understanding of the baseline nutrient loads, and a perception of acceptable costs and fairness in targeted reductions of these base line loads. This article presents a general framework for identifying the implications of divergence between different nutrient load quantification approaches, with regard to both cost and fairness criteria outcomes, for the international agreement to decrease nutrient loads into the Baltic Sea as presented in the BSAP. The results indicate that even relatively small divergence in the nutrient load quantification translates into relatively large differences in abatement cost for different Baltic Sea countries. A robust result, irrespective of differences in nutrient load assessments, is a conflict between abatement cost effectiveness and fairness, with relatively poor countries facing heavy abatement cost burdens for cost-effective international load abatement.

Keywords: Nutrient measurement divergences, Eutrophication, Cost effectiveness, Fairness, Baltic Sea

Introduction

Excess anthropogenic nutrient loads to aquatic ecosystems have led to worldwide eutrophication problems (Galloway 2008; Conley et al. 2009a) that require abatement solutions to reduce the proliferation of harmful algal blooms (Huisman et al. 2005) and “dead zones” in coastal marine ecosystems (Díaz and Rosenberg 2008). The Baltic Sea has been reported to contain the largest anthropogenic dead zone in the world (Díaz and Rosenberg 2008) and the effects of eutrophication in this system have been well described (Elmgren and Larsson 2001; Conley et al. 2009b). Mitigation of the damage from eutrophication has been on the agenda for the countries surrounding the Baltic Sea for decades, leading to the collaborative establishment of the Convention on the Protection of the Marine Environment of the Baltic Sea (Helsinki Commission, Helcom) in the late 1980s, working to implement a 50% reduction target for anthropogenic nutrient emissions and discharges (Backer and Leppänen 2008). In spite of the decades of attempts to combat eutrophication, however, there has so far been little progress in total nutrient reductions (http://www.helcom.fi/). Frustration over the lack of progress in achieving improvements in water quality can be one reason for the establishment of private foundations and initiatives which call for rapid and radical measures to combat the eutrophication in the Baltic Sea (e.g. BalticSea2020 2011; NEFCO 2008). Helcom has also reached a new international agreement to reduce the effects of eutrophication, the Baltic Sea Action Plan (BSAP), with targeted nutrient reductions for each Baltic Sea country (Helcom 2007).

The BSAP implies renewed efforts to achieve targeted reductions of nutrient discharges, as calculated to be needed for long-lasting improvement of marine water quality. The lack of results so far, however, clearly indicates an inability to implement effective strategies for such reductions. One important reason for the hesitation to reduce nutrient loads to the Baltic Sea is by all likelihood associated costs, which now start to increase at a higher rate than earlier because the low cost options, such as improved nutrient removal at wastewater treatment plants, have already been implemented in several countries (e.g. Helcom 2007). Therefore, careful cost calculations are now likely to be more important than earlier. Furthermore, successful implementation of international agreements such as the BSAP requires a perception of fairness by involved stakeholders (e.g. Carraro 2000; Bérubé and Cusson 2002; Lange et al. 2007). This may be of particular importance for the mitigation of eutrophication in the Baltic Sea since countries with relatively low income levels are likely to face the highest financial burdens in a cost effective solution (e.g. Gren 2008a). In general, such an allocation of cost burdens is regarded as unfair (e.g. Grasso 2007).

In order to calculate costs and evaluate financial burdens among contracting parties in an international agreement it is necessary to quantify the relation between inland activities, such as agriculture, and associated nutrient loads to the coastal and marine waters, where damages from excess nutrient loads occur. However, model interpretations of available nutrient budget and cycling data can differ considerably with respect to the representations and projections of sources, waterborne transport and retention processes, and future fate of nutrient loads from inland hydrological drainage basins to the coast (e.g. Helcom 2007; Destounit et al. 2008; Gren et al. 2008). Reported Baltic Sea wide estimates of nitrogen (N) and phosphorus (P) loads, for instance, vary between 684 and 745 kton N and 31 and 36 kton P, respectively, in reports by Helcom (2004, 2007), Destouni et al. (2008) and Gren et al. (2008). The main questions addressed in this paper are: if, how much, and in which respects such divergence in nutrient load measurements matters for successful achievement of internationally targeted nutrient load reductions.

The term nutrient load measurement refers here to the quantitative interpretation of available measured data, and not just to directly measured data. Such interpretation, by use of models, is always needed to fill in essential spatiotemporal gaps between the localities (points in space and time) of direct water flow and concentration measurement, and the total nutrient loads that eventually feed into the coast at different points in time, from all the different sources, and along all the different transport-reaction pathways of waterborne nutrients in the large spatial drainage basin scales of long coastlines and whole seas. However, all models and model interpretations of large-scale hydrological mass transport are inevitably associated with uncertainties, see e.g. Hannerz and Destouni (2006) and Destouni et al. (2006, 2008, 2010) for examples of both measurement gap analysis, and analysis of divergence and ambiguity between different models of nutrient loading to the Baltic Sea.

The problem of model interpretation is central in the above-formulated main questions of this study, and involves a different type of uncertainty than the randomness of stochastic model parameters (e.g. Gren et al. 2000, 2002, 2008b; Elofsson 2003; Khadam and Kaluarachchi 2006), and/or the different scenario assumptions of uncertain site characteristics, values of parameters or parameter statistics, or future developments (e.g. Baresel and Destouni 2005, 2007; Destouni et al. 2010), which have been considered in previous studies. For such statistically/scenario-quantifiable uncertainty, previous studies have addressed how the uncertainty propagates further into the problem of minimum costs for abating nutrient loads to international waters by comparing the sensitivity of minimum cost results to different assumptions in, and/or to quantifiable randomness around a single basic modelling approach to expected nutrient loads (e.g. Elofsson 2003, 2006; Bayramoglu 2006; Gren 2008b; Fernandez 2009; Kataria et al. 2010). This study considers instead the problem of how divergent results of different, independent nutrient load reports, based on different nutrient load modelling approaches, propagate into both minimum cost and fairness outcomes. No previous study has to our best knowledge investigated the implications of such divergence propagation to the both the costs and the fairness outcomes of an international agreement on nutrient load mitigation targets.

This study focuses particularly on impacts on the intergovernmental agreement of the BSAP, based on the different measurements of nutrient loads from the Baltic Sea Drainage Basin to the Baltic Sea reported in the three, independent studies of Helcom (2007), Destouni et al. (2008) and Gren et al. (2008). Also in the large literature on cost effective achievements of international environmental agreements (e.g. Carraro and Buchner 2002; Lange et al. 2007), there are few studies considering the present combination of both cost and fairness outcomes for national implementations and international agreements. One previous study has evaluated the BSAP suggestion of abatement target allocation among different countries with respect to both cost effectiveness and fairness (Gren 2008a), but that study did not consider the implications of divergence in different basic nutrient load assessments, which is the main focus of this study.

A few caveats are in order, which are due to the exclusions of benefits from BSAP and dynamics in nutrient transports in the drainage basins and in the Baltic Sea. There are a number of studies showing the importance of distribution of both benefits and abatement costs for agreements and implementations of international environmental agreements (for applications to the Baltic Sea, see Markowska and Zylicz 1999; Gren and Folmer 2003). However, there exists no study of the allocation of benefits among the riparian countries from the implementation of the BSAP. Even if such benefit estimates existed, it is unclear how they could be related to divergences in nutrient load estimates, which is the focus of this article. With respect to the second caveat, it is well known that the dynamics of nitrogen and phosphorus transports differ in the drainage basins (e.g. Destouni et al. 2010), and among marine basins in the Baltic Sea (e.g. Savchuck and Wulff 2009). This means that the time required for achieving certain nutrient reductions to the coastal waters and marine basins also differs among drainage basins, which, in turn, affects abatement costs. Lack of data on nutrient dynamics in the drainage basins is the main reason for the static approach applied in this paper Another justification is the relatively short time perspective of the BSAP, the targets are supposed to be achieved in 2021 (Helcom 2007).

This article is organised as follows: first we briefly present the numerical optimisation model which is used for identifying the implications of differences in nutrient load measurements. Second, we present the considered reports of such different nutrient load measurements for the Baltic Sea. Fourth section shows the calculated results for minimum costs and indicators of fairness for the BSAP implementation for the different nutrient load measurement reports, and the paper ends with some main conclusions from these calculations.

Cost Effectiveness and Fairness

There is an emerging literature in economics on the role of cost effectiveness and fairness for agreements on international environmental problems (e.g. Carraro 2000; Bérubé and Cusson 2002; Lange et al. 2007). The general approach is to treat the two issues separately by first identifying efficient allocations of load abatement requirements and then carry out an assessment with respect to different fairness criteria. This approach is also applied in this article, where we first present calculations of costs for different nutrient load reports and then present the quantification of different fairness criteria.

Calculations of Minimum Cost Solutions—A Brief Presentation of the Numerical Optimisation Model

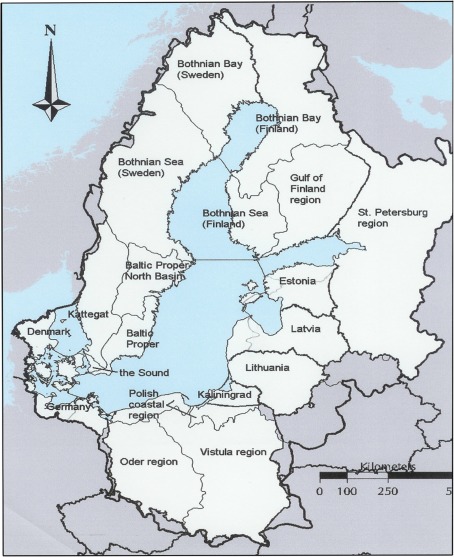
We apply a mathematical programming model described in Gren et al. (2008) for calculations of minimum cost solutions for achieving nutrient targets under different nutrient load reports. The Baltic Sea consists of seven interconnected marine basins (Fig. 1), and the ecological conditions of these basins differ. They are most severe in the largest basin, Baltic Proper, where large parts of the sea bottom lack oxygen and are without biological life due to excess nutrient loads (Conley et al. 2009a). 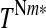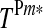For that purpose, the BSAP suggests different nitrogen, N, and phosphorus, P, load targets for the marine basins, denoted Inline graphic and Inline graphic where m = 1,…, n refers to the different marine basins. Each marine basin receives nutrient loads, DEmic, where E = N, P, from its hydrological catchment, where i = 1,…,r are the different sub-catchments, and c = 1,…,j the different riparian countries (or parts of countries) located within that whole catchment. The impacts of nutrient deposition in these catchments differ because of variation in climatic, hydrological, biogeochemical and biological conditions, and the entire basin is therefore divided into 24 sub-catchments (i), nine riparian countries (c), and seven marine basins (m) (Fig. 1).

Fig. 1.

Fig. 1

Open in a new tab

Hydrological catchments of the Baltic Sea (originally from Elofsson 2003) (catchments in Denmark, Germany, Latvia and Estonia are not named but are delineated by fine line)

The main question of this article—how management is affected by divergence in nutrient load measurements—is approached by investigating the implication for cost effective solutions and fairness outcomes from different quantifications of the loads DEmic under business as usual conditions, i.e. before any abatement activities. Measurement divergence is then here defined as a multiplicative relation, θSEmic, between a chosen reference report and other nutrient load reports S, where S = 1,…,v are the different load reports. The coefficient θSEmic is defined as 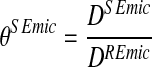Inline graphic where DREmic is the reference report and DSEmic are the other reports. When θSEmic = 1, there is no difference in load measurements between the reference and the S report. It is assumed that θSEmic is constant and unaffected by the level of abatement.

Nutrient loads from report S to each marine basin, TSEm, are the sum of loads from all sub-catchments located in different countries according to

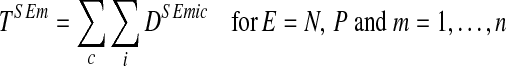graphic file with name M4.gif 1

The load DSEmic is determined by the business as usual scenario (BAU) or base line load, 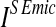Inline graphic, minus the abatement in each sub-catchment. The numerical model applies the nutrient load reports of Gren et al. (2008) as the base line load in the reference study, 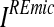Inline graphic, because it is the only report which connects nutrient loads with abatement measures which is necessary to calculate costs of nutrient load reductions. The loads are calculated from data on emissions from different sectors—agriculture, industry, and households—in the sub-catchments, which is necessary for calculations of cost effective solutions. Data on emissions quantify also the loads from sources with direct discharges into the Baltic Sea, such as industry and wastewater treatment plants discharging directly into coastal waters, and atmospheric deposition directly on the Baltic Sea itself. For all other sources, additional data are needed on the transformation of source emissions into coastal loads. This requires data on nutrient leaching for all sources with deposition on land, and on nutrient retention for all sources with discharges into streams. Deposition of nutrients on arable land includes manure and fertilisers. Estimates of discharges of nitrogen and phosphorus from households are based on data on annual emission per capita in different regions, and on connections of populations to wastewater treatment plants with different nutrient removal capacities. We refer to Gren et al. (2008) for a more detailed presentation of the calculations of nutrient loads to coastal waters.

Following earlier literature, we distinguish between two types of abatement measures: reductions in the emissions at sources, 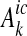Inline graphicwhere k = 1,…,l are different abatement measures, and land use change reducing nutrient transport between the emission source to the coastal waters, 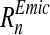Inline graphic, for n = 1,…,o different measures (e.g. Byström 1998; Gren 2008b). The first type of measure affects leaching of nitrogen and/or phosphorus, 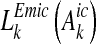Inline graphic, which is increasing at a decreasing rate in 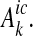Inline graphic The numerical model includes measures for reduction of loads from agriculture, wastewater treatment plants, industry, and households (Gren et al. 2008). In total, 12 different emission oriented measures (k) are included in each sub-catchment, and 1 measure (n) reducing nutrient loads during the transport from the source to the coastal water. Measures directly affecting the agricultural sector are reductions in fertilisers and livestock holding, change in spreading time of manure, and increased area with grassland, energy forests and catch crops. Nutrient loads from industry and wastewater treatment plants are decreased by increased nutrient removal capacity. Household loads are reduced by installation of private sewers in houses not connected to municipal waste water treatment plants, and by use of phosphorus-free detergents.

Construction of wetlands constitutes the second type of measures, 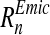Inline graphic, where upstream nutrient mass inputs to the wetlands are assimilated by plants or immobilized in sediments, or for nitrogen, transformed into gas by denitrification. Since only one abatement measure of the second class of measures is included we delete the subindex n in the following. Abatement by wetlands is determined by the area covered by wetland, Hic, and by the mass input to the wetland, which depends on the load from upstream areas. Abatement by wetlands is then a function that is assumed to be increasing in Hic and non-positive in Aick. Abatement at upstream emission sources reduces the load entering the wetlands and thereby decreases nutrient sequestration in the wetlands. For an emission source located at the coast, such as several wastewater treatment plants, the impact of abatement on wetland sequestration is assumed to be zero. Loads from a hydrological catchment into a marine basin in the reference report is then written as

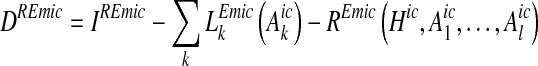graphic file with name M12.gif 2

Among the different load measurement reports considered and compared in this study, only the reference report models explicitly the relation between abatement measures and impacts on nutrient loads. It is therefore assumed here that these functional relations are the same for all nutrient reports, which then only differ with respect to the initial, or BAU, nutrient loads.

For all abatement measures, there exist either a cost function for reducing nutrient loads at the emission sources, 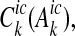Inline graphic or for the transport to the coastal waters, CicH(Hic), which are assumed to be increasing and convex in the arguments 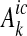Inline graphic and Hic. The model applies two methods for estimation of costs of the different abatement measures in each catchment—econometric and engineering methods—which differ with respect to consideration of the affected sectors’ actual behaviour in the market (see Gren et al. 2008 for a further description of cost estimations). Costs of reductions in fertiliser use are calculated as associated decreases in profit based on econometric estimates of demand for nutrient fertilisers in the different riparian countries. Market prices of land are used for assessing costs of conversion of land into relatively low leaching land-uses, such as grassland and wetlands. Due to lack of data, region-specific and constant unit abatement costs are assumed for the abatement measures that affect municipal wastewater treatment plants, industry and households.

Each abatement measure is subjected to capacity constraint, such as a maximum possible phosphorus removal at wastewater treatment plants by 90%, and maximum possible area of land suitable for wetland construction. Additional constraints consist of the number of households that can be connected to municipal wastewater treatment plants. Limitations on fertiliser and livestock reductions and land use changes are imposed in order to avoid drastic structural changes in the agricultural sector. The capacity constraints of the abatement measures differ between the regions due to differences in population size, area of arable land, livestock holdings, etc. For a more detailed presentation of abatement capacities and costs of all measures, see Gren et al. (2008).

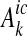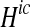The main decision problem is now defined as the choice of the allocation of Inline graphic and Inline graphic that minimises the sum of costs over all countries for achieving the BSAP nutrient load targets for different marine basins, 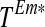Inline graphic, under alternative nutrient load reports S = 1,…,v. This decision problem is written as

graphic file with name M18.gif 3
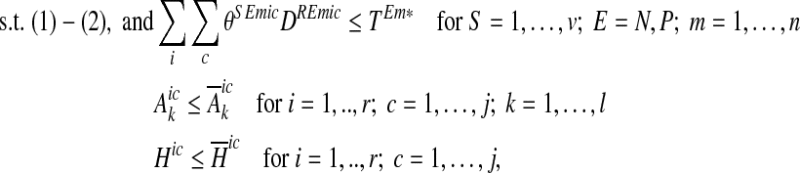graphic file with name M19.gif

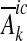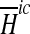where Inline graphic and Inline graphicare the maximum abatement capacities in subcatchment i in country c.

A direct first observation from the decision problem in (3) is the greater required load reduction for θSEmic > 1, which clearly increases total abatement cost relative to the reference case. However, this higher load reduction requirement is counteracted by a second observation of a larger impact from marginal abatement, which decreases total abatement costs for θSEmic > 1. The second observation is found by solving for the first-order conditions for a cost effective solution, which gives

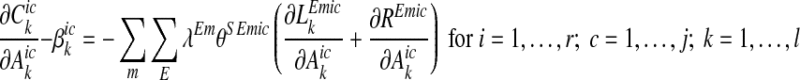graphic file with name M22.gif 4
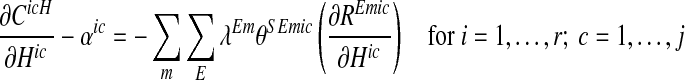graphic file with name M23.gif 5

where λEm ≤ 0 for E = N, P and m = 1,…,n are the Lagrange multipliers for the marine load targets in (3). In absolute values, these are interpreted as the marginal cost of achieving the target and they are increasing in the stringency of the target. The parameters 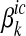Inline graphic ≤ 0 and αic ≤ 0 in (4) and (5) reflect the shadow values of additional nutrient removal capacities of abatement measures or areas of land with relatively low costs.

The left hand sides of (4) and (5) are the marginal cost of abatement in a catchment, and the right hand sides show the marginal impacts on the nutrient targets of a specific abatement measure. When summing the effects on the nutrient targets they are weighted by the Lagrange multipliers, λEm. The more nutrient targets that are affected by abatement in a catchment and the higher the value of the Lagrange multipliers the higher is the level of abatement allocated to the catchment. 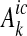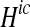This is also true for the value of θSEmic, where a higher θSEmic value implies larger impact on the load targets from a marginal increase in Inline graphic and Inline graphic, which reduces costs for achieving the targets. From the right hand side of (4), we can also note the negative impact of marginal abatement at emission sources on the wetland abatement, 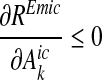Inline graphic, which reduces the marginal contribution to target achievement.

Measurements of Fairness

Not only total abatement cost, but also its distribution among countries can be an important factor for the actual implementation success of international abatement agreements. Cost effectiveness in a Baltic Sea perspective implies that relatively large abatement is carried out in countries with access to low abatement costs. Due to difference in factor prices, the costs of abatement measures are low in countries such as Poland, Latvia, Lithuania, Estonia, and Russia. If also the impact of measures located in the catchments within these low-cost countries is high due to high degree of loading from diffuse nutrient inputs and deposition, and/or low retention along the hydrological nutrient transport to the Baltic Sea, the cost effective allocation will result in relatively high abatement cost burdens for these countries. In general, such an allocation of cost burdens is regarded as unfair (e.g. Grasso 2007).

Although there is general consensus on the requirement of fairness for actual implementation of environmental restoration plans, there is less agreement on the operational definition of fairness. Usually, a distinction is made between the process of reaching agreements and the outcome of the agreements (e.g. Carraro 2000; Grasso 2007). This article focuses on fairness with respect to outcomes. In general, two principles can then be distinguished: egalitarian and equity. The egalitarian principle rests on equal human rights, where citizens have the right to, for example, the same amount of emission of nitrogen and phosphorus (e.g. Ringuis et al. 2002) The equity principle, based on the capability approach suggested by Sen (1999), relates burdens of actions to the agents’ ability to meet them. Based on these two principles of fairness with respect to allocation of abatement targets among countries, the fairness criteria sensitivity to divergence of different nutrient measurement reports is assessed according to three different criteria: nutrient load per capita, abatement cost per capita, and abatement cost in relation to gross domestic product (GDP). The first criterion relates to equal nutrient loading rights, and the second to equal cost burden. The third is related to equity by relating nutrient loading or abatement cost to the affordability in different countries, which is measured as their values of total production in the economy, GDP. Similar criteria are adopted in Carraro and Buchner (2002) when assessing equity outcomes from cost effective climate change policies.

There is a large literature on measuring inequality related to poverty, which rests on the egalitarian principle, within and between countries. A common approach is to calculate so-called Gini coefficients as a measurement of inequality (Gini 1921). The maximum value of the Gini coefficient is 1, which reflects the minimum level of equality. The lower the coefficient the larger is the equality level. There is a large literature on the calculation of the Gini coefficient (e.g. Sutcliffe 2005). This article will use a simple approach where the Gini coefficient calculation is based on cumulative percentages of nutrient loads, population, abatement costs, and GDP (e.g. Secondi 2008).

Nutrient Targets and Load Measurements

Nutrient load abatement targets for the Baltic Sea were set in autumn 2007 when the riparian countries adopted the BSAP (Helcom 2007). According to that action plan, phosphorus reductions are required for the marine basins Baltic Proper, Gulf of Finland and Gulf of Riga, and nitrogen reductions for the marine basins Baltic Proper, Danish straits and Kattegat. Phosphorus reductions in relation to initial, pre-abatement loads are largest for the Baltic Proper, and the largest nitrogen reductions are needed for Kattegat and the Danish Straits. It is expected that these reductions will reduce the hypoxia extension in the Baltic Proper by ~1/3, and the nitrogen fixation, an indicator of the intensity of cyanobacterial blooms, is expected to decrease by 2/3.

The BSAP nutrient reduction requirements are based on nutrient load estimates reported by Helcom (2007). Direct nutrient and pollutant discharges into the coastal waters are relatively easy to measure. The main difficulty is to obtain accurate estimates of the loads from upstream sources within the catchment areas, and in particular non-point sources, and of the distribution of diffuse discharges to the sea along long and mostly unmonitored coastlines (Destouni et al. 2008, 2010).

We consider here three principally different types of nutrient and pollutant load measurements from non-point sources: recipient, statistical, and emission-oriented approaches. The recipient-oriented approach is based on the available, yet still relatively few (Hannerz and Destouni 2006) actual field measurements of nutrient concentrations and water discharges close to the coastline, and uses model interpretations to fill in the gaps and estimate total nutrient loads to the sea (Helcom 2007). The emission-oriented approach is based on reported data of nutrient deposition and discharges into soil and water from different emission sources, such as agriculture, industry and households, which are available in official statistics (e.g. Gren 2008b; Elofsson 2003). Nutrient loads to the coastal waters are then in both of these approaches calculated by modelling, which accounts for reported data on nutrient leaching, retention and transport to the coast. To various degrees, both of these approaches thus rely on data and modelling account combinations of emissions at inland sources, and how these emissions are transported and retained along and among different transport pathways to the coast. The nutrient load results from different applications of these two types of approaches can differ considerably due to differences in both source input conceptualisation and data (e.g. Baresel et al. 2006) and transport-retention process account in underlying models (e.g. Destouni et al. 2006, 2008, 2010). In addition to such process-based methods, with principally different weights on emission-oriented or recipient-oriented data, the third, statistical type of approach is based on regression relations between reported coastal nutrient loads and emission pressure proxies, such as population, economic activity and, for diffuse source inputs, also contributing inland area in the hydrological catchments (Destouni et al. 2008).

In this article, we compare the effects on costs and fairness outcomes from three nutrient load measurement reports, with each of them being based on one of the three discussed types of measurement approaches: the recipient-oriented Helcom (2007) study for the period 1997–2003, which underlies the BSAP; the emission-oriented study by Gren et al. (2008) based on data for 2006; and the statistical study by Destouni et al. (2008) based on data for 2000. The Gren et al. (2008) study included also nutrient loads from air-borne emissions, which were not part of the other two studies. Therefore, air-borne emissions are here excluded from the Gren et al. (2008) results and, since that study also reported abatement costs, we use it here as the reference study of nutrient loads.

The nutrient load estimates from the three different load measurement reports are summarized in Table 1 for the different marine basins and riparian countries of the Baltic Sea, along with the BSAP targets on maximum N and P loads to the different marine basins.

Table 1.

Nutrient targets (BSAP) and loads (in ktons) based on the different load measurements of three different studies

BSAP targetsa Helcoma Destouni et al.b Gren et al.c
TP TN TP TN TP TN TP TN
Marine basins
Bothnian Bay 2.6 51 2.6 51 2.7 58 0.7 18
Bothnian Sea 2.5 57 2.5 57 2.7 52 0.9 18
Gulf of Finland 4.9 107 6.9 113 7.2 145 5.3 133
Baltic Proper 6.8 233 19.1 327 17.3 298 20.2 392
Gulf of Riga 1.4 78 2.2 78 1.5 48 2.7 51
Danish Straits 1.4 31 1.4 46 2.0 50 1.0 42
Kattegat 1.6 44 1.6 64 1.6 34 0.7 34
Countries
Germany 0.5 21 1.3 41 0.4 34
Sweden 4.2 126 6.2 111 1.6 66
Denmark 1.7 55 1.7 45 1.1 26
Finland 3.5 72 4.1 82 1.6 42
Poland 13.7 215 12.5 189 15.2 234
Estonia 1.3 32 1.1 40 1.6 55
Latvia 2.2 77 1.4 42 2.9 50
Lithuania 2.6 49 1.55 41 2.8 86
Russia 6.6 89 5.15 94 4.2 95
Total 21.1 601 36.3 736 35.0 685 31.4 688
Open in a new tab

aHelcom (2007), p 8, b Destouni et al. (2008), c Gren et al. (2008)

Results—Load Comparison, Costs and Fairness Outcomes

Load Comparison

Table 1 reveals the notable result that, in spite of the quite different approaches to estimate nutrient loads, the resulting total nutrient loads are quite similar. Among the present national data based reports, the Helcom study estimates the largest nutrient loads, which are ~15% larger than that of the reference study. This implies higher stringency of the targets in overall reduction of nutrients for the Helcom study, which tends to increase total abatement cost, and for most marine basins also the allocation of nutrient loads to them. Nutrient loads to the Bothnian Bay and Bothnian Sea are two to four times larger in the Helcom than in the reference study, and those to the Kattegat are approximately twice as large. For two basins—Baltic Proper and Gulf of Riga—all or most load estimates in the Helcom study are lower than in the reference study.

The relatively small result divergence in total nutrient load increases when the estimated BAU loads are further distributed among the riparian countries in the three studies. The largest relative difference is found for nutrient loads from Sweden, which are two to four times larger in the Helcom and Destouni et al. studies than in the reference study. On the other hand, the nutrient loads from Poland, Estonia and Lithuania are higher in the reference study. We thus have two counteracting effects on total abatement costs when using nutrient measurements from the Helcom (2007) and Destouni et al. (2008) studies compared with the reference study. However, due to the dominating role of Polish loads, the abatement costs of the reference study are likely to be highest, which tends to increase total abatement costs for relatively poor countries, and affects the equity criterion for the reference study.

Cost and Fairness Comparison

The calculations of cost effective solutions are carried out by use of the GAMS programme with the Conopt2 solver (Rosenthal 2008). Minimum cost solutions are presented in SEK (1 Euro = 9.20 SEK, July 14, 2011). In the calculation of the Gini coefficients for allocation of abatement cost per capita, there is a need to account for differences in purchasing power of a given income among the riparian countries. This is done by use of the purchasing power parity (PPP) index, which reflects the purchasing power of a dollar in each country. The index is calculated by comparing GDP in real prices with that measured in PPP (The World Bank 2011). Unless otherwise stated, all costs are measured in 2006 year prices and exchange rates.

Minimum total abatement costs and allocation among countries for meeting the BSAP targets are presented in Table 2.

Table 2.

Minimum total abatement costs and their allocation among countries (in mill SEK) for meeting the BSAP marine basin targets, based on the nutrient measurements of the same three studies as in Table 1

Country Helcom Destouni et al. Gren et al.
Germany 242 564 386
Sweden 1105 1155 344
Denmark 647 658 140
Finland 1 118 5
Poland 13279 12015 14877
Estonia 119 210 295
Latvia 723 203 1273
Lithuania 2499 1525 2838
Russia 1062 576 579
Total 19677 17024 20737
Open in a new tab

Total abatement costs are lowest based on the Destouni et al. study and largest based on the reference Gren et al. study. The main reason for this difference is the lower estimated nutrient loads from Poland into the Baltic Proper marine basin in the Destouni et al. study, combined with the relatively stringent nutrient abatement targets for the Baltic Proper basin. With respect to the allocation of abatement costs among countries, the dominating role of Polish costs can be noticed for all three measurement studies: they constitute 2/3 of total costs based on the Gren et al. and the Helcom studies, and 1/2 of total costs based on the Destouni et al. study. The abatement cost for Poland is approximately twice as large with nutrient estimates from the reference study compared with the Destouni et al. study. However, not all countries face the largest abatement cost under the load measurements of the reference study. Under national implementation of the cost effective solutions Sweden and Denmark face the lowest abatement cost with the nutrient reports of the reference study. Germany, Finland, and Estonia face the lowest cost burdens based on the Helcom study, and Latvia, Poland, Lithuania, Russia are favoured by the nutrient load estimates in the Destouni et al. study.

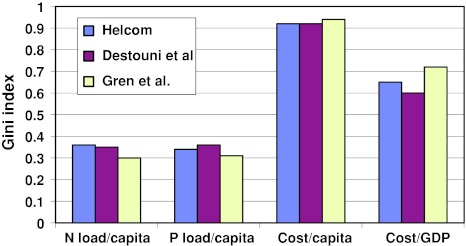
In spite of the differences in abatement cost for some countries between the different nutrient reports, the fairness outcomes with respect to Gini coefficients for two types of fairness criteria—egalitarian and equity—are quite similar (Fig. 2). Egalitarian fairness is calculated by comparing population shares with their corresponding nutrient load and cost shares. Equity is defined as the countries’ ability to pay for abatement and is measured as abatement costs in relation to GDP.

Fig. 2.

Fig. 2

Open in a new tab

Gini index for measurement of fairness with respect to the egalitarian principle (N load/capita, P load/capita, abatement cost/capita), and to the equity principle (abatement cost/GDP (gross domestic product)) in the cost effective solutions under the same three nutrient load reports as in Table 1

The calculated Gini coefficients for the different egalitarian criteria are similar for all measurement studies: relatively modest (i.e., modest equality level) for nutrient loads, but considerably higher (i.e., lower equality level) for the costs to abate these loads The main reason for the high coefficient (low equality) for costs/capita is the role of Poland, which accounts for 0.5 of total population but faces ~0.7 of the total cost burden. This is also the reason for the relatively high Gini (low equality) coefficient for the equity criterion; unequal division of abatement costs when related to the gross domestic product. It can also be concluded that there is no nutrient report study that performs best or worst (implies greater or smaller equality) according to all fairness criteria; the Gren et al. study gives the lowest Gini coefficients (highest equality level) for nitrogen and phosphorus load per capita, the Destouni report generates the lowest coefficient for abatement cost/capita, and the Helcom report the lowest for abatement cost/GDP. However, the differences in the Gini coefficients are quite small for each criterion. That is, the resulting fairness patterns are the same for all nutrient reports.

Conclusions

With respect to the main question posed in the title of this article—whether nutrient measurement divergence matters for successful international mitigation of eutrophication—the results allow us to answer both yes and no. On the one hand, relatively small divergence in nutrient measurements translates to relatively large differences in abatement cost for the different riparian countries. Ambiguity about the accuracy of nutrient load measurements may be a source of disagreement on how abatement targets should be allocated among different countries, and/or be used as a means for choosing only favourable measurement reports when postulating compliance with agreements. Even small divergence of nutrient measurements from application of different models and methods to interpret the same available national data can thus inhibit actual implementation performance with respect to nutrient reductions. This result sends a clear message to different scientific communities involved in nutrient and other pollutant load measurements and management: To explicitly recognise divergence in interpretation models, and work with open inter-model comparisons of nutrient loads as a basis for reaching international agreements on eutrophication management that may actually be implemented.

On the other hand, the result that relatively poor countries face the largest abatement cost burdens is robust and independent of the investigated differences in nutrient load measurements. Even with convergent nutrient load measurements by different methods, there is thus a remaining conflict between abatement cost effectiveness and fairness criteria. The unequal distribution of BSAP costs in relation to the countries’ population or GDP, as measured by the Gini coefficient, may in practice hinder its implementation unless compensation mechanisms are implemented for at least some Baltic Sea countries. Similarly to the implementation of international agreements on climate change mitigation, unfairness is likely to be a serious obstacle to implementation in practice, not only of the BSAP, but also of other international nutrient reduction agreements.

The inclusion of not only abatement costs but also environmental benefits may either enforce or counteract the results obtained in this study. There is currently no study of the allocation of benefits from the BSAP, but earlier studies reveal that the benefit from nutrient load reductions in per capita terms is significantly larger in Sweden, Finland, Germany and Denmark than in the other riparian countries (Söderquist 1998; Markowska and Zylicz 1999; Turner et al. 1999). If this relation in benefits is valid also for the BSAP the results obtained in this study are enforced. An international compensation mechanism, such as a nutrient trading system suggested by, among others, NEFCO (2008) may then have a potential in combating unfair financial burdens among the partners.

Acknowledgement

Destouni acknowledges support from Stockholm University’s Strategic Marine Environmental Research Funds through the BEAM Program.

Biographies

Ing-Marie Gren

is a professor in environmental and resource economics at Swedish University of Agricultural Sciences. She carries out research and teaching in the field of environmental economics applied to water management, biodiversity and valuation of ecosystem services.

Georgia Destouni

is a Professor in hydrology, hydrology and water resources at Stockholm University, and research leader in the Bert Bolin Centre for Climate Research. She is member of Royal Swedish Academy and its Energy Committee, and member of the Royal Swedish Academy of Engineering Sciences.

Contributor Information

Ing-Marie Gren, Phone: ++46-18-671753, Email: ing-marie.gren@slu.se.

Georgia Destouni, Phone: ++46-8-164785, Email: Georgia.destouni@natgeo.su.se.

References

  1. The World Bank. 2011. Data catalogue. http://data.worldbank.org/data-catalog. Accessed 20 Jan 2011.
  2. Backer H, Leppänen JM. The Helcom system of a vision, strategic goals and ecological objectives: implementing an ecosystem approach to the management of human activities in the Baltic Sea. Marine Freshwater Ecosystem. 2008;18:224–321. [Google Scholar]
  3. BalticSea2020. 2011. http://www.balticsea2020.org/english/. Accessed 30 April 2011.
  4. Baresel, C., and Destouni, G. 2005. Novel quantification of coupled natural and cross-sectoral water and nutrient/pollutant flows for environmental management. Environmental Science & Technology 39(16):6182–6190. doi:10.1021/es050522k. [DOI] [PubMed]
  5. Baresel C, Destouni G. Uncertainty-accounting environmental policy and management of water systems. Environmental Science and Technology. 2007;41(10):3653–3659. doi: 10.1021/es061515e. [DOI] [PubMed] [Google Scholar]
  6. Baresel C, Destouni G, Gren I-M. The influence of metal source uncertainty on cost-effective allocation of mine water pollution abatement in catchments. Journal of Environmental Management. 2006;78(2):138–148. doi: 10.1016/j.jenvman.2005.03.013. [DOI] [PubMed] [Google Scholar]
  7. Bayramoglu B. Transboundary pollution in the Black Sea: Comparison of institutional arrangements. Environmental & Resource Economics. 2006;35(4):289–325. doi: 10.1007/s10640-006-9016-0. [DOI] [Google Scholar]
  8. Bérubé G, Cusson C. The environmental legal and regulatory frameworks. Assessing fairness and efficiency. Energy Policy. 2002;30:291–298. [Google Scholar]
  9. Byström O. The nitrogen abatement cost in wetlands. Ecological Economics. 1998;26(3):321–331. doi: 10.1016/S0921-8009(97)00132-8. [DOI] [Google Scholar]
  10. Carraro C, editor. Efficiency and equity in climate change policy. Amsterdam, the Netherlands: Kluwer Academic Publisher; 2000. [Google Scholar]
  11. Carraro C, Buchner B. Equity, development and climate change policy. In: Carraro C, Kemfert C, Buchner B, editors. Climate change policy regimes, international trade and growth. Buxelles: CEPS-ESRI Collaboration studies; 2002. [Google Scholar]
  12. Conley DJ, Björck S, Bonsdorff E, Carstensen J, Destouni G, Gustafsson BG, Hietanen S, Kortekaas M, et al. Hypoxia-related processes in the Baltic Sea. Environmental Science and Technology. 2009;43:3412–3420. doi: 10.1021/es802762a. [DOI] [PubMed] [Google Scholar]
  13. Conley DJ, Bonsdorff E, Carstensen J, Destouni G, Gustafsson BG, Hansson LA, Rabalais NN, Voss M, Zillén L. Tackling hypoxia in the Baltic Sea: Is engineering a solution? Environmental Science and Technology. 2009;43(10):3407–3411. doi: 10.1021/es8027633. [DOI] [PubMed] [Google Scholar]
  14. Destouni G, Lindgren G, Gren I-M. Effects of inland nitrogen transport and attenuation modeling on coastal nitrogen load abatement. Environmental Science and Technology. 2006;40:6208–6214. doi: 10.1021/es060025j. [DOI] [PubMed] [Google Scholar]
  15. Destouni G., F. Hannerz, C. Prieto, J. Jarsjö, and Y. Shibuo. 2008. Small unmonitored near-coastal catchment areas yielding large mass loading to the sea. Global Biogeochemical Cycles 22: GB4003 (10 pp). doi:10.1029/2008GB003287.
  16. Destouni G, Persson K, Prieto C, Jarsjö R. General quantification of catchment-scale nutrient and pollutant transport through the subsurface to surface and coastal waters. Environmental Science and Technology. 2010;44:2048–2055. doi: 10.1021/es902338y. [DOI] [PubMed] [Google Scholar]
  17. Díaz RJ, Rosenberg R. Spreading dead zones and consequences for marine ecosystems. Science. 2008;321:926–929. doi: 10.1126/science.1156401. [DOI] [PubMed] [Google Scholar]
  18. Elmgren R, Larsson U. Europhication in the Baltic Sea area. Integrated coastal management issues. In: Bodugen BV, Turner RK, editors. Science and integrated coastal management. Berlin: Dahlem University Press; 2001. pp. 15–3527. [Google Scholar]
  19. Elofsson K. Cost effective reductions of stochastic agricultural nitrogen loads to the Baltic Sea. Ecological Economics. 2003;47(1):13–31. doi: 10.1016/j.ecolecon.2002.10.001. [DOI] [Google Scholar]
  20. Elofsson K. Cost uncertainty and unilateral abatement. Environmental & Resource Economics. 2006;36(2):143–162. [Google Scholar]
  21. Fernandez L. Waste water pollution abatement across international border. Environment and Development Economics. 2009;14(1):67–88. doi: 10.1017/S1355770X08004543. [DOI] [Google Scholar]
  22. Galloway JN. Transformation of the nitrogen cycle: Recent trends, questions, and potential solutions. Science. 2008;320:889. doi: 10.1126/science.1136674. [DOI] [PubMed] [Google Scholar]
  23. Gini C. Measurement of inequality of incomes. The Economic Journal. 1921;31:124–126. doi: 10.2307/2223319. [DOI] [Google Scholar]
  24. Grasso M. A normative ethical framework in climate change. Climatic Change. 2007;81:223–246. doi: 10.1007/s10584-006-9158-7. [DOI] [Google Scholar]
  25. Gren I-M. Evaluation of cost effectiveness and fairness of the Helcom Baltic Sea Action Plan. Vatten. 2008;4:271–281. [Google Scholar]
  26. Gren I-M. Mitigation and adaptation policies for stochastic water pollution: An application to the Baltic Sea. Ecological Economics. 2008;66(2–3):337–347. doi: 10.1016/j.ecolecon.2007.09.010. [DOI] [Google Scholar]
  27. Gren I-M, Folmer H. International cooperation of stochastic environmental damage: The case of the Baltic Sea. Ecological Economics. 2003;47(1):31–43. doi: 10.1016/j.ecolecon.2002.12.001. [DOI] [Google Scholar]
  28. Gren IM, Destouni G, Sharin H. Cost effective management of stochastic coastal water pollution. Environmental modelling and assessment. 2000;5(4):193–203. doi: 10.1023/A:1011588129892. [DOI] [Google Scholar]
  29. Gren IM, Destouni G, Tempone R. Cost effective policies for alternative distributions of stochastic water pollution. Journal of Environmental Management. 2002;66:145–157. doi: 10.1006/jema.2002.0569. [DOI] [PubMed] [Google Scholar]
  30. Gren, I.-M., Y. Jonzon, and M. Lindqvist. 2008. Calculation of costs for nutrient reductions to the Baltic Sea. Technical report. Working paper no. 1. Department of Economics, SLU, Uppsala.
  31. Hannerz F, Destouni G. Spatial characterization of the Baltic Sea drainage basin and its unmonitored catchments. Ambio. 2006;35(5):214–219. doi: 10.1579/05-A-022R.1. [DOI] [PubMed] [Google Scholar]
  32. Helcom. 2004. The fourth Baltic Sea pollution load compilation (PLC-4). Helsinki, Finland: Helsinki Commission.
  33. Helcom. 2007. An approach to set country-wise nutrient reduction allocations to reach good marine environment of the Baltic Sea. Helcom BSAP Eutro Expo. Helsinki, Finland: Helsinki Commission.
  34. Huisman, J., H.C.P. Matthijs, and P.M. Visser. 2005. Harmful cyanobacteria. Springer Aquatic Ecology Series 3. Dordrecht: Springer.
  35. Kataria M, Elofsson K, Hasler B. Distributional assumptions in chance-constrained programming models of stochastic water pollution. Environmental Modeling and Assessment. 2010;15(4):273–281. doi: 10.1007/s10666-009-9205-7. [DOI] [Google Scholar]
  36. Khadam I, Kaluarachchi J. Trade off between cost minimization and equity in water quality management for agricultural watersheds. Water Resources Research. 2006;42:W10404. doi: 10.1029/2005WR004434. [DOI] [Google Scholar]
  37. Lange A, Vogt C, Ziegler A. On the importance of equity in international climate policy: An empirical analysis. Energy Economics. 2007;29(3):545–562. doi: 10.1016/j.eneco.2006.09.002. [DOI] [Google Scholar]
  38. Markowska A, Zylizc T. Costing an international public good: The case of the Baltic Sea eutrophication. Ecological Economics. 1999;30:301–316. doi: 10.1016/S0921-8009(98)00138-4. [DOI] [Google Scholar]
  39. NEFCO. 2008. Framework for a nutrient quota and credit’s trading system for the contracting parties of Helcom in order to reduce eutrophication of the Baltic Sea. http://www.nefco.org/files/Nefco_BS%20NTS_GSN_Final%20Report_20080229.pdf. Accessed 27 Jan 2011.
  40. Ringuis L, Torvanger A, Underdal A. Burden sharing and fairness principles in international climate policy. International Environmental Agreements: Politics, Law and Economics. 2002;2:1–22. doi: 10.1023/A:1015041613785. [DOI] [Google Scholar]
  41. Rosenthal R. GAMS—a user’s guide. Washington, DC: GAMS Development Corporation; 2008. [Google Scholar]
  42. Savchuk OP, Wulff F. Long-term modelling of large-scale nutrient cycles in the entire Baltic Sea. Hydrobiologia. 2009;629:209–224. doi: 10.1007/s10750-009-9775-z. [DOI] [Google Scholar]
  43. Secondi G, editor. The development economics reader. Routledge: London; 2008. [Google Scholar]
  44. Sen A. Development as freedom. New York: Anchor; 1999. [Google Scholar]
  45. Söderquist T. Why give up money for the Baltic Sea? Motives for peoples’ willingness to pay. Environmental & Resource Economics. 1998;12/2:141–153. [Google Scholar]
  46. Sutcliffe B. World inequality and globalization. Oxford Review of Economic Policy. 2005;20(1):15–37. doi: 10.1093/oxrep/grh002. [DOI] [Google Scholar]
  47. Turner K, Georgiou S, Gren I-M, Wulff F, Barett S, Söderqvist T, Bateman IJ, Folke C, Langaas S, Zylicz T, Mäler K-G, Markowska A. Managing nutrient fluxes and pollution in the Baltic: An interdisciplinary simulation study. Ecological Economics. 1999;30:333–352. doi: 10.1016/S0921-8009(99)00046-4. [DOI] [Google Scholar]

Articles from Ambio are provided here courtesy of Springer

RESOURCES