Musculotendon Lengths and Moment Arms for a Three-Dimensional Upper-Extremity Model

Abstract

Generating muscle-driven forward dynamics simulations of human movement using detailed musculoskeletal models can be computationally expensive. This is due in part to the time required to calculate musculotendon geometry (e.g., musculotendon lengths and moment arms), which is necessary to determine and apply individual musculotendon forces during the simulation. Modeling upper-extremity musculotendon geometry can be especially challenging due to the large number of multi-articular muscles and complex muscle paths. To accurately represent this geometry, wrapping surface algorithms and/or other computationally expensive techniques (e.g., phantom segments) are used. This paper provides a set of computationally efficient polynomial regression equations that estimate musculotendon length and moment arms for thirty-two (32) upper-extremity musculotendon actuators representing the major muscles crossing the shoulder, elbow and wrist joints. Equations were developed using a least squares fitting technique based on geometry values obtained from a validated public-domain upper-extremity musculoskeletal model that used wrapping surface elements (Holzbaur et al., 2005). In general, the regression equations fit well the original model values, with an average root mean square difference for all musculotendon actuators over the represented joint space of 0.39 mm (1.1% of peak value). In addition, the equations reduced the computational time required to simulate a representative upper-extremity movement (i.e., wheelchair propulsion) by more than two orders of magnitude (315 versus 2.3 seconds). Thus, these equations can assist in generating computationally efficient forward dynamics simulations of a wide range of upper-extremity movement tasks.

Introduction

Forward dynamics simulations using detailed musculoskeletal models have been generated to gain insights into the biomechanics and neuromotor control of human movement tasks such as pedaling (e.g., Raasch et al., 1997; Umberger et al., 2006), walking (e.g., Liu et al., 2006; McGowan et al., 2009), running (e.g., Miller et al., 2011; Sasaki and Neptune, 2006), natural arm movements (e.g., Blana et al., 2008; Nikooyan et al., 2012) and wheelchair propulsion (e.g., Lin et al., 2004; Rankin et al., 2010). Many of these musculoskeletal models use complex wrapping surface algorithms and/or “phantom segments” to represent musculotendon geometry (i.e., musculotendon lengths and moment arms). Although these techniques help assure the geometry accurately represents corresponding empirical data, the wrapping algorithms are computationally expensive and phantom segments introduce additional system constraints. Both techniques can make simulating human movement computationally prohibitive. This is especially evident in models containing a large number of musculotendon actuators with complex or multi-articular muscle geometry (e.g., human upper-extremity) or when generating simulations using open-loop dynamic optimization techniques that require a large number of iterations (i.e., tens of thousands) to converge.

An alternative method to represent complex musculotendon geometry is to utilize regression equations. Because they are differentiable and computationally efficient compared to wrapping surfaces, they make simulating complex human movements feasible. Menegaldo et al (2004) presented a method for generating the regression equations for the musculotendon lengths and moment arms of 43 lower-extremity musculotendon actuators. This paper extends this work to provide a similar set of equations for 32 musculotendon actuators of the upper-extremity. A computationally efficient upper extremity musculoskeletal model would be useful in addressing a wide range of upper extremity research questions from identifying the optimal technique for wheelchair propulsion to assessing operational regions that minimize the risk for injuries.

Methods

Model Description

The regression equations for the musculotendon actuators were based on data obtained from a previously validated three-dimensional upper-extremity model originally developed in SIMM (Musculographics, Inc., Santa Rosa, CA, USA), which is now public-domain (Holzbaur et al., 2005, https://simtk.org). The original model was modified to contain rigid bodies representing the trunk, scapula, clavicle, humerus, forearm and hand and consisted of seven degrees-of-freedom representing shoulder, elbow, forearm and wrist articulations. Each model degree-of-freedom was represented by a generalized coordinate. Shoulder movement was modeled using three Euler rotations (Y,X,Y′) based on international recommendations (Wu et al., 2005), representing plane of elevation (SPE), elevation angle (SEA) and axial rotation (SRT). The shoulder abduction plane was defined as 0° SPE, the humerus was parallel to the thorax at 0° SEA and 0° SRT caused the forearm to lie in the sagittal plane during elbow flexion at 0° SEA. Scapular and clavicular motions were prescribed as a function of shoulder elevation based on an experimentally derived glenohumeral rhythm (de Groot and Brand, 2001). Elbow flexion-extension (EFE), forearm pronation-supination (PS), wrist flexion-extension (WFE) and wrist ulnar-radial deviation (WDV) were all modeled as rotations, defined such that 0° represents full elbow extension and positive PS, WFE, WDV values represent pronation, wrist flexion and wrist ulnar deviation, respectively. The ranges for each generalized coordinate were determined from values typically observed during upper-extremity movements (e.g., Magermans et al., 2005; van Andel et al., 2008) (Table 1).

Table 1.

Generalized coordinate abbreviations and corresponding range of motion used to develop the regression equations.

Generalized Coordinate	Abreviation	Range of Motion
		Minimum	Maximum
Shoulder Plane of Elevation	SPE	−60	60
Shoulder Elevation Angle	SEA	0	65
Shoulder Rotation	SRT	−20	85
Elbow Flexion-Extension	EFE	0	100
Forearm Pronation-Supination	PS	−45	45
Wrist Deviation	WDV	−10	25
Wrist Flexion-Extension	WFE	−45	45

The musculotendon actuator geometry and parameters were unchanged from the original model; however, muscles inserting distal to the carpometacarpal joints were excluded (Table 2). Actuator geometry was a function of up to five generalized coordinates based on the number of joints each muscle crossed.

Table 2.

Musculotendon actuators used in developing the regression equations and the corresponding generalized coordinates they are dependent on (SPE = shoulder plane of elevation, SEA = shoulder elevation angle, SRT = shoulder rotation, EFE = elbow flexion-extension, PS = forearm pronation-supination, WFE = wrist flexion-extension, WDV = wrist ulnar-radial deviation).

Muscle	Actuator	Description	Origin	Insertion	Generalized Coordinates
Deltoid	DELT1	Anterior Deltoid	Clavicle	Humerus	SPE, SEA, SRT
	DELT2	Middle Deltoid	Scapula	Humerus	SPE, SEA, SRT
	DELT3	Posterior Deltoid	Scapula	Humerus	SPE, SEA, SRT
Pectoralis Major	PECM1	Clavicular Head	Clavicle	Humerus	SPE, SEA, SRT
	PECM2	Sternal Head 1	Thorax	Humerus	SPE, SEA, SRT
	PECM3	Sternal Head 2	Thorax	Humerus	SPE, SEA, SRT
Supraspinatus	SUPSP		Scapula	Humerus	SPE, SEA, SRT
Infrapinatus	INFSP		Scapula	Humerus	SPE, SEA, SRT
Teres Minor	TMIN		Scapula	Humerus	SPE, SEA, SRT
Subscapularis	SUBSC		Scapula	Humerus	SPE, SEA, SRT
Latissimus Dorsi	LAT1	Upper	Thorax	Humerus	SPE, SEA, SRT
	LAT2	Middle	Thorax	Humerus	SPE, SEA, SRT
	LAT3	Lower	Thorax	Humerus	SPE, SEA, SRT
Teres Major	TMAJ		Scapula	Humerus	SPE, SEA, SRT
Biceps Brachii	BIClong	Long Head	Scapula	Radius	SPE, SEA, SRT, EFE, PS
	BICshort	Short Head	Scapula	Radius	SPE, SEA, SRT, EFE, PS
Coracobrachialis	CORB		Scapula	Humerus	SPE, SEA, SRT
Brachialis	BRA		Humerus	Ulna	EFE
Triceps	TRIlong	Long Head	Scapula	Ulna	SPE, SEA, SRT, EFE, PS
	TRImed	Medial Head	Humerus	Ulna	EFE
	TRIlat	Lateral Head	Humerus	Ulna	EFE
Anconeous	ANC		Humerus	Ulna	EFE
Brachioradialis	BRD		Humerus	Radius	EFE, PS
Pronator Teres	PT		Humerus	Radius	EFE, PS
Pronator Quadratus	PQ		Ulna	Radius	PS
Supinator	SUP		Ulna	Radius	PS
Extensor Carpi Radialis Longus	ECRL		Humerus	2nd Metacarpal	EFE, PS, WDV, WFE
Extensor Carpi Radialis Brevis	ECRB		Humerus	3rd Metacarpal	EFE, PS, WDV, WFE
Extensor Carpi Ulnaris	ECU		Humerus	5th Metacarpal	EFE, PS, WDV, WFE
Flexor Carpi Radialis	FCR		Humerus	2nd Meaecarpal	EFE, PS, WDV, WFE
Flexor Carpi Ulnaris	FCU		Humerus	5th Metacarpal	EFE, PS, WDV, WFE
Palmaris Longus	PL		Humerus	3rd Metacarpal	EFE, PS, WDV, WFE

Fitting Method

Regression equations were determined using a least-squares fitting method, which was previously used to develop lower extremity equations (Menegaldo et al., 2004). The determination of the regression equations consisted of identifying the coefficients c, a_i of a generic function g:

$$\begin{array}{l}\mathbf{g}({\text{Q}}_1,\dots ,{\text{Q}}_{\text{k}})=c+a_1{f}_1({\text{Q}}_1,\dots ,{\text{Q}}_{\text{k}})+a_2{f}_2({\text{Q}}_1,\dots ,{\text{Q}}_{\text{k}})\\ +\dots +a_n{f}_n({\text{Q}}_1,\dots ,{\text{Q}}_{\text{k}})\end{array}$$ (1)

where g represents the musculotendon length or moment arm, Q_i is a generalized coordinate, f_i is a predetermined polynomial function and n and k are positive integers. g can be expressed in matrix form as a vector product of the coefficient and function vectors a and b as:

$$\mathbf{g}=\mathbf{ba}$$ (2)

where,

$$\mathbf{a}={[c,a_1,a_2,\dots ,a_n]}^{\text{T}}$$ (3)

$$\mathbf{b}=[1,f_1,f_2,\dots ,f_n]$$ (4)

If m samples of data are available (i.e., for the values g and associated Qs) then Equation 2 can be expressed in matrix form as:

$$\mathbf{G}=\mathbf{Ba}$$ (5)

where G contains function values at each sample:

$$\mathbf{G}={[\mathbf{g}(1),\mathbf{g}(2),\dots ,\mathbf{g}(m)]}^{\text{T}}$$ (6)

and B is defined as:

$$\mathbf{B}=\left[\begin{array}{cccc}1& f_1(1)& \cdots & f_n(1)\\ 1& f_1(2)& \cdots & f_n(2)\\ ⋮& ⋮& \cdots & ⋮\\ 1& f_1(m)& \cdots & f_n(m)\end{array}\right]$$ (7)

The pseudo-inverse of Equation 5 can be taken to obtain the least-squares normal equation,

$$\mathbf{a}={({\mathbf{B}}^{\text{T}}\mathbf{B})}^{-1}{\mathbf{B}}^{\text{T}}\text{G}$$ (8)

Custom Matlab (Mathworks, Natick, MA, USA) code was used to generate generalized coordinate point meshes across the range of values (Q_i, Eq. 1). For musculotendon geometries dependent on one generalized coordinate, 80 points were evenly sampled across the coordinate’s range of motion. For geometries dependent on two to three generalized coordinates, twenty points were sampled over each coordinate to generate a coordinate mesh. Equations dependent on four or five generalized coordinates had meshes generated from fifteen or eleven points, respectively. Musculotendon lengths and moment arms were then placed in groups based on generalized coordinate dependence and values obtained from the SIMM model using the corresponding point mesh. The original wrapping surface values were used as base values (G, Eq. 8) when developing the fitting equations. However, these can be easily modified for new models or experimental data to obtain a corresponding set of regression equations.

Fitting equations were developed for each quantity by adding polynomial functions to Equation 8 until either: 1) a predetermined fit error criterion was reached, or 2) improvement in peak fit error was less than 2% relative to the previous equation. The accuracy fit criterion was either a maximum fit error <2 mm or <10% of the largest value in the joint space. To further evaluate fit accuracy, the root mean square (RMS) fit error over the entire range of motion was calculated.

To assess whether the regression equations provided a computational advantage, a previously described forward dynamics simulation of wheelchair propulsion (a 1.16 second duration movement, Rankin et al., 2010) was performed using both a) original wrapping surface/phantom segment elements, and b) regression equations on a standard workstation computer (3.16 GHz dual-core processor, 2 GB RAM), and the computational times were compared.

Results

Equations based on fifteen distinct forms with different levels of complexity were necessary to fit the 32 musculotendon actuators’ length and moment arm data. Each equation is a function of the generalized coordinate values (in radians) and returns a value in meters (see Web Supplementary Material, Sections 1–3). The form of each equation and coordinates Q₁, Q₂…Q_n are provided in Section 1. Sections 2 and 3 then provide additional details required to reconstruct the regression equation. For example, from Section 1, the BRD musculotendon length is of equation form 4 and based on two generalized coordinates (Q₁ represents EFE and Q₂ represents PS). The equation form and specific coefficient values (a, Eq. 3) can then be obtained from Sections 2 and 3 of the Web Supplementary Material.

Overall, the regression equations fit the muscle geometry data of the original SIMM model well, with an average RMS error over all musculotendon actuators of 0.39 mm or 1.1% of peak value (Table 3). Although some maximum fit errors were above the accuracy threshold (Table 3), increasing equation complexity did not reduce these errors. Further investigation revealed that the maximum errors occurred primarily when discontinuities existed in original model geometry due to the actuator moving across different wrapping surfaces. Because the regression equations are continuous functions, these discontinuities could not be represented (Fig. 1). However, the total number of points outside the desired accuracy was small for all equations (Fig. 2). The wheelchair simulation required 315 seconds of CPU processing time using the wrapping surface/phantom segment elements while the same simulation was completed in 2.3 seconds using the regression equations.

Table 3.

Fit equation errors for each musculotendon actuator. Values are presented in mm (% maximum value).

	LMT		SPE Moment Arm		SEA Moment Arm		SROT Moment Arm		EFE Moment Arm		PS Moment Arm		WDV Moment Arm		WFE Moment Arm
Actuator	RMS Fit Error (mm, %)	Maximum Error (mm, %)	RMS Fit Error (mm, %)	Maximum Error (mm, %)	RMS Fit Error (mm, %)	Maximum Error (mm, %)	RMS Fit Error (mm, %)	Maximum Error (mm, %)	RMS Fit Error (mm, %)	Maximum Error (mm, %)	RMS Fit Error (mm, %)	Maximum Error (mm, %)	RMS Fit Error (mm, %)	Maximum Error (mm, %)	RMS Fit Error (mm, %)	Maximum Error (mm, %)
DELT1	0.04 (0.02)	0.49 (0.21)	0.25 (0.44)	2.49 (6.15)	0.10 (0.24)	6.80 (11.96)	0.09 (0.97)	1.87 (19.40)
DELT2	0.33 (0.16)	1.94 (0.90)	0.50 (1.29)	1.08 (4.18)	0.20 (0.76)	2.59 (6.68)	2.47 (3.04)	11.20 (13.8)
DELT3	0.17 (0.13)	6.17 (3.94)	0.35 (0.51)	4.07 (7.58)	0.30 (0.55)	2.80 (4.05)	0.17 (1.49)	1.16 (10.27)
PECM1	0.15 (0.12)	1.05 (0.80)	0.14 (0.37)	1.33 (3.54)	0.15 (0.45)	1.53 (4.59)	0.11 (0.63)	1.19 (6.66)
PECM2	0.14 (0.08)	0.91 (0.48)	0.15 (0.39)	1.26 (3.26)	0.20 (0.38)	1.81 (3.41)	0.16 (0.93)	1.57 (9.31)
PECM3	0.16 (0.08)	1.70 (0.85)	0.13 (0.35)	1.12 (2.97)	0.40 (0.64)	3.97 (6.33)	0.27 (1.36)	1.59 (7.99)
SUPSP	0.04 (0.04)	0.38 (0.40)	0.15 (0.52)	2.11 (8.28)	0.17 (0.65)	1.70 (6.06)	0.16 (0.71)	2.65 (11.69)
INFSP	0.02 (0.02)	0.23 (0.18)	0.16 (0.85)	2.30 (12.42)	0.12 (0.67)	5.72 (29.7)	0.14 (0.57)	4.24 (16.9)
TMIN	0.58 (0.42)	6.58 (4.86)	0.38 (1.70)	2.62 (16.4)	0.37 (2.32)	5.54 (24.9)	0.24 (1.13)	2.36 (10.9)
SUBSC	0.06 (0.06)	0.42 (0.40)	0.09 (0.58)	0.44 (2.83)	0.05 (0.34)	1.14 (7.56)	0.10 (0.50)	0.64 (3.17)
LAT1	0.14 (0.06)	0.88 (0.35)	0.14 (0.43)	1.59 (5.05)	0.19 (0.51)	1.84 (4.96)	0.19 (1.59)	1.52 (12.80)
LAT2	0.14 (0.05)	0.87 (0.31)	0.14 (0.47)	1.20 (4.03)	0.24 (0.45)	1.40 (2.67)	0.18 (1.66)	1.39 (12.50)
LAT3	0.14 (0.04)	1.67 (0.52)	0.14 (0.64)	0.83 (3.70)	0.32 (0.57)	2.52 (4.51)	0.21 (1.64)	1.32 (10.55)
TMAJ	0.14 (0.11)	1.00 (0.83)	0.09 (0.24)	0.94 (2.42)	0.18 (0.40)	1.26 (2.57)	0.16 (1.48)	1.39 (12.80)
BIClong	1.01 (0.25)	7.30 (1.89)	0.39 (1.41)	1.49 (6.47)	0.18 (0.77)	2.72 (9.73)	0.32 (1.36)	2.60 (10.96)	0.27 (0.55)	1.72 (3.48)	0.18 (1.14)	0.96 (6.04)
BICshort	0.43 (0.13)	4.52 (1.47)	0.23 (0.75)	1.29 (4.28)	0.34 (0.80)	1.83 (3.87)	0.29 (3.73)	1.22 (15.90)	0.27 (0.55)	1.72 (3.48)	0.18 (1.14)	0.96 (6.04)
CORB	0.30 (0.19)	1.89 (1.28)	0.20 (0.64)	1.17 (3.83)	0.22 (0.42)	1.26 (2.42)	0.07 (2.45)	0.69 (25.83)
BRA	0.06 (0.04)	0.13 (0.09)							0.25 (1.05)	0.78 (3.30)
TRIlong	0.62 (0.20)	2.83 (1.05)	0.07 (0.23)	1.06 (3.29)	0.12 (0.34)	0.76 (2.11)	0.11 (1.11)	0.58 (5.97)	0.17 (0.70)	0.41 (1.68)
TRImed	0.01 (0.01)	0.04 (0.02)							0.17 (0.69)	0.51 (2.10)
TRIlat	0.01 (0.01)	0.04 (0.02)							0.17 (0.69)	0.51 (2.10)
ANC	0.01 (0.04)	0.03 (0.11)							0.07 (0.56)	0.22 (1.76)
BRD	0.18 (0.06)	0.87 (0.26)							1.07 (1.26)	3.83 (4.52)	0.13 (0.77)	0.60 (3.51)
PT	0.04 (0.02)	0.11 (0.07)							0.05 (0.31)	0.10 (0.65)	0.11 (1.09)	0.34 (3.48)
PQ	0.00 (0.00)	0.00 (0.00)									0.01 (0.10)	0.04 (0.54)
SUP	0.00 (0.00)	0.01 (0.01)									0.00 (0.04)	0.01 (0.12)
ECRL	0.97 (0.30)	3.27 (1.00)							0.46 (1.50)	1.36 (4.39)	0.11 (1.98)	0.43 (7.77)	0.19 (0.51)	0.84 (2.31)	0.54 (1.73)	1.33 (4.29)
ECRB	0.17 (0.06)	0.67 (0.22)							0.02 (0.26)	0.04 (0.76)	0.00 (0.16)	0.01 (0.53)	0.45 (2.38)	2.91 (15.31)	0.70 (2.02)	5.31 (15.25)
ECU	5.30 (1.76)	26.10 (8.18)							0.00 (0.01)	0.00 (0.01)	0.00 (0.06)	0.00 (0.10)	2.79 (9.47)	22.20 (75.47)	7.21 (20.45)	30.53 (86.63)
FCR	0.41 (0.14)	2.90 (1.05)							0.29 (2.17)	0.84 (6.27)	0.35 (0.64)	0.12 (2.27)	0.39 (2.39)	1.53 (9.47)	0.48 (1.47)	1.35 (4.13)
FCU	0.56 (0.19)	2.11 (0.75)							0.81 (5.81)	3.22 (23.12)	0.08 (2.47)	0.33 (10.02)	0.34 (1.40)	2.34 (9.65)	0.42 (1.09)	2.92 (7.62)
PL	0.85 (0.27)	3.08 (1.01)							0.42 (2.62)	1.68 (10.44)	0.05 (0.75)	0.22 (3.38)	0.78 (3.84)	2.17 (10.75)	2.45 (5.10)	6.72 (13.98)

Italicized values represent fit equations that did not meet the desired accuracy criterion (SPE = shoulder plane of elevation, SEA = shoulder elevation angle, SRT = shoulder rotation, EFE = elbow flexion-extension, PS = forearm pronation-supination, WFE = wrist flexion-extension, WDV = wrist ulnar-radial deviation).

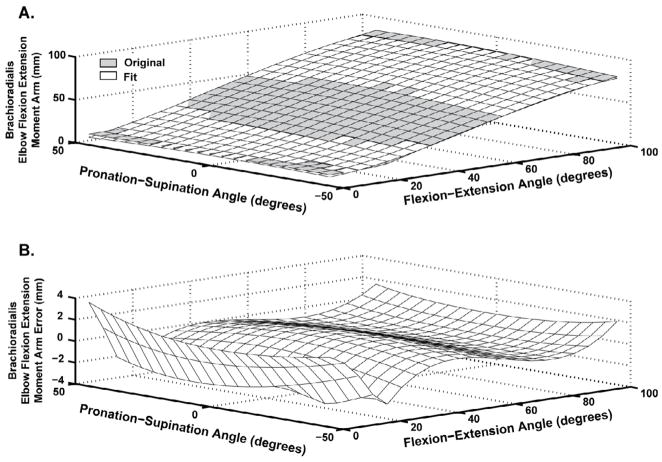
Figure 1.

Elbow Flexion extension moment arm comparisons for Brachioradialis (BRD). A) Surface plot of original (Grey) and regression equation (White) moment arm values (mm) over the entire range of motion for the elbow and forearm. B) Moment arm differences (mm) between the original and regression equation. Note the increase in error that occurs at flexion extension values less than 20 degrees flexion due to a non-smooth transition between wrapping surfaces in the original model.

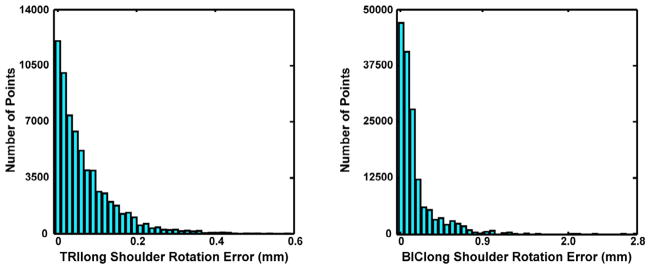
Figure 2.

Error histogram (i.e., difference between regression equation and original model values at each point) for two sample musculotendon actuator moment arms. A) Shoulder rotation moment arm of the long head of the triceps brachii (TRIlong, equation has desired fit accuracy). B) Shoulder rotation moment arm of the long head of the biceps brachii (BIClong, equation did not reach desired fit accuracy).

Discussion

This paper provides a set of regression equations that can be used to estimate musculotendon lengths and moment arms of 32 upper-extremity musculotendon actuators for a widely-used public-domain 3D upper-extremity musculoskeletal model. These equations were developed using the methods presented in Menegaldo et al (2004), which uses a least-squares regression technique on a mesh of points in the coordinate space, and therefore reproduces generalized coordinate interdependencies. Regression equations also account for scapula and clavicle movement, and therefore these segments do not need to be explicitly modeled to obtain accurate musculotendon geometry. The equations greatly reduced the computational cost of generating forward dynamics simulations relative to the original upper-extremity model. This is likely due to the elimination of the multiple wrapping surfaces and system constraints caused by phantom segments that are used to replicate the experimentally measured musculotendon geometry. For example, the total processing time required to simulate 1.16 seconds of wheelchair propulsion was reduced by more than two orders of magnitude relative to the original model (315 versus 2.3 seconds).

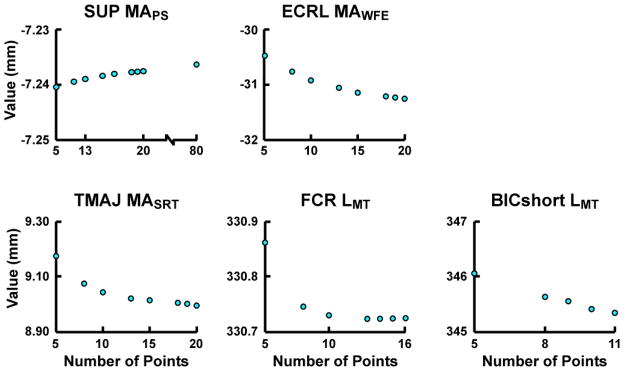
Because the regression equations were developed from a finite mesh of samples obtained from the original model, there exists the possibility of introducing errors by not sampling enough points. To investigate this possibility, a post-hoc sensitivity analysis was performed to determine the influence of the mesh size on each regression equation. This was done by generating each regression equation across a series of meshes and comparing the calculated equation value at a predetermined point in the coordinate space. With the exception of the two equations based on five generalized coordinates, the chosen mesh sizes were sufficiently large to reduce sampling error as values calculated near the chosen mesh point varied little over the number of points used (Fig. 3). Although equations based on five generalized coordinates appear to converge above 10 points per coordinate, this could not be verified because increasing the number of mesh points beyond 11 was computationally prohibitive due to the large number of data points (e.g., a 12 point mesh would have 248,832 points) required to generate the equation coefficients.

Figure 3.

Example results from the sensitivity analysis used to determine the influence of mesh size on the regression equation values. Each panel represents the value corresponding to a single point in the joint space when calculated from a regression equation developed from increasing the mesh size. Panels show equations dependent on different generalized coordinates: SUP MAPS – 1 coordinate, ECRL MAWFE – 2 coordinates, TMAJ MASRT – 3 coordinates, FCR LMT – 4 coordinates and BICshort LMT – 5 coordinates. All regression equations followed similar trends.

There are some potential limitations associated with these regression equations. First, the least-squares fitting method produces fit errors that systematically increase when approaching the generalized coordinate limits (Menegaldo et al., 2004). Although an effort was made to establish limits sufficiently large to encompass a large range of upper extremity movements (Table 1), care should be taken when implementing these equations during movements that approach or surpass these limits. If a larger range is needed, one can simply expand G in Equation 8 and refit the data. Second, these equations are only useful for muscle torque-driven models as they do not provide the musculotendon actuator’s line of action, which is necessary to apply its force vector to each body segment. As a result, compressive forces caused by muscles are not readily available to determine joint contact forces. Last, the glenohumeral rhythm used in the original model was obtained from healthy adults (de Groot and Brand, 2001). However, a recent study has shown that changes in external demand and muscle innervation level (i.e., pathology) influence scapular kinematics (Raina et al., 2011). Thus, future work should be performed to determine how these changes alter muscle geometry. Despite these potential limitations, the computationally efficient equations presented here will greatly assist in generating forward dynamics simulations of a wide range of upper extremity movements.