MULTI-SOURCE FEATURE LEARNING FOR JOINT ANALYSIS OF INCOMPLETE MULTIPLE HETEROGENEOUS NEUROIMAGING DATA

Abstract

Analysis of incomplete data is a big challenge when integrating large-scale brain imaging datasets from different imaging modalities. In the Alzheimer’s Disease Neuroimaging Initiative (ADNI), for example, over half of the subjects lack cerebrospinal fluid (CSF) measurements; an independent half of the subjects do not have fluorodeoxyglucose positron emission tomography (FDG-PET) scans; many lack proteomics measurements. Traditionally, subjects with missing measures are discarded, resulting in a severe loss of available information. In this paper, we address this problem by proposing an incomplete Multi-Source Feature (iMSF) learning method where all the samples (with at least one available data source) can be used. To illustrate the proposed approach, we classify patients from the ADNI study into groups with Alzheimer’s disease (AD), mild cognitive impairment (MCI) and normal controls, based on the multi-modality data. At baseline, ADNI’s 780 participants (172 AD, 397 MCI, 211 NC), have at least one of four data types: magnetic resonance imaging (MRI), FDG-PET, CSF and proteomics. These data are used to test our algorithm. Depending on the problem being solved, we divide our samples according to the availability of data sources, and we learn shared sets of features with state-of-the-art sparse learning methods. To build a practical and robust system, we construct a classifier ensemble by combining our method with four other methods for missing value estimation. Comprehensive experiments with various parameters show that our proposed iMSF method and the ensemble model yield stable and promising results.

1. Introduction

Alzheimer’s disease (AD) is a highly prevalent neurodegenerative disease, and is widely recognized as a major, escalating epidemic and a world-wide challenge to global health care systems (Kuljis, 2010). AD is the most common type of dementia, accounting for 60–80% of age-related dementia cases. The direct cost of care for AD patients by family members or healthcare professionals is more than $100 billion per year; this figure is expected to rise dramatically as the population ages during the next several decades (Reiman et al., 2010). In AD patients, neurons and their connections are progressively destroyed, leading to loss of cognitive function and ultimately death. The underlying pathology most probably precedes the onset of cognitive symptoms by many years (Braskie et al., 2008; Jack et al., 2011). Efforts are underway to find early diagnostic markers to evaluate AD risk pre-symptomatically in a rapid and rigorous way. Such findings will help establish early interventions that may prevent or at least postpone the onset of AD, or reduce the risk of developing the disease.

Neuroimaging is a powerful tool to measure disease progression and therapeutic efficacy in AD and mild cognitive impairment (MCI). Neuroimaging research offers great potential to discover features that can identify individuals early in the course of dementing illness; several candidate neuroimaging biomarkers have been examined in recent cross-sectional and longitudinal neuroimaging studies (Devanand et al., 2007; Fennema-Notestine et al., 2009). Past clinical and research studies show that reduced fluorodeoxyglucose (FDG) PET measurements of the cerebral metabolic rate for glucose in brain regions preferentially affected by AD, structural MRI measures of brain shrinkage, and cerebrospinal fluid (CSF) measurements are among the best established biomarkers of AD progression and pathology (Reiman et al., 2010). Realizing the importance of combining neuroimaging and genetics, NIH in 2003 funded the Alzheimer’s Disease Neuroimaging Initiative (ADNI (Mueller et al., 2005; Jack et al., 2008a), PI: Michael W. Weiner). The initiative is facilitating the scientific evaluation of neuroimaging data including magnetic resonance imaging (MRI), positron emission tomography (PET), other biomarkers, and clinical and neuropsychological assessments for predicting the onset and progression of MCI and AD. By identifying more sensitive and specific markers of very early AD progression, these efforts should make it easier to diagnose AD earlier as well as develop, assess, and monitor new treatments.

Clinical and research studies commonly acquire complementary brain images, neuropsychological and genetic data for each participant for a more accurate and rigorous assessment of the disease status and likelihood of progression. Advances in image analysis make it possible to use one image modality to support the analysis of a complementary image modality (Ashburner and Friston, 1997; Ibanez et al., 1998; Casanova et al., 2007; Jack et al., 2008b; Landau et al., 2011). However, only a few systems, e.g., (Worsley et al., 1997; Martinez-Montes et al., 2004; Fan et al., 2008; Ye et al., 2008; Calhoun and Adali, 2009; Chen et al., 2009; Vemuri et al., 2009a, 2009b; Correa et al., 2010; Kohannim et al., 2010; Wang et al., 2010; Yang et al., 2010; Groves et al., 2011; Lemm et al., 2011; Sui et al., 2011; Zhang et al., 2011), applied machine learning techniques such as the multivariate linear model, partial least squares, independent component analysis and canonical correlation analysis to characterize the linkage between the patterns of information from the same individual’s brain images and other biological measures. Instead, most researchers have performed statistical analyses by analyzing different images separately. In general, these “unimodal” analyses could be improved by considering other sources of relevant information from multiple imaging modalities, e.g., PET and MRI, and non-imaging datasets from genomics and proteomics. It is a common belief that by integrating multiple heterogeneous sources, one may not only provide more accurate information on AD progression and pathology, but also better predict cognitive decline before the onset of illness, or at least in the earliest stages of disease.

One common problem that hampers the adoption of multi-modality imaging approach is the problem of missing data. Missing data present a special challenge when integrating large-scale biomedical data. Incomplete data is ubiquitous in real-world biomedical applications. In ADNI, over half of the subjects lack CSF measurements; an independent half of the subjects do not have FDG-PET; many lack proteomics measurements. Missing data may be due to the high cost of certain measures (e.g., PET scans), poor data quality, dropout of the patients from the study, etc. Some measures, such as CSF biomarkers, require more invasive procedures (such as lumbar puncture) which not all study participants are willing to consent to. Some subjects in a longitudinal study may miss at least one of the regular assessments, or their data quality may be insufficient for accurate analysis at some time points.

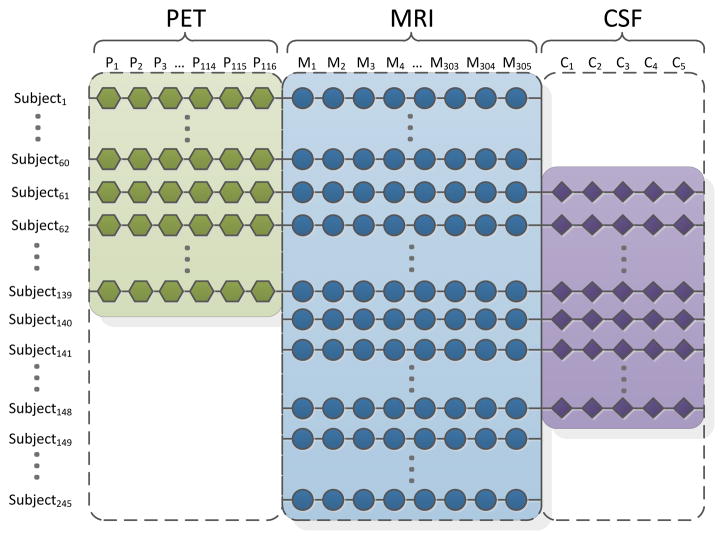
The simplest approach removes all samples with missing values, but this throws away a vast amount of useful information and dramatically reduces the number of samples in the analysis. As a result, a subject with incomplete data cannot be studied for classification and prognosis. Moreover, with this approach, the resource and time devoted to those subjects with incomplete data are totally wasted. A number of previous works have acknowledged the challenge of missing data and discussed general strategies (Van Ness et al., 2007; Hardy et al., 2009; Palmer and Royall, 2010). An alternative and popular approach is to estimate missing entries based on the observed values. Many algorithms have been proposed for this (Hastie et al., 1999; Schneider, 2001; Gao, 2004; Schott et al., 2010). While these methods work well when missing data are rare, they are less effective when a significant amount of data is missing, e.g., when all PET features from half of the subjects are missing. Recently, trace norm minimization has been proposed for missing data estimation (Cai et al., 2010; Candes and Tao, 2010). This can be effective even when a large amount of data is missing. However, it does assume that the missing locations are random; it is less effective when a complete block of the data is missing, e.g., the complete block of all PET features from half of the subjects. Therefore, computational methods are needed to integrate heterogeneous data with a block-wise missing pattern (“block-wise missing” means a large chunk of data is missing for one or more data sources - an example is shown in Figure 2). Without such a method, it is quite challenging to build a highly accurate classifier to process any real multi-modality imaging datasets.

Figure 2.

Here we illustrate the “block-wise” pattern of missing data for the ADNI dataset. In this figure, we show AD and normal control subjects only. For simplicity, we focus on those subjects with complete MRI measures. Note in our entire study, there are still 132 subjects who do not have MRI measures, as the UCSF group only released pre-processed baseline MRI imaging features for 648 subjects.

In this paper, we propose a novel multi-task sparse learning framework to integrate multiple incomplete data sources. In machine learning, multi-task means that the method can tackle many classification/regression problems simultaneously. Instead of removing samples with missing data or guessing the missing values from what is available, we observe and make full use of the block-wise missing pattern. Based on the availability of different feature sources, we divide the data set into several learning tasks, from each of which a unique classifier is learned. We then impose a structural sparse learning regularization^* onto these tasks, such that a common set of features is selected among these tasks. Therefore, we exploit the multi-task nature of the problem and the feature set is learned jointly among different tasks. To solve the parameter tuning problem and improve system performance, we construct an ensemble model to combine all the models together. As an illustrative application, we study clinical group (diagnostic) classification problems in the ADNI baseline imaging dataset. Comprehensive experiments demonstrate the promising and stable performance of the proposed system.

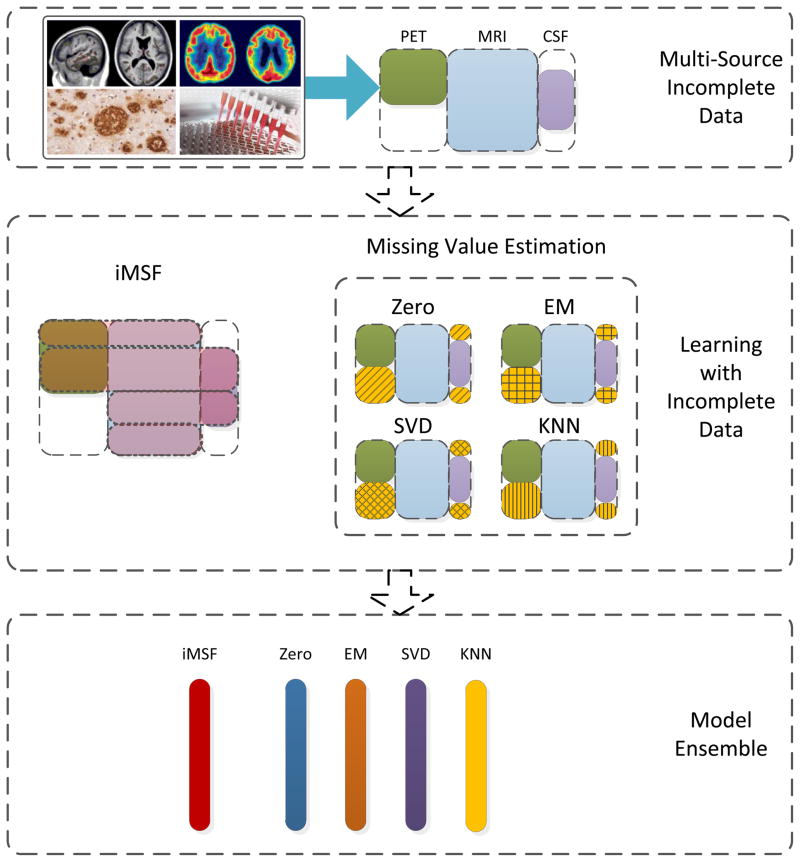
The overview of the complete system proposed in this paper is shown in Figure 1. 780 subjects in the ADNI baseline dataset have their diagnosis (AD, MCI or NC) available and have at least one type of features available (meaning an image or related clinical measure), including MRI, FDG-PET, CSF and proteomics. We set out to use these data to solve clinical group classification problems (AD-NC; AD-MCI and MCI-NC). For our experiments, we obtained MRI, CSF and proteomics feature sets from the ADNI web site (http://adni.loni.ucla.edu/) and we processed FDG-PET data using the image analysis package, SPM (SPM8, http://www.fil.ion.ucl.ac.uk/spm) using the statistical region of interest (sROI) method. Besides our multi-source learning framework for incomplete data, we also implement four other methods for missing value estimation: (1) the “Zero” method: a method for mean value imputation; (2) EM: a missing value imputation method based on the expectation-maximization (EM) algorithm (Schneider, 2001); (3) SVD (singular value decomposition): a method for matrix completion using a low rank approximation to the full matrix; and (4) KNN: a missing value imputation method based on the k-nearest neighbor principle (Hastie et al., 1999). Finally, by combining these classifiers, we develop a practical classifier ensemble system.

Figure 1.

Overview of the proposed system. We are given a multi-source data set with incomplete sources. Instead of removing valuable subjects if they have missing data, we use structured multi-task learning to enable feature learning from incomplete data. Then, along with other methods to impute missing values, we obtain a series of plausible models to aggregate into an even more robust one.

2. Subjects and Methods

In this section, we describe our proposed system. In Section 2.1, we discuss the data set used, and the multi-source feature learning framework is introduced in Section 2.2. As the proposed problem is numerically challenging, an efficient algorithm is presented in Section 2.3. The ensemble methods are introduced in Section 2.4; these allow a set of different models to be combined.

2.1 Subjects

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessments can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California – San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 adults, ages 55 to 90, to participate in the research, approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years and 200 people with early AD to be followed for 2 years.” For up-to-date information, see www.adni-info.org.

In terms of data collected at baseline, a total of 822 ADNI participants were recruited from 59 sites across the U.S. and Canada. These including 229 NC (normal elderly controls), 405 with MCI, and 188 with AD, ranging in age from 55 to 90 years. Phenotype data included structural MRI scans acquired on 1.5T MRI scanners, and clinical and neuropsychological assessments. Additional data such as 3-Tesla MRI, FDG-PET, PIB-PET (a PET scanning method using the amyloid-sensitive ligand, Pittsburgh compound B), and fluid biomarkers are available for some subjects as well. In our experiments, we use pre-processed 1.5 Tesla (T) MRI imaging features which were preprocessed by the team at the University of California at San Francisco (UCSF). There are a total of 648 subjects whose processed MRI imaging features were available. Besides these data, we were able to include other subjects who had at least one of three data types available: FDG-PET, CSF, and/or proteomics. For these subjects – those beyond the initial 648 subjects - we consider their MRI data as “missing” since the UCSF group did not release their pre-processed MRI imaging features. As a result, baseline data from a total of 780 participants (172 AD, 397 MCI, and 211 NC) were used to test our algorithm.

In ADNI, all participants received 1.5 Tesla (T) structural MRI. The MRI image features in this study were based on the imaging data from the ADNI database processed by the UCSF team, who performed cortical reconstruction and volumetric segmentations with the FreeSurfer image analysis suite (http://surfer.nmr.mgh.harvard.edu/). The processed MRI features come from a total of 648 subjects (138AD, 319 MCI and 191 NC), and can be grouped into 5 categories: average cortical thickness, standard deviation in cortical thickness, the volumes of cortical parcellations (based on regions of interest automatically segmented in the cortex), the volumes of specific white matter parcellations, and the total surface area of the cortex. There were 305 MRI features in total. Details of the analysis procedure are available at http://adni.loni.ucla.edu/research/mri-post-processing/. More details on ADNI MRI imaging instrumentation and procedures (Jack et al., 2008a) may be found at ADNI web site (http://adni.loni.ucla.edu). We also downloaded FDG-PET images of 327 subjects (74 AD, 172 MCI, and 81 NC) from the ADNI website. With SPM8 (http://www.fil.ion.ucl.ac.uk/spm/), we processed these FDG-PET images. We applied Automated Anatomical Labeling (AAL) (Tzourio-Mazoyer et al., 2002) to extract each of the 116 anatomical volumes of interest (AVOI) and derived average image values from each AVOI, for every subject. Baseline CSF samples were acquired from 416 subjects (102 AD, 200 MCI and 114 NC) by the ADNI Biomarker Core laboratory at the University of Pennsylvania Medical Center (Tzourio-Mazoyer et al., 2002). In our study, we use 5 measures obtained from the CSF, including levels of beta amyloid 1-42 (Aβ_1-42), tau protein (Tau), phosphorylated-tau protein 181 (pTau_181p) along with two CSF ratios (Tau/Aβ_1-42 and pTau_181p/Aβ_1-42). The proteomics data set (97 AD, 345 MCI, and 54 NC) was produced by the Biomarkers Consortium Project “Use of Targeted Multiplex Proteomic Strategies to Identify Plasma-Based Biomarkers in Alzheimer’s Disease”^† (see URL in footnote). We use 147 measures from the proteomic data downloaded from the ADNI web site. As a result, for a subject with all four types of data available, a total of 573 measures were studied in our classification experiment. The number of samples from each category corresponding to each type of feature utilized in this study is summarized in Table 1.

Table 1.

Summaries of number of available samples and features utilized for each source in this study.

	MRI	PET	CSF	Proteomics
Number of AD subjects	138	74	102	97
Number of MCI subjects	319	172	200	345
Number of NC subjects	191	81	114	54
Number of features	305	116	5	147

2.2 Multi-Source Feature Learning Framework with Block-wise Missing Values

In many applications, multiple data sources may suffer from a considerable amount of missing data. For example, in the ADNI data acquisition phase, many subjects lack a subset of measures, resulting in a scenario shown in Figure 2, where large chunks of missing data are marked by the white areas. A simple and popular approach is to remove all the subjects with missing values, but this greatly reduces the number of samples and fails to make full use of the information in the dataset. In Figure 2, only 79 subjects (Subjects 61-139) out of a total of 245 subjects do not have missing values. In our feature learning framework described below, we fully use the multiple heterogeneous data with a block-wise missing pattern by exploiting the underlying structure in the multi-source data. Our proposed framework formulates the prediction problem as a multi-task learning problem (Ando and Zhang, 2005; Argyriou et al., 2008; Liu et al., 2009a) by first decomposing the prediction problem into a set of tasks, one for each combination of data sources available, and then building the models for all tasks simultaneously.

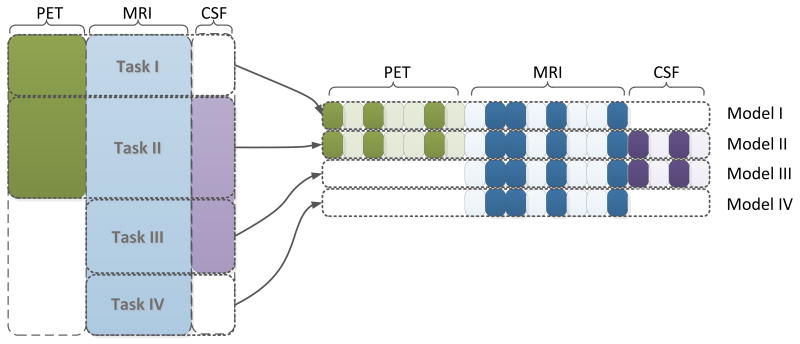
For example, considering a dataset with three sources (CSF, MRI, PET) and assuming all samples have MRI measures, we first partition the samples into multiple blocks (4 in this case), one for each combination of data sources available: (1) PET, MRI; (2) PET, MRI, CSF; (3) MRI, CSF; and (4) MRI. We then build four models, one for each block of data, resulting in four prediction tasks (Figure 3).

Figure 3.

Illustration of the proposed multi-task feature learning framework for incomplete multi-source data fusion. In the proposed framework, we first partition the samples into multiple blocks (four blocks in this case), one for each combination of data sources available: (1) PET, MRI; (2) PET, MRI, CSF; (3) MRI, CSF; (4) MRI. We then build four models, one for each block of data, resulting in four prediction tasks. We use a joint feature learning framework that learns all models simultaneously. Specifically, all models involving a specific source are constrained to select a common set of features for that particular source. As shown above, all four tasks select a common subset of MRI features (the selected features for all four tasks are highlighted).

A simple approach to deal with the missing data is to build these four models separately, but that does not fully use the information in the multi-source data. Indeed, the sample size for each of these four tasks is even smaller, resulting in the large dimension small sample size problem. We address this by employing a joint feature learning formulation. We formulate our proposed framework as follows. Suppose the data set is divided into m tasks: $T^i=\{x_j^i,y_j^i\}$, i =1 …m, j= 1 … N_i, where N_i is the number of subjects in the i-th task, and ( $x_j^i,y_j^i$) is the j-th subject from the i-th task. Suppose for each task, we consider the following linear model:

$$f^i(x_j^i)={({\beta }^i)}^T{x}_j^i$$

where βⁱ is the weight vector, including the model parameters for the i-th task. Denote β = {β¹, ···, β^m} as the collection of all model parameters. Assume that we have a total of S data sources, and the feature dimensionality of the s-th source is denoted as p_s = |g_s|. For notational convenience, we introduce an index function I(s,k) as follows: β_I(s,k) denotes all the model parameters corresponding to the k-th feature in the s-th data source. The proposed multi-task feature learning framework is given by:

$$\underset{\beta }{min}\frac{1}{m}\sum _{i=1}^m\frac{1}{N_i}\sum _{j=1}^{N_i}L(x_j^i,y_j^i,{\beta }^i)+\lambda \sum _{s=1}^S\sum _{k=1}^{p_s}{\left|\right|{\beta }_{I(s,k)}\left|\right|}_2$$

where L(·) is the loss function. In our study, we use the logistic loss function, defined as follows:

$$L(x_j^i,y_j^i,{\beta }^i)=ln\left(1+exp\left(-y_j^i{({\beta }^i)}^T{x}_j^i\right)\right)$$

The second part of the formulation, which is essentially an ℓ_2,1-norm regularization on the model parameters (Yuan and Lin, 2006), leads to a solution with the desired sparsity, that is, all models involving a specific source are constrained to select a common set of features for this particular source. The proposed formulation is novel as it (1) formulates the incomplete multi-source fusion as a multi-task learning problem, and (2) extends existing multi-task feature learning formulations to accommodate missing feature values.

2.3 Efficient Optimization

The optimization problem proposed in Section 2.2 is the composition of a smooth term and a non-smooth term, which is challenging to solve. In this paper, we propose to solve it using the accelerated gradient descent (AGD) method (Nesterov 2003, 2007) because of its fast convergence rate. Denote the empirical loss as

$$\ell (\beta )=\frac{1}{m}\sum _{i=1}^m\frac{1}{N_i}\sum _{j=1}^{N_i}L(x_j^i,y_j^i,{\beta }^i),$$

and the non-smooth regularization as ${\phi }_{\lambda }(\beta )=\lambda {\sum }_{s=1}^S{\sum }_{k=1}^{p_s}{\left|\right|{\beta }_{I(s,k)}\left|\right|}_2$. We first approximate ℓ(β) + φ_λ(β) as

$$f_{L,\beta }(\theta )=\ell (\beta )+\langle {\ell }^{\prime }(\beta ),\theta -\beta \rangle +{\phi }_{\lambda }(\theta )+\frac{L}{2}{\left|\right|\theta -\beta \left|\right|}^2$$

In the i-th step, a search point s_i is computed based on the past solutions of the previous steps by s_i = β_i + τ_i(β_i − β_i−1). Then, the new solution β_i+1 is obtained via the minimization of the model at the current search point, that is, β_i+1 = argmin_θ f _L,si(θ). This sub-problem is the key component to the optimization, and is often called the proximal operator (Combettes and Pesquet, 2009). A detailed discussion of how to solve this subproblem efficiently can be found in our previous work (Liu et al., 2009a). By doing so, we successfully bypass the difficulty of computing the subgradient of φ_λ(·); algorithm details are summarized in Algorithm 1.

Algorithm 1.

Efficient Optimization for the Multi-Source Framework

Input: L0, λ, β0, n

Output: βn+1 Initialize β1 =β0, α−1 = 0, α0 = 1, and L = L0 for i = 1 to n do: Set ${\tau }_i=\frac{{\alpha }_{i-2}-1}{{\alpha }_{i-1}}$, si = βi + τi(βi − βi−1) Find the smallest L = Li−1, 2Li−1, … such that ℓ(βi+1) + φλ(βi+1) ≤ f L,si (βi+1) holds, where $${\beta }_{i+1}=\underset{\theta }{\text{argmin}}{f}_{L,s_i}(\theta )$$ Set Li = L and ${\alpha }_{i+1}=\frac{1+\sqrt{1+4{\alpha }_i^2}}{2}$ end for

2.4 Ensemble Methods

In practice, the regularization parameter λ in our proposed model controls how sparse the solution will be, and should be tuned via a set of possible selections. In other words, during the training, a series of models are constructed and one of them can be adopted. In addition, there are several different missing value estimation methods, therefore we will have a fairly large collection of models to choose from. One intuitive question to ask is: can we bypass the difficulty of choosing the best one and the possibility of over-fitting, by trying to combine all of the base models? This leads to the idea of model ensemble (Dietterich, 2000). One simple form of ensemble method is majority voting (which we refer to as “Voting” for the rest of the paper). For each previously unseen testing sample, each of the models will give a decision, either positive or negative, and the majority is considered as the final decision. An extension of majority voting is uniformly weighted voting (here denoted by “Uniform”), where each model gives a decision with a confidence level, and the final prediction is decided based on the votes weighted by the confidence in them.

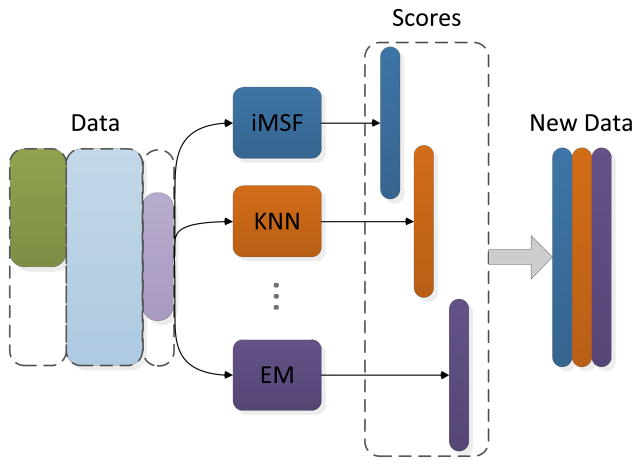
Recently, one particular ensemble method has shown quite promising performance in practice (Dietterich, 2000), where the weight assigned to each models is learned (so we call it “Learned” for the rest of the paper). The framework of this method is shown in Figure 4. For a given data set, different methods (with different parameters if necessary) will be applied; each of them gives a classification score on each sample (training or testing). Then, these scores are considered as the new dataset on which the final training and testing is performed, during which the weight or the “importance” of each base model are determined.

Figure 4.

Illustration of the learning-based ensemble method. For a given dataset, different base models (with different parameters if necessary) are applied and each of them gives a classification score on each sample (training or testing). Then, these scores are considered as the new dataset on which the final training and testing are performed.

3. RESULTS

In this section, we perform experimental studies to demonstrate the effectiveness of our proposed methods. As noted earlier, we used all the subjects who had at least one feature type available among four different data sources including MRI, PET, CSF and proteomics, and challenge our method with the problem of distinguishing AD, MCI and NC subjects from each other. As in other diagnostic classification papers, we consider the clinical diagnosis (as defined by ADNI) as the ground truth, and the goal is to classify people into the 3 groups based on their imaging and other biomarkers that were not used to make the clinical diagnosis. In Section 3.1, we compare different ensemble methods with the base methods that were combined; in Section 3.2, we compare the performance of the proposed iMSF and missing value estimation methods. In our binary classification test scenarios (e.g. AD vs. control, AD vs. MCI vs. control), the relative performances of different methods are evaluated using metrics of accuracy, sensitivity and specificity, defined as follows:

$$\begin{array}{l}\text{accuracy}(\%)=\frac{\text{number}\text{of}\text{true}\text{positives}+\text{number}\text{of}\text{true}\text{negatives}}{\text{number}\text{of}\text{total}\text{samples}}\times 100\%\\ \text{sensitivity}(\%)=\frac{\text{number}\text{of}\text{true}\text{positives}}{\text{number}\text{of}\text{true}\text{positives}+\text{number}\text{of}\text{false}\text{negatives}}\times 100\%\\ \text{specificity}(\%)=\frac{\text{number}\text{of}\text{true}\text{negatives}}{\text{number}\text{of}\text{true}\text{negatives}+\text{number}\text{of}\text{false}\text{positives}}\times 100\%\end{array}$$

In the statistical tests, the sensitivity measures the proportion of true positives that are correctly identified as such; specificity measures the proportion of negatives that are correctly identified. The accuracy measures the overall correct classification rate in the whole ADNI cohort.

3.1 Comparison of the Ensemble Classifier to Other Methods

In our first set of experiments, we apply our proposed system to the full multi-source dataset including MRI, PET, proteomics and CSF for distinguishing ADNI subjects into 3 diagnostic groups (AD, MCI and NC). 780 subjects were analyzed. Among them, 648 subjects have MRI measures and each subject has at least one of the four data sources (MRI, FDG-PET, CSF and proteomics features) available. We first randomly select a portion (from 50% to 75%) of samples as the training set to learn the model, and then apply the model to predict the labels on the remaining data, used as a non-overlapping test set. We repeated this process 30 times, and the average performance is reported.

For comparison purposes, we implemented the following missing value estimation methods:

• Zero: this is the most intuitive way to impute missing values - we assign zero to any element that is missing. When the data set is first normalized to have zero mean and unit standard deviation, this is equivalent to mean value imputation.

• KNN: missing value imputation using the k-nearest neighbor method (Hastie et al., 1999). The KNN method replaces the missing value in the data matrix with the corresponding value from the nearest column. That is to say, KNN will first identify the most similar feature to the current one with a missing value, and then use this feature as a guess for the missing one.

• EM: this method imputes missing values using the expectation-maximization (EM) algorithm (Schneider, 2001). An iteration of the EM algorithm includes two steps. In the E step, we estimate the mean and covariance matrix from the data matrix (with missing values filled with guesses from previous M step, or initialized as zeros); then in the M step, the missing value of each data column is filled in with their conditional expectation values based on the available values and the estimated mean and the covariance. We then re-estimate the mean and the variance based on the new estimates, therefore entering the next EM iteration.

• SVD: this is a standard method for matrix completion based on low rank approximation. SVD based estimation works in a similar way to the EM method above. We first provide some initial guesses (such as 0) to the missing data values, and then we apply singular value decomposition (SVD) to obtain a low-rank approximation of the filled-in matrix. Next, we update the missing values as their corresponding values in the low-rank estimation. Finally, we apply SVD to the updated matrix again and the process is repeated until convergence.

For our proposed iMSF method, five values (0.001, 0.01, 0.1, 0.2 and 0.4) were used for the regularization parameter λ. Combining this with the four missing value estimation methods mentioned before, we have a total of 9 different models for the ensemble classifier. The performance for different classification problems, in terms of accuracy, sensitivity and specificity is summarized in Table 2 to Table 4, where the best performance in each case is underlined. For a clear comparison with the individual classifier, only the best and average performances out of the 9 methods are illustrated.

Table 2.

AD/NC classification comparison of the ensemble methods (Voting, Uniform and Learned) and the other methods (Best and Average) in terms of accuracy, sensitivity and specificity when the training percentage varies from 1/2 to 3/4. For this experiment, we used the full multi-source data including MRI, PET, proteomics and CSF from 383 subjects in total.

Accuracy	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.7703	0.8925	0.8949	0.8737	0.8427
	66.7%	0.8248	0.8994	0.9013	0.889	0.8642
	75.0%	0.8177	0.9026	0.9026	0.8887	0.8629
Sensitivity	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.9662	0.8862	0.8897	0.8879	0.8424
	66.7%	0.9659	0.8818	0.8889	0.8838	0.8511
	75.0%	0.9588	0.8809	0.8862	0.885	0.8481
Specificity	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.5685	0.9016	0.9019	0.879	0.8458
	66.7%	0.6712	0.9184	0.9144	0.9142	0.8787
	75.0%	0.6675	0.9294	0.923	0.9102	0.8814

Table 4.

MCI/NC classification comparison of the ensemble methods (Voting, Uniform and Learned) and the other methods (Best and Average) in terms of accuracy, sensitivity and specificity when the training percentage varies from 1/2 to 3/4. In this experiment, we used the full multi-source dataset including MRI, PET, proteomics and CSF, from 608 subjects in total.

Accuracy	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.8832	0.8754	0.8845	0.8872	0.8504
	66.7%	0.9105	0.8865	0.8967	0.9033	0.8591
	75.0%	0.9026	0.8821	0.893	0.8927	0.8573
Sensitivity	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.7829	0.4446	0.5051	0.6228	0.3698
	66.7%	0.8393	0.5119	0.582	0.6922	0.414
	75.0%	0.846	0.5031	0.5639	0.7162	0.4139
Specificity	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.9121	0.995	0.9901	0.9955	0.9837
	66.7%	0.9321	0.9938	0.9883	0.9956	0.9855
	75.0%	0.9212	0.9925	0.9888	0.9982	0.985

In terms of overall accuracy, we find that the ensemble methods (especially the Uniform and Learned method) can always achieve similar, if not better, performance as the best of the 9 base methods. This is quite encouraging since in practice, we will never know which parameter will be the best. This shows that our ensemble system is practical and able to produce robust results.

Comparing the best and the average performances of the 9 base methods, we can see that the variance in their performance is quite large. Since for a different problem, the best choice may vary, combining them instead of choosing one of them should offer a distinct advantage. It was also acknowledged in the neuroimaging literature that “weak learner”, or classifiers whose performance alone is relatively weak may be combined to produce a powerful classifier (Kuncheva and Rodríguez, 2010; Morra et al., 2010); this is the principle of adaptive boosting and other methods based on weak learners.

We also found that among the three ensemble methods, the uniformly weighted and the “learned” method gave comparable performance in most cases, while the majority voting method yielded much better sensitivity. This may provide some practical guidance for designing future ensemble methods for incomplete data classification.

3.2 Comparison of iMSF and imputation methods

In this section, we compare our proposed iMSF method with several missing value estimation methods. Experiments follow the same sequence as in the previous section. We first randomly select a portion (from 50% to 75%) of samples as the training set to learn the model, and then apply the model to predict the labels (diagnosis) for the remaining test set. We repeat this process 30 times, and the average performance is reported. For the ease of comparison of our methods with the previous works, here we also present the leave-one-out (LOO) results. The results are illustrated in Table 5 to Table 7, where the best performance in each case is underlined.

Table 5.

AD/NC classification comparison of our proposed method (iMSF) and missing value estimation methods (Zero, KNN, SVD and EM) in terms of accuracy, sensitivity and specificity when the training percentage varies from 1/2 to 3/4 as well as leave-one-out (LOO). In this experiment, we used the full multi-source data including MRI, PET, proteomics and CSF with 383 subjects in total.

Accuracy	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.8658	0.8571	0.8737	0.8615	0.8404
	66.7%	0.889	0.8667	0.8814	0.8733	0.8494
	75.0%	0.8848	0.8662	0.8887	0.8701	0.8554
	LOO	0.9082	0.8671	0.8987	0.8797	0.8481
Sensitivity	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.8552	0.8808	0.8879	0.8842	0.8539
	66.7%	0.8706	0.8838	0.8785	0.8818	0.8468
	75.0%	0.8667	0.8793	0.885	0.8849	0.8523
	LOO	0.8951	0.8889	0.8951	0.8827	0.8519
Specificity	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.879	0.8354	0.861	0.8407	0.8279
	66.7%	0.9142	0.8481	0.8844	0.8636	0.8523
	75.0%	0.9102	0.8551	0.8942	0.8569	0.8593
	LOO	0.9351	0.8442	0.9026	0.8766	0.8442

Table 7.

MCI/NC classification comparison of our proposed method (iMSF) and missing value estimation methods (Zero, KNN, SVD and EM) in terms of accuracy, sensitivity and specificity when the training percentage varies from 1/2 to 3/4 as well as leave-one-out (LOO). In this experiment, we used the full multi-source data including MRI, PET, proteomics and CSF with 608 subjects in total.

Accuracy	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.8872	0.8346	0.8095	0.8142	0.8115
	66.7%	0.9033	0.843	0.8132	0.8113	0.8193
	75.0%	0.8927	0.8462	0.8088	0.8106	0.8165
	LOO	0.9116	0.8481	0.8204	0.8287	0.8204
Sensitivity	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.6228	0.2537	0.1573	0.174	0.1678
	66.7%	0.6922	0.3055	0.1726	0.1768	0.2092
	75.0%	0.7162	0.3184	0.1709	0.1741	0.2093
	LOO	0.7375	0.3125	0.2125	0.2625	0.2
Specificity	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.9907	0.9955	0.9901	0.9915	0.9898
	66.7%	0.9934	0.9956	0.9931	0.9895	0.9906
	75.0%	0.9949	0.9982	0.9907	0.9912	0.9893
	LOO	0.9965	1	0.9929	0.9894	0.9965

Table 5 shows the AD – NC classification results - all algorithms achieved very good results and the accuracy rates are around 88%. However, as shown in Table 6–7, in the more challenging settings where MCI subjects are involved, iMSF performs much better, especially in terms of sensitivity. It may be due to the fact that our algorithm took a more systematic approach to use multiple sources of information for classification. A detailed comparison with published results using the ADNI data set can be found in the discussions.

Table 6.

AD/MCI classification comparison of our proposed method (iMSF) and missing value estimation methods (Zero, KNN, SVD and EM) in terms of accuracy, sensitivity and specificity when the training percentage varies from 1/2 to 3/4 as well as leave-one-out (LOO). In this experiment, we used the full multi-source data including MRI, PET, proteomics and CSF with 569 subjects in total.

Accuracy	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.8278	0.804	0.8025	0.7963	0.8059
	66.7%	0.8335	0.812	0.812	0.8035	0.8149
	75.0%	0.8401	0.8242	0.8148	0.8091	0.8148
	LOO	0.8563	0.8209	0.813	0.8091	0.8071
Sensitivity	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.4339	0.1406	0.1232	0.1021	0.159
	66.7%	0.4424	0.1663	0.1552	0.1192	0.1848
	75.0%	0.4514	0.1907	0.1467	0.1286	0.1649
	LOO	0.5	0.1964	0.1696	0.1607	0.1607
Specificity	Training Size	iMSF	Zero	EM	KNN	SVD
	50.0%	0.9628	0.9894	0.9924	0.9902	0.9867
	66.7%	0.9643	0.9898	0.9923	0.9913	0.9879
	75.0%	0.967	0.9946	0.9946	0.9923	0.9899
	LOO	0.9697	0.9975	0.9949	0.9924	0.9899

Interestingly, the four different missing value estimation methods perform comparably to each other. That is to say, estimating the missing values does not give much edge over simply substituting missing elements with zeros. This is somehow counterintuitive and it may be because of the data distribution in the ADNI dataset. Whether it is true for other studies needs more exploration.

4. DISCUSSION

This paper has two major contributions. First, we were able to use a large multi-modal dataset for classification, even when large segments of the data were missing. Secondly, we built a multi-task learning framework with an efficient numerical stable scheme, and used it to create an automatic, robust classifier based on ensemble models, whose performances were compared. In our experiments, the classifier ensemble significantly improved the classification accuracy on the ADNI dataset. Our method (iMSF) has two major advantages: 1) All subjects, so long as at least one of the feature sources is available, can be used for feature learning, and all of them can contribute to the feature selection jointly; 2) the difficulty of guessing unknowns is bypassed, as the feature learning is only based on what data is available. To the best of our knowledge, in the ADNI dataset, we are the first group who tried to utilize all the available information for classification by allowing the use of subjects with incomplete data. In our current pilot work, we assessed whether our incomplete feature learning models help to boost the statistical power in the whole dataset. Except for some of the PET imaging measures (such as Pittsburgh compound B), we used all other measures that are publicly available at ADNI web site. We hope our work will increase interest in this important problem and that other groups might consider using this approach (not throwing out data) when performing future ADNI classification studies.

Pioneering work has been done on the automated diagnosis problem using the ADNI dataset. López et al. (1995) applied principal component analysis to extract features from FDG-PET. In a dataset of 211 subjects (53 AD, 114 MCI and 52 NC), they achieved a best leave one out (LOO) accuracy 82% for classifying people into groups of AD/NC and a best LOO accuracy of 81% on MCI/NC. Cuingnet et al. (2011) evaluated the performance of ten high dimensional classification methods using the ADNI MRI data. In their dataset of 509 subjects, the best of the ten classifiers achieved 81%/95%, 65%/94% sensitivity/specificity for classification of AD/NC, MCI/NC, respectively. In our earlier work (Kohannim et al., 2010), we used support vector machines to combine several MRI measures, as well as PET and CSF biomarkers, etc. and we achieved a 90% LOO accuracy on AD/NC and a 75% LOO accuracy on MCI/NC classification. Notably, all of these prior studies were applied to a subset of the full available ADNI data used here. For example, in Kohannim et al. (2010), 635 subjects were studied when only MRI-based measures were needed, but when both CSF and PET were also added to the set of predictors, the available sample size dropped dramatically to 166 subjects. Without a method to include subjects with missing data, it becomes quite difficult to build an accurate classifier. The approach we outlined here still achieved comparable or better results than those in prior works.

Comparison with single source classification

Though it is a common belief that by integrating multiple heterogeneous sources, one can provide more accurate prediction of AD progression, it is still interesting to see how much classification performance we can improve by utilizing multi-modality data. Therefore, we extract the 648 subjects that have MRI features available (with complete data), and perform leave-one-out classification on the same problems we discussed before. We then extract the classification results for the same 648 subjects from our iMSF method, such that the comparison can be made using the same sample pool. The results are summarized in Table 8.

Table 8.

Classification comparison of using multi-modality data (iMSF) and just using MRI data. The classification is done on the same set of samples so that a fair comparison can be made. Leave-one-out is used and the accuracy, sensitivity and specificity are reported.

	AD/NC			AD/MCI			MCI/NC
	Accuracy	Sensitivity	Specificity	Accuracy	Sensitivity	Specificity	Accuracy	Sensitivity	Specificity
Baseline	0.8645	0.8333	0.8936	0.6993	0.2246	0.8903	0.6941	0.3979	0.8715
iMSF	0.9231	0.9085	0.9389	0.8254	0.5093	0.959	0.9022	0.7101	0.996

As we can observe from Table 8, using multiple data sources greatly improves the performance in each case. This is because we not only learn from additional information from the current samples (when data sources other than MRI are available); we also utilize the information from other samples that are thrown away in the unimodal case.

Comparison with methods that throw out missing data

An intrinsic advantage of our iMSF method over throwing out missing data is that no sample will be wasted. The final learned model will be able to benefit from all the samples as long as one of the data sources is available. Also, unlike the one learned from a complete data set, our final model will be able to give the prediction for a newly arrived sample with any combination of the data sources. Still, it is interesting to investigate if utilizing all these additional information will be beneficial for the classification performance. Therefore, we extract the complete data set where each sample has all the four data sources (MRI, CSF, PET and proteomics) available. We then extract the classification results for the same 153 subjects from our iMSF method, such that the comparison can be made using the same sample pool. The results are summarized in Table 9.

Table 9.

Classification comparison of using multi-modality data (iMSF) and using the complete MRI + CSF + PET + Proteomics data. The classification is done on the same set of samples so that a fair comparison can be made. Leave-one-out is used and the accuracy, sensitivity and specificity are reported.

	AD/NC			AD/MCI			MCI/NC
	Accuracy	Sensitivity	Specificity	Accuracy	Sensitivity	Specificity	Accuracy	Sensitivity	Specificity
Baseline	0.8772	1	0.6316	0.7203	0.2105	0.9625	0.8081	0	1
iMSF	0.9825	0.9737	1	0.822	0.5263	0.9875	0.8485	0.5789	1

As we can observe from Table 9, by only utilizing 153 subjects (about 20% of the 780 subjects iMSF used), the baseline method results in very unsatisfactory performance. We can conclude that our method not only makes use of all the possible information, but also greatly improves classification performance.

Effects of different λ in the proposed iMSF

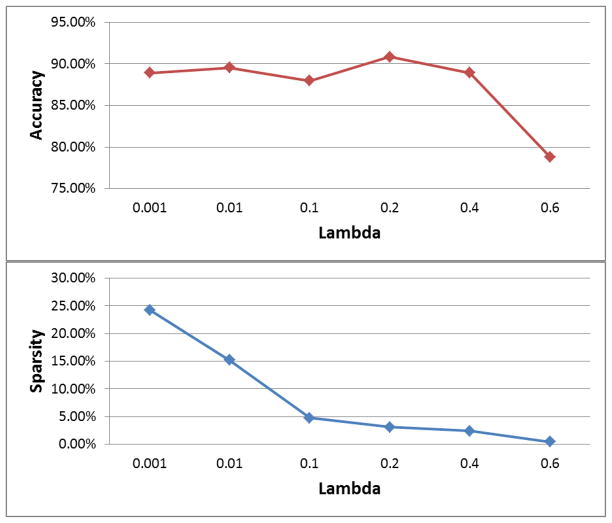
Here we use a particular example to illustrate how the results vary when different λ values are chosen in our proposed iMSF method in Figure 5. We use the AD/NC problem, and report leave-one-out results when we use different choices of λ values (0.001, 0.01, 0.1, 0.2, 0.4 and 0.6). As we can observe from the figure, as we increase λ, the number of features selected will gradually decrease, from about 25% of the features to 0.5%. We can also observe that the best choice of λ lies in the middle of the region (in this example 0.2). This justifies the advantage of our proposed ensemble system, since it bypasses the difficulty of selecting the parameters.

Figure 5.

Illustration of the results obtained using different λ in our proposed iMSF method. The AD/NC problem is used, and leave-one-out performance is reported. We vary the λ value from 0.001 to 0.6 (x-axis) and report the accuracy obtained (y-axis) in the top figure. In the bottom figure, we report the proportion of selected features (Sparsity, y-axis) when we increase λ from 0.001 to 0.6 (x-axis).

Contribution of iMSF in Model Ensemble

In this experiment, we demonstrate the benefits the iMSF method brought to the model ensemble. Using the “Learned” ensemble method discussed earlier as an example, we first remove all the iMSF models and then build the model ensemble using only the data completion methods. The comparison in terms of classification performance is summarized in Table 10.

Table 10.

Classification comparison of model ensembles with and without iMSF. Here the “Learned” method is used. 75% of the data is used as training; accuracy and sensitivity are reported.

	AD/NC		AD/MCI		MCI/NC
	Accuracy	Sensitivity	Accuracy	Sensitivity	Accuracy	Sensitivity
with iMSF	0.9026	0.8862	0.8401	0.315	0.893	0.5639
w/o iMSF	0.8905	0.8939	0.8228	0.1802	0.8238	0.2301

We can see from Table 10 that our iMSF models contribute significantly to our final model ensemble, especially for the more challenging tasks such as AD/MCI and MCI/NC.

The work reported here is related to ongoing research on structured sparse learning. We recently developed a prototype software package called “SLEP” (Sparse Learning with Efficient Projections) (Liu et al., 2009b). SLEP achieves state-of-the-art performance for many sparse learning models, such as Fused Lasso (Liu et al., 2010), Tree Lasso (Liu and Ye, 2010) and Overlapping Group Lasso (Yuan et al., 2011), and it has become one of the most popular sparse learning software packages. The SLEP tools have been applied successfully for biological image analysis (Ji et al., 2008), joint gene expression and network data analysis (Ji et al., 2009; Yuan et al., 2011), and even brain connectivity analysis in AD (Sun et al., 2009).

There are several possibilities for extending our current work. In this paper, we used numerical summary measures from MRI scans of 648 subjects, whose data were available in ADNI dataset. In some of our earlier studies (Hua et al., 2011), we used tensor-based morphometry to study baseline and longitudinal MRI scans in ADNI, and these could be added to the feature set in the future. In addition, the second phase of the ADNI initiative is now collecting data from diffusion tensor imaging, arterial spin labeling, and resting state functional MRI. Although each of these features is likely to help with classification and for predicting decline, the 3 new imaging modalities will not all be performed on the same subjects – in fact, each of the ADNI subjects will be scanned using only one of the 3 additional modalities, because it was not feasible to prolong the scanning session to include all three in every subject. Such a situation lends itself to the machine learning approach developed here, as there will be considerable joint information available about the relationships between the new modalities and the traditional biomarkers, but not in the same subjects.

Also, by combining various models produced with different parameters, or even models from different methods, the ensemble methods used here may become even more stable and robust. A natural question to ask is, can we add more models to improve performance? Ensemble learning (Dietterich, 2000) can boost performance in general machine learning problems. In the future, we plan to enrich our model set and add new models to tackle the incomplete data problem.

Table 3.

AD/MCI classification comparison of the ensemble methods (Voting, Uniform and Learned) and the other methods (Best and Average) in terms of accuracy, sensitivity and specificity when the training percentage varies from 1/2 to 3/4. In this experiment, a multi-source data including MRI, PET, Proteomics and CSF with 569 subjects in total.

Accuracy	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.8183	0.8177	0.8291	0.8278	0.8095
	66.7%	0.8288	0.8269	0.8337	0.8335	0.8182
	75.0%	0.8419	0.8298	0.8401	0.8401	0.8231
Sensitivity	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.5877	0.1965	0.2857	0.4339	0.2365
	66.7%	0.5926	0.2251	0.3017	0.4424	0.2598
	75.0%	0.5954	0.2218	0.315	0.4514	0.2631
Specificity	Training Size	Voting	Uniform	Learned	Best	Average
	50.0%	0.884	0.9916	0.9818	0.9924	0.9701
	66.7%	0.8953	0.9926	0.9804	0.9923	0.9722
	75.0%	0.9088	0.994	0.9818	0.9946	0.9743

APPENDIX

Choosing the number of repeated experiments

When we use a certain proportion of the data as training and the rest as testing, the major purpose of performing this split randomly several times is to reduce the effect of randomness and obtain a proper estimate. Here, we perform a simple experiment to demonstrate the effects of number of random splits. We use the MRI data source only applied to AD/NC classification. We use half of the data set as training and the rest as testing. 1~100 random training/testing splits are generated and the average classification accuracies are obtained for each number of random splits. The results are summarized in Table 11:

Table 11.

Effects of number of random splits on the obtained average performance. MRI is used for AD/NC classification, and different numbers (1 – 100) of training/testing partitions are generated. The average accuracies are obtained and reported.

Number of Splits	1	10	20	30	50	100
Accuracy	0.8667	0.8473	0.8409	0.8404	0.8421	0.843

As we can observe from Table 11, starting from 20 splits, the results become quite stable (the fluctuation is within 0.5%). Therefore, our choice of 30 times of repeated experiments provides a quite stable estimate of the overall performance.

Comparison with trace norm minimization

Recently, trace norm minimization has been proposed for missing data estimation (Cai et al., 2010; Candes and Tao, 2010). This can be effective even when a large amount of data is missing. Therefore, it will be interesting to see how this algorithm (singular value thresholding or SVT) performs in our particular setting. We acquire the SVT program online (http://svt.stanford.edu) and follow their suggestions for parameter setting. We use the classification problems AD/NC and MCI/NC as examples, and used 75% of total data set as training. The results are summarized in Table 12.

Table 12.

AD/NC and MCI/NC classification comparison of our proposed iMSF method and missing data estimation methods (Zero, EM, KNN and SVD) as well as the state-of-the-art matrix completion method SVT. We use a 75% training percentage and the accuracy, sensitivity and specificity are reported.

	AD/NC			MCI/NC
	Accuracy	Sensitivity	Specificity	Accuracy	Sensitivity	Specificity
iMSF	0.8879	0.8716	0.9092	0.8945	0.716	0.9967
Zero	0.8649	0.8806	0.8513	0.8429	0.3106	0.9963
EM	0.8896	0.8854	0.8954	0.8073	0.1653	0.9903
KNN	0.8732	0.882	0.8666	0.8139	0.1819	0.9935
SVD	0.8593	0.8578	0.8623	0.8154	0.2017	0.9893
SVT	0.5658	0.5938	0.5373	0.8136	0.2893	0.9649

As we have discussed before, in this particular setting with block-wise missing pattern, most missing value estimation method we applied here do not out-perform simply filling the missing entries with zeros. We can also observe that in our case, the SVT algorithm does not yield very stable results. In the MCI/NC setting, it is comparable to other imputation methods, while in the AD/NC case, the resulting accuracy is very low (less than 60%) compared to others.

Comparison of Computational Time

Here we provide some brief discussions on the differences in computational times between our iMSF method and the data completion methods. We use the “Zero” method as an example, since its data completion step is very efficient. We perform experiments using both methods on different partitions of training/testing data, and the average computation time is reported in Table 13. The experiments are performed using Matlab R2010b on a Windows 7 desktop machine with Intel Core2 2.66GHz processor.

Table 13.

Computational time comparison between iMSF and the data completion method “zero” in different problem settings. The time is presented in seconds.

	AD/NC	AD/MCI	MCI/NC
iMSF	3.4733	3.6571	2.4879
Zero	5.2886	11.4902	6.1825

We can see from Table 13 that iMSF generally runs faster in these problems. This is because in the training and testing steps of iMSF, only the selected features are used; while in the Zero method, after all missing data is filled with zeros, the complete feature set, which is much larger than the one used in the iMSF method, takes longer training and testing time (we use random forest to train the final model in this paper).