Whereas normalization methods for mRNA-Seq data have been properly described, there has been no unbiased evaluation of normalization methods on microRNA-Seq data. Furthermore, it was not known whether the normalization methods used for mRNA-Seq data can be adequately adapted to process microRNA-Seq data. This paper evaluates seven commonly used normalization methods for high-throughput data of microRNA-Seq data. The authors concluded that Lowess normalization and quantile normalization are recommended for normalizing microRNA-Seq data, whereas the Trimmed Mean Method, which is most appropriate for RNA-Seq data, should be used with caution when applied to miRNA-Seq data.
Keywords: microRNA-Seq, next generation sequencing, statistical normalization, high-throughput data analysis
Abstract
Simple total tag count normalization is inadequate for microRNA sequencing data generated from the next generation sequencing technology. However, so far systematic evaluation of normalization methods on microRNA sequencing data is lacking. We comprehensively evaluate seven commonly used normalization methods including global normalization, Lowess normalization, Trimmed Mean Method (TMM), quantile normalization, scaling normalization, variance stabilization, and invariant method. We assess these methods on two individual experimental data sets with the empirical statistical metrics of mean square error (MSE) and Kolmogorov-Smirnov (K-S) statistic. Additionally, we evaluate the methods with results from quantitative PCR validation. Our results consistently show that Lowess normalization and quantile normalization perform the best, whereas TMM, a method applied to the RNA-Sequencing normalization, performs the worst. The poor performance of TMM normalization is further evidenced by abnormal results from the test of differential expression (DE) of microRNA-Seq data. Comparing with the models used for DE, the choice of normalization method is the primary factor that affects the results of DE. In summary, Lowess normalization and quantile normalization are recommended for normalizing microRNA-Seq data, whereas the TMM method should be used with caution.
INTRODUCTION
The next generation sequencing (NGS) technology has been widely used recently to study a variety of biological problems, such as quantifying the mRNA transcripts expression (RNA-Seq), chromosome DNA–DNA bound protein interactions (CHIP-Seq), and small microRNA expression. It has been shown that NGS provides higher reproducibility, wider range, and better quality of data, compared with the microarray method. Moreover, the open-platform of NGS enables discoveries of new mRNA transcripts and new microRNA strands.
Mammalian microRNAs are small RNAs of ∼22 nt in length (Bartel 2004). They are regarded to destabilize target mRNAs or inhibit translation machinery by binding to specific regions of mRNA transcripts such as 3′ UTRs (Baek et al. 2008). Though new microRNAs are being discovered continuously, the total number of known microRNAs is much smaller than mRNAs. For example, so far there are <1000 annotated microRNAs in human that are expected to regulate ∼30% of genes. It has been shown that microRNAs act as “micro-regulators” to fine-tune gene expression, and are involved in various diseases such as cancers and immune-related diseases (Fabbri et al. 2007; O'Connell et al. 2010). microRNA-Seq profiling can directly yield information of the abundance of microRNAs under certain conditions, and thus infer the regulatory outcome of the microRNAsome (Creighton et al. 2009; Lu et al. 2009; Ramsingh et al. 2010; Schulte et al. 2010).
It is critical to normalize the different libraries of microRNA-Seq data due to the fact that different total tag counts are generated in different microRNA-Seq libraries. One could expect microRNA-Seq normalization methods could be adapted from the mRNA-Seq normalization methods. However, currently there are only a few software packages that are designed to normalize mRNA-Seq data prior to the test of differential expression (DE), such as the Trimmed Mean Method in edgeR (Robinson et al. 2010) and DEseq that uses a negative binomial model (Robinson and Oshlack 2010), and there are only a few statistical studies evaluating normalization methods in mRNA-Seq data (Bullard et al. 2010; Srivastava and Chen 2010). Contrary to mRNA-Seq, there has been no unbiased evaluation of normalization methods on microRNA-Seq data. Moreover, it remains questionable whether the normalization method used for mRNA-Seq data can be adequately adapted to process microRNA-Seq data, given the fact that the total number of mRNA transcripts is magnitudes larger than the total number of microRNA strands.
To answer these questions, we systematically evaluated seven commonly used normalization methods for high-throughput data, namely global normalization, Lowess normalization, Trimmed Mean Method (TMM), quantile normalization, scaling normalization, variance stabilization (VSN), and invariant method (INV). These methods make different assumptions about the true biological difference and the random noise in order to be able to estimate the systematic variation. They can be classified into two categories, according to the application of linear scaling or not. (1) The first category includes scaling, global, Lowess, and TMM. Scaling normalization assumes the ranges of data are the same and that the noise and the stochastic variations of microRNAs are proportional to the signal intensity (Smyth et al. 2003). Global normalization is another linear scaling approach that scales all the data of the experimental condition against the control condition by a factor of the difference in the means of two data (Smyth et al. 2003). Lowess normalization does not use a global scaling factor; instead, it calculates local scaling factors within a certain window size (Smyth et al. 2003). TMM, a more recent normalization method applied to mRNA-Seq data, also assumes the majority of the mRNAs in NGS output are similar, except the data points that lie within the extreme M-value and A-value ranges. It derives a simple scaling factor after trimming the data points located in extreme M-value and A-value ranges (Robinson et al. 2010). (2) The second category includes quantile, VSN, and INV. Quantile normalization is nonscaling and assumes that the overall distribution of signal intensity does not change (Bolstad et al. 2003). VSN assumes that most microRNAs do not change and transform the data such that the transformed variance is constant among different expression levels. Therefore, it allows better precision in low expression regions, which generally suffer from greater variance (Huber et al. 2002). INV assumes that a subpopulation of expressed microRNAs does not change, and it learns a set of “invariants” through algorithms, instead of assigning “housekeeping genes” subjectively (Perkins et al. 2007; Pradervand et al. 2009).
We carried out the pairwise comparisons on two publicly available microRNA-Seq profiling data sets. One is the comparison between activated versus inactivated natural killer cells (abbreviated as F-data) (Fehniger et al. 2010), and the other is the comparison between pro-B cells and pre-B cells (abbreviated as K-data) (Kuchen et al. 2010). These data sets are chosen because of the availability of quantitative PCR results for the assessment of sensitivity and specificity. We used a combination of criteria to evaluate the performance of each normalization method, including metrics such as mean square error (MSE) and Kolmogorov-Smirnov (K-S) statistic, validation from quantitative PCR data, and the abnormality diagnosis based on the results of DE test.
RESULTS
Necessity of normalization beyond simple tag count normalization
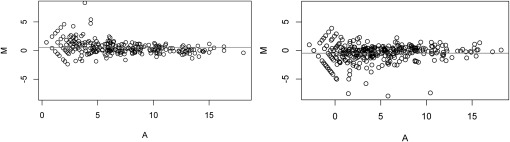
MA-plot is a plot of log-intensity ratios (M-values) versus log-intensity averages (A-values). It is commonly used to illustrate the dependency on intensities in the high-throughput data. Currently, most studies use a simple scaling factor, which is equal to the ratio of summed tag counts between two conditions, to normalize the experimental lane to the control lane. Using MA-plots, we evaluated such normalization on the two public data sets (see Materials and Methods), denoted as F-data (Fehniger et al. 2010) and K-data (Kuchen et al. 2010). Figure 1 shows the distribution of M-values between two comparison samples after the standard normalization procedure of accounting for the total tag counts among known, detectable microRNAs. The centers of the distributions of M-values are significantly deviated from zero, with a median of 0.57 for F-data, and −0.47 for K-data, indicating that additional normalization procedure is needed. In the following sections, we systematically evaluate seven normalization methods, namely global normalization, Lowess normalization, TMM, quantile normalization, scaling normalization, VSN, and INV. These methods were previously applied to high-throughput data, such as microarray and mRNA-Seq data.
FIGURE 1.
MA-plots after simple tag count normalization. MA-plots show the distribution of microRNAs in paired samples of comparison after the simple total tag count normalization among the known, detectable microRNAs. The horizontal lines denote the mean of the M-values, which are significantly deviated from zero in both data sets, with a median of 0.57 for F-data (left) and −0.47 for K-data (right).
Effect of normalization on data distribution
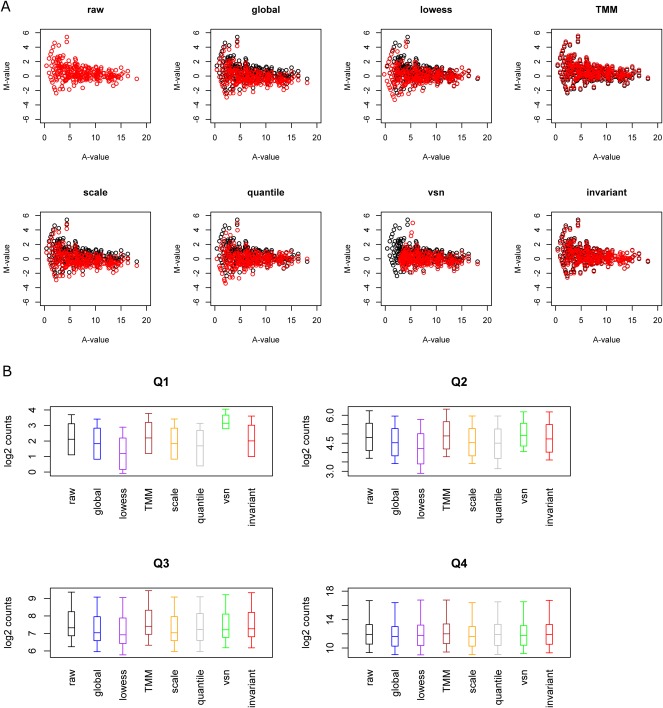
We first examined the effects of different normalization on the distribution of data using the MA-plots that are commonly done in microarray analysis, exemplified by F-data. As shown in Figure 2A, the greatest change among MA data occurs in global normalization, Lowess normalization, scaling, quantile, and VSN. Global normalization shifts the center of M-values of data to 0, and thus the observed changes on all levels of A-values are expected. Similarly, the scaling method enforces equal median absolute deviations in both M- and A-values. Lowess, quantile, and VSN present bigger changes in normalized log2 tag counts in the lower A-value range (Fig. 2A,B). Lowess takes account of local weighting to adjust the data points, and quantile normalization assumes the quantile distribution of data in two conditions is the same. They both redistribute normalized M-values around M-values prior to normalization, especially at the lower level of A-values. On the other hand, VSN aims to have uniform variance across different expression levels, and shifts M-values at lower levels of A-values toward a higher A-value region (Fig. 2B). Although less obvious, a similar pattern was observed in the K-data (Supplemental Fig. 1), except that many normalization methods pull the M-values toward more positive directions due to the fact that the control condition has larger mean M-value (Fig. 1B).
FIGURE 2.
Effect of normalization on F-data distribution. (A, top) MA-plots before and after applying different normalization schemes to F-data described in the text (Fehniger et al. 2010). Except the raw data plot, in all the other MA-plots, black circles are data before normalization, and red circles are after normalization. (B, bottom) Box plots list the transformed log2 counts in the treatment condition after normalization (except raw data) separated by quartiles: Q1, Q2, Q3, and Q4. Q1 is the lowest quartile and Q4 is the highest quartile. The color codes for box plots from left to right are as follows: black (raw data), blue (global normalization), purple (Lowess normalization), brown (TMM normalization), orange (scaling normalization), gray (quantile normalization), green (VSN normalization), and red (INV normalization).
Evaluation of normalization based on empirical statistics
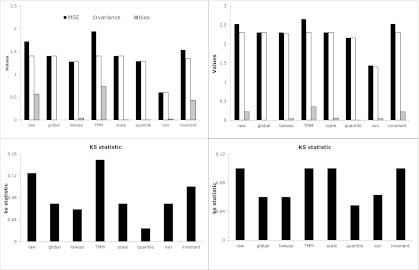
MSE is a comparison criterion that is widely used to measure statistical models, such as the alternative normalization methods in this study and others (Xiong et al. 2008). MSE can be decomposed into the summation of variance and the square of bias. Small MSE indicates better normalization overall, within which variance is a metric for precision and bias is a measurement of accuracy. In this report, we use MSE to calculate the difference between M-values and the center of M-values. We present the results using this metric to compare all normalization methods on both F-data and K-data (Fig. 3). As mentioned before, the average of M-values in the data without normalization is deviated from 0, resulting in bias in MSE. Expectedly, global normalization eliminates the bias of M, resulting in smaller MSE. Using the MSE of global normalization as the reference point, Lowess, quantile, and VSN normalizations consistently produce smaller MSE. These smaller MSEs can be decomposed into smaller variances and smaller biases comparing with those of unnormalized data. On the other hand, TMM, a method that trims data strongly affected by treatment conditions, and INV are worse than global normalization as evidenced by even greater MSEs than no normalization. TMM also produces the largest biases among all, most likely because it throws away valuable data information through trimming M-values by 30% and A-values by 5% by default (Robinson et al. 2010). Although this approach could be beneficial while dealing with thousands of mRNAs in the mRNA-Seq normalization, it can be harmful among the small body of hundreds of microRNAs.
FIGURE 3.
Evaluation of normalization methods with empirical statistics. (Top) Comparison of mean squared errors (or MSE, black bar), as well as the two decomposed forms of MSE, variance (empty bar) and bias (gray bar), in various normalization methods. (Bottom) Comparison of K-S statistics calculated from the M-values before and after different normalization methods. The left plot is based on F-data and the right plot is based on K-data.
The K-S test is a goodness-of-fit test to measure similarities between two distributions by counting the largest deviation between the two accumulative distributions. Based on the rationale that an effective normalization method would generate two similar distributions and thus a small K-S statistic, we also measured the K-S statistics that were calculated from the M-values before and after different normalizations on both data sets and show the results in Figure 3. Similar results to the MSEs are observed. Global normalization does decrease the K-S statistic compared with no normalization. Lowess and quantile normalization produce smaller or equal K-S statistics relative to the global normalization. Both VSN and scaling methods give similar K-S values to the global normalization. On the other hand, TMM and INVs consistently generate larger K-S statistics relative to the global normalization. Similar to the largest MSE from TMM, K-S statistics from TMM is also the largest.
Evaluation of normalization with quantitative PCR results
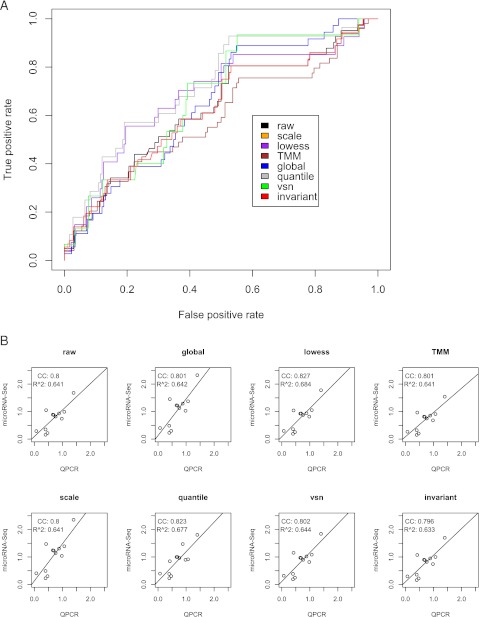
Quantitative PCR (QPCR) is an effective alternative method to assess the expression profile of microRNAs. Over 100 QPCR experiments were conducted in parallel with the microRNA-Seq results from F-data, making them an ideal set to evaluate gains in sensitivity and specificity after normalization. The “true positives” from QPCR results were assigned to microRNAs with at least twofold changes in the activated versus inactivated states. We found there is more noise in the miRs that are of low tag counts in the microRNA-Seq data, when comparing microRNA-Seq DE data (twofold cutoff) with the assumed “truth” of QPCR DE data (twofold cutoff). Both false positive and false negative microRNAs have lower tag counts (data not shown). To compare the sensitivity and specificity of the different methods, we obtained standard receiver operating characteristic (ROC) plots where the area under the curves can be used for evaluations (Fig. 4A). Some normalization methods improved the sensitivity and specificity compared with no normalization, whereas others did not. Consistent with the results of MSE and K-S statistics, quantile and Lowess normalization perform the best, followed by VSN, global, and scaling normalization, all of which are better than no normalization. INV appears to have a similar ROC curve to that of no normalization. Clearly, TMM has the worst under-curve coverage even when compared with no normalization. This result is consistent with the conclusions based on MSE and K-S statistics.
FIGURE 4.
Evaluation of normalization methods with QPCR results. (A) ROC plot of sensitivity and specificity of the various normalization methods, based on F-data. The color codes of ROC curves for the normalization methods are the same as those in Figure 2. A “true difference” of value 1 is assigned to the microRNAs whose QPCR expression ratios are at least twofold different between activated and inactivated state, but 0 otherwise. A “predicted difference” is the absolute value of the normalized M-value of microRNA-Seq tag counts. Note: the ROC curves of the scaling and global normalization methods are identical and the global normalization (blue) is superimposed on the scaling method (orange). (B) Linear regression of microRNA-Seq log2 fold change results versus QPCR log2 fold change results based on K-data, over various normalization methods. The correlation coefficient (CC) and R-square (R^2) are two metrics to measure the correlation between the two types of data. The lines are the best linear regression fits to the data. For comparison, all x- and y-axes are uniformized to the same scales.
The QPCR results are available for 12 microRNAs in the K-data. Though the ROC plot is not possible, correlation study of microRNA-Seq data versus QPCR of the 12 microRNAs is achievable, as shown in Figure 4B. As expected, global normalization performs slightly better than no normalization. It has better correlation coefficient (CC) and better R-square (R^2) value from a linear regression between log2 transformed microRNA-Seq data and log2 transformed QPCR data. Lowess normalization has the best correlation among all, with a CC = 0.677 and R^2 = 0.459 from the linear regression, closely followed by quantile normalization which has a CC of 0.652 and R^2 of 0.426. VSN produces slightly better CC and R^2, compared with global normalization. TMM and INVs do not show much difference in correlation from no normalization, whereas scaling had the worst correlations among all methods. Overall, the correlation results of K-data are also consistent with the previous conclusions based on MSE and K-S statistics, in the sense that Lowess and quantile normalization have the highest correspondence to the QPCR results.
Test of differential expression
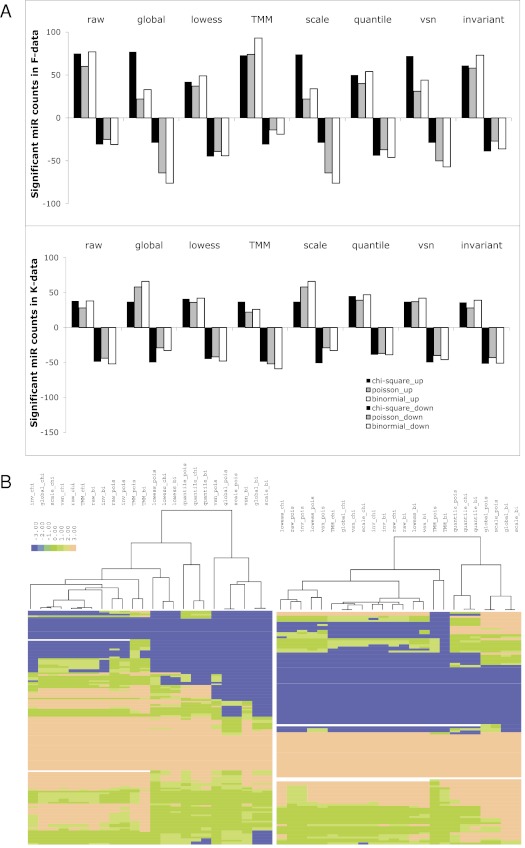
It was shown in mRNA-Seq studies that normalization is a primary factor affecting the test of DE (Taslim et al. 2009; Anders and Huber 2010; Bullard et al. 2010; Robinson and Oshlack 2010). We therefore also used the results in DE to reflect the performance of the normalization methods. Based on previous studies (Taslim et al. 2009; Bullard et al. 2010; Robinson and Oshlack 2010), we used three different tests of DE, namely χ2 test, Poisson distribution, and binomial distribution. We define significantly changed microRNAs as those that have P-values <0.05 after Bonferroni corrections, and we present the DE test results in Figure 5. Comparing with all other methods, TMM has an abnormally large amount of up-regulated microRNAs versus an abnormally small amount of down-regulated microRNAs in F-data, and the least amount of up-regulated microRNAs versus the most amount of down-regulated microRNAs in K-data, reflecting the distortion of tags in sample pairs with the scaling method (Fig. 5A). Global normalization and scaling normalization have similar total numbers of differentially expressed genes, as expected. Both Poisson distribution and binomial distribution have assumptions that there is an equal probability of individual microRNAs within normalized, paired samples, therefore the DE counts from Poisson test and binomial test are similar to each other, compared with those from the χ2 test (Fig. 5A). Perhaps most importantly, heat maps reveal that different DE results under the same normalization method tend to cluster closer, suggesting that variations within the same normalization method but different DE tests are smaller than variations within the same DE test but different normalization methods (Fig. 5B). This result confirms that the normalization method, rather than the model of DE, is a primary factor affecting the results of DE.
FIGURE 5.
Test of differential expression based on different normalizations. (A) Bar graphs show the results of DE based on χ2/Fisher's test (chi-square), Poisson model (poisson), and binomial model (binomial) for different normalization schemes. The color codes for the tests of DE are as follows: black bar (χ2), gray bar (Poisson), and empty bar (binominal). The normalization methods upon which the DE tests are performed are listed above the bars. “Up-regulated” microRNAs are plotted above y = 0 and “down-regulated” microRNAs below y = 0. The top plot is from F-data, and the bottom plot from K-data. (B) Heat maps show the hierarchical clustering results of all significant microRNAs that are defined in A. The values are transformed from P-values of specific microRNAs. Blue color represents down-regulation whereas brown color represents up-regulation. pois, Poisson model; bi, binomial model; and chi, χ2/Fisher's test.
DISCUSSION
Analyzing microRNA profiles with NGS is becoming a new trend of microRNA-related discoveries in many different organisms. The high volume and digitized information make microRNA-Seq highly competitive to the probe-based microRNA-array method. It is generally believed that statistical normalization is beneficial compared with no normalization. So far, most normalizations for RNAs generated by NGS use simple total tag count normalization to remove differences in sequencing depths between libraries. There is an urgent need to propose more sophisticated normalization methods. However, currently most microRNA-Seq experiments do not use biological replicates, thus impeding the estimation of true biological variations. This problem will likely disappear in a year or two due to the competition of lowering the cost of deep sequencing. Nevertheless, the library normalization issue still needs to be addressed before any test of DE. It seems reasonable to assume that the majority body of the microRNAs are expressed similarly, on the closely related biological samples, such as the activated versus inactivated natural killer cells and pro-B cells versus pre-B cells that are exemplified in this study. Normalization could remove the technical artifacts arising from unintended noise; however, it maintains the true differences between the samples.
These above normalization methods and their assumptions were evaluated by multiple independent data sets on several levels. Although each level of evaluation was based on some specific assumptions, the consensus of multiple levels of evaluations helps to draw unbiased conclusions. First, we used the generic, empirical statistics MSE and K-S statistics to measure the fitness of normalization methods. The MSE metric is based on the rationale that better normalization methods should create small variations and trivial bias within the data. And K-S statistics is based on the assumption that good normalization methods could maximize the distribution similarities between two data sets. Due to these reasons, the MSE and K-S statistics may bias toward the normalization methods whose assumptions favor to minimize them (such as quantile normalization), as observed and discussed by others (Xiong et al. 2008). These empirical metrics need to be used together with other evaluation criteria to draw unbiased conclusions. We did so using two other approaches: QPCR validation and results from test of DE. QPCR is an orthogonal, quantitative method to RNA-Seq. We assumed that a better normalization method for the microRNA-Seq data should yield better correlations between the QPCR and microRNA-Seq, and evaluated the methods with ROC plots and linear regression. We found that Lowess and quantile normalizations are consistently superior to other methods, whereas TMM normalization performs the poorest. Lastly, we also compared results of DE, as ways to reveal the consequences of normalization and diagnose abnormalities in the normalized data. These evaluations gave consistent results over all. Lowess and quantile normalizations are the best among tested methods, whereas TMM behaved abnormally and extremely. Similar to our results, Bullard and colleagues also found that, in mRNA-Seq experiments, the quantile-based method yields better concordance with qRT-PCR methods than the linear total scaling method. Our study supports the speculation on the advantage of quantile normalization over scaling in small RNA-Seq (Bullard et al. 2010), while discouraging the usage of TMM application to microRNA-Seq as recently proposed (McCormick et al. 2011). More broadly speaking, microRNA-Seq data are a portion of the bigger data set that is generated from the small RNA (<30 nt in length) sequencing. Small RNA libraries also include other RNAs, such as siRNA and piRNA. We speculate that Lowess and quantile normalization are also suitable for other small RNA deep sequencing data, conditional on that the total species in the small RNA library are within thousands, instead of tens of thousands (the range that TMM method is good for). It will be of interest to test this once in the future.
Due to the high-cost of NGS, most experiments are done without replicates currently, thus we limit this study to between-library normalization under no replicate condition. We intend to evaluate normalizations under multiple biological and technical replicates in the future. Additionally, mRNA-Seq is known to have gene-length bias toward genes of larger lengths, and the within-library normalization to normalize individual genes within the same libarary was proposed (Oshlack and Wakefield 2009). However, we found this length-variation effect was trivial in microRNA-Seq due to the small variation of mature microRNA lengths (data not shown). More sophisticated models such as mixed-effect models and multiple-step normalization will also be valuable to explore when the appropriate experimental designs are made prior to the microRNA-Seq and when the cost yield ratio of NGS is sufficiently economical.
MATERIALS AND METHODS
microRNA-Seq data
Raw tag count and relevant data are obtained from their online sources (Fehniger et al. 2010; Kuchen et al. 2010). The inactivated versus activated natural killer cell data, including the microRNA-Seq and microarray data, are downloaded from: http://genome.cshlp.org/content/20/11/1590/suppl/DC1. The pro-B cells versus pre-B cells data are downloaded from the record GSE21630 in the Gene Expression Omnibus (GEO): http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE21630. Additional QPCR data were courtesy from authors.
Normalization methods used in the study
Existing normalization methods were implemented in R through installing the appropriate R and Bioconductor libraries. Limma package was used for MAD-scaling, quantile, and VSN normalization (Smyth 2005). LPE package was used for Lowess normalization (Jain et al. 2003). An implementation of invariant normalization was modified from the original R script (Pradervand et al. 2009) at http://www.unil.ch/dafl/page58744.html, which selects invariants and normalizes arrays with robust regression. The edgeR package was used for TMM normalization (Robinson and Oshlack 2010; Robinson et al. 2010). MSE was defined as the averaged sum square of M-values on all nonzero data points, and variance is the averaged, squared deviation of M-values from the mean M-values, on all nonzero data points.
ROCR package in R was used to generate ROC plots. The “true differences” based on QPCR results are assigned to the microRNAs whose QPCR expression ratios are at least twofold different between activated and inactivated state. And the “predicted difference” is actually the absolute value of the normalized M-value (or, an absolute value of the Z-score calculated from the M-value) of microRNA-Seq tag counts.
Test of differential expression
Test of DE was modeled by χ2/Fisher's exact test, binomial test, and Poisson tests, similar to others (Taslim et al. 2009; Bullard et al. 2010; Robinson and Oshlack 2010). Briefly, in the χ2/Fisher's exact test, each microRNA is associated with a 2 × 2 contingency table, with the tag counts of specific microRNAs in control versus treatment condition, as well as with the summed tag counts of all other microRNAs in the population. If all tag counts are above five, χ2 test was applied. Otherwise, Fisher's exact test was applied for accuracy. A microRNA is called “up-regulated” (or “down-regulated”) when the observed tag counts are greater (or less) than the expected tag counts, with a Bonferroni-corrected P-value <0.05. The binomial test was carried out by assuming each microRNA is independent from each other, and follows the binomial distribution bin (p = 0.5, n = [n_con + n_treat]), where p is the expected probability of tags appearing in either the control sample or the treatment sample, and n is the summation of tag counts for that microRNA in the control sample (n_con) and treatment sample (n_treat). The same P-value criteria were applied as the χ2/Fisher's exact test. Poisson test was done similarly to the binomial test.
To visualize the overlapping microRNAs that were called “differentially expressed” in all the above three DE tests, over the seven different normalization methods, a perl script was written to take the union microRNAs in all conditions. Hierarchical clustering and the heat map visualization were then done by Cluster (http://rana.lbl.gov/EisenSoftware.htm; Eisen et al. 1998), based on the transformed P-values. For simplicity, a significant Bonferroni-corrected P-value is assigned a value of −3/+3 (down/up-regulated); a nonsignificant P-value is −1.5/+1.5 (down/up-regulated); and a Bonferroni-corrected P-value of 1 is assigned −0.5/+0.5 in the color coding.
SUPPLEMENTAL MATERIAL
Supplemental material is available for this article.
ACKNOWLEDGMENTS
This work was supported by the NIGMS Large Scale Collaborative “Glue” Grant U54 GM069338 to S.S. We thank Dr. Chris Benner for valuable discussion. We thank Dr. Estelle Wall and Dr. Jason Nathanson for the communication about the microRNA-Seq library preparation process.
Footnotes
Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.030916.111.
REFERENCES
- Anders S, Huber W 2010. Differential expression analysis for sequence count data. Genome Biol 11: R106 doi: 10.1186/gb-2010-11-10-r106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek D, Villén J, Shin C, Camargo FD, Gygi SP, Bartel DP 2008. The impact of microRNAs on protein output. Nature 455: 64–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartel DP 2004. MicroRNAs: Genomics, biogenesis, mechanism and function. Cell 116: 281–297 [DOI] [PubMed] [Google Scholar]
- Bolstad BM, Irizarry RA, Astrand M, Speed TP 2003. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 19: 185–193 [DOI] [PubMed] [Google Scholar]
- Bullard JH, Purdom E, Hansen KD, Dudoit S 2010. Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. BMC Bioinformatics 11: 94–107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Creighton CJ, Reid JG, Gunaratne PH 2009. Expression profiling of microRNAs by deep sequencing. Brief Bioinform 10: 490–497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisen MB, Spellman PT, Brown PO, Botstein D 1998. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci 95: 14863–14868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabbri M, Ivan M, Cimmino A, Negrini M, Calin GA 2007. Regulatory mechanisms of microRNAs involvement in cancer. Expert Opin Biol Ther 7: 1009–1019 [DOI] [PubMed] [Google Scholar]
- Fehniger TA, Wylie T, Germino E, Leong JW, Magrini VJ, Koul S, Keppel CR, Schneider SE, Koboldt DC, Sullivan RP, et al. 2010. Next-generation sequencing identifies the natural killer cell microRNA transcriptome. Genome Res 20: 1590–1604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber W, von Heydebreck A, Sültmann H, Poustka A, Vingron M 2002. Variance stabilization applied to microarray data calibration and to the quantification of differential expression. Bioinformatics (Suppl1) 18: S96–S104 [DOI] [PubMed] [Google Scholar]
- Jain N, Thatte J, Braciale T, Ley K, O'Connell M, Lee JK 2003. Local-pooled-error test for identifying differentially expressed genes with a small number of replicated microarrays. Bioinformatics 19: 1945–1951 [DOI] [PubMed] [Google Scholar]
- Kuchen S, Resch W, Yamane A, Kuo N, Li Z, Chakraborty T, Wei L, Laurence A, Yasuda T, Peng S, et al. 2010. Regulation of microRNA expression and abundance during lymphopoiesis. Immunity 32: 828–839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu YC, Smielewska M, Palakodeti D, Lovci MT, Aigner S, Yeo GW, Graveley BR 2009. Deep sequencing identifies new and regulated microRNAs in Schmidtea mediterranea. RNA 15: 1483–1491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick KP, Willmann MR, Meyers BC 2011. Experimental design, preprocessing, normalization and differential expression analysis of small RNA sequencing experiments. Silence 2: 2 doi: 10.1186/1758-907X-2-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Connell RM, Rao DS, Chaudhuri AA, Baltimore D 2010. Physiological and pathological roles for microRNAs in the immune system. Nat Rev Immunol 10: 111–122 [DOI] [PubMed] [Google Scholar]
- Oshlack A, Wakefield MJ 2009. Transcript length bias in RNA-seq data confounds systems biology. Biol Direct 4: 14 doi: 10.1186/1745-6150-4-14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perkins DO, Jeffries CD, Jarskog LF, Thomson JM, Woods K, Newman MA, Parker JS, Jin J, Hammond SM 2007. MicroRNA expression in the prefrontal cortex of individuals with schizophrenia and schizoaffective disorder. Genome Biol 8: R27 doi: 10.1186/gb-2007-8-2-r27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pradervand S, Weber J, Thomas J, Bueno M, Wirapati P, Lefort K, Dotto GP, Harshman K 2009. Impact of normalization on miRNA microarray expression profiling. RNA 15: 493–501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsingh G, Koboldt DC, Trissal M, Chiappinelli KB, Wylie T, Koul S, Chang LW, Nagarajan R, Fehniger TA, Goodfellow P, et al. 2010. Complete characterization of the microRNAome in a patient with acute myeloid leukemia. Blood 16: 5316–5326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson MD, Oshlack A 2010. A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol 11: R25 doi: 10.1186/gb-2010-11-3-r25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson MD, McCarthy DJ, Smyth GK 2010. edgeR: A Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26: 139–140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulte JH, Marschall T, Martin M, Rosenstiel P, Mestdagh P, Schlierf S, Thor T, Vandesompele J, Eggert A, Schreiber S, et al. 2010. Deep sequencing reveals differential expression of microRNAs in favorable versus unfavorable neuroblastoma. Nucleic Acids Res 38: 5919–5928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth GK. 2005. Limma: Linear models for microarray data. In Bioinformatics and computational biology solutions using R and bioconductor (ed. R Gentleman et al.), pp. 397–420. Springer, New York. [Google Scholar]
- Smyth GK, Yang YH, Speed TP 2003. Statistical issues in microarray data analysis. Methods Mol Biol 224: 111–136 [DOI] [PubMed] [Google Scholar]
- Srivastava S, Chen L 2010. A two-parameter generalized Poisson model to improve the analysis of RNA-seq data. Nucleic Acids Res 38: e170 doi: 10.1093/nar/gkq670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taslim C, Wu J, Yan P, Singer G, Parvin J, Huang T, Lin S, Huang K 2009. Comparative study on ChIP-seq data: Normalization and binding pattern characterization. Bioinformatics 25: 2334–2340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong H, Zhang D, Martyniuk CJ, Trudeau VL, Xia X 2008. Using Generalized Procrustes Analysis (GPA) for normalization of cDNA microarray data. BMC Bioinformatics 9: 25 doi: 10.1186/1471-2105-9-25 [DOI] [PMC free article] [PubMed] [Google Scholar]