Abstract
Quantification of nerve fibers in peripheral and central nervous systems is important for the understanding of neuronal function, organization and pathological changes. However, current methods to quantify nerve fibers are resource-intensive and often provide an indirect measurement of nerve fiber density. Here, we describe an automated and efficient method for nerve fiber quantification, which we developed by making use of widely available software and analytical techniques, including Hessian-based feature extraction in NIH ImageJ and line intensity scan analysis. The combined use of these analytical tools through an automated routine enables reliable detection and quantification of nerve fibers from low magnification, non-uniformly labeled epifluorescence images. This allows for time-efficient determination of nerve density and also comparative analysis in large brain structures, such as hippocampus or between various regions of neural circuitry. Using this method, we have obtained accurate measurements of cholinergic fiber density in hippocampus and a large area of cortex in mouse brain sections immunolabeled with an antibody against the vesicular acetylcholine transporter (VAChT). The density values are comparable among animals tested, showing a high degree of reproducibility. Because our method can be performed at relatively low cost and in large tissue sections where nerve fibers can be labeled by various antibodies or visualized by expression of reporter proteins, such as green fluorescent protein in transgenic mice, we expect our method to be broadly useful in both research and clinical investigation. To our knowledge, this is the first method to reliably quantify nerve fibers through a rapid and automated protocol.
Keywords: Hessian-based feature extraction, line intensity scan analysis, epifluorescence image, cholinergic nerve fiber density, cortex, hippocampus
1. Introduction
Neurons are connected to each other and function through a vast network of circuits made up of axons and dendrites. In the central nervous system (CNS), these axons and dendrites, also called nerve fibers, are either locally distributed or travel for long distances across different brain regions, such as cortico-cortical interconnections between the left and right hemispheres (Nieuwenhuys et al., 1998). Current research has revealed numerous subtypes of nerve fibers expressing distinct cell markers. The fiber densities of individual subtypes vary significantly in different regions of the brain, reflecting physiological function of the regions and circuit strength, as well as aging and pathological changes. Various diseases, such as autosomal dominant cerebellar ataxia, amyotrophic lateral sclerosis (ALS), Alzheimer’s disease (AD), Huntington’s disease (HD) and Parkinson’s disease (PD) are known to be associated with pathological changes in nerve fiber density (Geula and Mesulam, 1996; Li et al., 2009; Schols et al., 2004; Tandan and Bradley, 1985; Vonsattel and DiFiglia, 1998). Thus, it is necessary to develop efficient tools for the quantitative assessment of nerve fiber density as it provides important insight into physiological functions as well as disease development and recovery.
However, quantitative determination of nerve fiber density is challenging, especially for measuring nerve fibers in large areas of tissue sections. The traditional way of counting fibers manually via grid-based methods is both time consuming and labor intensive. In addition, fluorescence immunolabeling and transgenic expression of reporter proteins, such as green fluorescent protein (GFP) are commonly used in modern research, which greatly improve the identification and visualization of specific types of nerve fibers.
However, these approaches have introduced new challenges for nerve fiber quantification. Often, immunolabeling experiments are done using relatively thick tissue sections. For example, free-floating sections are usually 25 to 50 µm-thick, which retain good spatial orientation of nerve fibers in large regions as well as reduce the number of sampling sections. However, immunofluorescence labeling is often non-uniform in these sections. Furthermore, images taken from common epifluorescence microscopes from relatively thick sections are often blurred due to out-of-focal-plane fluorescence signals, making distinction of fine nerve fibers difficult. While thinner tissue sections, such as 2–7 µm-thick sections could limit blurred fluorescence and uneven staining, it is difficult to determine the spatial orientation of nerve fibers. To obtain sample regions that are equivalent to those of thick sections, researchers would have to increase the number of sections processed, which would consume more labor and time. For density measurement of fluorescently labeled nerve fibers in thicker sections, confocal microscopy is generally used to obtain sharp images of nerve fibers, which requires expensive equipment and highly trained personnel. Further, confocal images are often limited to small areas in tissue sections.
Recently, in a study investigating the effect of nerve growth factors on spinal afferent sprouting, a computer-assisted fiber quantification technique was used in which nerve fibers were identified by an edge-detection filter and the images were converted to binary images for density measurement (Ramer et al., 2007). However, this method can cause distortions resulting in artifacts in the binary images (Grider et al., 2006). More recently, the conventional edge detection filter has been replaced by Hessian image filters before binary conversion (Grider et al., 2006), because Hessian-filtering extracts line-like structures (Hladuvka and Groller, 2002) and is more suitable to detecting nerve fibers. The binary image conversion by a threshold level fails to pick up weakly labeled fibers, resulting in under-counting of nerve fibers. Further, the previous computer-assisted methods often use an indexing approach to quantify the fibers, which does not count the actual number of fibers. The indexed values provide the only information of total amount of fibers in the measured area (Liu et al., 2009; Ziehn et al., 2010). One potential problem of this type of measurement is that in the same size of image area, a smaller number of fibers with large diameters would generate an indexed value similar to that of a large number of fibers with small diameters. Therefore, the indexed value may not represent the actual number of fibers. Furthermore, the use of expensive software programs also limits their application.
We sought to develop an automated method to directly and objectively quantify nerve fiber density in both epifluorescence and confocal images in a fast and cost-effective manner. We first modified the line intensity scan analysis technique, which has been widely used in scanning densitometric analyses wherein the intensity of a spatially discrete signal is plotted along the length of a ‘scan’ through the region of interest. Our modified line-intensity scan allows us to reliably and efficiently detect and quantify fluorescently labeled nerve fibers in brain tissue sections. In addition, we made use of Hessian-based feature extraction and baseline adjustment to overcome the limitation of blurred signals and uneven labeling in epifluorescence images, allowing a subtraction of unwanted background. We used a computerized routine to automatically generate fiber counts from line scans in processed images. We have stringently evaluated our method in the hippocampus and cerebral cortex using low magnification epifluorescence images, where cholinergic fibers are fluorescently labeled with an anti-VAChT antibody and have obtained reliable and consistent results. We also performed line scans in images taken with both conventional epifluorescence and confocal microscopes and compared the fiber density values, which are highly comparable. Further, we demonstrated that our method is capable of distinguishing cell bodies from nerve fibers labeled by the same antibody. Thus, our newly developed method provides a reliable and both cost- and time-efficient means to quantify density of nerve fibers.
2. Materials and Methods
2.1. Animals
Three to six months old C57BL/6 mice of both genders were used in this study. All animal care and experimental procedures were approved by the Institutional Animal Care and Use Committee of the University of Maryland, Baltimore County.
2.2. Immunhistochemistry
The procedure for immunohistochemistry was adapted from our previous studies (Ogura et al. 2010, 2011). Briefly, mice were anesthetized and transcardially perfused with 0.1 M phosphate-buffered fixative containing 0.019 M L-lysine-monohydrochloride, 3% paraformaldehyde, and 0.23% sodium m-periodate. The brain tissue was removed and postfixed for 1.5 hours before being transferred into 0.1 M phosphate-buffered saline (PBS, pH 7.4) with 25% sucrose overnight at 4°C. The tissue was embedded in optimal cutting temperature (OCT) compound (Sakura finetek USA Inc, Torrance CA) and cut sagittally using a cryostat (Microm international, Walldorf, Germany) into 35µm-thick free-floating sections.
Brain sections were incubated in PBS buffered blocking solution containing 2% normal donkey serum, 0.3% Triton X-100 and 1% bovine serum albumin for 1.5 hours, followed by incubation with a primary antibody against VAChT (1:500, Sigma) for 48–72 hours at 4°C. The sections were rinsed and incubated with a secondary antibody conjugated with Alexa 555 (Invitrogen, Eugene, OR) for 1 hour at room temperature before being washed and mounted on slides.
2.3. Image acquisition
Low magnification fluorescence images were taken using an Olympus BX 41 epifluorescence compound microscope equipped with a Retiga 4000R digital camera (Qimaging, British Columbia, Canada) and Image-Pro Plus 6.2 (Media cybernetics, Bethesda, MD). The image resolution was 1.86 µm/ pixel with a 4× objective lens. We used the same parameters for image capture, including exposure time and camera gain, which obtain a good dynamic range of grayscale for all the images obtained from different sections and animals. Confocal fluorescence images were taken using an Olympus BX 61 epifluorescence microscope equipped with a spinning disc confocal unit and Hamamatsu Orca-AG digital camera (Hamamatsu Photonics, Japan). Slidebook 4.0 software (3i, Denver, CO) was used for confocal image capturing and processing. The confocal image resolution was 0.64 µm/ pixel with a 10× objective lens. We took all the images under the same exposure time, camera gain, and neutral density filter. Also, we used the same optical section step (0.4 µm) and imaged almost the same thickness for all the sections (Z-stack thickness: 22.0 to 22.8µm). The confocal Z-stack images were then processed to display maximum projection images, which were used for our data analysis. All the epifluorescence and confocal images were saved as 8-bit gray scale TIF format.
2.4. Image processing
2.4.1 Hessian-based image filter
Mathematically, fluorescently labeled fibers can be represented as curvilinear structures possessing local intensity variations (minima or maxima). Such local intensity extrema can be detected using a Hessian matrix, which describes the second-order information or curvature of these intensity variations (Sato et al., 1998). Thus, image-filtering based on the Hessian matrix specifically extracts line-like information from the input image. Accordingly, fluorescence images were feature-extracted for VAChT-labeled nerve fibers through a Hessian-based filter in NIH ImageJ (version 1.44) software plugin, FeatureJ (Meijering, 2003). Several parameters are selectable in this plugin. Based on the best results obtained with our “line-scan profile analysis” described in the paragraph below, we selected the following parameter options empirically: 1) “Largest eigenvalue of Hessian tensor” option, and 2) “Absolute eigenvalue comparison” option, and set the “Smoothing scale” factor to 0.5. This setting generates a resulting image of largest eigenvalues after comparing the absolute values of the Hessian matrices. We chose the absolute comparison option since the change in sign (positive or negative) of the intensity value, depending on the curvature along a line is irrelevant to our purpose of fiber count. The resulting images were converted to 8-bit before line scan analysis.
2.4.2 Binary image conversion
We compared our approach of Hessian-based image filter with the method described in Grider et al. (2006), which used the same ImageJ plugin, but with different filter parameters. Grider et al. generated images by using the “smallest eigenvalue” setting of the Hessian tensor and keeping the default value of 1 for the “smoothing scale factor”. In addition, they converted processed images to binary images with “auto” threshold setting in ImageJ. For comparison, we applied their technique to our raw images and performed fiber density measurement on the raw, binary processed images as well as the processed images obtained using our method.
2.5. Line scan profile analysis
2.5.1 Line Scan
Lines were drawn using ImageJ’s “line tool” through the region of interest (ROI). Either straight or segmented line could be drawn depending on the morphology of the brain structures. Pixel Intensity along the line was plotted using the “Plot Profile” tool. We conducted two series of scans for each ROI. The first set of scans was parallel to the outer edge of the brain structure under investigation, which we refer as “parallel scan”. The second set of scans was performed perpendicular to the “parallel” scans at equidistant points along the outer edge of the brain structure in order to sample the entire region. We refer to these scans as “perpendicular scans”. Background line scans were taken from a region of the corpus callosum immediately dorsal to the hippocampus in the images, where we observed no detectable VAChT labeling. All line scan data was imported into MATLAB (version 2011a, MathWorks, Natick, MA) for further analysis.
2.5.2 Baseline adjustment
The line scans were baseline-adjusted in MATLAB. Baseline estimation depends on how peaks (signal) are distinguished from background. We used the "msbackadj" command of the MATLAB bioinformatics toolbox to estimate the true baseline of the line scans. Using this command, the baselines are determined based on the Expectation-Maximization algorithm. This method classifies the data points into two groups (background and peaks) both of which have a normal distribution. The mean value of the background class is treated as the final estimated baseline. For fiber-density measurements using longer scans greater than 200 µm in length, we employed a window-size of 10 and 25 datapoints in 4× and 10× images, respectively, which roughly equals 20 µm in length. For fiber density measurements using shorter scans, 5 datapoints in 4× image, which is about 10 µm in length, was employed. We chose these criteria empirically based on how stringently the baseline was adjusted. The MATLAB algorithm performed this baseline adjustment in steps of desired size across the entire length of the scan. We chose a step-size equal to the window-size for baseline adjustment. For fiber intensity value distributions, we included a “PreserveHeights” condition as part of the baseline adjustment algorithm to more effectively preserve the intensity values of peaks counted.
2.5.3 Peak detection
Intensity matrices with adjusted baselines were then processed through a peak-detection algorithm, “mspeaks” in MATLAB to detect fibers represented as intensity peaks on individual line scans. Average background intensity obtained from the scans in the corpus callosum was used as the threshold-filter and local maxima above the threshold in adjusted line-scans were deemed to be peaks. The total number of peaks was then divided by the length of each line to yield the average number of peaks per µm scan.
2.5.4 Volume density calculation
For each ROI in the image, peaks per µm from parallel and perpendicular line scans were averaged separately to obtain the average number of peaks per µm along the parallel (x) or perpendicular (y) line scan vectors (Nx and Ny, respectively). To estimate fiber density per volume, we obtained the product of Nx and Ny, taking into account the thickness of the section (z). The value of tissue thickness for the 4x epifluorescence images was taken directly from the cryostat setting. For confocal images, the thickness value was the confocal Z-distance. Final values for volumetric fiber density obtained through measurements on the 4X epifluorescence images were calculated using the following formula:
| (Equation 1) |
In eqn. 1, Dv is volumetric fiber density and z is thickness of the section in µm. To account for the random orientation of fibers, we included a factor of cos45° in the denominator (Soghomonian et al., 1987). To account for optical losses in signal as well as attenuated epifluorescence signal from fibers deeper in tissue, we introduced a dimensionless empirical factor ε, which was calculated by comparing average number of peaks per µm line scan in ROIs of images obtained from epifluorescence to values obtained from confocal imaging. This factor was estimated prior to all the measurements and ranged from 1.4–1.6.
2.5.5 Calculation of difference in linear density
Linear scan density was represented as linear density per 10 µm, i.e., Nx or Ny multiplied by a factor of 10. Difference between parallel and perpendicular fiber components was calculated using the following equation:
| (Equation 2) |
Values obtained from eqn. 2 could be negative or positive, e.g., for any Nx and Ny, a higher perpendicular fiber component (Nx; detected by the parallel scan) would yield a positive value of difference and higher parallel fiber component (Ny; detected by the perpendicular scan) would yield a negative value of difference. Note that the directional nature of the fiber component (running parallel or perpendicular to the outer edge of the brain component e.g. hippocampus) is detected by the scan vector perpendicular to it.
2.5.6 Fiber intensity histogram
Fiber/peak intensities measured in each line scan was normalized to maximum values obtained in a particular image. The bin size for the intensity histogram was 0.1 a.u. (arbitrary unit of normalized fluorescence intensity)
2.5.7 Full width at half-height (FWHH) measurements
For each peak, the intensity value and the full width at half-height (FWHH) of that peak, were obtained as an output of the peak detection algorithm. The FWHH correlates directly to the width or diameter of the objects, which can represent either nerve fibers or cell bodies in our study. For the FWHH histogram of fibers in the molecular layer of dentate gyrus (MolDG), bin size equals 0.1µm. Using Origin 6.1 graphing software (Origin Lab, Northampton, MA), data were fitted to a multi-peak Gaussian function.
2.6. Statistical analysis
An independent or unpaired Student’s t-test was used to compare fiber scan densities. One-way ANOVA was used to determine the significance of the difference between parallel and perpendicular fiber density components. Tukey’s multiple comparison test was used as posthoc test for the ANOVA. Data obtained from two separate tissue sections at least 210 µm apart from the same mouse were averaged, and then the averaged data from 3–4 mice were used for the statistical analysis. In figures, a single asterisk (*) denotes p<0.05 and double asterisks (**) denote p<0.01. Statistical analyses were performed using Origin 6.1 graphing software and Prism 2.01 (GraphPad software, La Jolla, CA).
3. Results
3.1. Extraction and enhancement of curvilinear features of fluorescently labeled nerve fibers in low magnification images
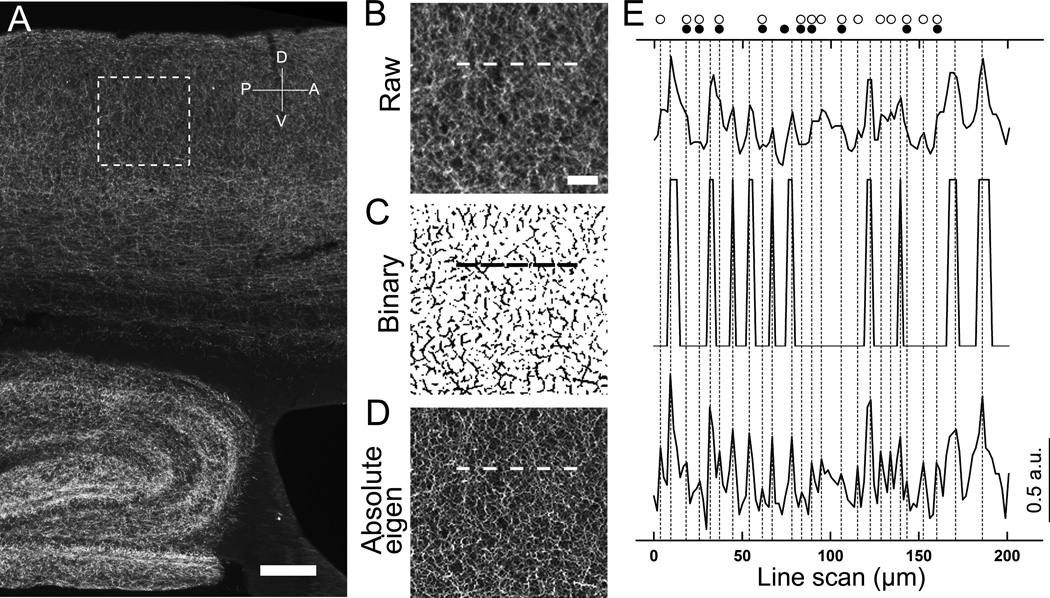
Quantifying fluorescently labeled nerve fibers in conventional epifluorescence images using automatic computerized routines is challenging. One major problem is uneven fluorescent labeling. We fluorescently labeled cholinergic fibers in sagittal mouse brain sections, using an antibody against the cholinergic maker VAChT. In a typical low magnification epifluorescence image of VAChT taken with a 4× objective lens, numerous labeled cholinergic fibers were seen in the hippocampus and cortex (Fig. 1A). Whereas many fibers exhibited very strong fluorescence labeling, some are relatively weak. Another major problem is the presence of background fluorescence signal, which is mostly caused by scattered fluorescence and non-specific staining. These uneven background signals result in low S/N (signal to noise) ratio and low dynamic range of the fluorescence label. We applied a line intensity scan to an enlarged raw image from a cortical region (Fig. 1B). In the line scan (Fig. 1E top scan), fluorescence intensity along the line drawn on the image was profiled and nerve fibers were detected and quantified as individual intensity peaks in the profile. Due to low S/N and low dynamic range of the raw epifluorescence image, some fibers with low intensity value did not appear as distinct peaks in the line scan profile and failed to be detected. To improve the S/N ratio, we tested a published method which incorporated image-filtering. Grider et al., (2006) had used a Hessian-filtering approach to better detect axonal densities from fluorescence confocal images of the serotonergic system. In their method, a raw image is processed using FeatureJ plugin (Meijering, 2003) based on a “non-absolute” Eigenvalue comparison in Hessian-based approach, to enhance curvilinear features, namely nerve fibers, and then converted to a binary image. We applied the Grider et al. method to process the raw image (Fig. 1B). The binary image is shown in Fig. 1C, in which the S/N ratio is significantly increased. However, a line intensity scan of approximately 200 µm across the test-region in the binary image revealed a number of false negatives, as compared to the raw image line scan profile (Fig. 1E middle vs. top). This result clearly indicates that Grider et al., method is not suitable for quantifying nerve fibers in low magnification epifluorescence images. Since the low intensity signals were lost mainly due to the binary conversion, we did not convert our images. Instead, we tried to optimize the parameters of the feature-extraction plugin FeatureJ to increase the rate of true positives in line intensity scans. We manually evaluated the accuracy of the fiber count in the processed image by different parameter settings and compared them to the count from the raw image. We found that the largest eigenvalue image generated by absolute eigenvalue comparison with a smoothing scale factor of 0.5 (as opposed to the default value of 1.0) exhibits a drastic enhancement of nerve fiber feature-extraction due to a higher S/N ratio and better resolution between fibers (Fig. 1D, Absolute eigen). The line scan profile from the absolute eigenvalue image shows more distinct peaks (i.e. better resolution, see Fig 1E, bottom line-scan), which is highly useful for accurate fiber count by both manual and automated methods. Because most manual methods involve observer-bias, we employed a computer-assisted automatic peak detection algorithm (see next section for automatic counting). Thus, our technique is superior in feature-extracting nerve fibers in terms of both higher S/N ratios and better resolution between fibers, which result in more accurate fiber counts by computer-assisted line intensity scan profile analysis.
Figure 1. Detection of individual fluorescently labeled nerve fibers in raw, binary and feature-extracted images.
(A) A low magnification epifluorescence image of VAChT-immunolabeled cholinergic nerve fibers in the cortex and hippocampus. Dotted square: Area of the cortex enlarged in panels B–D. (B) Raw image. (C) Binary image. This image was generated by binary conversion of the raw image after smallest eigenvalues Hessian extraction using the method of Grider et al (2006). (D) Absolute-eigen image. This image was obtained by processing the raw image with the Hessian-filter plugin with parameter setting for the highest eigenvalues and absolute comparison. Dotted lines (in panels B, C and D) indicate the location of the line used for measuring the fluorescence intensity by line scan as shown in panel E. (E) Nerve fibers are detected as intensity peaks in line scans from Raw image (top), Binary image (middle) and Abslolute-eigen image (bottom). Vertical dotted lines correspond to the peak locations of the line scan from Absolute-eigen image. Open circles indicate peaks missed in the Binary image. Filled circles indicate peaks missed in the Raw image. Note, Absolute-eigen image processing allows more efficient detection of nerve fibers as peaks in line scans. Scale: A, 200 µm, B–D, 50 µm.
3.2. Determination of cholinergic fiber density in the cortex using automated line-intensity scan analysis
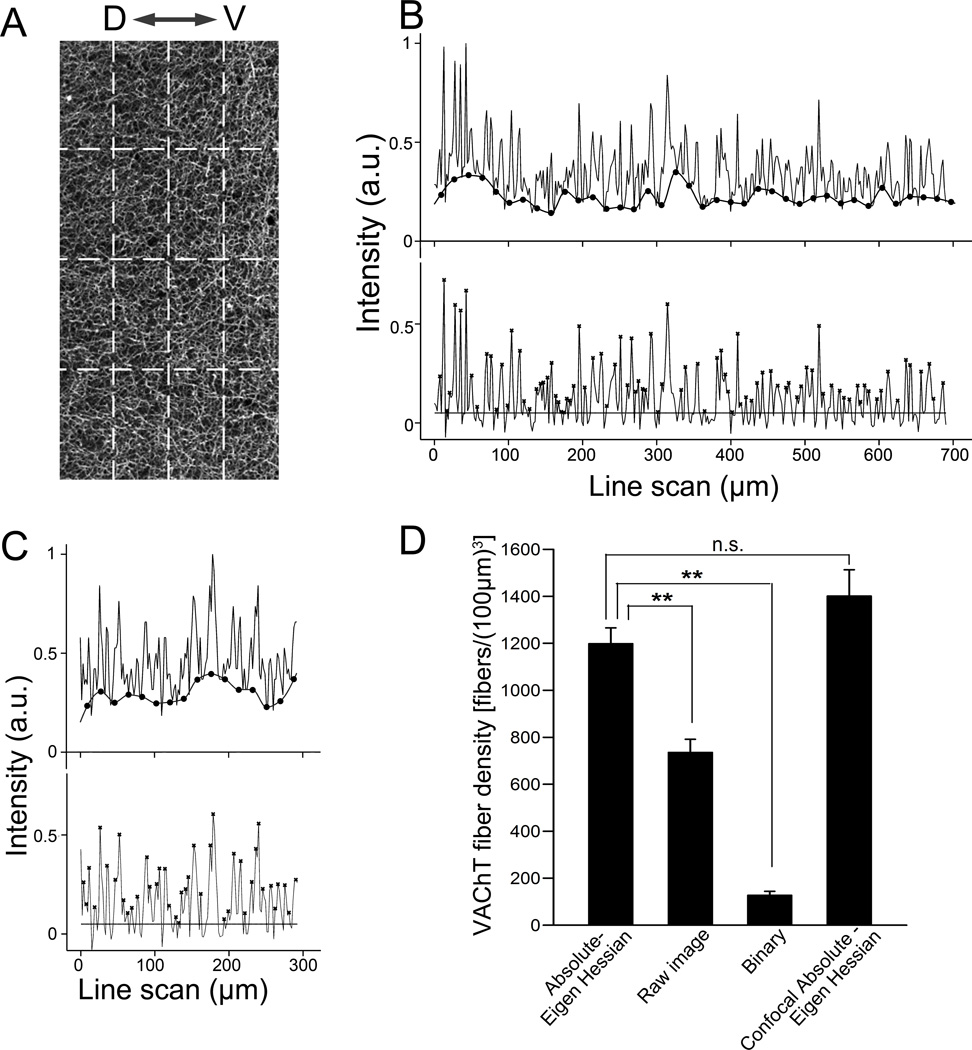
We next evaluated our method with high stringency by applying our absolute-eigenvalue Hessian protocol and line scan to quantify the density of VAChT-positive cholinergic fibers in a large cortical region in 4× low magnification epifluorescence images. We obtained images of VAChT immunolabeling in sagittal brain sections 0.4–0.5 mm lateral to the mid-plane. In all images, we defined a 800 µm × 400 µm window as region of interest (ROI) in layer II/IV of the retrosplenial granular cortex (RSA) (Fig. 2A), as determined from the mouse brain atlas (Paxinos and Franklin, 2001). The three parallel scans conducted were spaced 100 µm apart and the three perpendicular scans were spaced 200 µm apart (dashed lines in Fig. 2A). We obtained line intensity profiles for each of the scans. Representative scan profiles from the parallel and perpendicular scans are shown in the top line profiles in Fig. 2B and C, respectively. In each of the profiles, the intensity values were normalized to the highest intensity value from a set of scans in the same images. In the normalized line intensity profiles (Fig 2B and C upper line profiles), the variable levels of the baseline across the scan length were calculated using MATLAB function msbackadj (the calculated baseline is shown as the smooth lower line marked with filled circles) and subtracted from individual corresponding intensity values. This baseline adjustment generates a uniform baselines across the scan length (Fig 2B and C, lower line profiles), allowing the use of a threshold for peak detection. The threshold value was the average intensity value from a set of line scans conducted through the corpus callosum, where we observed negligible VAChT immunoreactivity. We applied the threshold value (marked as a horizontal line in Fig. 2B and C, lower line profiles) above which local maxima were treated as peaks (Fig 2B and C, asterisks). We used the automatic peak detection routine of MATLAB, “mspeaks”, to generate fiber counts. Fiber counts from 3 parallel scans and 3 perpendicular scans were averaged, respectively, which yielded average fiber counts in two orientations (Nx and Ny). We then applied the values of Nx and Ny to the equation (1) in method section 2.5.4. to calculate the volumetric fiber density. The average cholinergic fiber density in the cortical region measured from the Absolute-eigenvalue image is presented in Fig. 2D. For comparison, we also conducted the same line scans and calculated the fiber density from the original raw images and the binary processed images using the method of Grider et al., (2006). Density values obtained in raw and binary images are significantly smaller than those obtained in our optimized Absolute-eigen Hessian filtered images (** p<0.01, n=4 mice, Fig. 2D). To further evaluate the density values obtained in 4× epifluorescence images processed with our approach of Absolute-eigen Hessian filtering, we obtained confocal images captured using a 10× lens from the same tissue sections where the 4× epifluorescence images were taken and applied our optimized Absolute-eigenvalue Hessian feature extraction. The average fiber densities obtained from 4× epifluorescence images was close to 85.5% of the values obtained from the 10× confocal images. The difference between the two values is not statistically significant. In addition, we compared values obtained using raw and binary processing paradigms for confocal images. The value from confocal Hessian is not statistically significant from the value from confocal raw (paired t-test, p=0.073). But the value from confocal binary is significantly lower than the value from confocal Hessian (paired t-test, p=0.017), which demonstrates that the binary paradigm is inaccurate for low magnification confocal images. These results indicate our technique can be used reliably to measure fiber density in large areas in low magnification images with reasonable accuracy.
Figure 2. Density measurement of fluorescently labeled nerve fibers.
(A) A raw image of VAChT-immunolabeled fibers in cerebral cortex captured with 4× lens. Dotted lines indicate the location used for line scans. “D–V” denotes dorsal and ventral directions. The 3 parallel scans (vertical dashed lines) are 100 µm apart. The 3 perpendicular scans (horizontal dashed lines) are 200 µm apart. (B, top scan) A representative parallel line scan in panel A with baseline displayed (lower line marked with filled circles). (B, bottom) The same line scan after baseline-adjustment. Background intensity level is marked as a horizontal line. Nerve fibers are marked as peaks (x) detected by MATLAB function “mspeaks”. (C) A representative perpendicular line scan from panel A (top), and the baseline adjusted line scan (bottom). (D) Bar graph showing average VAChT fiber densities obtained from the same set of images processed differently (n = 4 mice). Volumetric fiber densities are calculated from the line scan analysis using equation 1. Data of Abosolute-Eigen-Hessian, Raw and Binary images are obtained from 4× epifluorescence image processed similarly shown in Fig. 1. Similar values of fiber density are obtained from 4× epifluorescence and 10× confocal Abosolute-Eigen images. **; p<0.01. n.s.; not significant.
3.3. Comparing cholinergic fiber density among different hippocampal layers
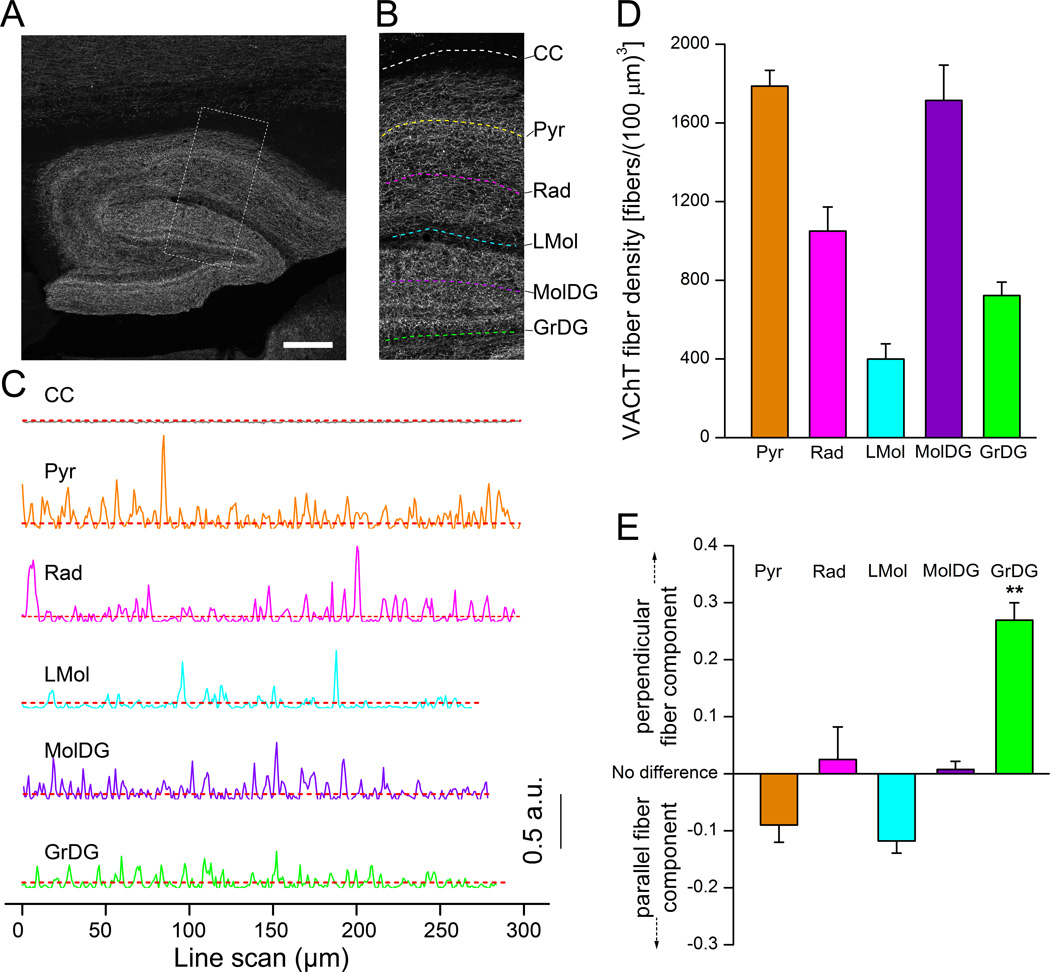
Having established the reliability of our technique in measuring fiber density, we applied this method to detect sub-regional variations in the cholinergic fiber density. We chose to examine the hippocampus as it is a critical region, responsible for learning and memory (Maguire et al., 2000; Squire et al., 1992). These functions are modulated by cholinergic activities (Frotscher et al., 1986; Mitchell et al., 1982). We imaged fluorescently-labeled VAChT nerve fibers in hippocampus using a 10× lens, which covered the entire hippocampal region in saggital brain sections (Fig. 3A). The hippocampal layers we analyzed included the pyramidal cell (Pyr), stratum radiatum (Rad), Lacunosum moleculare layer (LMol), molecular layer dentate gyrus (MolDG) and granular layer dentate gyrus (GrDG). For each of the five layers, we performed an individual parallel scan through the center of the layers in images processed with Absolute-eigenvalue Hessian filter (Fig. 3A). The length of the individual scans varied depending on the size of the layer (for Pyr, Rad, LMol, MolDG and GrDg, ~1.5 mm, ~1.0 mm, ~0.3 mm, ~1.7 mm and ~1.3 mm, respectively). Typical positions of the line scans in each individual layers are indicated in Fig. 3B, which is enlarged from the dotted square in Fig. 3A. Fig. 3C shows individual scan profiles from the dashed lines in Fig. 3B. We also obtained a parallel scan through the corpus callosum (CC) for determining threshold level for automated peak detection. The baseline intensity-adjusted parallel scans in 5 hippocampus layers demonstrate that the peak numbers per µm line scan varied among the layers (Fig 3C). To further obtain volumetric fiber densities, we also performed a series of six perpendicular scans approximately equidistant from each other along the length of the parallel scans, which were through the entire layers. The calculated volumetric fiber densities for VAChT fibers in each of the hippocampal layers, using averaged fiber counts in parallel scans and perpendicular scans (Nx and Ny, respectively) and the equation (1), are shown in Fig. 3D (n = 4 mice). We observed highest fiber densities in the MolDG and the Pyr layers - 1787.3 fibers/(100 µm)3 and 1714.3 fibers/(100 µm)3, respectively. The LMol layer had the least density with 399.5 fibers/(100 µm)3. These values agree well with an earlier quantitative investigation of cholinergic fiber density in the rodent hippocampus (Aznavour et al., 2002). Thus, our method is sensitive and able to detect sub-regional changes in fiber density.
Figure 3. Density measurements of cholinergic nerve fibers in the hippocampus.
(A) An epifluorescence image of VAChT-immunolabeled fibers. Dotted square region denotes the enlarged image in panel B. (B) Dotted lines in various layers indicate locations of representative line scans shown in C. Only the parallel scans are shown. Corpus callosum (CC). Pyramidal cell layer (Pyr). Stratum radiatum (Rad). Lacunosum moleculare layer (LMol). Molecular layer dentate gyrus (MolDG). Granular layer dentate gyrus (GrDG). (C) Line scans in different areas after baseline adjustment. CC is for determining background intensity levels shown as dotted red lines. (D) Average values of VAChT fiber densities in different layers of the hippocampus. For each layer, the density was calculated from one parallel scan crossing through the entire layer and 6 perpendicular scans evenly distributed across each layer. (n = 4 mice). (E) Plot of differences in linear densities between the perpendicular and parallel scans, showing distinct orientation of the cholinergic fibers in individual layers. Difference between fiber components was calculated using equation 2 of Method section 2.5.5. Perpendicular fiber component in GrDG is significantly higher than the parallel fiber component (**; p<0.01). Scale: 200 µm.
3.4. Determining gross orientation of the cholinergic nerve fibers in hippocampal layers through differences in the parallel and perpendicular line scans
In addition to variations in fiber density, sub-regions may possess nerve fibers running grossly in different directions. We compared the differences in the linear fiber scan density of the parallel (Nx) and perpendicular scan (Ny) in each hippocampus layer. Fig. 3E shows that Pyr and LMol layers had a greater parallel fiber component, Layers Rad and MolDG had close to no difference in orientation preference, which implies an equal contribution of perpendicular and parallel fiber components. The GrDG, however, had a significantly higher perpendicular component (p<0.01, One-way ANOVA with post hoc Tukey’s multiple comparison test, n = 4 mice). The results were confirmed by manual observation of the GrDG, where we noticed a stronger presence of fibers traversing the layer in a direction perpendicular to the curvature of the outer edge than of parallel fibers.
3.5. Measuring inter-regional differences in fiber density across a large sampling area
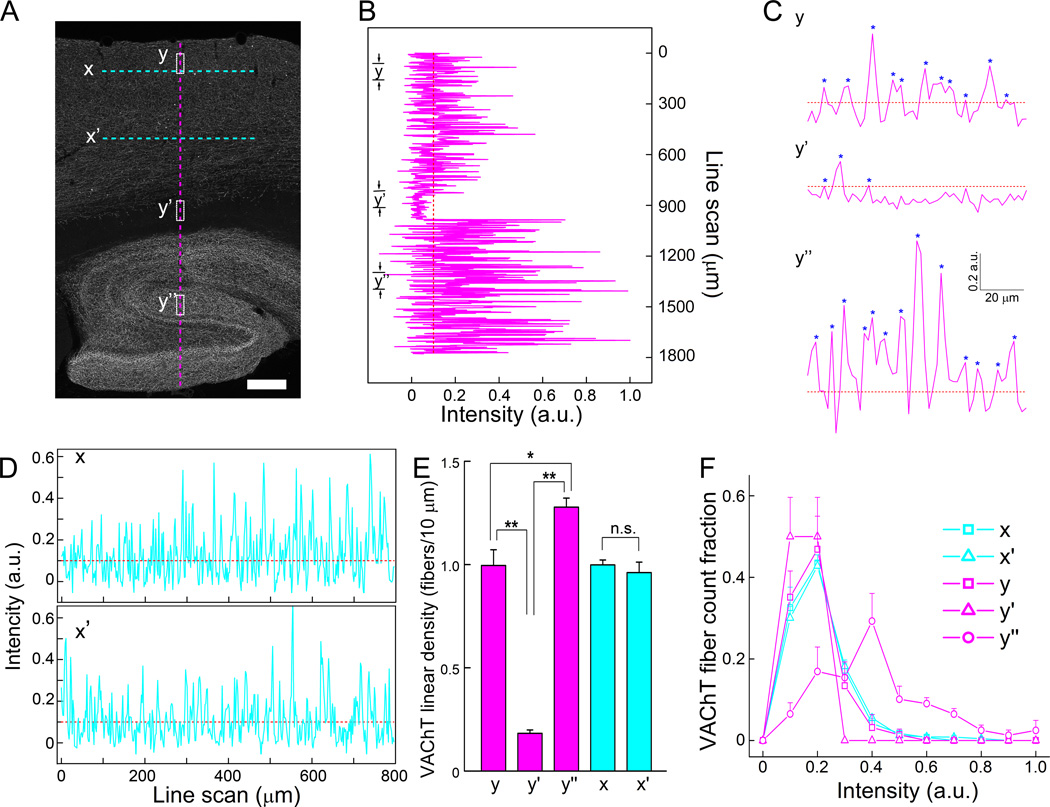
In many cases, it becomes necessary to monitor fiber density in different regions of the brain simultaneously. For example, in Alzheimer’s disease, cholinergic innervations are altered in cortical as well as hippocampal regions (Bierer et al., 1995; Boncristiano et al., 2002; Ransmayr et al., 1992). Using line scan profile analysis of low magnification (4X) Hessian-filtered VAChT epifluorescence images, we can perform rapid and reliable fiber density measurements for cholinergic fibers on a large scale. Fig. 4A is a fluorescence image of VAChT labeling in cortical and hippocampal regions. We performed line intensity scan analysis across cortex as well as hippocampus using an extended, individual perpendicular line scan, totaling about 1900 µm. As shown in the overall view of perpendicular line scan (Fig. 4B), as well as the enlarged views of the line scans for the 3 specific brain areas (Fig. 4C), the fiber densities and the intensity of fluorescence labels were different among these brain regions. We calculated linear fiber density of 90 µm length of 3 specific areas; cortex, cortical edge and corpus callosum, and hippocampus (labeled as y, y’, and y’’, respectively in Fig. 4). The averaged fiber density of hippocampus (y’’) was significantly higher than other two regions y and y’ (Fig. 4E, n = 3 mice). Similarly, we performed two parallel scans through layers II and IV of the cortex labeled as X and X’ in Fig. 4A and scan profiles are shown in Fig. 4D. We did not observe a significant difference in the averaged VAChT fiber density between these two parallel scans (Fig. 4E, n= 3 mice). Our method is thus well suited to examine fiber densities of large area of the brain regions and compare them in different sample sections quantitatively and rapidly.
Figure 4. Quantitative comparison of density and intensity of fluorescently labeled nerve fibers in large areas.
(A) A raw image of VAChT-immunolabled fibers in cortical and hippocampal regions. (B) A long perpendicular line scan from cerebral cortex to hippocampus, which is marked as a vertical dotted magenta line in A. (C) Three sections of line scans labeled as y, y’ and y” in panel A and B are enlarged. Fibers detected are marked with (*), showing differences in both density and fluorescence intensity. (D) Two long parallel line scans in the cortex, which is marked as two horizontal cyan dotted lines labeled as x and x’ in A. Straight dotted lines in B,C, and D indicate background (threshold) level after the base line correction was applied. (E) Graph of average linear densities of VAChT fibers in different areas (n = 3 mice). “n.s.”, not significant. * and **, p<0.05 and 0.01, respectively. (F) Histogram of fibers with different intensity of VAChT-immunoreactivity. Note, in the y’’ line scan, a higher fraction of fibers shows greater intensity of immunolabeling. Bin size is 0.1 intensity (a.u.). Scale, 200 µm.
3.6. Determining VAChT fiber Intensity distribution
The line intensity scans shown in Fig. 4B and C also display differences in the intensity levels of VAChT labeling among nerve fibers of various brain regions. Immunolabeling intensity often indicates expression levels of a particular protein labeled. We can derive functional implications for the protein expression by quantifying the fluorescence intensity levels. Using the peak-detection algorithm of MATLAB, we analyzed 5 different brain areas, similar to those shown in x, x’, y, y’ and y’’ in Fig. 4A, from images of three mice and extracted the intensity of each fibers (peaks) detected in the line scans. Fibers were grouped by their intensity value (bin size = intensity value of 0.1 a.u.) and the number of the fibers in the same intensity levels were counted. The summarized data are plotted as a histogram of fiber distributions for different intensity levels (Fig. 4F). The histogram revealed that in all line scan areas except y’’, a considerable percentage of fibers (~20–50%) have an intensity value less than 0.3 a.u. In the scan area y’’ in the hippocampus, the distribution is broader with certain fractions reaching up to 0.7 a.u. This indicates VAChT is expressed at higher levels in this region of the hippocampus than in the region of cortex where we obtained measurements, supporting the greater functional significance of the cholinergic system in the hippocampus.
3.7. Distinguishing objects of different sizes using line intensity analysis
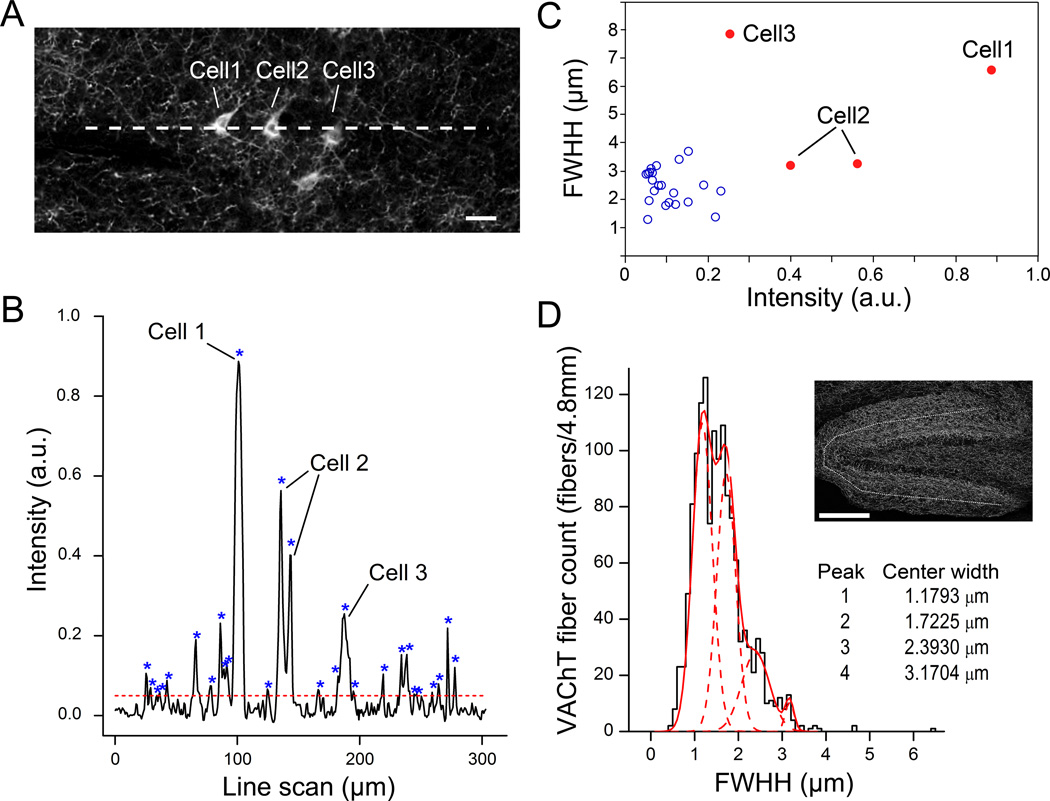
In many cases, immunolabeling of a certain protein is not exclusive to nerve fibers (axons and dendrites) as the somata are often labeled. Fig. 5A is a 10× confocal image from a mid-brain region, where both cell bodies and nerve fibers were fluorescently labeled with the VAChT antibody. In such instances, it becomes useful to exclude the intensity peaks representing the cell bodies in the line scan profile for nerve fiber count (Fig. 5B). Fortunately, we can readily extract the “full width at half height (FWHH)” for each peak detected by the built-in “mspeaks” algorithm of MATLAB. This value is a direct correlate of the detected object’s (fiber or cell body) size and in some cases may closely match it. We employed this strategy to count only fibers by excluding peaks above a certain FWHH and intensity, because both size and intensity values of most VAChT fibers is smaller than those of somata. In a line scan of approximately 300 µm across three cell bodies immunolabeled for VAChT, we were able to distinguish soma peaks based on their unique combination of high FWHH (> 3 µm) and a high intensity value (> 0.3 a.u) (Fig. 5C). Further, we sought to use this approach as a tool for classifying fibers of varying sizes. We pooled FWHHs of 1397 peaks (nerve fibers) detected from parallel line scans of the MolDG layer of the hippocampus in 10× confocal images (n = 3 mice, 4.8 mm total line scan length). We constructed a FWHH histogram with 0.1 µm bins and fitted a Gaussian distribution with multiple peaks. A 4-peak Gaussian fit resembled the data considerably well (Fig. 5D, solid red line). Individual peaks yielded the average fiber diameters for each population of fibers (Fig 5D, dashed red lines), which closely matched the observed sizes of axonal fibers in earlier studies (Shepherd et al., 2002).
Figure 5. Distinguishing different-size objects using line scan analysis.
(A) A 10× confocal image of VAChT-immunolabeled fibers with cell bodies taken from the mid-ventral brain. A dashed line indicates the location of line scan shown in B. (B) Line scan across fibers and three cell bodies. “*” marks Intensity peaks. Cell 2 has two peaks due to scanning through the nucleus where the intensity is low. Horizontal dashed line represents threshold for peak detection. (C) Scatter plot of peaks in B. Cell bodies (red filled circle) can be distinguished from fibers (blue open circle) based on both intensity value and full width at half-height (FWHH) of the peaks. (D) Histogram of fiber FWHH, showing different diameter of cholinergic fibers in MolDG layer. VAChT fibers are counted from the line scans of 10× confocal images at MolDG layer of hippocampus from 3 mice (total 4.8 mm scan). Location of line scan is shown in the inset image as a dotted line. The histogram is fitted to four Gaussian distributions (4 dotted curves) based on the fiber FWHH. Scale, 20 µm and 200 µm in A and D, respectively.
4. Discussion
We have demonstrated that our newly developed automated method, which makes unique use of several broadly available software and techniques, can efficiently determine nerve fiber density in fluorescence images. Using the method, we have obtained reliable and reproducible nerve density measurement for VAChT fibers in large regions of the cortex and hippocampus from brain sections with a high degree of stringency and efficiency. In addition, we have demonstrated that our method can differentiate nerve fibers from cell bodies immunolabeled by the same antibody, making computerized fiber count accurate. Further, we have illustrated that our method is sensitive and efficient in detecting regional changes in cholinergic fiber density across large brain regions. Thus, our method is applicable to a wide variety of basic neuroscience research and clinical investigations. The capability, efficiency and accuracy of our method represent a significant improvement over currently available computer-assisted methods of nerve fiber quantification.
4.1. The advantages and improvements of our current method
A significant advantage of our technique is that it works well to quantify nerve fibers in low magnification images without significant loss in efficiency as compared to the use of higher magnification confocal images. This is mainly due to the usage of already built-in software tools and techniques. One is the baseline correction algorithm, which makes reliable baseline adjustment to overcome the problem of non-uniform signal intensity in epifluorescence images. The other is a more efficient Hessian-based feature extraction that we selected to enhance features of curvilinear nerve fibers. Another significant advantage of our method is that it allows direct and objective measurement of nerve fiber density without biases due to observer/examiner judgment. This is because our technique uses a threshold intrinsic to the images to distinguish objectively between signal and noise. Although several techniques are currently available for fiber density measurement, most of these methods either yield indices, such as fluorescent intensity per area (Ziehn et al., 2010), area of fibers per area of measurement window or a manually scored axon density index (Geula and Mesulam, 1996). All of these methods provide an indirect quantitative measurement. In addition, methods that yield fiber count per area or volume measured are subject to observer bias. An example of such a method is the protocol conventionally used for quantifying intraepithelial nerve fiber density (IENFD) in skin biopsies (Lauria et al., 2010). Further, these methods heavily depend on examiners and are labor intensive, time-consuming and in some cases, expensive. Casanova-Molla et al. (2011) designed a semi-automated method to better estimate axonal densities in biopsies of patients suffering from small fiber neuropathy (SFN). However, the use of an examiner to count cutaneous axon fibers could not be eliminated. Thus, existing methods are not sufficient to provide reliable fiber quantification in a time-efficient and objective manner. We believe our method fulfills this need through a highly flexible automated routine.
4.2. Principles and applications of Line intensity profile and hessian-based image filter
The two major techniques used in our method are well-established and have been used widely. However, applying them in unique combination to quantify nerve fibers has not been explored. The first is line intensity profile analysis, which has been employed in chromatographic techniques, such as thin layer chromatography (TLC) and also in electrophoretic techniques to quantify the amount of given unknown sample based on known standard concentration curves (Ghosh et al., 1988; Kastner, 2000; Scott, 1995). The second is Hessian-based filters, which have been used as an image-processing procedure to enhance features of curvilinear structures, such as bronchi, brain vessels and portal veins from medical images obtained through magnetic resonance imaging (MRI) and computerized tomography (CT)(Frangi et al., 1998; Sato et al., 1998). The basic parameters affecting hessian-filtering of images are choice of eigenvalue comparison and value of the smoothing derivative. The Hessian-filter allocates an eigenvalue to each pixel based on its initial intensity as well as its local position on the image. This conveys information about : 1) the “magnitude” or shape identity of an object (“blob” or “line”) and 2) the “direction” or the local curvature (location on an object). Thus, a non-absolute filtering process yields a Hessian image with sign-intact eigenvalues. Pixels belonging to a curvilinear object on the concave part possess a positive eigenvalue and those on the convex part have a negative value. For fiber density count, the curvature information is irrelevant. In fact, in our analysis, we have noted that an absolute comparison of eigenvalues results in a higher signal to noise ratio for fiber density analysis.
4.3. Reliability and accuracy of our method
We have tested our method on epifluorescence as well as confocal images processed with Absolute-eigenvalue Hessian filter. The cholinergic fiber density measured from the cortical region of the epifluorescence images is comparable to the density value measured from similar region of the confocal images. The results are consistent and reproducible among animals tested. In addition, our results are comparable to earlier quantitative studies of cholinergic fibers in the rodent cortex (Mechawar et al., 2000) and hippocampus (Aznavour et al., 2002). Although the methods used by these investigators are different due to the use of non-fluorescence immunohistochemistry and a net length estimate of labeled axons, we can nevertheless draw important parallels with our study. For example, the percent differences of the length estimates of cholinergic axons according to Aznavour et al., 2002 in the hippocampal layers of Pyr, Rad, MolDG and GrDG over the net axon length in the LMol layer are 91%, 49%, 101% and 71% respectively. This trend is maintained in our results with percent differences (in same order) of 127%, 90%, 124% and 58% over that of the fiber density estimate in the LMol layer. It should be emphasized that our technique combines the advantages of fluorescence immunolabeling (as compared to earlier detection techniques) as well as a low magnification microscopy. As mentioned earlier, Casanova-Molla et al. (2011) developed a method, allowing quantification of neuronal fiber density from confocal immunofluorescence images of skin biopsies. However, confocal images usually are limited to small areas. In this regard, we believe our technique to be more robust and highly efficient in processing large ROIs.
4.4. Factors and limitations influencing the accuracy of nerve fiber quantification
4.4.1 Resolution in low magnification images
Using a 4× objective lens for low magnification immunofluorescence images has its distinct set of advantages, such as large field of view, high focal depth and easy acquisition, however, it is not without its tradeoffs. One obvious limitation is the image resolution, which directly affects fiber density measurements. We tested our method with high stringency by using 4X images and were able to mathematically enhance the “resolution” between closely spaced peaks to obtain reliable and accurate measurement of fiber density. However, one cannot stretch this technique beyond its obvious systemic constraints. This also means that one cannot readily use low magnification images to obtain details such as FWHH to a high degree of precision. This is reflected in our use of images captured through a 10× objective to investigate the ability of our technique to obtain meaningful information about differences in nerve diameters (Fig. 5E). Another tradeoff inherent to low-magnification epifluorescence images has to do with the thickness of the tissue sections. We performed our immunolabeling experiments using 35 µm thick free-floating brain sections so that the antibody has better and even access to the tissues. Too thick a section can lead to uneven labeling, higher background and lesser discrimination between peaks in low magnification images. Thus, in order for a good imaging and analysis routine, the thickness of the tissue sections has to be considered. In our calculations of fiber density, we have included the empirical constant ε, which corrects for the optical limitation of the 4× objective and also accounts for the thickness of the tissue sections and imaging settings used. Because the value of ε depends on the combination of imaging techniques used, it may be different for different experimental and laboratory settings. Although initially, for a given imaging setup, few confocal images may be required for calculating the value of ε, this does not necessitate the use of confocal imaging before the start of every experiment. Using ε, we can minimize the difference and variability between different imaging settings, which allows comparison of results from different studies.
4.4.2 Overlapping of fibers and cell bodies labeled by the same antibodies
In order to obtain accurate measurements of neuronal fiber density, it is important that we can separate intensity peaks of cell bodies from the peaks of nerve fibers. Using our technique one can readily weed out the counts of extraneous effects of cell bodies, since they have a larger diameter than fibers and their peaks on the line scan would consequently exhibit a larger FWHH. It is important to note that a direct FWHH threshold can sometimes prove ineffective since the line scan can pass through a nuclear region where there is little or no immunoreactivity, leading to a double peak separated by a defined minimum (representing the unlabeled nucleus, Fig. 5A). In such instances, it becomes useful to apply two thresholds – intensity and FWHH. This follows from the assumption of differential immunolabeling between the nerve processes and cell bodies, although this may not always hold up. In our method we applied a threshold for intensity and FWHH, effectively eliminating the effects due to cellular peaks. Further, we could even obtain a count of the cells encountered by the line scan, for example, by dividing the plot in Fig. 5C into four quadrants obtained by the FWHH and intensity thresholds. The points in the upper right quadrant represent a direct count of cells but those in the lower right quadrant represent cells in the line scan separated by the nuclear minimum. Ideally, the number of points in this quadrant divided by a factor of two would yield the remaining number of cells encountered by the line scan.
4.4.3 Cross cut fiber counting
Immunolabeled fibers in tissue sections which are “cross-cut” would appear circular rather than curvilinear. Marina et al (2010) describe a semiquantitative method to quantify loss of axonal density in such cross-cut fiber images using a “nucleus-counter” ImageJ plugin. Since we used low magnification images taking from 35 µm thick tissue sections and scanned large tissue areas, such encountering in our line scan is much less frequent and loss in fiber count is minimal.
4.4.4 Unbiased sample selection
Since we focus on method development in this study, we only sampled and analyzed limited tissue sections. For a truly unbiased and thorough measurement of nerve fiber density, it is important to conduct measurement on tissue sections systematically obtained and processed from the region of interest. For example, processing of every sixth section of a region of interest may allow for more unbiased sampling to be achieved.
4.5. Potential applications
The ability to quantify fluorescently labeled nerve fibers in large regions of tissue section is advantageous and valuable for a wide variety of basic neuroscience research. In addition, our method has a high potential to be used as a diagnostic tool for the measurement of nerve fiber density in clinical applications. For example, as we showed in this study, we can obtain accurate and reproducible measurement of cholinergic fiber densities in large cortical and the hippocampal regions. Both these regions undergo changes in cholinergic fiber density upon the onset or development of neurodegenerative diseases, such as Alzheimer’s (Boncristiano et al., 2002; Bronfman et al., 2000; Geula and Mesulam, 1996; Ikonomovic et al., 2007; Wong et al., 1999) and Parkinson’s (Jellinger et al., 1991; Kuhl et al., 1996) as well as psychosocial conditions, such as addiction (Lehmann et al., 2004; Trauth et al., 2000). Our technique can be readily used in a clinical setting or disease models to obtain nerve fiber density estimates in a quick and reliable manner as opposed to observer/examiner dependent estimates, which mostly yield an index of fiber density rather than a count (Nolano et al., 2010). Also, many neurodegenerative disorders result in axon swelling as well as alteration of the number and size of presynaptic boutons (Wong et al., 1999). Marina et al (2010) used high magnification (63×) images for analysis and differentiated between different kinds of damaged axons, such as those with thinner diameters. Our protocol to differentiate between objects of different diameter/size corresponding to the FWHH measurements can be very useful for quantifying such changes and guiding diagnosis or prognosis, especially in images obtained from tissue biopsy. In addition, our method can be applied in combination with the latest in vivo nerve imaging techniques, such as diffusion tensor imaging (DTI) (Mandl et al., 2008) and high resolution optical coherence tomography (OCT) (Bonin et al., 2010) to estimate changes in fiber density. Currently, in vivo fluorescent nerve imaging is being developed using the rodent model (Misgeld & Kerschensteiner, 2006; Whitney et al., 2011) and it is only a matter of time when such techniques may be applied to study and treat the human brain in vivo. Future directions for our automated method lie in the development of a real-time functional analysis suite, working in conjunction with the aforementioned imaging techniques.
In summary, we have developed a tool to rapidly and reliably quantify neuronal fibers in biomedical research as well as clinical settings using widely established software. This technique can also be used for 1) global analysis of changes in density and intensity in large areas of the brain or other tissue sections with a particular component labeled, and also for 2) fine analysis of diameters or sizes of particular subjects, such as nerve fibers and cell bodies in a particular system. Further, our method is highly flexible and can be adapted and modified according to research interest.
Highlights.
We developed an automated method to quantify fluorescently labeled nerve fibers.
Our method makes unique use of line intensity scan, NIH ImageJ plugin and built-in peak detection algorithms of MATLAB.
Our method enables efficient and reliable nerve fiber density measurement in large tissue areas from low magnification epifluorescence images.
We measured cholinergic nerve fiber density in cortical and hippocampal regions and our results are accurate and highly reproducible.
Our method is highly adaptable and can be broadly useful in both research and clinical investigation.
Acknowledgments
We thank Wangmei Luo, Sarah Ashby and Kurt Krosnowski for technical assistance, Varsha Rao for critical reading of the manuscript. This work was supported by NIH/NIDCD 009269 and ARRA administrative supplement to WL.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aznavour N, Mechawar N, Descarries L. Comparative analysis of cholinergic innervation in the dorsal hippocampus of adult mouse and rat: a quantitative immunocytochemical study. Hippocampus. 2002;12:206–217. doi: 10.1002/hipo.1108. [DOI] [PubMed] [Google Scholar]
- Bierer LM, Haroutunian V, Gabriel S, Knott PJ, Carlin LS, Purohit DP, Perl DP, Schmeidler J, Kanof P, Davis KL. Neurochemical correlates of dementia severity in Alzheimer's disease: relative importance of the cholinergic deficits. J Neurochem. 1995;64:749–760. doi: 10.1046/j.1471-4159.1995.64020749.x. [DOI] [PubMed] [Google Scholar]
- Boncristiano S, Calhoun ME, Kelly PH, Pfeifer M, Bondolfi L, Stalder M, Phinney AL, Abramowski D, Sturchler-Pierrat C, Enz A, Sommer B, Staufenbiel M, Jucker M. Cholinergic changes in the APP23 transgenic mouse model of cerebral amyloidosis. J Neurosci. 2002;22:3234–3243. doi: 10.1523/JNEUROSCI.22-08-03234.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonin T, Franke G, Hagen-Eggert M, Koch P, Huttmann G. In vivo Fourier-domain full-field OCT of the human retina with 1.5 million A-lines/s. Optics letters. 2010;35:3432–3434. doi: 10.1364/OL.35.003432. [DOI] [PubMed] [Google Scholar]
- Bronfman FC, Moechars D, Van Leuven F. Acetylcholinesterase-positive fiber deafferentation and cell shrinkage in the septohippocampal pathway of aged amyloid precursor protein london mutant transgenic mice. Neurobiol Dis. 2000;7:152–168. doi: 10.1006/nbdi.2000.0283. [DOI] [PubMed] [Google Scholar]
- Casanova-Molla J, Morales M, Sola-Valls N, Bosch A, Calvo M, Grau-Junyent JM, Valls-Sole J. Axonal fluorescence quantitation provides a new approach to assess cutaneous innervation. J Neurosci Methods. 2011;200:190–198. doi: 10.1016/j.jneumeth.2011.06.022. [DOI] [PubMed] [Google Scholar]
- Frangi AF, Niessen WJ, Vincken KL, Viergever MA. Multiscale vessel enhancement filtering. Lect Notes Comput Sci. 1998;1496:130–137. [Google Scholar]
- Frotscher M, Schlander M, Leranth C. Cholinergic neurons in the hippocampus. A combined light- and electron-microscopic immunocytochemical study in the rat. Cell Tissue Res. 1986;246:293–301. doi: 10.1007/BF00215891. [DOI] [PubMed] [Google Scholar]
- Geula C, Mesulam MM. Systematic regional variations in the loss of cortical cholinergic fibers in Alzheimer's disease. Cereb Cortex. 1996;6:165–177. doi: 10.1093/cercor/6.2.165. [DOI] [PubMed] [Google Scholar]
- Ghosh S, Gepstein S, Heikkila JJ, Dumbroff EB. Use of a scanning densitometer or an ELISA plate reader for measurement of nanogram amounts of protein in crude extracts from biological tissues. Anal Biochem. 1988;169:227–233. doi: 10.1016/0003-2697(88)90278-3. [DOI] [PubMed] [Google Scholar]
- Grider MH, Chen Q, Shine HD. Semi-automated quantification of axonal densities in labeled CNS tissue. J Neurosci Methods. 2006;155:172–179. doi: 10.1016/j.jneumeth.2005.12.021. [DOI] [PubMed] [Google Scholar]
- Hladuvka J, Groller E. Exploiting the Hessian matrix for content-based retrieval of volume-data features. Visual Comput. 2002;18:207–217. [Google Scholar]
- Ikonomovic MD, Abrahamson EE, Isanski BA, Wuu J, Mufson EJ, DeKosky ST. Superior frontal cortex cholinergic axon density in mild cognitive impairment and early Alzheimer disease. Arch Neurol. 2007;64:1312–1317. doi: 10.1001/archneur.64.9.1312. [DOI] [PubMed] [Google Scholar]
- Jellinger K, Braak H, Braak E, Fischer P. Alzheimer lesions in the entorhinal region and isocortex in Parkinson's and Alzheimer's diseases. Ann N Y Acad Sci. 1991;640:203–209. doi: 10.1111/j.1749-6632.1991.tb00218.x. [DOI] [PubMed] [Google Scholar]
- Kastner M. Protein liquid chromatography. 1st ed. Amsterdam ; New York: Elsevier; 2000. [Google Scholar]
- Kuhl DE, Minoshima S, Fessler JA, Frey KA, Foster NL, Ficaro EP, Wieland DM, Koeppe RA. In vivo mapping of cholinergic terminals in normal aging, Alzheimer's disease, and Parkinson's disease. Ann Neurol. 1996;40:399–410. doi: 10.1002/ana.410400309. [DOI] [PubMed] [Google Scholar]
- Lauria G, Hsieh ST, Johansson O, Kennedy WR, Leger JM, Mellgren SI, Nolano M, Merkies ISJ, Polydefkis M, Smith AG, Sommer C, Valls-Sole J, Force T. European Federation of Neurological Societies/Peripheral Nerve Society Guideline on the use of skin biopsy in the diagnosis of small fiber neuropathy. Report of a joint task force of the European Fe-deration of Neurological Societies and the Peripheral Nerve Society. Eur J Neurol. 2010;17:903–912. doi: 10.1111/j.1468-1331.2010.03023.x. e44-9. [DOI] [PubMed] [Google Scholar]
- Lehmann K, Hundsdorfer B, Hartmann T, Teuchert-Noodt G. The acetylcholine fiber density of the neocortex is altered by isolated rearing and early methamphetamine intoxication in rodents. Experimental Neurology. 2004;189:131–140. doi: 10.1016/j.expneurol.2004.05.017. [DOI] [PubMed] [Google Scholar]
- Li YP, Liu WC, Oo TF, Wang L, Tang Y, Jackson-Lewis V, Zhou C, Geghman K, Bogdanov M, Przedborski S, Beal MF, Burke RE, Li CJ. Mutant LRRK2(R1441G) BAC transgenic mice recapitulate cardinal features of Parkinson's disease. Nature Neuroscience. 2009;12:826–828. doi: 10.1038/nn.2349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu ZW, Zhang RL, Li Y, Cui YS, Chopp M. Remodeling of the Corticospinal Innervation and Spontaneous Behavioral Recovery After Ischemic Stroke in Adult Mice. Stroke. 2009;40:2546–2551. doi: 10.1161/STROKEAHA.109.547265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maguire EA, Gadian DG, Johnsrude IS, Good CD, Ashburner J, Frackowiak RS, Frith CD. Navigation-related structural change in the hippocampi of taxi drivers. Proc Natl Acad Sci U S A. 2000;97:4398–4403. doi: 10.1073/pnas.070039597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandl RC, Schnack HG, Zwiers MP, van der Schaaf A, Kahn RS, Hulshoff Pol HE. Functional diffusion tensor imaging: measuring task-related fractional anisotropy changes in the human brain along white matter tracts. PloS one. 2008;3:e3631. doi: 10.1371/journal.pone.0003631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marina N, Bull ND, Martin KR. A semiautomated targeted sampling method to assess optic nerve axonal loss in a rat model of glaucoma. Nature protocols. 2010;5:1642–1651. doi: 10.1038/nprot.2010.128. [DOI] [PubMed] [Google Scholar]
- Mechawar N, Cozzari C, Descarries L. Cholinergic innervation in adult rat cerebral cortex: a quantitative immunocytochemical description. J Comp Neurol. 2000;428:305–318. doi: 10.1002/1096-9861(20001211)428:2<305::aid-cne9>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- Meijering E. FeatureJ: A Java Package for Image Feature Extraction. 2003 http://www.imagescience.org/meijering/software/featurej/
- Misgeld T, Kerschensteiner M. In vivo imaging of the diseased nervous system. Nature reviews. Neuroscience. 2006;7:449–463. doi: 10.1038/nrn1905. [DOI] [PubMed] [Google Scholar]
- Mitchell SJ, Rawlins JN, Steward O, Olton DS. Medial septal area lesions disrupt theta rhythm and cholinergic staining in medial entorhinal cortex and produce impaired radial arm maze behavior in rats. J Neurosci. 1982;2:292–302. doi: 10.1523/JNEUROSCI.02-03-00292.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuys R, Donkelaar HJt, Nicholson C. The central nervous system of vertebrates. Berlin ; New York: Springer; 1998. [Google Scholar]
- Nolano M, Provitera V, Caporaso G, Stancanelli A, Vitale DF, Santoro L. Quantification of pilomotor nerves A new tool to evaluate autonomic involvement in diabetes. Neurology. 2010;75:1089–1097. doi: 10.1212/WNL.0b013e3181f39cf4. [DOI] [PubMed] [Google Scholar]
- Ogura T, Krosnowski K, Zhang L, Bekkerman M, Lin W. Chemoreception regulates chemical access to mouse vomeronasal organ: role of solitary chemosensory cells. PloS One. 2010;5:e11924. doi: 10.1371/journal.pone.0011924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogura T, Szebenyi SA, Krosnowski K, Sathyanesan A, Jackson J, Lin W. Cholinergic microvillous cells in the mouse main olfactory epithelium and effect of acetylcholine on olfactory sensory neurons and supporting cells. J Neurophysiol. 2011;106:1274–1287. doi: 10.1152/jn.00186.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, Franklin KBJ. The mouse brain in stereotaxic coordinates. 2nd ed. San Diego: Academic Press; 2001. [Google Scholar]
- Ramer LM, McPhail LT, Borisoff JF, Soril LJJ, Kaan TKY, Lee JHT, Saunders JWT, Hwi LPR, Ramer MS. Endogenous TrkB ligands suppress functional mechanosensory plasticity in the deafferented spinal cord. Journal of Neuroscience. 2007;27:5812–5822. doi: 10.1523/JNEUROSCI.0491-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ransmayr G, Cervera P, Hirsch EC, Berger W, Fischer W, Agid Y. Alzheimer's disease: is the decrease of the cholinergic innervation of the hippocampus related to intrinsic hippocampal pathology? Neuroscience. 1992;47:843–851. doi: 10.1016/0306-4522(92)90034-y. [DOI] [PubMed] [Google Scholar]
- Sato Y, Nakajima S, Shiraga N, Atsumi H, Yoshida S, Koller T, Gerig G, Kikinis R. Three-dimensional multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. Med Image Anal. 1998;2:143–168. doi: 10.1016/s1361-8415(98)80009-1. [DOI] [PubMed] [Google Scholar]
- Schols L, Bauer P, Schmidt T, Schulte T, Riess O. Autosomal dominant cerebellar ataxias: clinical features, genetics, and pathogenesis. Lancet Neurol. 2004;3:291–304. doi: 10.1016/S1474-4422(04)00737-9. [DOI] [PubMed] [Google Scholar]
- Scott RPW. Techniques and practice of chromatography. New York: Marcel Dekker; 1995. [Google Scholar]
- Shepherd GM, Raastad M, Andersen P. General and variable features of varicosity spacing along unmyelinated axons in the hippocampus and cerebellum. Proc Natl Acad Sci U S A. 2002;99:6340–6345. doi: 10.1073/pnas.052151299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soghomonian JJ, Doucet G, Descarries L. Serotonin innervation in adult rat neostriatum. I. Quantified regional distribution. Brain Res. 1987;425:85–100. doi: 10.1016/0006-8993(87)90486-0. [DOI] [PubMed] [Google Scholar]
- Squire LR, Ojemann JG, Miezin FM, Petersen SE, Videen TO, Raichle ME. Activation of the hippocampus in normal humans: a functional anatomical study of memory. Proc Natl Acad Sci U S A. 1992;89:1837–1841. doi: 10.1073/pnas.89.5.1837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tandan R, Bradley WG. Amyotrophic lateral sclerosis: Part 1. Clinical features, pathology, and ethical issues in management. Ann Neurol. 1985;18:271–280. doi: 10.1002/ana.410180302. [DOI] [PubMed] [Google Scholar]
- Trauth JA, McCook EC, Seidler FJ, Slotkin TA. Modeling adolescent nicotine exposure: effects on cholinergic systems in rat brain regions. Brain Res. 2000;873:18–25. doi: 10.1016/s0006-8993(00)02465-3. [DOI] [PubMed] [Google Scholar]
- Vonsattel JP, DiFiglia M. Huntington disease. J Neuropathol Exp Neurol. 1998;57:369–384. doi: 10.1097/00005072-199805000-00001. [DOI] [PubMed] [Google Scholar]
- Whitney MA, Crisp JL, Nguyen LT, Friedman B, Gross LA, Steinbach P, Tsien RY, Nguyen QT. Fluorescent peptides highlight peripheral nerves during surgery in mice. Nature biotechnology. 2011;29:352–356. doi: 10.1038/nbt.1764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong TP, Debeir T, Duff K, Cuello AC. Reorganization of cholinergic terminals in the cerebral cortex and hippocampus in transgenic mice carrying mutated presenilin-1 and amyloid precursor protein transgenes. J Neurosci. 1999;19:2706–2716. doi: 10.1523/JNEUROSCI.19-07-02706.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziehn MO, Avedisian AA, Tiwari-Woodruff S, Voskuhl RR. Hippocampal CA1 atrophy and synaptic loss during experimental autoimmune encephalomyelitis, EAE. Lab Invest. 2010;90:774–786. doi: 10.1038/labinvest.2010.6. [DOI] [PMC free article] [PubMed] [Google Scholar]