Computational adaptive optics for broadband optical interferometric tomography of biological tissue

Abstract

Aberrations in optical microscopy reduce image resolution and contrast, and can limit imaging depth when focusing into biological samples. Static correction of aberrations may be achieved through appropriate lens design, but this approach does not offer the flexibility of simultaneously correcting aberrations for all imaging depths, nor the adaptability to correct for sample-specific aberrations for high-quality tomographic optical imaging. Incorporation of adaptive optics (AO) methods have demonstrated considerable improvement in optical image contrast and resolution in noninterferometric microscopy techniques, as well as in optical coherence tomography. Here we present a method to correct aberrations in a tomogram rather than the beam of a broadband optical interferometry system. Based on Fourier optics principles, we correct aberrations of a virtual pupil using Zernike polynomials. When used in conjunction with the computed imaging method interferometric synthetic aperture microscopy, this computational AO enables object reconstruction (within the single scattering limit) with ideal focal-plane resolution at all depths. Tomographic reconstructions of tissue phantoms containing subresolution titanium-dioxide particles and of ex vivo rat lung tissue demonstrate aberration correction in datasets acquired with a highly astigmatic illumination beam. These results also demonstrate that imaging with an aberrated astigmatic beam provides the advantage of a more uniform depth-dependent signal compared to imaging with a standard Gaussian beam. With further work, computational AO could enable the replacement of complicated and expensive optical hardware components with algorithms implemented on a standard desktop computer, making high-resolution 3D interferometric tomography accessible to a wider group of users and nonspecialists.

The light microscope is a fundamental tool underpinning many historic developments in medicine and biology. Modern optical microscopy, capitalizing on the development of the laser, has provided capabilities to image thick specimens and visualize microstructure deeper into scattering tissues. The confocal laser scanning microscope uses a pinhole to reject light from out-of-focus planes to achieve superior optical sectioning and enable 3D imaging (tomography). With two-photon microscopy, imaging depth can be increased to hundreds of micrometers in biological tissue (1).

The development of optical coherence tomography (OCT) has enabled in vivo tomography with a relatively large imaging depth (1–3 mm) in scattering tissues (2–6). OCT has achieved widespread clinical use in ophthalmology (7), and applications in cardiology, oncology, gastroenterology, and dermatology are currently undergoing translation from the research lab into clinical practice (3, 8, 9). OCT has also found applications in developmental biology (10). In addition to imaging the structure of tissue, it can be adapted to perform molecular imaging (11, 12). Near-infrared broadband sources can provide micrometer scale axial resolution (13), but transverse resolution, which is inversely proportional to N.A., is typically low, resulting in an asymmetric 3D point-spread function (PSF). The use of higher N.A. optics (14) has enabled cellular resolution (15), but with significant reduction of the depth of field. One solution is to combine tomograms obtained at different focal depths (16), at the expense of acquisition time and mechanical scanning. Interferometric synthetic aperture microscopy (17, 18), a computed imaging technique based on a solution to the inverse scattering problem for OCT, enables object reconstruction with spatially invariant focal-plane resolution without having to scan the focus in depth. Although interferometric synthetic aperture microscopy (ISAM) corrects defocus for all depths, it does not account for aberrations of the incident beam (19).

Aberrations in optical microscopy degrade resolution and reduce the signal-to-noise ratio (SNR). Defined as deviations from ideal optical wavefronts, aberrations can be caused by the optical imaging system or by the sample itself. Adaptive optics provides a means to correct aberrations by physically modifying the effective pupil phase profile of the objective lens, enabling significant improvements in resolution and SNR (20–24). Adaptive optics has enabled high-resolution imaging of the rods and cones of the human retina, with confocal microscopy (24) and OCT (25–27). A disadvantage of adaptive optics (AO) methods is that they require relatively elaborate and expensive optical components, and any optimization of the aberration correction needs to be achieved at the time of imaging. Additionally, existing AO hardware is incompatible with catheter-based endoscopic OCT systems (6, 8, 9, 28) for imaging deep within the human body, as well as needle-based OCT systems (29). Both of these imaging configurations experience problems with astigmatism that are expected to become more prominent at higher resolution.

Computational correction of aberrations provides an alternative method of aberration correction, providing the flexibility of post-data-acquisition correction without the hardware overhead of AO. An example of this method is numerical aberration correction in digital holography (30–36). Aberration correction in digital holographic microscopy (DHM), however, has only been demonstrated for nonbiological samples or “thin” biological samples (e.g., a single cell) using discrete-wavelength optical sources, and not for broadband tomography of bulk biological tissue. A different computational AO (CAO) method proposed space-variant deconvolution to compensate sample-specific aberrations (37). Demonstrated by imaging of a fluorescent bead under an oil droplet, this method used a separate measurement of the sample by Nomarski differential interference microscopy to map its refractive index. This map was then used to perform 3D optical ray tracing to compute the magnitude of the aberrated PSF used for deconvolution. This CAO method is suited for noninterferometric imaging of fluorescence from relatively weakly scattering biological samples, and performed deconvolution based only on the magnitude of a computed PSF.

In this paper, we present a method for post-data-acquisition aberration correction that computationally modifies the effective pupil phase profile corresponding to the complex PSF of an OCT system, and demonstrate tomographic imaging of bulk biological tissue with computational aberration correction. An OCT tomogram is a record of both amplitude and phase of the backscattered field, and therefore it can be considered to be related to DHM (38). As in digital holography, the acquired signal is an invertible transformation of the optical field, suggesting it may be possible to compensate for beam aberrations. However, an OCT system possesses distinct advantages that make it well suited to performing high-resolution tomography in scattering (turbid) biological tissue. Unlike with DHM, in OCT and ISAM a broadband optical signal is collected. With a spectral-domain OCT system, reconstruction is simplified by the simultaneous (therefore phase-stable) recording of the wavelength-dependent interferometric signal at each lateral scan coordinate.

Another distinguishing characteristic of OCT from DHM is scanned acquisition with a focused beam, similar to a confocal microscope, which rejects cross-talk from adjacent regions and out-of-plane scattering in turbid samples. A challenge is presented by the fact that object reconstruction may need to account for spatially dependent phase noise from random fluctuations of interferometric optical path length or from beam scanning errors. We have developed algorithms to correct phase noise in order to generate phase-stable data for CAO and subsequent ISAM reconstruction. Additionally, the theoretical treatment of aberrations should account for the double-pass detection (reflection geometry) of an OCT system. In addition to providing a unique capability for correcting aberration effects in OCT and ISAM, our CAO technique is easily adaptable to other broadband interferometric imaging geometries, and for nonbiological imaging applications as well.

Results and Discussion

Fig. 1 demonstrates aberration correction of 3D, broadband, interferometric data acquired from a silicone phantom with subresolution titanium-dioxide (TiO₂) microparticles, acquired with a highly astigmatic beam (see Methods for details of the experimental setup and data acquisition). This sparse phantom provides a convenient measure of the depth-dependent 3D PSF of the system. An astigmatic optical system is characterized by asymmetry that results in two axially separated line foci that are orthogonal to each other in the transverse plane. The so-called circle of least confusion, where the transverse PSF of an aberrated optical system has the minimum circular cross-section, occurs midway between the two line foci, in the plane of least confusion. After standard OCT processing (see Methods for details of standard OCT, CAO, and ISAM processing), the 3D tomogram of the subresolution scatterers clearly shows the presence of two line foci associated with astigmatism (see OCT in Fig. 1). A plane of least confusion can be identified approximately midway between them, where the (aberrated) transverse PSF associated with each subresolution scatterer has a minimum circular cross-section. After CAO aberration correction, the plane of least confusion is restored as the nominal astigmatism-free focal plane, and the line foci are transformed into circular symmetric transverse PSFs free of astigmatism (see aberration-corrected OCT in Fig. 1). Subsequent ISAM resampling results in a 3D reconstruction of the phantom with the defocus removed (see aberration-corrected ISAM in Fig. 1).

Fig. 1.

Computational aberration correction of astigmatism in a silicone tissue phantom containing 1 μm titanium-dioxide particles. These images were generated from a single 3D dataset that was acquired with a highly astigmatic illumination beam. The OCT images show the two en face (x-y) planes with the best line foci, located 300 μm above and 300 μm below the plane of least confusion. The aberration-corrected OCT and aberration-corrected ISAM images show en face planes corresponding to the same depths as the OCT images. Dimensions of the 3D dataset are 256 × 256 × 1230 μm (x × y × z), where the units of the z axis denote optical path length.

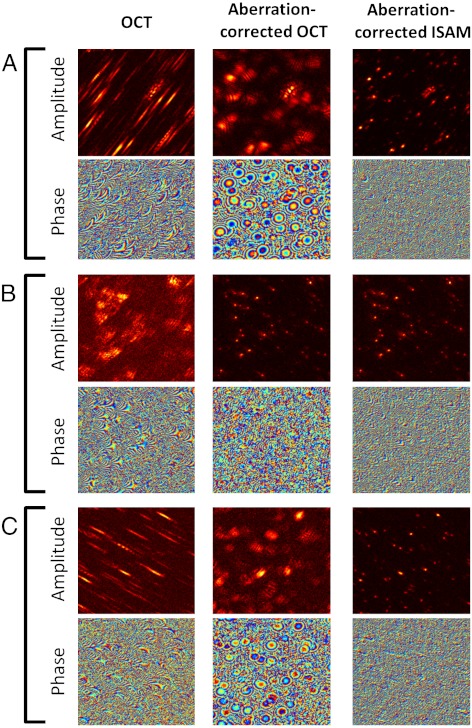
The effect of aberrations in the spatial domain is to broaden the complex system PSF and potentially introduce additional (non-Gaussian) structure. Fig. 2 and Movie S1 show the effect of CAO correction of astigmatism on both the amplitude and phase of the data. In particular, the phase of the aberration-corrected OCT at depths corresponding to the two line foci have circular symmetry, and the depth-dependent OCT resolution (Fig. 3A) is characteristic of imaging with a Gaussian beam. After CAO and ISAM, the 3D object scattering potential, η(x,y,z), is reconstructed with spatially invariant resolution at all depths (Figs. 1 and 3A). The procedure for computing the curves in Fig. 3 is given in Methods. Deviations from the ideal focal-plane resolution can be attributed to a non-Gaussian PSF (most likely from the presence of high-order aberrations), or to overlap between the PSFs of neighboring microparticles. Movie S1 demonstrates real-time tuning of the CAO correction for individual en face depths using the Zernike polynomials (39) for astigmatism (Z₅, Z₆) and defocus (Z₄), as well as spherical aberration (Z₁₁). The quartic term of Z₁₁ was isolated by applying a Z₄ defocus phase correction of equal and opposite sign to cancel the quadratic phase term of Z₁₁. Fig. S1 shows a plot of image metrics (as a function of the frame number in Movie S1), based on sensorless AO techniques (40–42) that provided feedback on the optimization of the aberration correction. Although the dominant aberration was astigmatism, the correction of quartic spherical aberration produced an appreciable improvement of the image metrics over the correction of only astigmatism and defocus, even at this relatively low N.A. of 0.1.

Fig. 2.

Complex signals from the silicone phantom data, showing the impact of computational correction of astigmatism on both the amplitude and phase. Images are arranged in columns according to the type of processing applied. The en face (x-y) planes shown are from the 3D silicone phantom dataset near (A) the upper line focus (z = 300 μm), (B) the plane of least confusion (z = 0 μm), and (C) the lower line foci (z = -300 μm), where the units of the z axis denote optical path length. Dimensions of all images are 256 × 256 μm.

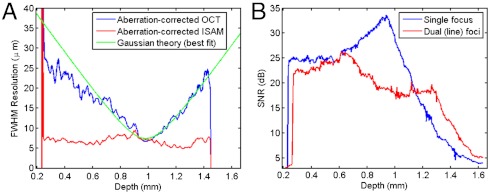
Fig. 3.

Depth-dependent resolution and signal-to-noise ratio in the silicone tissue phantom. (A) Resolution (along the x axis) vs. depth for the aberration-corrected OCT and ISAM, and (B) signal-to-noise ratio after ISAM reconstruction, comparing the cylindrical lens setup producing two axially separated line foci to a standard single-focus setup. The optical focus appears at z ≈ 1 mm because depth is plotted relative to zero optical path delay in the interferometer.

Aberrations are usually viewed as detrimental in optical microscopy. However, CAO provides the ability to exploit potential advantages of imaging with aberrated beams. An example of such a benefit is shown in Fig. 3B, which compares ISAM reconstructions with and without the astigmatism-producing cylindrical lens added to the sample arm optics. ISAM reconstructions after CAO demonstrate the advantage of a more uniform depth-dependent signal, thereby reducing the dynamic range required to represent the signal. At a given depth deep within the sample (e.g., z = 1.4 mm), this more uniform signal is also seen to increase SNR. The change in depth-dependent SNR can be attributed to the presence of two axially separated line foci, effectively forming two (partial) confocal gates within the sample. This result is of even greater benefit for high N.A. OCT, where the steep roll-off in signal strength with distance from focus demands data acquisition with a larger dynamic range.

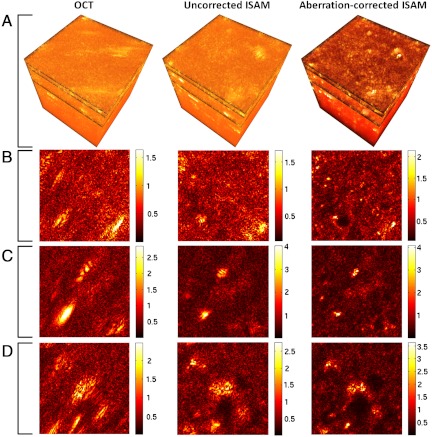
Fig. 4 demonstrates CAO in a biological sample, ex vivo rat lung tissue. Three-dimensional data were obtained using the same astigmatic setup used to acquire the phantom data in Fig. 1 and processed using the same computational aberration correction. The standard OCT tomogram shows astigmatic blurring of tissue structures, particularly evident in highly scattering regions. The application of ISAM without aberration correction corrects some defocus, but does not resolve fine sample structure, indicating that when aberrations are present, they must be accounted for in the reconstruction. (Note that this uncorrected ISAM processing is different to the aberration-corrected OCT processing in Figs. 1 and 2.) However, CAO followed by ISAM is seen to reconstruct the fine structure of the sample. In particular, correction of both astigmatism and defocus is clearly demonstrated at highly scattering regions of the sample.

Fig. 4.

Computational aberration correction of astigmatism in ex vivo rat lung tissue. The three-dimensional volumes and images were generated from a single dataset acquired with an astigmatic illumination beam, and are arranged in columns corresponding to the type of processing applied. (Note that the uncorrected ISAM processing is different to the aberration-corrected OCT processing in Figs. 1 and 2.) (A) Three-dimensional volumes with dimensions 256 × 256 × 270 μm (x × y × z), where the units of the z axis denote optical path length. (B–D) En face (x-y) planes at depths of (B) 640 μm above the plane of least confusion, (C) 620 μm above the plane of least confusion, and (D) 570 μm above the plane of least confusion. The tissue surface was 660 μm above the plane of least confusion. The tissue was thawed from storage at −80 °C before imaging. Gamma correction was used for dynamic range compression in the en face images, with γ = 0.8, γ = 0.7, and γ = 0.8 for the rows B, C, and D, respectively.

Computational AO is based on the ability to correct aberrations of a virtual (or computed) pupil rather than the physical pupil of the objective lens (see SI Text for a detailed treatment of the following description). From Fourier optics, the (transverse) optical field distribution at the beam focus, g(x,y,z = 0; k), at optical wavenumber k, is related to the objective lens pupil function by the Fourier transform (43). Therefore, from a measurement of the optical field at the nominal focus, such as g(x,y,0; k), a corresponding (virtual) pupil function can be computed via the transverse Fourier transform. The complex system PSF can be measured using a sparse phantom consisting of subresolution scatterers, such as the one in Figs. 1 and 2. However, due to the double-pass imaging geometry, this system PSF, h(x,y,z; k) ∝ g²(x,y,z; k), is a product of the (identical) illumination and collection beams (44, 45).

According to the convolution theorem, the transverse Fourier transform of the complex system PSF is the convolution of these virtual pupil functions. As with hardware-based AO, we express pupil aberrations using Zernike polynomials, but compute an aberration-correction filter as the (transverse) convolution of these aberrated (virtual) pupil functions. This aberration-correction filter, applied to the 3D Fourier transform of the OCT tomogram, “rephases” components in the transverse frequency domain of the focal-plane PSF to restore constructive interference across the band. This constructive interference results in recovery of diffraction-limited resolution at the nominal focus, accompanied by increased SNR (Figs. 1 and 2).

The 3D aberration correction filter implemented here corrects for phase deviations from the ideal transverse-frequency response of the system PSF. Although these results show that it works well in practice, we note that, in general, the convolution in Eq. S5 can manifest (depth-dependent) amplitude structure in the transverse frequency domain. This depth-dependent amplitude structure is relevant when combining CAO with ISAM, in order to reconstruct object structure away from the nominal aberration-free focus. Space-variant deconvolution (Fig. 6) can be used to correct such depth-dependent amplitude structure in the transverse frequency domain, at the expense of computation time.

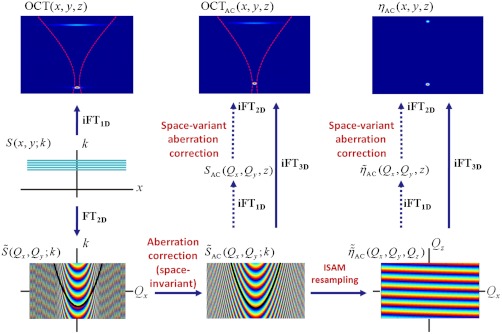
Fig. 6.

Overview of data processing showing the relationship between spectral data, S(x,y; k), and the intermediate signals resulting in the aberration-corrected OCT tomogram, OCT_AC(x,y,z), and aberration-corrected ISAM reconstruction of the scattering potential, η_AC(x,y,z). The dashed red curves in the OCT(x,y,z) and OCT_AC(x,y,z) images represent one transverse scan position of the incident optical beam with respect to the two-scatterer sample. The frequency domain images (Bottom) show the phase profile associated with the out-of-focus scatterer, with an ISAM resampling curve (corresponding to a fixed value of Q_z) superimposed in black. FT and iFT denote the Fourier transform and inverse Fourier transform, respectively. Bold arrows denote processing steps for space-invariant aberration correction, and the dashed arrows indicate the steps enabling space-variant aberration correction (i.e., at specific en face depths).

An important consideration for CAO and ISAM is phase stability, particularly for the case of in vivo measurements. Phase instabilities during data acquisition can degrade resolution and raise the noise floor of the reconstruction. The ISAM signal model recognizes that transverse beam scanning results in the acquisition of data at sequential spatial frequencies, (dependent on illumination angle), with a predictable phase profile (see the ISAM resampling curve in Fig. 6). The “interrogation time” for a given object coordinate increases with its distance from focus; thus, the (resolution) requirements on phase stability are expected to increase with distance from focus. For future in vivo applications of CAO and ISAM, the axial phase-correction procedure in this paper can be modified to use the cross-correlation of A scans based on sample data, and thereby not require a coverslip phase reference in contact with the sample. Additionally, significant increases in acquisition speed are feasible (8), which will minimize phase instabilities resulting from the motion of in vivo samples.

In conclusion, these results demonstrate computational aberration correction for broadband optical interferometric tomography. CAO provides the flexibility of postacquisition aberration control on a desktop computer without the need for complex and expensive AO hardware, and could enable aberration-free imaging with compact and inexpensive optics. Three-dimensional reconstructions of a tissue phantom using CAO and ISAM demonstrated spatially invariant ideal focal-plane resolution despite being imaged with a highly astigmatic beam. Additionally, the reconstruction based on imaging with the highly astigmatic beam, with dual line foci, had the advantage of a more uniform depth-dependent SNR as compared to that obtained from imaging with a standard single-focus beam. Real-time correction of astigmatism, defocus, and spherical aberration was demonstrated in the tissue phantom for discrete en face planes. Three-dimensional ISAM reconstructions of ex vivo rat lung demonstrate tomographic results in biological tissue that incorporate computational aberration correction. With the appropriate phase-correction algorithms, CAO may be applied retrospectively to existing OCT datasets; e.g., for retinal imaging, or for the correction of astigmatism typically encountered in catheter and needle-based OCT applications.

Computational adaptive optics could open new directions for optical science. For example, the formation of a high-resolution focal spot in biological tissue has benefited from AO via pupil segmentation techniques (46) that offer the capability of correcting large pupil phase gradients. The computed pupil in CAO provides the flexibility of a large number of independent segments and permits arbitrary phase profiles with unlimited range of phase correction, but without the limiting requirement of having to determine the phase correction at the time of imaging. CAO could also provide a new (numerical) capability for wavefront phase conjugation and enable related investigations into the phenomenon of subdiffraction focusing (47) via disorder introduced by biological tissues.

Methods

Experimental Setup and Data Acquisition.

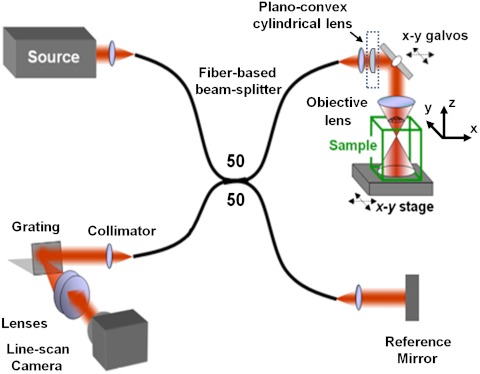
Measurements were acquired with a previously reported spectral-domain OCT system (17), with modifications to the sample arm optics. The sample arm (Fig. 5) was constructed using off-the-shelf optics, with nominal N.A. = 0.1 (calculated from the divergence angle corresponding to the 1/e² beam width). The design that minimized aberrations used identical doublets with focal length f = 19 mm (Thorlabs; AC127-019-B) for the collimator and objective lens. This optical configuration imaged the mode field diameter of the fiber with magnification M = 1, resulting in focal-plane resolution (1/e² beam width) of 5.6 μm and Rayleigh range of 30 μm. Astigmatism was introduced by adding a plano-convex cylindrical lens with focal length f = 1,000 mm (Thorlabs; LJ1516RM-B) directly after the collimator. The beam was steered using an x-y galvanometer pair (Cambridge Technology; 6220HM40B), with mirror apertures of 10 mm.

Fig. 5.

Schematic of the fiber-based spectral-domain OCT system. The sample arm of the standard OCT setup was modified using a plano-convex cylindrical lens (dashed box) in order to acquire datasets with astigmatism.

Three-dimensional datasets of 2,048 × 1,000 × 600 pixels (k × x × y) were acquired with isotropic spatial sampling in the x and y dimensions of 1 μm. Data were acquired at a rate of 10 kHz and with an exposure time of 40 μs. The frame rate was 9 Hz, allowing time between frames to rearm the frame trigger.

Data Processing and Phase Noise Correction.

An overview of the data processing and aberration correction for OCT and ISAM is shown in Fig. 6. The background spectrum was subtracted from the raw data, a Hilbert transform was performed along the k axis, and fixed and material dispersion were corrected (48) to obtain the complex interferometric signal S(x,y; k). Taking the inverse Fourier transform to obtain OCT(x,y,z), the focus depth was shifted to the depth corresponding to zero optical path delay (z = 0) by applying a circular shift. After a 3D Fourier transform, the 3D aberration correction filter was applied to the signal (the mathematical form of this filter is derived in SI Text). The aberration-corrected OCT tomogram was then obtained by taking a 3D inverse Fourier transform, and the aberration-corrected ISAM reconstruction was obtained via ISAM resampling (see SI Text for the mathematical form of the resampling curves) followed by a 3D inverse Fourier transform. For the ISAM resampling, cubic B-spline interpolation was used after first upsampling the data along the k axis by a factor of two (using the Fourier transform and zero padding) to increase interpolation accuracy.

Before CAO or ISAM processing, a phase-correction algorithm was applied to OCT(x,y,z) in order to remove axial and transverse phase noise resulting from interferometer axial path-length fluctuations or from beam scanning instabilities. Axial phase noise dominated and was corrected through the use of a phase reference coverslip placed in contact with the sample (17). To correct transverse shifts, the complex cross-correlation between frames (depth averaged in the transverse frequency domain) was calculated, and the transverse frequency domain phase ramp (transverse group delay in the space domain) between frames was compensated.

Image-Based Metrics for Optimizing the Aberration Correction Filter.

Two image metrics were computed based on sensorless AO techniques (40–42) and applied to the focal-plane amplitude image (Fig. S1 plots these image metrics during optimization of the aberration correction filter). The first metric was based on the peak values of the intensity, and the second on the image spatial frequency content. The intensity-based image metric was based on the underlying principle that the optimal pupil phase results in constructive interference at the focal plane and therefore the highest peak intensity, and was computed from an array of maximum values that were calculated for each row and separately for each column of the image (see the maximum intensity projection method described below, under Calculation of the Depth-Dependent Resolution and SNR). The metric was evaluated as the average ratio between the highest 10% of maxima values after aberration correction to the highest 10% of maxima values before aberration correction. The second metric was based on the assumption that the mid- to high-frequency content of an amplitude image should increase as the resolution improves (i.e., when aberrations are minimized). This metric was calculated as the ratio of energy within a bandpass frequency range of the transverse Fourier transform of the amplitude image, normalized to the total energy contained within the upper frequency limit.

Calculation of the Depth-Dependent Resolution and SNR.

The depth-dependent resolution in the sparse TiO₂ tissue phantom (Fig. 3A) was calculated using a previously reported method (18). The depth-dependent SNR in the tissue phantom (Fig. 3B) was estimated from the peak (magnitude) signals of point scatterers about a given depth, and the corresponding tomogram noise floor. Due to the sparse nature of the sample, the signal (in the SNR) was computed as the (depth-dependent) histogram mode of the maximum signals corresponding to an ensemble of particles over a depth range (rolling window of 26 depths spanning 52 μm), and the corresponding noise floor was computed as the histogram mode of the minimum signals. These two modes were calculated from the maximum intensity projection (MIP) taken over the range of depths in the rolling window to reduce sparcity, resulting in a 2D array of x by y pixels. From this MIP, an array of maximum values was calculated for each row and separately for each column, producing a total of x + y maxima values for calculating the signal histogram. An array of x + y minima values were similarly obtained for each depth. A robust estimation of the mode was obtained by fitting a quadratic function about the peak of each histogram and computing the turning point of the fit.