Influence of water on the work function of certain metals

Abstract

Experiments were carried out to explore the effect of light on Au, Pt and Cu surfaces immersed in water, in order to study the changes of work function arising from the interaction between the metallic surfaces and water. The results show an action of liquid water about three times larger than that of low-temperature ice. Theoretical calculations, present in literature, have predicted values much lower than those we measured. The substantial changes in work function measured here appear to arise from the complex structure of water in the vicinity of the metal surface.

1. Introduction

In exploring the electrochemical behavior of various metals in aqueous solution we recently came upon an unexpected finding: certain metals showed solute-exclusion zones similar to those found next to hydrophilic polymers, gels, and biological surfaces. These zones exclude solutes and particles. With physical properties different from liquid water, this so-called “exclusion zone” has been considered possibly another phase of water (see, as for instance, http://www.youtube.com/watch?v=V7jKL2-B0QA&feature=related). Exclusion zones are sensitive to light [1], especially in the infrared range, and particularly 3.1 μm. All such experiments were carried out with polymeric substances. Since exclusion zones are sensitive to light and they are found as well next to metals, we explored whether they might play some role in the interaction between light and metal surfaces. In spite of numerous studies [2–5], the behavior of the water–metal interface is not fully understood, and, understanding would be of considerable interest due to its importance in fuel cells for hydrogen production, storage, and conversion.

Of special interest is the effect of light on metals immersed in water. Some investigators have tackled this issue both from a theoretical [6,7] and an experimental point of view. The experiments have been conducted at very low temperatures with water in the solid state. The effect, limited to a decrease on the order of 1 eV [8], appears to depend on the number of water layers grown on the metal surfaces [9]. Considering the peculiar characteristics of liquid water, it seemed interesting to us to study the influence of this phase on metals. Some theoretical papers foresee some effect of water on the work function, W, of metals even at room temperature [6], supposing that the effect comes from only the first layer of water. Experimental results in this frame could provide information on the robustness of these theoretical approaches and, due to the dependence of the measured W changes on the number of layers, provide information also on how many layers are involved. Therefore, we have explored the effects of light on the electrode potential of some metals immersed in water at room temperature.

2. Materials and methods

Water

Deionized water was obtained from a NANOpure Diamond ultrapure water system, and had a resistivity > 18 m cm.

Chemicals and metals

CH₃COOH (>99.8%) and Na₂SO₄ (ACS grade) were obtained from Fisher Scientific, Fairlawn (NJ), (NH₄)₂SO₄ (ACS grade) from S.T. Maker Inc. Phillipsburg (NJ), NaCl (ACS grade), NaOH (>99.99), Cu, Pt and Au (all 99.99% purity) from Sigma Aldrich, St. Louis (MO).

The metal foils were cut to suitable pieces whose illuminated area was 44 mm². After the initial preparation the metals were cleaned following standard procedures [10]. Before and after each measurement day, Pt and Au surfaces were lightly buffed with an ultrapure water-soaked lab tissue. In the case of Cu the oxidation layer was removed using sandpaper of 400 grit and then the sample was accurately rinsed with ultrapure water.

All experiments were carried out at room temperature, 21–22°C. The temperature of the illuminated sample was stable during illumination time inside 0.1° C.

Conductivity of water and solutions was measured by a CON 110 meter (OAKTON Instruments, Vernon Hills, IL). pH values were measured using a Corning Pinnacle 530 PH meter (Nova Analytics, Woburn, MA).

As reference electrode for the potential measurements, the Ag/AgCl half-cell FLEX-REF 138362 (World Precision Instruments, Sarasota FL) was used. The difference of potential between the metals and the reference electrode, was measured by a Keithley Model 6512 Electrometer, (measurement range 10 μV – 200 V, sensitivity 4½ digits, input resistance 200 T) and by a Tektronix TDS2004B Oscilloscope, with a high input impedance (10 G), instrumentation amplifier.

Different LEDs were used as light sources. If their spectral half-width exceeded 10 nm it was reduced using suitable bandpass filters. We used 5 LEDs produced by Luxeon Philips Lumileds San Jose, Ca: LXML-PR01-0500 (448 nm), LXML-PB01-0040 (470 nm), LXML-PE01-0080 (505 nm), LXML-PM01-0100 (530 nm), LXML-PL01-0040 (590 nm). Each one of them was coupled with a reflecting parabola and a bandpass interference filter. The filters (Edmund Optics Inc., Barrington, NJ) had a spectral half-width of 10 nm and their central wavelengths were 450, 470, 505, 532 and 589 nm.

Moreover two other LEDs were used: a UVTOP270 (270 nm) by Sensor Electronic Technology Inc., Columbia SC and a NSHU551A (375 nm) by Nichia Corporation, Tokushima, JAPAN. The light power reaching the metal position was measured with a Newport 1918-C meter equipped with a 818UV quantum detector.

Figure 1 shows the spectrum (according to the provider’s information), and the relative intensity of the light sources measured with the Newport meter. Each measurement required one full day: At the beginning the metal and reference electrode were put in freshly produced water. In about 30 minutes the metal reached a stable electrode potential V_M. At this point the metal was illuminated and the changes of V_M were detected. When the Keithley Electrometer was used the metal was illuminated for 60 s and V_M was measured every 10 s. When the Tektronix Oscilloscope was used the signal was continuously recorded for 225 s. Within this interval the sample was illuminated for 120 s and the values of V(t), during the illumination time, were sampled every 30 s, starting from the start time of the illumination. The light sources did not illuminate the reference electrode.

Fig. 1.

Overall spectra of the light sources used during the experiments, normalized to the intensity of the 448 nm LED.

After every illumination, V_M recovers its previous value in 20 minutes. A single sample was used every day, and it was illuminated four times with all the light sources. To avoid systematic errors, the order of the different wavelengths was changed each time.

At the end of a measurement day we obtained an array of values of the electrode potential of the metal M, V_M (λ, t), for the different wavelengths and the different times from illumination onset. Because the LED intensity and the optical absorbance of the metals depend on wavelength, the measured values were normalized to the value measured at 450 nm according to the following expression

$$\mathrm{\Delta }{\overline{V}}_M(\lambda )=\frac{I_S(450)\ast (1-R_M(\lambda ))}{I_S(\lambda )\ast (1-R_M(450))}\frac{{\displaystyle \sum _{t=1}^N}\frac{\mathrm{\Delta }{V}_M(\lambda ,t)}{\mathrm{\Delta }{V}_M(450,t)}}{N}$$ (1)

Where

• I_S(λ) is the intensity of the source with wavelength,

• I_S(450) is the intensity of the 450 nm source,

• R_M(λ) is the reflectivity of the metal at wavelength,

• R_M(450) is the reflectivity of the metal at 450 nm,

• V_M(λ,t) and V_M(450,t) are the voltage respect to the standard electrode measured, for the values and 450 of the wavelength, at the time t from the illumination onset, and

• V_M(λ): is the value of the normalized difference of potential averaged over the whole illumination time.

3. Results and discussion

The metal electrode dipped in freshly produced pure water (pH=5.5±0.2) presents, respect to the reference electrode, a potential difference V_M depending on the nature of metal (470 ±20 mV for Pt, 380 ±15 mV for Au and 100 ± 10 mV for Cu) [10]. During an experiment going on all day, the pH value slightly decreases, of about 0.2, probably due to the solution of atmospheric CO2 in water. This little change has no remarkable influence on measured values of VM. At first we checked the influence of solution conductivity and pH on these values. The conductivity was changed by adding either sodium sulphate, sodium chloride, or ammonium sulphate, whereas pH was increased by adding sodium hydroxide, or decreased by adding acetic acid. We found that V_M is independent of the conductivity, but it is strongly influenced by pH (V_{Pt (pH=4)}=650mV, V_{Pt (pH=7)}=130mV).

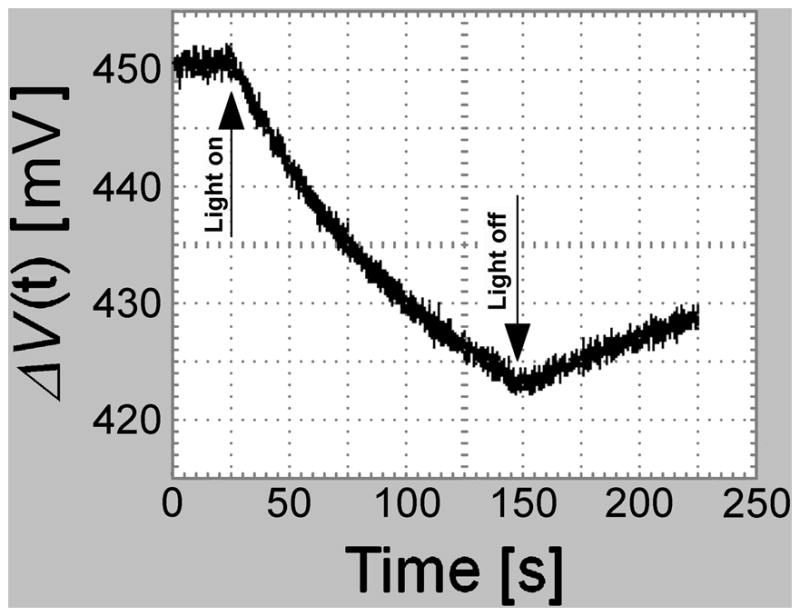
Figure 2 shows that during illumination, platinum’s V_Pt decreases in a well-defined way. After illumination it slowly recovers its initial value. The amplitude of the response V_M (λ, t) depends both on conductivity and pH. On increasing the conductivity of the water, V_M (λ, t) tends to zero, and is measurable only with the higher intensity sources. An increase of pH produces an effect similar to the increase of conductivity, strongly diminishing V_M (λ, t). A decrease of pH, instead, amplifies the effect.

Fig. 2.

Pt: Influence of the illumination on the time trend of V(t) for Pt illuminated by the LED LXML-PR01-0500 (448 nm) with a 910 mW radiometric power The Pt electrode was immersed in freshly prepared water (pH= 5.5±0.2).

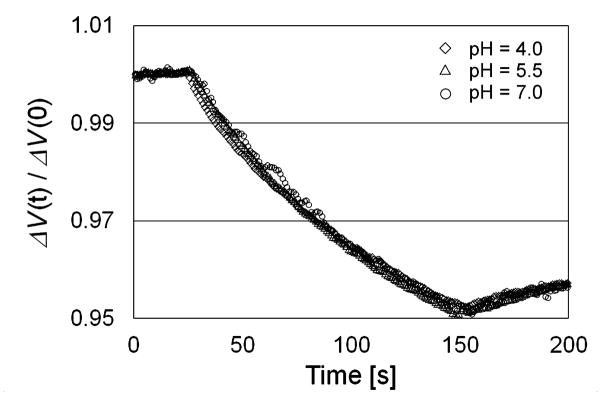
Interestingly, a change of pH has a proportional effect on both V_M and V_M (λ, t). This is shown in Figure 3, where the trends for three pH values have been compared after normalizing the starting potential to a common value of 1.0.

Fig. 3.

Relative effects of Pt illumination at different pH values.

Experiments, conducted on water with pH 5.5±0.2, showed that, on increasing the wavelength, the effect of light became progressively weaker.

This suggests that a kind of photoelectric effect is at work. In this case, the squared intensity of the measured effect should depend linearly on the energy of the impinging photons [11] and the energy threshold of the effect should give information on the minimum energy E₀ needed to remove an electron from the metal to a point in the water immediately outside its surface. To obtain the work function it should be necessary to add to E₀ the value of V₀, the liquid electron affinity of water. But, according to recent literature [12], V₀ in pure water is of the order of 0.1 eV or perhaps even slightly positive. So we consider the work function equal to E₀.

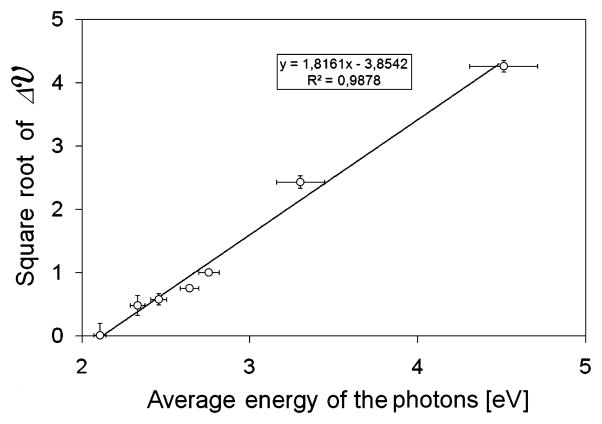
Fig. 4 shows the square root of V_Pt(λ) as a function of the energy of the corresponding photons.

Fig. 4.

Square root of V_Pt (λ)as a function of the energy of the corresponding photons. The horizontal error bars represent the spectral half-widths of the sources while the vertical error bars represent the standard deviation of V_Pt (λ).

It is possible to see that the square root of V_M (λ) can be described as a linear function of the energy of the photons with a high R² value. This trend is typical for the photoelectric effect [11]. W can be easily obtained because it is the horizontal intercept of the linear trend. In figure 4 this value is 2,12 ± 0,09 eV.

Table I summarizes the results of all experiments. It shows that the values obtained from the different experiments on the same metal are well reproducible. The Table shows also that the presence of water causes a substantial decrease of W for all metals, achieving a value that is about 40% of the value in vacuum. The W values for the three metals appear to be slightly different but it is not possible to conclude that these differences are statistically significant.

Table 1.

Values for W obtained in our different experiments compared with literature values for the same metals in vacuum.

Metal	Exp. 1	Exp. 2	Exp. 3	Average	In vacuum
Pt	2.14 ± 0.13	2.12 ± 0.09	2.12 ± 0.5	2.12 ± 0.09	5.12–5.93
Au	2.24 ± 0.10	2.26 ± 0.10	2.23 ± 0.6	2.26 ± 0.10	5.10–5.47
Cu	1.98 ± 0.16	2.08 ± 0.08	2.05 ± 0.6	2.08 ± 0.08	4.53–5.10

4. Conclusion

The photoelectric effect has been experimentally studied in vacuum for metals covered by monolayers of water, at 77 K [8] or with several ice layers in the range 100 – 180 K [9]. To our knowledge, no data are present in literature about metals immersed in water at room temperature. Our results show an action of liquid water on the work function of some metals much larger than predicted from theoretical calculations.

According to reference [9], the change in W increases with the number of ice layers and depends on the structure of the monolayer. Moreover simulations predict, with good approximation, the behavior of a single layer of ice deposited on a metal surface. In some cases the simulations have been extended to predict the behavior of liquid water at room temperature, suggesting a lowering of W on the order of 1 eV for platinum and 0.5 eV for gold.⁶

Our results do not agree with those predictions. The simulations explain the decrease in W by the creation of a highly polarized layer at the surface between metal and ice. On the other hand, the dependence of the change in W on the number of ice layers grown on the surface has been experimentally observed.

Following the same line of thought, it therefore seems reasonable to suppose that the substantial changes in W measured here are due to a complex structure of water in the vicinity of the metal surface, given the substantial difference with the theoretical predictions for a single bilayer.

This would be a fact confirmed by recent observations of the formation of extensive “exclusion zones” in water in the vicinity of metal surfaces [10]. Further studies will be needed to explore the nature of these zones and the mechanism by which they impact the metal work function.

Highlights.

• Light changes the electrode potential of some metals immersed in water.

• Relative intensity of the changes don’t depend on pH or water conductivity.

• Work function at water-metal interfaces is much higher than expected.