Abstract
Anomaly detection involves identifying rare data instances (anomalies) that come from a different class or distribution than the majority (which are simply called “normal” instances). Given a training set of only normal data, the semi-supervised anomaly detection task is to identify anomalies in the future. Good solutions to this task have applications in fraud and intrusion detection. The unsupervised anomaly detection task is different: Given unlabeled, mostly-normal data, identify the anomalies among them. Many real-world machine learning tasks, including many fraud and intrusion detection tasks, are unsupervised because it is impractical (or impossible) to verify all of the training data. We recently presented FRaC, a new approach for semi-supervised anomaly detection. FRaC is based on using normal instances to build an ensemble of feature models, and then identifying instances that disagree with those models as anomalous. In this paper, we investigate the behavior of FRaC experimentally and explain why FRaC is so successful. We also show that FRaC is a superior approach for the unsupervised as well as the semi-supervised anomaly detection task, compared to well-known state-of-the-art anomaly detection methods, LOF and one-class support vector machines, and to an existing feature-modeling approach.
Keywords: Anomaly detection, Unsupervised learning
1 Background
Anomaly detection involves the identification of instances that come from a different distribution or class than the majority. Examples of this type of task include fraud detection (e.g., identify fraudulent credit card transactions among a majority of valid ones), and intrusion detection (e.g., distinguish an attack from normal network activity). As a learning task, anomaly detection may be semi-supervised or unsupervised.1 In a semi-supervised anomaly detection task, we assume all the training instances come from the “normal” class and our goal is to distinguish future instances that come from a different distribution (“anomalies”). In an unsupervised anomaly detection task, we are given one sample that is a mixture of normal and anomalous instances, and the goal is to differentiate them. The proportion of anomalies is generally small, but its exact value is often unknown and varies from task to task.
We focus on tasks where data instances are represented by feature vectors. That is, we are given a training set of N examples
 = {x1,
x2, …,
xN }. Each example xj is a fixed-length vector of D features xj = 〈xj1, xj2, …, xj D〉 of types t = 〈t1, t2, …, tD〉. Our goal is to learn a function f: t → ℝ that maps a query vector xq to a real-valued anomaly score. In the semi-supervised anomaly detection task, we assume all of
= {x1,
x2, …,
xN }. Each example xj is a fixed-length vector of D features xj = 〈xj1, xj2, …, xj D〉 of types t = 〈t1, t2, …, tD〉. Our goal is to learn a function f: t → ℝ that maps a query vector xq to a real-valued anomaly score. In the semi-supervised anomaly detection task, we assume all of
 come from the normal class, and f is used to classify or rank future instances. In the unsupervised anomaly detection task, we assume that a majority of
come from the normal class, and f is used to classify or rank future instances. In the unsupervised anomaly detection task, we assume that a majority of
 are normal, and use f to classify or rank each x
j ∈
are normal, and use f to classify or rank each x
j ∈
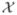 .
.
1.1 Distance- and density-based approaches
Most current approaches make judgments based on the distance among instances. That is, they map each instance to a point in some representation of feature space, and then measure the distance among these points.2 For example, one approach is to cluster the points, and then identify anomalies as points that are far away from any cluster centroid (Smith et al. 2002). Alternatively, one may rank each instance by the distance to its kth nearest neighbor (the larger the distance, the more likely the instance is to be anomalous, Byers and Raftery 1998; Guttormsson et al. 1999). The local outlier factor method (LOF) (Breunig et al. 2000) compares the distance between a point and its nearest neighbors to the density among those neighbors. It identifies anomalies as points relatively far from local groups. That is, LOF is a density-based approach that has the advantage of distinguishing between a point near the boundary of a sparse cluster and a point that does not appear to be part of any cluster or distribution at all. This is an important consideration and makes LOF one of the best general approaches to anomaly detection. Classification is also used in anomaly detection. For example, given a set of labeled training data for multiple “normal” classes, classification algorithms can be used to distinguish the normal classes from each other. Anomalies are instances that do not appear to be part of any normal class (Chandola et al. 2009). These approaches require labels that are often not available. However, one-class support vector machines (SVMs) are able to learn models from one class of training instance (Schölkopf et al. 2000). They attempt to separate the training examples from the rest of feature space and rank anomalies according to their distance from this region. For a survey of anomaly detection problems and current approaches, see Chandola et al. (2009).
1.2 Feature modeling approaches
All of the approaches above assume that anomalies can be identified by their distance to normal instances in feature space. An alternative framework is to model features individually, as shown by Huang et al. (2003) and our own approach (Noto et al. 2010). Feature-modeling anomaly detection approaches use supervised learning algorithms to learn predictive models of each feature, based on the other features. The intuition is that these models represent the underlying relationships among features that hold for the normal class. These relationships may not hold for an alternative distribution and therefore feature models that predict the wrong feature value provide evidence of an anomaly.
Any implementation of feature-modeling involves three key design decisions:
For which features do we learn a predictive model, and which other features do we use in each model?
Which supervised learning algorithm(s) do we use to train the feature models?
How do we combine the set of feature models
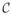 into a single anomaly score for a query instance xq? That is, what is the definition of f (
into a single anomaly score for a query instance xq? That is, what is the definition of f (
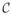 ,
xq) → ℝ?
,
xq) → ℝ?
Without any feature-specific background knowledge, there is no basis to choose to model particular features over others. A natural choice is therefore to learn predictors for all features and use all other features (potentially) in their predictive models. That is, if ρi is the function mapping a vector x to just the components of x that are used to predict feature i, then we choose
| (1) |
for all i. This means that
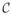 = {C1, C2, …, CD} consists of one predictive model for each feature and each Ci is a function mapping the subset of features ρi (xq) of a query instance xq to a prediction of its ith feature value. Its type is Ci: ρi(t) → ti, where t = 〈t1, t2, …, tD〉 are the types of each of the D features.
= {C1, C2, …, CD} consists of one predictive model for each feature and each Ci is a function mapping the subset of features ρi (xq) of a query instance xq to a prediction of its ith feature value. Its type is Ci: ρi(t) → ti, where t = 〈t1, t2, …, tD〉 are the types of each of the D features.
For the second decision, any supervised learning algorithm can be used in principle to infer a feature predictor Ci, as long as it is compatible with the feature types. This holds for any feature type, but by and large it means that Ci must be a regression model if ti is numeric, and Ci must be a classifier if ti is nominal.3
For the third design choice, the definition of f(
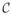 , xq) → ℝ, Huang et al. first suggest using the average match count, defined as the average number of correct predictions per example:
, xq) → ℝ, Huang et al. first suggest using the average match count, defined as the average number of correct predictions per example:
| (2) |
If xq is an anomaly, then fewer Ci classifiers will predict the observed xqi values correctly. Therefore, the lower the average match count, the more likely the instance is anomalous. Recall that Ci (ρi (xq)) returns a feature value of type ti. This means that average match count is not compatible with real-valued features, because the prediction can never exactly match the observed value.
Average match count does not account for the classifier’s uncertainty, however. The observation, that Ci (ρi (xq)) is not equal to xqi, is more significant if the classifier is more confident in its prediction. Huang et al. therefore suggest the alternative average probability:
| (3) |
P(xqi |Ci, ρi (xq)) is the likelihood of an observed feature value xqi given the feature model Ci and the other features ρi (xq), and Eq. 3 requires that this quantity be defined. Fortunately, it is the natural output of some classifiers such as naïve Bayes, and there are standard ways of estimating likelihoods from many other classifiers, such as decision trees (Quinlan 1990). In (Huang et al. 2003), present cross-feature analysis (CFA), which uses average probability. CFA discretizes all numeric features so they can be modeled by a classifier.4 In (Huang et al. 2003), the authors experiment with C4.5 (decision trees) (Quinlan 1993), RIPPER (a rule learner) (Cohen 1995), and the naïve Bayes classifier (Mitchell 1997), and use the likelihood associated with observed feature values according to these classifiers.
We recently presented feature regression and classification (FRaC) (Noto et al. 2010), another feature modeling approach that measures the log-loss, or amount of surprisal (Shannon 1948), of the observation xq, given its feature predictions.
| (4) |
We interpret the surprisal as the amount of evidence (measured in bits of information, if we use log base 2) that an instance is anomalous, and FRaC uses the sum of surprisal over all features to produce the surprisal anomaly score:
| (5) |
FRaC does not use the classifier Ci directly to define P(xqi). Instead, it uses cross-validation to compute Ai, a set of (observed, predicted) feature i values, one pair for each training set example, and builds an error model, Ei, to model the distribution of prediction errors in Ai. FRaC defines p(xqi) in terms of Ei and Ci (ρi (xq)).
This technique has the important advantage of being compatible with any feature type, as long as an appropriate error model is defined. For numeric and nominal features, it is straightforward to model the error.
In our experiments with FRaC, we define the error of a numeric feature as the difference between an observed and a predicted value, xqi – Ci (ρi (xq)). We divide the real line of possible error values into bins (N is the training set size). For each bin, we count how often an error in the corresponding range occurs in Ai. We then normalize the resulting histogram of counts, making it a probability distribution. (In our experiments, we also smooth the distribution with a Gaussian-shaped kernel that has a standard deviation of one bin (John and Langley 1995; Noto et al. 2010).) Finally, we calculate P(xqi | Ei, Ci (ρi (xq))) as the mass of the bin corresponding to xqi – Ci (ρi (xq)).
It is important to note that discretizing the error after training is not the same as discretizing the numeric features into nominal features before training, and does not have the same affect on performance. In Sect. 3.1 we empirically investigate the cost of discretizing numeric features.
If i is a nominal feature, then the error distribution Ei takes the form of a confusion matrix. Put simply, given a query instance xq, FRaC will predict its i th feature value to be g. If i is nominal, then we estimate the likelihood of the observed value y to be the frequency in Ai of the value y when it was predicted to be g. Formally, the type ti of a nominal feature is a set of ki possible values. Let δ(·) map each possible value in ti to a unique integer 1, 2, …, ki. The error distribution for i is then a confusion matrix M where each Mδ(g), δ(y) is the number of pairs in Ai equal to (y, g) (i.e., xj has the predicted value Ci (ρi (xj)) = g and the observed value xji = y). After normalizing each row of M so that for all g, P(xqi|Ei, Ci (ρi (xq))) is given by the matrix entry Mδ(Ci(ρi(xq))), δ(xqi). (In our experiments, we smooth the error distribution by adding a pseudocount of one to each entry of M before normalizing.)
The choice of supervised learning algorithm used to infer feature models is not a fundamental part of the feature modeling approaches, and may seem arbitrary for a general-purpose anomaly detector. Different supervised algorithms use different hypothesis spaces, and there is no one hypothesis space ideal for all features. FRaC learns multiple models for each feature, each with its own bias, and combines them in a “feature ensemble,” in an attempt to benefit from all of them.
Using surprisal, it is straightforward to combine the results for P models by simply adding the scores associated with each model Cpi, p ∈ {1, 2, … P}.5 In Sect. 3.2, we empirically demonstrate the benefits of doing so.
Finally, in the cases where the query instance feature value xqi is missing, FRaC uses the entropy (this is the expected surprisal) of feature i’s training set distribution in place of the surprisal score. This is equivalent to subtracting the entropy from each surprisal score and using zero when the feature value is missing. We call this anomaly score normalized surprisal. This is the definition of f (
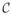 , xq) → ℝ that FRaC uses. If there are P feature prediction models, then normalized surprisal is defined as:
, xq) → ℝ that FRaC uses. If there are P feature prediction models, then normalized surprisal is defined as:
| (6) |
The entropy of a collection
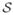 is given by
is given by
| (7) |
where ν corresponds to each of the k distinct values in
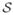 and pν is the proportion in
and pν is the proportion in
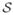 of items that have that value. If ti is nominal, it is straightforward to use Eq. 7. If ti is numeric, we discretize the values in {x1i, …, xNi} into
bins and use Eq. 7. A detailed description of our entire approach is given in Algorithm 1.
of items that have that value. If ti is nominal, it is straightforward to use Eq. 7. If ti is numeric, we discretize the values in {x1i, …, xNi} into
bins and use Eq. 7. A detailed description of our entire approach is given in Algorithm 1.
Algorithm 1.
Outline of our approach, showing the use of cross-validation to estimate training set error and the use of multiple prediction models. The running time depends on the supervised feature prediction algorithm(s) and is otherwise linear in the number of features and feature predictors.
input:N training examples
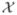 = {x1,x2, …,xN }, any number of test examples xq = {x1,x2, …,xN }, any number of test examples xq
|
| for each feature i ∈ {1, 2, …, D} do |
| for each feature prediction model p ∈ {1, 2, …, P} do |
| Ap,i ← ∅//Ap,i will be a set of training set |
| //(observed feature value, predicted feature value) pairs we can use to |
| //build an error model to estimate P(xqi |Cp,i (ρi (xq))) for anyxq |
| for each cross-validation fold fdo |
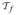 , ,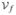 ← divide( ← divide(
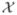 , f)//divide , f)//divide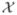 into a training set into a training set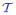
|
//and a validation set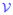 , unique to this fold , unique to this fold
|
valsetf ← (ρi (x), xji) for each xj ∈
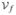
|
trainset f ← (ρi (x), xji) for each xj ∈
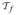
|
| Cp,i, f ← train p(trainset f)//learn a feature i predictor using model p |
| Ap,i ← Ap,i ∪ (xji, Cp,i, f (ρi (xj))) for each xj ∈ valset f |
| end for |
| Ep,i ← error_model(A p,i)//model the distribution of error A p,i |
| //(the model type depends on the type of feature i, see text) |
trainset ← (ρi (xj), xji) for each xj ∈
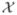
|
| Cp,i ← train(trainset)//the “final” predictor trained on the entire |
//training set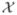 , used to make test set predictions , used to make test set predictions
|
| end for |
| end for |
| for each test example xqdo |
| //output the normalized surprisal score as the sum |
| //over P feature prediction models. |
| //P(xqi) depends on C p,i (ρi (xq))) and E p,i. |
| output: |
| end for |
In Noto et al. (2010), we introduced FRaC and compared it to LOF and one-class SVMs. The contributions of this paper are as follows: (i) we compare FRaC to cross-feature-analysis (Huang et al. 2003) on semi-supervised anomaly detection tasks (Sect. 2), (ii) we explain why FRaC succeeds, using extensive new experiments and several examples of feature models learned by FRaC on real data sets (Sect. 3), and (iii) we present and defend FRaC as a superior approach for the unsupervised anomaly detection task (Sect. 4).
2 Semi-supervised experiments
To evaluate FRaC as a general-purpose approach to the semi-supervised anomaly detection problem, we run it on several independent data sets and compare its performance to that of local outlier factor (LOF) (Breunig et al. 2000), a one-class SVM (Schölkopf et al. 2000), and cross-feature analysis (CFA) (Huang et al. 2003).6–7
2.1 Evaluation testbed
As a testbed, we select all classification data sets from the UCI machine learning repository (Asuncion and Newman 2007) with at least 100 examples that are (i) listed as being classification tasks in feature-vector format at http://archive.ics.uci.edu/ml, and (ii) have a .data file in the corresponding machine-learning-databases public directory at ftp.ics.uci.edu. If the directory contains multiple data sets, we select one arbitrarily. The resulting testbed contains 47 data sets, listed in Table 1.
Table 1.
The 47 UCI data sets we use to evaluate our anomaly detection methods. All data sets are publicly available
| Data set | Examples | Features |
|---|---|---|
| abalone | 4,177 | 8 |
| acute | 120 | 6 |
| adult | 32,561 | 14 |
| annealing | 798 | 18 |
| arrhythmia | 452 | 266 |
| audiology | 200 | 62 |
| balance-scale | 625 | 4 |
| blood-transfusion | 748 | 4 |
| breast-cancer-wisconsin | 569 | 31 |
| car | 1,728 | 6 |
| chess | 3,196 | 36 |
| cmc | 1,473 | 9 |
| connect-4 | 67,557 | 42 |
| credit-screening | 690 | 15 |
| cylinder-bands | 540 | 37 |
| dermatology | 366 | 34 |
| echocardiogram | 132 | 7 |
| ecoli | 336 | 7 |
| glass | 214 | 9 |
| haberman | 306 | 3 |
| hayes-roth | 132 | 4 |
| hepatitis | 155 | 19 |
| horse-colic | 300 | 27 |
| image | 210 | 18 |
| internet_ads | 3,279 | 1,558 |
| ionosphere | 351 | 33 |
| iris | 150 | 4 |
| letter-recognition | 20,000 | 16 |
| libras | 360 | 90 |
| magic | 19,020 | 10 |
| mammographic-masses | 961 | 5 |
| mushroom | 8,124 | 21 |
| nursery | 12,960 | 8 |
| ozone | 2,536 | 72 |
| page-blocks | 5,473 | 10 |
| parkinsons | 195 | 22 |
| pima-indians-diabetes | 768 | 8 |
| poker | 25,010 | 10 |
| secom | 1,567 | 474 |
| spambase | 4,601 | 57 |
| statlog | 1,000 | 20 |
| tae | 151 | 5 |
| tic-tac-toe | 958 | 9 |
| voting-records | 435 | 16 |
| wine | 178 | 13 |
| yeast | 1,484 | 8 |
| zoo | 101 | 16 |
For our experiments, all of the features in this testbed are considered to be either (i) nominal, taking on one of a finite number of values, or (ii) numeric, taking on either integer or real values. Any features with complex types (e.g., hierarchical features) are reduced to either nominal or numeric types.
For each data set, we assign the most-represented class the label “normal.” All other classes are assigned the label “anomaly.” We take 75% of the normal examples for training. The remaining 25% of the normal examples and all “anomalous” examples are held aside for testing.
2.2 Evaluation criteria
Note that our test sets may be larger than our training sets, and the relative proportion of test set instances labeled ‘anomalous’ may be large (indeed, ‘normal’ instances may be a minority in the test set). This is in contrast to most traditional anomaly detection scenarios, where anomalies are particularly rare events. We therefore choose an evaluation metric that depends only on the relative order of test set instances, when ranked by an anomaly score (i.e., the real-valued output of an anomaly detection method). To evaluate an anomaly detection method on a test set, we construct an ROC curve (Spackman 1989) and report the area under the curve (AUC).8 This allows us to use all test instances in our measure of performance and avoid committing to a particular anomaly score threshold, which in practice depends on a cost analysis particular to the data set in question.
The anomaly detection methods we compare in this section are listed in Table 2. The AUC for each data set varies depending on which examples are randomly assigned to the training set and which are held aside for testing. Therefore we replicate each of our experiments at least 25 times and report the average AUC.
Table 2.
Description of the anomaly detection methods we compare in this section. Each method is described in Sect. 1
| Approach | Description |
|---|---|
| LOF | Local outlier factor (Breunig et al. 2000) |
| SVM | One-class SVMs (Schölkopf et al. 2000) |
| CFA | Cross-feature analysis (Huang et al. 2003), using average probability (Eq. 3) |
| FRaC | Our approach, feature regression and classification Noto et al. (2010), using normalized surprisal (Eq. 6) |
We also compare the AUC of anomaly detection methods to that of a supervised classifier trained on labeled examples from both normal and anomalous classes. The reported supervised AUC is the best test set AUC of three supervised models: Decision trees, SVM with a linear kernel and SVM with a RBF kernel. This is meant to judge the difficulty of the learning task—we expect the AUC of the supervised classifier to be a rough estimate of the upper-bound for any anomaly detection approach.
2.3 Methods
LOF is a density-based approach, fundamentally based on a feature distance metric. For our experiments, we use the Euclidean distance between feature vectors, where the distance for a single numeric feature is the difference in value divided by the range of that feature’s value (i.e., the maximum distance is 1.0), and the distance for a nominal feature is the Hamming distance (i.e., 1 if the feature values are different, 0 if they are identical). We compute the LOF separately for each test set example, such that a test set example cannot receive a low LOF score due to other test set examples in the same neighborhood. LOF has one parameter, Min Pts, which is the size of the neighborhood. Following a suggestion in Breunig et al. (2000), we calculate the anomaly score by taking the maximum LOF over a range of values.9
One-class SVMs learn from numeric features, thus when using SVMs, we replace k-valued nominal features with k binary features, each set to 0, except for the one corresponding to the feature’s value, which is set to 1. We use the LIBSVM implementation (Chang and Lin 2001) of one-class SVMs with a radial basis kernel (RBF). There is no standard way of choosing one-class SVM parameters for an anomaly detection task. This is in contrast to supervised classification, where one is able to set parameters to optimize an objective that depends on training set labels, such as the accuracy of a validation set. In our experiments, we use the default LIBSVM parameter values, but we have run our experiments with several different parameter settings and we have confirmed using t-tests that test set performance does not improve for any of these parameter settings. Specifically, we altered the default LIBSVM RBF model by setting the model type to linear, quadratic, cubic, and sigmoid, the SVM c parameter to all powers of ten 0.001 ≤ c ≤ 100, and the RBF parameter γ to all powers of ten 0.001 ≤ γ ≤ 100. Therefore, we can say with confidence that the parameter settings we use in our analysis are a fair representation of the SVM approach.
For our approach using feature regression and classification (FRaC), we combine multiple feature prediction methods: (i) support vector machines (SVMs) using a linear kernel (trained for regression in the case of numeric features) (ii) SVMs using a radial basis function (RBF) kernel, and (iii) decision trees (regression trees for numeric features). We choose these methods because they represent a variety of hypothesis spaces. We use the LIBSVM implementation for multi-class SVMs and support vector regression (Chang and Lin 2001; Fan et al. 2008). When learning SVM models, we replace the nominal predictor features with multiple binary features as described above. We use the WEKA implementation for C4.5 classification decision trees and decision/regression trees (Hall et al. 2009). We use normalized surprisal as our anomaly detection score (Eq. 6).
Like FRaC, Cross-feature analysis (CFA) is a “wrapper” algorithm that uses supervised learning algorithms as a subroutine to predict feature values. The choice of feature prediction algorithm is important, but any algorithm will work, as long as it is compatible with the feature types, and the equation used to combine feature predictions. In their evaluation of CFA, Huang et al. experiment with three feature predictors C4.5, RIPPER, and naïve Bayes (Huang et al. 2003). However, in order to compare CFA with FRaC as fairly as possible, we run a version of CFA that uses the same feature models as FRaC. Recall that CFA combines predictions using average probability (Eq. 3). This means that feature predictors must produce a probability and therefore the feature in question must be nominal. In our implementation of CFA, following Huang et al. (2003), we discretize numerically-valued features into five bins, with approximately the same number of instances in each. We use C4.5, linear-kernel SVMs, and RBF-kernel SVMs as feature predictors. We use Platt scaling to convert the natural output of SVMs to a probability. To produce an anomaly score, we use the average probability (Eq. 3) of all three feature predictors.10
2.4 Experimental results
The results are shown in Table 3. We make the following observations:
Table 3.
Average test set area under the ROC curve (AUC) on UCI classification datasets that have been modified to be semi-supervised anomaly detection tasks using four anomaly detection methods: one-class support vector machines, local outlier factor, cross-feature-analysis, and our approach, feature regression and classification
| Data set | Estimated upper-bound | One-class SVM | LOF | CFA | FRaC | p-value |
|---|---|---|---|---|---|---|
| abalone | 0.64 | 0.58 | 0.51 | 0.39 | 0.48 | |
| acute | 1.00 | 0.97 | 0.84 | 1.00 | 1.00 | |
| adult | 0.88 | 0.61 | 0.47 | 0.53 | 0.61 | |
| annealing | 0.95 | 0.63 | 0.85 | 0.80 | 0.82 | |
| arrhythmia | 0.77 | 0.62 | 0.72 | 0.65 | 0.78 | 9.04e – 13 |
| audiology | 0.95 | 0.77 | 0.77 | 0.78 | 0.80 | 0.00152 |
| balance-scale | 0.99 | 0.96 | 0.95 | 0.94 | 0.97 | 0.00022 |
| blood-transfusion | 0.62 | 0.57 | 0.57 | 0.51 | 0.59 | 0.000306 |
| breast-cancer-wisconsin | 0.93 | 0.51 | 0.93 | 0.30 | 0.96 | 5.42e – 15 |
| car | 0.99 | 0.98 | 0.91 | 0.97 | 0.97 | |
| chess | 1.00 | 0.71 | 0.89 | 0.94 | 0.93 | |
| cmc | 0.75 | 0.45 | 0.45 | 0.42 | 0.41 | |
| connect-4 | 0.87 | 0.53 | 0.85 | 0.76 | 0.65 | |
| credit-screening | 0.88 | 0.69 | 0.73 | 0.84 | 0.85 | 0.822 |
| cylinder-bands | 0.81 | 0.81 | 0.68 | 0.82 | 0.69 | |
| dermatology | 1.00 | 0.96 | 0.99 | 0.86 | 1.00 | 2.15e – 08 |
| echocardiogram | 0.77 | 0.66 | 0.65 | 0.58 | 0.67 | 0.090 |
| ecoli | 0.99 | 0.98 | 0.98 | 0.50 | 0.97 | |
| glass | 0.79 | 0.61 | 0.70 | 0.64 | 0.65 | |
| haberman | 0.66 | 0.67 | 0.64 | 0.67 | 0.67 | |
| hayes-roth | 0.92 | 0.87 | 0.68 | 0.89 | 0.92 | 1.43e – 06 |
| hepatitis | 0.84 | 0.58 | 0.46 | 0.81 | 0.83 | 0.108 |
| horse-colic | 0.81 | 0.68 | 0.65 | 0.71 | 0.82 | 1.27e – 13 |
| image | 1.00 | 0.83 | 0.94 | 0.66 | 0.98 | 7.62e – 08 |
| internet_ads | 0.92 | 0.79 | 0.79 | 0.92 | 0.94 | 0.00459 |
| ionosphere | 0.98 | 0.84 | 0.91 | 0.87 | 0.97 | 7.67e – 18 |
| iris | 1.00 | 1.00 | 1.00 | 0.97 | 1.00 | |
| letter-recognition | 1.00 | 0.99 | 0.99 | 1.00 | 1.00 | |
| libras | 0.95 | 0.63 | 0.69 | 0.81 | 0.89 | 4.9e-05 |
| magic | 0.88 | 0.78 | 0.81 | 0.60 | 0.83 | 5.22e-14 |
| mammographic-masses | 0.89 | 0.74 | 0.58 | 0.72 | 0.73 | |
| mushroom | 1.00 | 0.95 | 1.00 | 1.00 | 1.00 | |
| nursery | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| ozone | 0.88 | 0.39 | 0.48 | 0.43 | 0.34 | |
| page-blocks | 0.94 | 0.57 | 0.95 | 0.72 | 0.89 | |
| parkinsons | 0.89 | 0.75 | 0.67 | 0.45 | 0.64 | |
| pima-indians-diabetes | 0.83 | 0.65 | 0.71 | 0.50 | 0.75 | 3.74e-14 |
| poker | 0.54 | 0.53 | 0.51 | 0.55 | 0.56 | 4.53e-06 |
| secom | 0.53 | 0.50 | 0.53 | 0.52 | 0.57 | 8.95e-13 |
| spambase | 0.94 | 0.78 | 0.58 | 0.82 | 0.84 | 1.15e-11 |
| statlog | 0.69 | 0.55 | 0.58 | 0.58 | 0.63 | 5.3e-14 |
| tae | 0.66 | 0.51 | 0.35 | 0.54 | 0.55 | 0.557 |
| tic-tac-toe | 0.98 | 0.85 | 0.98 | 1.00 | 0.99 | |
| voting-records | 0.99 | 0.98 | 0.83 | 0.77 | 0.95 | |
| wine | 0.99 | 0.79 | 0.88 | 0.33 | 0.96 | 4.93e-14 |
| yeast | 0.73 | 0.69 | 0.72 | 0.56 | 0.72 | |
| zoo | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | |
| Number of data sets with the maximum AUC score | 5 | 5 | 3 | 23 |
The highest average AUC score among the anomaly detection methods is shown in bold. On data sets where FRaC has the best AUC, we report the p-value of a paired, one-tailed t-test comparing FRaC to the alternative method with the best AUC. p-values under 0.05 are shown in bold. The estimated upper-bound reports the average AUC score for the corresponding supervised classification task, i.e., when training on both “normal” and “anomalous” examples
The performance of FRaC is better than that of all of the other three anomaly detectors on about half of the data sets, and has the maximum score more often than the other methods combined, by a wide margin.
The AUC is as good as or better than the estimated upper-bound on 34% of the data sets. Recall that the reported estimated upper-bound is itself the best of three supervised classifiers.
FRaC does not have the worst performance in any data set, excluding a few where all anomaly detectors are worse than random guessing. It is important that an anomaly detector be robust in this sense because, without labeled anomalies available for training, it is often difficult to judge the accuracy of an anomaly detector or even the difficulty of an anomaly detection task.
On the average, the AUC scores for FRaC are superior to all of the other anomaly detection methods. To test if the differences are statistically significant, we run one-tailed, paired t-tests, comparing the AUC of FRaC to that of the next best anomaly detection method for each data set. p-values are shown in Table 3. The p-values are shown in Table 3.11 With few exceptions, the superior average AUC scores of FRaC shown in Table 3 are statistically significant.
The results in Table 3 raise some important questions. Why is FRaC successful? Why does it outperform the other feature-modeling approach? Why are some of the AUC scores less than 0.5 (i.e., worse than random guessing)? In the next section, we address these questions.
3 Discussion
3.1 Analysis of feature-based methods
Distance-based methods such as LOF work well when anomalous instances are separated in feature space from the observed set of normal training instances (see Fig. 1). FRaC works by identifying key relationships among features instead of computing a distance from all features (Noto et al. 2010). However, Cross-feature analysis (CFA) is also a feature modeling approach. In the examples above, CFA models the same features as FRaC. Why does FRaC typically outperform CFA?
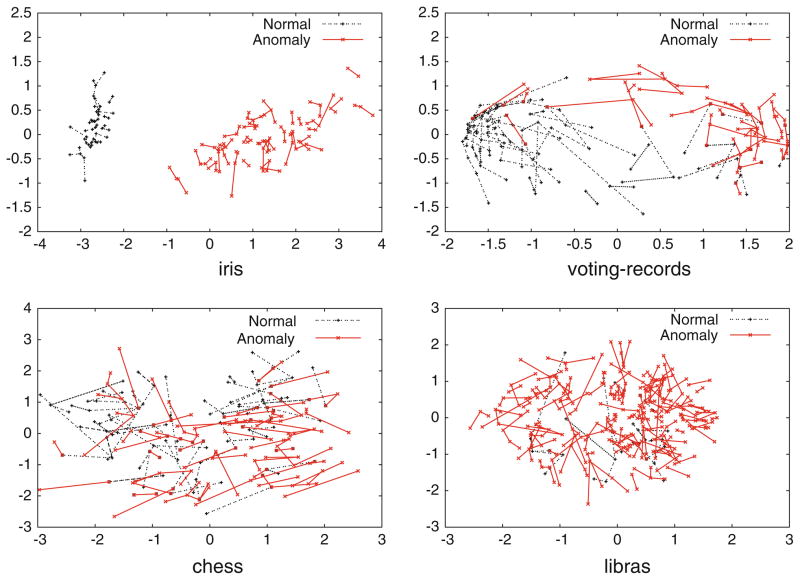
Fig. 1.
A visualization of feature space for four of the data sets in Table 1 that we discuss in this section. Following (Leon et al. 2005), these graphs are created by performing non-metric multidimensional scaling on each data set using Kruskal’s normalized stress1 criterion, and connecting each instance to the point that is its nearest neighbor in the original high-dimensional feature space. Overlapping lines are an indication that points are difficult to separate in feature space. Note that there is a clear separation between classes in the iris data set, which indicates that distance-based methods should work well
There are two key differences between FRaC and CFA. The first is that FRaC is able to handle numerical features by learning regression feature models. CFA, in contrast, first discretizes these features so that it can estimate the probability of each observed feature value. This discretization loses information about the feature values, and may adversely affect the performance of the anomaly detector. The second difference is the equation used to combine feature predictions. FRaC uses surprisal, and CFA uses average probability.
To measure the extent to which each of these differences affects the performance of the anomaly detectors, we create two new versions of FRaC, “discrete FRaC,” which discretizes all numerically-valued features before they are modeled by FRaC, and “Average Probability (AP) FRaC,” which uses Eq. 3 instead of Eq. 6 to compute anomaly scores.
We rerun all of the experiments in Sect. 2 using both new methods. These experiments allow us to estimate the effect of surprisal (by comparing CFA to discrete FRaC and AP FRaC to FRaC) and that of discretization (by comparing CFA to AP FRaC and discrete FRaC to FRaC). The results of these experiments are shown in Tables 4, 5, 6, and 7.
Table 4.
A comparison between cross-feature analysis (CFA) and a version of FRaC that models numeric features as discrete value ranges to measure the extent to which the use of surprisal affects anomaly detection
| Feature predictor | CFA | Discrete FRaC | p-value |
|---|---|---|---|
| Naïve Bayes | 13 | 29 | 0.00258 |
| RIPPER | 10 | 30 | 0.000416 |
| Decision tree | 12 | 28 | 0.00203 |
| Linear Kernel SVM | 15 | 25 | 0.13 |
| RBF Kernel SVM | 14 | 19 | 0.376 |
| Tree, linear and RBF SVM combined | 9 | 25 | 0.00178 |
The second and third columns indicate the number of data sets from Table 1 with superior AUC for each feature model type, and the fourth column shows the p-value from a one-tailed paired t-test comparing the AUC scores across all data sets. (Due to ties, neither of the two compared methods has the superior AUC for some data sets.)
Table 5.
A comparison between FRaC using average probability (Eq. 3 Huang et al. (2003)) and using normalized surprisal (Eq. 6, Noto et al. 2010) to measure the extent to which using surprisal affects anomaly detection
| Feature predictor | AP FRaC | FRaC (Eq. 6) | p-value |
|---|---|---|---|
| Decision/regression tree | 17 | 19 | 0.106 |
| Linear Kernel SVM | 24 | 20 | 0.268 |
| RBF Kernel SVM | 11 | 26 | 0.00826 |
| Tree, linear and RBF SVM combined | 11 | 22 | 0.0272 |
Columns have the same meaning as in Table 4. (Rows for naïve Bayes and RIPPER are not shown because these approaches require discretization which reduces the comparison to that between CFA and discrete FRaC)
Table 6.
A comparison between CFA Huang et al. (2003) and FRaC using average probability (Eq. 3) to measure the extent to which discretization affects anomaly detection
| Feature predictor | CFA | AP FRaC | p-value |
|---|---|---|---|
| Decision/regression tree | 10 | 32 | 0.000133 |
| Linear Kernel SVM | 9 | 33 | 0.000697 |
| RBF Kernel SVM | 13 | 28 | 0.00416 |
| Tree, linear and RBF SVM combined | 11 | 29 | 0.000925 |
Columns have the same meaning as in Table 4. (Rows for naïve Bayes and RIPPER are not shown because these approaches are the same when discretization is required)
Table 7.
A comparison between FRaC with and without discretizing numeric features
| Feature predictor | Discrete FRaC | FRaC | p-value |
|---|---|---|---|
| Decision/regression tree | 9 | 25 | 0.000528 |
| Linear Kernel SVM | 10 | 27 | 0.000244 |
| RBF Kernel SVM | 12 | 26 | 0.00123 |
| Tree, linear and RBF SVM combined | 9 | 26 | 0.00146 |
Columns have the same meaning as in Table 4 (Rows for naïve Bayes and RIPPER are not shown because these algorithms are not compatible with numeric targets and therefore the ability of FRaC to handle numeric features is not an advantage when using these models)
These tables indicate that both of the differences mentioned above are reasons why FRaC performs better than CFA. However, there is a particular reason why discretization can lead to bad performance. Note in Table 3 that the performance of CFA alone is significantly less than 0.5 on breast-cancer-wisconsin, parkinsons, and wine, all of which have many continuous features.
These data sets reveal a fundamental flaw in the discretization of numeric features by feature-modeling approaches, which is that discretization replaces real values with ranges of values. Errors within one of the ranges cannot be detected.
Consider the following example. On the breast-cancer-wisconsin data set, CFA learns that if feature 14 (variance of perimeter) of a benign cell is large, then feature 12 (variance of cell radius) is also large.12 However, for the CFA models, “large” refers to a range of values. Malignant cells (anomalies) do not have quite the same relationship between perimeter and radius variance as do benign cells, and FRaC can detect the numeric differences,13 but malignant cells tend to be larger than benign cells and have more perimeter and radius variance measurements that CFA simply labels as “large.” This means that the rule CFA learned to predict radius variance still holds for many of the “anomalous” test cases, and CFA incorrectly regards them as normal. Situations like this explain why CFA may tend to rank normal instances ahead of anomalies and suffer poor performance as a result.
3.2 Combining multiple feature models
As the data sets in Table 1 represent a variety of tasks, it is not surprising that the performance of our anomaly detector depends on our choice of feature prediction model. For example, the connect-4 data set is best represented by a decision tree, and the tic-tac-toe data set is best represented by a support vector machine.14 In general, we may not know which hypothesis space is the best choice for a given data set, therefore we advocate the approach of combining the normalized surprisal from multiple predictors. The intuition for why this works is that normalized surprisal is influenced the most by accurate predictors. That is, if the set of predictors using one type of feature model contains few accurate predictors, but the set of predictors using another type of feature model contains many accurate predictors, then normalized surprisal will be controlled primarily by the second set of predictors, which uses the superior hypothesis space for the task in question. The FRaC AUC scores in Table 3 are computed from the combined normalized surprisal of three feature models (RBF kernel SVMs, linear kernel SVMs, and decision trees), and Table 8 compares the AUC scores using the normalized surprisal of each of these models individually and those of adding the normalized surprisal of all three model types.
Table 8.
Test set area under the ROC curve (AUC) using normalized surprisal for three types of feature prediction model, and for the combined normalized surprisal of all three of them. The best AUC scores are shown in bold
| Data set | Linear Kernel SVM | RBF Kernel SVM | Decision tree | Combined |
|---|---|---|---|---|
| abalone | 0.50 | 0.51 | 0.43 | 0.48 |
| acute | 0.99 | 1.00 | 0.93 | 1.00 |
| adult | 0.64 | 0.64 | 0.53 | 0.61 |
| annealing | 0.73 | 0.79 | 0.84 | 0.82 |
| arrhythmia | 0.77 | 0.77 | 0.78 | 0.78 |
| audiology | 0.81 | 0.79 | 0.78 | 0.80 |
| balance-scale | 0.94 | 0.96 | 0.94 | 0.97 |
| blood-transfusion | 0.56 | 0.60 | 0.56 | 0.59 |
| breast-cancer-wisconsin | 0.94 | 0.96 | 0.96 | 0.96 |
| car | 0.95 | 0.91 | 0.96 | 0.97 |
| chess | 0.89 | 0.91 | 0.92 | 0.93 |
| cmc | 0.41 | 0.42 | 0.42 | 0.41 |
| connect-4 | 0.51 | 0.54 | 0.75 | 0.65 |
| credit-screening | 0.83 | 0.84 | 0.84 | 0.85 |
| cylinder-bands | 0.62 | 0.75 | 0.63 | 0.69 |
| dermatology | 0.98 | 1.00 | 0.99 | 1.00 |
| echocardiogram | 0.64 | 0.68 | 0.65 | 0.67 |
| ecoli | 0.96 | 0.96 | 0.96 | 0.97 |
| glass | 0.61 | 0.65 | 0.65 | 0.65 |
| haberman | 0.67 | 0.66 | 0.66 | 0.67 |
| hayes-roth | 0.92 | 0.91 | 0.88 | 0.92 |
| hepatitis | 0.80 | 0.80 | 0.84 | 0.83 |
| horse-colic | 0.78 | 0.79 | 0.80 | 0.82 |
| image | 0.97 | 0.96 | 0.98 | 0.98 |
| internet_ads | 0.96 | 0.89 | 0.95 | 0.94 |
| ionosphere | 0.96 | 0.97 | 0.96 | 0.97 |
| iris | 0.99 | 1.00 | 0.99 | 1.00 |
| letter-recognition | 0.99 | 1.00 | 0.99 | 1.00 |
| libras | 0.89 | 0.88 | 0.89 | 0.89 |
| magic | 0.80 | 0.74 | 0.86 | 0.83 |
| mammographic-masses | 0.72 | 0.74 | 0.71 | 0.73 |
| mushroom | 1.00 | 1.00 | 1.00 | 1.00 |
| nursery | 0.99 | 1.00 | 1.00 | 1.00 |
| ozone | 0.37 | 0.37 | 0.34 | 0.34 |
| page-blocks | 0.88 | 0.83 | 0.90 | 0.89 |
| parkinsons | 0.54 | 0.67 | 0.65 | 0.64 |
| pima-indians-diabetes | 0.73 | 0.74 | 0.72 | 0.75 |
| poker | 0.56 | 0.57 | 0.53 | 0.56 |
| secom | 0.54 | 0.56 | 0.61 | 0.57 |
| spambase | 0.79 | 0.85 | 0.84 | 0.84 |
| statlog | 0.61 | 0.60 | 0.62 | 0.63 |
| tae | 0.60 | 0.48 | 0.49 | 0.55 |
| tic-tac-toe | 0.96 | 0.97 | 0.78 | 0.99 |
| voting-records | 0.93 | 0.94 | 0.91 | 0.95 |
| wine | 0.95 | 0.94 | 0.91 | 0.96 |
| yeast | 0.72 | 0.72 | 0.71 | 0.72 |
| zoo | 0.99 | 0.99 | 1.00 | 1.00 |
| Number of data sets with the maximum AUC score | 3 | 8 | 6 | 11 |
Our empirical results show that the AUC of FRaC combining all three models is as good as the best AUC of FRaC using any individual feature model on 57% of the data sets. Indeed, the AUC of FRaC combining three feature models is strictly better than that of FRaC with any individual model 23% of the time. Based on these observations, we advocate combining multiple feature prediction models.
3.3 Implicit feature selection
In any learning task, there are many potentially irrelevant features that distort the feature space, affecting the shapes of clusters and the relative distance among examples. LOF and one-class SVMs treat all features equally, but by using normalized surprisal to combine the output of feature predictors, FRaC implicitly selects features, because normalized surprisal is only very high for accurate predictors. CFA does not treat all features equally, but it averages the likelihood estimates of inaccurate predictors with those of accurate predictors.
To show that FRaC is robust to irrelevant features, we perform the following experiment. We take all of the data sets from Table 3 for which all of the anomaly detection methods do well (AUC ≥ 0.9), then add a number of synthetic features to each. Each of these new features is of the same type and value distribution as one of the original features, but its value in each data instance is independent of the class label and of any of the other features. This type of noise makes each learning task more difficult. We then rerun the experiments from Sect. 2 on the resulting data sets. We hypothesize that the performance of FRaC will be more robust to the additional noise than that of one-class SVMs, LOF and CFA.
For this experiment, we include one additional anomaly detection method: LOF with feature bagging, which was developed specifically for data sets that contain noisy or irrelevant features (Lazarevic and Kumar 2005). It involves running LOF multiple times with random feature subsets and combining the results.15
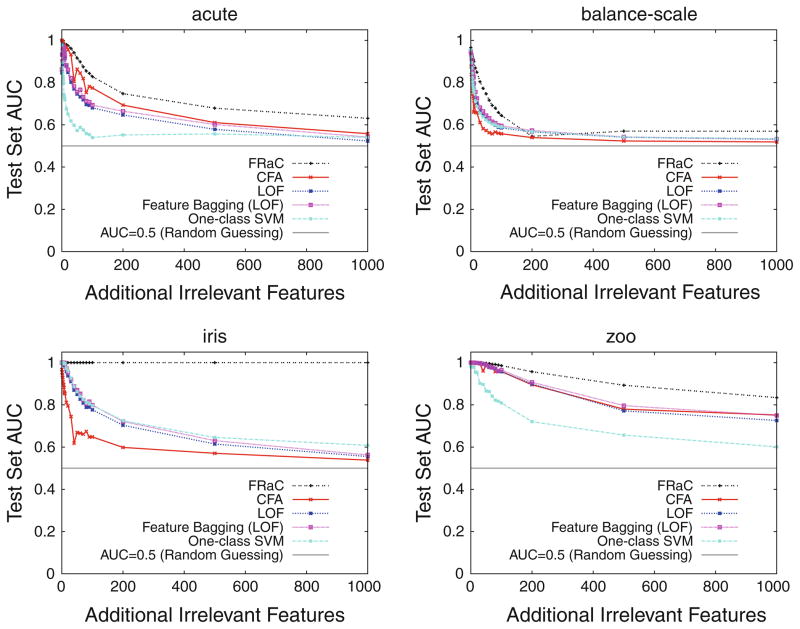
Table 9 shows the performance (average AUC) on data sets with 10 additional features. Table 10 shows the performance with 100 irrelevant features. The performance of FRaC is the least affected by the added noise. Indeed, only once does an anomaly detection method retain more AUC than FRaC (one-class SVMs on the data set, car).
Table 9.
AUC on data sets with 10 additional irrelevant features
| Data set | One-class SVM | LOF | LOF with feature bagging | CFA | FRaC |
|---|---|---|---|---|---|
| Acute | 0.70 | 0.91 | 0.93 | 0.97 | 0.98 |
| Balance-scale | 0.75 | 0.77 | 0.80 | 0.71 | 0.90 |
| Car | 0.97 | 0.87 | 0.91 | 0.86 | 0.95 |
| Iris | 0.99 | 0.99 | 1.00 | 0.85 | 1.00 |
| Mushroom | 0.93 | 1.00 | 1.00 | 1.00 | 1.00 |
| Tic-tac-toe | 0.67 | 0.65 | 0.68 | 0.99 | 0.99 |
| Zoo | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 |
Table 10.
AUC on data sets with 100 additional irrelevant features
| Data set | One-class SVM | LOF | LOF with feature bagging | CFA | FRaC |
|---|---|---|---|---|---|
| Acute | 0.54 | 0.68 | 0.69 | 0.76 | 0.83 |
| Balance-scale | 0.59 | 0.59 | 0.60 | 0.56 | 0.64 |
| Car | 0.89 | 0.63 | 0.70 | 0.62 | 0.80 |
| Iris | 0.80 | 0.77 | 0.80 | 0.65 | 1.00 |
| Mushroom | 0.83 | 0.97 | 0.97 | 0.97 | 1.00 |
| Tic-tac-toe | 0.55 | 0.54 | 0.55 | 0.58 | 0.61 |
| Zoo | 0.80 | 0.95 | 0.96 | 0.94 | 0.98 |
To show how the performance of each anomaly detector degrades as a function of task difficulty, we plot several points of a curve at increasing levels of noise. These experiments involve hundreds of trials for each anomaly detector (as before, we replicate each experiment 25 times and report an average AUC), so we choose the four smallest data sets from Tables 9 and 10. The results are shown in Fig. 2. On these data sets, FRaC’s performance nearly dominates that of the other anomaly detection methods over all data set sizes.16 We expect that this trend would hold in general for the other data sets in Table 1.
Fig. 2.
Test set performance of five anomaly detection methods as a function of irrelevant features that are synthetically added to a data set to make it more difficult
Many real-world data sets are likely to contain features that are irrelevant, but identifying which features are irrelevant is extremely difficult because only one class of training instance is provided. These results suggest that FRaC is robust in the presence of irrelevant features.
3.4 Discovery of key feature relationships
To further demonstrate the principle that FRaC works by discovering key feature relationships, we point out a few illustrative examples.
Consider the voting records data set. Each feature is a vote made by a Democratic (political party) representative. The distance between each pair of instances is a function of the number of votes on which the representatives disagree. Republican voters are anomalous in this training set, but Democrats disagree often enough that both parties overlap in feature space.17 However, there is one vote in particular (“physician fee freeze”) that goes mostly along party lines. FRaC learns that Democrats are unlikely to vote ‘yes,’ and therefore measures a high degree of surprisal when it observes almost all of the Republicans. This feature is a large part of the reason that FRaC performs well. It makes sense that one-class SVMs also do well on this data set, because ‘no’ values for this particular vote should fall outside of the region containing a large majority of the normal instances.
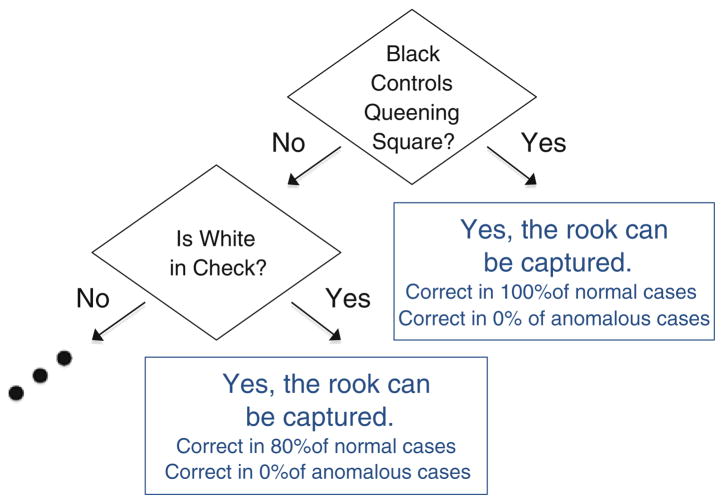
In general, however, feature models will depend on multiple features. Consider the chess (KR vs. KP) data set, which represents a set of chess scenarios where black has a king and a rook, but white can win with a king and a pawn. Scenarios where white cannot win are anomalous, and the task is to identify these. One of the features is, “can white capture the rook?” Among anomalies (where white cannot win), the value is almost always ‘no,’ but it is usually ‘no’ among normal instances as well, so that value is not surprising by itself. There are situations among the normals, however, when the value is usually ‘yes.’ Part of the decision tree model for this feature is shown in Fig. 3. This model identifies the other features of normal scenarios when the black rook can be captured. Among anomalous instances that follow these same decision tree paths, the rook cannot be captured. Given the other features and the model, this observation is surprising, and therefore FRaC is able to identify the corresponding anomalies.
Fig. 3.
Part of the decision tree model learned by FRaC for the feature, “can white capture the rook?” of the chess (KR vs. KP) data set. (Note that the model only applies to “normal” cases where white can win. If black controls the queening square, then it is likely that white can capture the black rook—otherwise no progress toward winning would be made.)
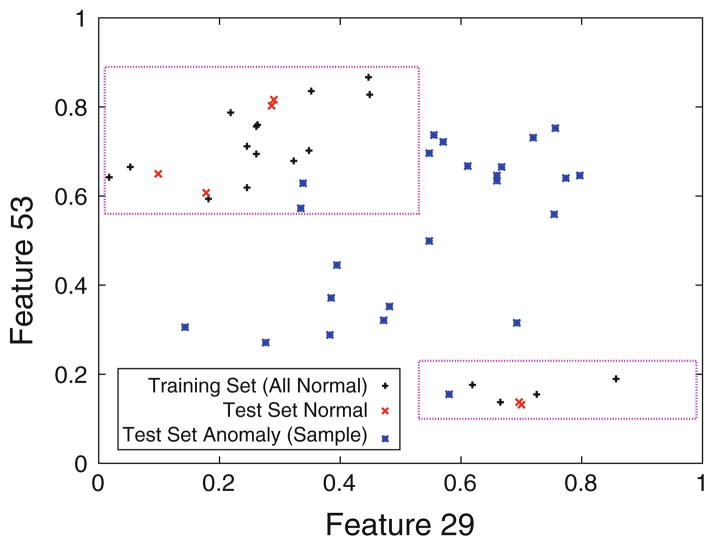
Finally, we examine the model of a real-valued feature. On the libras (Brazilian sign language) data set, FRaC is trained on instances of a particular sign. This is a high-dimensional data set: features are the positions in two dimensions of a hand at 45 different time steps during the process of making the sign. FRaC learns that feature 29 is a good predictor of feature 53, and in fact they have roughly an inverse relationship. The regression tree model is shown in Fig. 4. Using cross-validation on the training set, FRaC learns that normal instances are unlikely to fall outside the delimited regions. Different signs are anomalies in this task, and many of them do not have the same relationship between features 29 and 53. FRaC is able to recognize these as anomalies, and together with the other accurate feature predictors, perform well on this data set.
Fig. 4.
The regression tree model learned by FRaC for feature 53 of the libras data set. FRaC learns that normal instances are unlikely to appear outside the delimited regions, but a large percentage of anomalies do not follow this rule
3.5 Difficult anomaly detection tasks
Recall that the area under the ROC curve is equal to the likelihood of a randomly selected test set anomaly being judged as more likely to be anomalous than a randomly selected test set normal instance. This means that an AUC of 0.5 is equivalent to assigning anomaly scores at random. However, several of the average AUC scores in Table 3 are conspicuously close to or worse than 0.5 for all or most of the anomaly detection methods.
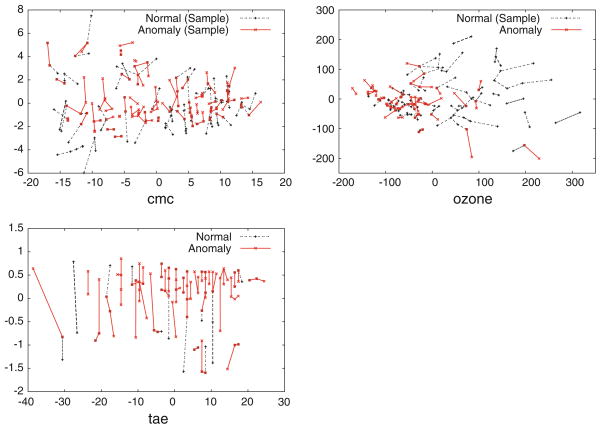
The performance of all of the anomaly detection methods is worse than random guessing on the data sets cmc and ozone. There are three data sets for which the average distance among normal instances is greater than the average distance between normal and anomalous instances, and the average distance among instances from each anomalous class is even smaller than that. These data sets are cmc, ozone, and tae (see Fig. 5). In other words, these are simply extremely difficult tasks where the anomalies in these data sets form tighter clusters than do normal examples, and these clusters of anomalies are near (possibly within) the region of feature space where normal examples are located.
Fig. 5.
A visualization of feature space for three especially difficult anomaly detection tasks, cmc, ozone, and tae. These are generated in the same way as Fig. 1
Why are CFA and FRaC alone worse than chance on the abalone data set? The task of the abalone data set is to identify female or infant abalones, after training on male abalones (the “normal” class in our experiments). There are several features based on weight measurements, such as whole weight, weight of shucked abalone, and weight after being dried. As you might expect, CFA and FRaC learn to predict each of the abalone weight measurements from the remaining weight measurements fairly accurately. However, these predictors, trained exclusively on male abalones, turn out to be even more accurate for female and especially for infant abalones.18 Abalone presents an unusual set of circumstances where anomalies have the same patterns among features, but less variance.19–20
4 Unsupervised anomaly detection experiments
FRaC was designed to be a general approach to the semi-supervised anomaly detection problem, and in Sect. 2, we showed that it is superior to several state-of-the-art approaches on a variety of data sets. Recall that this learning scenario is semi-supervised because we assume that we can trust that the training set consists of correctly labeled normal instances. However, such labels are often unavailable. Unsupervised anomaly detection is the learning scenario where we are given just one data set that is a mixture of normal and anomalous instances, none of which are labeled, and our task is to identify the anomalous instances.
We do not assume that we know the proportion of anomalies in our data set, but they are by definition infrequent, and we hypothesize that because the proportion of anomalies is small, we can use FRaC and the feature predictors will still be accurate enough despite the presence of anomalies in the training set.
To test this hypothesis, we use the same 47 UCI data sets that we use in Sect. 4. However, for this set of experiments, we create data sets that contain only a small portion of “anomalies.” Specifically, for each data set, we (i) add all “normal” instances to the experimental data set. We then (ii) select a portion of anomalies uniformly at random. The number of anomalies will be at least one, but no more than 5%. We add a random sample of “anomalous” instances of the chosen sample size to the experimental data set. Finally (iii), we randomize the order of the data set instances. We carry out this procedure over 25 replicates, so the portion of anomalies and the individual instances representing anomalies are different each time (although the exact same data sets are used to compare across different anomaly detection methods). We compare the same anomaly detection methods as in Sect. 2: One-class SVMs (using an RBF kernel), LOF, CFA (using the average probability of C4.5, linear-kernel and RBF-kernel SVMs), and FRaC (using the normalized surprisal of C4.5, linear-kernel and RBF-kernel SVMs). Note that, although LOF is applicable to both semi-supervised and unsupervised anomaly detection scenarios, it is designed for the unsupervised scenario.
The results of these experiments are shown in Table 11. It is not surprising that LOF improves the most relative to the semi-supervised tasks,21 but FRaC still clearly outperforms the other three methods on these data sets.
Table 11.
Average area under the ROC curve (AUC) on unsupervised anomaly detection tasks. The highest average AUC score among the anomaly detection methods is shown in bold. When FRaC has the highest average AUC score, we show the p-value of a paired, one-tailed t-test comparing the AUC scores of FRaC to the next best anomaly detection method. p-values under 0.05 are shown in bold
| Data set | One-class SVM | LOF | CFA | FRaC | p-value |
|---|---|---|---|---|---|
| abalone | 0.56 | 0.48 | 0.42 | 0.46 | |
| acute | 0.94 | 0.83 | 1.00 | 0.98 | |
| adult | 0.48 | 0.47 | 0.52 | 0.59 | 9.86e – 15 |
| annealing | 0.63 | 0.83 | 0.77 | 0.79 | |
| arrhythmia | 0.44 | 0.75 | 0.43 | 0.80 | 0.00263 |
| audiology | 0.70 | 0.72 | 0.75 | 0.77 | 0.0241 |
| balance-scale | 0.95 | 0.96 | 0.95 | 0.97 | 0.00289 |
| blood-transfusion | 0.51 | 0.56 | 0.45 | 0.56 | |
| breast-cancer-wisconsin | 0.51 | 0.92 | 0.28 | 0.96 | 1.7e – 11 |
| car | 0.98 | 1.00 | 0.97 | 0.96 | |
| chess | 0.70 | 0.89 | 0.90 | 0.90 | |
| cmc | 0.48 | 0.47 | 0.41 | 0.43 | |
| connect-4 | 0.52 | 0.86 | 0.70 | 0.63 | |
| credit-screening | 0.51 | 0.69 | 0.78 | 0.84 | 0.00252 |
| cylinder-bands | 0.37 | 0.71 | 0.68 | 0.61 | |
| dermatology | 0.95 | 0.98 | 0.74 | 0.99 | 0.063 |
| echocardiogram | 0.54 | 0.67 | 0.51 | 0.71 | 0.0138 |
| ecoli | 0.98 | 0.98 | 0.34 | 0.96 | |
| glass | 0.64 | 0.75 | 0.50 | 0.65 | |
| haberman | 0.60 | 0.67 | 0.70 | 0.70 | |
| hayes-roth | 0.94 | 0.67 | 0.91 | 0.94 | |
| hepatitis | 0.51 | 0.42 | 0.74 | 0.83 | 0.0187 |
| horse-colic | 0.64 | 0.62 | 0.56 | 0.78 | 4.01e – 06 |
| image | 0.55 | 0.93 | 0.31 | 0.97 | 0.0316 |
| internet_ads | 0.77 | 0.78 | 0.89 | 0.91 | 0.000689 |
| ionosphere | 0.84 | 0.90 | 0.50 | 0.96 | 8.85e-08 |
| iris | 1.00 | 1.00 | 0.58 | 1.00 | |
| letter-recognition | 0.99 | 0.99 | 0.91 | 1.00 | 0.00316 |
| libras | 0.57 | 0.76 | 0.56 | 0.86 | 7.8e – 06 |
| magic | 0.50 | 0.81 | 0.57 | 0.81 | |
| mammographic-masses | 0.74 | 0.57 | 0.67 | 0.71 | |
| mushroom | 0.94 | 0.99 | 0.79 | 0.91 | |
| nursery | 1.00 | 1.00 | 1.00 | 1.00 | |
| ozone | 0.49 | 0.45 | 0.33 | 0.30 | |
| page-blocks | 0.49 | 0.93 | 0.37 | 0.81 | |
| parkinsons | 0.52 | 0.66 | 0.31 | 0.56 | |
| pima–indians-diabetes | 0.52 | 0.71 | 0.47 | 0.75 | 7.89e – 07 |
| poker | 0.53 | 0.52 | 0.54 | 0.56 | 0.00017 |
| secom | 0.50 | 0.53 | 0.52 | 0.54 | 0.064 |
| spambase | 0.77 | 0.58 | 0.77 | 0.80 | 0.0308 |
| statlog | 0.50 | 0.57 | 0.56 | 0.62 | 0.0112 |
| tae | 0.44 | 0.37 | 0.55 | 0.58 | 0.260 |
| tic-tac-toe | 0.83 | 1.00 | 1.00 | 0.99 | |
| voting-records | 0.98 | 0.69 | 0.60 | 0.87 | |
| wine | 0.48 | 0.87 | 0.11 | 0.94 | 1e – 05 |
| yeast | 0.66 | 0.71 | 0.51 | 0.70 | |
| zoo | 0.99 | 1.00 | 1.00 | 1.00 | |
| Number of data sets with the maximum AUC score | 5 | 9 | 1 | 22 | |
FRaC often has the best performance among all four compared anomaly detection methods, and it is never the worst, except in the case of ozone (a difficult data set on which all methods perform worse than random guessing) and one other data set: car, on which FRaC has an average AUC of 0.96.
5 Conclusions
FRaC is a new, general-purpose approach to anomaly detection. We showed that it effectively models a set of normal data with just the key, conserved feature relationships that characterize those data. FRaC can then discover anomalies effectively by testing their consistency with these characteristic models.
We showed the importance of learning regression models for real-valued features and modeling the prediction error instead of discretizing numeric features and learning classifier models only.
We showed experimentally that FRaC is robust to noisy and high-dimensional feature sets because it implicitly reduces feature space to the relevant features. It is also robust across a wide variety of data sets; our experiments show that it is most often the best, and consistently among the best, compared with state-of-the-art general-purpose approaches to anomaly detection, including LOF and one-class SVMs.
Finally, we showed that FRaC is also a superior anomaly detection method on the (arguably more general) unsupervised anomaly detection task.
Supplementary Material
Acknowledgments
This research was supported by award number R01-HD-058880 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development. The content is solely the responsibility of the authors and does not necessarily reflect the views of the NICHD or the National Institutes of Health. C. B. was supported by NSF Grant IIS-0803409. Availability: All code, documentation, and complete experimental results are available online at bcb.cs.tufts.edu/frac.
Footnotes
Supervised learning with a class imbalance is sometimes referred to as supervised anomaly detection.
Euclidean distance is a common measurement, and is naturally applicable to numeric features. Other feature types, and especially combinations of different feature types, may require complex mappings or distance functions.
By numeric features, we mean both real-valued features and discrete numerical features with a large number of possible values (e.g., age measured in years, or number of network packets received) that are better modeled as continuous values.
Note that numeric features need only be modeled as a nominal-valued; their numeric values may be used in models of other features.
In our experiments, we ensure that each feature has the same number of predictors by choosing a clas-sification “version” (e.g., decision tree) and a regression version (e.g., regression tree) of each feature predictor p.
The experiments in this section are similar to the ones carried out in Noto et al. (2010). There are two important differences: First, we replicate each experiment several times and report a robust average. Second, we include a comparison to CFA.
We also ran all the experiments described in this section using connectivity-based outlier factor (COF) (Tang et al. 2002), but we find that its performance does not differ significantly from that of LOF.
The area under the ROC curve is equal to the probability that a randomly selected anomaly will have a higher score than a randomly selected normal example. An AUC of 1.0 is perfect, and an AUC of 0.5 is no better than random guessing.
In our experiments, we use the range 10 = Min Pts = 100. In Noto et al. (2010), we tried a number of alternative ranges and found that LOF is not very sensitive to this choice.
The authors of CFA do not explicitly suggest combining feature models this way, but it appears to be an improvement. On the data sets in Table 1, the average performance (area under the ROC curve) of CFA combining feature models is 0.014 higher than the average performance of CFA with the individual feature models. We also carried out the same CFA experiments using C4.5, RIPPER, and naïve Bayes. On the data sets in Table 1, RIPPER performs best, but the performance of combining C4.5, linear and RBF-kernel SVMs is, on average, 0.025 higher than that.
The t-test assumes the pairwise differences in AUC scores are normally distributed. According to the Shapiro-Wilk test for normality (Shapiro and Wilk 1965), this does not always appear to be the case. However, we believe the vast majority of t-test comparison p-values are small enough to be convincing.
This is one of the rules inferred by the C4.5 decision tree model. The average probability is most heavily influenced by the tree (compared to the SVM models) on this data set.
FRaC’s tree model on the same training set uses feature 15 (variance of cell radius) as well as feature 14, but the rule is effectively the same: large perimeter (and area) variance predicts large radius variance.
tic-tac-toe is the familiar 3 × 3 naughts and crosses game. The object of the two-player game connect-4 is to place four checkers in a row on a 7 × 6 board with specific rules about how checkers may be placed. Although these seem like similar domains, the task for tic-tac-toe is to determine the winner of a completed game and the task for connect-4 is to predict the eventual winner from an incomplete game.
The effect of feature bagging on the experiments in Sect. 2 is minimal (on average, it slightly lowered the AUC of LOF), but we include it here because it was proposed specifically for data sets with irrelevant or noisy features.
FRaC’s performance does not degrade at all on the iris data set because the anomalous feature values are so unlikely according to FRaC’s feature models that the surprisal measures hundreds of bits. We estimate that FRaC’s performance would remain consistent for several thousand more features.
Democrats also disagree with each other more than Republicans do. The average distance among Democrats is 3.62, among Republicans it is 3.02.
The Pearson correlation between two “weight” features for male abalones ranges from 0.84 to 0.96, and the corresponding correlation among infant abalones ranges from 0.91 to 0.97 and is always higher. One may speculate that there is less variance in the shape of the infants.
Indeed, if we train on infant abalone and attempt to detect males and females as anomalies, then the performance of all anomaly detectors (and the supervised estimated upper-bound) markedly increases.
In practice, one would consider attempting to eliminate redundant features, but we intentionally experiment with unaltered public data sets.
In general, the unsupervised anomaly detection tasks are more difficult than the semi-supervised tasks, and this fact is reflected in the performances reported in Tables 3 and 11. For the semi-supervised experiments in Sect. 2, we hold aside 25% of the normal instances for testing, but in order to use the available data instances to the fullest extent possible, we use 100% of the normal instances in the unsupervised experiments. As a result of the additional data, the performance in some cases may be better on the unsupervised task.
Contributor Information
Keith Noto, Email: noto@cs.tufts.edu, Department of Computer Science, Tufts University, 161 College Ave., Medford, MA 02155, USA.
Carla Brodley, Email: brodley@cs.tufts.edu, Department of Computer Science, Tufts University, 161 College Ave., Medford, MA 02155, USA.
Donna Slonim, Email: slonim@cs.tufts.edu, Department of Computer Science, Tufts University, 161 College Ave., Medford, MA 02155, USA.
References
- Asuncion A, Newman D. UCI machine learning repository. 2007 http://www.ics.uci.edu/~mlearn/MLRepository.html.
- Breunig M, Kriegel H, Ng R, Sander J. LOF: identifying density-based local outliers. ACM SIGMOD Rec. 2000;29(2):93–104. [Google Scholar]
- Byers S, Raftery AE. Nearest-neighbor clutter removal for estimating features in spatial point processes. J Am Stat Assoc. 1998;93(442):577–584. [Google Scholar]
- Chandola V, Banerjee A, Kumar V. Anomaly detection: a survey. ACM Comput Surv. 2009;41(3):1–58. [Google Scholar]
- Chang CC, Lin CJ. LIBSVM: a library for support vector machines software. 2001 http://www.csie.ntu.edu.tw/~cjlin/libsvm.
- Cohen WW. Fast effective rule induction. Proceedings of the twelfth international conference on machine learning. 1995:115–123. [Google Scholar]
- Fan RE, Chang KW, Hsieh CJ, Wang XR, Lin CJ. LIBLINEAR: a library for large linear classification. J Mach Learn Res. 2008;9:1871–1874. [Google Scholar]
- Guttormsson SE, Marks RJ, El-Sharkawi MA, Kerszenbaum I. Elliptical novelty grouping for on-line short-turn detection of excited running rotors. IEEE Trans Energy Convers. 1999;14(1):16–22. [Google Scholar]
- Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software: an update. SIGKDD Explor. 2009;11(1):10–18. [Google Scholar]
- Huang YA, Fan W, Lee W, Yu PS. Cross-feature analysis for detecting ad-hoc routing anomalies. ICDCS ’03: proceedings of the 23rd international conference on distributed computing systems; Washington, DC, USA: IEEE Computer Society; 2003. [Google Scholar]
- John G, Langley P. Estimating continuous distributions in Bayesian classifiers. Proceedings of the eleventh conference on uncertainty in artificial intelligence; San Mateo: Morgan Kaufmann; 1995. pp. 338–345. [Google Scholar]
- Lazarevic A, Kumar V. Feature bagging for outlier detection. Proceedings of the eleventh ACM SIGKDD international conference on knowledge discovery and data mining; 2005. pp. 157–166. [Google Scholar]
- Leon D, Podgurski A, Dickinson W. Visualizing similarity between program executions. Proceedings of the 16th IEEE international symposium on software reliability engineering; 2005. pp. 311–321. [Google Scholar]
- Mitchell T. Machine learning. McGraw-Hill; New York: 1997. [Google Scholar]
- Noto K, Brodley C, Slonim D. Anomaly detection using an ensemble of feature models. Proceedings of the 10th IEEE international conference on data mining (ICDM 2010); 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinlan JR. Probabilistic decision trees. 3, chap 5. Morgan Kaufmann; San Mateo: 1990. pp. 140–153. [Google Scholar]
- Quinlan J. C4.5: programs for machine learning. Morgan Kaufmann; San Mateo: 1993. [Google Scholar]
- Schölkopf B, Smola AJ, Williamson RC, Bartlett PL. New support vector algorithms. Neural Comput. 2000;12(5):1207–1245. doi: 10.1162/089976600300015565. [DOI] [PubMed] [Google Scholar]
- Shannon CE. A mathematical theory of communication. Bell Syst Tech J. 1948;27:379–423. (Part I) [Google Scholar]
- Shapiro SS, Wilk MB. An analysis of variance test for normality (complete samples) Biometrika. 1965;52(3–4):591–611. [Google Scholar]
- Smith R, Bivens A, Embrechts M, Palagiri C, Szymanski B. Clustering approaches for anomaly based intrusion detection; Proceedings of intelligent engineering systems through artificial neural networks; 2002. pp. 579–584. [Google Scholar]
- Spackman KA. Signal detection theory: valuable tools for evaluating inductive learning. Proceedings of the sixth international workshop on machine learning; San Francisco, CA, USA: Morgan Kaufmann Publishers Inc; 1989. pp. 160–163. [Google Scholar]
- Tang J, Chen Z, Fu A, Cheung D. Enhancing effectiveness of outlier detections for low density patterns. Lecture notes in computer science. Springer; New York: 2002. pp. 535–548. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.