Abstract
When environmental conditions vary stochastically, individuals accrue fitness benefits by exhibiting phenotypic plasticity. Here we analyze a general dynamic-programming model describing an individual’s optimal energy allocation in a stochastic environment. After maturation, individuals repeatedly decide how to allocate incoming energy between reproduction and maintenance. We analyze the optimal fraction of energy invested in reproduction and the resultant degree of plasticity in dependence on environmental variability and predictability. Our analyses reveal unexpected patterns of optimal energy allocation. When energy availability is low, all energy is allocated to reproduction, although this implies that individuals will not survive after reproduction. Above a certain threshold of energy availability, the optimal reproductive investment decreases to a minimum and even vanishes entirely in highly variable environments. With further improving energy availability, optimal reproductive investment gradually increases again. Costs of plasticity affect this allocation pattern only quantitatively. Our results show that optimal reproductive investment does not increase monotonically with growing energy availability and that small changes in energy availability can lead to major variations in optimal energy allocation. Our results help to unify two apparently opposing predictions from life-history theory, that organisms should increase reproductive investment both with improved environmental conditions and when conditions deteriorate (“terminal investment”).
Keywords: phenotypic plasticity, stochastic environment, energy allocation, reproductive investment
Introduction
Phenotypic plasticity is the ability of a genotype to produce alternative phenotypes in different environments. Organisms can benefit from such an ability to adjust their phenotype to a range of environmental conditions (e.g., Lively 1986; Schlichting 1986; Kaitala 1991; Travis 1994; Dorn et al. 2000), especially if environments are heterogeneous in space or time (e.g., Clark and Harvell 1992; Gabriel and Lynch 1992; Gomulkiewicz and Kirkpatrick 1992; Houston and McNamara 1992; Ernande and Dieckmann 2004; Lind and Johansson 2007). The evolution of phenotypic plasticity requires that plastic individuals have a higher fitness than nonplastic individuals, with fitness defined as an average of the environment-specific fitness values over all possible environments an individual may encounter (Releya 2002b). Because of this averaging, the frequency distribution according to which environments are encountered influences how much trait values resulting from evolutionarily optimal plasticity in a given environment differ from trait values that would be evolutionarily optimal if that environment were the only one encountered. Naturally, a better match is expected in environments that are encountered frequently and that provide high energy levels, compared with rare and/or poor environments (Zhivotovsky et al. 1996; Ernande and Dieckmann 2004).
In stochastically fluctuating environments, the evolutionarily optimal degree of plasticity will typically depend on the statistical characteristics of the environmental stochasticity (Kaitala 1991; Gabriel and Lynch 1992), suggesting that being highly plastic is not always a superior strategy. Phenotypic plasticity should be reduced or absent when conditions are constant (Levins 1968; Via and Lande 1985) or when costs associated with plasticity are high (Van Tienderen 1991; De Witt 1998). Theoretical studies showed that evolutionarily optimal reaction norms for the phenotypic plasticity of life-history traits result from a balance between perfect adaptation and the avoidance of costs originating from the effort of maintaining plasticity (Van Tienderen 1991; Ernande and Dieckmann 2004).
Plasticity in reproductive investment strategies appears to depend strongly on the degree of environmental heterogeneity. Several empirical studies (e.g., Kaitala 1991; Ellers and van Alphen 1997) have shown that, in a variable environment, reduced survival prospects caused by a sudden reduction in energy availability may lead to decreased reproductive investment in favor of a higher allocation of energy to maintenance and survival. On the other hand, there is empirical evidence that reduced energy availability and the ensuing loss of survival probability favor a high allocation to reproduction as a form of “terminal investment” (e.g., Stelzer 2001). As yet, a theoretical framework is lacking that reconciles these two opposing predictions of life-history theory. Moreover, it has not yet been systematically explored how important characteristics of stochastic environments, namely their variability and predictability in time, influence the evolution of phenotypic plasticity in reproductive investment strategies.
Here we introduce a conceptual model to investigate the influence of stochastic environments (1) on energy allocation to reproduction and (2) on the degree of phenotypic plasticity in reproductive investment. In our model, the amount of energy available in the environment varies with time, and the model organisms can repeatedly adjust their energy allocation. Using dynamic programming, we investigate the evolutionarily optimal reaction norm for energy invested in reproduction versus in maintenance during an organism’s lifetime, when energy availability varies stochastically. We analyze how this reaction norm and the implied degree of phenotypic plasticity depend on environmental variability and predictability, and we extend our model to investigate how costs of plasticity affect optimal energy allocation.
Model Description
We consider an individual at a specific moment in time after it has reached maturation. Growth is assumed to be determinate, and hence no energy is allocated to growth after maturation. We model the life history from the age at maturation onward. The age a is a discrete variable with values a = 0, 1, 2, … , T, with a = 0 referring to the age at maturation. At each age a, the individual has access to a certain amount of energy e ≥ 0 available in the environment, which characterizes the current state of the environment. The individual’s allocation of available energy to reproduction versus to maintenance may plastically depend on e. For each age a, the reaction norm f(a, e), where 0 ≤ f ≤ 1, describes how the fraction of energy allocated to reproduction varies with the energy e currently available in the individual’s environment. As we will show, the evolutionarily optimal allocation reaction norm f is independent of age a. In line with this result and to keep notation simple, we do not make all arguments explicit but write f(e) when referring to f(a, e).
The energy enet available for allocation (which could be lower than the energy e available in the environment owing to costs of plasticity; see eq. [5] below) is split between reproduction, er(a), and maintenance, em(a):
| 1 |
with the reaction norm f(e) specifying the split:
| 2a |
| 2b |
Survival increases monotonically with maintenance energy. We thus assume that the dependence on em of the survival probability at age a is of Holling type II,
| 3 |
where e1/2 is the energy allocation at which survival probability reaches one-half. The smaller the value of e1/2, the steeper the initial increase of survival probability with em.
As we investigate energy allocation in stochastically fluctuating environments, the energy availability e is a random variable. We construct a stochastic process to describe how energy availability varies over time. This process depends on two environmental characteristics, environmental variability λ and predictability τ, which we will vary independently in our analysis (fig. 1). Appendix A details the definition of this stochastic process and describes how the two environmental parameters λ and τ emerge from this definition.
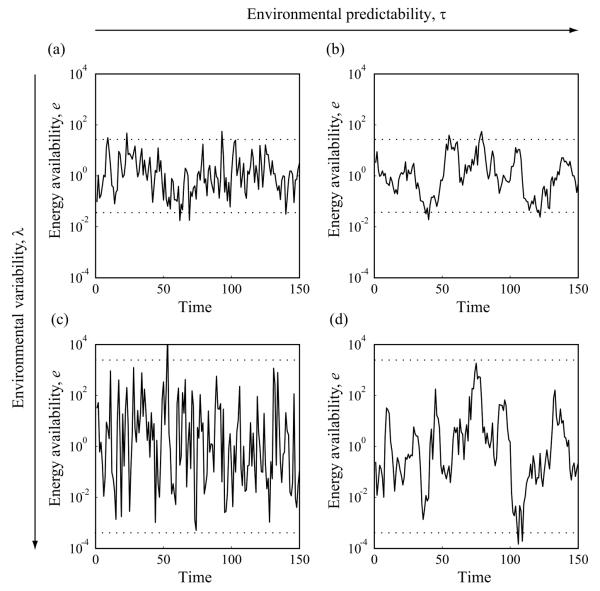
Figure 1.
Stochastic fluctuations in energy availability in four environments with different variability and predictability. The average amplitude of the time series increases with environmental variability λ, whereas its average frequency decreases with environmental predictability τ. Dotted lines show the resultant 95% confidence intervals for energy availability. Environmental variability λ is larger in the bottom row (c, d) than it is in the top row (a, b), while environmental predictability τ is larger in the right column (b, d) than it is in the left column (a, c): a, λ = 5, τ = 1; b, λ = 5, τ = 10; c, λ = 50, τ = 1; and d, λ = 50, τ = 10. Note that the vertical axes are scaled logarithmically.
Our aim is to find the evolutionarily optimal allocation reaction norm f(e) that maximizes an individual’s lifetime reproductive success. For this purpose, we use the technique of dynamic programming. Dynamic programming is a backward-iteration approach for optimizing an inter-dependent sequence of decisions (Houston and McNamara 1999; Clark and Mangel 2000). Because the fitness benefits of immediate reproduction will usually depend on how an individual chooses to reproduce in the future, it is natural to work backward in time when searching for optimal allocation strategies. Dynamic programming is a deterministic procedure that allows us to identify the evolutionarily optimal allocation reaction norm for each age a before some terminal age T and for a given combination of model parameters. For each possible energy availability e, we find the optimal allocation strategy at age a by choosing f so that the reproductive success from age a onward, R(a, e), is maximized. The dynamic-programming equation specifies R(a, e):
| 4 |
We thus see that R(a, e) comprises two components: (1) current reproductive success at age a as determined by the energy allocated to reproduction at age a, f(e) · e, and (2) expected future reproductive success E(R(a + 1, e)) from age a + 1 onward, weighted by the survival probability S(a, (1 – f(e)) · e) from age a to age a + 1. The expected future reproductive success is a function of future energy availabilities and future allocation decisions. The dynamic-programming equation thus is recursive and can be best solved backward in time: starting at a chosen final age a = T, reproductive success R(a, e) is maximized iteratively for younger and younger ages until a = 0 is reached. Determining the optimal values of f for all energy availabilities e in this manner yields the optimal allocation reaction norm f(e) that maximizes lifetime reproductive success. A more detailed description of the dynamic programming technique is provided in appendix B.
Our evolutionary allocation model contains three parameters: the variability λ of the environmental dynamics, the autocorrelation time τ of the environmental dynamics, and the energy level e1/2 at which survival probability reaches one-half. In this article, we will systematically analyze how the evolutionarily optimal allocation reaction norm f(e) and the implied degree of plasticity depend on these parameters. We define the degree of plasticity of a reaction norm f as the range fmax – fmin of reproductive investments across all possible environments on the basis of the maximum reproductive investment fmax = maxe f(e) and the minimum reproductive investment fmin = mine f(e).
As an extension of the model specified above, we consider possible costs of phenotypic plasticity C(a, f). The energy available at age a, e(a), is reduced by costs of phenotypic plasticity, C(a, f),
| 5 |
yielding the net energy enet(a) at age a. We assume that maintaining plasticity may result in costs for an individual (De Witt et al. 1998) and that these costs increase with the range of trait values that can be expressed as a result of plasticity. Plasticity costs for a reaction norm f(e) are defined as
| 6 |
where fmax – fmin is the degree of plasticity and c scales the plasticity costs. The more plastic an individual’s energy allocation, and hence the more reproductive allocation f (e) varies across energy availabilities e, the higher are these plasticity costs. If f(e) does not vary with energy availability so that fmax = fmin, plasticity costs vanish. Constant reaction norms in our model are thus cost free, which was also assumed in the models of Van Tienderen (1991) and Ernande and Dieckmann (2004).
The parameter b, where 0 ≤ b ≤ 1, determines how strongly plasticity costs decrease the energy allocated to reproduction and maintenance:
| 7a |
| 7b |
For b = 0, plasticity costs only affect the energy allocated to maintenance, whereas for b = 1, plasticity costs only influence the energy allocated to reproduction. For comparison, we also analyze the implications of plasticity costs being split in proportion to energy allocation, b = f:
| 8a |
| 8b |
When costs of plasticity are included in the model, the mutual dependence between an evolutionarily optimal reaction norm f and the associated plasticity cost necessitates an additional iteration loop when solving equation (4). When we are determining the optimal f at age a, we start with costs set to 0, calculate the resultant optimal f, calculate the resultant plasticity costs of f, and iterate the last two steps until f and its plasticity cost converge. This ensures that we have found a self-consistent solution through which energy allocation is optimized.
The evolutionary allocation model extended by costs of plasticity has two additional parameters: the maximum plasticity costs c, which result when the degree of plasticity equals 1, and the proportion b at which plasticity costs affect reproduction rather than maintenance.
Results
Our evolutionary allocation model possesses the property of strong backward convergence (Houston and McNamara 1999, p. 43). This means that, in the backward iteration process of solving equation (4), the evolutionarily optimal reaction norms essentially do not change with age (so that for all ages a of interest, |f(a + 1) – f(a)| falls below some small threshold such as 10−5). For ages a that are sufficiently less than a = T, the evolutionarily optimal reaction norm f is thus not only independent of the terminal reward R(T, e) but also of the age a, f(a, e) = f(e).
The age-independent evolutionarily optimal allocation reaction norms resulting from our model do not predict that reproductive investment will increase monotonically with energy availability, but instead they consistently show a characteristic nonmonotonic shape. When energy availability is very low, it is optimal to invest in reproduction alone (fig. 2). With increasing energy availability, the evolutionarily optimal reproductive investment rapidly decreases to a unique minimum (fig. 2b) or may even vanish completely (fig. 2a, 2c, 2d). When energy availability improves further, reproductive investment gradually increases again until almost all energy is allocated to reproduction. Depending on the precise shape of the evolutionarily optimal allocation reaction norm, we distinguish between two classes of outcomes: (1) the optimal reproductive investment is positive for all energy availabilities, so the unique minimum in reproductive investment is greater than 0 (fig. 2b); or (2) the optimal reproductive investment decreases to 0 over an intermediate range of energy availabilities, so reproduction is skipped within that range (fig. 2a, 2c, 2d). The four reaction norms in figure 2 are nothing more than examples and thus cannot capture all aspects of the dependence of evolutionarily optimal reaction norms on environmental variability λ and predictability τ. A full exploration of these effects is provided in figure 3, which highlights, for example, that the dependence of the degree of plasticity on τ is not always monotonic.
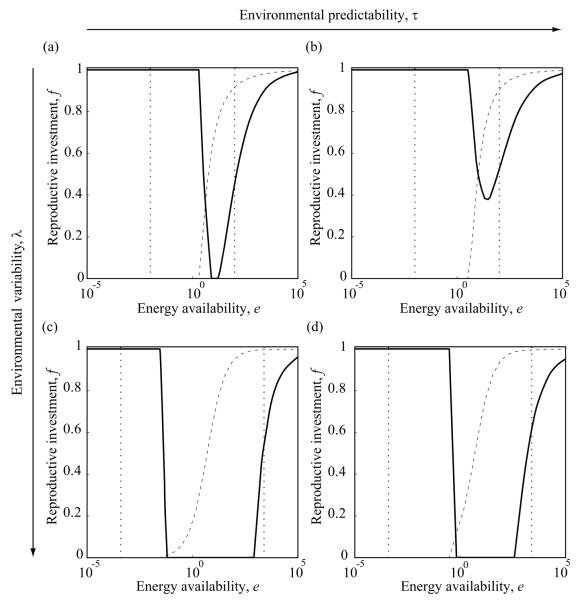
Figure 2.
Evolutionarily optimal allocation reaction norms, describing the dependence of the optimal reproductive investment f on energy availability e, in four environments with different variability and predictability (fig. 1). Dotted lines show the resultant 95% confidence intervals for energy availability. Dashed curves show the survival probabilities resulting from the presented reaction norm at different energy availabilities. Environmental variability λ is larger in the bottom row (c, d) than it is in the top row (a, b), while environmental predictability τ is larger in the right column (b, d) than it is in the left column (a, c): a, λ = 10, τ = 20; b, λ = 10, τ = 50; c, λ = 50, τ = 20; and d, λ = 50, τ = 50. Note that the horizontal axes are scaled logarithmically. Other parameters: e1/2 = 5.
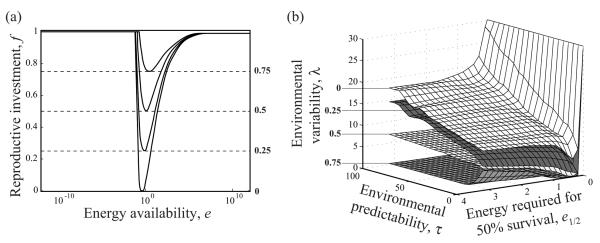
Figure 3.
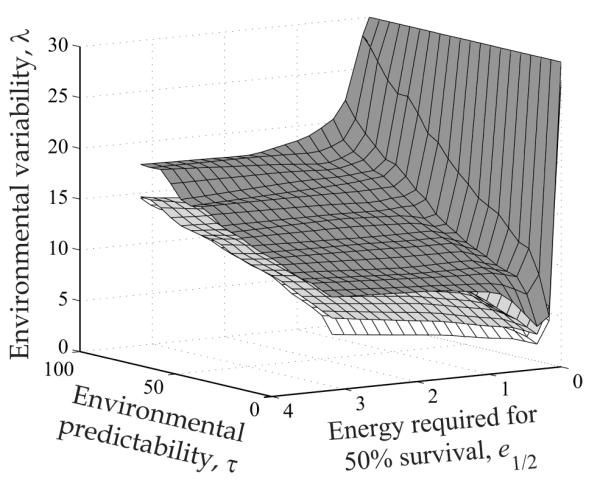
Classification of evolutionarily optimal allocation reaction norms. a, Examples of reaction norms f(e) with minima at f = 0, 0.25, 0.5, or 0.75. b, Surfaces of parameter combinations (e1/2, τ, λ) resulting in optimal reaction norms with these minima. Plasticity thus increases from bottom to top.
As the degree of plasticity is determined by the range fmax – fmin of reproductive investments across all possible energy availabilities that an individual may encounter, and because for all evolutionarily optimal allocation reaction norms, the maximum expressed reproductive investment was found to be 1, the degree of plasticity resulting from an optimal reaction norm is 1 – fmin and thus was determined by the minimal value fmin. We can therefore focus on fmin for characterizing how the evolutionarily optimal degree of plasticity depends on model parameters in general, and on the statistical characteristics of environmental stochasticity in particular. Each point in the three-dimensional parameter space in figure 3b represents a combination of the three parameters e1/2 (energy required for 50% survival), τ (environmental predictability), and λ (environmental variability). The surfaces in the figure divide this parameter space into five ranges, with different degrees of phenotypic plasticity being exhibited by the optimal reaction norms resulting for each parameter combination. In the range above the surface for fmin = 0, optimal reaction norms possess an intermediate region of skipped reproduction, whereas below this surface, optimal reproductive investment is always positive (fig. 3a, 3b). The three surfaces for fmin = 0, 0.25, and 0.5 continuously rise with increasing environmental predictability τ. Surprisingly, the surface for fmin = 0.75 first drops with increasing environmental predictability but eventually rises again, although only very slowly, as predictability is further increased. Thus, as environmental predictability τ is enhanced, the evolutionarily optimal degree of plasticity drops when environmental variability λ is high, but it rises when environmental variability is low. Also, the parameter e1/2 affects plasticity. We recall that, when e1/2 is low, little energy is needed to ensure survival. The shown surfaces first slightly drop with decreasing e1/2, but when e1/2 becomes small, the drop first becomes steeper and then the behavior changes entirely: the surfaces suddenly curve upward and thereby indicate how the optimal degree of plasticity rapidly decreases as e1/2 approaches 0 (fig. 3b). Because survival becomes assured when e1/2 approaches 0, it is intuitive that reproductive investment increases. The evolutionarily optimal allocation reaction norms thus approach f(e) = 1 for all energy availabilities e. As a result, the range of parameter combinations below each of the shown surfaces expands. Of all three parameters, environmental variability λ, which determines the amplitude of stochastic fluctuations in energy availability, has the strongest influence on the evolutionarily optimal degree of plasticity and thus on the shapes of the corresponding reaction norms. When λ is increased, the minimum fmin of the optimal reaction norm lowers. For each combination of τ and e1/2, one value of λ exists for which the minimum fmin of the optimal reaction norm reaches 0. Increasing λ beyond that value, thus broadening and flattening the distribution of energy availabilities, enlarges the intermediate range of energy availability for which reproduction is skipped (fig. 4).
Figure 4.
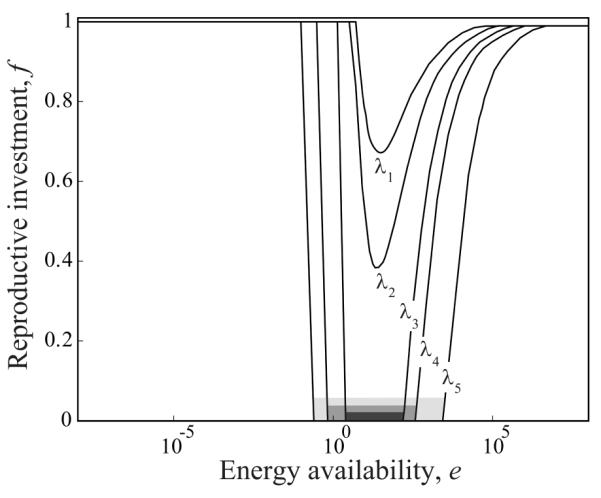
Effects on evolutionarily optimal allocation reaction norms of environmental variability. Optimal reaction norms f(e) are shown for different levels of environmental variability λ: λ1 = 1, λ2 = 10, λ3 =20, λ4 = 50, and λ5 = 100. Increased environmental variability leads to skipped reproduction across wider ranges of energy availability (gray bars). Other parameters: e1/2 = 5 and τ = 50.
Costs of phenotypic plasticity influence evolutionarily optimal energy allocation patterns only quantitatively. As expected, the minimum of the optimal reaction norm rises with increasing magnitude of plasticity costs c, such that the degree of plasticity decreases (fig. 5a, 5b). Analysis of the effect of increased plasticity costs in interaction with the other parameters reveals that the qualitative dependence of optimal reaction norms on the parameters λ and τ is not altered for different values of c. As can be expected, the region in parameter space in which plasticity is maximal shrinks with increasing values of c (fig. 5b): the more costly it is to be plastic, the lower the evolutionarily optimal degree of plasticity is. The line of combinations (τ, λ) separating reaction norms with maximum plasticity from those with less plasticity does not change shape, but it only moves toward larger values of λ (and, equivalently, smaller values of τ) as plasticity costs increase. Less plastic strategies thus become optimal under a wider range of conditions and occur for higher environmental variability and lower environmental predictability (fig. 5b).
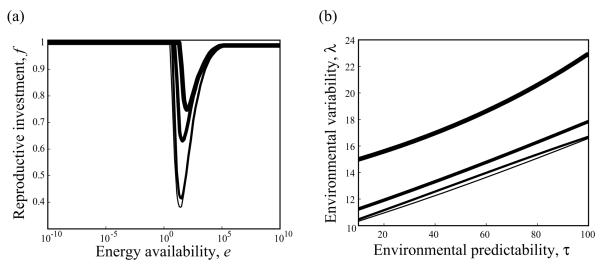
Figure 5.
Effects on evolutionarily optimal allocation reaction norms of the scale c of plasticity costs. a, Optimal reaction norms for different values of c, with τ = 50 and λ = 10. Increased plasticity costs reduce the optimal degree of plasticity. b, Lines of parameter combinations (τ, λ) resulting in optimal reaction norms with a minimum f = 0 for different values of c: c = 0, 10, 100, and 1,000 are indicated by growing line widths. Other parameters: e1/2 = 5 and b = 1.
As well, the parameter b, which determines the relative extent by which plasticity costs reduce the energy available for reproduction, affects the optimal reaction norms only quantitatively. When b is decreased, the surface of combinations (e1/2, τ, λ) separating reaction norms with maximum plasticity from those with less plasticity hardly changes shape, but only moves toward smaller values of λ (fig. 6). Decreasing b causes the minimum of the optimal reaction norms to decrease and, hence, plasticity to increase. We obtained qualitatively similar results (not shown) when assuming that costs affect maintenance and reproductive energy in proportion to energy allocation, such that b = f.
Figure 6.
Effects on evolutionarily optimal allocation reaction norms of the proportion b at which plasticity costs affect reproduction as opposed to maintenance. Surfaces of parameter combinations (e1/2, τ, λ) resulting in optimal reaction norms with a minimum at f = 0 for different values of b: b = 0 (white), b = 0.5 (light gray), and b = 1 (dark gray). Increased allocations of plasticity costs to reproduction reduce the optimal degree of plasticity. Other parameters: c = 1.
We tested the influence of a mortality component that cannot be diminished by higher energy allocation em to maintenance by investigating survival functions S = αem/(em + e1/2) that reach their asymptotes at some maximal survival value α where 0 < α < 1 instead of where α = 1, as in equation (3). Including this additional mortality component again does not change evolutionarily optimal reaction norms qualitatively but only leads to a rise of their minimum fmin values (results not shown). Because the potential for future reproduction diminishes when α is lowered, it is intuitive that evolution responds by an increase in immediate reproduction.
Reproductive investment f in our model varies between 0 and 1, and evolution fixes it at 1 for very low energy availability. We tested the influence of physiological limits that restrict the fraction f of the available energy e that can be invested in reproduction by introducing an upper limit fl, where 0 < fl < 1, for reproductive investment f, such that evolution had to respect the constraint f≤fl. Once again, this does not alter the U shape of the evolutionarily optimal allocation reaction norm but only prevents f from increasing all the way up to 1 for very low or very high values of energy availability e. As a result, f equals fl for energy availabilities close to 0, decreases to a minimum as e grows, and then rises again up to fl for increasing e. In other words, reproductive investment is as high as the physiological limit allows for low and high energy availability, whereas it drops to a minimum in between.
Discussion
We have investigated how evolutionarily optimal reproductive investment depends on the predictability and variability of energy availability in stochastic environments. Our model shows that, at certain energy levels, a slight change in energy availability must be expected to cause a major change in optimal energy allocation. Investment in reproduction alone is optimal when energy availability is low: mortality due to starvation is then likely, and options for future reproduction are virtually nonexistent. When energy availability is intermediate, the probability of future reproductive success becomes high enough to outweigh the benefits of immediate reproduction. Reproductive investment is then drastically reduced and reaches a unique intermediate minimum, or reproduction is even skipped altogether. When energy availability is high, a high reproductive investment occurs even in very variable environments.
Skipped reproduction is frequently observed in nature (in fish: Bull and Shine 1979; Engelhard and Heino 2005; Rideout et al. 2005; Jørgensen and Fiksen 2006; Jørgensen et al. 2006; in amphibians: Bull and Shine 1979; Harris and Ludwig 2004; in reptiles: Bull and Shine 1979; Brown and Weatherhead 2004; in birds: Illera and Diaz 2006). Poor individual condition or poor environmental quality are thought of as the main causes for skipped reproduction (Bull and Shine 1979; Dutil 1986; Rideout et al. 2005), which is expected to occur when future reproductive success outweighs the benefits of immediate reproduction (Engelhard and Heino 2005; Jørgensen et al. 2006). However, to our knowledge, no previously analyzed life-history model has predicted the occurrence of skipped reproduction only for intermediate environmental qualities, with high reproductive investment being optimal at both ends of a gradient of environmental quality.
Interestingly, previous life-history theory made two apparently contradictory predictions about optimal reproductive investment in stochastic environments. Theoretical studies concluded that worsened environmental conditions favor decreased reproductive investment per reproductive event (Erikstad et al. 1998). This is supported by empirical evidence (Kaitala 1991; Ellers and van Alphen 1997), and it agrees with the right-hand side of the evolutionarily optimal allocation reaction norm resulting from our model. On the other hand, it has been hypothesized that, when survival is suddenly reduced because of worsened environmental conditions, reproductive investment should be increased as a form of “terminal investment” (Gadgil and Bossert 1970; Michod 1979). Also, this prediction is supported by empirical results (Stelzer 2001) and it agrees with the left-hand side of the evolutionarily optimal allocation reaction norm resulting from our model. Although so far these two predictions were regarded as separate phenomena, our results suggest that they may apply to different ranges of energy availability and are thus, in fact, part of the same reaction norm. Our model results hence help to reconcile these apparently contradictory previous life-history predictions.
Why have U-shaped reaction norms for optimal reproductive investment in stochastic environments not been detected in earlier studies? In contrast to most previous theoretical studies, our analysis describes reproductive investment by a reaction norm and thus as a function of energy availability. Early studies instead compared the fitness of fixed reproductive strategies in variable and constant environments (Murphy 1968; Schaffer 1974) and found that increased environmental variability leads to a decrease in the optimal reproductive investment per reproductive event. Neither of these models allowed for plasticity in reproductive investment but considered only fixed reproductive strategies. The models of iteroparous life histories by Gadgil and Bossert (1970) and Michod (1979) considered variations in reproductive investment at different ages but again did not allow for plasticity in reproductive investment at any specific age. Gurney and Middleton (1996) demonstrated in a population model that mixed investment in both reproduction and growth can become a superior strategy in highly variable environments, as opposed to investment in growth followed by a switch to reproduction at a certain time in an individual’s life. They also did not allow for plasticity in allocation strategies, nor did they derive reaction norms. More recently, Benton and Grant (1999) studied a matrix population model of optimal resource allocation that included density dependence and stochastic fluctuations in survival and fecundity. They demonstrated through numerical simulations that, as environmental variability increases, the resultant change in the evolutionarily stable reproductive investment also increases, on average, which qualitatively agrees with our findings. Also in this study, no reaction norms were considered. To our knowledge, Erikstad et al. (1998) is the only preceding theoretical study that analyzed the reaction norm of optimal reproductive investment for a range of environmental conditions in a stochastic environment. They reported that optimal reproductive investment increases monotonically with improving environmental conditions. Erikstad et al. (1998) designed their model to describe long-lived bird species with a fixed clutch size. Below a certain threshold of environmental quality, they defined current reproduction as 0, because the available energy would not suffice for producing a clutch. Hence, although their findings agree with the right-hand side of the U-shaped evolutionarily optimal allocation reaction norm found in our study, their model did not allow detection of the left-hand side of this reaction norm, because reproduction at very low energy levels was prevented a priori.
An experimental study on rotifers nicely illustrated that a single organism can exhibit both of the effects predicted above when exposed to a full spectrum of food concentrations, from very low to ad lib. (Stelzer 2001). Reproductive investment of rotifers, which was measured as energy flow into the ovary during an egg-laying interval, was highest at very low food concentrations and decreased when food availability was improved. High reproductive investment at low food concentrations was often followed by immediate death after reproduction. When food concentration was improved further, however, the reproductive rate of individuals increased, with more offspring being produced per time unit. This translates into a high reproductive investment when food availability was high. Both of these observations are thus in agreement with our predictions.
Costs of phenotypic plasticity have been predicted to impede the evolution of phenotypic plasticity (e.g., Via and Lande 1985; Gomulkiewicz and Kirkpatrick 1992; Scheiner 1993; De Witt et al. 1998; Ernande and Dieckmann 2004; Pigliucci 2005). A number of experimental studies identified costs of plasticity in different taxa and traits, including plasticity in behavioral, morphological, and life-history traits as a response to predators in amphibian larvae (Releya 2002a) and freshwater snails (DeWitt 1998); plasticity in morphological traits in response to light cues and resources in plants (Dorn et al. 2000; Van Kleunen et al. 2000; Weinig et al. 2006; Dechaine et al. 2007), and plasticity in flowering time in response to temperature (Stinchcombe et al. 2004). Each of these studies established support for the existence of costs of plasticity for at least some of the traits investigated. Still, the frequency of studies in which plasticity costs have been detected is low relative to the total number of tests, and even when detected, the magnitude of such costs often turns out to be small, rendering difficult the general conclusions about the importance of plasticity costs. It has been suggested that plasticity costs have not often been detected unequivocally because of the employed experimental setups and the genetic background of the studied genotypes (Agrawal 2001; Weinig et al. 2006). In particular, most studies testing for plasticity costs sampled genotypes from natural populations even though genotypes with high plasticity costs, which may have been present initially, might subsequently have been removed during protracted evolution by natural selection (Weinig et al. 2006).
Bearing in mind that the more general importance of plasticity costs is still unclear, we first reported our main results in the absence of any such costs and then demonstrated the robustness of these results in an extended model in which plasticity costs were taken into account. As expected, our extended results show that, when plasticity is costly, a reduced degree of plasticity is optimal. Surprisingly, however, our extended results reveal that evolutionarily optimal allocation reaction norms were not qualitatively altered by plasticity costs. High plasticity costs just moved the optimal reaction norm toward the cost-free flat-reaction norm, in agreement with previous findings by Van Tienderen (1991) and Ernande and Dieckmann (2004).
It may be worth highlighting that we modeled costs of phenotypic plasticity as “maintenance costs” sensu DeWitt et al. (1998) and also that our definition of plasticity costs includes costs of acquiring information about the environment. Because we focus on the phenotypic expression of plasticity and do not study the underlying genetic architecture, we do not address the consequences of potential genetic costs of, or constraints on, plasticity originating from linkages or epistasis between loci underlying plasticity and loci affecting other fitness-relevant traits (DeWitt et al. 1998). We tested the robustness of our results against the use of another cost function that was based on the variance of reaction norms (Ernande and Dieckmann 2004) and did not find any qualitative departures from the predictions presented above (results not shown). This confirms that our results for the influence of plasticity costs are qualitatively robust and do not depend on a particular form of the underlying cost function.
Our model allows us to vary how strongly the costs of plasticity reduce the energy available for maintenance as opposed to that available for reproduction. When plasticity costs mainly reduce maintenance energy, the evolutionarily optimal degree of plasticity is enhanced by limiting reproductive investment when energy availability is low, so as to ensure survival.
Various model approaches have been employed to explore the conditions favoring the evolution of phenotypic plasticity (e.g., Via and Lande 1985; Van Tienderen 1991; Gomulkiewicz and Kirkpatrick 1992; Moran 1992; Ernande and Dieckmann 2004). Our results agree with findings based on optimality models and quantitative genetics models in that plastic strategies are always superior to fixed strategies in variable environments (e.g., Clark and Harvell 1992; Scheiner 1993). In contrast to earlier models (e.g., Houston and McNamara 1992; Moran 1992), we analyzed the gradual degree of plasticity rather than just consider its presence or absence: a unique property of our model is that we considered both environmental quality and the phenotypic response to the environment, in terms of reproductive investment, as continuous variables. This allowed us to demonstrate how minor changes in environmental quality can imply major changes in the evolutionarily optimal reproductive investment.
Some assumptions underlying our model might limit the generality of our results. We derived the evolutionarily optimal allocation reaction norms as evolutionary endpoints in stochastic environments with different statistical characteristics. At these endpoints, the selection pressures on energy allocation vanish. Such optima are, of course, unlikely to be exactly tracked by natural populations, for three reasons. First, as with any evolutionary endpoint, selection pressures diminish as the endpoint is approached, such that evolution close to the endpoint becomes increasingly slow. Second, ecological systems are changing continuously, such that their statistical characteristics, even in terms of features as general as environmental variability and predictability, might change faster than adaptation can occur. However, when evolutionary rates are not too slow and changes in the statistical characteristics of the stochastic environment are not too fast, we can expect evolution by natural selection to take populations close to the identified endpoints. Third, as already mentioned above, we assume that evolving populations do not run out of genetic variance as they respond to the existing selection pressures on energy allocation.
Our approach assumes that the evolutionarily optimal allocation reaction norm is independent of density. Although density would influence resource abundance and, thus, energy availability, it should not alter an individual’s allocation decisions at a given energy level. Likewise, even though density-dependent competition could change environmental variability and predictability, these effects can be accounted for in our model, because it treats environmental variability and predictability as parameters. What our model does not capture is frequency-dependent selection. If, for example, environmental variability and predictability become dependent on the reaction norm that is currently prevalent in the population, an environmental feedback is created that precludes the use of any optimality model.
Another critical assumption underlying our analysis is that the modeled organisms are “income breeders” who can acquire energy for reproduction and maintenance only during the current reproductive period and who must thus spend all such energy during the current season (Stearns 1992; Jönsson 1997). This may explain why we found full investment in reproduction close to starvation. An interesting extension of the framework presented here would be to investigate how allocation decisions are affected by the possibility of energy storage between seasons, which is a widespread strategy helping individuals to cope with temporarily poor environmental conditions (e.g., Rogers 1987; Rogers and Smith 1993; Kooi and Troost 2006). Even though the possibility of energy storage will affect evolutionarily optimal allocation reaction norms, it should be borne in mind that there usually exists a fundamental asymmetry between investments in reproduction and in maintenance. When energy availability is high, many organisms can increase their reproductive success by investing more energy in reproduction by increasing, within physiological limits, their reproductive frequency, their clutch size, and their investment in each individual offspring. In contrast, all investments in maintenance cannot push the probability of survival above 1. This asymmetry is captured by the saturating survival function in our model and serves as a conceptual cornerstone for understanding elevated investment into reproduction at high energy availability.
We conclude that stochastic environments can cause unexpected patterns of plastic energy allocation, with evolutionarily optimal reproductive investment not necessarily just increasing or decreasing monotonically with energy availability. The U-shaped allocation reaction norms predicted here imply maximal reproductive investment at the extreme ends of environmental quality and minimal reproductive investment for intermediate conditions. We find that the transitions between these three outcomes are quite sharp; consequently, evolutionarily optimal reproductive investment in stochastic environments can be very sensitive to small changes in energy availability.
Acknowledgments
We thank F. Johnston for valuable comments on an earlier version of this manuscript and D. Urbach for helpful discussions. This study was funded by the Austrian Science Fund (FWF; grant P18647-B16 to B.T.) and by the Swiss National Foundation (grant 3100A0-111796 to B.T.). U.D. acknowledges financial support by the Vienna Science and Technology Fund (WWTF) and by the European Commission, through the European Research Training Network on Fisheries-induced Adaptive Changes in Exploited Stocks (FishACE; contract MRTN-CT-2204-005578) and the European Research Network on Fisheries-induced Evolution (FinE; contract SSP-2006-044276).
APPENDIX A
Definition of Stochastically Fluctuating Environments
A time series of environmental states {e1, e2, e3, …, eT} is a realization of a stochastic process describing varying energy availability (fig. 1), with the individual states applying at ages a = 1, 2, … , T of the model organism. Considering all possible realizations, we obtain the frequency distribution of e at each age a. Thus, for defining the stochastic process, we need to make assumptions about the distribution of e at each age a.
In nature, the abundance of organisms and resources often follows a lognormal distribution (Limpert et al. 2001), owing to the central limit theorem for multiplicative stochastic variables. We thus assume that energy availability e is lognormally distributed with mean μ and variance σ2, which implies that the logarithm of e is normally distributed, with mean μN and variance In line with this, we assume environmental dynamics to follow a multiplicative autoregressive process of order 1, AR(1), which means that energy availability at a given age depends on two factors, the energy availability at the previous age and a noise term. Consequently, energy availability at age a + 1, ea+1, is given by the product of energy availability at the previous age a, ea, and an age-specific noise term εa, which is the source of randomness:
| A1 |
where φ ≥ 0. The parameter φ describes how much ea influences ea+1. When φ = 0, subsequent environmental states are not correlated, and ea+1 is independent of ea and is thus fully determined by the error term εa. Because correlations between ages are thus captured by φ, εa can be assumed to be uncorrelated between ages. Because ea and ea+1 are lognormally distributed, the noise term εa must also follow a lognormal distribution. The logarithm of εa is thus a normally distributed white-noise process, with mean με,N and variance . This white noise serves as the source of randomness for the environmental fluctuations in our model. We assume this stochastic process to be stationary, which means that the mean and variance of ea are independent of a, which in turn implies that με,N = 0. Taking the logarithm of equation (4) and subsequently taking variances, this results in , which implies that φ < 1. The variance of the logarithm of e and the parameter φ thus determine the variance of the noise term. Because με,N = 0 and are independent of age a, the noise process is stationary, εa = ε.
The autocorrelation time τ of the stochastic environmental dynamics of e measures the duration over which the correlation between successive energy availabilities decreases to 1/e ≈ 36.8% (where e ≈ 2.718, denoting Euler’s number); τ is given by
| A2 |
We use τ as a convenient measure of environmental predictability. To reduce the number of parameters needed to describe the environmental dynamics, and because we can freely choose the unit for e, we set the geometric mean of e to 1, which is equivalent to μN = 0; we thus measure energy availability relative to its geometric mean. With this, we obtain σ2 = (eσ2N – 1) · eσ2N and μ = eσ2N/2 for the mean and variance of the lognormal distribution of e. We use the coefficient of variation,
| A3 |
to quantify environmental variability. Using the two parameters λ and τ to characterize the fluctuating environment allows us to independently vary the variability and predictability of fluctuating energy availability (fig. 1).
APPENDIX B
Determination of Evolutionarily Optimal Reaction Norms through Dynamic Programming
Evolutionarily optimal reaction norms in our model are computed by applying the technique of dynamic programming. For this purpose, we need to discretize the energy scale to obtain a vector of n discrete energy states ei, i = 1, 2, … , n. For each of these, we find the optimal allocation strategy at age a by choosing f so that the reproductive success from age a onward, R(a, ei), is maximized. The recursive dynamic-programming equation is
| B1 |
where the transition probability p(ej|ei) determines the likelihood of the transition from energy state ei at age a to state ej at age a + 1. These transition probabilities follow directly from the definition of the autoregressive process:
| B2 |
and can be assembled in an n × n matrix P with elements Pij = p(ej|ei), where i, j = 1, 2, … , n. This last step follows from the fact that ε = ei−φ · ej is lognormally distributed, and it is accurate when n is large. Starting with R(T, ej) at age a = T, equation (B1) is solved iteratively for younger and younger ages until a = 0 is reached. At each age and for each energy state ei, f(ei) is chosen so as to maximize the expression in square brackets (this is the meaning of the argmax function). The set of numbers f(ei), i = 1, 2, … , n that result when a = 0 then describes the evolutionarily optimal allocation reaction norm.
It is important to understand that this f(e) is potentially very different from the function f′(e) we would obtain by optimizing energy allocation separately for each energy state ei when assuming the absence of stochastic fluctuations in energy availability. Whereas f(e) describes the expected endpoint of evolution by natural selection in a single population exposed to a fluctuating environment, f′(e) would describe the collection of evolutionary endpoints in many completely separated populations, each of which is exposed to a constant environment with a specific energy availability e. The formal reason for this biologically crucial distinction is that, for evolution in stochastically fluctuating environments, energy states are coupled by the considered stochastic environmental process, with this coupling being reflected in equation (B1) by the sum across all possible energy states. More specifically, the evolutionarily optimal energy allocation f(ei) at age a and energy state ei not only depends on (1) how likely it is that the individual will survive until a + 1, S(a, (1 – f(ei)) · ei), but also on (2) how likely the energy state ej is encountered at age a + 1, p(ej|ei) and on (3) how valuable that encounter will be in terms of future reproductive success, R(a + 1, ej).
We choose a terminal age T that is so large that virtually no survival from age a = 0 until age a = T is possible. Hence the terminal reward R(T, e), denoting the vector of reproductive success for all energy states ei from age T onward, has no effect on results at ages of interest (for which survival from age a = 0 is nonnegligible) and can thus be assumed to vanish, R(T, e) = 0. At the terminal age, future reproductive success is obviously maximized by allocating all available energy to reproduction, f(ei) = 1 for all ei at age T.
Literature Cited
- Agrawal AA. Phenotypic plasticity in the interactions and evolution of species. Science. 2001;294:321–326. doi: 10.1126/science.1060701. [DOI] [PubMed] [Google Scholar]
- Benton TG, Grant A. Optimal reproductive effort in stochastic, density-dependent environments. Evolution. 1999;53:677–688. doi: 10.1111/j.1558-5646.1999.tb05363.x. [DOI] [PubMed] [Google Scholar]
- Brown GP, Weatherhead PJ. Sexual abstinence and the cost of reproduction in adult male water snakes, Nerodia sipedon. Oikos. 2004;104:269–276. [Google Scholar]
- Bull JJ, Shine R. Iteroparous animals that skip opportunities for reproduction. American Naturalist. 1979;114:296–303. [Google Scholar]
- Clark CW, Harvell CD. Inducible defenses and the allocation of resources: a minimal model. American Naturalist. 1992;139:521–539. [Google Scholar]
- Clark CW, Mangel M. Dynamic state variable models in ecology: methods and applications. Oxford University Press; New York: 2000. [Google Scholar]
- Dechaine JM, Johnston JA, Brock MT, Weinig C. Constraints on the evolution of adaptive plasticity: costs of plasticity to density are expressed in segregating progenies. New Phytologist. 2007;176:874–882. doi: 10.1111/j.1469-8137.2007.02210.x. [DOI] [PubMed] [Google Scholar]
- DeWitt TJ. Costs and limits of phenotypic plasticity: tests with predator-induced morphology and life history in a freshwater snail. Journal of Evolutionary Biology. 1998;11:465–480. [Google Scholar]
- DeWitt TJ, Sih A, Wilson D. Costs and limits of phenotypic plasticity. Trends in Ecology & Evolution. 1998;13:77–81. doi: 10.1016/s0169-5347(97)01274-3. [DOI] [PubMed] [Google Scholar]
- Dorn LA, Pyle EH, Schmitt J. Plasticity to light cues and resources in Arabidopsis thaliana: testing for adaptive value and costs. Evolution. 2000;54:1982–1994. doi: 10.1111/j.0014-3820.2000.tb01242.x. [DOI] [PubMed] [Google Scholar]
- Dutil J-D. Energetic constraints and spawning interval in the anadromous Arctic charr (Salvelinus alpinus) Copeia. 1986;1986:945–955. [Google Scholar]
- Ellers J, van Alphen JJM. Life history evolution in Asobara tabida: plasticity in allocation of fat reserves to survival and reproduction. Journal of Evolutionary Biology. 1997;10:771–785. [Google Scholar]
- Engelhard GH, Heino M. Scale analysis suggests frequent skipping of the second reproductive season in Atlantic herring. Biology Letters. 2005;1:172–175. doi: 10.1098/rsbl.2004.0290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erikstad KE, Fauchald P, Tveraa T, Steen H. On the cost of reproduction in long-lived birds: the influence of environmental variability. Ecology. 1998;79:1781–1788. [Google Scholar]
- Ernande B, Dieckmann U. The evolution of phenotypic plasticity in spatially structured environments: implications of intraspecific competition, plasticity costs, and environmental characteristics. Journal of Evolutionary Biology. 2004;17:613–628. doi: 10.1111/j.1420-9101.2004.00691.x. [DOI] [PubMed] [Google Scholar]
- Gabriel W, Lynch M. The selective advantage of reaction norms for environmental tolerance. Journal of Evolutionary Biology. 1992;5:41–59. [Google Scholar]
- Gadgil M, Bossert WH. Life historical consequences of natural selection. American Naturalist. 1970;104:1–24. [Google Scholar]
- Gomulkiewicz R, Kirkpatrick M. Quantitative genetics and the evolution of reaction norms. Evolution. 1992;46:390–411. doi: 10.1111/j.1558-5646.1992.tb02047.x. [DOI] [PubMed] [Google Scholar]
- Gurney WSC, Middleton DAJ. Optimal resource allocation in a randomly varying environment. Functional Ecology. 1996;10:602–612. [Google Scholar]
- Harris RN, Ludwig PM. Resource level and reproductive frequency in female four-toed salamanders, Hemidactylium scutatum. Ecology. 2004;85:1585–1590. [Google Scholar]
- Houston AI, McNamara JM. Phenotypic plasticity as a state-dependent life-history decision. Evolutionary Ecology. 1992;6:243–253. [Google Scholar]
- Houston AI, McNamara JM. Models of adaptive behaviour: an approach based on state. Cambridge University Press; Cambridge: 1999. [Google Scholar]
- Illera JC, Diaz M. Reproduction in an endemic bird of a semiarid island: a food-mediated process. Journal of Avian Biology. 2006;37:447–456. [Google Scholar]
- Jönsson KI. Capital and income breeding as alternative tactics of resource use in reproduction. Oikos. 1997;78:57–66. [Google Scholar]
- Jørgensen C, Fiksen Ø. State-dependent energy allocation in cod (Gadus morhua) Canadian Journal of Fisheries and Aquatic Sciences. 2006;63:186–199. [Google Scholar]
- Jørgensen C, Ernande B, Fiksen Ø, Dieckmann U. The logic of skipped spawning in fish. Canadian Journal of Fisheries and Aquatic Sciences. 2006;63:200–211. [Google Scholar]
- Kaitala A. Phenotypic plasticity in reproductive behaviour of waterstriders: trade-offs between reproduction and longevity during food stress. Functional Ecology. 1991;5:12–18. [Google Scholar]
- Kooi BW, Troost TA. Advantage of storage in a fluctuating environment. Theoretical Population Biology. 2006;70:527–541. doi: 10.1016/j.tpb.2006.07.005. [DOI] [PubMed] [Google Scholar]
- Levins R. Evolution in changing environments: some theoretical explorations. Princeton University Press; Princeton, NJ: 1968. [Google Scholar]
- Limpert E, Stahel WA, Abbt M. Log-normal distributions across the sciences: keys and clues. BioScience. 2001;51:341–352. [Google Scholar]
- Lind MI, Johansson F. The degree of adaptive phenotypic plasticity is correlated with the spatial environmental heterogeneity experienced by island populations of Rana temporaria. Journal of Evolutionary Biology. 2007;20:1288–1297. doi: 10.1111/j.1420-9101.2007.01353.x. [DOI] [PubMed] [Google Scholar]
- Lively CM. Predator-induced shell dimorphism in the acorn barnacle Chthamalus anisopoma. Evolution. 1986;40:232–242. doi: 10.1111/j.1558-5646.1986.tb00466.x. [DOI] [PubMed] [Google Scholar]
- Michod RE. Evolution of life histories in response to age-specific mortality factors. American Naturalist. 1979;113:531–550. [Google Scholar]
- Moran NA. The evolutionary maintenance of alternative phenotypes. American Naturalist. 1992;139:971–989. [Google Scholar]
- Murphy GI. Pattern in life history and the environment. American Naturalist. 1968;102:391–403. [Google Scholar]
- Pigliucci M. Evolution of phenotypic plasticity: where are we going now? Trends in Ecology & Evolution. 2005;20:481–486. doi: 10.1016/j.tree.2005.06.001. [DOI] [PubMed] [Google Scholar]
- Relyea RA. Costs of phenotypic plasticity. American Naturalist. 2002a;159:272–282. doi: 10.1086/338540. [DOI] [PubMed] [Google Scholar]
- Relyea RA. Local population differences in phenotypic plasticity: predator-induced changes in wood frog tadpoles. Ecological Monographs. 2002b;72:77–93. [Google Scholar]
- Rideout RM, Rose GA, Burton MPM. Skipped spawning in female iteroparous fishes. Fish and Fisheries. 2005;6:50–72. [Google Scholar]
- Rogers CM. Predation risk and fasting capacity: do wintering birds maintain optimal body mass? Ecology. 1987;68:1051–1061. [Google Scholar]
- Rogers CM, Smith JNM. Life-history theory in the nonbreeding period: trade-offs in avian fat reserves. Ecology. 1993;74:419–426. [Google Scholar]
- Schaffer W. Optimal reproductive effort in fluctuating environments. American Naturalist. 1974;108:783–790. [Google Scholar]
- Scheiner SM. Genetics and evolution of phenotypic plasticity. Annual Review of Ecology and Systematics. 1993;24:35–68. [Google Scholar]
- Schlichting C. The evolution of phenotypic plasticity in plants. Annual Review of Ecology and Systematics. 1986;17:667–693. [Google Scholar]
- Stearns SC. The evolution of life histories. Oxford University Press; New York: 1992. [Google Scholar]
- Stelzer CP. Resource limitation and reproductive effort in a planktonic rotifer. Ecology. 2001;82:2521–2533. [Google Scholar]
- Stinchcombe JR, Dorn LA, Schmitt J. Flowering time plasticity in Arabidopsis thaliana: a reanalysis of Westerman and Lawrence (1970) Journal of Evolutionary Biology. 2004;17:197–207. doi: 10.1046/j.1420-9101.2003.00641.x. [DOI] [PubMed] [Google Scholar]
- Travis J. Evaluating the adaptive role of morphological plasticity. In: Wainwright P, Reilly S, editors. Ecological morphology: integrative organismal biology. University of Chicago Press; Chicago: 1994. pp. 99–122. [Google Scholar]
- Van Kluenen M, Fischer M, Schmid B. Costs of plasticity in foraging characteristics of the clonal plant Ranunculus reptans. Evolution. 2000;54:1947–1955. [PubMed] [Google Scholar]
- Van Tienderen PH. Evolution of generalists and specialists in spatially heterogeneous environments. Evolution. 1991;45:1317–1331. doi: 10.1111/j.1558-5646.1991.tb02638.x. [DOI] [PubMed] [Google Scholar]
- Via S, Lande R. Genotype-environment interaction and the evolution of phenotypic plasticity. Evolution. 1985;39:505–522. doi: 10.1111/j.1558-5646.1985.tb00391.x. [DOI] [PubMed] [Google Scholar]
- Weinig C, Johnston J, German ZM, Demink LM. Local and global costs of adaptive plasticity to density in Arabidopsis thaliana. American Naturalist. 2006;167:826–836. doi: 10.1086/503530. [DOI] [PubMed] [Google Scholar]
- Zhivotovsky LA, Feldman MW, Bergman A. On the evolution of phenotypic plasticity in a spatially heterogeneous environment. Evolution. 1996;50:547–558. doi: 10.1111/j.1558-5646.1996.tb03867.x. [DOI] [PubMed] [Google Scholar]