The functional role of cross-frequency coupling

Abstract

Recent studies suggest that cross-frequency coupling (CFC) may serve a functional role in neuronal computation, communication, and learning. In particular, the strength of phase-amplitude CFC differs across brain areas in a task-relevant manner, changes quickly in response to sensory, motor, and cognitive events, and correlates with performance in learning tasks. Importantly, while high-frequency brain activity reflects local domains of cortical processing, low-frequency brain rhythms are dynamically entrained across distributed brain regions by both external sensory input and internal cognitive events. CFC may thus serve as a mechanism to transfer information from large-scale brain networks operating at behavioral timescales to the fast, local cortical processing required for effective computation and synaptic modification, thus integrating functional systems across multiple spatiotemporal scales.

Neuronal oscillations and brain function

What role, if any, do neuronal oscillations play in shaping computation and communication in large-scale brain networks? There is increasing interest in this question for several reasons. First, electrical brain activity is now commonly recorded at a variety of different scales, each of which exhibits oscillatory activity correlated with functional activation. Recordings from these different spatial scales include not only spikes from single neurons but also measures of synchronized population activity such as the local field potential (LFP) – recorded from penetrating microelectrodes and reflecting the activity of several tens of thousands of nerve cells – to the subdural electrocorticogram (ECoG) – recorded from clinical macroelectrodes and reflecting activity of several million cells – to the noninvasive electro- and magneto-encephalogram (EEG/MEG) at the largest scales, reflecting the simultaneous activity of multiple cortical areas [1]. Despite the wide range of population sizes generating each type of signal, decades of research have revealed distinct frequency bands common across different signal types that exhibit characteristic changes in response to sensory, motor, and cognitive events [2–4].

Second, accumulating evidence suggests that information and processing is integrated across these multiple spatial and temporal scales, and that a hierarchy of mutually-interacting oscillations would be well-positioned to regulate this multi-scale integration [5, 6]. Neuronal oscillations can be viewed as rhythmic changes in cortical excitability [7]. Therefore, brain rhythms affect local computation since neuronal activity associated with stimulus processing differs depending on its timing relative to the phase of ongoing oscillations. If high neuronal excitability is associated with the trough of an LFP oscillation, then stimuli time-locked to the LFP trough may be processed faster or more comprehensively than stimuli time-locked to the peak of the oscillatory waveform [7]. Similarly, long-range communication between areas may also be influenced by oscillatory activity by modulating the effective gain of communication [7–9]. For example, for a given phase difference between two areas, spikes leaving one area will arrive when the other area is maximally excitable, while a shift in the relative phase implies that spikes will arrive when the receiving area is less excitable, making communication less effective.

The impact of oscillations on local computation and long-range communication is rendered more complex by the presence of several distinct brain rhythms. In vitro work investigating the local cellular origins of different rhythms shows that application of chemicals and neurotransmitters (i.e., carbachol, kainate, glutamate, etc) to isolated cortical slices reliably evokes electrical activity within a set of distinct modal frequencies [10]. These modal rhythms correspond to band-specific activity observed in vivo, including the traditional delta (1–4 Hz), theta (4–8 Hz), alpha (8–12 Hz), beta (12–30 Hz), and gamma (>30 Hz) bands as well as finer subdivisions within each band [5, 11–15]. Importantly, while different frequencies provide distinct temporal windows for processing (corresponding to the duration required to complete one oscillatory cycle), different rhythms are also associated with different spatial scales and therefore different cell population sizes. For a given spatial separation, the two-point spatial autocorrelation function is often larger for low-frequency electrical activity than for high-frequency activity [1, 16]. For example, two ECoG electrodes separated by 10 mm will often have highly-correlated theta activity while gamma activity exhibits a lower correlation [17, 18]. This suggests that low frequencies modulate activity over large spatial regions in long temporal windows, while high frequencies modulate activity over small spatial regions and short temporal windows [19]. Therefore, distinct frequency bands appear to parse ongoing neuronal activity into discrete packets, each of which has a characteristic spatial and temporal scale [20, 21]. This parsing does not appear to be a strict binary classification, but is more akin to a statistical weighting or membership within a fuzzy set [22].

The basic “activity packet” building blocks defined by distinct frequencies can give rise to more complex regulatory structure through interactions between different frequency bands, a phenomenon termed cross-frequency coupling (CFC). In particular, phase-amplitude CFC provides an effective means to integrate activity across different spatial and temporal scales. Phase-amplitude CFC describes the statistical dependence between the phase of a low-frequency brain rhythm and the amplitude (or power) of the high-frequency component of electrical brain activity.

The relationship of low-frequency phase to high-frequency amplitude has gained greater theoretical importance given recent findings that low-frequency brain rhythms are often entrained by external sensory and motor events as well as internal cognitive processes associated with decision making, motivation, and memory [23]. That is, low-frequency phase entrainment combined with phase-amplitude CFC provides a plausible mechanism to coordinate fast, spike-based computation and communication with slower external and internal state events guiding perception, cognition, and action. To clarify this connection, this review examines the different varieties of CFC, current empirical evidence of phase-amplitude CFC and methods to assess it, the relation of high frequency power to local cortical activity, the dynamic entrainment of low-frequency phase, the transient and task-relevant modulation of CFC strength, and the role of CFC in learning and memory.

Evidence for CFC

This review focuses primarily upon phase-amplitude CFC, but other types of coupling across frequencies exist. Two other varieties of coupling that have been studied are cross-frequency phase synchronization (phase-phase CFC), and cross-frequency amplitude envelope correlation (amplitude-amplitude CFC).

Phase synchronization has been suggested to play a number of different roles in brain function. Cross-location, same-frequency phase coupling between different brain areas has been studied extensively because of its potential role in regulating inter-area communication [7–9, 24, 25]. Similarly, same-location, cross-frequency phase coupling may serve as a potential mechanism to regulate communication between different spatiotemporal scales [6, 26–28]. Phase-phase CFC provides a plausible physiological mechanism for linking activity that occurs at significantly different rates. For example, patterns of firing-rate correlations observed during learning repeat during NREM sleep, but at a 6–7 times speedup [29, 30]. Similar temporal compression of spike sequences has been reported in the hippocampus [31]. Mechanisms to explain such pattern compression remain unknown, but the dependence of spiking upon LFP phases at different frequencies suggests phase-phase CFC as an explanatory hypothesis deserving further investigation.

Amplitude-amplitude CFC has also been observed [24, 32, 33], but despite correlations with behavior, the functional role of amplitude-amplitude CFC remains unclear. Phase-amplitude CFC, on the other hand, has functional correlations and plausible physiological mechanisms. Low frequency phase reflects local neuronal excitability, while high frequency power increases reflect either a general increase in population synaptic activity (broad-band power increase) or the selective activation of a connected neuronal subnetwork (narrow-band power increase).

Phase-amplitude CFC has been observed in the rodent hippocampus [34–39], rodent basal ganglia [37], and macaque neocortex [5]. In humans, phase-amplitude CFC has been observed across multiple cortical and subcortical sites under a variety of experimental conditions [40–55] and using a variety of different measures (see Box 1). For example, Figure 1A is a phase-locked time-frequency plot showing that high frequency amplitude is modulated by low frequency (theta, 4–8 Hz) phase. Figure 1B shows that across a wide range of phase and amplitude frequency pairs, theta/high-gamma phase-amplitude CFC is strongest. This example of theta/high gamma phase-amplitude coupling in human neocortex is consistent with the theta/gamma coupling observed in rodent hippocampus, and may have similar cellular and network origins.

Box 1. Assessing phase-amplitude cross-frequency coupling.

The study of phase-amplitude cross-frequency coupling is an emerging area of research, with a diversity of quantitative methods in use. A variety of different measures demonstrating CFC makes it less likely that CFC is due to an artifact inherent to a given analysis method, but can make it difficult to compare results across studies. Here we briefly describe quantitative methods in current use; interested readers will find detailed mathematical accounts in [47, 82–85].

Tort and colleagues recently compared eight different phase-amplitude measures [82]. These include:

• --The heights ratio (HR) [5], where high frequency (HF) amplitude values are binned and averaged as a function of low frequency (LF) phase, and the maximum difference in average amplitude values divided by the maximum average amplitude is used as a metric.
• --The Kullback-Liebler (KL) based modulation index (KL-MI) [37, 39]. Like the heights ratio measure, this index starts with the average binned HF amplitude as a function of LF phase, and then determines the deviation of this distribution-like function from a uniform distribution using KL divergence.
• --The mean vector length modulation index (MVL-MI) [43]. This index computes the modulus of the average value of a complex-valued time series where each sample point has a modulus of the HF amplitude and a phase of the LF phase.
• --The phase-locking value (PLV) [47, 85]. Here the HF amplitude is filtered to extract a LF phase, which is then compared with the LF phase extracted from the raw (unfiltered) signal.
• --The envelope-to-signal correlation (ESC) [40; 47]. Here the correlation coefficient between the (real-valued) LF filtered signal and the HF amplitude envelope is computed. A normalized envelope-to-signal (NESC) can be computed by using the (real-valued) cosine of the LF phase (to remove LF amplitude information).
• --The general linear model (GLM) measure [47]. This generalization of the NESC measure removes the dependence of CFC detection upon the phase of coupling, and can detect CFC for any LF phase.
• --The power spectral density (PSD) of the high frequency amplitude envelope [85]. One advantage of this method is that only the HF is fixed and multiple low frequencies can be examined at once, unlike the methods discussed above.
• --The coherence value (CV) [86], where the coherence spectrum between the HF amplitude envelope and the raw (unfiltered) signal is computed.

Of these eight measures, no “gold standard” has yet emerged; each metric has different advantages and disadvantages, depending on the goals of the experimenters. In comprehensive simulation studies, Penny et al. [47] compared four of the above measures (MVL-MI, PLV, ESC, GLM), showing that MVL-MI has the weakest sensitivity of the four under conditions of low SNR or short data epochs, and recommend use of the GLM metric [Penny 2008]. However, as shown by Tort et al. [82], the CV, PLV, ESC, and GLM metrics can only detect the presence or absence of phase-amplitude CFC, but cannot assess the intensity of CFC, as can the KL-MI, MVL-MI, PSD and HR metrics. Note, however, that a PSD (or CV) peak is a necessary but not sufficient condition for phase-amplitude CFC; HF activity may exhibit LF amplitude modulations without being phase coupled to LF activity. In general, the selection of a metric should be based on experimenter goals, with different metrics proving useful for different purposes.

Lastly, distinguishing brain-based phase-amplitude CFC from artifactual coupling is a prime concern. Kramer and colleagues explored possible sources of spurious CFC, focusing on the effects of non-sinusoidal waveforms [84]. They show that even slight deviation from sinusoidality can impact CFC measures, and demonstrate that cross-frequency phase-phase coupling can be used to detect spurious phase-amplitude CFC [84].

Figure 1. Phase-amplitude cross-frequency coupling (CFC) occurs between distinct brain rhythms, but varies as a function of cortical area and task demands.

A) Example of theta phase-locked modulation of low and high gamma power. (Top) time-frequency plot of mean power modulation time-locked to the theta trough. (Bottom) Theta trough-locked average of raw electrocorticogram (ECoG) signal. B) Modulation strength as a function of frequency for amplitude and frequency for phase. Note that the strongest modulation for this electrode occurs between theta phase and high gamma amplitude. C) During auditory tasks, theta/gamma CFC is stronger than alpha/gamma CFC over anterior sites. Theta/gamma CFC is equal across the cortex whereas posterior alpha/gamma CFC is larger than anterior alpha/gamma CFC. D) During visual tasks, alpha/gamma CFC is stronger on average at posterior electrode sites and is greater than theta/gamma CFC. For both C and D, electrode color signifies the low frequency bias in coupling with high gamma amplitude; red indicates greater theta/gamma CFC compared to alpha/gamma CFC; blue indicates greater alpha/gamma CFC compared to theta/gamma CFC. E) Optimal low (phase) and high (amplitude) frequency bands depend on working memory load. F) The frequency of modulating theta oscillations (frequency for phase) shifts toward lower frequencies with increased working memory load (colored circles indicate values for individual subjects). G) In contrast, there is no change in high frequencies (frequency for amplitude), probably due to high intersubject variability. H) Interestingly, the ratio of high-to-low frequencies remains constant across different load conditions. A and B reproduced with permission from Ref. [43]; C and D reproduced with permission from Ref. [55]; E–H reproduced with permission from Ref. [53].

Recently, however, investigators have found evidence for regional- and task-dependent variation of the dominant low frequency rhythm providing the phase for phase-amplitude CFC. For example, using magnetoencephalography (MEG), Osipova and colleagues observed that gamma power was locked to posterior alpha phase, not theta phase [45]. Similarly, Cohen et al. observed alpha/gamma phase-amplitude coupling in the human nucleus accumbens [48]. Furthermore, the amplitude frequency need not be in the gamma range: Cohen and colleagues found that delta/theta phase modulated alpha/beta amplitude in human medial frontal cortex, and that phase-amplitude CFC strength in this competitive decision making task differed between losses and wins [49].

Importantly, high frequency power can be modulated by the phase of multiple slow brain rhythms simultaneously. In particular, Voytek and colleagues showed that the theta (4–8 Hz) rhythm dominated phase-amplitude CFC with gamma (30–80 Hz) band activity in anterior frontal and temporal sites during an auditory task (Figure 1C), while the strongest CFC over occipital areas during a visual task depended on the phase of the alpha (8–12 Hz) rhythm (Figure 1D) [55]. Gamma power was phase-locked to both theta and alpha phase, but the relative influence of each low-frequency rhythm varied as a function of brain area and task modality. Given the functional association of alpha band activity with visual cortical areas and processing, alpha-based phase-amplitude CFC may play a role in computation within visual cortical areas.

Further evidence that phase-amplitude CFC may play a functional role in cortical processing comes from a study by Axmacher and colleagues [53]. Recording from multiple hippocampal sites in humans, Axmacher et al showed that the frequency for phase in phase-amplitude CFC depends on working memory load, with higher working memory load corresponding to a lower frequency for phase. That is, while the phase frequency remained within the theta range throughout the working memory task, a load of one item corresponded to a CFC peak at the upper end of the frequency range while a load of four items corresponded to a CFC peak at the lower end of the theta frequency range (Figure 1E–G).

Dynamic entrainment of low frequency phase

It is possible that phase-amplitude CFC exists but is unrelated to functional activity, computation or communication. However, recent research has shown that low frequency activity can be entrained by rhythmic external sensory and motor events [56–58], as well as internal cognitive processes related to learning and memory [59]. Therefore, low frequency phase entrainment combined with the presence of phase-amplitude CFC implies that the modulation of high-frequency power by CFC will be entrained and coordinated with the occurrence of slower, behaviorally-relevant internal and external events.

Dynamic entrainment of low frequency phase appears puzzling from a viewpoint that focuses primarily on perception and considers action to be a secondary phenomenon evoked by percepts through conditioned associations. However, a case can be made for reversing this order and viewing action as the primary purpose of the brain – evolution works via survival selection, and survival depends on appropriate action taken by an organism. In this view of motor primacy, the purpose of the brain is to guide action, and perception and cognition arose as ‘error-correction’ mechanisms to adjust and optimize an actively ongoing process of action selection [60]. This purpose is best served if sensory organs are under direct and active motor control. Under ecologically valid conditions organisms will actively control the timing and targeting of their own sensory experience – contrast seeing vs. looking, hearing vs. listening, or smelling vs. sniffing. Importantly, the time course of motor actions – including the motor control of active sensing – will often exhibit rhythmic patterns [61]. Therefore, the arrival of neuronal spikes carrying information about stimuli to early sensory areas will occur in rhythmic volleys, introducing a volitionally-controlled rhythmicity to perception and multisensory integration.

As an example of how neuronal oscillations can impact cortical processing, Figure 2A–E provides an example of low frequency phase entrainment in a multisensory task in macaque V1 [56]. In this task, rhythmic stimuli entrain the phase of the ongoing delta rhythm and influence local spiking and synaptic population activity. This attention-dependent entrainment has behavioral consequences, reflected in decreased reaction times. Similar results were observed by Saleh and colleagues in human motor cortex [57]. These two tasks, examining different cortical areas, both show that rhythmicity in the external world impacts internal sensory and motor processing in an attention-dependent fashion.

Figure 2. Low frequency phase is entrained by rhythmic behavioral events.

A) From [56], intermodal auditory/visual selective-attention task. Light bulbs and speakers represent visual and auditory stimuli in the mixed stimulus stream. Visual and auditory deviants are marked by light blue and magenta arrows, respectively. Stimulus onset asynchrony (SOA) within modality was jittered around a mean of 650 ms; SOA between modalities had a mean of 300 ms. B) Color maps show current source density (CSD) profiles related to standard visual stimuli in the attend-visual (AV) and attend-auditory (AA) conditions. Red arrowhead indicates the visual event used as trigger (0 ms). C) Current source density (CSD) from a supragranular electrode in the AV and AA conditions. D) Distribution of single-trial supragranular prestimulus (0 ms) delta oscillatory phases in the same experiment. E) Pooled prestimulus mean (across trials) delta phase for all experiments. Reproduced with permission from Ref. [56].

How does this dynamic entrainment of low frequency phase have an effect upon local computation and long-range communication? First, LFP phase modulates the instantaneous spike probability and can shift spike timing [34, 62–66]. Therefore, low-frequency phase entrainment will shift the relative timing of spiking and synaptic activity. This may have important consequences for cognitive processing, since the strength of theta frequency phase-locking of neuronal spikes is correlated with memory performance [67]. Second, coherent low-frequency oscillations appear to be important in regulating large-scale networks [68, 69], such that phase entrainment in one area may have effects that propagate throughout a larger network due to inter-regional phase locking. These patterns of phase coupling between multiple brain areas can impact the spiking of single cells and may help bind together anatomically-dispersed functional cell assemblies [70]. Therefore, dynamic entrainment of low frequency phase is positioned to have a broad impact on processing at multiple spatial and temporal scales, from the spike timing of single neurons to the integrated action of inter-regional functional brain networks.

Cellular and network origins of phase-amplitude CFC

It is critical to distinguish between two different ways of thinking about CFC: 1) as an observed statistical dependence between filtered signals derived from electrical brain activity, and 2) as a transient but mechanistic coupling (mediated by spikes and synaptic activity) between the functionally distinct neuronal subpopulations that give rise to recorded electrical activity. CFC can have a functional role under option 2, but not under option 1. Therefore, saying that theta/gamma phase-amplitude CFC has a functional role is equivalent to saying that dynamic interactions between the pyramidal-interneuron cell sub-networks that give rise to theta and gamma frequency activity has a functional role. So first, how are these different brain rhythms generated, and second, what is the mechanism of their interaction?

Over the past decade in vitro slice work has revealed much about the cellular and network origins of low gamma (LG, 30–80 Hz) [71] and high gamma (80–200 Hz) activity (see Box 2). LG activity arises primarily due to interactions within the highly-interconnected GABAergic (inhibitory) interneuron network (interneuron network gamma or ING), as well as from network interactions between populations of (excitatory) pyramidal cells and local interneuron networks (pyramidal-interneuron network gamma or PING) [13]. Recent in vivo work employed light-driven activation of interneurons or pyramidal cells to investigate the causal impact of these distinct populations upon gamma activity [72]. This study revealed a cell-type specific double dissociation supporting the ING gamma model. Similarly, it appears that theta activity is also generated locally [73] and is regulated by interneuronal networks [74] with both pyramidal cells and interneurons exhibiting a resonance peak in the theta range due to intrinsic membrane properties [75].

Box 2. High frequency power and local cortical activity.

The association of high gamma (HG, 80–200 Hz) activity with local functional activation has been firmly established over the past two decades, but the cellular and network origins of HG remain a matter of vigorous debate. While increased HG power is associated with increased spiking activity in a local cortical area, the direct contribution of population spiking activity to HG activity, and the relation of HG to low gamma (30–80 Hz), remains to be determined.

As shown by Figure I, LG and HG occur independently in spontaneous and task-related activity in the hippocampus [86]. That is, both LG and HG may appear simultaneously, or just LG alone or just HG alone, indicating that different mechanism are giving rise to activity in these bands. HG reflects both active and passive dendritic current flows as well as axonal spikes. However, HG is not just “buzz” from multi-unit activity, since significant event-related power changes are often restricted to <200 Hz, while the sharp spike waveforms have broadband power contributions above that range. In other words, there appears to be cellular and network mechanisms in place to create resonant peak in the 80–200 Hz range (but see [87, 88] for an alternate view).

One candidate mechanism for HG generation, supported by simulation studies [89] as well as anatomical data [90], focuses on axo-axonal gap junction connections between pyramidal cells. These gap junction connections between pyramidal cells create local, electrically-coupled networks supporting the propagation of spikelets from one axon to adjacent axons, with the degree and distance of connections controlling the resonant frequency peak generated by network activity. This peak is in the HG range, suggesting that HG reflects local coordination of spike timing to maximize the post-synaptic impact of convergent population activity.

An alternative mechanism holds that HG activity, similar to LG activity, depends on purely synaptic network mechanisms and transiently engages different subgroups of interneurons to shape pyramidal cell activity. Support comes from investigations of ripple oscillations in humans [91]. Human hippocampal ripple events have a frequency content and event duration similar to HG activity, with a center frequency ~100 Hz. Le Van Quyen and collegues [91] show that 1) different interneuron populations appear to shape the duration of ripple events (~ 40 ms, or 3–5 ripple cycles), 2) pyramidal cell firing rates track the amplitude envelope of ripple activity, and 3) both pyramidal cell and interneuron spiking is phase-locked to individual ripple cycles. Similar mechanisms in neocortex could help HG serve as a natural information processing window that quickly establishes a local increase in pyramidal cell spike rate and spike timing coincidence, followed by a swift quenching of this activity to permit downstream processing.

Importantly, Wulff and colleagues recently showed that the theta/gamma interactions depend on a particular class of GABAergic interneurons [38]. They used genetically-modified mice to show that synaptic inhibition onto parvalbumin-positive cells is critical for regulating theta/gamma interactions. These findings were supported by similar results within a computational model of the hippocampal CA1 region [38].

Dynamic and transient CFC

Low frequency phase entrainment to behaviorally-relevant events suggests a functional role for phase-amplitude CFC, but CFC could not serve as an effective control mechanism if CFC strength were constant over time and across different tasks. The findings of Tort and colleagues [37] are illuminating as they show dynamic modulation of CFC strength in rodent hippocampus and striatum during a simple T-maze task. Interestingly, in addition to showing that CFC strength can quickly go from no coupling to strong phase-amplitude coupling and back within hundreds of milliseconds (Figure 3), this study also revealed different patterns of coupling and temporal modulation within different brain structures. In particular, the temporal modulation of phase-amplitude CFC in the hippocampus differed from that in the striatum, as did the high and low frequencies that were coupled. Furthermore, this study showed that CFC can span different areas, with hippocampal low frequency phase affecting high frequency amplitude in the striatum and vice versa. The distinct coupling frequencies observed in each area may provide a form of frequency domain modularity that allows simultaneous communication in independent channels.

Figure 3. Cross-frequency coupling is dynamic and exhibits fast task- and event-related changes in coupling strength.

A) T-maze with task events and run trajectories from a representative session with 39 trials. B) Phase-to-amplitude comodulograms for electrode in the striatum plotted for each task-event window. Pseudocolor scale represents CFC strength; positive values indicate significant phase-to-amplitude CFC. C) As in B, for a hippocampal electrode. Note the difference in onset, duration, and offset times of strong CFC in these two brain areas. Reproduced with permission from Ref. [37].

CFC and learning

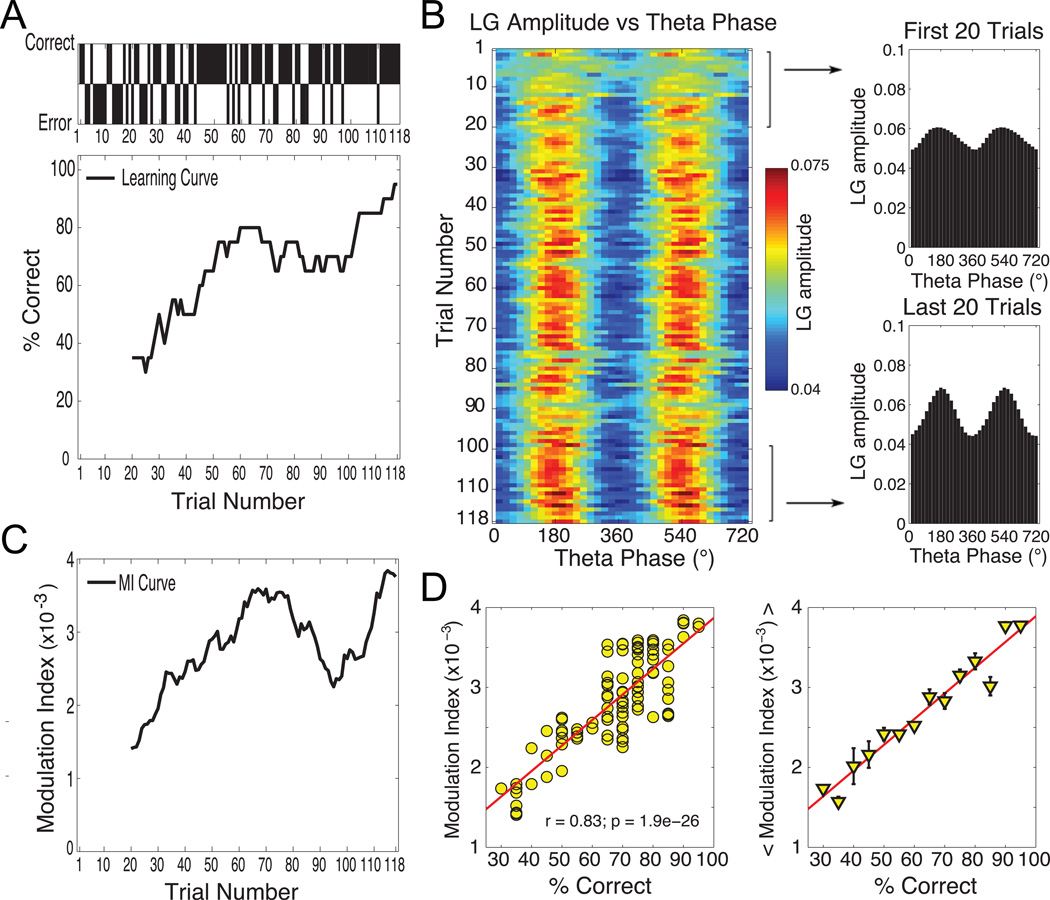
The findings described above, which show that CFC can be entrained to behavioral events and dynamically and independently modulated in multiple task-relevant areas, support the claim that phase-amplitude CFC has a functional role but does not provide a clear and unambiguous link to performance. Such a link is provided by a recent study showing a strong correlation of CFC strength to performance in a learning task [39]. In this learning task the strength of hippocampal CFC increased over time as the rodent improved performance, with CFC strength and task performance both reaching a plateau (Figure 4). Early in the training phase, however, both CFC strength and task performance are low, suggesting that CFC is not simply an epiphenomenon occurring independent of behavior. In fact, phase-amplitude CFC strength appears to be the most predictive neurophysiological marker of learning yet found, and promises to be a valuable tool for future experimentalists.

Figure 4. Hippocampal theta/gamma cross-frequency coupling correlates with learning and task performance.

Theta modulation of low gamma (LG) amplitude in the CA3 region during context exploration increases with learning. A) Behavioral profile of a representative rat during learning of the task. Shown is the animal’s performance (correct, black bar up; error, black bar down) at each trial of the session (Upper) and the associated learning curve computed by using a sliding window of 20 trials (Lower). B) Pseudocolor scale representation of the mean CA3 LG amplitude as a function of the theta phase for each trial in the session (Left). The mean LG amplitude per theta phase averaged over the first and last 20 trials is also shown (Right). C) CFC modulation index (MI) curve computed by using a 20-trial sliding window. (D) Linear correlation between theta-LG coupling strength and task performance. The correlation between the MI and learning curves (Left) and the average MI value over each mean performance percentage (Right) are shown. Reproduced with permission from Ref. [39].

Why should phase-amplitude CFC, and theta/HG CFC in particular, show any relation to learning and memory? One clue comes from the literature focused on the induction of long-term synaptic potentiation (LTP). Several distinct protocols for inducing LTP are used by experimentalists, but one of the most effective uses a high-frequency (~100 Hz) burst of 6–7 stimulations, with bursts repeated at a slower (~3–5 Hz) interburst interval [76, 77]. This pattern corresponds to a high gamma burst recurring at theta rates – exactly what is produced by strong theta/HG phase-amplitude CFC. Furthermore, shifting the timing of such a burst relative to the phase of the ongoing endogenous theta rhythm can depotentiate previously-established LTP or induce long-term depression (LTD) [78, 79]. That is, artificial LTP/LTD induction protocols may be tapping into a naturally occurring process whereby synaptic strength is regulated by theta/HG CFC. Support for this hypothesis also comes from the observation that theta-burst transcranial magnetic stimulation (TMS) at the scalp is the most effective protocol for potentiating the motor cortical evoked potential [80]. These results, combined with the fact that CFC is modulated by centralized cholinergic control via the nucleus basalis [81] – a structure in the basal forebrain associated with plasticity and learning – supports a key role for CFC in learning. Given the strong correlation between CFC strength and learning performance, on the one hand, and learning and synaptic LTP/LTD, on the other, the hypothesis that phase-amplitude CFC provides a mechanism for regulating synaptic strength deserves further study.

Concluding remarks

The past decade has seen several lines of research converge on the idea that phase-amplitude CFC may play an important functional role in local computation and long-range communication in large-scale brain networks. The discovery that strong CFC exists in multiple brain areas including the neocortex, hippocampus, and basal ganglia suggests that CFC reflects functional activation of these areas. The finding that the exact frequencies coupled together vary as a function of area and task imply that independent channels of coupling may coexist simultaneously during task performance. The dynamic regulation of coupling strength indicates that CFC has the necessary temporal resolution required for the effective modulation of distinct functional networks. Finally, the discovery that hippocampal CFC strength is correlated with learning task performance suggests that phase-amplitude CFC may help regulate the network of synaptic connections vital for memory and learning. Together, these findings suggest a framework where phase-amplitude CFC parses neuronal computation into discrete chunks of activity that are ideal for attention, learning, and memory, and that these multi-scale building blocks are entrained to both rhythmic, external sensory and motor activity as well as the internal fronto-limbic activity associated with motivation, decision making, and memory. In conclusion, evidence of a functional role of phase-amplitude CFC in regulating multi-scale networks continues to accumulate, and promises an interesting avenue for future research.

Box 2, Figure I. The hippocampal CA1 region exhibits two distinct gamma bands (y-axis), and both are modulated by the phase of the theta rhythm (x-axis).

Time frequency representations of power for a representative recording, averaged across (i) all theta cycles, (ii) theta cycles with slow gamma, (iii) theta cycles with fast gamma and (iv) the minority of theta cycles exhibiting both slow and fast gamma. v) The averaged unfiltered theta cycle. Reproduced with permission from Ref. [86].

Box 3. Questions for future research.

• Are the cellular and network mechanisms of phase-amplitude cross-frequency coupling similar across neocortex, basal ganglia, and hippocampus?

• How do the different varieties of cross-frequency coupling (phase-phase, amplitude-amplitude, and phase-amplitude coupling) relate to each other? Is one type more general than another, or serve as necessary and/or sufficient conditions for another?

• What is the relation of phase-amplitude cross-frequency coupling to existing measures of phase coupling across space? Can these different measures be integrated into more informative composite measures?

• Is phase-amplitude cross-frequency coupling, especially theta/high gamma phase-amplitude coupling, associated with long-term changes in local synaptic strength (LTP/LTD)?

• Is phase-phase cross-frequency coupling involved in the compressed replay and spontaneous reactivation of previously stored patterns of neuronal activity during sleep?

Glossary

Neuronal oscillation

a transient, rhythmic variation in neuronal activity. Often detected as fluctuations in the electric field generated by the summed synaptic activity of a local neuronal population

Frequency (band)

Oscillations generated by active neuronal tissue often exhibit characteristic rhythms. Traditionally, neuronal oscillations have be divided into different bands, including: slow oscillations (< 1 Hz), delta (1–4 Hz), theta (4–8 Hz), alpha (8–12 Hz), beta (12–30), and gamma (> 30 Hz), with further subdivisions becoming more common.

Phase

A measure of position within a full cycle of an oscillatory waveform. Typically measured in radians [−π, π) or degrees [−180, 180). For example, the peak of a sinusoidal waveform has a phase of 0 radians, while the trough as a phase of π radians

Amplitude (envelope)

The instantaneous magnitude of a complex-valued signal. Intuitively, a function that interpolates from peak to peak of an oscillatory waveform