Including Robustness in Multi-criteria Optimization for Intensity Modulated Proton Therapy

Abstract

We present a method to include robustness into a multi-criteria optimization (MCO) framework for intensity modulated proton therapy (IMPT). The approach allows one to simultaneously explore the tradeoff between different objectives as well as the tradeoff between robustness and nominal plan quality. In MCO, a database of plans, each emphasizing different treatment planning objectives, is pre-computed to approximate the Pareto surface. An IMPT treatment plan that strikes the best balance between the different objectives can be selected by navigating on the Pareto surface. In our approach, robustness is integrated into MCO by adding robustified objectives and constraints to the MCO problem. Uncertainties (or errors) of the robust problem are modeled by pre-calculated dose-influence matrices for a nominal scenario and a number of pre-defined error scenarios (shifted patient positions, proton beam undershoot and overshoot). Objectives and constraints can be defined for the nominal scenario, thus characterizing nominal plan quality. A robustified objective represents the worst objective function value that can be realized for any of the error scenarios and thus provides a measure of plan robustness. The optimization method is based on a linear projection solver and is capable of handling large problem sizes resulting from a fine dose grid resolution, many scenarios, and a large number of proton pencil beams. A base of skull case is used to demonstrate the robust optimization method. It is demonstrated that the robust optimization method reduces the sensitivity of the treatment plan to setup and range errors to a degree that is not achieved by a safety margin approach. A chordoma case is analysed in more detail to demonstrate the involved tradeoffs between target underdose and brainstem sparing as well as robustness and nominal plan quality. The latter illustrates the advantage of MCO in the context of robust planning. For all cases examined, the robust optimization for each Pareto optimal plan takes less than 5 minutes on a standard computer, making a computationally friendly interface possible to the planner. In conclusion, the uncertainty pertinent to the IMPT procedure can be reduced during treatment planning by optimizing plans that emphasize different treatment objectives, including robustness, and then interactively seeking for a most-preferred one from the solution Pareto surface.

1 Introduction

Radiation therapy is an effective way to treat cancer by irradiating and killing cancer cells. An ideal radiation therapy treatment delivers sufficiently high dose to the target volume but completely spares radiation-sensitive organs. Intensity modulated proton therapy (IMPT) [6, 21] is one of the treatment modalities that comes closest to this goal. Compared with the exponential depth dose curve of a photon beam, the dose deposited by a proton beam increases dramatically at the end of range (controlled by the energy of the proton pencil beam) and then falls off to almost zero. Compared to proton therapy delivery based on passive scattering techniques, the comformality of the dose distribution can be improved through IMPT. In comparison to photon therapy the integral dose in healthy tissues sourounding the target is greatly reduced. In IMPT, a proton beam is magnetically scanned over the tumor volume. By using mathematical optimization techniques to optimize the intensity of the proton beam at every location, highly conformal treatment plans can be achieved [26].

However, due to the steep dose fall-off, IMPT is more sensitive to errors than IMRT. An IMPT dose distribution can be largely distorted even under small setup errors [7]. This is inherently due to the relatively large dose discrepancy caused by distally or laterally shifted Bragg peaks. Another important source of uncertainty for IMPT is range uncertainty, i.e. uncertainty of the Bragg peak location in depth. Range uncertainty arises because the range of a proton beam in the patient depends on the traversed tissue and is thus flawed if the planning CT scan does not adequately represent the patient geometry. See [7, 8] for a review on the uncertainties of IMPT. Heuristics such as selecting the beam angles with small tissue heterogeneity in their paths, avoiding metal implants, etc., are methods used to increase the robustness of plans [20]. In photon therapy, setup uncertainty and organ motion is typically accounted for using the concept of a planing target volume (PTV). This approach is successful because a photon dose distribution in treatment room coordinates is approximately invariant to changes of the patient geometry. In IMPT, this approximation is not valid in general and the usefulness of PTVs in IMPT is therefore limited. This has recently been discussed by [19].

On the other hand, robust optimization has been introduced to produce high quality plans that are acceptable even under uncertainty. This is achieved by incorporating the uncertainty information into the optimization [5, 2, 9]. Robust optimization approaches can be probabilistic or non-probabilistic depending on whether the underlying probability distribution of uncertainty is known and utilized in the optimization. The work of [3, 2] assumes a normal distribution of uncertainties, and optimizes the expected value of a weighted sum of quadratic dose deviations. Without assuming a probability distribution for the uncertainty, the works in [5, 9] optimize treatment plans that are as good as possible for the worst error that can occur. The approach in [9] solves a minimax optimization problem: it optimizes the worst score of an objective function evaluated for a set of pre-defined error scenarios. The approach presented in [5] optimizes a weighted sum of two terms. The first term is the objective function evaluated for the nominal scenario (i.e. no error occurs). The second term is the objective function evaluated for the worst case dose distribution is introduced by Lomax [7]. This worst case dose distribution is an artificial one in which every target voxel takes the lowest dose that can occur for any error scenario, and every healthy tissue voxel takes the highest dose. Since the worst dose value corresponds to different error scenarios for different voxels, the worst case dose distribution cannot be physically realized. In contrast to the approach in [5], the minimax method in [9] uses only realizable uncertainty scenarios.

Previously published works on robust optimization for IMPT share the weakness of optimizing a weighted sum of multiple objectives, which can lead to a tedious trial-and-error process of adjusting the weights and redoing the expensive optimization in order to find the right balance of objectives. MCO allows the planner to explicitly see the tradeoff between different objectives and navigate on the Pareto surface in real time. In [1] we published a fast and memory-efficient approach for optimizing IMPT in an MCO setting. The work in this paper is an immediate extension of that approach to robust IMPT optimization. Robust optimization is wrapped in an MCO framework by adding robustified objectives to the MCO problem formulation. In addition to objectives defined for the nominal scenario as done for non-robust planning, the treatment planner can define robustified objectives for the target and important organs at risk. Thus, the data base of Pareto optimal treatment plans contains both robust and non-robust treatment plans. By navigating the Pareto surface, the treatment planner can explore the tradeoff between robustness and nominal plan quality.

In our implementation, robust optimization performs minimax optimization similar to the work by Fredriksson [9]. Thus, robustified objectives correspond to worst-case objectives that return the worst objective function value that can occur for any error scenario. By assigning discrete probabilities to the uncertainty scenarios, our method also allows to optimize the expected mean dose to an organ which may be a good indicator of the protection of a parallel organ. However, in contrast to the work by Fredriksson [9], which uses a general non-linear constrained optimization method, we use a customized solver for piecewise-linear convex constrained optimization. The large-scale optimization can be solved in minutes by the projection solver we proposed in [1]. The robust IMPT MCO will be implemented in our in-house IMPT treatment planning system “ASTROID” [1] at Massachusetts General Hospital. ASTROID takes advantage of modern multi-core computers to parallelize the multiple optimization tasks.

The remainder of this paper is organized as follows: In section 2 we present the robust MCO framework. In section 3.1 we demonstrate the robust optimization method for a base-of-skull case and compare the result to a non-robust plan optimized on a PTV. In 3.2 we illustrate the tradeoffs involved in robust IMPT planning for a chordoma case.

2 Methods

2.1 Preliminaries

We consider IMPT treatment planning for the 3D spot scanning technique [21]. The spot size we model, expressed as the standard deviation of the Gaussian dose distribution, is approximately 5 mm at patient surface, depending on the energy layer the spot locates. The spacing of Bragg peaks in depth is given by the proximal 80% to distal 80% width of the most distal peak. This leads to a typical spacing of the energy layers corresponding to 5-7 mm in water equivalent range.

2.1.1 Dose calculation

The dose calculation of the chordoma case is done with our in-house dose calculation algorithms for proton pencil beams at Massachusetts General Hospital¹. Proton pencil beam, in this context, refers both to the physical nature of the proton beam, i.e., delivery by numerous individual narrow proton beams, and to the computational nature of the underlying transport model, i.e., the approximation of bulk transport as the summation of numerous computational pencil beams. The physical model is described in [17]. Our implementation, however, differs. We first transport a large set of zero-width pencil beams through the patient. These pencil beams only model the effects of multiple Coulomb scatter. These pencil beams, indexed by k, yield the dose D_ik to each point i. The physical pencil beams j are computed by summing over the mathematical pencil beams k to yield the dose D_ij from each pencil beam j.

2.2 Uncertainty model

The uncertainties in IMPT are numerous. In this paper we consider range uncertainty and systematic setup errors. We do not consider other potential errors like intra-fraction or inter-fraction organ motion, which can be significant in certain sites like lung and liver. Both, range and setup errors are modeled via a discrete set of K possible error scenarios. For each error scenario I, we use the dose calculation engine to calculate a dose influence matrix $D_{ij}^I$ that stores the dose contribution of a pencil beam j to voxel i in error scenario I.

2.2.1 Range uncertainty

We model range uncertainty via two error scenarios: one overshoot scenario and one undershoot scenario. Overshoot and undershoot is modeled by a scaling of the CT Hounsfield numbers. Hence, both error scenarios correspond to a synchronized overshoot/undershoot of all pencil beams. This model of range uncertainty is applicable to the components of range uncertainty that influence all proton pencil beams in the same way. This includes, e.g., errors in the conversion of Hounsfield numbers to relative stopping powers as well as, to some extent, weight loss or weight gain. It is a simplification for errors that influence different proton pencil beams in different ways (e.g., imaging artifacts due to metal implants).

2.2.2 Setup uncertainty

Setup uncertainty refers to a misalignment of the patient relative to the treatment beam. It can be modeled as a rigid shift of the patient with respect to the isocenter. In this paper, we characterize the magnitude of the setup error by a single number that corresponds to the length of the three-dimensional vector for the patient shift. It is assumed that the patient shift can occur in any direction. For practical purpose, we represent the possible shifts by a discrete set of equal distance shifts that are evenly distributed on the surface of a 3D sphere. We distinguish two sets of error scenarios:

K=9 Only setup errors along the three coordinate axes are considered, i.e., anterior-posterior, left-right, and cranial-caudal. This leads to 6 setup error scenarios. Assuming that the length of the three-dimensional shift vector is λ mm, those patient shifts are given by (±λ, 0, 0) mm, (0, ±λ, 0) mm, and (0, 0, ±λ) mm. Together with the nominal scenario and two range error scenarios, this yields a total of 9 scenarios.

K=29 additional to the above 9 scenarios, 20 additional setup error scenarios are considered. In those 20 scenarios the patient is shifted by $(\pm \lambda ∕\sqrt{2},\pm \lambda ∕\sqrt{2},0)\mathrm{mm}$, $(\pm \lambda ∕\sqrt{2},0,\pm \lambda ∕\sqrt{2})\mathrm{mm}$, $(0,\pm \lambda ∕\sqrt{2},\pm \lambda ∕\sqrt{2})\mathrm{mm}$ or, $(\pm \lambda ∕\sqrt{3},\pm \lambda ∕\sqrt{3},\pm \lambda ∕\sqrt{3})\mathrm{mm}$. This yields a total of 29 scenarios.

We only consider setup shifts of a given length. This is motivated by the assumption that smaller setup errors will generally lead to smaller dosimetric errors. In the context of worst-case optimization methods as described below, these smaller error scenarios are expected to have none or negligible influence on the treatment plan.

2.3 Multi-criteria robust method

2.3.1 General problem formulation

In this section we formulate the multi-criteria robust optimization problem. Let K denote the number of error scenarios. The dose-influence matrix of scenario I is denoted by D^I for 1 ≤ I ≤ K. The nominal scenario is indexed by I = 1. Given an intensity vector x, the dose vector realized in scenario I is d^I = D^Ix, for 1 ≤ I ≤ K. For notational convenience, let d be a concatenation of the dose vectors realized in the K scenarios: d = (d¹, , d², …, d^K). Objective functions f(d) and constraint functions g(d) are scalar functions of the dose vector d. The formulation of the robust IMPT MCO problem is:

$$\begin{array}{c}\hfill Minimize\{f_1\left(d\right),f_2\left(d\right),\dots ,f_M\left(d\right)\},\hfill \\ \hfill Subjectto{g}_i\left(d\right)\le b_i,fori=1,2,\dots ,N,\hfill \\ \hfill x\ge 0,\hfill \end{array}$$

where M is the number of objectives, N is the number of constraints, and b_i are bounds on the values of the constraint functions.

2.3.2 Objective and constraint functions

We now further define the objective and constraint functions. Objective functions can be characterized by a triple

$$\{TYPE,STRECTURES,SCENARIOS,\},$$

where TYPE refers to the functional form. In our implementation this can be minimize the maximum dose, maximize the minimum dose, minimize/maximize the mean dose, or minimize the ramp function (see Subsection 2.3.3). STRUCTURES can be one structure or a set of structures whose voxels will be involved in the function. SCENARIOS indicates whether the objective is robustified or not. A non-robust objective function is evaluated for the nominal scenario only and thus is a measure for nominal plan quality. A robustified objective is evaluated for all scenarios and its value is given by the extremum taken over the scenarios. Hence, this method implements a worst-case optimization approach, also referred to as minimax optimization. For example, the robustified version of the objective that minimizes the maximum dose to an organ at risk minimizes the maximum dose to that organ that can occur for any of the error scenarios. In addition to nominal and robust objectives, an objective function can be evaluated for a weighted sum of scenario doses. This is used for the mean dose objective, which is the only objective function for which the weighted sum of objective values for different scenarios equals the objective function evaluated for a weighted sum of dose values. The objectives that we use are stated explicitly in Table 1.

Table 1.

Objective/Constraint function definitions for a structure that has |V| voxels in volume V.

Objective f(d)	Nominal	Robust	Expected
Mean dose	$\frac{1}{\mid V\mid }{\Sigma }_{i\in V}{d}_i^1$	$\min ∕{\max }_{I=1}^K\frac{1}{\mid V\mid }{\Sigma }_{i\in V}{d}_i^I$	$\frac{1}{K}{\Sigma }_{I=1}^K\left(w^I\frac{1}{\mid V\mid }{\Sigma }_{i\in V}{d}_i^I\right)$
Min dose	${\min }_{i\in V}{d}_i^1$	${\min }_{I=1}^K{\min }_{i\in V}{d}_i^I$
Max dose	${\max }_{i\in V}{d}_i^1$	${\max }_{I=1}^K{\min }_{i\in V}{d}_i^I$
Overdose ramp	$\frac{1}{\mid V\mid }{\Sigma }_{i\in V}\max (0,d_i^1-d^{pres})$	${\max }_{I=1}^K\frac{1}{\mid V\mid }{\Sigma }_{i\in V}\max (0,d_i^I-d^{pres})$
Underdose ramp	$\frac{1}{\mid V\mid }{\Sigma }_{i\in V}\max (0,d^{pres}-d_i^1)$	${\max }_{I=1}^K\frac{1}{\mid V\mid }{\Sigma }_{i\in V}\max (0,d^{pres}-d_i^I)$

For the constraint functions g we use exactly the same functions we use as objectives. It should be noted that for these functions the bounds b_i on the right hand side of the constraints are given in the unit Gray (Gy), and therefore have interpretable values.

2.3.3 Ramp function

If an OAR is located close to the target, the objectives that minimize the maximum dose to the OAR or maximize the minimum dose to the target are typically not sufficient to generate an acceptable treatment plan. An objective is needed that minimizes underdose to the target even though minimum dose is below the desired prescription dose due to geometrical/physical reasons. We adopt the ramp function to be a powerful complementary to the types of objectives and constraints we deal with. An overdose (underdose) ramp function is the average overdose (underdose) over the total number of voxels in one structure [22]. It is the linear analog to the standard quadratic overdose (underdose) function. Let d_i, i ∈ V be the dose to the voxel i in a structure V, d be the dose vector (d_i)_{i ∈ V}, and let d^pres be the prescription dose level. The overdose ramp function is given by:

$$r(d,d^{pres})=\frac{1}{\mid V\mid }\sum _{i\in V}\max (0,d_i-d^{pres}),$$ (1)

where |V| is the number of voxels in the structure V. For any voxel dose d_i larger than the prescribed level d^pres, an amount equal to the deviation is added to the overdose ramp function. If this function is 0 it means that all voxel doses are less than or equal to d^pres. The underdose ramp function can be similarly defined and is useful for minimizing the underdose to a target. The overdose ramp function applies to both target and critical structures.

2.3.4 Combining MCO and robustness

We introduce robustness into the MCO framework by adding robustified objectives and constraints to the problem formulation. For example, if minimizing the maximum dose to an organ at risk is an objective in the conventional problem formulation, we add an additional objective that minimizes the worst-case maximum dose to the organ at risk that can occur for any error scenario. The advantage of this method is that previously developed MCO methods for database generation and Pareto surface navigation are applicable. In addition, the formulation reflects the fact that robustness is not a global property of a treatment plan. Instead, a treatment plan can be robust regarding the sparing of an organ at risk but not robust regarding target coverage. In our approach this is accounted for by adding separate robustified objectives for different structures. In our formulation, the error scenarios are fixed. The tradeoff between nominal plan quality and robustness is controlled by forming convex combinations of plans optimized for the nominal scenario and robust plans optimized for the given set of error scenarios. Since the linear feasibility constraints stay the same for all the optimizations, the convex combinations of any feasible plans are still feasible.

2.3.5 Optimization solver

The computational challenge for this formulation is that the size of the system matrix and therefore the number of constraints is up to K times as large as in the non-robust optimization. We solve the problem by the fast and memory-efficient linear feasibility and optimality solver for large scale linear programs called ART3+O [1]. The method is primarily designed for handling constraints that are linear in the beam weights so that a projection onto the constraint can be done in closed form. This is intrinsically the case for the mean constraint and the min/max dose constraint in Table 1. In order to project onto a ramp constraint we use an iterative heuristic as described in the appendix. The fast convergence at sufficient precision and nearly zero memory overhead make ART3+O among very few choices to solve the robust IMPT MCO problem as formulated herein.

2.3.6 MCO database generation and navigation

After generating the anchor plans for the M objectives (i.e., minimizing each of the objectives individually), additional Pareto surface plans can be computed as described in [1]. Briefly, the intermediate Pareto optimal plans can be solved by the bounded objective function method [12], in which the objective values of the average of the M anchor plans are set as constraints, and another M anchor plans are generated for each of the M objectives subject to these updated constraints. The final optimal plan is a user chosen linear combination of all the anchor plans [13].

3 Results

We demonstrate our method on two clinical cases: a base of skull tumor and a chordoma case. For the base of skull case a treatment plan can be obtained without tradeoffs involved to satisfy all clinical goals. This case is used to demonstrate the robust optimization method independent of the MCO framework and provide a comparison with a margin based plan. The chordoma case involves a tradeoff between brainstem sparing and CTV coverage. We use this case to show the tradeoffs between the target coverage, the OAR sparing and the robustness of the plan.

3.1 Base of skull

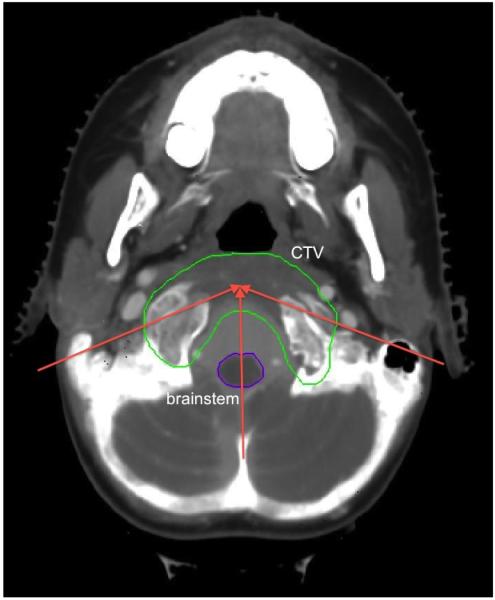
A representative CT slice of the patient is shown in Figure 1. Three proton beams are used in the plan for the base of skull case. Two beams are in the transverse plane at gantry angles of 75 and 270 degrees. The third one is an obliquely incident superior-anterior beam, which is at a couch angle of 90 degrees and gantry angle of 300 degrees. The total number of beamlets is 7,778. The dose grid is 125×125×99 voxels. The voxel size is 2.5 mm × 2.5 mm × 2.5 mm. We assume 3 mm setup uncertainty and 3.5% range uncertainty. For robust optimization we use 9 error scenarios as defined in section 2.2.2. The raw dose-fluence matrices of the 9 scenarios total to 11 Gb in size.

Figure 1.

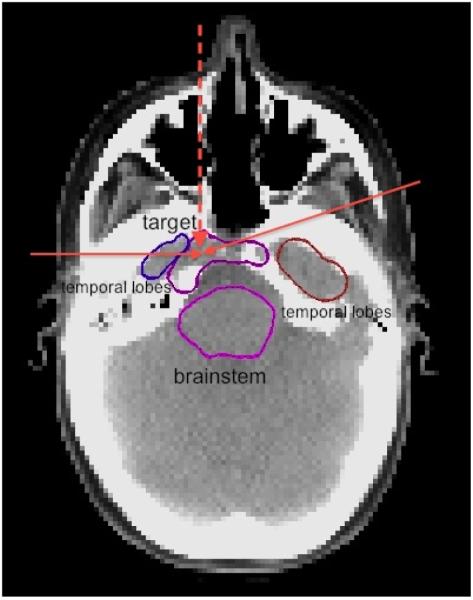
A slice of the CT of the base of skull case. The two solid red arrows show the directions of the IMPT beams in the transverse plane at gantry angles of 75 degrees and 270 degrees. The vertical dashed red arrow shows the projection of the IMPT beam at a couch angle of 90 degrees and gantry angle 300 degrees. The top purple structure is the target, the bottom purple structure is the brainstem, the brown and blue structures are the temporal lobes.

For this case, in order to highlight the difference between the scenario method and the margin method, we do not use an MCO formulation. Instead, we solve for a feasible plan that satisfies the set of constraints given in Table 2. For the margin plan, the PTV was constructed by a 3 mm isotropic expansion of the CTV. For treatment planning, set of constraints is applied to the nominal scenario only and the set of constraints for CTV is applied to PTV.

Table 2.

Constraints of the robust method for the base of skull case. The “weighted” scenario is the nominal scenario with weight 0.2 and the other 8 scenarios with weight 0.1.

Base of skull (Rx = 74 Gy)
Structures	Type	Scenarios	Bound (in Gy)
CTV	min	all	≥ 70
CTV	max	all	≤ 80
CTV	min	nominal	≥ 74
CTV	max	nominal	≤ 77
CTV	overdose ramp (dpres = Rx)	nominal	≤ 0:5
brainstem	max	all	≤ 60
brainstem	mean	nominal	≤ 10
brainstem	mean	weighted (see caption)	≤ 11
optic chiasm	max	all	≤ 62
brain, brain-CTV, R/L temporal lobe	mean	nominal	≤ 30
all structures	max	all	≤ 90

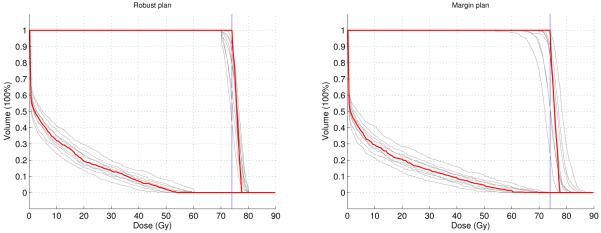
Figure 2 compares the DVHs of the CTV and the brainstem of the robust plan and the margin plan evaluated in all 9 scenarios. For both plans, the nominal DVHs (the red lines) are almost equally good. They both satisfy all constraints. However, the target coverage of the margin plan is much worse than the robust plan due to large underdose and overdose in some of the error scenarios. And unlike the margin plan, the robust plan restricts the maximum brainstem dose to 60 Gy in all the scenarios. This comparison demonstrates that by incorporating range and setup uncertainty information in the optimization, the sensitivity of IMPT plans against errors can be reduced.

Figure 2.

The DVHs of CTV and brainstem for the 9 scenarios. The DVH for the nominal scenario is in red and the DVHs for 8 error scenarios are in gray. Left is the robust plan, right is the margin plan. The vertical blue line is the prescribed dose to the target.

3.2 Chordoma

3.2.1 Patient geometry, problem size and Calculation time

Three proton beams are used in the plan for this chordoma case. They are in the transverse plane at gantry angles of 110 degrees, 180 degrees and 250 degrees (see the CT image in Figure 3). The total number of beamlets is 9,623. The dose grid is 88×103×77 voxels. The voxel size of the dose grid is 2 mm × 2 mm × 2.5 mm. We assume 3 mm setup uncertainty and 5% range uncertainty. The raw dose-fluence matrices of the 29 scenarios used for this case total to 16.3 Gb in size. Each individual Pareto optimal plan optimization takes up to 5 minutes on a single 2.66G Intel Xeon CPU.

Figure 3.

A slice of the CT of the chordoma case. The three red arrows show the directions of the three IMPT beams in the transverse plane at gantry angles of 110 degrees, 180 degrees and 250 degrees. The green structure is the CTV and the purple structure is the brainstem.

3.2.2 Analysis of tradeoffs

For this case, the two main conflicting objectives are tumor coverage and brainstem sparing. Those objectives are implemented via a maximum dose objective for the brainstem and an underdose ramp objective for the CTV. All other critical structures are handled via constraints. All dose constraints and objectives we use are summarized in Table 3.

Table 3.

Objectives and constraints of the robust method for the chordoma case. The brainstem and cord are unioned for the objective.

Chordoma (Rx = 78 Gy)
Structures	Type	Scenarios	Bound (in Gy) / Direction
Objectives
CTV	underdose ramp (dpres = Rx)	all	minimize
brainstem, spinal cord	max	all	minimize
Constraints
CTV	min	nominal	≥ 60
CTV	max	nominal	≤ 85:8
R/L cochlea	max	9	≤ 50
R/L parotid	mean	9	≤ 26

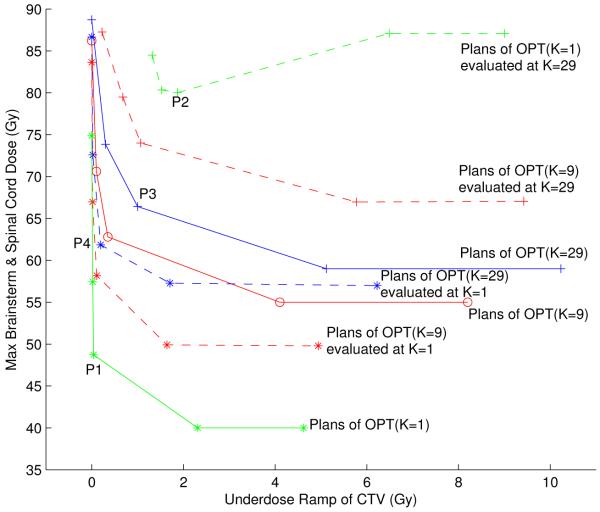
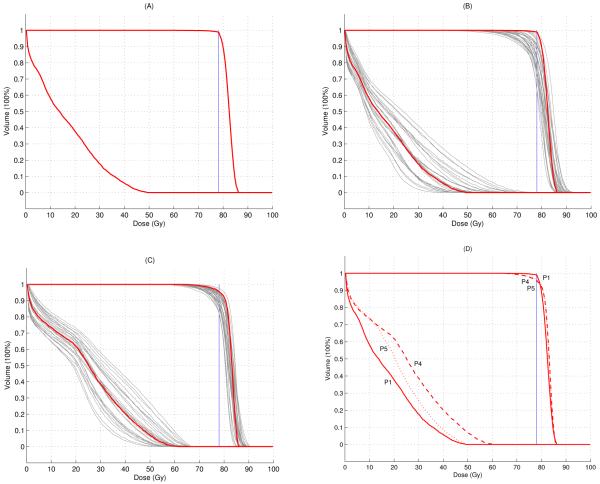
We start the discussion of this case by characterizing the tradeoff between target coverage and brainstem sparing for the nominal, non-robust case. The solid green line in Figure 4 shows the Pareto surface that corresponds to the optimization problem in Table 3 (except that objectives and constraints are evaluated for the nominal scenario only). Here, the Pareto surface has been approximated by the two anchor plans plus three intermediate plans. The treatment plan labeled as P1 represents a good tradeoff between the two objectives. The corresponding DVHs for CTV and brainstem for the nominal scenario are shown in Figure 5(A), indicating that satisfying both CTV coverage and brainstem sparing can be achieved.

Figure 4.

Pareto surfaces of the chordoma case for three scenario set sizes K = 1, 9, 29, and the same plans evaluted for different scenario sets. The solid green line is the Pareto surface when the two objectives only apply to the nominal scenario (K = 1). The solid red line is the Pareto surface when the two objectives are robustified by the 9 scenarios (K = 9). The solid blue line is the Pareto surface when the two objectives are robustified by the 29 scenarios (K = 29). The dashed green line shows the 5 plans on the K = 1 Pareto surface evaluated at 29 scenarios. The dashed blue line is the 5 plans on the K = 29 Pareto surface evaluated at the nominal scenario. The upper dashed red line is the 5 plans on the K = 9 Pareto surface evaluated at 29 scenarios. The lower dashed red line is the 5 plans on the K = 9 Pareto surface evaluated at the nominal scenario.

Figure 5.

(A) The nominal DVH of the non-robust plan (P1 in Figure 4). (B) The DVHs in 29 scenarios of the non-robust plan (P2 in Figure 4). (C) The DVHs in 29 scenarios of the 29 scenarios optimized robust plan (P3 in Figure 4). (D) Comparison of the nominal DVHs for three plans: solid line: nominal plan (P1 in Figure 4), dashed line: robust plan (P4 in Figure 4), dotted line: robust plan with optimized nominal brainstem dose (P5 in Figure 6). Nominal scenario DVHs are in red and error scenarios are in gray.

If we evaluate this treatment plan for the 29 error scenarios defined in Subsection 2.2.2, we observe that the treatment plan quality is insufficient for several error scenarios. This is demonstrated in Figure 5(B), which shows the DVHs for CTV and brainstem for the 29 error scenarios. In order to visualize the degradation of plan quality in Figure 4, we can evaluate the robustified objectives (i.e., the maximum brainstem dose that occurs in any of the 29 scenarios and the worst-case underdose ramp value for the CTV) for the 5 treatment plans that approximate the Pareto surface for the nominal optimization problem. The result is given by the dashed green line in Figure 4.

In order to obtain a treatment plan that is robust against errors, we can calculate the Pareto surface for the robustified objectives, i.e., the only two objectives are given by the robustified brainstem maximum dose and the robustified CTV underdose ramp. Nominal plan quality is not explicitly incorporated into treatment plan optimization. The result is shown as the solid blue line in Figure 4. Comparing the solid blue line to the dashed green line indicates that the robustness of the treatment plan could be improved through robust optimization. This is also illustrated via the DVHs for the treatment plan labeled as P3. Figure 5(C) shows DVHs for the 29 error scenarios; a comparison to Figure 5(B) reveals the improved robustness.

Another important interpretation of the blue and the green Pareto surface (solid lines) in Figure 4 is that the tradeoff between brainstem sparing and CTV coverage becomes harder if we include robustness. In the nominal case (solid green line) it is unproblematic to determine a treatment plan that fulfills clinical goals. As soon as robustness is enforced, the tradeoff is harder, meaning that, e.g., worse target coverage has to be accepted in order to maintain a given level of brainstem sparing.

We further observe that the improvement in plan robustness is associated with a deterioration of nominal plan quality. This can be visualized if we evaluate the nominal objectives for the 5 robust treatment plans that define the solid blue line in Figure 4. The result is given by the dotted blue line. The compromised nominal plan quality is also illustrated in Figure 5(D), which shows the DVHs for the nominal scenario for the treatment plan labeled as P4.

In the following paragraphs we further analyse the tradeoff between robustness and nominal plan quality. Intuitively, we can assume that there is a tradeoff between the nominal brainstem dose and robustness of CTV coverage. If we want to cover the CTV under uncertainty, it is likely that we have to accept higher brainstem doses even in the nominal case. Looking at Figure 4 we can ask the following question: To what extent can the nominal brainstem dose be improved by slightly worsening the robustness in CTV coverage?

Generally, we can consider the treatment planning problem as an MCO problem with four objectives: (1) nominal brainstem maximum dose, (2) robustified brainstem maximum dose, (3) nominal CTV underdose ramp, and (4) robustified CTV underdose ramp. The treatment plans on the solid blue and green lines in Figure 4 are all Pareto optimal in this four-objective problem. However, they are extreme plans in the sense that they consider either the nominal objectives or the robustified objectives, but not both simultaneously.

We now want to visualize the tradeoff between nominal brainstem dose and robustness of CTV coverage. In order to do this, we start off with the treatment plan labeled P3. The location of P3 in the diagram of Figure 4 yields optimal objective values for the robustified objectives. The point P4, which corresponds to the same treatment plan, indicates the corresponding values of the nominal objectives. We now impose a constraint on the value of the robustified brainstem maximum dose objective and the nominal CTV underdose ramp objective. The constraint level is given by P3 and P4, i.e., approximately 67 Gy and 0.2 Gy, respectively. Given these constraints, we can calculate the two-dimensional Pareto surface that characterizes the tradeoff between nominal brainstem dose and robust CTV coverage. The result is shown in Figure 6.

Figure 6.

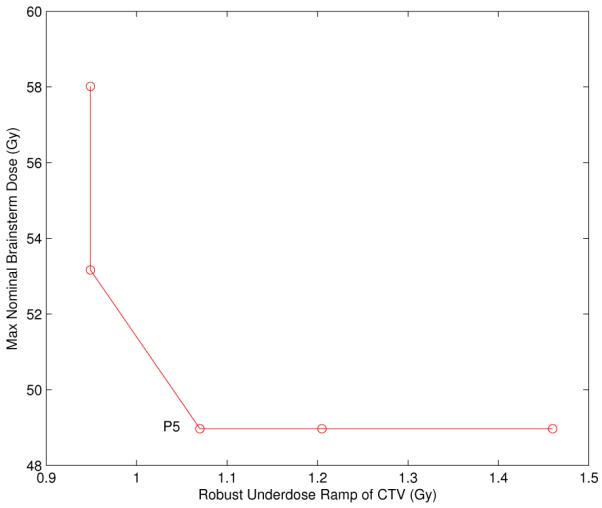
The Pareto surface visualizing the trade-off between nominal brainstem dose and robust underdose ramp of the CTV.

It is apparent that one can reduce the nominal brainstem maximum dose substantially without worsening the robustness of the CTV coverage. Whereas the nominal brainstem dose is 62 Gy for the plan P4 in Figure 4, it can be reduced to at least 53 Gy without worsening the robust CTV objective noticeably. The nominal DVHs for the plan labeled P5 in Figure 6 is shown as the dotted line in Figure 5(D).

3.2.3 The number of error scenarios

Above, we discussed the Pareto surface for robust treatment plans that were optimized for 29 error scenarios. Figure 4 also shows the Pareto surface of robust plans that are optimized using the smaller set of K = 9 error scenarios (red solid line). In addition, the dashed red line shows 5 plans on the red Pareto surface when the values of the robustified objective functions are evaluated for 29 error scenarios. Similarly, the dotted red curve shows the reevaluation of the same plans for the nominal scenario. The discrepancy between the solid line and the dashed line indicates that if a plan is robustified only against 9 error scenarios, there may be error scenarios among the larger set of 29 scenarios that show larger maximum brainstem doses or worse target coverage. On the other hand, not robustifying against the additional 20 setup error scenarios leads to better nominal plan quality (dotted line).

4 Discussion and conclusion

Compared to photon radiation therapy, proton therapy offers the chance for superior dose distributions due to the shape of the dose deposition curve of a proton pencil beam. The exact location of the dose peak depends on the incident pencil beam energy and the (line integral of) stopping powers along the proton pencil beam path. In IMPT, the intensity of thousands of pencil beams, incident from a small number of angles, are optimized to collectively produce a dose distribution that best conforms to the target and spares critical structures. Due to the sensitivity of the individual Bragg peaks to the amount and type of physical matter that each pencil beam passes through, an optimized dose distribution can be highly sensitive to errors in patient setup and discrepancies in the actual versus predicted range of the Bragg peaks. Robust optimization provides a numerical technique to compute plans (i.e., the fluence contribution from each pencil beam) that are less sensitive to these possible errors.

It is not trivial to determine what to strive for regarding a “robust” plan. For one, a plan that robustly covers the target will necessarily produce more dose to critical structures. Conversely, a plan that robustly spares a nearby critical structure will likely underdose the target. Additionally, the level of robustness needs to be determined, and this may be best decided only after observing how robustness changes the overall plan quality. Such observations indicate that an interactive system, where a user can explore various robustness options and levels, will be useful. In the present work we have presented such a system in the form of Pareto-surface based MCO utilizing multiple scenarios to model IMPT delivery errors.

4.1 Robust optimization: exploiting the redundancy of constraints

Compared to single scenario optimization, multiple scenario optimization has a greatly increased problem size and therefore will in general stress the computational environment of this already large problem (millions of voxels and thousands of pencil beams). In terms of the computational burden of requiring a large number of error scenarios K, the projection solver that we use, ART3+O, is well-suited. Computational burden (used loosely to mean both memory requirements and computation time) of typical gradient-based and linear programming algorithms scale at least linearly with the input problem size. In the case of ART3+O, only active constraints are in the working memory, and while more scenarios add more constraints to the problem, only a fraction of those constraints are binding for a given optimization run. For example, a worst-case (i.e. all scenarios) constraint on a spinal cord maximum dose level will be dominated by the scenario(s) that have the spinal cord shifted in the direction of the target and/or the Bragg peaks shifted into the spinal cord. Thus even though the constraints will be written to constrain the spinal cord doses for all scenarios, most of these constraints will be redundant and only the constraints for selected scenarios will be important. The ART3+O solver naturally exploits such redundancy of constraints, as described in more detail in [1].

4.2 Combining robust optimization with MCO

Given a solver capable of handling large IMPT instances and the observation that the notion of robustness in radiotherapy planning is inherently a question of trading off between nominal plan quality and robustified plan quality, we have implemented and demonstrated a robust MCO system that pre-computes a set of Pareto optimal plans as a way to expose these tradeoffs to treatment planners. To our knowledge, this is the first such system to be described.

In Subsection 3.2 for the chordoma case, we have gone through a typical tradeoff analysis that a physicist might experience in the course of navigating the Pareto surface. Although we have not described a navigation system in this paper, the technique detailed in [13] is applicable to this setting. The concept of using weighted averages of pre-computed Pareto optimal plans to approximate the continuous Pareto surface is well fitted to IMPT planning, where the average of multiple plans is deliverable (i.e., the fluence map sequencing step that is needed in IMRT planning, and adds a complication to the navigation procedure, is not needed here).

In our approach to robust MCO, the error scenarios are fixed. The tradeoff between nominal plan quality and robustness is controlled by forming convex combinations of plans optimized for the nominal scenario and robust plans optimized for the given set of error scenarios. An alternative approach to controlling plan robustness would be to vary the magnitude of the error. This approach is however not pursued here, the reason being that existing methods for database generation and navigation are not only applicable to such an approach.

A limitation in the current implementation of the projection solver is the Pareto optimal plan database generation method. In its current form, the solver is built to optimize single objectives, which is why we generate interior Pareto surface plans by adjusting constraint levels for a set of the objectives and then minimizing another one of them. More advanced Pareto surface generation strategies [24, 25], which compute additional interior points on the surface in such a way to minimize the gap between the upper and lower Pareto surface bounds, require solvers to be able to optimize weighted sums of the underlying objectives. Using the solver ART3+O for weighted sum minimization requires the introduction of auxiliary variables (the details of such techniques are well known in the linear optimization literature, see for example [23]). While this is straightforward, it has not been pursued at this point.

4.3 Remarks

The hard constraints set up for the constrained optimization problem define the feasible plan space where the planner will later navigate. Therefore those constraint bounds should be selected loosely to make room for the navigation to find a satisfactory Pareto optimal plan. Of course, more user experience on the specific disease site will help in determining typical values of those constraint bounds.

For simplicity of presentation, we have ignored the clinical IMPT concepts of single field uniform dose (SFUD) and fraction groups. SFUD is an additional constraint that specifies that the dose to a target from a single beam needs to be uniform, within some specified tolerance. This greatly restricts the degrees of freedom in IMPT planning; it is used clinically to produce more robust plans without explicitly performing robust optimization. Using auxiliary variables it is straightforward to include such a constraint in the system, and indeed our initial release of ASTROID includes this option.

In this work we have used both K = 9 and K = 29 scenarios, and we observe that the two choices result in different Pareto surfaces. Since one dose-fluence matrix is computed for each scenario, it is desirable computationally to keep K as low as possible, but in general the choice of K will depend on the disease site and the uncertainty settings (magnitude of setup and range errors modeled). Further experimentation is required to be able to make statements about how many scenarios are needed. Furthermore, investigating the number of error scenarios required for optimization is linked to the question how the robustness of a treatment plan should be measured and visualized. Minimax optimization by its nature aims at optimizing treatment plans for worst case that is considered in the uncertainty model. In practice, however, a focus on the worst case may not always be desired. Instead, the clinical goal may be that a treatment plan is acceptable for the majority of patients, suggesting statistical measures for robustness evaluation. It can be hypothesized that a large number of error scenarios is needed if the worst case scenario is criterion for robustness. Instead, a smaller number of scenarios may be sufficient if average plan quality is the criterion of choice.

The questions regarding the best robustness evaluation measure, the number of error scenarios used in robust optimization, the magnitude of the assumed errors, and the type of robust optimization method that is to be used are all linked. Gaining further experience in clinical IMPT planning may be needed to address these questions. Partly for this reason, from a system design point of view, we have opted for “user has complete control”. Because these are the early days of IMPT, and it is not clear exactly how much emphasis should be put on robust plan quality versus nominal plan quality, we opt for a system that allows planners to view the spectrum of possibilities. The point of this paper is to introduce a system that is capable of studying these issues, not to answer them. It is likely that they can only be answered in a site specific (or even patient specific) way, and that the answers depend on the characteristics of the pencil beam scanning system under consideration.

4.4 Summary

In summary, we presented a new method for robust IMPT optimization. In our approach, uncertainty is modeled by a discrete set of error scenarios. For each error scenario, a separate dose-influence matrix is pre-computed to calculate the dose distribution under those errors. The current implementation performs minimax optimization, i.e. treatment plans are optimized such that an objective is minimized for the worst error scenario that can occur. Our solver is customized for linear constraints and exploits the redundancy in the constraint set that is inherent to minimax optimization. In addition, we present an approach to incorporate robustness into a multi-criteria optimization. The approach can take advantage of existing methods for database generation and Pareto surface navigation. In the context of robust optimization, there is a special need for MCO planning methods, first because tradeoffs between different volumes of interests become harder, and second because it leads to a tradeoff between robustness and nominal plan quality. This has been illustrated for a Chordoma case.

Appendix: Projection to satisfy the ramp constraint

In our previous work in [1] we have presented most of the optimization method used in this paper. However, the ramp function was added to the pool of objective/constraint functions. The ramp function can be formulated as a linear problem with the help of auxiliary variables. By introducing auxiliary variables thesame projection methods applied in [1] can be used to handle a ramp constraint. In the current implementation though we avoid the introduction of auxiliary variables and use an iterative heuristic to project onto a violated ramp constraint.

For example, we consider an underdose ramp constraint for the target. Let D be the dose-fluence matrix for the target voxels and let the beamlet intensity vector be x. Then the dose vector to the target voxels is d = Dx. Assume we are at a solution x₀ where the constraint r(Dx₀, d^pres) ≤ b is violated. The projection operator needs to return a solution P(x₀) that is closest to x₀ and satisfies the constraint. When the ramp constraint is violated, it means some of the voxels are underdosed. Consider only this set of underdosed target voxels. Summing up the rows of the corresponding sub-matrix of D gives the gradient of the mean dose to these voxels, i.e., the direction of maximal increase of the mean dose of the underdosed voxels. A move in this direction will increase the dose to these underdosed voxels and update x from x₀ to x₁. Such an incremental move is made iteratively. During each iteration the list of underdosed voxels and the solution are updated. This procedure is repeated, until the ramp constraint is satisfied. The overdose ramp constraint is treated similarly. Note that ramp objectives are handled as constraints by the projection solver [1].