Influence of robust optimization in intensity-modulated proton therapy with different dose delivery techniques

Wei Liu; Yupeng Li; Xiaoqiang Li; Wenhua Cao; Xiaodong Zhang

doi:10.1118/1.4711909

. 2012 May 11;39(6):3089–3101. doi: 10.1118/1.4711909

Influence of robust optimization in intensity-modulated proton therapy with different dose delivery techniques

Wei Liu ^1,^a), Yupeng Li ¹, Xiaoqiang Li ¹, Wenhua Cao ², Xiaodong Zhang ³

PMCID: PMC3360691 PMID: 22755694

Abstract

Purpose: The distal edge tracking (DET) technique in intensity-modulated proton therapy (IMPT) allows for high energy efficiency, fast and simple delivery, and simple inverse treatment planning; however, it is highly sensitive to uncertainties. In this study, the authors explored the application of DET in IMPT (IMPT-DET) and conducted robust optimization of IMPT-DET to see if the planning technique’s sensitivity to uncertainties was reduced. They also compared conventional and robust optimization of IMPT-DET with three-dimensional IMPT (IMPT-3D) to gain understanding about how plan robustness is achieved.

Methods: They compared the robustness of IMPT-DET and IMPT-3D plans to uncertainties by analyzing plans created for a typical prostate cancer case and a base of skull (BOS) cancer case (using data for patients who had undergone proton therapy at our institution). Spots with the highest and second highest energy layers were chosen so that the Bragg peak would be at the distal edge of the targets in IMPT-DET using 36 equally spaced angle beams; in IMPT-3D, 3 beams with angles chosen by a beam angle optimization algorithm were planned. Dose contributions for a number of range and setup uncertainties were calculated, and a worst-case robust optimization was performed. A robust quantification technique was used to evaluate the plans’ sensitivity to uncertainties.

Results: With no uncertainties considered, the DET is less robust to uncertainties than is the 3D method but offers better normal tissue protection. With robust optimization to account for range and setup uncertainties, robust optimization can improve the robustness of IMPT plans to uncertainties; however, our findings show the extent of improvement varies.

Conclusions: IMPT’s sensitivity to uncertainties can be improved by using robust optimization. They found two possible mechanisms that made improvements possible: (1) a localized single-field uniform dose distribution (LSFUD) mechanism, in which the optimization algorithm attempts to produce a single-field uniform dose distribution while minimizing the patching field as much as possible; and (2) perturbed dose distribution, which follows the change in anatomical geometry. Multiple-instance optimization has more knowledge of the influence matrices; this greater knowledge improves IMPT plans’ ability to retain robustness despite the presence of uncertainties.

Keywords: robust optimization, IMPT, distal edge tracking

INTRODUCTION

Proton therapy, especially intensity-modulated proton therapy (IMPT), can result in highly conformal target coverage while sparing adjacent organs at risk (OARs).¹ This is mainly facilitated by the flexibility to set nonuniform intensities of “beamlets” with a sequence of energies of multiple beams incident from different directions. A beamlet is a thin scanning beam of protons that exits the nozzle and is incident on the patient or phantom surface; all the beamlets from a given angle make up the beam from that angle. Proton beams’ intensity maps are derived using inverse treatment planning systems that optimize some objective functions to achieve an optimum compromise between delivering a tumoricidal dose to the target and sparing critical normal structures.² A common strategy in intensity-modulated radiation therapy and IMPT optimization involves first computing the contribution of each of thousands of beamlets to each dose voxel in volumes of interest (the target and critical structures) using appropriate pencil-beam algorithms. The contributions to voxels from all the beamlets per unit intensity within the range of influence have been called an influence matrix (IM).³ The optimized dose to each voxel is then calculated by adding up the contributions from all beamlets weighted with optimized intensities.

Lomax² described 4 delivery techniques for IMPT. Typical IMPT uses the full 3D modulation technique (IMPT-3D) proposed by Brahme et al.,⁴ in which multiple energies are used at each lateral position to form a spread-out Bragg peak that covers the target from the distal edge to the proximal edge. The full 3D modulation method is the most flexible proton scanning beam modulation technique; however, it is not energy efficient because of the dozens of energy layers needed per lateral position. This lack of efficiency is especially a concern when the number of energy layers provided by an accelerator is limited or when a more cost-effective accelerator for IMPT is desired, such as a dielectric wall accelerator.⁵ In addition, reducing the number of beamlets by reducing the number of the energy layers used in the machine would simplify inverse treatment planning and treatment delivery. Thus, a more energy-efficient delivery technique for proton scanning beam therapy is needed.

Another delivery technique for IMPT, the distal edge tracking technique (IMPT-DET) proposed by Deasy et al.,⁶ uses only 1 Bragg peak for each lateral position (i.e., the Bragg peak stops at the distal edge of the target). Proton scanning beams used in IMPT have thin pristine Bragg peaks; thus, more beams from different angles are needed in IMPT-DET treatment plans than in IMPT-3D treatment plans to deliver a homogeneous dose in the target volume. Although the DET method uses only a limited number of Bragg peaks, it can result in dose distributions that are similar to those of the full 3D method,⁷^,⁸^,⁹^,¹⁰^,¹¹^,¹² depending on the tumor size and number of treatment beams. The DET technique is favored for centrally located targets and can minimize the total dose delivered to the patient.¹¹

One complicating factor is that IMPT’s effectiveness can be greatly diminished by range uncertainties, patient setup uncertainties, and interfractional and intrafractional organ motion,⁹^,¹⁰^,¹³^,¹⁴^,¹⁵^,¹⁶^,¹⁷^,¹⁸ which necessitates some means of accounting for robustness. IMPT planning is usually based on the PTV, which is an accurate planning method when the given dose distribution is invariant.¹⁹ This assumption is, in general, not true for protons. Therefore, PTV-based planning is not appropriate in IMPT. In multibeam IMPT optimization, the intensities of spots placed in the CTV and the corresponding dose distributions per beam are highly inhomogeneous. Beamlets from a given beam direction may not even reach the distal edge of the target. Inhomogeneous dose distributions within the target for individual beams are compensated for by doses deposited by beamlets of other beams. Therefore, range uncertainties may lead to overshooting (exceeding the expected range) or undershooting (not reaching the expected range), which could result in hot or cold spots in the targets. Furthermore, changes in proton path lengths due to changes in patient setup would result in similar effects on the dose distribution. In assessments of treatment plans using rigorous uncertainty analyses, such as density-differentiated error and motion-differentiated error distributions, the DET approach was found to be more sensitive to uncertainties than the 3D approach.⁹^,¹⁰ However, Albertini et al.¹¹^,¹² discovered that in cases of stringent dose-volume constraints to OARs, IMPT plans are less sensitive to uncertainties when they use the DET approach rather than the 3D approach.

Some robust optimization methods for IMPT-3D have been proposed. Probabilistic nonlinear programming and robust linear programming approaches have been used to account for range and setup uncertainties.¹⁶^,¹⁷^,¹⁸ Similarly, worst-case robust optimization was applied in a clinical case (for a tumor near the spinal cord) by Pflugfelder et al.¹⁵ Fredriksson et al.²⁰ used minimax optimization to handle range and setup uncertainties in proton therapy. The resulting treatment plans all showed reduced sensitivity to uncertainties.

However, to our knowledge, no one has applied robust optimization to IMPT-DET. The results of IMPT-3D planning suggest that if range and patient setup uncertainties were considered in the optimization algorithm, robust optimization would reduce the sensitivity of target coverage to uncertainties, making previously unreliable plans reliable.¹⁵^,¹⁶^,¹⁷^,¹⁸ The primary goal of the present study was to determine whether robust optimization can likewise improve IMPT-DET plans. In addition, an improved understanding of the behavior to incorporate systematic uncertainties into the IMPT-DET optimization process will help us understand how robust optimization works in IMPT-3D. In Sec. 2 of this paper, we briefly introduce our patient data and beam configurations, the beam angle optimization algorithm, the robust optimization algorithm, the dose calculation algorithm, the plan evaluation metrics, and the robustness evaluation technique. In Sec. 3, the quality, delivery efficiency, and plan robustness of the 36 beam IMPT-DET plan are compared with those of the 3-beam IMPT-3D plan for a prostate cancer case and a base of skull (BOS) cancer case. Our conclusions from these analyses and discussion of the results are presented in Sec. 4.

METHODS

Patient data and beam configurations

The various treatment planning techniques were tested using historical data for a representative patient with prostate cancer (adenocarcinoma) and a representative patient with a BOS chordoma. For IMPT-3D, we created plans using 3 beams in the transverse plane (gantry angles of 10°, 140°, and 270° for prostate, and gantry angles of 60°, 290°, and 320° for BOS), and for IMPT-DET, we created plans using 36 beams with uniformly spaced angles (10°). The 3-beam IMPT-3D plan angles were derived from a beam angle optimization algorithm developed previously (see Sec. 2A). The lateral margin and spot spacing of the beam configuration used in both plans were 1.0 and 0.5 cm, respectively. The numbers of energy layers used in the IMPT-3D plan were 27, 29, and 20 for the prostate cancer case and 30, 27, and 34 for the BOS cancer case. The nominal energies used in the IMPT-3D for every beam were 143.2, 183.4, and 190.5 MeV (48 distinct proton energies were used for these 3 beams) for the prostate cancer case and 134.6, 141.6, and 144.9 MeV (36 distinct proton energies were used for these 3 beams) for the BOS cancer case. For every IMPT-DET beam, only the spots with the highest and second-highest energy levels (calculated by allowing each beam to use only the highest and second-highest energy layers) were chosen so that the Bragg peak would be placed at the distal edge of the target (i.e., the near-DET technique was adopted for better plan quality). Twenty-four and 21 distinct proton energies were used in IMPT-DET plans for the prostate and BOS cancer cases, respectively.

In our center, when using image-guided radiation therapy, a 5-mm margin is used for clinical target volume (CTV)-to-PTV expansion for prostate cancers and a 3-mm margin is used for BOS cancers. We consider lateral margins for proton plans to be the same as those for photon plans. Thus, in the current study, we used 5 mm as the lateral margin for the prostate cancer case and 3 mm as the lateral margin for the BOS cancer case. We also assumed a 3.5% range uncertainty, as is standard for patients treated at our center.

The prescribed dose to the target was 76 Gy for the prostate cancer case and 66 Gy for the BOS cancer case. At MD Anderson, the dose-volume constraints in prostate cancer irradiations are as follows: for the rectum, the volume of rectum receiving a dose of 70 Gy (denoted by V₇₀) is no greater than 25%; for bladder, the volume of bladder receiving a dose of 65 Gy (denoted by V₆₅) and 40 Gy (denoted by V₄₀) is no greater than 25% and 50%, respectively; for femoral heads, the volume of rectum receiving a dose of 50 Gy (denoted by V₅₀) is no greater than 10%. The dose constraints in BOS cancer irradiations are: for brain stem, the maximum dose (D_max) should be less than 54 Gy; for spinal cord, D_max should be less than 45 Gy; for brain, D_max should be less than 50 Gy; and for the optic chiasm, D_max should be less than 54 Gy.

Beam angle optimization algorithm

We used a local neighborhood search algorithm (LNS)²¹ to optimize beam angles. The LNS algorithm is designed to find a locally optimal solution subject to a neighborhood definition for a given starting feasible solution. In our implementation, the neighborhood of a beam angle set was defined by a one-angle-exchange algorithm. In such an algorithm, the local search procedure first enumerates all elements of the neighborhood of a starting feasible solution. Next, one angle from the feasible solution set is selected. For this given angle, one angle from the neighborhood set is selected and exchanged with the angle from the current solution set, and the objective function is evaluated with this new angle set. This procedure is repeated until all angles in the neighborhood set are evaluated. The current solution is then updated with the one yielding the most improvement in the objective function value among those elements, and the process continues until no more improving solutions exist. In our implementation, the starting angle set we fed to the algorithm consisted of equally spaced beam angles (e.g., 0°, 120°, and 240°).

The objective of this beam angle optimization scheme is to both ensure target dose coverage and uniformity and minimize OAR dose. The beam angles in the current analysis were selected on the basis of the conventional plan’s quality. Robustness analysis was then performed a posteriori.

Robust optimization algorithm

We enhanced the worst-case robust optimization method proposed by Pflugfelder et al.¹⁵ by modifying the objective function to penalize hot spots within the target as described below (Ref. ²²). The methods we used to design and compare robustly and conventionally optimized plans differs from those used by many other investigators;¹⁵^,¹⁶^,¹⁷^,¹⁸ many previous investigators designed the conventional plans on the basis of the CTV or compared robustly optimized plans with CTV-based plans [but see Fredriksson et al.²⁰ and Chen et al.²³]. In this work, we chose the PTV as the target for the conventional PTV-based plan and the CTV as the target for the robustly optimized plan. The PTV was formed by isotropic expansion of the CTV using a method similar to that used in photon therapy.²⁴ We then compared the two plans’ quality and robustness. We believe that the comparison of robustly optimized plan with CTV-based optimized plan is not valid since the latter does not incorporate uncertainties.²² For fair comparison, we renormalized the plans for all cases to have at least 98% of the CTV covered by the prescribed dose in the nominal changed other dose distributions accdose distribution and ordingly.

The intensity weight of beamlet j is denoted by the non-negative quantity $ω_{j}^{2}$ . Thus, the constrained optimization problem with respect to weights can be addressed by optimizing the square roots of the beamlet weights instead of optimizing the beamlet weights directly. The weight array $ω_{j}^{2}$ (or the fluence map) can be optimized by minimizing the objective function.

By following the strategy published by Lomax et al.,²⁵ we computed a simple worst-case dose distribution as follows: For any given beam arrangement, we computed the nominal dose distribution (i.e., without consideration of uncertainties) and dose distributions incorporating (1) setup uncertainties by shifting the patient’s planning computed tomography (CT) image and (2) range uncertainties by scaling the planning image’s CT numbers by a set percentage (e.g., ±3.5%). To incorporate setup uncertainties, we shifted the patient isocenters along the anterior–posterior (A–P), superior–inferior (S–I), and lateral (R–L) directions, yielding 6 dose distributions and 6 corresponding influence matrixes (IMs). To incorporate range uncertainties, we modified stopping power ratios by −3.5% and +3.5% to generate 2 additional IMs corresponding to maximum and minimum proton ranges, respectively. The worst-case dose distribution was then represented by the minimum of the 9 doses in each voxel in the CTV and the maximum of the 9 doses in each voxel outside the CTV. This is analogous to using the PTV dose distribution for photons, which implicitly represents the worst-case dose distribution for the CTV.

For robust optimization, we used a standard quadratic objective function

F (ω_{j}) = \sum_{i \in CTV} p_{CTV, \min} {(D_{i, \min} - D_{0, CTV})}^{2} + \sum_{i \in CTV} p_{CTV, \max} {(D_{i, \max} - D_{0, CTV})}^{2} + \sum_{i \in OARs} p_{OARs} H (D_{i, \max} - D_{0, OARs}) \times {(D_{i, \max} - D_{0, OARs})}^{2},

(1)

where p denotes the penalty weight of the corresponding term and D₀ denotes the prescribed dose for the corresponding organ. The underlined term is the modification that minimizes hot spots. The Heaviside function, $H (⟨ D_{i} ⟩ - D_{0})$ , is defined conventionally (i.e., its value is unity if ⟨D_i⟩ > D₀ but zero if ⟨D_i⟩ ≤ D₀). In our current study, we used only “relaxed” dose constraints, which were adjusted by trial and error to meet the dose-volume constraints used in our clinic. The terms $D_{i, \min} = \min_{m} {D_{i}^{m}}$ and $D_{i, \max} = \max_{m} {D_{i}^{m}}$ in Eq. 1, and they, respectively indicate the minimum and maximum dose among the m possible doses $D_{i}^{m}$ in voxel i (m = 9 here), which are calculated using $D_{i}^{m} = \sum_{i} {IM}_{i, j}^{m} ω_{j}^{2}$ in each iteration. The m IMs ${IM}_{i, j}^{m}$ , incorporating range and setup uncertainties, were precalculated using an in-house dose calculation engine for proton pencil beams of a finite size³ and stored in local memory for efficient optimization. Our robust optimization approach inherits the simplicity of worst-case robust optimization and does not require a detailed model for uncertainties.

Optimization was performed using the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method. The L-BFGS algorithm is a member of the broad family of quasi-Newton optimization methods. Unlike the original BFGS method, which stores a dense Hessian matrix approximation, the L-BFGS stores only a few vectors that implicitly represent the approximation. Because of its moderate memory requirement, the L-BFGS method is particularly well suited for optimization problems with a large number of variables.

Dose calculation engine

We developed an improved analytic formula based on the Bortfeld’s work;²⁶ this improved formula was designed to generate a full set of integral dose distribution (IDD) data for all proton energies required for our treatment planning system commissioning using the measured IDD data at only a few selected energies.²⁷ We adopted the same CT calibration table as Bortfield did; this table contains stopping power ratios relative to water for the clinical range of Hounsfield units. These ratios scale the geometric depth to compute the water-equivalent depth (WED), so the depth dose distribution in water can be associated with that in a patient or a heterogeneous medium.

Correctly acquiring the low-dose halos in single-spot profiles is crucial to correcting IDD data for nuclear interactions²⁷ and generating modeling parameters for in-medium single-spot profiles. For the in-air spot profile, we found that the approximation of an in-air profile using 1 Gaussian function was sufficient in terms of the final calculated dose’s accuracy when a modified Cauchy–Lorentz function was used in addition to 2 Gaussian functions to describe the dose distribution in a given medium. Once a spot enters a patient or phantom, the single Gaussian function characterizing the spot in air continues to be widened by the multiple Coulomb scattering and nuclear interactions in the medium. Increases in the spot’s standard deviation contributed by in-patient scattering as a function of the WED can be evaluated by using the method of Hong et al.²⁸ In addition to the primary Gaussian component, a second Gaussian function with a large standard deviation and a modified Cauchy–Lorentz distribution function were used to describe the long-range scattering caused by nuclear interactions and the large-angle Coulomb scattering that are not accounted for by the primary Gaussian component.

In brief, we developed a modified version of the algorithm of Soukup et al.²⁹ to describe the weight and width of the second Gaussian function and added a Cauchy–Lorentz component to better model the long-range effects that cannot be taken into account by using Gaussian functions alone.

Plan evaluation metrics

The following dosimetric parameters were used in comparisons for the prostate cancer case: the dose that covered 99% of the CTV (D_99%), which was composed of the prostate and seminal vesicles; the dose that covered 1% of the CTV (D_1%); the normalized volume as a percentage of the rectum and bladder that received more than 10, 20, 40, 60, and 70 Gy (V₁₀, V₂₀, V₄₀, V₆₀, and V₇₀); maximum D_max and mean dose D_mean to the rectum and bladder; D_max and mean dose D_mean to the femoral heads; and the mean dose to the body. The following dosimetric parameters were used in comparisons for the BOS cancer case: D_99%; D_1%; V₂₀, V₃₀, V₄₀, V₅₀, and V₆₀ to the brainstem; D_max and D_mean to the brainstem; and D_max and D_mean to the spinal cord. The heterogeneity index (HI) was defined as the difference between D_1% and D_99%, divided by the prescribed dose.

Robustness quantification

To evaluate or compare IMPT plans, we used a robustness quantification technique that displayed the envelope of all dose-volume histograms (DVHs) in band graphs of the 9 dose distributions associated with the corresponding range or setup uncertainties.³⁰ For convenience, the DVHs derived by choosing the nominal dose of a voxel were also displayed in the robust quantification. This robust quantification technique is effective at determining an IMPT plan’s sensitivity to setup and range uncertainties.³¹

RESULTS

Prostate cancer case

Conventional optimization

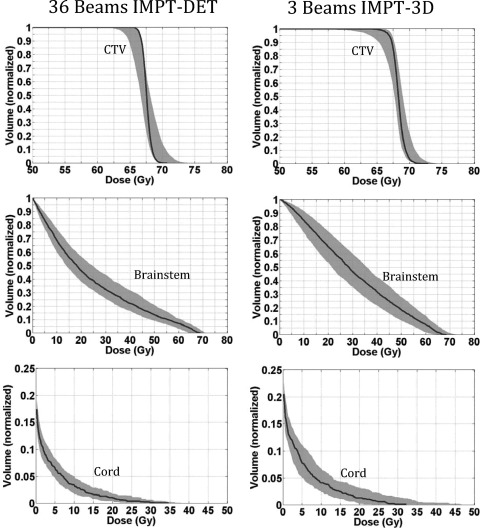
For the representative prostate cancer case, we first compared IMPT-DET plans with IMPT-3D plans derived from conventional PTV-based optimization without considering uncertainties. Figure 1 shows the robustness quantification of the CTV and various OARs from the 3-beam IMPT-3D plan and 36-beam IMPT-DET plan for the prostate cancer case, derived from conventional optimization. The details of dosimetric parameters are shown in Table TABLE I.. The qualities of the robustly optimized IMPT-DET and IMPT-3D plans are shown in Fig. 1.

DVHs derived from the robustness quantification of the CTV and various OARs from the 36-beam IMPT-DET plan (left) and 3-beam IMPT-3D plan (right) with conventional PTV-based optimization for the prostate cancer case. The solid lines are the DVHs derived using the nominal dose of every voxel. All curves are normalized to the total volume of the corresponding organs.

TABLE I.

Values of dosimetric parameters in the 3-beam IMPT-3D plan and 36-beam IMPT-DET plan from conventional PTV-based optimization for the prostate cancer case.

Tissue	Dosimetric parameter	3-beam IMPT	36-beam IMPT-DET
CTV	D_99% (Gy)	75.9	75.8
	D_1% (Gy)	76.8	77.9
Rectum	V₁₀ (%)	66.4	36.7
	V₂₀ (%)	42.4	26.4
	V₄₀ (%)	13.9	17.5
	V₆₀ (%)	8.5	11.8
	V₇₀ (%)	5.7	8.2
	D_mean (Gy)	20.9	16.8
Bladder	V₁₀ (%)	35.2	29.5
	V₂₀ (%)	27.0	20.6
	V₄₀ (%)	14.1	13.8
	V₆₀ (%)	8.9	9.4
	V₇₀ (%)	6.4	6.8
	D_mean (Gy)	14.8	13.2
Femoral heads	D_max (Gy)	25.2	39.1
Femoral heads	D_mean (Gy)	3.4	2.7

Open in a new tab

The target coverage of the IMPT-3D plan (D_99% = 75.9 Gy) was slightly higher than that of the IMPT-DET plan (D_99% = 75.8 Gy). The IMPT-3D plan produced a slightly more homogeneous dose distribution in the target (HI = 1.2%) than did the IMPT-DET plan (HI = 2.8%). The DET method generated plans that had a less homogeneous dose distribution in the target volume than the 3D method did, but CTV coverage remained about the same in the prostate cancer case.

In terms of normal tissue protection in the prostate cancer case (i.e., sparing of the rectum and bladder), IMPT-DET plan performed worse (spared less volume) than the IMPT-3D plan at high doses, while the converse was true at low doses (<20 Gy). The mean doses to the femoral heads, rectum, and bladder were always lower in the DET plans than in the 3D plans (Table TABLE I.). The mean dose for the body was reduced from 2.3 Gy in 3D plans to 2.0 Gy in DET plans. The constraint of D_max to the femoral heads ≤45 Gy was satisfied in both plans. Figure 1 clearly shows that the DET method was much more sensitive to uncertainties than the 3D method (largest CTV band widths were about 16.6 Gy for DET versus about 2.8 Gy for 3D).

Worst-case robust optimization

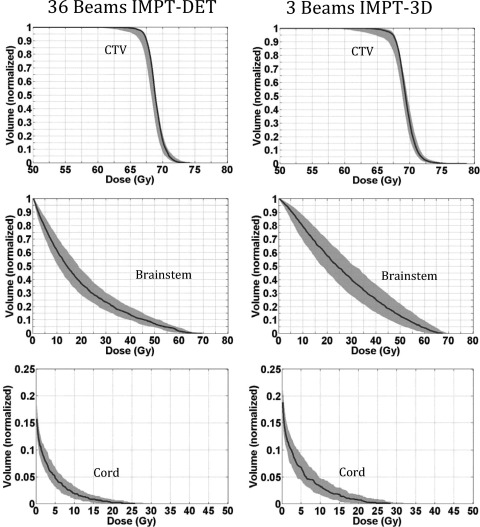
We also sought to determine whether robust optimization would improve IMPT-DET plan robustness as it does IMPT-3D plan robustness for the prostate cancer case.¹⁵^,¹⁶^,¹⁷^,¹⁸ Figure 2 shows the robustness quantification of the CTV and various OARs from the 3-beam IMPT-3D plan and 36-beam IMPT-DET plan of the prostate cancer case, derived from robust optimization. The details of the dosimetric parameters are shown in Table TABLE II.. The qualities of plans robustly optimized by means of IMPT-DET and IMPT-3D are also shown in Fig. 2.

DVHs derived from the robustness quantification of the CTV and various OARs from the 36-beam IMPT-DET plan (left) and 3-beam IMPT-3D plan (right) with robust optimization for the prostate cancer case. The solid lines are the DVHs derived using the nominal dose of every voxel. All curves are normalized to the total volume of the corresponding organs.

TABLE II.

Values of dosimetric parameters in the 3-beam IMPT-3D plan and 36-beam IMPT-DET plan with robust optimization for the prostate cancer case.

Tissue	Dosimetric parameter	3-beam IMPT	36-beam IMPT-DET
CTV	D_99% (Gy)	76.0	75.7
	D_1% (Gy)	77.2	79.9
Rectum	V₁₀ (%)	63.6	49.1
	V₂₀ (%)	42.7	36.9
	V₄₀ (%)	11.8	21.7
	V₆₀ (%)	5.0	13.5
	V₇₀ (%)	2.5	9.2
	D_mean (Gy)	19.6	21.1
Bladder	V₁₀ (%)	26.7	29.6
	V₂₀ (%)	17.0	20.6
	V₄₀ (%)	9.0	11.4
	V₆₀ (%)	5.1	6.2
	V₇₀ (%)	3.0	3.3
	D_mean (Gy)	10.1	10.7
Femoral heads	D_max (Gy)	12.1	29.3
Femoral heads	D_mean (Gy)	2.37	3.9

Open in a new tab

The D_99% of the CTV from the IMPT-3D plan (76.0 Gy) was similar to that from the IMPT-DET plan (75.7 Gy), which means that the target coverage was similar in both plans. However, the dose inside the CTV from the IMPT-3D plan was more homogeneous (HI = 1.6%) because part of the CTV was overdosed in the IMPT-DET plan (HI = 5.5%). The IMPT-3D plan typically spared more normal tissue than did the IMPT-DET plan, although the pattern was reversed at low doses (<20 Gy).

The sensitivity of the dose distribution to uncertainties from the IMPT-DET plan was not much reduced by robust optimization for this prostate cancer case. The maximal width of the CTV in the robustly optimized IMPT-3D plan was about 0.8 Gy, compared with about 2.8 Gy from the nonrobust optimization; the reduction in sensitivity was considerably smaller when comparing optimization methods in the IMPT-DET plan (the maximal width of the CTV was about 14.2 Gy for robust optimization and about 16.6 Gy for nonrobust optimization).

BOS cancer case

To determine if the above findings could be generalized, we performed a similar study for 1 representative BOS cancer case. We found that for the BOS cancer case, the DET method (with HI = 4.8%) generated plans with more homogeneous dose distributions in the CTV than did the IMPT-3D method (with HI = 7.4%) and offered better CTV coverage. In addition, the DET method provided better normal tissue protection (Fig. 3). The details of the dosimetric parameters are shown in Table TABLE III..

TABLE III.

Values of dosimetric parameters in the 3-beam IMPT-3D plan and 36-beam IMPT-DET plan from conventional PTV-based optimization for the BOS cancer case.

Tissue	Dosimetric parameter	3-beam IMPT	36-beam IMPT-DET
CTV	D_99% (Gy)	65.4	65.8
	D_1% (Gy)	70.4	69.1
Brainstem	V₂₀ (%)	64.9	46.2
	V₃₀ (%)	46.5	32.3
	V₄₀ (%)	31.7	22.0
	V₅₀ (%)	18.3	13.6
	V₆₀ (%)	7.3	7.2
	Max (Gy)	68.3	68.6
	D_mean (Gy)	30.2	23.7
Spinal cord	D_max (Gy)	32.0	34.5
Spinal cord	D_mean (Gy)	1.2	0.95

Open in a new tab

The D_99% of the CTV from the IMPT-3D plan (65.4 Gy) was similar to that from the IMPT-DET plan (65.8 Gy), which means that the target coverage was similar in both plans. However, the dose inside the CTV in the IMPT-DET plan was more homogeneous (HI = 5.0%) because part of the CTV was overdosed in the IMPT-3D plan (HI = 7.8%). The IMPT-DET plan spared more normal tissue than did the IMPT-3D plan. These results are the inverse of those observed in the prostate cancer case and might have resulted from the more stringent dose constraints used in this case than in the prostate cancer case to nearby OARs (see Sec. 4).

Although the DET was less robust to uncertainties than was the 3D method (Fig. 3), we observed that for the BOS cancer case our robust optimization method could improve the robustness of the IMPT-DET plan to uncertainties (Fig. 4). The details of the dosimetric parameters are shown in Table TABLE IV.. Please note that the DET plan (without robust optimization) for the BOS cancer case was not as sensitive to uncertainties as the prostate cancer case. This result might give us some hints why the robust optimization could improve the BOS cancer case but not the prostate cancer case, as discussed in Sec. 4.

TABLE IV.

Values of dosimetric parameters in the 3-beam IMPT-3D plan and 36-beam IMPT-DET plan with robust optimization for the BOS cancer case.

Tissue	Dosimetric parameter	3-beam IMPT	36-beam IMPT-DET
CTV	D_99% (Gy)	65.3	65.3
	D_1% (Gy)	73.4	71.9
Brainstem	V₂₀ (%)	57.5	36.8
	V₃₀ (%)	39.5	23.3
	V₄₀ (%)	24.9	13.9
	V₅₀ (%)	12.8	7.1
	V₆₀ (%)	4.1	1.8
	D_max (Gy)	67.3	69.1
	D_mean (Gy)	26.6	18.9
Cord	D_max (Gy)	28.3	25.6
Cord	D_mean (Gy)	0.93	0.67

Open in a new tab

Figure 5 shows the dose distributions for the BOS cancer case in the transverse plane derived from the 36-beam IMPT-DET plans developed with conventional PTV-based optimization and with robust optimization. Dose distributions with the nominal range of doses and with a range 3.5% higher than the nominal one are shown. It is clear that the dose distribution in the robustly optimized plan was less affected by the range uncertainty than the PTV-based plan. Figure 6 shows the dose distributions resulting from setup uncertainties, in which the patient was moved to the right by 3 mm. The shift affected the PTV-based plan to a markedly greater degree than the robustly optimized plan. Robust optimization led to robust IMPT-DET and IMPT-3D plans that were both resistant to uncertainties for this BOS cancer case.

Dose distributions in the transverse plane for the BOS cancer case illustrating that the robustly optimized 36-beam IMPT-DET plan was insensitive to range uncertainty compared with the conventionally PTV-based optimized 36-beam IMPT-DET plan. Left panels: PTV-based plans. Right panels: robustly optimized plans. Top row: nominal position. Bottom row: with 3.5% larger range. CTV: orange color wash (middle filled area); brainstem: magenta color (bottom enclosed area).

Dose distributions in the transverse plane for the BOS cancer case illustrating that the robustly optimized 3-beam IMPT-3D plan was relatively insensitive to setup uncertainty compared with the conventional PTV-based optimized 3-beam IMPT-3D plan. Left panels: PTV-based plans. Right panels: robustly optimized plans. Top row: nominal position. Bottom row: with patient moved to the right by 3 mm. CTV: orange color wash (middle filled area); brainstem: magenta color (bottom enclosed area); red solid arrows: beam directions.

DISCUSSION

In this paper, we evaluated the use of the DET in IMPT treatment planning. In this study, we did not adopt a commonly used clinical beam arrangement with 2 lateral opposed fields in IMPT-3D for the prostate cancer case because our goal was not to compare our 36-beam plan with the common clinical plan. Some published studies have also described 5-beam plans to treat a prostate cancer, such as in Albertini et al.¹¹ In our current study, we used only relaxed dose constraints for all results presented here, which were adjusted by trial and error to meet the dose-volume constraints used in our clinics. Dose-volume constraints may be incorporated using the method described by Wu and Mohan,³² which we plan to do in our future studies.

We conclude that with no uncertainties considered, the DET is less robust to uncertainties than is the 3D method but offers better normal tissue protection. With robust optimization to account for range and setup uncertainties, we can improve the robustness of IMPT plans to uncertainties; however, our findings show the extent of improvement varies. It is important to remember that these conclusions are preliminary and are limited in scope, but we have other evidence that supports them. Space limitations permitted us to include only illustrative examples in this paper; however, we have conducted a robust optimization study of IMPT-3D for 20 cancer patients, including 9 head and neck, 7 lung, and 4 prostate cancer patients. For IMPT-DET, we have studied fewer cases, but our results and conclusions are consistent with those reported in this paper. We found at least two possible mechanisms to improve the robustness of IMPT plans to uncertainties: (1) a localized single-field uniform dose distribution (LSFUD) mechanism, in which the optimization algorithm attempts to produce an single-field uniform dose (SFUD) while minimizing the patching field as much as possible and (2) a perturbed dose distribution, which follows the change in anatomical geometry. Both mechanisms are implemented by multiple-instance optimization.³³ The multiple-instance optimization procedure described in Sec. 2C has more knowledge of the IMs than the single-instance optimization used in the conventional PTV-based optimization, which makes it possible to retain plan robustness despite uncertainties.

Figure 7 demonstrates how our robust optimization led to a plan that was more robust to uncertainties in the prostate cancer case. The figure shows the dose distribution (isosurface) in the transverse plane of single beams from the conventionally optimized PTV-based plan and from the robustly optimized plan. The range uncertainties were dominant in this case. In conventional optimization, fields 2 and 3 were patched together to produce a uniform distribution. However, robust optimization resulted in each field covering the target uniformly, leading to an LSFUD. This idea can be seen more clearly in Fig. 8, which shows the dose profiles of different fields along the R-L direction from the conventionally optimized PTV-based plan and the robustly optimized plan of the prostate cancer case. For comparison, the figure also shows the total dose distributions on the transverse plane of the prostate cancer case. The slopes of the dose profiles are considerably flatter inside the target.

Dose distribution (color wash) of fields in the transverse plane of the 3-beam IMPT plan for the prostate cancer case. *Toprow*: beam 2 (gantry angle: 140°); *bottomrow*: beam 3 (gantry angle: 270°). *Leftcolumn*: PTV-based plan; *rightcolumn*: robust plan. Cyan (bottom filled area): rectum; yellow (top enclosed area): bladder; red (middle enclosed area): CTV; red solid arrows: beam directions. The PTV-based plan was generated from the IMPT-3D inverse treatment plan, which was optimized on the basis of the PTV.

Dose distribution (color wash) of fields in the transverse plane of the 3-beam IMPT plan for the prostate cancer case. *Toprow*: total dose distribution; *bottomrow*: dose profiles of different fields along the R-L direction indicated in the top row as red middle arrows. *Leftcolumn*: PTV-based plan; *rightcolumn*: robust plan. Cyan (bottom filled area): rectum; yellow (top enclosed area): bladder; red (middle enclosed area): CTV. The PTV-based plan was generated from the IMPT-3D inverse treatment plan, which was optimized on the basis of the PTV.

The optimization algorithm attempts to produce an SFUD while minimizing the patching field as much as possible (i.e., it employs an LSFUD mechanism). The LSFUD mechanism greatly improved the robustness to range uncertainties in the IMPT-3D plan for this prostate cancer case. However, no such improvement could be gained in IMPT-DET because, by definition, it is impossible to cover a regular-sized target uniformly with just 1 field. Therefore, the possible mismatch between beamlets due to range uncertainties greatly diminished the IMPT-DET plan’s robustness.

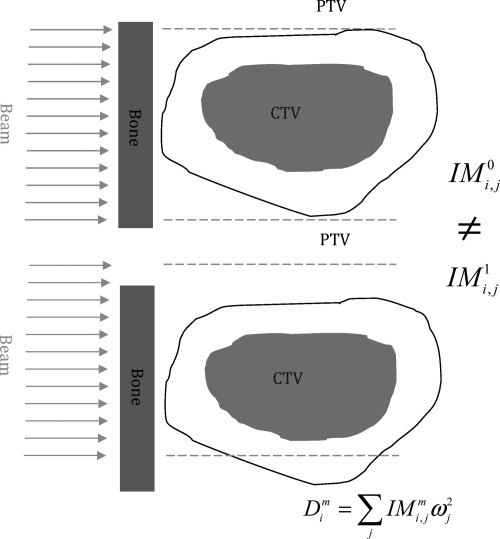
Unfortunately, the above LSFUD mechanism does not work in all cases. In some such cases, the mechanism of perturbed dose distribution to follow the change of anatomy geometry is very important. A schematic depiction of the second mechanism illustrates how the optimization method may affect plan robustness to uncertainties (Fig. 9). The top panel of Fig. 9 shows the nominal anatomical geometry without any uncertainties considered; its IM is represented by ${IM}_{i, j}^{0}$ . The bottom panel shows changes in the anatomical geometry due to an uncertainty (both setup and range uncertainties can be accounted for, although only one setup uncertainty scenario is shown here for convenience); its influence matrix is represented by ${IM}_{i, j}^{1}$ . Because IMPT is very sensitive to uncertainties, there is a big difference between ${IM}_{i, j}^{0}$ and ${IM}_{i . j}^{1}$ . In other words, the dose distribution of IMPT could be easily perturbed by the uncertainties. It is worth noting that it is this unique characteristic of protons that makes it possible for multiple-instance optimization to achieve a more robust IMPT plan without sacrificing plan optimality. If there were no differences between the IMs corresponding to different uncertainty scenarios as for photons, both robust optimization and PTV-based conventional optimization would lead to same robust plans. As the differences of the IMs grow, both methods become worse, but comparatively larger benefits can be obtained from the robust optimization because it can compensate for the differences of the IMs in a better way than conventional methods can. In our robust optimization, the optimizer can find a desired beamlet weight solution from the degenerate solution space by means of multiple-instance optimization. Although the beamlet weights solution (fluence maps) $ω_{j}^{2}$ remain unchanged in different uncertainty scenarios, the dose distribution $D_{i}^{m} = \sum_{j} {IM}_{i, j}^{m} ω_{j}^{2}$ derived from such a fluence map can be perturbed so that it follows the changes in anatomical geometry, thus improving the robustness of IMPT plans in the face of uncertainties. The current method is limited in its ability to handle range uncertainties and rigid shifts in patient isocenters due to setup uncertainties. The intra-fractional anatomical changes necessitate 4D robust optimization using 4D CT and deformable image registration; this will be the subject of a future study in our laboratory.

Illustration showing how multiple-instance optimization improves the robustness of IMPT plans to uncertainties. Red (middle filled area): CTV; *black lines:* PTV margin; blue (left rectangle): bones; *green arrows:* beams. The green dashed lines indicate that the beams were not moved; only the patient was shifted downward. *Top:* nominal anatomical geometry without any uncertainties with its influence matrix represented by ${IM}_{i, j}^{0}$ ; *bottom*: anatomical geometry changed due to a setup uncertainty, with its influence matrix represented by ${IM}_{i, j}^{1}$ .

We chose to use the CTV rather than the PTV as the target for optimization. Instead of expanding the CTV to form a PTV with a fixed, predefined margin to account for setup uncertainties, our worst-case robust optimization itself generated a patient-specific, “customized,” and as-small-as-necessary margin (i.e., the margin itself was optimized by the optimizer), which led to an effectively smaller margin than if we had used a fixed and predefined margin to expand the CTV to form the PTV. Therefore, we were able to achieve better normal tissue protection than the conventional PTV-based optimization without compromising the target coverage. This mechanism can be seen clearly from Figs. 5 6 in both IMPT-DET and IMPT-3D plans for the BOS cancer case.

It would be of interest to determine why the planning techniques behaved differently for the prostate and BOS cancer treatment plans. Albertini et al.³⁴ pointed out that whether the relaxed or “stringent” constraints were employed for nearby organs played an important role in the robustness of conventional PTV-based plans when uncertainties were present, since relaxed constraints to the organs could lead to quasi-SFUD individual fields (thus rendering the plans insensitive to uncertainties), whereas stringent constraints to the organs could lead to individual fields with large in-field dose gradients (thus rendering the plans sensitive to uncertainties).³⁴

For our prostate cancer case, only relaxed volume constraints were given to the OARs (e.g., less than 25% of rectum volume should receive 92% of the prescribed dose). One could satisfy these relaxed constraints simply by patching quasi-SFUD individual fields in the conventional PTV-based IMPT-3D plans. These resulted in more robust conventional PTV-based plans in IMPT-3D compared with in IMPT-DET. The robust optimization further improves the robustness of the IMPT-3D plans via LSFUD. However, patching quasi-SFUD individual fields are not possible with the DET approach because of the very nature of DET. For the BOS cancer case, in which stringent dose constraints were given to the neighboring OARs (e.g., 0% of the brainstem volume could receive 82% of the prescribed dose), the IMPT plans needed to generate individual fields with large in-field dose gradients. These kinds of fields can be generated with both the 3D and DET approaches, thus both of them are almost equally sensitive to uncertainties. However, the robustness of the BOS plans can be much improved after robust optimization since now the multiple-instance optimization works well here.

The choice of the initial starting beamlet intensity map might also play an important role in the robustness of the final IMPT plans,¹¹ especially if dose-volume constraints are used. It is worthy to emphasize here that in our IMPT-DET planning, the optimization process was started by setting the beamlet weight universally to zero except for the most and second most distal beamlets [i.e., these were set for initial condition (d) of Albertini et al.,¹¹] while in our IMPT-3D planning, optimizations used constant initial beamlet weights [initial condition (a) of Albertini et al.¹¹]. The influence of the initial starting conditions on the IMPT-3D plans’ robustness was beyond the scope of this analysis but should be explored in a future study.

It would also be interesting to know to what degree the number of energies is a determining factor that makes it hard to improve the robustness of DET plans. For the prostate cancer case presented here, we have tried to use the highest one, two, three, and five energy layers (data not shown) and have found that when three or fewer of the highest energy layers are used, the robustness of the IMPT-DET plan in the face of uncertainties cannot be much improved. However, if the highest five energy layers are used, we can markedly improve the robustness of the IMPT-DET plan. This result can be explained by the first mechanism discussed in this paper (i.e., the absence of an LSFUD mechanism in IMPT-DET for the prostate cancer case) if a small number of energy layers are used. However, if the highest five energy layers are used in IMPT-DET, the number of distinct proton energy layers used increases from 21 (with the highest two energy layers used) to 36, or the same as in IMPT-3D. Therefore, no energy efficiency benefits from IMPT-DET over IMPT-3D can be attained if the highest five energy layers are used in IMPT-DET.

IMPT-DET is highly sensitive to uncertainties; thus, radiation oncologists have been slow to adopt DET in IMPT treatment planning. We believe that our results might partly eliminate their concerns about applying this highly promising treatment modality to treat cancers.

ACKNOWLEDGMENTS

The authors thank Dr. Kazumichi Suzuki for his insightful discussion. This research is supported by National Cancer Institute (NCI) Grant No. P01CA021239, by the University Cancer Foundation via the Institutional Research Grant program at The University of Texas MD Anderson Cancer Center, and by the MD Anderson Cancer Center support Grant No. CA016672 from the NCI.

References

Zhang X. D., Li Y. P., Pan X. N., Li X. Q., Mohan R., Komaki R., Cox J. D., and Chang J. Y., “Intensity-modulated proton therapy reduces the dose to normal tissue compared with intensity-modulated radiation therapy or passive scattering proton therapy and enables individualized radical radiotherapy for extensive stage IIIB non-small-cell lung cancer: A virtual clinical study,” Int. J. Radiat. Oncol., Biol., Phys. 77, 357–366 (2010). 10.1016/j.ijrobp.2009.04.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
Lomax A., “Intensity modulation methods for proton radiotherapy,” Phys. Med. Biol. 44, 185–205 (1999). 10.1088/0031-9155/44/1/014 [DOI] [PubMed] [Google Scholar]
Li Y. P., Zhang X. D., and Mohan R., “An efficient dose calculation strategy for intensity modulated proton therapy,” Phys. Med. Biol. 56, N71–N84 (2011). 10.1088/0031-9155/56/4/N03 [DOI] [PubMed] [Google Scholar]
Brahme A., Källman P., and Lind B. K., “Optimization of proton and heavy ion therapy using an adaptive inversion algorithm,” Radiother. Oncol. 15, 189–197 (1989). 10.1016/0167-8140(89)90132-1 [DOI] [PubMed] [Google Scholar]
Caporaso G. J., Mackie T. R., Sampayan S., Chen Y. J., Blackfield D., Harris J., Hawkins S., Holmes C., Nelson S., Paul A., Poole B., Rhodes M., Sanders D., Sullivan J., Wang L., Watson J., Reckwerdt P. J., Schmidt R., Pearson D., Flynn R. W., Matthews D., and Purdy J., “A compact linac for intensity modulated proton therapy based on a dielectric wall accelerator,” Phys. Med. 24, 98–101 (2008). 10.1016/j.ejmp.2008.01.010 [DOI] [PubMed] [Google Scholar]
Deasy J. O., Shepard D. M., and Mackie T. R., Proceedings of the 12th International Conference on the Use of Computers in Radiation Therapy, Madison, WI (unpublished).
Nill S., Bortfeld T., and Oelfke U., “Inverse planning of intensity modulated proton therapy,” Z Med. Phys. 14, 35–40 (2004). [DOI] [PubMed] [Google Scholar]
Oelfke U. and Bortfeld T., “Inverse planning for photon and proton beams,” Med. Dosim. 26, 113–124 (2001). 10.1016/S0958-3947(01)00057-7 [DOI] [PubMed] [Google Scholar]
Lomax A. J., “Intensity modulated proton therapy and its sensitivity to treatment uncertainties 1: The potential effects of calculational uncertainties,” Phys. Med. Biol. 53, 1027–1042 (2008). 10.1088/0031-9155/53/4/014 [DOI] [PubMed] [Google Scholar]
Lomax A. J., “Intensity modulated proton therapy and its sensitivity to treatment uncertainties 2: The potential effects of inter-fraction and inter-field motions,” Phys. Med. Biol. 53, 1043–1056 (2008). 10.1088/0031-9155/53/4/015 [DOI] [PubMed] [Google Scholar]
Albertini F., Hug E. B., and Lomax A. J., “The influence of the optimization starting conditions on the robustness of intensity-modulated proton therapy plans,” Phys. Med. Biol. 55, 2863–2878 (2010). 10.1088/0031-9155/55/10/005 [DOI] [PubMed] [Google Scholar]
Albertini F., Lomax A. J., Hug E. B., and Ctr Proton Radiat T., “In regard to Trofimov et al.: Radiotherapy treatment of early-stage prostate cancer with IMRT and protons: A treatment planning comparison (Int. J. Radiat. Oncol. Biol. Phys. 69, 444–453 (2007)),” Int. J. Radiat. Oncol., Biol., Phys. 69, 1333–1334 (2007). 10.1016/j.ijrobp.2007.06.077 [DOI] [PubMed] [Google Scholar]
Kang Y. X., Zhang X. D., Chang J. Y., Wang H., Wei X., Liao Z. X., Komaki R., Cox J. D., Balter P. A., Liu H., Zhu X. R., Mohan R., and Dong L., “4D proton treatment planning strategy for mobile lung tumors,” Int. J. Radiat. Oncol., Biol., Phys. 67, 906–914 (2007). 10.1016/j.ijrobp.2006.10.045 [DOI] [PubMed] [Google Scholar]
Lomax A. J., Boehringer T., Coray A., Egger E., Goitein G., Grossmann M., Juelke P., Lin S., Pedroni E., Rohrer B., Roser W., Rossi B., Siegenthaler B., Stadelmann O., Stauble H., Vetter C., and Wisser L., “Intensity modulated proton therapy: A clinical example,” Med. Phys. 28, 317–324 (2001). 10.1118/1.1350587 [DOI] [PubMed] [Google Scholar]
Pflugfelder D., Wilkens J. J., and Oelfke U., “Worst case optimization: A method to account for uncertainties in the optimization of intensity modulated proton therapy,” Phys. Med. Biol. 53, 1689–1700 (2008). 10.1088/0031-9155/53/6/013 [DOI] [PubMed] [Google Scholar]
Unkelbach J., Bortfeld T., Martin B. C., and Soukup M., “Reducing the sensitivity of IMPT treatment plans to setup errors and range uncertainties via probabilistic treatment planning,” Med. Phys. 36, 149–163 (2009). 10.1118/1.3021139 [DOI] [PMC free article] [PubMed] [Google Scholar]
Unkelbach J., Chan T. C. Y., and Bortfeld T., “Accounting for range uncertainties in the optimization of intensity modulated proton therapy,” Phys. Med. Biol. 52, 2755–2773 (2007). 10.1088/0031-9155/52/10/009 [DOI] [PubMed] [Google Scholar]
Unkelbach J., Soukup M., Alber M., and Bortfeld T., “Range, setup and dose calculation errors in IMPT and their interrelation,” World Congr. Med. Phys. Biomed. Eng. 25, 900–903 (2009). 10.1007/978-3-642-03474-9_253 [DOI] [Google Scholar]
Schwarz M., “Treatment planning in proton therapy,” Eur. Phys. J. Plus 126, 67–76 (2011). 10.1140/epjp/i2011-11067-y [DOI] [Google Scholar]
Fredriksson A., Forsgren A., and Hardemark B., “Minimax optimization for handling range and setup uncertainties in proton therapy,” Med. Phys. 38, 1672–1684 (2011). 10.1118/1.3556559 [DOI] [PubMed] [Google Scholar]
Lim G. J. and Cao W., “A two-phase method for selecting IMRT treatment beam angles: Branch-and-Prune and local neighborhood search,” Eur. J. Oper. Res. 217, 609–618 (2012). 10.1016/j.ejor.2011.09.038 [DOI] [Google Scholar]
Liu W., Zhang X., Li Y., and Mohan R., “Robust optimization in intensity-modulated proton therapy,” Med. Phys. 39, 1079–1091 (2012). 10.1118/1.3679340 [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen W., Unkelbach J., Trofimov A., Madden T., Kooy H., Bortfeld T., and Craft D., “Including robustness in multi-criteria optimization for intensity-modulated proton therapy,” Phys. Med. Biol. 57, 591–608 (2012). 10.1088/0031-9155/57/3/591 [DOI] [PMC free article] [PubMed] [Google Scholar]
Meyer J., Bluett J., Amos R., Levy L., Choi S., Nguyen Q. N., Zhu X. R., Gillin M., and Lee A., “Spot scanning proton beam therapy for prostate cancer: treatment planning technique and analysis of consequence of rotional and translational alignment errors,” Int. J. Radiat. Oncol., Biol., Phys. 78, 428–434 (2010). 10.1016/j.ijrobp.2009.07.1696 [DOI] [PubMed] [Google Scholar]
Lomax A. J., Pedroni E., Rutz H., and Goitein G., “The clinical potential of intensity modulated proton therapy,” Z Med. Phys. 14, 147–152 (2004). [DOI] [PubMed] [Google Scholar]
Bortfeld T., “An analytical approximation of the Bragg curve for therapeutic proton beams,” Med. Phys. 24, 2024–2033 (1997). 10.1118/1.598116 [DOI] [PubMed] [Google Scholar]
Zhang X., Liu W., Li Y., Li X., Quan M., Mohan R., Anand A., Sahoo N., Gillin M., and Zhu R. X., “Parameterization of multiple Bragg curves for scanning proton beams by simultaneously fitting multiple curves,” Phys. Med. Biol. 56, 7725–7735 (2011). 10.1088/0031-9155/56/24/003 [DOI] [PubMed] [Google Scholar]
Hong L., Goitein M., Bucciolini M., Comiskey R., Gottschalk B., Rosenthal S., Serago C., and Urie M., “A pencil beam algorithm for proton dose calculations,” Phys. Med. Biol. 41, 1305–1330 (1996). 10.1088/0031-9155/41/8/005 [DOI] [PubMed] [Google Scholar]
Soukup M., Fippel M., and Alber M., “A pencil beam algorithm for intensity modulated proton therapy derived from Monte Carlo simulations,” Phys. Med. Biol. 50, 5089–5104 (2005). 10.1088/0031-9155/50/21/010 [DOI] [PubMed] [Google Scholar]
Trofimov A., Kang J., Unkelbach J., Adams J. A., Zhang X., Bortfeld T., Liebsch N. J., and DeLaney T. F., “Evaluation of dosimetric gain and uncertainties in proton therapy delivery with scanned pencil beam in treatment of base-of-skull and spinal tumors,” Int. J. Radiat. Oncol., Biol., Phys. 78, S133–S134 (2010). 10.1016/j.ijrobp.2010.07.334 [DOI] [Google Scholar]
Li Y., Liu W., Li X., Quan E., and Zhang X., “Toward a thorough evaluation of IMPT plan sensitivity to uncertainties: Revisit the worst-case analysis with an exhaustively sampling approach,” Med. Phys. 38, 3853 (2011). 10.1118/1.3613506 [DOI] [Google Scholar]
Wu Q. W. and Mohan R., “Algorithms and functionality of an intensity modulated radiotherapy optimization system,” Med. Phys. 27, 701–711 (2000). 10.1118/1.598932 [DOI] [PubMed] [Google Scholar]
Lin A., Moran J. M., Marsh R. B., Balter J. M., Fraass B. A., McShan D. L., Kessler M. L., and Pierce L. J., “Evaluation of multiple breathing states using a multiple instance geometry approximation (MIGA) in inverse-planned optimization for locoregional breast treatment,” Int. J. Radiat. Oncol., Biol., Phys. 72, 610–616 (2008). 10.1016/j.ijrobp.2008.06.1488 [DOI] [PMC free article] [PubMed] [Google Scholar]
Albertini F., Hug E. B., and L. A. J., “Is it necessary to plan with safety margins for actively scanned proton therapy?,” Phys. Med. Biol. 56, 4399–4413 (2011). 10.1088/0031-9155/56/14/011 [DOI] [PubMed] [Google Scholar]

[c1] Zhang X. D., Li Y. P., Pan X. N., Li X. Q., Mohan R., Komaki R., Cox J. D., and Chang J. Y., “Intensity-modulated proton therapy reduces the dose to normal tissue compared with intensity-modulated radiation therapy or passive scattering proton therapy and enables individualized radical radiotherapy for extensive stage IIIB non-small-cell lung cancer: A virtual clinical study,” Int. J. Radiat. Oncol., Biol., Phys. 77, 357–366 (2010). 10.1016/j.ijrobp.2009.04.028 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c2] Lomax A., “Intensity modulation methods for proton radiotherapy,” Phys. Med. Biol. 44, 185–205 (1999). 10.1088/0031-9155/44/1/014 [DOI] [PubMed] [Google Scholar]

[c3] Li Y. P., Zhang X. D., and Mohan R., “An efficient dose calculation strategy for intensity modulated proton therapy,” Phys. Med. Biol. 56, N71–N84 (2011). 10.1088/0031-9155/56/4/N03 [DOI] [PubMed] [Google Scholar]

[c4] Brahme A., Källman P., and Lind B. K., “Optimization of proton and heavy ion therapy using an adaptive inversion algorithm,” Radiother. Oncol. 15, 189–197 (1989). 10.1016/0167-8140(89)90132-1 [DOI] [PubMed] [Google Scholar]

[c5] Caporaso G. J., Mackie T. R., Sampayan S., Chen Y. J., Blackfield D., Harris J., Hawkins S., Holmes C., Nelson S., Paul A., Poole B., Rhodes M., Sanders D., Sullivan J., Wang L., Watson J., Reckwerdt P. J., Schmidt R., Pearson D., Flynn R. W., Matthews D., and Purdy J., “A compact linac for intensity modulated proton therapy based on a dielectric wall accelerator,” Phys. Med. 24, 98–101 (2008). 10.1016/j.ejmp.2008.01.010 [DOI] [PubMed] [Google Scholar]

[c6] Deasy J. O., Shepard D. M., and Mackie T. R., Proceedings of the 12th International Conference on the Use of Computers in Radiation Therapy, Madison, WI (unpublished).

[c7] Nill S., Bortfeld T., and Oelfke U., “Inverse planning of intensity modulated proton therapy,” Z Med. Phys. 14, 35–40 (2004). [DOI] [PubMed] [Google Scholar]

[c8] Oelfke U. and Bortfeld T., “Inverse planning for photon and proton beams,” Med. Dosim. 26, 113–124 (2001). 10.1016/S0958-3947(01)00057-7 [DOI] [PubMed] [Google Scholar]

[c9] Lomax A. J., “Intensity modulated proton therapy and its sensitivity to treatment uncertainties 1: The potential effects of calculational uncertainties,” Phys. Med. Biol. 53, 1027–1042 (2008). 10.1088/0031-9155/53/4/014 [DOI] [PubMed] [Google Scholar]

[c10] Lomax A. J., “Intensity modulated proton therapy and its sensitivity to treatment uncertainties 2: The potential effects of inter-fraction and inter-field motions,” Phys. Med. Biol. 53, 1043–1056 (2008). 10.1088/0031-9155/53/4/015 [DOI] [PubMed] [Google Scholar]

[c11] Albertini F., Hug E. B., and Lomax A. J., “The influence of the optimization starting conditions on the robustness of intensity-modulated proton therapy plans,” Phys. Med. Biol. 55, 2863–2878 (2010). 10.1088/0031-9155/55/10/005 [DOI] [PubMed] [Google Scholar]

[c12] Albertini F., Lomax A. J., Hug E. B., and Ctr Proton Radiat T., “In regard to Trofimov et al.: Radiotherapy treatment of early-stage prostate cancer with IMRT and protons: A treatment planning comparison (Int. J. Radiat. Oncol. Biol. Phys. 69, 444–453 (2007)),” Int. J. Radiat. Oncol., Biol., Phys. 69, 1333–1334 (2007). 10.1016/j.ijrobp.2007.06.077 [DOI] [PubMed] [Google Scholar]

[c13] Kang Y. X., Zhang X. D., Chang J. Y., Wang H., Wei X., Liao Z. X., Komaki R., Cox J. D., Balter P. A., Liu H., Zhu X. R., Mohan R., and Dong L., “4D proton treatment planning strategy for mobile lung tumors,” Int. J. Radiat. Oncol., Biol., Phys. 67, 906–914 (2007). 10.1016/j.ijrobp.2006.10.045 [DOI] [PubMed] [Google Scholar]

[c14] Lomax A. J., Boehringer T., Coray A., Egger E., Goitein G., Grossmann M., Juelke P., Lin S., Pedroni E., Rohrer B., Roser W., Rossi B., Siegenthaler B., Stadelmann O., Stauble H., Vetter C., and Wisser L., “Intensity modulated proton therapy: A clinical example,” Med. Phys. 28, 317–324 (2001). 10.1118/1.1350587 [DOI] [PubMed] [Google Scholar]

[c15] Pflugfelder D., Wilkens J. J., and Oelfke U., “Worst case optimization: A method to account for uncertainties in the optimization of intensity modulated proton therapy,” Phys. Med. Biol. 53, 1689–1700 (2008). 10.1088/0031-9155/53/6/013 [DOI] [PubMed] [Google Scholar]

[c16] Unkelbach J., Bortfeld T., Martin B. C., and Soukup M., “Reducing the sensitivity of IMPT treatment plans to setup errors and range uncertainties via probabilistic treatment planning,” Med. Phys. 36, 149–163 (2009). 10.1118/1.3021139 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c17] Unkelbach J., Chan T. C. Y., and Bortfeld T., “Accounting for range uncertainties in the optimization of intensity modulated proton therapy,” Phys. Med. Biol. 52, 2755–2773 (2007). 10.1088/0031-9155/52/10/009 [DOI] [PubMed] [Google Scholar]

[c18] Unkelbach J., Soukup M., Alber M., and Bortfeld T., “Range, setup and dose calculation errors in IMPT and their interrelation,” World Congr. Med. Phys. Biomed. Eng. 25, 900–903 (2009). 10.1007/978-3-642-03474-9_253 [DOI] [Google Scholar]

[c19] Schwarz M., “Treatment planning in proton therapy,” Eur. Phys. J. Plus 126, 67–76 (2011). 10.1140/epjp/i2011-11067-y [DOI] [Google Scholar]

[c20] Fredriksson A., Forsgren A., and Hardemark B., “Minimax optimization for handling range and setup uncertainties in proton therapy,” Med. Phys. 38, 1672–1684 (2011). 10.1118/1.3556559 [DOI] [PubMed] [Google Scholar]

[c21] Lim G. J. and Cao W., “A two-phase method for selecting IMRT treatment beam angles: Branch-and-Prune and local neighborhood search,” Eur. J. Oper. Res. 217, 609–618 (2012). 10.1016/j.ejor.2011.09.038 [DOI] [Google Scholar]

[c22] Liu W., Zhang X., Li Y., and Mohan R., “Robust optimization in intensity-modulated proton therapy,” Med. Phys. 39, 1079–1091 (2012). 10.1118/1.3679340 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c23] Chen W., Unkelbach J., Trofimov A., Madden T., Kooy H., Bortfeld T., and Craft D., “Including robustness in multi-criteria optimization for intensity-modulated proton therapy,” Phys. Med. Biol. 57, 591–608 (2012). 10.1088/0031-9155/57/3/591 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c24] Meyer J., Bluett J., Amos R., Levy L., Choi S., Nguyen Q. N., Zhu X. R., Gillin M., and Lee A., “Spot scanning proton beam therapy for prostate cancer: treatment planning technique and analysis of consequence of rotional and translational alignment errors,” Int. J. Radiat. Oncol., Biol., Phys. 78, 428–434 (2010). 10.1016/j.ijrobp.2009.07.1696 [DOI] [PubMed] [Google Scholar]

[c25] Lomax A. J., Pedroni E., Rutz H., and Goitein G., “The clinical potential of intensity modulated proton therapy,” Z Med. Phys. 14, 147–152 (2004). [DOI] [PubMed] [Google Scholar]

[c26] Bortfeld T., “An analytical approximation of the Bragg curve for therapeutic proton beams,” Med. Phys. 24, 2024–2033 (1997). 10.1118/1.598116 [DOI] [PubMed] [Google Scholar]

[c27] Zhang X., Liu W., Li Y., Li X., Quan M., Mohan R., Anand A., Sahoo N., Gillin M., and Zhu R. X., “Parameterization of multiple Bragg curves for scanning proton beams by simultaneously fitting multiple curves,” Phys. Med. Biol. 56, 7725–7735 (2011). 10.1088/0031-9155/56/24/003 [DOI] [PubMed] [Google Scholar]

[c28] Hong L., Goitein M., Bucciolini M., Comiskey R., Gottschalk B., Rosenthal S., Serago C., and Urie M., “A pencil beam algorithm for proton dose calculations,” Phys. Med. Biol. 41, 1305–1330 (1996). 10.1088/0031-9155/41/8/005 [DOI] [PubMed] [Google Scholar]

[c29] Soukup M., Fippel M., and Alber M., “A pencil beam algorithm for intensity modulated proton therapy derived from Monte Carlo simulations,” Phys. Med. Biol. 50, 5089–5104 (2005). 10.1088/0031-9155/50/21/010 [DOI] [PubMed] [Google Scholar]

[c30] Trofimov A., Kang J., Unkelbach J., Adams J. A., Zhang X., Bortfeld T., Liebsch N. J., and DeLaney T. F., “Evaluation of dosimetric gain and uncertainties in proton therapy delivery with scanned pencil beam in treatment of base-of-skull and spinal tumors,” Int. J. Radiat. Oncol., Biol., Phys. 78, S133–S134 (2010). 10.1016/j.ijrobp.2010.07.334 [DOI] [Google Scholar]

[c31] Li Y., Liu W., Li X., Quan E., and Zhang X., “Toward a thorough evaluation of IMPT plan sensitivity to uncertainties: Revisit the worst-case analysis with an exhaustively sampling approach,” Med. Phys. 38, 3853 (2011). 10.1118/1.3613506 [DOI] [Google Scholar]

[c32] Wu Q. W. and Mohan R., “Algorithms and functionality of an intensity modulated radiotherapy optimization system,” Med. Phys. 27, 701–711 (2000). 10.1118/1.598932 [DOI] [PubMed] [Google Scholar]

[c33] Lin A., Moran J. M., Marsh R. B., Balter J. M., Fraass B. A., McShan D. L., Kessler M. L., and Pierce L. J., “Evaluation of multiple breathing states using a multiple instance geometry approximation (MIGA) in inverse-planned optimization for locoregional breast treatment,” Int. J. Radiat. Oncol., Biol., Phys. 72, 610–616 (2008). 10.1016/j.ijrobp.2008.06.1488 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c34] Albertini F., Hug E. B., and L. A. J., “Is it necessary to plan with safety margins for actively scanned proton therapy?,” Phys. Med. Biol. 56, 4399–4413 (2011). 10.1088/0031-9155/56/14/011 [DOI] [PubMed] [Google Scholar]

PERMALINK

Influence of robust optimization in intensity-modulated proton therapy with different dose delivery techniques

Wei Liu

Yupeng Li

Xiaoqiang Li

Wenhua Cao

Xiaodong Zhang

Abstract

INTRODUCTION

METHODS

Patient data and beam configurations

Beam angle optimization algorithm

Robust optimization algorithm

Dose calculation engine

Plan evaluation metrics

Robustness quantification

RESULTS

Prostate cancer case

Conventional optimization

Figure 1.

TABLE I.

Worst-case robust optimization

Figure 2.

TABLE II.

BOS cancer case

Figure 3.

TABLE III.

Figure 4.

TABLE IV.

Figure 5.

Figure 6.

DISCUSSION

Figure 7.

Figure 8.

Figure 9.

ACKNOWLEDGMENTS

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases