A wireless handheld probe with spectrally constrained evolution strategies for diffuse optical imaging of tissue

Abstract

We present a low-cost, portable, wireless diffuse optical imaging device. The handheld device is fast, portable, and can be applied to a wide range of both static and dynamic imaging applications including breast cancer, functional brain imaging, and peripheral artery disease. The continuous-wave probe has four near-infrared wavelengths and uses digital detection techniques to perform measurements at 2.3 Hz. Using a multispectral evolution algorithm for chromophore reconstruction, we can measure absolute oxygenated and deoxygenated hemoglobin concentration as well as scattering in tissue. Performance of the device is demonstrated using a series of liquid phantoms comprised of Intralipid^®, ink, and dye.

INTRODUCTION

Diffuse optical imaging (DOI) uses near-infrared light to probe tissue in vivo and extract information about the absorption and scattering. Tissue absorption in the near-infrared range is primarily affected by the concentration of oxy- and deoxy-hemoglobin, lipid, and water. These properties make optical measurements well suited to a variety of clinical applications including breast cancer, functional brain imaging, and peripheral artery disease.^{1, 2, 3} DOI requires instrumentation to illuminate and detect the light passing through the tissue, which typically involves large, expensive cameras, or bulky fiber-based systems. Here, we present a handheld device that miniaturizes the detection hardware so that all processing is performed at the detector and transmitted wirelessly to the host computer. This design eliminates the need for optical fibers or a camera-based design and allows for a handheld device whose small form factor and ease of use make it suitable for a number of clinical applications.

In the field of breast cancer imaging a number of handheld probes have been developed for detecting breast tumors and monitoring tumor response to therapy.^{4, 5, 6, 7} These handheld probes image in reflectance mode with a 0.5–3.5 cm source-detector separation in order to probe beneath the tissue surface. They use a range of near-infrared wavelengths to determine the concentration of chromophores relevant to detecting tumors including oxy- and deoxy-hemoglobin, lipid, water, and scattering. Many of these probes operate in the frequency domain (FD), where the source light is modulated in intensity at frequencies between 100 and 1000 MHz. These systems can extract both the change in phase and amplitude from the detected light. Current handheld FD imaging systems require bundles of optical fibers to bring the detected light back to large systems that house the detection hardware.

Continuous-wave (CW) systems use illumination with constant (or radio-frequency modulated) light intensities and, as a result, only extract the change in amplitude of the light through the tissue. Therefore, less information is collected as compared to FD systems. However, CW systems are much less expensive, allow for faster data acquisition, and the detection electronics can be miniaturized. Recently, Xu et al.^{5, 8} demonstrated a handheld CW system for pressure-induced dynamic breast imaging. Their approach integrates the detection electronics into the handheld portion of the device and relays the measured data to a laptop computer via a serial port. No wireless handheld breast imaging devices have been published to date.

In other areas, wireless optical imaging devices have recently been developed for wearable technologies^{9, 10} and endoscopy.^{11, 12} A wearable patchlike device designed by Muehlemann et al.⁹ uses four CW sources and four detectors with two wavelengths. A flexible printed circuit board holds the illumination, detection, and wireless transmission electronics. Similarly, a larger, but still portable wearable brain-imaging system developed by Atsumori et al.¹⁰ uses eight CW sources and eight detectors with two wavelengths for imaging the frontal cortex. Along with a portable pack that attaches to the subject's waist, the wireless system allows for the subject to move around during imaging. Both of these systems focus on differential imaging and use the modified Beer-Lambert law to look at relative changes in the concentration of oxy- and deoxy-hemoglobin. In endoscopy, capsulelike wireless devices have been designed for spectral, fluorescent, and bright field imaging of the gastrointestinal tract.^{11, 12} These devices use small complementary metal-oxide semiconductor or charged couple device sensors to perform qualitative imaging for identifying suspicious regions at the surface of the tissue.

Despite this progress, there are currently no wireless optical imaging devices that perform diffuse optical tissue measurements with absolute reconstruction of the concentrations of tissue chromophores, including the contribution of tissue scattering. Here, we present the first prototype of such a device. The device is handheld, wireless, and can resolve actual optical properties of scattering, oxy- and deoxy-hemoglobin using four source wavelengths and two detectors at 2.3 Hz. The device uses radio-frequency modulated illumination to eliminate background light and reduce noise artifacts. Using digital detection techniques developed in our laboratory,^{13, 14} we are able to perform the majority of the signal detection and demodulation in the digital domain, which allows for the wireless transmission of the final signal amplitude. The device is inexpensive, portable, runs off of a 9 V D-type battery, and can seamlessly interface via Bluetooth^® to a host computer. A multispectral evolution algorithm uses the measured valued to calculate absolute values for tissue-scattering, and concentrations of oxy- and deoxy-hemoglobin in tissue.

INSTRUMENT DESIGN

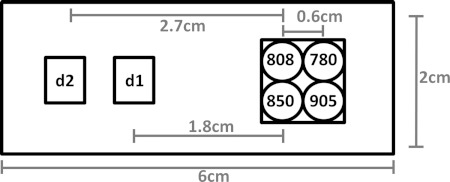
The instrument uses four near-infrared wavelengths of light to illuminate tissue. The light passes through the sample and is absorbed and scattered as it travels to two detectors configured in reflectance geometry and located 1.8–2.4 cm and 2.7–3.3 cm away from the sources as shown in Fig. 1.

Figure 1.

Source and detector layout.

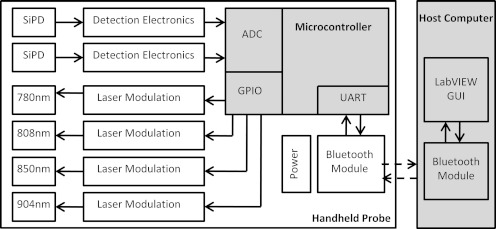
The light is detected by a silicon photodiode and both quantized and demodulated by a microcontroller that then passes the result back to the host computer via Bluetooth^®. The instrument is powered by a 9 V D-type battery. A block diagram of the system is shown in Fig. 2.

Figure 2.

System block diagram for the handheld wireless probe.

The current version of the device is a prototype that is enclosed by a plastic case measuring 11.5 cm × 16 cm × 2.5 cm. This makes the device easy to hold and bring in contact with a variety of tissue surfaces. A photograph of the probe is shown in Fig. 3a. Figure 3b shows the instrument with the enclosure opened to expose the inner electronics.

Figure 3.

Photograph of (a) the device and (b) with the enclosure opened to expose the electronics.

Light illumination

The input light is generated by 10 mW 5.6 mm-diameter laser diodes at wavelengths of 780 nm, 808 nm, 850 nm, and 904 nm (L780P010, L808P010, L850P010, L904P010, Thorlabs). The wavelengths are selected to provide a range of spectral information to reconstruct oxygenated hemoglobin ([HbO₂]), deoxygenated hemoglobin ([Hb]) and scattering while working within the limited selection of wavelengths available in this small package. The laser diodes are driven by the 15 V Laser Diode Driver (iC-WKN, iC Haus). Each wavelength has the ability to modulate the amplitude at a frequency ranging from 1 to 8 KHz, controllable by 20 kΩ potentiometers. The modulation signal is generated using a combination of a 1 kHz–33 MHz Oscillator (LTC1799, Linear Technology), a binary counter (M74HC4820, STMicroelectronics) and a low-pass filter (LTC1067, Linear Technology). The power of the laser diode can be controlled using a 20 kΩ potentiometer that regulates the current to the laser driver.

The modulation of the input light provides several advantages including superior noise rejection (including ambient light) as well as the ability to illuminate the tissue simultaneously with multiple wavelengths. Due to the fact that the speed of this particular system is limited by the processing power of the microcontroller (discussed further in Sec. 2D), the probe is configured to sequentially illuminate the target which each wavelength. However, future iterations of this design involving a more powerful microcontroller could simultaneously illuminate the sample with all wavelengths, modulated at different frequencies, thereby improving the frame rate by a factor of 4.

Light detection

Light is detected using a silicon photodiode (SiPD) (Hamamatsu S1337-33BR) and a transimpedance amplifier (TIA). The amplifier has 4 possible gain settings including 10 kV/A, 100 kV/A, 1 MV/A, and 10 MV/A. For laser power between 1 and 5 mW, the closer detector (d1) uses the 1 MV/A setting for most applications, while the further detector (d2) uses the 10 MV/A setting. The 1 MV/A and 10 MV/A gain settings utilize a bandwidth-extension technique previously described in Ref. 15. Following the TIA, the signal is high-pass filtered to remove any dc component of the light. The signal is also passive low-pass filtered to prevent aliasing at the analog-to-digital converter (ADC). In the final stage the signal is offset to 1.5 V to fully optimize the dynamic range of the input to the ADC.

The microcontroller used in this design (ADUC7020, Analog Devices) has built-in 12-bit ADC conversion circuitry. The ADC logic is configured to sample at 75 kHz and to acquire 150 samples for each measurement. Upon acquisition, the microcontroller performs digital lock-in detection to extract the amplitude from the detected sinusoidal signal. This algorithm, previously outlined by Masciotti et al., uses averaging filters combined with modulation and sampling constraints to digitally extract the amplitude while reducing noise.¹⁶ The demodulated amplitude is transmitted to the Bluetooth^® module via a universal asynchronous receiver/transmitter interface.

The Bluetooth^® module (RN-41, Roving Networks) was selected for this instrument due to its small form factor (13.4 mm × 25.8 mm × 2.0 mm) and low power consumption (<100 mA @ 3 V). The RN-41 Bluetooth^® module provides secure communication with 128-bit encryption, error correction for guaranteed packet transfer, and a Class 1 antenna that provides up to 100 m of wireless range. Any Bluetooth^®-capable computer can pair with the Bluetooth^® module (by providing the correct pairing code) and communicate via a virtual serial communication port to a LabVIEW user interface.

Power supply

All power to the device is supplied by a 9 V D-type battery. This could easily be replaced with any battery that can provide more than 120 mA @ 3 V. Care was taken in selecting components for the device that operate at 3 V, so that only one voltage rail is required for the device operation. A low-dropout voltage regulator takes any input voltage between 3 and 12 V and converts it to 3 V.

System performance

With no incident light on the detector the dark noise of the system is 160 μV. This is far below the typical values recorded for tissue of between 0.05 and 1 V. The largest possible input value is 3 V peak-to-peak, giving the device a dynamic range of 85 dB for the single 10 MV/A gain setting. From measurements made on a tissuelike optical phantom, the signal-to-noise ratio (SNR) of the wavelengths was between 36 dB and 51 dB. This range is due in part to the differences in absorption at the various wavelengths.

The system speed is currently limited by the time required to demodulate the acquired signal. It takes 2 ms to acquire 150 samples followed by 52 ms to demodulate the data and send it to the Bluetooth^® module. This 54 ms acquisition time must be repeated for each of the four wavelengths and each of the detectors, ultimately giving a sampling speed of 2.3 Hz. It takes the laser diodes ∼5 ms to settle following switching. This settling time is coordinated to take place during the time that the microcontroller is demodulating the data from the previous wavelength. A summary of the probe's parameters and performance is shown in Table 1.

Table 1.

Summary of the wireless handheld probe parameters and performance.

Parameter	Value
Wavelengths	4: 780 nm, 805 nm, 850 nm, 904 nm
Detectors	2
Mode	CW
Frame rate	2.3 Hz
Dynamic range	85 dB
Dark noise	160 μV
SNR	∼50 dB
Power consumption	120 mA @ 3 V
Size	11.5 cm × 16 cm × 2.5 cm

RECONSTRUCTION ALGORITHM

Background

We present here a brief description of diffuse reflectance spectroscopy that derives optical properties of scattering, [Hb], and [HbO₂] in tissue. The diffuse spectroscopic technique is based on the reflectance measured at multiple locations on the surface of the medium, where the diffuse reflectance depends solely on the absorption coefficient μ_a and the reduced scattering coefficient ${\mu }_s^{\prime }$ and the source-detector separation d. Under the assumption of a semi-infinite homogeneous medium, the closed-form analytic solution for the spatially resolved reflectance is given by Farrell et al.¹⁷ as

$$\begin{array}{ccc}\hfill R{\left(d\right)}_{\mathrm{dc}}& =& \frac{1}{4\pi {\mu }_t^{\prime }}[\left({\mu }_{eff}+\frac{1}{r_1^2}\right)\frac{\exp (-{\mu }_{eff}{r}_1)}{r_1^2}\hfill \\ \hfill & & +\left(\frac{4}{3}A+1\right)\left({\mu }_{eff}+\frac{1}{r_2}\right)\frac{\exp (-{\mu }_{eff}{r}_2)}{r_2^2}],\hfill \end{array}$$ (1)

where

$$r_1=\sqrt{{\left(\frac{1}{{\mu }_t^{\prime }}\right)}^2+d^2},r_2=\sqrt{{\left(\frac{{\displaystyle \frac{3}{4}}A+1}{{\mu }_t^{\prime }}\right)}^2+d^2}.$$ (2)

Here μ_eff is the effective attenuation coefficient (${\mu }_{eff}=\sqrt{3{\mu }_a{\mu }_s^{\prime }}$), ${\mu }_t^{\prime }$ is the total transport coefficient $({\mu }_t^{\prime }={\mu }_a+{\mu }_s^{\prime })$ and A is the internal reflection parameter¹⁸ that takes into account the refractive index mismatch at air-tissue interface.

The common approach to find μ_a and ${\mu }_s^{\prime }$ is to fit the analytic solution (Eq. 1) to the measured values of R(d), which makes use of the linear correlation between R(d) and d. In other words, a plot of log(d²R(d)) versus d can be used to estimate μ_eff. To separate μ_a and ${\mu }_s^{\prime }$, Patterson et al.¹⁹ used the absolute overall diffuse reflectance over the entire surface, whereas Farrell et al.²⁰ exploited the reflectance at small d to obtain ${\mu }_s^{\prime }$, Liu et al.²¹ used the intercept of d²R(d) versus d to estimate ${\mu }_s^{\prime }$, and Matcher et al.²² simply use time-resolved techniques to assume ${\mu }_s^{\prime }$. Once μ_a and ${\mu }_s^{\prime }$ are obtained at multiple wavelengths, the results are combined to obtain [HbO₂] and [Hb]. Clinical applications of this technique can be found in the literature.^{23, 24, 25, 26, 27}

Although the slope-based approach is widely used, it is highly sensitive to noise. Small errors in the measurement can lead to a large error in the slope obtained through a least squares fitting procedure. To reduce this error, one can increase the amount of data by increasing the number of detectors, which in turn leads to an increase in the size of a probe, a solution that is not preferred in the design of handheld probes. To overcome these difficulties with the slope-based approach, we employ here a multispectral direct method that uses data from all wavelengths simultaneously for the estimation of optical properties.

Multispectral direct approach

The multispectral direct method exploits the following relations that describe the tissue absorption, chromophore concentration, and scattering as

$${\mu }_a\left(\lambda \right)=\sum _{i=1}^{N_c}{\varepsilon }_i\left(\lambda \right)C_i\mathrm{and}{\mu }_s^{\prime }=A{\lambda }^{-b},$$ (3)

where ɛ_i(λ) and C_i are the absorption extinction coefficient and the concentration for the ith chromophore in tissue. N_c is the number of tissue chromophores that contribute to the absorption at wavelength λ. The scattering parameters A and b are the scattering amplitude and the scattering power, respectively. The multispectral direct method reconstructs C_i, A, and b directly instead of retrieving μ_a and ${\mu }_s^{\prime }$ independently for each wavelength and decomposing the results as is done in the standard two-step method. The greatest value of the direct approach lies in the fact that it enables using all wavelengths data simultaneously to recover the parameters C_i, A, and b which are wavelength independent, thereby making improvements to the non-uniqueness problem of diffuse optical imaging.^{28, 29, 30, 31}

In this work, we make use of these benefits of the direct approach for spatially resolved spectroscopy (SRS) where bulk optical properties are to be obtained for a semi-infinite medium. The SRS problem with the direct approach can be formulated as the following inverse problem where the optimal solution can be found by minimizing the misfit between predictions R_d and measurements z_d of the reflectance on the tissue surface

$$F\left(x\right)=\sum _{\lambda ,d}{\left(R_d^{\lambda }-z_d^{\lambda }\right)}^2,$$ (4)

where x is the vector of all unknowns, e.g., x = (C_j, A, b). Traditional nonlinear least-squares methods may be available to solve Eq. 4, but as reported by Farrell et al.²⁰ traditional gradient-based search methods are sensitive to random noise and can fail to find the global least-squared minimum. To circumvent this problem, we present here a global-search multispectral SRS algorithm that is based on evolution strategies^{32, 33, 34} that do not require a calculation of the noise-sensitive gradient, and has been shown to reliably find the global minimum of the problem (Eq. 4).^{33, 35, 36}

Evolution strategies

Evolution strategies are algorithms that imitate the principles of evolution and heredity in nature for inverse problems in engineering applications. The general structure of the ES algorithm used here can be described as follows.

Consider a population of individuals P_k = (x₁, …, x_n)_k at iteration k, where each individual x_j represents a potential solution to the inverse problem under investigation. Each individual x_j is evaluated using the objective function (Eq. 4). Next individuals are randomly recombined and mutated to give more than n individuals and then each individual is evaluated again with the objective function, and the n fittest individuals are selected to generate the new population P_k+1 = (x₁, …, x_n)_k+1. This process is repeated until the fittest individual is selected. Table 2 shows the pseudo-code of the ES algorithm.

Table 2.

Pseudo-code of the evolution strategy algorithm.

1. Set k = 0

2. Initialize Pk = (x1, …, xn) with $x_j={(C_{{\mathrm{HbO}}_2},C_{\mathrm{Hb}},A,b)}_j$

3. Evaluate Pk

4. Repeat while (not converged)

a. Recombine ${\tilde{P}}_k=\left({\tilde{x}}_1,...,{\tilde{x}}_m\right)$ (m > n)

b. Mutate $P_k={\tilde{P}}_k+Z_k$

c. Evaluate Pk

d. Select n best individuals

e. k = k + 1

5. End

In Step 4.a of Table 2, a temporary population vector ${\tilde{P}}_k=\left({\tilde{x}}_1,...,{\tilde{x}}_m\right)$ is first built through the recombination process. The recombination can be performed according to the following formula:³³

$${\tilde{x}}_j^i=\frac{1}{2}\left(x_{a,j}^i+x_{b,j}^i\right),$$ (5)

where ${\tilde{x}}_j^i$ denotes the ith component of the jth temporary individual vector and $x_a^i$ and $x_b^i$ are the ith components of two individuals randomly chosen from the population vector. Using this temporary population vector ${\tilde{P}}_k$, the next m individuals (m > n) are created by the following mutation process (Step 4.b):³⁴

$$\begin{array}{ccc}\hfill x_j^{mut}& =& {\tilde{x}}_j+{\sigma }_j^{\prime }·N_j\left(0,1\right),\mathrm{where}\hfill \\ \\ \hfill {\sigma }_j^{\prime }& =& {\sigma }_j\exp \left({\tau }^{\prime }{N}_j\left(0,1\right)+\tau N_j\left(0,1\right)\right),\hfill \end{array}$$ (6)

where σ_j is a mutation step size for the update of the jth individual and here is set to be 0.0001 multiplied by some typical value of each unknown parameter, and N(0, 1) denotes the normally distributed random variable sampled only once during the kth iteration and N_j(0, 1) denotes the normally distributed random variable sampled anew for each jth individual. Here, the proportionality factors τ and τ^′ are set as according to the literature τ ∝ 1/(2n)^1/2 and τ^′ ∝ 1/(2n^1/2)^1/2.³²

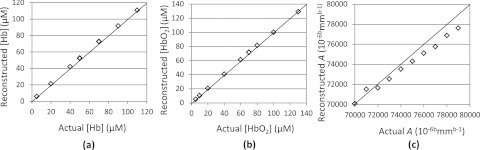
The ES algorithm as described here is evaluated through numerical experiments using the same setup described in Sec. 4. Note that for the scattering parameters, we focus on the reconstruction of A alone since there exists a well-known strong cross talk between A and b, and four wavelengths of data (available from our current wireless probe) is not sufficient to reliably reconstruct both A and the scattering power b.³⁰ To this end, synthetic data corrupted by noise level of 15 dB were generated using the analytic solution (Eq. 1) for semi-infinite approximation for a number of cases with different optical properties which vary from 20 μM to 100 μM for [HbO₂] and [Hb] and from 7000 to 8000 10^−6bmm^b-1 for A with a fixed b of 1.34, a typical value for Intralipid^® (and bulk breast tissue) scatterers.³⁰ Figure 4 shows reconstructed [HbO₂], [Hb], and A values versus their respective true values in the numerical phantom. The results show that for all cases considered here the ES algorithm can retrieve the actual values of absorption and scattering parameters within reasonable accuracy, although the scattering coefficients are slightly underestimated due to the lower sensitivity of CW data in comparison to FD data. While CW instrumentation is lower cost and provides faster measurements, it is sensitive to inter-parameter cross talk and has difficulty accurately separating absorption and scattering.³¹

Figure 4.

Reconstructed values of (a) [Hb], (b) [HbO₂], and (c) A versus the actual values expected for various cases tested with a numerical phantom.

EXPERIMENTAL RESULTS

Experimental studies on an optical phantom were performed to validate the handheld probe. Using a series of liquid phantoms we explored the relationship between the expected value of absorption, scattering, and chromophore concentration and our reconstructed values. To reconstruct the absolute values of absorption and scattering parameters in the medium, we normalized the target measurement data to a reference medium with known optical properties.²⁹ Measurements were made at the surface of an 8 cm × 8 cm × 8 cm box filled with 500 ml of 30 different solutions. Each solution consisted of an aqueous mixture made up of Intralipid^® (Baxter Intralipid^® 20% Fat Emulsion), black ink (Higgins India Ink), and near-infrared dye (Epolight^™ 2735, Epolin Inc.). We chose Intralipid^® for its well-documented optical properties and prior use in phantom studies to mimic tissue optical properties.^{37, 38} Likewise, black ink is commonly used in optical phantoms and is a water-soluble absorber that has a flat absorption spectrum in our wavelength range. Epolight^™ 2375 is a water-soluble near-infrared dye that has peak absorption at 970 nm, and therefore displays a different spectral response from India ink in the near-infrared range. The ranges for μ_a and ${\mu }_s^{\prime }$ were selected based on the typical optical properties of breast tissue.⁴

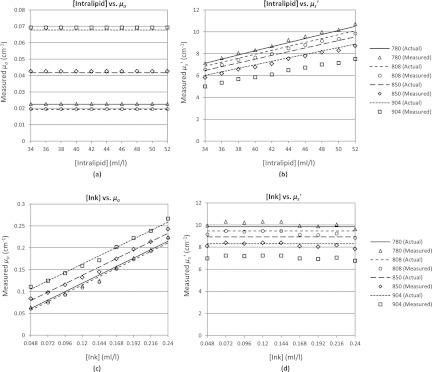
In the first experiment, we used a reference solution of 3.2% by volume (32 ml/l) of Intralipid^® 20% with no added ink or dye. This provides a medium where the absorption is predominantly due to water, which results in higher absorption at higher wavelengths (expected μ_a: 0.023, 0.019, 0.042, 0.068, cm⁻¹ @ 780, 808, 850, 904 nm).³⁹ The scattering in the medium is due to the Intralipid^® scatterers and decreases at higher wavelengths (expected ${\mu }_s^{\prime }$: 6.74, 6.48, 6.12, 5.70 cm⁻¹ @ 780, 808, 850, 904 nm).^{37, 38} We increased the reduced scattering coefficient by increasing the concentration of Intralipid^® from 3.4% (34 ml/l) to 5.2% (52 ml/l) in increments of 0.2% (2 ml/l) resulting in a ${\mu }_s^{\prime }$ ranging from ∼6 to 10 cm⁻¹. Note that an increase in the Intralipid^® concentration does not change the absorption of the solution. In Fig. 5a, we show both the theoretical (solid and dashed lines) and the experimentally derived values (markers) for μ_a for varying concentrations of Intralipid^®. As expected, μ_a shows no dependence on the Intralipid^® concentration and the calculated values for absorption closely match the expected values for water. Conversely, Fig. 5b shows that ${\mu }_s^{\prime }$ increases linearly with the increasing Intralipid^® concentration due to the increased concentration of scatterers. Our setup tends to underestimate the reduced scattering and has an average relative error of 6%, an effect also observed in the simulations shown in Fig. 4b.

Figure 5.

Reconstructed values of μ_a and ${\mu }_s^{\prime }$ for linearly increasing amounts of Intralipid^® [(a) and (b)] and Ink [(c) and (d)] added to the phantom.

For the second experiment, we used a reference solution of 4.8% (48 ml/l) Intralipid^® and 0.024 ml/l of our ink dilution. In this case, the absorption is due to both water and ink (expected μ_a: 0.042, 0.038, 0.060, 0.086 cm⁻¹ @ 780, 808, 850, 904 nm) while scattering is due to Intralipid^® (expected ${\mu }_s^{\prime }$: 9.84, 9.46, 8.93, 8.31 cm⁻¹ @ 780, 808, 850, 904 nm). We increased the absorption coefficient by increasing the ink concentration by 0.024 ml/l per step from 0.048 ml/l to 0.24 ml/l (resulting in an increase in μ_a of ∼0.0192 cm⁻¹ per step). Note that increasing the ink concentration does not affect the scattering properties of the medium. The results are shown in Figs. 5c, 5d, where the theoretical values of absorption and scattering are shown by the solid and dashed lines and the experimentally derived values are shown by the markers. In Fig. 5c, μ_a shows a linear relationship to the ink concentration with an average relative error of 3%. The increased ink concentration does not affect the scattering of the solution, as reflected by Fig. 5d, where ${\mu }_s^{\prime }$ is constant across the various concentrations of ink. Similar to the first experiment the scattering is underestimated by 7% on average, an effect that appears accentuated at the longer wavelengths.

In order to explore the probe's ability to accurately separate two chromophores (such as oxy- and deoxy-hemoglobin), we performed measurements on a series of liquid optical phantoms with varying amounts of ink (Black India Ink) and dye (Epolight^™ 2735, 0.05 g in 50 ml deionized water). In each experiment, we used a low and high absorbing solution to calibrate the probe. In the first experiment, we measured a solution of 4% Intralipid^® (40 ml/l), 0.5 ml/l of dye, and 1.5 ml/l to 3.5 ml/l of ink in steps of 0.5 ml/l (Phantom 1 through 5). The expected and measured values of the ink and dye volumes are shown in Fig. 6a. In the second experiment, we measured a solution of 4% Intralipid^® (40 ml/l), 1 ml/l of a 1% ink dilution, and 1 ml/l to 3 ml/l of dye in steps of 0.5 ml/l (Phantom 6 through 10). The expected and measured values of the ink and dye volumes are shown in Fig. 6b. Note that increasing the ink or dye concentration does not affect the scattering properties of the medium. The expected and measured values for the scattering parameter A are shown for the increasing ink (Fig. 6c) and increasing dye (Fig. 6d) experiments. The results shown in Fig. 6 demonstrate that the probe can distinguish between two different optically absorbing chromophores. The small error in deriving the precise ink and dye volumes is due to the fact that the wavelengths used in the probe are optimized for differentiating oxy- and deoxy-hemoglobin, not for differentiating the spectra of ink and dye.

Figure 6.

Reconstructed volumes of ink (grey) and dye (black) in Intralipid^® solution for (a) linearly increasing amounts of ink and (b) linearly increasing amounts of dye. Also shown is the reconstructed scattering A for each experiment [(c) and (d)]. Dashed lines represent the actual values, while the markers indicated measured values.

DISCUSSION AND SUMMARY

We have presented a new handheld wireless device for diffuse optical tissue spectroscopy. The prototype was created using low-cost components and presents an inexpensive, portable, and user-friendly device for clinical optical measurements. The size of the device is currently suited for handheld operation, but could be further scaled down in size by selecting smaller component footprints, a smaller battery, and using a denser board layout. Furthermore, while the device can image at 2.3 Hz, which is suitable for most dynamic imaging experiments, the speed could be increased by selecting a more powerful microcontroller and using simultaneous illumination by multiple wavelengths. Using four wavelengths and two detector positions we have demonstrated that we can accurately resolve absolute measurements of absorption and scattering using a multispectral evolutionary reconstruction algorithm.

This device and accompanying algorithm will facilitate future clinical studies exploring the optical signatures of tumor regions in the breast, but is not limited to breast imaging. Indeed, this device provides a fast and easy way to make static and dynamic measurements on many other tissues, including, for example, the brain or limbs without the need for specific interfaces for each application. The ease of use, portability, and low cost of this device will complement many existing clinical optical studies by providing real-time measurements and will create opportunities for new clinical applications.