Natural Language Processing with Dynamic Classification Improves P300 Speller Accuracy and Bit Rate

Abstract

The P300 speller is an example of a brain-computer interface that can restore functionality to victims of neuromuscular disorders. Although the most common application of this system has been communicating language, the properties and constraints of the linguistic domain have not to date been exploited when decoding brain signals that pertain to language. We hypothesized that combining the standard stepwise linear discriminant analysis with a Naive Bayes classifier and a trigram language model would increase the speed and accuracy of typing with the P300 speller. With integration of natural language processing, we observed significant improvements in accuracy and 40%–60% increases in bit rate for all six subjects in a pilot study. This study suggests that integrating information about the linguistic domain can significantly improve signal classification.

1. Introduction

High brain stem injuries and motor neuron diseases such as amyotrophic lateral sclerosis (ALS) can interrupt the transmission of signals from the central nervous system to effector muscles, impairing a patient’s ability to interact with the environment or to communicate and causing them to become “locked-in.” Brain-computer interfaces (BCI) restore some of this ability by detecting electrical signals from the brain and translating them into computer commands [1]. The computer can then perform actions dictated by the user, whether it be typing text [2], moving a cursor [3], or even controlling a robotic prosthesis [4] [5].

The P300 Speller is a common BCI system that uses electroencephalogram (EEG) signals to simulate keyboard input [2]. The system works by presenting a grid of characters on a graphical interface and instructing the user to focus on the desired letter. Groups of characters are then flashed randomly and flashes containing the attended character will elicit an evoked response (i.e., a P300 signal). The computer then classifies EEG responses based on features differentiating attended and non-attended flashes and selects the character that falls in the intersection of the groups with a positive response.

Since the signal to noise ratio is low, several trials must be combined in order to correctly classify responses. The resulting typing speed can therefore be slow, prompting many reports focusing on system optimization. Sellers et al. showed that although a 3 × 3 character grid has a higher online accuracy, a 6 × 6 grid provides a better bit rate [6]. McFarland et al. showed that the optimal interstimulus interval (ISI) varies between 62.5 and 250 ms depending on the subject[7]. Various signal processing methods have also been implemented such as support vector machines [8] and independent component analysis [9] [10], but the original stepwise linear discriminant analysis (SWLDA) still yields competitive results [11]. Finally, different flashing paradigms have been developed to decrease trial time [12] and to improve signal classification [13].

While the P300 speller is designed to provide a means for communication, most attempts at system optimization have not taken advantage of existing knowledge about the language domain. Existing analyses treat character selections as independent elements chosen from a set with no prior information. In practice, we can use information about the domain of natural language to create a prior belief about the characters to be chosen. By adding a bias to the system based on this prior, we hypothesize that both system speed and accuracy can be improved.

Statistical natural language processing (NLP) is an engineering field dedicated to achieving computer understanding of natural language. One application often used in domains such as speech recognition is to apply a language model to create probabilities for different interpretations of an input audio signal [14]. We can use this method in a BCI system by finding the probabilities of all possible continuations of the text entered in previous trials. This probability provides a prior for subsequent character selections so that text agreeing with the language model is more likely to be selected.

This study exploits prior information using NLP to improve the speed and accuracy of the P300 speller. The system will determine the confidence of a classification by weighting the output of the SWLDA algorithm with prior probabilities provided by a language model. The number of flashes used to classify a character is dynamically set based on the amount of time required for the system to reach a predetermined confidence threshold.

2. Methods

The subjects were six healthy male graduate students and faculty with normal or corrected to normal vision between the ages of 20 and 35. Only one subject (subject 2) had previous BCI experience. The system used a six by six character grid, row and column flashes, an ISI of 125 ms, and a flash duration that varied between 31.25 and 62.5 ms. Each subject underwent nine trials consisting of spelling a five letter word (Table 1) with 15 sets of 12 flashes (six rows and six columns) for each letter. The choice of target words for this experiment was independent of the language model used in the NLP method.

Table 1.

Target words for the nine trials

UNITS	MINUS	NOTED
DAILY	SCORE	GIANT
HOURS	SHOWN	PANEL

BCI2000 was used for data acquisition and analysis was performed offline using MATLAB (version 7.10.0, MathWorks, Inc, Natick, MA). Three analysis methods were compared: a static method where the number of flashes is predetermined, a dynamic method that uses a threshold probability and a uniform prior, and an NLP method that incorporates a character trigram language model.

2.1. Static Method

SWLDA is a classification algorithm that selects a set of signal features to include in a discriminant function [15]. Training is performed using nine-fold cross-validation where the test set is one of the trial words and the other eight are the training set. The signals in the training set are then assigned labels based on two classes: those corresponding to flashes containing the attended character and those without the attended character. Each new signal is then reduced to a score that reflects how similar it is to the attended class.

The algorithm uses ordinary least-squares regression to predict class labels for the training set. It then adds the features that are most significant in the forward stepwise analysis and removes the least significant features in the backward analysis step. These steps are repeated until either the target number of features is met or it reaches a state where no features are added or removed [11].

The score for each flash in the test set, $y_t^i$, is then computed as the dot product of the feature weight vector, w, with the features from that trial’s signal, ${\mathbf{z}}_t^i$.

$$y_t^i=\mathbf{w}•{\mathbf{z}}_t^i$$ (1)

For the static classification, the score for each possible next character, x_t, is the sum of the individual scores for flashes that contain that character.

$$g(x_t)=\sum _{i:x_t\in {\mathbf{A}}_t^i}{y}_t^i$$ (2)

where ${\mathbf{A}}_t^i$ is the set of characters illuminated for the i^th flash for character t in the sequence.

The number of flashes is predetermined in the static method, so the classifier will choose arg max_xt g(x_t) after the set number of flashes is reached. In order to optimize this method, the number of flashes was varied from 1 to 15 and the associated speeds, accuracies, and bit rates were recorded (see section 2.4). For each subject, the number of flashes was chosen that optimized the bit rate (Table 2).

Table 2.

Results for the Static, Dynamic and NLP methods optimized for bit rate.

	SR (sel/min)			Accuracy (%)			Bit Rate (bits/min)
Subject	Static	DYN	NLP	Static	DYN	NLP	Static	DYN	NLP
1	7.50	10.29	10.91	95.56	88.89	93.33	35.10	44.03	48.81
2	6.32	7.06	8.07	86.67	91.11	97.78	24.76	30.22	39.57
3	5.45	6.95	8.33	97.78	100.00	100.00	26.74	35.93	43.08
4	7.50	5.16	5.81	66.67	93.33	95.56	19.07	23.08	27.17
5	4.80	5.22	4.92	68.89	68.89	84.44	12.86	13.98	18.43
6	3.87	4.04	5.83	82.22	95.56	88.89	13.87	18.89	21.83
AVG	5.91	6.45	7.31	82.97	89.63	93.33	22.07	27.69	33.15

2.2. Dynamic Method

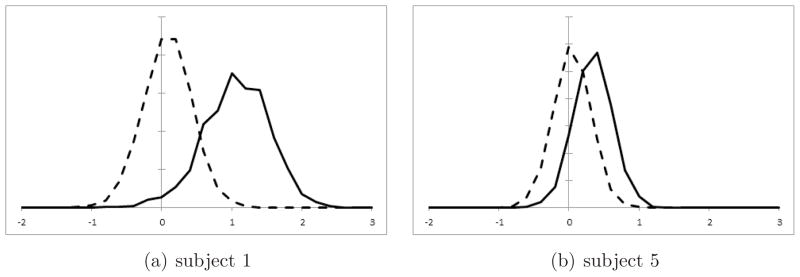
As in the static method, the dynamic classification method (DYN) uses nine-fold cross-validation to obtain a training set for SWLDA. Instead of summing the scores as in equation 2, scores into probabilities and selects characters once a probability threshold is met. The classifier is first trained as in section 2.1. Scores for each flash in the training set were then computed and the distributions for the attended and non-attended signals were found (Fig 4).

Figure 4. SWLDA Score Distributions.

Histograms of the attended (solid curve) and non-attended (broken curve) scores from SWLDA.

While it has been shown that consecutive flashes are not independent [16], we made the simplifying assumption that each flash’s score was drawn independently from one of these distributions. We made the further assumption that the distributions were Gaussian which was tested using Kolmogorov-Smirnov tests for normality [17]. The probability density function (pdf) for the likelihood probability can then be computed:

$$f(y_t^i\mid x_t)=\{\begin{array}{ll}\frac{1}{\sqrt{2\pi {\sigma }_a^2}}{e}^{\frac{1}{2{\sigma }_a^2}{(y_t^i-{\mu }_a)}^2}\hfill & \text{if}{x}_t\in {\mathbf{A}}_t^i\hfill \\ \frac{1}{\sqrt{2\pi }{\sigma }_n^2}{e}^{\frac{1}{2{\sigma }_n^2}{(y_t^i-{\mu }_n)}^2}\hfill & \text{if}{x}_t\notin {\mathbf{A}}_t^i\hfill \end{array}$$ (3)

where μ_a, ${\sigma }_a^2$, μ_n and ${\sigma }_n^2$ are the means and variances of the distributions for the attended and non-attended flashes, respectively.

A Naive Bayes classifier was used to determine the probability of each character given the flash scores and the previous decisions [18]. If we assume that the individual flashes are conditionally independent given the current attended character, the posterior probability is:

$$\begin{array}{l}P(x_t\mid {\mathbf{y}}_t,x_{t-1},\dots ,x_0)=\frac{P(x_t\mid x_{t-1},\dots ,x_0)P({\mathbf{y}}_t\mid x_t,\dots ,x_0)}{P({\mathbf{y}}_t\mid x_{t-1},\dots ,x_0)}\\ =\frac{1}{Z}P(x_t\mid x_{t-1},\dots ,x_0)\prod _{i}f(y_t^i\mid x_t)\end{array}$$ (4)

where P (x_t|x_t−1, …, x₀) is the prior probability of a character given the history, $f(y_t^i\mid x_t)$ are the pdfs from equation 3, and Z is a normalizing constant. Since the dynamic method uses a uniform prior probability, the posterior simplifies to:

$$P(x_t\mid {\mathbf{y}}_t,x_{t-1},\dots ,x_0)=\frac{1}{Z}\prod _{i}f(y_t^i\mid x_t)$$ (5)

A threshold probability, P_Thresh, is then set to determine when a decision should be made. The program flashes characters until either max_xt P (x_t|y_t, x_t−1, …, x₀) ≥ P_thresh or the number of sets of flashes reaches 15. The classifier then selects the character that satisfies arg max_xt P (x_t|y_t, x_t−1, …, x₀). The speeds, accuracies, and bit rates were found for values of P_thresh between 0 and 1 in increments of 0.01. The threshold probability that maximized the bit rate was chosen for each subject.

2.3. NLP Method

The NLP model builds on the dynamic methodology. While the dynamic method had uniform prior probabilities, here NLP is integrated to provide language-specific prior probabilities.

Prior probabilities for characters were obtained from frequency statistics in an English language corpus. This probability was simplified using the second-order Markov assumption to create a trigram model [19]. The prior probability that the next character is x_t given that the last two characters chosen were x_t−1 and x_t−2 is then equal to the number of times that all three characters occurred together in the corpus divided by the number of times the last two characters occurred together.

$$P(x_t\mid x_{t-1},\dots ,x_0)=\frac{c(x_{t-2},x_{t-1},x_t)}{{\sum }_{x_t}c(x_{t-2},x_{t-1},x_t)}=\frac{c(x_{t-2},x_{t-1},x_t)}{c(x_{t-2},x_{t-1})}$$ (6)

where c(x_t−2, x_t−1, x_t) is the number of occurrences of the string “x_t−2x_t−1x_t” in the corpus.

For the first two characters in a word, x_t−1 and x_t−2 are not defined. In the case of the first character, the prior probability is the number of words that start with that character divided by the number of words in the corpus. Similarly, the probability for the second character in the word is the number of words that start with “x_t−1x_t” divided by the number of words that start with “x_t−1.”

$$P(x_t\mid x_{t-1},\dots ,x_0)=\{\begin{array}{ll}\frac{c(\mathit{start},x_t)}{c(\mathit{start})}\hfill & \text{if}t=0\hfill \\ \frac{c(\mathit{start},x_{t-1},x_t)}{c(\mathit{start},x_{t-1})}\hfill & \text{if}t=1\hfill \\ \frac{c(x_{t-2},x_{t-1},x_t)}{c(x_{t-2},x_{t-1})}\hfill & \mathit{otherwise}\hfill \end{array}$$ (7)

where c(start, x_t−1, x_t) and c(start, x_t) are the numbers of words that start with “x_t−1x_t” and “x_t” respectively and c(start) is the total number of words in the corpus. Combining equations 3, 4, and 7 yields a posterior probability biased by the language model.

Trigrams for the English language were obtained from the Brown corpus [20]. The Brown corpus contains over two million words compiled from various types of documents published in the United States in 1961.

2.4. Evaluation

Evaluation of a BCI system must take into account two factors: the ability of the system to achieve the desired result and the amount of time required to reach that result. The efficacy of the system can be measured as the selection accuracy, which we evaluated by dividing the number of correct selections by the total number of trials.

For each model we also calculated the selection rate (SR). First, the average amount of time for a selection is found by adding the gap between flashes (3.5 s) to the product of the amount of time required for a flash (.125 s), the average number of sets of flashes (s̄), and the number of flashes in each set (12). The selection rate measured in selections per minute is then the inverse of the average selection time.

$$\text{SR}=\frac{60}{3.5+.125\ast 12\ast \overline{s}}$$

Since there is a tradeoff between speed and accuracy, we also use bit rate as a metric which takes both into account. The bits per symbol, B, is a measure of how much information is transmitted in a selection taking into account the accuracy and the number of possible selections [21].

$$B={log}_{2}N+P{log}_{2}P+(1-P){log}_2\frac{1-P}{N-1}$$

Where N is the number of characters in the grid (36) and P is the selection accuracy. The bit rate (in bits/minute) can then be found by multiplying the selection rate by the bits per symbol. Significance was tested using paired two-sample t-tests with 5 degrees of freedom.

Although the number of flashes was fixed for all trials, different selection rates were simulated by limiting the amount of data available for the classification algorithm. For example, if the confidence threshold is reached after six sets of flashes, the classification algorithm only uses the data from the first six sets and omits the remaining nine.

3. Results

3.1. Static Method

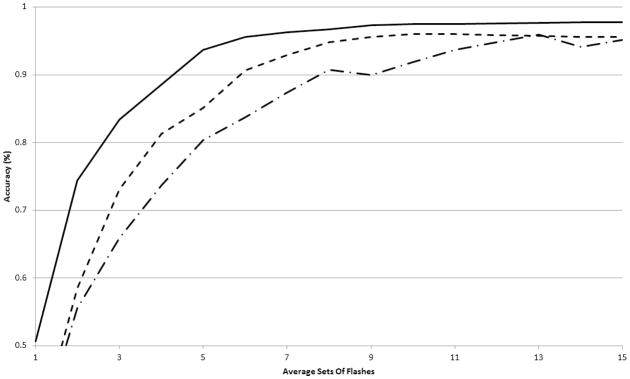
Using the static method, all subjects were able to type with varying levels of performance. The best performer (subject 1) was able to achieve 95% accuracy after 3 sets of flashes, while the worst performer (subject 5) reached a maximum of 82% after 15 flashes. The accuracy increased with the number of flashes for all subjects and five out of six were able to exceed 90% accuracy within 15 sets of flashes (Fig. 1 and 2).

Figure 1. Average accuracies.

Average accuracy across subjects for the static (chain curve), dynamic (broken curve), and NLP (full curve) methods versus the average number of sets of flashes required to make a decision.

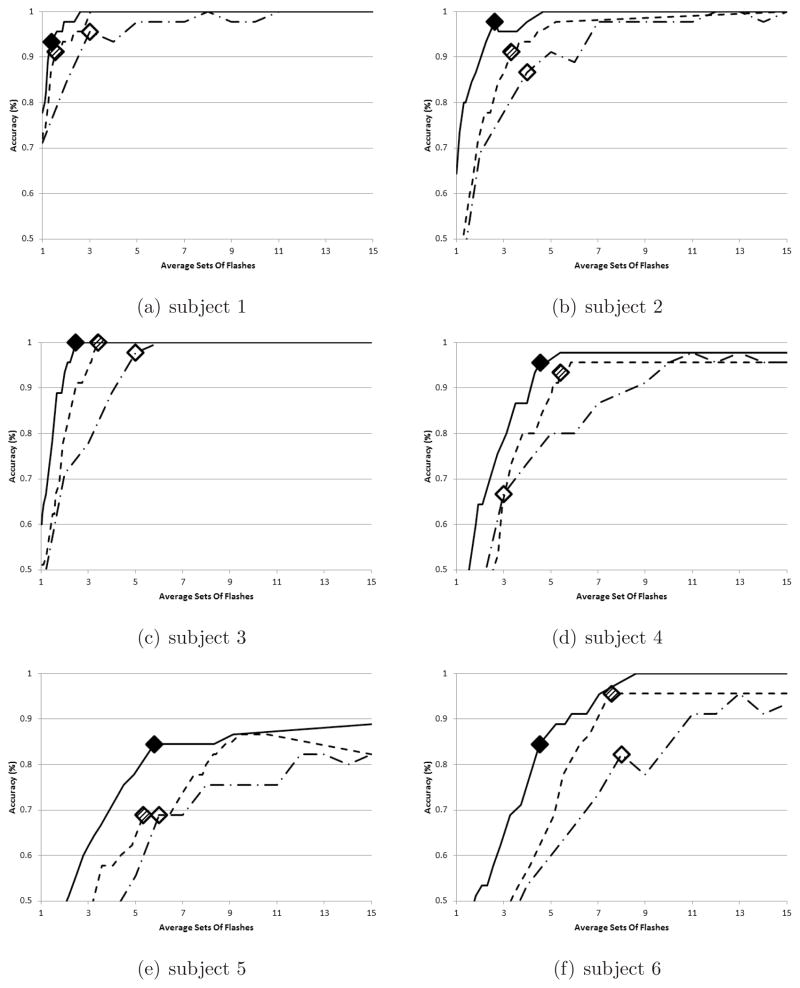
Figure 2. Subject accuracies.

Average accuracy for each subject using the static (chain curve), dynamic (broken curve), and NLP (full curve) methods versus the average number of sets of flashes required to make a decision. The markers represent the values on the curve that correspond to the optimal bit rate for each method.

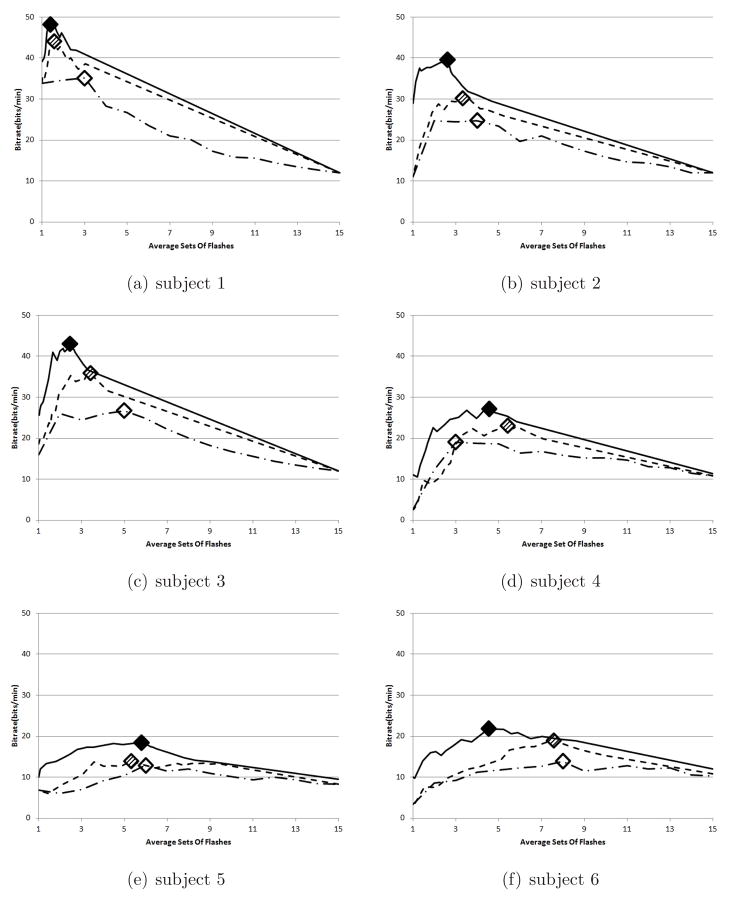
The optimal number of sets of flashes varied from 3 to 8, which yielded bit rates from 12.86 to 35.10 (Table 2). In general, subjects that performed better achieved an optimal bit rate in fewer flashes (Fig. 3). On average, the subjects had a 36% accuracy after a single set of flashes which increased to about 95% after 15 sets (Fig. 1). The average selection rate for the static method was 5.91, the average accuracy was 82.97%, and the average bit rate was 22.07.

Figure 3. Subject bit rates.

Average bit rate for each subject using the static (chain curve), dynamic (broken curve), and NLP (full curve) methods versus the average number of sets of flashes required to make a decision. The markers represent the values on the curve that correspond to the optimal bit rate for each method.

3.2. Dynamic Method

Score distributions were found by taking the histograms of the scores from the attended and non-attended signals for each subject (Fig. 4). Kolmogorov-Smirnov tests for normality were performed to verify our Gaussian assumption and none were found to be significant after Šidák correction for multiple comparisons. While the shape of the distributions was similar for all subjects, some exhibited better separation between the attended and non-attended scores (Fig. 4(a)).

The maximum bit rates using dynamic classification improved by 25% overall (p=0.003), ranging from 8% (subject 5) to 36% (subject 3) compared to the static method (Table 2). On average, the accuracy and selection rate trended upward, but were not statistically significant (p=0.11 and p=0.23 respectively). In some cases, however, a decreased accuracy (subject 1) or selection rate (subject 4) was reported for the dynamic method relative to the static method because of the optimization based on bit rate. In these cases, the optimal bit rate may occur at a lower accuracy but a much higher selection rate or vice versa.

3.3. NLP method

As the threshold probability varied for the NLP method, it achieved the best accuracies for any given selection rate (Fig. 2). Four of the subjects had 100% accuracies within 9 sets of flashes and subject 4 had all characters but one correct within 6 sets of flashes. Only subject 5 failed to reach 90% accuracy, but an improvement to 84% accuracy was seen within 6 sets of flashes.

The overall improvement from the static method to the NLP method was between 40% and 60% for each subject. The average bit rate across subjects improved by 50% from 22.07 to 33.15 (p=0.0008). The accuracy increased from 82.97% to 93.33% (p=0.03) and the selection rate trended up from 5.91 to 7.31, but was not statistically significant (p=0.06).

4. Discussion

Current BCI communication systems ignore domain knowledge when processing natural language. Most systems also use static trial lengths so that all classifications are given the same amount of input information regardless of classification difficulty. Integration of dynamic classification and NLP addresses these shortcomings, improving performance in offline analysis.

4.1. Prior Knowledge and Dynamic Classification

The dynamic method was able to improve speed by rendering a decision as soon as it became confident of a classification. At the same time, it increases accuracy by analyzing additional flashes to improve confidence in more challenging classifications. There is also the potential that faster feedback afforded by the dynamic method could improve user attentiveness, but this would require online analysis to observe.

The NLP method added a prior probability to the dynamic method based on the language model. This helped the system reach the threshold probability more quickly by adding additional probabilistic information from the linguistic domain rather than presuming equal a priori probabilities for all characters. It also improved accuracy as it increased the probability of selections that were consistent with natural language.

4.2. Significant Advance

The static method achieved an average bit rate of 22.07 across subjects, which is consistent with previous studies [13] [22]. Our dynamic method improves the bit rate by 25% on average to 27.69. Using the language model for prior probabilities increased the bit rate by 40–60 percent for each subject in this study for an average of 33.15. To put this in context, Townsend et al. reported an average bit rate increase of 19.85 to 23.17 using their improved flashing paradigm [13].

4.3. Similar Work

Serby et al. implemented a maximum likelihood (ML) method which varies the number of flashes used to classify a character using a threshold as in our dynamic method [10]. Their method differs in that it makes a decision when a target score is met rather than a confidence threshold. In situations where the classifier gives high scores to multiple characters, their method makes a decision if any of them exceed the target score. Since our method converts scores into a confidence probability, it continues flashing until there is enough information to confidently choose one of the characters.

Ryan et al. created a system that attempted to take advantage of the language domain by adding suggestions for word completion [22]. Their system differs in that it does not use a language model, but instead performs dictionary lookups as characters are selected. This language information is incorporated into the user interface as several of the cells in their character matrix are reserved for word completions.

Their approach has several limitations. Characters are removed from their interface to make room for word completions, resulting in a smaller possible output vocabulary and a reduced system bit rate. Also, their graphical interface was more complicated resulting in a lower reported accuracy.

Nevertheless, their study showed that word completion can improve the speed of a BCI system, so it could be beneficial to use it in conjunction with our method. Since our system integrates the language information into the signal processing method and their changes are exclusively in the user interface, they are essentially parallel tracks that can be integrated.

4.4. Limitations and Future Directions

More advanced models that better utilize knowledge of linguistic structure will likely provide even greater improvements than the work presented here. For example, a simple improvement would be to include a model with word probabilities. The corpus used in this study contains part of speech tags which could provide additional prior information. Discourse and context information can also be integrated into this system.

The corpus used in this model was chosen because it is large enough to give reliable trigram counts and because it contains text samples from a variety of domains. Clinical implementations of this system may prefer corpora that are more specific to the patients’ needs.

This method is independent of system parameters, grid size, and flashing paradigm, so it can be incorporated into most other systems as well. Also, the Naive Bayes method and language model prior can be combined with any classifier that returns a likelihood probability. Studying the effects of NLP in such systems remains as future work.

This study was performed to demonstrate a proof of concept for the use of a language model in BCI communication. While the results are encouraging, it remains to be seen if the improvement in bit rate translates into improved performance in a live communication system. The next step is to implement NLP in an online system and to measure the realized bit rate increase.

5. Conclusion

Natural language contains many well-studied structures and patterns. Understanding of this domain information can greatly improve the processing and creation of language. This study showed that utilizing natural language information can dramatically increase the speed and accuracy of a BCI communication system.