Abstract
Maternal care is critical to offspring growth and survival, which is greatly improved by building an effective nest. Some suggest that genetic variation and underlying genetic effects differ between fitness-related traits and other phenotypes. We investigated the genetic architecture of a fitness-related trait, nest building, in F2 female mice intercrossed from inbred strains SM/J and LG/J using a QTL analysis for six related nest phenotypes (Presence and Structure pre- and postpartum, prepartum Material Used and postpartum Temperature). We found 15 direct-effect QTLs explaining from 4 to 13% of the phenotypic variation in nest building, mostly with non-additive effect. Epistatic analyses revealed 71 significant epistatic interactions which together explain from 28.4 to 75.5% of the variation, indicating an important role for epistasis in the adaptive process of nest building behavior in mice. Our results suggest a genetic architecture with small direct effects and a larger number of epistatic interactions as expected for fitness-related phenotypes.
Keywords: maternal behavior, fitness, QTL, epistasis, mice
Introduction
Maternal care is a complex and flexible phenotype with critical importance to fitness (Mousseau and Fox, 1998). The environment created by the mother modifies several phenotypes such as survival, growth, body size, and the emotional development of their offspring (Francis and Meaney, 1999; Caspi and Moffitt, 2006; Räsänen and Kruuk, 2007), and is more important than any other single factor during the first days of life (Lee et al., 1991). The performance of a mother is related to specific maternal care characteristics such as milk production and ejection (Horseman et al., 1997), aggression against intruders (Bateson, 1994), and nest building (Lynch, 1981, 1994; Bult and Lynch, 1997).
Nest building has an essential role in offspring viability (Wallace, 1981), being important for protection against predators (Boake, 1994), for temperature maintenance (Lynch, 1994; Gaskill et al., 2011), for fostering pup’s development by an increase of growth hormone (Marple et al., 1972; Zimmerberg and Shartrand, 2004), for reduction of water loss (Friedman and Bruno, 1976), and for keeping pups in closer contact with their mother (Fleming et al., 1999). Nest building is also common in adult mice (males and non-pregnant females) for thermoregulation (Weber and Olsson, 2008), and the behavior for maternal and non-maternal nests probably shares some genetic basis (Lynch, 1981). Mice selected for adaptations to cold temperatures build better adult nests (Barnett and Dickson, 2008) which lead to more successful offspring (Bult and Lynch, 1997). General nest building behavior also has, in male and female mice, a high to moderate broad-sense heritability (H2 from 0.4 to 0.6) and low narrow-sense heritability (h2 around 0.2; Lee, 1973; Lynch, 1994), suggesting that natural selection is removing disadvantageous additive genetic variation.
Although there is abundant information on nest building, little is known about the evolution of this behavior and its genetic architecture (Boake, 1994; Weber and Olsson, 2008). By genetic architecture of a phenotype, we refer to the total number of genetic regions involved, their direct effects (additivity), inter-allelic interactions at the same locus (dominance), interactions between different loci (epistasis), and the extension of effects across other phenotypes (pleiotropy) (Falconer and Mackay, 1996; Erickson, 2005). Taking into account multiple genetic components simultaneously allows the understanding of phenotypes with complex genetic architectures that would be unpredictable if we consider only one component at a time (Rockman, 2008). Knowledge of the underlying genetic architecture leads to inferences about the causal physiological networks involved and aids in the discovery of genes responsible for phenotypic differences. Also, genes’ interactions and effects contain important information about past and future phenotypic evolution (Templeton, 2006; Levy and Siegal, 2008; Parter et al., 2008).
The genetic architecture for phenotypes critical to survival and reproduction (fitness-related traits) may be dramatically different from that of phenotypes not directly related to fitness (Peripato et al., 2004). Fitness-related traits usually have a larger number of underlying genes, and, consequently, higher levels of additive and interaction variance because there are more targets for mutational events (Houle et al., 1996). However, due to natural selection acting on the direct effects through generations, fitness-related traits are expected to have less relative (per gene) additive genetic variation and, because of the high number of possible interactions, more dominance, and epistatic genetic variation than other complex traits (Lynch and Walsh, 1998; Merilä and Sheldon, 1999). Moreover, traits related to fitness may have proportionally more genes with intermediate effects in comparison with other phenotypes due to the balance between natural selection and genetic drift (Ohta, 1973; Merilä and Sheldon, 1999).
We have been studying the genetic architecture of maternal care features in LG/J × SM/J mice females (Peripato and Cheverud, 2002; Peripato et al., 2002, 2004; Góes, C. P., Sauce, B., and Peripato, A. C., unpublished data). Females grouped by maternal performance for offspring survival from SM/J and LG/J strains and their intercross differ in pre- and postpartum nest building (Peripato and Cheverud, 2002; Peripato et al., 2002; Chiavegatto et al., 2012). Here, we used QTL (Quantitative Trait Loci) analysis to investigate the genetic architecture of nest building behavior in mice. Furthermore, because nest building is a complex maternal behavior critical to offspring’s survival and development, its study can add to the question of expected genetic architecture for fitness-related traits.
Materials and Methods
Animals
We used inbred mouse strains Small (SM/J) and Large (LG/J), and their F2 intercross. The parental strains were acquired from The Jackson Laboratories (Bar Harbor, ME, USA). The LG/J strain originated from an albino population selected for large body size at 60 days and SM/J from a separate selection for small body size at 60 days (for history and details, see Hrbek et al., 2006). Many phenotypes have been genetically studied in this intercross, including maternal performance (Peripato et al., 2002), prepulse inhibition (Samocha et al., 2010), growth (Cheverud et al., 1996; Kramer et al., 1998; Vaughn et al., 1999), bone length (Norgard et al., 2008), obesity (Cheverud et al., 2001, 2004; Ehrich et al., 2005), and litter size (Peripato et al., 2004).
We mated 10 SM/J males with LG/J females and 10 LG/J males with SM/J females, resulting in 68 F1 animals. We performed 29 crosses among F1 mice in all combinations of sex and origin to attain an F2 progeny with chromosome X derived from both strains. We then randomly mated F2 mice among families (258 crosses) to generate the pre- and postpartum data of this study. We analyzed all mothers during the first week after delivery for a set of behavioral tests. At the third week after delivery, we weaned all pups and placed them in single-sex cages with at most five animals. We weighed these mice weekly until their seventh week, when they were separated by couples to mate. Whenever pregnancy was detected, we removed the male and started monitoring maternal behaviors.
Animals were fed ad libitum with Nuvilab CR1/Nuvital (Colombo, PR, Brazil) and maintained at a constant temperature of 21 ± 1°C with 12 h light/dark cycles (lights on at 6 a.m.) at Federal University of São Carlos. To improve environment’s homogeneity, we performed all tests and observations during the same period (8:00 to 12:00) inside a laminar flow cabinet in the animal room. Experiments were carried out in accordance to the Ethics Committee of the Federal University of São Carlos (Brazil).
Nest building
As soon as pregnancy was detected, females were each maintained in a single cage and provided with pieces of cotton of similar sizes (average 3.67 ± 0.48 g) at the cage’s food/water level to be used for nest building. To compare possible differences in material usage described in some studies (Sherwin, 1997; van de Weerd et al., 1998), we also added paper (average 1.08 ± 0.03 g) under the cotton for most animals. During the prepartum period, we daily removed all nests, cotton, and paper to increase the confidence that the scores for a nest reflect a consistent building behavior (Schneider and Chenoweth, 1970; Lee, 1973; Lynch and Roberts, 1984). We evaluated prepartum nest building daily by classifying it as open or closed, by the presence of material (cotton or paper) above the nest, and by the nests’ height. To measure the amount of material used for nest building, we daily weighed the added cotton and paper and subtracted the value remaining at the cage’s food/water level. The quantification of postpartum nest building followed the same categories and procedures as the prepartum period, but, to guarantee maternal closeness with pups for other tests, we avoided daily disturbances such as destroying the nest and weighting the material used. In the postpartum period, we measured the difference between the nest’s inner and outer temperatures during 1 min at the second and fourth days after birth.
In sum, we investigated the following nest building phenotypes in F2 females in maternal phase: Nest Presence (0 = absent; 1 = present) prepartum and postpartum; Nest Closure (0 = opened; 1 = closed) prepartum and postpartum; Nest Height (centimeters) prepartum and postpartum; Cotton Used (grams) prepartum; Paper Used (grams) prepartum; Temperature Difference (degrees Celsius) postpartum.
We weighed all nest building variables according to the relative importance of each day. Females, in general, spend more time building nests during pregnancy and birth, decreasing this behavior afterward (Lisk et al., 1969), so we gave more weight to days closer to birth because they probably have higher importance to fitness by reflecting the conditions pups would normally meet. For the prepartum period, being X the highest number of prepartum days analyzed, we multiplied each value by: X/X in the day before birth, (X − 1)/X in the second day before birth, (X − 2)/X in the third day before birth, and progressively. For the postpartum period, the highest number of days was 7, so we multiplied each value by: 7/7 in the first day after birth, 6/7 in the second day after birth, 5/7 in the third day after birth, and progressively. The final phenotype of each female was the sum of those weighed values divided by the sum of days phenotypes were measured for that female. In order to bring this back to the correct scale, we then multiply each value by the number of days each phenotype was measured (multiplied by the maximum number of days measured, in our case, seven) divided by the sum of indices considering all days in which measurements were taken. By doing this, we also reduced biases due to different number of days being scored for different animals, like the ones caused by differences in pregnancy detection during the prepartum period.
Principal component analysis in nest building data
We assessed the correlations among all measured phenotypes to understand the similarity of their information. A Principal Component Analysis (PCA) of correlations performed in SYSTAT 13 (Systat Software Inc., USA) of the already described weighted means across all the days for each animal and phenotype revealed that Nest Presence, Nest Closure, and Nest Height have correlations that range from 0.237 to 0.496 prepartum and 0.213 to 0.478 postpartum. The correlation between Paper Used and Cotton Used is 0.892 whereas some other correlations range from 0.037 to 0.094. To compare the same information between pre- and postpartum phenotypes, we combined the common variables Nest Presence, Nest Closure, and Nest Height in a PCA for each period. We performed a separate PCA for Cotton Used and Paper Used and maintained the original values of Temperature Difference. The analysis, then, allowed us to reduce the number of meaningful phenotypes for the subsequent QTL analysis by using, for each female, factor scores (values of the best planes explaining all variance) instead of the original values. With this, we increased the phenotypes’ repeatability, since the new variables aggregate similar measures with minimal error, while also increasing the degrees of freedom for the epistatic QTL analysis. We used six phenotypic variables for the QTL analysis: Prepartum Nest Structure (1) and Nest Presence (2) resulting from standardized vectors of the PCA between original prepartum phenotypes Nest Presence, Nest Closure, and Nest Height; Material Used (3) from the resulting standardized vector of the PCA between original phenotypes of Cotton Used and Paper Used; Postpartum Nest Presence (4) and Nest Structure (5) from the standardized vectors of the PCA between original postpartum phenotypes Nest Presence, Nest Closure, and Nest Height; and finally Temperature Difference (6), unchanged from original.
Genotyping
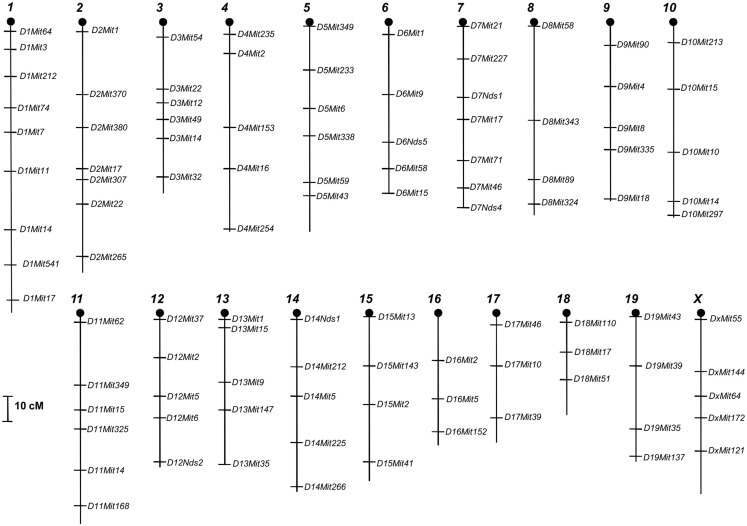
We genotyped 234 F2 females for 101 microsatellites markers previously shown to be polymorphic for SM/J and LG/J strains that uniformly cover all 19 autosomal chromosomes and the sex chromosome X (Figure 1).
Figure 1.
Microsatellite marker’s location used in all 20 chromosomes of mice genome.
We used a Guanidine Thiocyanate protocol (Nelson and Krawetz, 1992) to extract total DNA from the liver of 234 F2 females previously sacrificed and necropsied. We then used a PCR amplification protocol for microsatellites (Dietrich et al., 1992) modified by Routman and Cheverud (1994) to efficiently genotype a high number of samples. PCR products were visualized and genotyped using 5% agarose gels and ethidium bromide staining.
Statistical analysis
Nest building
We used the parametric Multivariate analysis of variance (MANOVA), with the Wilks lambda (λ) test in SYSTAT 13 (Systat Software Inc., USA) to investigate the differences between nest building phenotypes during pre- and postpartum periods of the F2 females. A significance threshold of 0.05 was used in all phenotypic tests.
Quantitative trait loci analysis
We performed QTL analysis of the F2 females in maternal phase to correlate the segregating phenotypes and polymorphic genetic markers covering a genome (Liu, 1997). First, the linkage map of the 101 markers for the F2 females was created using the Kosambi function, with the program Map Manager QTX (Manly et al., 2001). We, then, used interval mapping (2 cM intervals) and multiple regression analysis (Haley and Knott, 1992) to estimate additive (a) and dominance (d) genotypic values for each interval (Falconer and Mackay, 1996). We calculated these values using the MIXED procedure in SAS 9 (SAS Institute Inc., USA).
The statistical significance of the tests was measured by LOD scores in each analysis against two different significance thresholds, chromosome-wide, and genome-wide, based on the multilocus model of Li and Ji (2005). The 5% genome-wide specific threshold value for the F2 mice is 3.27, while the 5% chromosome-wide threshold values ranged from 1.77 to 2.13, depending on the chromosome, with a mean of 1.97. LOD scores higher than the chromosome-wide significance threshold only suggest an association of the genomic region with the phenotype (Weller et al., 1998). LOD scores higher than the genome-wide significance threshold are a strong evidence of such association (Lander and Kruglyak, 1995). Confidence intervals for each QTL were specified by the one-LOD-drop-rule (Lynch and Walsh, 1998).
The epistatic QTL analysis was performed by an interchromosomal two-way genome-wide scan performed at every two cM using the F2 Model (Cockerham, 1954) extended to two loci by Cockerham and Zeng (1996) in SAS 9 (SAS Institute Inc., USA). We did not evaluate epistasis among genotypes within chromosomes because of difficulties in interpretation caused by linkage disequilibrium. For each pair of chromosomes, we plotted all F values generated from these analyses which had probabilities below 0.05. We considered as potential epistatic QTLs only those positions exhibiting the highest F values in a plot. Distant F peaks separated by low F values were taken as distinct epistatic signals (Leamy et al., 2005) and epistatic QTLs found within 10 cM were treated as the same locus. Due to the problem of false positives arising through multiple comparisons, we estimated a significance threshold based in the Bonferroni criteria for gene–gene interactions using the Li and Ji (2005). The total number of independent epistasis tests per phenotype, calculated by the cross products’ sum of markers for all pairs of chromosomes, was 3,137. This suggests that we might expect about 157 tests to be significant at the 5% level, 31 at the 1% level, and 3 at the 0.1% level due of chance alone. In our study, the 0.05 significance threshold for interactions was 0.05/3137 = 1.63 × 10−5 which corresponds to a LOD score of 4.79. We considered epistatic tests with probability below this P value as significant evidence for epistasis (Peripato et al., 2002; Leamy et al., 2009). We also considered epistasis significant if one of the four types of epistasis (additive by additive, additive by dominant, dominant by additive, and dominant by dominant) was below 4.09 × 10−6 (1.63 × 10−5/4) which corresponds to a LOD score of 5.33, even if the overall epistasis model was not significant.
We used a GLM model in SYSTAT 13 (Systat Software Inc., USA) to estimate the percentage of variation in each nest building phenotype explained by direct-effect QTLs. We also estimated the contribution of all direct-effect and epistatic QTLs together in models with and without interactions to evaluate the effect of all regions and the importance of epistasis to nest building.
Results
Nest building
Pre- and postpartum nest building data for the F2 females are listed in Table 1. We found significant differences between the pre- and postpartum sets of phenotypes Nest Presence, Nest Closure, and Nest Height (Wilks λ3.36 = 0.87, P = 10−10). Nest Presence is greater in the postpartum period (F1 = 13.66, P = 10−3), but prepartum values are greater for Nest Closure (F1 = 29.18, P = 10−6) and Nest Height (F1 = 29.18, P = 10−6).
Table 1.
Nest building for pre- and postpartum periods, in F2 females in maternal phase.
| Phenotype | n | Mean | |
|---|---|---|---|
| Prepartum | Nest presence (0–1) | 231 | 0.873 ± 0.015a |
| Nest closure (0–1) | 224 | 0.145 ± 0.015b | |
| Nest height (cm) | 224 | 3.752 ± 0.055c | |
| Cotton used (g) | 116 | 1.862 ± 0.081 | |
| Paper used (g) | 106 | 0.761 ± 0.042 | |
| Postpartum | Nest presence (0–1) | 241 | 0.958 ± 0.010a |
| Nest closure (0–1) | 238 | 0.072 ± 0.010b | |
| Nest height (cm) | 139 | 3.217 ± 0.089c | |
| Temperature difference (°C) | 232 | 2.613 ± 0.075 |
Means are expressed as mean ± SEM. Upper script letters indicate that there is significant difference (P < 10−6) between pre- and postpartum equivalent phenotypes.
Principal component analysis in nest building data
Using the PCA, we reduced the number of nest building phenotypes for the QTL analyses. Prepartum variables Nest Closure, Nest Height, and Nest Presence were represented by the resulting first two vectors, Nest Structure and Nest Presence, which explain 54.6 and 28.7% of the original variation, respectively. The vector Material Used, resulting from the prepartum variables Cotton Used and Paper Used explains 94.6% of their variation. Likewise, postpartum variables Nest Closure, Nest Height, and Nest Presence were represented by the resulting two vectors, Nest Structure and Nest Presence, explaining 51 and 32.9% of the original variation, respectively.
Direct-effect and epistatic QTL analysis
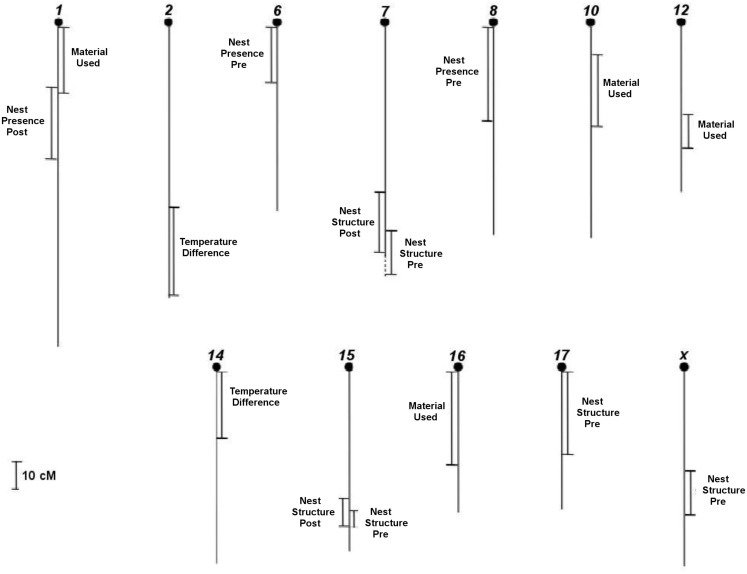
We searched for direct-effect QTLs in F2 females in maternal phase using regressions of genotypic values imputed for every 2 cM with the nest building phenotypes Nest Presence pre- and postpartum, Nest Structure pre- and postpartum, Material Used prepartum, and Temperature Difference postpartum. In total, we obtained 15 regions that, individually, are significantly associated with the variation in the six pre- and postpartum phenotypes analyzed (Figure 2), after correcting for multiple tests. Of these, five QTLs are above the genome-wide threshold and the other 10 regions are above the chromosome-wide threshold.
Figure 2.
Location of all direct-effect QTLs that we found in F2 females in 12 chromosomes of 20 total from mice genome for the nest building phenotypes pre- and postpartum with respective confidence intervals, in cM.
Out of the 10 prepartum direct-effect QTLs (Table 2), four regions have mainly direct (additive) effects: preNP8, preNS7, preNS17, and preNSX, whereas the other six QTLs showed mostly dominance effects, with four showing overdominance (preNS15, preMU1, preMU10, and preMU16) and two under-dominance (preNP6 and preMU12). Considering the additive and dominance effects, QTLs explain, together, 7% of the variation for Nest Presence, with QTL effects of 3.4 and 4.3%. QTLs explain, together, 16.1% of variation for Nest Structure, with QTL effects ranging from 4.4 to 6.4%, whereas QTLs explain 26.6% of the variation for Material Used, with QTL effects varying from 9.1 to 11.2%.
Table 2.
Direct-effect QTLs of pre- and postpartum nest building phenotypes in F2 females in maternal phase.
| Nest building | QTL name | Chr | Location (CI) | Additive effect | Dominance effect | Variance explained (%) | LOD score |
|---|---|---|---|---|---|---|---|
| Prepartum nest presence | preNP6 | 6 | 10 (0–20) | −0.531* | −0.423* | 4.3 | 2.10 |
| preNP8 | 8 | 14 (0–34) | −0.750* | 0.007 | 3.4 | 2.57 | |
| Prepartum nest structure | preNS7 | 7 | 82 (74–90) | −0.747* | −0.282 | 6.4 | 3.58 |
| preNS15 | 15 | 56 (50–56) | −0.046 | 0.521* | 4.4 | 2.92 | |
| preNS17 | 17 | 12 (0–30) | 0.945* | −0.062 | 5.3 | 3.34 | |
| preNSX | X | 42 (36–52) | −0.659* | −0.037 | 5.0 | 3.25 | |
| Prepartum material used | preMU1 | 1 | 10 (0–24) | 0.787* | 0.562* | 11.2 | 2.77 |
| preMU10 | 10 | 26 (10–36) | 0.142 | 0.838* | 9.1 | 2.74 | |
| preMU12 | 12 | 38 (32–44) | −0.082 | −0.682* | 9.2 | 2.82 | |
| preMU16 | 16 | 12 (0–34) | 0.908* | 0.506* | 11.0 | 2.65 | |
| Postpartum nest presence | postNP1 | 1 | 36 (22–48) | 0.281 | −0.762* | 3.6 | 9.80 |
| Postpartum nest structure | postNS7 | 7 | 74 (60–82) | −0.793* | −0.917* | 3.9 | 12.90 |
| postNS15 | 15 | 56 (46–56) | 0.749* | 0.522* | 2.6 | 8.70 | |
| Postpartum temperature difference | postTD2 | 2 | 80 (66–98) | −0.409* | −0.442* | 2.5 | 4.60 |
| postTD14 | 14 | 10 (0–24) | 0.117 | −0.497* | 2.4 | 3.10 |
Direct-effect QTLs are listed by phenotype affected, name, chromosome, location from centromere in centiMorgans and Confidence Interval of 1 LOD (CI), Standardized additive effect, 2a/σp, and Standardized dominant effect, d/σp (with asterisks indicating significance), and percentage of variation explained. Genome-wide threshold is 3.27.
The five postpartum direct-effect QTLs we found (Table 2) have only significant dominance effects. Heterozygous females have a higher score structured nest than parental ones based on overdominance effect for postNS15. Nonetheless, poor nest performance in heterozygous females (under-dominance) is found at the QTLs postNP1, postNS7, postTD2, and postTD14. The postNP1 QTL explains 9.8% of the variation of this phenotype. QTLs for Nest Structure explain, together, 20.3% of its variation, with QTL effects of 8.7 and 12.9%, whereas QTLs explain 7% of the variation for Temperature Difference, with QTL effects of 3.1 and 4.6%.
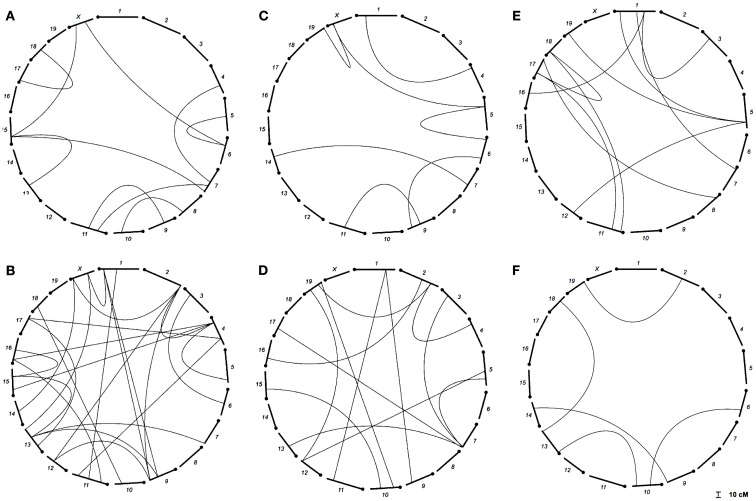
We found several interactions in the analysis of epistatic QTL for nest building phenotypes in the F2 females in maternal phase. We detected close to 1,900 significant tests for epistasis at the 5% level considering all the phenotypes here investigated, which is about twice as many as we would have expected by chance. Furthermore, 500 were significant at the 0.1% level though we would expect 19 by chance and 71 that were significant at the corrected 5% level (P < 1.63 × 10−5), though we expected less than one by chance. The analyses on prepartum variables revealed 10 significant epistatic interactions at the corrected 5% level affecting Nest Presence involving 17 regions (Figure 3A; Table A1 in Appendix), seven interactions for Nest Structure involving seven regions (Figure 3C; Table A2 in Appendix) and 10 for Material Used involving 15 regions (Figure 3E; Table A3 in Appendix). The comparison of epistatic QTLs for prepartum nest building phenotypes revealed a region at medial chromosome 7 which is common for Nest Presence and Nest Structure and another at proximal chromosome 11 which is common for Nest Presence and Material Used. We found direct-effect QTLs located inside the confidence interval of some of the epistatic QTLs detected, at chromosome 6 for prepartum Nest Presence (0–20 cM) and at chromosomes 1, 12, and 16 for Material Used.
Figure 3.
Location of epistatic QTLs for nest presence and nest structure pre- and postpartum, material used prepartum, and temperature difference postpartum across the total 20 chromosomes. (A) Nest presence prepartum; (B) Nest Presence postpartum; (C) Nest Structure prepartum; (D) Nest Structure postpartum; (E) Material Used prepartum; (F) Temperature Difference postpartum.
In the postpartum period, we found 26 epistatic interactions for Nest Presence involving 29 regions (Figure 3B; Table A4 in Appendix), 13 interactions for Nest Structure involving 22 regions (Figure 3D; Table A5 in Appendix), and five for Temperature Difference involving 10 regions (Figure 3F; Table A6 in Appendix). Among epistatic QTLs of postpartum nest building phenotypes, we found regions in common in proximal chromosome 3, distal chromosomes 5, 7, and 11, and medial chromosomes13 and 16 for Nest Presence and Nest Structure. There were direct-effect and epistatic QTLs in common at chromosome 1 for postpartum Nest Presence, at chromosome 7 for postpartum Nest Structure and at chromosome 2 for Temperature Difference.
When we contrasted pre- and postpartum phenotypes, we found several regions in common for Nest Presence, at chromosomes 4, 10, 13, 15, and X, whereas for Nest Structure we found common regions at chromosomes 4, 9, and 19.
All direct-effect and epistatic QTLs and their interactions together explain 28.4% of Nest Presence prepartum, 45.1% of Nest Structure prepartum, 62.3% of Material Used, 75.7% of Nest Presence postpartum, 34.9% and of Nest Structure postpartum, 40% for Temperature Difference.
Discussion
Nest building is a common behavior for thermoregulation in adult rodents (Weber and Olsson, 2008) which is typical during the maternal phase for mother/offspring aspects beyond thermoregulation (Marple et al., 1972; Boake, 1994; Lynch, 1994; Zimmerberg and Shartrand, 2004; Gaskill et al., 2011). LG/J and SM/J dams exhibit similar maternal performance of prepartum nest building (Chiavegatto et al., 2012). Additionally, when we contrast the Nest Presence in F2 females in prepartum stage and in adult F2 males and females that were not in maternal phase we found similar values (data not shown), suggesting that they may share some genetic basis (Lynch, 1981). However, F2 females in maternal phase have significantly higher values for Nest Height (on average, 1.28 times higher than F2 males) and Nest Closure (on average, 7.17 times more frequently closed than females that were not in maternal phase; data not shown). These results are similar to studies in rodents showing that maternal nests are more structured than non-maternal nests, two times higher and usually closed (Denenberg et al., 1969; Weber and Olsson, 2008). Maternal nests may also be structurally different depending on maternal stage. Generally, mothers show some programmed hormonal stimulus response during pregnancy and sensorial stimuli after birth coming from pups (Rosenblatt, 1975). Consequently, we would expect differences in nest building behavior in these two phases. Indeed, here we observed significant differences between pre- and postpartum phenotypes of nest building in F2 females. Even though LG/J and SM/J females build a pre- and postpartum nest, the postpartum nest differ in quality between the strains (Chiavegatto et al., 2012) with SM/J females building higher score nests than LG/J females. The LG/J × SM/J genetic background for females from this intercross generates a poor quality postpartum nest, as seen in F2 females. This may suggest interactions among genes modulating maternal performance of nest building. Nonetheless, even if mothers built similar nests before and after giving birth, the pups alone could alter the postpartum phenotypes measured. The decrease of postpartum Nest Closure and Nest Height quality in F2 could come from difficulties faced by mothers to keep nests structured with pups interfering. LG/J and SM/J females have smaller litter size (6.59 and 4.05, respectively) when compared to F2 females (8.73) (Góes, C. P., Sauce, B., and Peripato, A. C., unpublished data) and the interference of pups in the nest may be less pronounced in the parental strains. Since litter size has a positive correlation with Nest Presence (r = 0.21) and negative correlations with Nest Closure (r = −0.25) and Nest Height (r = −0.04) in the F2 females (Sauce, 2010), the number of pups may be impacting the quality of postpartum nest building.
The direct-effect QTL analysis of prepartum nest building detected 10 significant regions that explain, individually, between 3.4 and 11.2% of the variation, which indicates effects of moderate intensity compared to other genetic regions and phenotypes (Ramos et al., 1999; Turri et al., 2001). Six of the 10 direct-effect QTLs detected showed significant non-additive effects of over- and under-dominance. We also found direct-effect QTLs overlapping in pre- (preNS7 and preNS15) and postpartum (postNS7 and postNS15) nest building phenotypes. Considering that pre- and postpartum nest building may be distinct phenotypes, as indicated by our results on nest quality (closure and height) and considering that quality is also the difference between maternal and non-maternal nests in mice, the presence of common QTLs for pre- and postpartum Nest Structure suggests common genetic components in mothers shared with thermoregulatory nest building behavior in non-pregnant adults (Lynch, 1981; Weber and Olsson, 2008).
The analysis of epistasis revealed a vast number of interactions modulating prepartum nest building variation (Figures 3A,C) that ratify the participation of non-additive effects for this phenotype. We detected half as many direct-effect QTLs for postpartum nest building when compared to the prepartum period. This may not be surprising considering the smaller sample size of the former compared to the later. Interestingly, though, all postpartum QTLs showed over or under-dominance instead of only additive effects, which is not expected if you consider the higher degrees of freedom (sample size) required to detect interactions. It is possible that several of the loci with additive effects have small direct effects that would not show up as significant in our analysis, perhaps because alleles with larger direct effects might have been eliminated by natural selection. Hence, additive effects in the F2 females could be hidden from selection by epistatic interactions or be dependent on changes in environment and genetic architecture (Templeton, 2006). It is expected that, due to the Beavis effect (Beavis, 1998), the number of QTLs detected in analyses performed with less than 1000 individuals may be biased downward whereas their average effects will be biased upward. These effects are more pronounced with dominance, because there is higher variance associated with its detection, since in general there is more power to detect additive than dominance effects. We only detected dominance effects for postpartum nest building and a combination of additive and dominance for prepartum nest building. Because pre- and postpartum data have roughly the same sample size, this difference might not be due to the Beavis effect, but, instead, might suggest the existence of more interaction effects in the postpartum, possibly due to increased levels of complexity brought by the offspring. The mother-offspring interaction may be a source of epistasis because genes expressed in the offspring may interact with genes expressed in the mother (Wolf et al., 2002). Furthermore, the care of a mother affects many behaviors in the offspring (Varki et al., 2008), which may create a network of more complex behavioral interactions. This is exactly what we found, with even more complexity for the interactions in postpartum nest phenotypes (Figures 3B,D) that may reflect that pups foster more interactions among hormones than in pregnancy in which pups show only indirect effects. Moreover, because the postpartum period may have greater importance for pup survival (Wallace, 1981; Weber and Olsson, 2008), it is possible that these differences support the hypothesis that phenotypes more closely related to fitness have proportionally less additive genetic variance (Merilä and Sheldon, 1999).
Even though this study was performed in a cross between LG/J and SM/J, two strains which have been selected for size and have been maintained in the lab for more than 50 years, we may still consider broad evolutionary considerations to explain our results. Because the phenotypes here studied may be important to fitness, it is possible that the strains were exposed to direct selection favoring their survival in the lab during their formation. Nonetheless, the phenotypes here investigated failed to show significant correlations with size (data not shown), indicating that the alleles here studied were not subject to the same selection pressure as those at loci underlying variation in body size. As discussed previously (Peripato et al., 2004), we are investigating the effects of these alleles in an F2 intercross, a situation in which the alleles provide the largest genetic variance and are most easily detected, but this should not limit our ability to generalize these conclusions to natural populations because these alleles should have been randomly drawn from natural populations. The fact that even in this F2 cross, in which we might expect more additive variation distinguishing different lineages, a large portion of the variation segregating comes from dominance and epistasis, suggests that non-additivity may be just as relevant, or even more relevant, in natural populations.
There are several genomic regions associated with nest building in these mice that also interact with other locations across the genome. Even the regions with direct effects also have indirect effects due to interactions with other regions, such as preMU16 that has an additive effect but is involved in an epistatic interaction with the distal region of chromosome 1. We found a similar number of dominance and additive effects for the prepartum period and only dominance effects in the postpartum period. More importantly, we found a large number of epistatic interactions for all phenotypes. The presence of many dominance and epistatic effects supports a genetic architecture compatible with a pattern where natural selection has biased direct and interaction variation on nest building behavior (Merilä and Sheldon, 1999; Templeton, 2006). Even if natural selection has not reduced additive genetic variation, phenotypes related with fitness might have higher epistatic and dominance variation due to more underlying genes being targets of mutational events and, consequently, more interactions per gene (Houle et al., 1996; Lynch and Walsh, 1998).
The results of the direct-effect and epistatic QTL analyses in the pre- and postpartum periods highlight the complexity in nest building’s genetic architecture. We expect that this phenotype, being a complex maternal behavior and a fitness-related trait, may have intermediate genetic effects and several regions with dominance and epistatic interactions. Using the same intercross, we found the same pattern in other maternal aspects related to fitness such as maternal performance for offspring survival (Peripato et al., 2002), litter size (Peripato et al., 2004), and milk provision (Góes, C. P., Sauce, B., and Peripato, A. C., unpublished data). On the other hand, studying non-fitness-related traits, such as morphology and body composition, in the same intercross, we found more direct-effect locus QTL of small additive effect and fewer epistatic QTLs than compared to those fitness-related traits (Norgard et al., 2008; Leamy et al., 2009). Considering the higher degrees of freedom in direct-effect QTLs tests, we should expect more direct effects than epistatic effects, particularly considering the reduced sample sizes here investigated. Therefore, the greater number of epistatic QTLs when compared to direct-effect QTLs in our study suggests that genetic interactions are modulating maternal behavior of nest building.
Nest building in mammals is set by an important array of maternal behaviors that ensures pups survival and it is directly associated with fitness, as well as milk provision (Falconer and Mackay, 1996), suggesting that genetic interactions could play a major role in the adaptive process as stocks of new additive variation (Phillips, 2008). The QTL effects found in pre- and postpartum nest building behaviors show low to moderate values. This is expected in a genetic architecture of fitness-related traits because, according to some models, mutations with intermediate effects are more favored during evolution of traits closely related to fitness (Merilä and Sheldon, 1999). In conclusion, our results provide important information about the genetic architecture of the maternal behavior of nest building in mice. We found 15 individual QTLs with effects ranging from 4 to 13% of the phenotypic variation in nest building, but when all significant epistatic interactions (71 overall) are considered, they explain on average 47.7% of the variation per nest building phenotype (ranging from 28.4 to 75.5%), indicative of the important role played by epistasis in the adaptive process of nest building behavior in mice.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Dr. James M. Cheverud and Dr. Iderval S. Sobrinho Jr. for comments on a previous version of this manuscript. This study was supported by grant from the Sao Paulo State Foundation for Research Support (FAPESP: 04/14583-9, and 05/56353-2 to Andrea Cristina Peripato). Bruno Sauce was recipient of a FAPESP master’s fellowship.
Appendix
Table A1.
Epistatic QTLs of prepartum nest presence in F2 females.
| Locus 1 | Locus distance to marker (cm) | Locus distance (cm) | Locus 2 | Locus distance to marker (cm) | Locus distance (cm) | Prob. epistasis | Type | Genotypic value | Prob. genotypic value |
|---|---|---|---|---|---|---|---|---|---|
| D4Mit16 | 8 | 68 | D7Mit227 | 10 | 32 | 4.48 × 10−8 | AD | 0.645 | 1.53 × 10−3 |
| DD | −0.952 | 9.51 × 10−8 | |||||||
| D5Mit6 | 4 | 46 | D6Mit1 | 16 | 16 | 1.6 × 10−5 | AD | −0.534 | 1.31 × 10−3 |
| DA | 0.615 | 5.12 × 10−5 | |||||||
| D6Mit9 | 0 | 22 | DXMit172 | 16 | 58 | 7.26 × 10−6 | AD | 0.351 | 1.30 × 10−2 |
| DD | 0.556 | 2.23 × 10−6 | |||||||
| D7Mit227 | 22 | 44 | D11Mit62 | 26 | 26 | 5.1 × 10−6 | AA | 0.669 | 6.45 × 10−4 |
| DA | 0.680 | 9.05 × 10−5 | |||||||
| D7Mit71 | 8 | 92 | D15Mit143 | 2 | 18 | 3.52 × 10−7 | AA | −0.650 | 2.31 × 10−3 |
| DA | −0.588 | 2.03 × 10−3 | |||||||
| DD | 0.693 | 4.75 × 10−5 | |||||||
| D8Mit89 | 8 | 76 | D10Mit10 | 14 | 62 | 2.53 × 10−7 | AA | −0.741 | 1.32 × 10−4 |
| AD | 0.442 | 3.89 × 10−3 | |||||||
| DD | 0.524 | 1.75 × 10−4 | |||||||
| D9Mit90 | 22 | 22 | D11Mit15 | 0 | 48 | 5.13 × 10−8 | DA | 0.862 | 9.30 × 10−6 |
| DD | −0.709 | 7.21 × 10−6 | |||||||
| D13Mit115 | 40 | 52 | D15Mit143 | 8 | 24 | 1.45 × 10−5 | AA | −0.732 | 2.82 × 10−4 |
| AD | 0.487 | 9.11 × 10−3 | |||||||
| DA | −0.545 | 4.25 × 10−3 | |||||||
| D15Mit143 | 10 | 26 | DXMit144 | 14 | 34 | 6.48 × 10−7 | AA | −0.534 | 5.23 × 10−3 |
| DA | 0.979 | 5.35 × 10−7 | |||||||
| D17Mit46 | 0 | 0 | D18Mit17 | 18 | 38 | 1.44 × 10−6 | DA | −0.308 | 2.36 × 10−2 |
| DD | −0.612 | 2.03 × 10−7 |
Epistasis type: AA, additive by additive; AD, additive by dominance; DA, dominance by additive; DD, dominance by dominance. Markers in bold were considered the same region in that respective chromosome.
Table A2.
Epistatic QTLs of prepartum nest structure in F2 females.
| Locus 1 | Locus distance to marker (cm) | Locus distance (cm) | Locus 2 | Locus distance to marker (cm) | Locus distance (cm) | Prob. epistasis | Type | Genotypic value | Prob. genotypic value |
|---|---|---|---|---|---|---|---|---|---|
| D1Mit212 | 8 | 26 | D4Mit235 | 6 | 6 | 3.79 × 10−5 | DD | 0.687 | 9.63 × 10−7 |
| D5Mit233 | 6 | 26 | D6Mit1 | 0 | 0 | 1.38 × 10−4 | DD | −0.675 | 3.19 × 10−6 |
| D5Mit233 | 4 | 24 | DXMit55 | 10 | 10 | 5.44 × 10−5 | AD | 0.805 | 8.12 × 10−7 |
| D6Mit58 | 10 | 62 | D9Mit8 | 14 | 68 | 2.26 × 10−7 | DD | 0.681 | 5.82 × 10−9 |
| D7Nds1 | 2 | 52 | D14Mit225 | 8 | 48 | 7.05 × 10−5 | AD | 0.827 | 1.54 × 10−6 |
| D9Mit4 | 10 | 46 | D11Mit14 | 0 | 66 | 6.56 × 10−6 | AD | 0.461 | 5.51 × 10−4 |
| DA | −0.561 | 1.40 × 10−4 | |||||||
| D19Mit35 | 8 | 66 | DXMit55 | 18 | 18 | 9.28 × 10−6 | AA | 0.351 | 3.38 × 10−2 |
| AD | 0.629 | 2.74 × 10−5 | |||||||
| DD | 0.356 | 9.70 × 10−3 |
Epistasis type: AA, additive by additive; AD, additive by dominance; DA, dominance by additive; DD, dominance by dominance. Markers in bold were considered the same region in that respective chromosome.
Table A3.
Epistatic QTLs of prepartum Material Used in F2 females.
| Locus 1 | Locus distance to marker (cm) | Locus distance (cm) | Locus 2 | Locus distance to marker (cm) | Locus distance (cm) | Prob. epistasis | Type | Genotypic value | Prob. genotypic value |
|---|---|---|---|---|---|---|---|---|---|
| D1Mit14 | 2 | 80 | D3Mit22 | 6 | 28 | 1.97 × 10−5 | DD | 1.038 | 2.60 × 10−6 |
| D1Mit3 | 6 | 10 | D5Mit59 | 6 | 70 | 1.72 × 10−4 | AA | −1.071 | 2.80 × 10−6 |
| D1Mit11 | 2 | 60 | D7Mit21 | 0 | 0 | 5.63 × 10−6 | AD | 0.789 | 1.89 × 10−4 |
| DD | 0.781 | 3.85 × 10−5 | |||||||
| D1Mit14 | 2 | 80 | D16Mit5 | 8 | 30 | 9.71 × 10−8 | AA | 0.802 | 7.06 × 10−4 |
| AD | 0.766 | 9.63 × 10−4 | |||||||
| DA | 0.916 | 6.19 × 10−6 | |||||||
| D5Mit338 | 10 | 60 | D12Mit2 | 10 | 28 | 8.17 × 10−6 | AD | 0.869 | 7.51 × 10−5 |
| DD | 0.732 | 3.29 × 10−4 | |||||||
| D5Mit59 | 2 | 66 | D19Mit43 | 10 | 10 | 1.19 × 10−5 | AA | −0.734 | 3.11 × 10−2 |
| AD | −1.075 | 7.33 × 10−4 | |||||||
| DA | −0.774 | 6.03 × 10−3 | |||||||
| DD | −0.796 | 6.67 × 10−3 | |||||||
| D8Mit58 | 6 | 6 | D17Mit10 | 18 | 60 | 6.98 × 10−7 | DA | 2.402 | 2.27 × 10−8 |
| D11Mit349 | 0 | 36 | D17Mit46 | 18 | 18 | 2.74 × 10−6 | AD | −2.401 | 1.49 × 10−7 |
| D11Mit62 | 0 | 0 | D18Mit17 | 0 | 20 | 4.62 × 10−5 | DD | 0.950 | 2.46 × 10−6 |
| D17Mit46 | 22 | 22 | D18Mit110 | 14 | 14 | 5.28 × 10−6 | AA | 0.945 | 4.98 × 10−2 |
| DA | 1.529 | 1.09 × 10−2 | |||||||
| DD | 2.897 | 1.81 × 10−6 |
Epistasis type: AA, additive by additive; AD, additive by dominance; DA, dominance by additive; DD, dominance by dominance. Markers in bold were considered the same region in that respective chromosome.
Table A4.
Epistatic QTLs of postpartum nest presence in F2.
| Locus 1 | Locus distance to marker (cm) | Locus distance (cm) | Locus 2 | Locus distance to marker (cm) | Locus distance (cm) | Prob. epistasis | Type | Genotypic value | Prob. genotypic value |
|---|---|---|---|---|---|---|---|---|---|
| D1Mit3 | 6 | 10 | D9Mit355 | 14 | 88 | 1.04 × 10−7 | AA | 1.395 | 1.23 × 10−7 |
| DA | −0.631 | 5.61 × 10−3 | |||||||
| D1Mit3 | 4 | 8 | D9Mit4* | 12 | 48 | 1.24 × 10−5 | AA | 1.181 | 1.27 × 10−6 |
| D1Mit7 | 6 | 48 | D11Mit325 | 0 | 58 | 6.67 × 10−6 | AA | 0.944 | 2.88 × 10−4 |
| AD | 0.624 | 1.42 × 10−3 | |||||||
| DD | 0.495 | 1.12 × 10−2 | |||||||
| D1Mit3 | 8 | 12 | DXMit172 | 12 | 54 | 1.94 × 10−5 | DD | 0.899 | 2.83 × 10−6 |
| D2Mit22 | 20 | 128 | D4Mit235 | 10 | 10 | 1.57 × 10−5 | AA | 0.609 | 1.17 × 10−2 |
| AD | 0.761 | 2.09 × 10−4 | |||||||
| DD | 0.618 | 2.32 × 10−3 | |||||||
| D2Mit22 | 12 | 120 | D9Mit355 | 18 | 92 | 9.13 × 10−7 | AA | 0.838 | 6.54 × 10−4 |
| DD | 1.095 | 2.1 × 10−6 | |||||||
| D2Mit22 | 10 | 118 | D12Mit5 | 6 | 44 | 1.21 × 10−8 | AA | −0.943 | 6.92 × 10−5 |
| DD | 1.122 | 4.51 × 10−8 | |||||||
| D2Mit22 | 12 | 120 | DXMit55 | 2 | 2 | 3.28 × 10−6 | AA | 0.762 | 1.87 × 10−3 |
| AD | −0.653 | 1.28 × 10−3 | |||||||
| DA | −0.719 | 1.67 × 10−3 | |||||||
| D3Mit22 | 4 | 26 | D6Nds5 | 0 | 36 | 2.64 × 10−7 | AA | −1.831 | 5.22 × 10−5 |
| AD | 1.052 | 1.15 × 10−3 | |||||||
| DA | −0.750 | 3.21 × 10−2 | |||||||
| DD | 0.915 | 2.64 × 10−3 | |||||||
| D4Mit235 | 10 | 10 | D5Mit59 | 18 | 82 | 1.7 × 10−10 | AA | −0.748 | 7.23 × 10−3 |
| AD | 1.073 | 9.98 × 10−7 | |||||||
| DA | −0.817 | 2.16 × 10−4 | |||||||
| DD | 0.735 | 8.58 × 10−5 | |||||||
| D4Mit16* | 8 | 68 | D11Mit14 | 14 | 80 | 1.61 × 10−6 | DA | −0.745 | 1.74 × 10−4 |
| DD | 0.781 | 8.72 × 10−6 | |||||||
| D4Mit235 | 4 | 4 | D15Mit143 | 8 | 24 | 7.52 × 10−5 | AD | −1.372 | 3.74 × 10−6 |
| D4Mit2 | 4 | 18 | D16Mit2 | 2 | 2 | 1.39 × 10−6 | DA | −1.379 | 5.16 × 10−7 |
| DD | 0.525 | 3.78 × 10−2 | |||||||
| D4Mit16* | 16 | 76 | D17Mit10 | 26 | 68 | 2.63 × 10−6 | AA | −1.051 | 7.50 × 10−4 |
| DA | −1.038 | 1.93 × 10−5 | |||||||
| D7Mit17 | 12 | 78 | D13Mit115 | 34 | 46 | 3.28 × 10−6 | DA | 1.513 | 8.79 × 10−8 |
| D9Mit355 | 12 | 86 | D12Mit5 | 10 | 48 | 8.25 × 10−13 | AA | −1.097 | 2.92 × 10−6 |
| DD | 1.200 | 2.28 × 10−11 | |||||||
| D9Mit4* | 2 | 38 | D13Mit115 | 40 | 52 | 2.54 × 10−8 | AA | −1.035 | 3.31 × 10−4 |
| AD | 0.654 | 6.66 × 10−3 | |||||||
| DA | −0.970 | 3.30 × 10−5 | |||||||
| DD | 0.663 | 3.60 × 10−3 | |||||||
| D10Mit15 | 22 | 44 | D15Mit143 | 18 | 34 | 2.62 × 10−11 | AA | −1.518 | 1.76 × 10−4 |
| AD | 1.369 | 2.65 × 10−5 | |||||||
| DA | −1.174 | 2.66 × 10−4 | |||||||
| DD | 1.327 | 2.91 × 10−6 | |||||||
| D10Mit14 | 2 | 66 | D18Mit17 | 0 | 20 | 5.76 × 10−10 | AA | 1.738 | 3.36 × 10−4 |
| AD | −1.770 | 3.77 × 10−6 | |||||||
| DA | −1.320 | 1.93 × 10−4 | |||||||
| DD | 1.035 | 1.32 × 10−3 | |||||||
| D11Mit14 | 14 | 80 | D13Mit115 | 28 | 40 | 6.07 × 10−10 | AA | 1.753 | 3.67 × 10−8 |
| AD | −1.233 | 1.09 × 10−4 | |||||||
| DA | −0.515 | 3.13 × 10−2 | |||||||
| DD | 0.631 | 3.36 × 10−2 | |||||||
| D11Mit349 | 6 | 42 | D16Mit2 | 0 | 0 | 5.11 × 10−7 | AA | −1.147 | 4.18 × 10−5 |
| AD | 0.621 | 5.39 × 10−3 | |||||||
| DD | 0.671 | 5.62 × 10−4 | |||||||
| D13Mit115 | 34 | 46 | D15Mit2* | 20 | 56 | 3.44 × 10−7 | AA | −1.097 | 2.56 × 10−4 |
| AD | −0.952 | 1.06 × 10−4 | |||||||
| DA | 0.871 | 3.01 × 10−3 | |||||||
| D13Mit115 | 8 | 20 | D17Mit10 | 24 | 66 | 2.02 × 10−7 | AA | 4.388 | 2.94 × 10−4 |
| AD | −3.092 | 8.69 × 10−4 | |||||||
| DA | −3.191 | 5.02 × 10−4 | |||||||
| DD | 1.819 | 2.52 × 10−2 | |||||||
| D13Mit147 | 26 | 98 | DXMit172 | 10 | 52 | 4.83 × 10−6 | AA | −0.939 | 3.10 × 10−4 |
| DD | 0.822 | 1.78 × 10−5 | |||||||
| D14Mit5 | 10 | 38 | DXMit55 | 0 | 0 | 3.5 × 10−7 | AA | 0.712 | 7.06 × 10−4 |
| AD | −0.754 | 1.99 × 10−5 | |||||||
| DA | −0.439 | 1.45 × 10−2 | |||||||
| D15Mit2* | 20 | 56 | D16Mit5 | 14 | 36 | 1.31 × 10−6 | AA | −0.953 | 5.11 × 10−5 |
Epistasis type: AA, additive by additive; AD, additive by dominance; DA, dominance by additive; DD, dominance by dominance. Markers in bold were considered the same region in that respective chromosome. *After marker means a different set that is considered as same region in the same chromosome.
Table A5.
Epistatic QTLs of postpartum nest structure in F2 females.
| Locus 1 | Locus distance to marker (cm) | Locus distance (cm) | Locus 2 | Locus distance to marker (cm) | Locus distance (cm) | Prob. epistasis | Type | Genotypic value | Prob. genotypic value |
|---|---|---|---|---|---|---|---|---|---|
| D1Mit14 | 14 | 92 | D9Mit8 | 6 | 60 | 7.73 × 10−6 | AA | 0.672 | 5.02 × 10−3 |
| DA | −0.764 | 1.30 × 10−4 | |||||||
| DD | 0.505 | 7.24 × 10−3 | |||||||
| D1Mit541 | 2 | 96 | D11Mit14 | 14 | 80 | 1.95 × 10−9 | AA | 0.844 | 5.04 × 10−4 |
| AD | −0.676 | 4.72 × 10−4 | |||||||
| DA | −0.839 | 2.43 × 10−5 | |||||||
| DD | 0.579 | 8.92 × 10−4 | |||||||
| D2Mit307 | 0 | 88 | D4Mit235 | 12 | 12 | 1.12 × 10−5 | AA | −0.767 | 2.55 × 10−4 |
| DA | 0.620 | 3.63 × 10−4 | |||||||
| D2Mit380 | 18 | 68 | D16Mit5 | 4 | 26 | 6.36 × 10−8 | DA | 0.412 | 3.22 × 10−2 |
| DD | −1.025 | 1.15 × 10−8 | |||||||
| D2Mit307 | 0 | 88 | D19Mit39 | 14 | 42 | 7.67 × 10−6 | AD | −0.606 | 1.63 × 10−2 |
| DD | 1.019 | 2.82 × 10−6 | |||||||
| D3Mit54 | 20 | 20 | D7Mit71 | 6 | 90 | 8.12 × 10−7 | AA | 1.358 | 3.51 × 10−3 |
| AD | 1.000 | 6.03 × 10−3 | |||||||
| DA | 0.903 | 6.52 × 10−3 | |||||||
| DD | 1.152 | 1.81 × 10−4 | |||||||
| D5Mit59 | 12 | 76 | D7Mit71 | 0 | 84 | 6.26 × 10−9 | AA | −1.037 | 2.61 × 10−4 |
| AD | −0.774 | 3.67 × 10−4 | |||||||
| DA | 0.505 | 3.50 × 10−2 | |||||||
| DD | 0.905 | 1.16 × 10−5 | |||||||
| D5Mit338 | 8 | 58 | D12Mit6 | 14 | 64 | 7.34 × 10−6 | AA | 1.074 | 8.66 × 10−4 |
| AD | 0.792 | 1.32 × 10−3 | |||||||
| DA | 0.637 | 9.6 × 10−3 | |||||||
| D7Mit17 | 12 | 78 | D13Mit115 | 18 | 30 | 1.25 × 10−6 | DD | 1.706 | 5.79 × 10−8 |
| D7Mit46 | 8 | 116 | D17Mit46 | 20 | 20 | 1.26 × 10−5 | AD | 0.752 | 3.50 × 10−2 |
| DA | 1.155 | 8.93 × 10−5 | |||||||
| DD | −0.928 | 7.99 × 10−3 | |||||||
| D10Mit10 | 8 | 56 | D15Mit143 | 10 | 26 | 3.9 × 10−6 | AA | 1.220 | 1.66 × 10−4 |
| AD | −1.097 | 2.49 × 10−4 | |||||||
| D10Mit213 | 10 | 10 | D19Mit39 | 28 | 56 | 8.18 × 10−6 | AD | 0.626 | 4.57 × 10−3 |
| DA | −0.714 | 8.44 × 10−3 | |||||||
| DD | 0.912 | 1.12 × 10−4 | |||||||
| D12Mit6 | 14 | 64 | D19Mit43 | 22 | 22 | 5.29 × 10−7 | AA | −0.752 | 2.82 × 10−3 |
| AD | 0.800 | 3.44 × 10−4 | |||||||
| DA | −0.767 | 1.95 × 10−4 |
Epistasis type: AA, additive by additive; AD, additive by dominance; DA, dominance by additive; DD, dominance by dominance. Markers in bold were considered the same region in that respective chromosome.
Table A6.
Epistatic QTLs of postpartum temperature difference in F2 females.
| Locus 1 | Locus distance to marker (cm) | Locus distance (cm) | Locus 2 | Locus distance to marker (cm) | Locus distance (cm) | Prob. epistasis | Type | Genotypic value | Prob. genotypic value |
|---|---|---|---|---|---|---|---|---|---|
| D2Mit380 | 18 | 68 | D19Mit35 | 6 | 64 | 1.95 × 10−6 | AA | −0.569 | 5.06 × 10−3 |
| DA | 0.666 | 3.71 × 10−4 | |||||||
| DD | 0.552 | 9.76 × 10−4 | |||||||
| D6Nds5 | 14 | 50 | D10Mit15 | 0 | 22 | 1.19 × 10−5 | AD | −0.638 | 3.21 × 10−3 |
| DA | −0.496 | 1.1 × 10−2 | |||||||
| DD | 0.630 | 9.00 × 10−4 | |||||||
| D9Mit355 | 24 | 98 | D14Mit225 | 16 | 56 | 3.08 × 10−10 | DD | 1.314 | 8.70 × 10−12 |
| D10Mit14 | 6 | 70 | D13Mit1 | 0 | 0 | 1.54 × 10−5 | AD | 0.352 | 2.39 × 10−2 |
| DA | 0.702 | 6.59 × 10−6 | |||||||
| D13Mit147 | 20 | 92 | D18Mit17 | 18 | 38 | 3.69 × 10−6 | AD | −0.882 | 3.87 × 10−7 |
Epistasis type: AA, additive by additive; AD, additive by dominance; DA, dominance by additive; DD, dominance by dominance.
References
- Barnett S. A., Dickson R. G. (2008). Wild mice in the cold: some findings on adaptation. Biol. Rev. Camb. Philos. Soc. 64, 317–340 [DOI] [PubMed] [Google Scholar]
- Bateson P. (1994). The dynamics of parent offspring relationship in mammals. Trends Ecol. Evol. (Amst.) 9, 399–403 10.1016/0169-5347(94)90066-3 [DOI] [PubMed] [Google Scholar]
- Beavis W. D. (1998). “QTL analyses: power, precision, and accuracy,” in Molecular Dissection of Complex Traits, ed. Paterson A. H. (New York: CRC Press; ), 145–162 [Google Scholar]
- Boake C. R. B. (1994). Quantitative Genetic Studies of Behavioral Evolution. Chicago: The University of Chicago Press [Google Scholar]
- Bult A., Lynch C. B. (1997). Nesting and fitness: lifetime reproductive success in house mice bidirectionally selected for thermoregulatory nest-building behavior. Behav. Genet. 27, 231–240 10.1023/A:1025610130282 [DOI] [PubMed] [Google Scholar]
- Caspi A., Moffitt T. (2006). Gene-environment interactions in psychiatry: joining forces with neuroscience. Nat. Rev. Neurosci. 7, 583–590 10.1038/nrn1925 [DOI] [PubMed] [Google Scholar]
- Cheverud J. M., Ehrich T. H., Hrbek T., Kenney J. P., Pletscher L. S., Semenkovich C. F. (2004). Quantitative trait loci for obesity- and diabetes-related traits and their dietary responses to high-fat feeding in LGXSM recombinant inbred mouse strains. Diabetes 53, 3328–3336 10.2337/diabetes.53.10.2700 [DOI] [PubMed] [Google Scholar]
- Cheverud J. M., Routman E. J., Duarte F. A. M., van Swinderen B., Cothran K., Perel C. (1996). Quantitative trait loci for murine growth. Genetics 142, 1305–1319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheverud J. M., Vaughn T. T., Pletscher L. S., Peripato A. C., Adams E. S., Erikson C. F., King-Ellison K. J. (2001). Genetic architecture of adiposity in the cross of LG/J and SM/J inbred mice. Mamm. Genome 12, 3–12 10.1007/s003350010218 [DOI] [PubMed] [Google Scholar]
- Chiavegatto S., Sauce B., Ambar G., Cheverud J. M., Peripato A. C. (2012). Hypothalamic expression of Peg3 gene is associated with maternal care differences between SM/J and LG/J mouse strains. Brain Behav. 10.1002/brb3.58 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cockerham C. C. (1954). An extension of the concept of partitioning hereditary variance for analysis of covariances among relatives when epistasis is present. Genetics 39, 859–882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cockerham C. C., Zeng Z. B. (1996). Design III with marker loci. Genetics 143, 1437–1456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denenberg V. H., Taylor R. E., Zarrow M. X. (1969). Maternal Behavior in the rat: an investigation and quantification of nest building. Behaviour 34, 1–16 10.1163/156853969X00369 [DOI] [PubMed] [Google Scholar]
- Dietrich W., Katz H., Lincoln S., Shin H.-S., Friedman J., Dracopoli N., Lander E. S. (1992). A genetic map of the mouse suitable for typing intraspecific crosses. Genetics 131, 423–447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehrich T. H., Hrbek T., Kenney-Hunt J. P., Pletscher L. S., Wang B., Semenkovich C. F., Cheverud J. M. (2005). Fine-mapping gene-by-diet interactions on chromosome 13 in a LG/J SM/J murine model of obesity. Diabetes 54, 1863–1872 10.2337/diabetes.54.6.1863 [DOI] [PubMed] [Google Scholar]
- Erickson D. (2005). Mapping the future of QTL’s. Heredity 95, 417–418 10.1038/sj.hdy.6800699 [DOI] [PubMed] [Google Scholar]
- Falconer D. S., Mackay T. F. C. (1996). Introduction to Quantitative Genetics. New York: Longman Press [Google Scholar]
- Fleming A. S., O’Day D. H., Kraemer G. W. (1999). Neurobiology of mother-infant interactions: experience and central nervous system plasticity across development and generations. Neurosci. Biobehav. Rev. 23, 673–685 10.1016/S0149-7634(99)00011-1 [DOI] [PubMed] [Google Scholar]
- Francis D. D., Meaney M. J. (1999). Maternal care and the development of stress responses. Curr. Opin. Neurobiol. 9, 128–134 10.1016/S0959-4388(99)80016-6 [DOI] [PubMed] [Google Scholar]
- Friedman M. I., Bruno J. P. (1976). Exchange of water during lactation. Science 197, 409–410 10.1126/science.1246627 [DOI] [PubMed] [Google Scholar]
- Gaskill B. N., Rohr S. A., Pajor E. A., Lucas J. R., Garner J. P. (2011). Working with what you’ve got: changes in thermal preference and behavior in mice with or without nesting material. J. Therm. Biol. 36, 193–199 10.1016/j.jtherbio.2011.02.004 [DOI] [Google Scholar]
- Haley C. S., Knott S. A. (1992). A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69, 315–324 10.1038/hdy.1992.131 [DOI] [PubMed] [Google Scholar]
- Horseman N. D., Zhao W., Montecino-Rodriguez E., Tanaka M., Nakashima K., Engle S. J., Smith F., Markoff E., Dorshkind K. (1997). Defective mammopoiesis, but normal hematopoiesis, in mice with a targeted disruption of prolactin gene. EMBO J. 16, 6926–6935 10.1093/emboj/16.23.6926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houle D., Morikawa B., Lynch M. (1996). Comparing mutational variabilities. Genetics 143, 1467–1483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hrbek T., de Brito R. A., Wang B., Pletscher L. S., Cheverud J. M. (2006). Genetic characterization of a new set of recombinant inbred lines (LGXSM) formed from the intercross of SM/J and LG/J inbred mouse strains. Mamm. Genome 17, 417–429 10.1007/s00335-005-0038-7 [DOI] [PubMed] [Google Scholar]
- Kramer M., Vaughn T. T., Pletscher L. S., King-Ellison K., Adams E., Erikson C., Cheverud J. M. (1998). Genetic variation for body weight gain and composition in the intecross of Large (LG/J) and Small (SM/J) inbred strains of mice. Genet. Mol. Biol. 21, 211–218 10.1590/S1415-47571998000200007 [DOI] [Google Scholar]
- Lander E. S., Kruglyak L. (1995). Genetic dissection of complex traits: guidelines for interpreting and reporting linkage results. Nat. Genet. 11, 241–247 10.1038/ng1195-241 [DOI] [PubMed] [Google Scholar]
- Leamy L. J., Pomp D., Lightfoot J. T. (2009). Genetic variation for body weight change in mice in response to physical exercise. BMC Genet. 10, 58. 10.1186/1471-2156-10-58 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leamy L. J., Workman M. S., Routman E. J., Cheverud J. M. (2005). An epistatic genetic basis for fluctuating asymmetry of tooth size and shape in mice. Heredity 94, 316–325 10.1038/sj.hdy.6800637 [DOI] [PubMed] [Google Scholar]
- Lee C. T. (1973). Genetic analysis of nest-building behavior in laboratory mice (Mus musculus). Behav. Genet. 3, 247–256 10.1007/BF01067601 [DOI] [PubMed] [Google Scholar]
- Lee P. C., Majluf P., Gordon I. J. (1991). Growth, weaning and maternal investment from a comparative perspective. J. Zool. 225, 99–114 10.1111/j.1469-7998.1991.tb03804.x [DOI] [Google Scholar]
- Levy S. F., Siegal M. L. (2008). Network hubs buffer environmental variation in Saccharomyces cerevisiae. PLoS Biol. 6, e264. 10.1371/journal.pbio.0060264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J., Ji L. (2005). Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlation matrix. Heredity 95, 221–227 10.1038/sj.hdy.6800717 [DOI] [PubMed] [Google Scholar]
- Lisk R. D., Pretlow R. A., III, Friedman S. T. (1969). Hormonal stimulation necessary for elicitation of maternal nest- building in the mouse (Mus musculus). Anim. Behav. 17, 730–737 10.1016/S0003-3472(69)80020-5 [DOI] [PubMed] [Google Scholar]
- Liu B.-H. (1997). Statistical Genomics: Linkage, Mapping, and QTL Analysis. New York: CRC [Google Scholar]
- Lynch C. B. (1981). Genetic correlation between two types of nesting in Mus musculus: direct and indirect selection. Behav. Genet. 11, 267–272 10.1007/BF01065463 [DOI] [PubMed] [Google Scholar]
- Lynch C. B. (1994). “Evolutionary inferences from genetic analyses of cold adaptation in laboratory and wild populations of the house,” in Quantitative Genetic Studies of Behavioral Evolution, ed. Boake C. R. B. (Chicago: The University of Chicago Press; ), 278–301 [Google Scholar]
- Lynch C. B., Roberts R. C. (1984). Aspects of temperature regulation in mice selected for large and small size. Genet. Res. 43, 299–306 10.1017/S0016672300026082 [DOI] [PubMed] [Google Scholar]
- Lynch M., Walsh B. (1998). Genetics and Analysis of Quantitative Traits. Sunderland: Sinauer Associates [Google Scholar]
- Manly K. F., Cudmore R. H., Jr., Meer J. M. (2001). Map Manager QTX, cross-platform software for genetic mapping. Mamm. Genome 12, 930–932 10.1007/s00335-001-1016-3 [DOI] [PubMed] [Google Scholar]
- Marple D. N., Aberle E. D., Forrest J. C., Blake W. H., Judge M. D. (1972). Effects of humidity and temperature on porcine plasma adrenal corticoids, acth and growth hormone levels. J. Anim. Sci. 34, 809–812 [DOI] [PubMed] [Google Scholar]
- Merilä J., Sheldon B. C. (1999). Genetic architecture of fitness and nonfitness traits: empirical patterns and development of ideas. Heredity 83, 103–109 10.1046/j.1365-2540.1999.00585.x [DOI] [PubMed] [Google Scholar]
- Mousseau T. A., Fox C. W. (1998). Maternal Effects as Adaptations. New York: Oxford University Press [Google Scholar]
- Nelson J. E., Krawetz S. A. (1992). Purification of cloned and genomic DNA by guanidine thiocyanate/isobutyl alcohol fractionation. Anal. Biochem. 207, 197–201 10.1016/0003-2697(92)90523-A [DOI] [PubMed] [Google Scholar]
- Norgard E. A., Roseman C. C., Fawcett G. L., Pavlicev M., Morgan C. D., Pletscher L. S. (2008). Identification of quantitative trait loci affecting murine long bone length in a two-generation intercross of LG/J and SM/J Mice. J. Bone Miner. Res. 23, 887–895 10.1359/jbmr.080210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohta T. (1973). Slightly deleterious mutant substitutions in evolution. Nature 246, 96–98 10.1038/246096a0 [DOI] [PubMed] [Google Scholar]
- Parter M., Kashtan N., Alon U. (2008). Facilitated variation: how evolution learns from past environments to generalize to new environments. PLoS Comput. Biol. 4, e1000206. 10.1371/journal.pcbi.1000206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peripato A. C., Cheverud J. M. (2002). Genetic influences on maternal care. Am. Nat. 160, 173–185 10.1086/341014 [DOI] [PubMed] [Google Scholar]
- Peripato A. C., de Brito R. A., Matioli S. R., Pletscher L. S., Vaughn T. T., Cheverud J. M. (2004). Epistasis affecting litter size in mice. J. Evol. Biol. 17, 593–602 10.1111/j.1420-9101.2004.00702.x [DOI] [PubMed] [Google Scholar]
- Peripato A. C., de Brito R. A., Vaughn T. T., Pletscher L. S., Matioli S. R., Cheverud J. M. (2002). Quantitative trait loci for maternal performance for offspring survival in mice. Genetics 162, 1341–1362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips P. C. (2008). Epistasis – the essential role of gene interactions in the structure and evolution of genetic systems. Nat. Rev. Genet. 9, 855–867 10.1038/nrg2452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramos A., Moisan M. P., Chaouloff F., Mormède C., Mormède P. (1999). Identification of female-specific QTLs affecting an emotionality-related behavior in rats. Mol. Psychiatry 4, 453–462 10.1038/sj.mp.4000546 [DOI] [PubMed] [Google Scholar]
- Räsänen K., Kruuk L. E. B. (2007). Maternal effects and evolution at ecological time-scales. Funct. Ecol. 21, 408–421 10.1111/j.1365-2435.2007.01246.x [DOI] [Google Scholar]
- Rockman M. V. (2008). Reverse engineering the genotype-phenotype map with natural genetic variation. Nature 456, 738–744 10.1038/nature07633 [DOI] [PubMed] [Google Scholar]
- Rosenblatt J. S. (1975). Prepartum and postpartum regulation of maternal behaviour in the rat. Ciba Found. Symp. 33, 17–37 [DOI] [PubMed] [Google Scholar]
- Routman E. J., Cheverud J. M. (1994). A rapid method of scoring simple sequence repeat polymorphisms with agarose gel electrophoresis. Mamm. Genome 5, 187–188 10.1007/BF00352355 [DOI] [PubMed] [Google Scholar]
- Samocha K. E., Lim J. E., Cheng R., Sokoloff G., Palmer A. A. (2010). Fine mapping of QTL for prepulse inhibition in LG/J and SM/J mice using F2 and advanced intercross lines. Genes Brain Behav. 9, 759–767 10.1111/j.1601-183X.2010.00613.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sauce B. (2010). Arquitetura Genética do Comportamento Materno de Construção de Ninho. Masters Thesis, Universidade Federal de São Carlos, Brazil, 74 [Google Scholar]
- Schneider C. W., Chenoweth M. E. (1970). Effects of hallucinogenic and other drugs on the nest-building behaviour of mice. Nature 225, 1262–1263 10.1038/2251262a0 [DOI] [PubMed] [Google Scholar]
- Sherwin C. M. (1997). Observations on the prevalence of nest-building in non-breeding to strain mice and their use of two nesting materials. Lab. Anim. 31, 125–132 10.1258/002367797780600134 [DOI] [PubMed] [Google Scholar]
- Templeton A. R. (2006). Population Genetics and Microevolutionary Theory. New Jersey: John Wiley and Sons Inc [Google Scholar]
- Turri M. G., Datta S. R., DeFries J., Henderson N. D., Flint J. (2001). QTL analysis identifies multiple behavioral dimensions in ethological tests of anxiety in laboratory mice. Curr. Biol. 15, 725–734 10.1016/S0960-9822(01)00206-8 [DOI] [PubMed] [Google Scholar]
- van de Weerd H. A., Van Loo P. L. P., Van Zutphen L. F. M., Koolhaas J. M., Baumans V. (1998). Strength of preference for nesting material as environmental enrichment for laboratory mice. Appl. Anim. Behav. Sci. 55, 369–382 10.1016/S0168-1591(97)00043-9 [DOI] [PubMed] [Google Scholar]
- Varki A., Geschwind D. H., Eichler E. E. (2008). Explaining human uniqueness: genome interactions with environment, behaviour and culture. Nat. Rev. Genet. 9, 749–763 10.1038/nrg2428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughn T. T., Pletscher L. S., Peripato A., King-Ellison K., Adams E., Erikson C., Cheverud J. M. (1999). Mapping quantitative trait loci for murine growth: a closer look at genetic architecture. Genet. Res. 74, 313–322 10.1017/S0016672399004103 [DOI] [PubMed] [Google Scholar]
- Wallace M. E. (1981). The breeding, inbreeding and management of wild mice. Symp. Zool. Soc. Lond. 47, 183–204 [Google Scholar]
- Weber E. M., Olsson A. I. S. (2008). Maternal behaviour in Mus musculus sp.: an ethological review. Appl. Anim. Behav. Sci. 114, 1–22 10.1016/j.applanim.2008.06.006 [DOI] [Google Scholar]
- Weller J. I., Song J. Z., Heyen D. W., Lewin H. A., Ron M. (1998). A new approach to the problem of multiple comparisons in the genetic dissection of complex traits. Genetics 150, 1699–1706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf J. B., Vaughn T. T., Pletscher L. S., Cheverud J. M. (2002). Contribution of maternal effect QTL to genetic architecture of early growth in mice. Heredity 89, 300–310 10.1038/sj.hdy.6800140 [DOI] [PubMed] [Google Scholar]
- Zimmerberg B., Shartrand A. M. (2004). Temperature-dependent effects of maternal separation on growth, activity, and amphetamine sensitivity in the rat. Dev. Psychobiol. 25, 213–226 10.1002/dev.420250306 [DOI] [PubMed] [Google Scholar]