A Model Combining Oscillations and Attractor Dynamics for Generation of Grid Cell Firing

Abstract

Different models have been able to account for different features of the data on grid cell firing properties, including the relationship of grid cells to cellular properties and network oscillations. This paper describes a model that combines elements of two major classes of models of grid cells: models using interactions of oscillations and models using attractor dynamics. This model includes a population of units with oscillatory input representing input from the medial septum. These units are termed heading angle cells because their connectivity depends upon heading angle in the environment as well as the spatial phase coded by the cell. These cells project to a population of grid cells. The sum of the heading angle input results in standing waves of circularly symmetric input to the grid cell population. Feedback from the grid cell population increases the activity of subsets of the heading angle cells, resulting in the network settling into activity patterns that resemble the patterns of firing fields in a population of grid cells. The properties of heading angle cells firing as conjunctive grid-by-head-direction cells can shift the grid cell firing according to movement velocity. The pattern of interaction of oscillations requires use of separate populations that fire on alternate cycles of the net theta rhythmic input to grid cells.

Introduction

Neurophysiological recordings from the entorhinal cortex of rats foraging in an open field environment have demonstrated neurons termed grid cells (Moser and Moser, 2008). Grid cells exhibit spiking activity when the rat visits specific locations in the environment that are laid out in a regular array of locations that fall on the vertices of tightly packed equilateral triangles (Fyhn et al., 2004; Hafting et al., 2005; Moser and Moser, 2008). This regular firing pattern of grid cells indicates that these neurons effectively encode the location of the rat as it moves along a complex trajectory. Grid cells at different dorsal to ventral positions in the medial entorhinal cortex show differences in the size and spacing between their firing fields (Hafting et al., 2005; Sargolini et al., 2006).

A number of models have addressed potential mechanisms for the firing pattern of grid cells that can be categorized based on different features (see Zilli, 2012, this special issue, for review). Among other things, models can be categorized in terms of how they code location. Many attractor models code location with sustained fixed-point attractor states (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Guanella et al., 2007; Burak and Fiete, 2009). In contrast, another class of models code location by the relative phase of oscillations (Blair et al., 2007; Burgess et al., 2007; Hasselmo et al., 2007; Burgess, 2008; Hasselmo, 2008; Zilli and Hasselmo, 2010; Welday et al., 2011). The second class of models is commonly referred to as oscillatory interference models (Burgess et al., 2007), though the oscillatory interference in these models is involved in generating the model output, and the relative phase code itself does not require interference (Zilli, 2012). Both classes of models address certain features of the experimental data.

Many continuous attractor models generate the hexagonal array of firing based on synaptic connectivity between neurons in the entorhinal cortex. The synaptic connectivity is circularly symmetric on average and depends on the distance between the environmental locations coded by individual grid cells. The firing can be updated by velocity input shifting the network attractor. Attractor models can account for the shared orientation of grid cells recorded close to each other in entorhinal cortex (Hafting et al., 2005; Fyhn et al., 2007), for the discrete quantal jumps in grid cell spacing (Barry et al., 2007), and for the sometimes irregular distribution of grid cell firing fields.

In contrast, oscillatory interference models generate the spatial pattern of firing due to interference between oscillations of different frequency (Burgess et al., 2007; Blair et al., 2008; Burgess, 2008; Hasselmo, 2008). In existing implementations of this model, the difference in frequency is driven by the running velocity of the animal, coded by neurons sensitive to head direction and to running speed. Oscillatory interference models provide a framework for generating the theta phase precession of grid cells (Hafting et al., 2008) in models (Burgess, 2008), and for linking the spacing of grid cells to the intrinsic frequency of these neurons as measured with both extracellular recording in vivo (Jeewajee et al., 2008) and with intracellular recording of the resonance frequencies of membrane potential dynamics in vitro (Giocomo et al., 2007; Giocomo and Hasselmo, 2008). The link to intrinsic properties is supported by recent data showing that changes in intrinsic properties due to knockout of the HCN1 subunit of the h current channel alters the spacing and size of entorhinal grid cell firing fields (Giocomo et al., 2011).

None of the existing models yet account for the full range of data on grid cells. Most initial attractor dynamic models did not require theta rhythm oscillations (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burak and Fiete, 2009), did not show theta phase precession, and did not link grid cell properties to intrinsic properties. However, a recent model using attractor dynamics does address all of these issues (Navratilova et al., 2011). Continuous attractor models rely on structured circularly symmetric synaptic connectivity to create the pattern of grid cell firing fields. A difference in the gain of velocity input on frequency could generate the change in firing patterns observed with changes in environment size (Barry et al., 2007) or shape (Derdikman et al., 2009). Oscillatory interference models have less dependence on synaptic connectivity, but they require velocity controlled oscillators regulated by speed and with preferred movement direction at intervals distributed at multiples of 60° in order to generate hexagonal patterns of interference. The continuous attractor models do not require this fixed interval of head direction input. Instead, continuous attractor models generate hexagons due to the interaction of circularly symmetric connectivity, consistent with theorems showing that hexagons provide the densest packing of circles (Fuhs and Touretzky, 2006).

The initial proposal of oscillatory interference models addressed both network and single cell implementations (Burgess et al., 2005, 2007; Burgess, 2008). Recent oscillatory interference models have used interactions of network oscillations (Zilli and Hasselmo, 2010) to overcome the issues preventing implementation with single neurons, including the variability of the temporal period of membrane potential oscillations or bistable persistent spiking (Zilli et al., 2009), the tendency of oscillations within single neurons to synchronize (Remme et al., 2009, 2010) and the lack of a linear relationship between membrane potential oscillations and depolarization (Yoshida et al., 2011). However, models using network oscillations (Zilli and Hasselmo, 2010), do not yet explain the link of grid cell spacing to the intrinsic membrane current properties of entorhinal neurons (Giocomo et al., 2007, 2011).

Recent data shows a loss of the spatial periodicity of grid cells when network theta rhythm oscillations are reduced by inactivation of the medial septum (Brandon et al., 2011; Koenig et al., 2011). These recent results along with the data on the cellular frequency of medial entorhinal neurons (Giocomo et al., 2007; Jeewajee et al., 2008) provide impetus for trying to understand how network theta oscillations and single cell intrinsic frequency contribute to the mechanism of grid cell generation. As a step in this direction, the model presented here combines oscillations and attractor dynamics to generate simulations of grid cell firing fields.

Materials and Methods

Overview of model

The model uses two populations of neurons inspired by experimental data. One population represents grid cells without head direction selectivity in medial entorhinal cortex, as described initially in the Moser laboratory (Fyhn et al., 2004; Moser and Moser, 2008). Cells in the second population are termed heading angle cells, and they are inspired by conjunctive cells that combine sensitivity to head direction with the spatially periodic firing of grid cells, as discovered in the Moser laboratory (Sargolini et al., 2006) and replicated in later work (Hafting et al., 2008; Brandon et al., 2011). Similar to conjunctive cells, this second population in the model contains cells that increase their activity when the rat is moving and the current head direction angle matches their preferred head direction, but they also have a background level of activity for all current head directions. This population has fixed, unchanging connections to the grid cell population with a pattern of connections that depends on each cells preferred heading angle in the environment. The rationale for these neurons is that the ability to shift the grid cell representation for movement in any arbitrary heading could arise from transitions between heading angle cells coding sequential spatial phases along that heading. The grid cell population has fixed, unchanging connections back to the heading angle cells such that grid cells coding a specific spatial phase of locations connect to an array of heading angle cells coding that same spatial phase.

Heading angle cells

In the model, the heading angle cells are divided into separate sub-populations referred to here as arrays. Each array of heading angle cells codes a specific spatial phase designated by spatial phase indices x and y. Spatial phases have integer values x = [1, 2…30] and y = [1,2…30] for a total of 900 arrays of heading angle cells. Within each heading angle cell array there are cells coding a full range of 24 heading angles (at 15° intervals), and each heading angle is coded by 10 cells that oscillate with different temporal phases. These cells have fixed, unchanging matrices of synaptic connections to a population of grid cells that contains a single grid cell coding each spatial phase (i.e., 900 total grid cells).

The fixed pattern of synaptic connections from heading angle cells to grid cells is based on the allocentric heading angle ϕ coded by individual heading angle cells, for example toward the East (0° heading angle), or the Northeast (45° heading angle). The structure of the model is summarized in Figures 1 and 2. In the figures, the activity of the heading angle cells is usually shown as the pattern of synaptic output to the grid cell population from individual heading angle arrays, filtered by the fixed pattern of synaptic connectivity between the heading angle array and the grid cell population. In the figures, the neurons will be plotted according to how their spatial phase maps to the environment, but this does not imply that neurons are laid out with anatomical topography within the entorhinal cortex, as data shows they are not (Hafting et al., 2005).

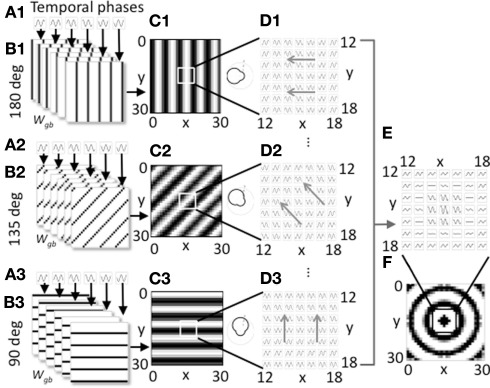
Figure 1.

Overview of model components for a single spatial phase. (A1–A3). Three groups of heading angle cells described by Eq. 1 show oscillations over time with different temporal phases (six phases shown). (B1–B3) The three groups project to grid cells with synaptic connectivity that depends on the six different temporal phases and the heading angles of 180° (B1), 135° (B2), and 90° (B3). Only 3 of 24 heading angles are shown. Connectivity also depends upon spatial phase. The groups shown all code a single spatial phase. (C1–C3) At a single time t, the synaptic input to the grid cell population from a full set of temporal phases coding an individual heading angle and spatial phase contains bands of higher amplitude (black). The polar plots on the right show how the output amplitude for each heading angle will change dependent on the direction of movement. (D1–D3) The full time course plotted for a 7 by 7 array of synaptic inputs shows that they oscillate over time with different temporal phases and align to form different spatial bands. Different spatial phases reach the peak of the oscillation at different times resulting in a shift in the bands over time in the direction of the gray arrows. (E) Synaptic input to a 7 by 7 array of grid cells is shown summed across all heading angles for a group of cells coding the spatial phase in the center of the grid cell plane (x = 15, y = 15). (F) At a single point in time, for this single spatial phase, the distribution of synaptic input to the full 30 by 30 array of the grid cell plane when summed over all heading angles has a circularly symmetric pattern.

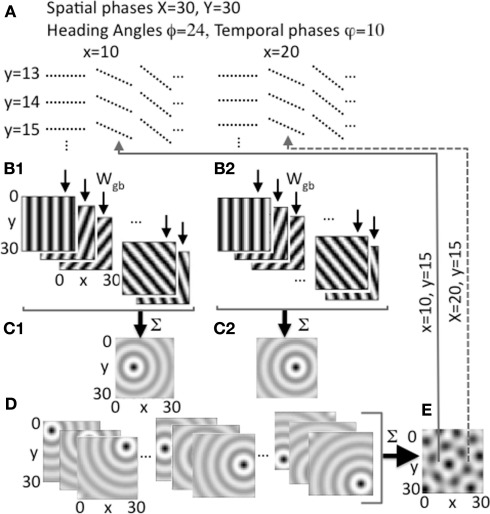
Figure 2.

Heading angle input across the full range of spatial phases. (A) Each spatial phase (x, y) is coded by a heading angle array that includes 24 different heading angles with 10 different temporal phases in each heading angle. Examples show 3 out of 24 angles for individual spatial phases y = 13, 14, 15 and x = 10, 20, with 10 temporal phases (dashed lines) for each angle. (B1,B2) Examples show synaptic output to the grid cell plane from different heading angle cell groups coding 5 out of 24 angles for a single spatial phase at a single point in time t, with bands of higher amplitude synaptic input shown in black. (B1) Shows example output for a single pair of spatial phases x = 10, y = 15, and (B2) shows output for x = 20, y = 15. (C1) Sum of all heading angle output plotted at a single time t for a single spatial phase (x = 10, y = 15). The sum over heading angles creates an amplitude pattern of circles in the grid cell plane centered on the grid cell spatial phase x = 10, y = 15. (C2) The sum of the synaptic output over all heading angles for spatial phase x = 20, y = 15. (D) Examples show synaptic output for a range of different spatial phases (left: y = 5, x = 5, 15, 25; center: y = 15, x = 5, 15, 25; right: y = 25, x = 5, 15, 25). (E) The synaptic output from heading angles is summed across all spatial phases in the grid cell plane. The example shows that differences in the relative amplitude of the heading angle input will result in a grid cell pattern. Arrows show examples of feedback from individual grid cells in the grid cell plane that project back to regulate input from heading angle cell arrays coding x = 10, y = 15 (solid line) and x = 20, y = 15 (dashed line).

Note that the model equates head direction with the direction of movement by the rat, making the assumption that when the rat is moving its head direction is usually in the direction of movement. In contrast to many oscillatory interference models, this model does not focus on heading angles that fall at intervals of 60°. Instead, this model utilizes neurons coding a large number of heading angles at regular intervals (at 15° intervals). The spatial phases of each array of heading angle cells are similar to the spatial phases of the firing fields of conjunctive cells (Sargolini et al., 2006; Brandon et al., 2011). This corresponds to the relative position coded by the heading angle cell in the environment, but because the coding is periodic it does not limit the spatial range that can be coded by the network.

The heading angle cells at each spatial phase x, y, and each heading angle ϕ_i have temporal dynamics of their membrane potential b(t) described by a difference equation:

$$\begin{array}{rcll}{b}_{\varphi ,\text{φ},x,y}\left(t\right)& =\tau b\left(t-1\right)+sin\left(2\pi \left(ft+{\phi }_k\right)\right)& & \\ & \times {\left[g_{x,y}\left(t\right)-{\lambda }_g\right]}_{+}∕{max}_{x,y}\left(g\left(t\right)\right)& & \text{(1)}\end{array}$$

This difference equation models the persistence of activity from the previous time step according to tau (τ= 0.2). The equation also includes oscillatory input from the medial septum with a temporal frequency f which was set to 4 Hz to replicate properties of theta cycle skipping, so that the grid cell population would generate a frequency of 8 Hz as described below. For each pair of spatial phases x, y, and heading angle ϕ_i (with index i) there is a full array of neurons with different temporal phases φ_k described by the index k. The temporal phase φ_k, the spatial phases x, y, and the heading angle ϕ_i all determine the pattern of connectivity of a given heading angle cell to the array of grid cells. The temporal phase determines the position along each heading angle for connections to the grid cell array. The oscillatory activity described by equation 1 is shown for different temporal phases in Figures 1A1–A3. The figure also shows the synaptic output of these cells that is described below in the section on Connectivity with Grid Cells.

Equation 1 for heading angle cell activity also includes feedback from the grid cell population g(t), where each array of heading angle cells coding a specific spatial phase x, y have their oscillatory input multiplied by the corresponding activity of the grid cell g_x,y. That is, the grid cell with spatial phase coordinates x,y regulates the activity of the array of heading angle cells with spatial phase coordinates x,y. If the activity of both regions were laid out as vectors, the connectivity would be an identity matrix. The feedback from grid cells has a threshold linear input-output function designated by []₊ that takes the value of the grid cell activity g(t) − λ_g when it is above the threshold λ_g = 0.6 and stays at zero below threshold. In addition, the grid cell output was sometimes normalized to the maximum activity level of individual grid cells max_x,y(g(t)) at time t measured over all spatial phases x,y. This normalization helps to prevent the system from exploding or dying out in activity. This normalization was used in Figure 5 to provide greater stability during movement, but was not used in the other figures in order to allow the time courses to be more visible in the plots in Figure 7. This effect could be mediated by feedback inhibition.

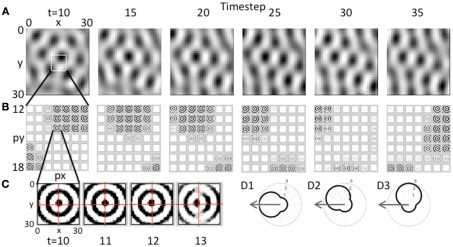
Figure 5.

Movement of the grid cell activity induced by speed modulation of head direction input. (A) With constant speed and with head direction facing West, the network receives greater input from the heading angle line coding West. This causes a progressive shift in the population activity of the grid cell plane, resulting in the hexagonal pattern shifting to the West. (B) This shift occurs because of the distortion in the circular pattern of synaptic input. The synaptic weights do not change, but the greater amplitude of oscillations in heading angle cells coding angles closer to West distorts the magnitude of synaptic input from each array of heading angle cells, resulting in a progressive shift of grid cell activity to the West. Feedback from the grid cell plane to the heading angle plane causes a progressive shift in the synaptic input. (C) Expansion of the synaptic input from the heading angle neurons coding a single spatial phase shows that on successive time steps 11–13 the circles show a distortion toward the West. Rhythmic regulation of the network prevents activity during the period when the same heading angle input would distort the pattern toward the East. (D1) A polar plot shows the amplitude of response of a heading angle cell with an angle of 180° (West). The arrow shows how the input velocity causes a maximum change in amplitude (3.0) for this heading angle cell. (D2) A heading angle cell with angle of 135° (Northwest) has a smaller change in amplitude (2.4). (D3) A heading angle cell with angle of 90° (North) shows no change in response for this velocity, but maintains the background amplitude (1.0).

Figure 7.

Plots of neural activity over time. (A) Time course of activity of the heading angle cells in Group (A) representing different angles for a 7 by 7 array of heading angle spatial phases from the center of the population used in Figures 3–4. (B) Time course of activity of the heading angle cells in Group (B) representing the same angles and spatial phases, but regulated to be active at different temporal phase (see text). (C) Time course of total synaptic input to the grid cell population showing oscillations that are double the frequency of the oscillations in Group (A) and Group (B). The activity in (A,B) shows theta cycle skipping relative to activity in (C).

Connectivity with grid cells

The heading angle cells project to the grid cells via patterns of synaptic connections that depend upon the heading angle cell properties including assigned spatial phase, heading angle and temporal phase. As shown in Figure 1B, each heading angle cell sends connections to grid cells arranged in lines in the grid cell plane with angles across the plane that depend upon the heading angle of the originating cell. The connections from the heading angle cell array b to the grid cell population g is described by a multi-dimensional matrix W_gb. This can be considered as an array of individual matrices, each of which connects a vector of heading angle cells with different temporal phases (but the same spatial phase and heading angle) to grid cells with different spatial phases x, y. The synaptic weights have values of 0 or 1. The index k for weights to be set to 1 is determined by the following equation:

$$W_{gb}\left(x,y,px,py,k,i\right)=1$$ (2)

if:

$$\begin{array}{l}k=\text{round(}K(\mathrm{mod}(f_s(\cos ({\phi }_{\text{i}}\text{)(}x-px)/X\\ +\sin ({\phi }_i)(y-py)/Y),1)))\end{array}$$

where x, y describe the spatial phase in the grid cell population. For computing connectivity from the heading angle cell population, px and py describe the spatial phase in this equation, ϕ_i describes the heading angle. The value k is the index for the heading angle cell with temporal phase φ_k and K is the total number of different temporal phases of the heading angle cells coding a specific spatial phase px, py, and heading angle ϕ_i. The value f_s is the spatial frequency which in the simulations shown here ranged between three and five cycles across the full range of spatial phases in the population. X is the total number of discrete spatial phases along the spatial phase dimension indexed by x (and px), and Y is the total number of discrete spatial phases along the dimension of spatial phase indexed by y (and py). The use of the mod function mod() ensures that values beyond the range of the matrix are mapped back into the matrix.

Equation 2 is not particularly intuitive, but the connectivity pattern is relatively simple as shown in Figure 1B. Each heading angle cell connects to the plane of grid cells in bands that have heading angle ϕ_i, a spatial phase offset px, py, and a position within each cycle of spatial phase that depends upon temporal phase φ_k. The connections for six heading angle cells with different temporal phases are shown in Figure 1B1 (for cells with heading angle 180), in part B2 for cells with heading angle of 135° and in part B3 for cells with heading angle of 90°. This results in synaptic output with bands of shared phase to the grid cell plane (Figures 1C,D).

Figure 1 shows how the individual sets of heading angle cells have different temporal phases for different relative positions along an individual heading angle. The position of these temporal phases is offset for neurons with different two-dimensional spatial phases. As shown in Figure 1C, each set of active cells multiplied by the fixed synaptic connectivity matrix W_gb produces synaptic output with temporal phases of oscillation that appear in bands across the environment that are perpendicular to the preferred heading angle. Each square in Figure 1C shows the result of multiplying the synaptic connectivity matrices in Figure 1B with the vector of heading angle cells with different temporal phases that code an individual spatial phase with an individual heading angle. For a single snapshot in time, as shown in Figure 1C, the differences in temporal phase result in bands of higher amplitude that are perpendicular to the preferred heading angle. A movie of this activity over time shows waves of activity that move across the plane of spatial phases in the direction of the heading angle, as indicated by the gray arrows in Figure 1D. When the output of heading angle cells is summed across all heading angles, this results in a standing wave pattern of concentric circles as shown across time in Figure 1E and at a single point in time in Figure 1F. The polar plots in Figure 1C show that the amplitude of the oscillations depends upon the heading direction of the virtual rat. There is a background oscillation of amplitude one for all heading angles regardless of the heading of the virtual rat, but this amplitude is increased when the rat runs in a heading that matches the heading angle for individual heading angle cells. The heading angle cell amplitude is also influenced by the feedback from the grid cells which show spatial periodicity, so these heading angle cells have properties of spatial periodicity, theta rhythmicity, and heading angle sensitivity similar to conjunctive cells (but with a baseline response during all directions of movement).

Interaction between heading angle cells and grid cells

The array of heading angle cells sends input to the array of grid cells via the connectivity matrix W_gb. The activation of the grid cells is described by:

$$g_{x,y}\left(t\right)=\tau g\left(t-1\right)+\sum _{\varphi ,px,py}{W}_{gb}{b}_{px,py,\varphi ,\phi }\left(t\right)∕{max}_{x,y}\left(W_{gb}b\left(t\right)\right)$$ (3)

Where g_x,y(t) represents the activation of an individual grid cell with spatial phase described by x, y. The activity of the grid cell shows persistence of activity from the previous timestep according to the parameter tau (τ= 0.3). As described above, for each group of heading angle cells with a specific spatial phase px, py and heading angle ϕ, individual heading angle cells with temporal phase φ send output to grid cells at periodic spatial phases x, y. The number of spatial bands of this periodic output are determined by the spatial frequency f_s of the synaptic connectivity and the total number of spatial phases X and Y being simulated. As shown in Eq. 3, the inputs to the grid cell are summed over the array of heading angles ϕ (Figures 1F and 2C,D) and are also summed over the different spatial phases px,py and of the heading angle cell population (Figure 2E). In most simulations, the activity is normalized to the spatial phase x,y with maximum value at time t of the synaptic input from the heading angle plane that was summed across angles (the maximum is taken from the full set of possible combinations of postsynaptic spatial phases x,y and presynaptic spatial phases px,py). The activity in the grid cell plane starts out with random activity drawn from a uniform distribution between 0 and 1.

As shown previously in Eq. 1, the heading angle cells receive feedback from the grid cells via direct one to one connections from grid cells coding the corresponding spatial phase x = px and y = py. Thus, if we consider only the spatial phase index px, py of the heading angle cells and lay them out in a single vector, then the feedback connectivity matrix from grid cells to heading angle cells would be an identity matrix. The normalization of the feedback from the grid cell layer in Eq. 1 is sufficient to keep the network within a stable range of activity when implemented alone, but in most simulations normalization to a maximum was used in both Eqs 1 and 3.

The input arising from the heading angle population is summarized in Figure 2 which shows examples of the synaptic output for different heading angles. Note that Figures 1C and 2B plot the amplitudes at one point in time of the full set of synaptic inputs from each heading angle to the grid cell plane. This results in input to the grid cell population that constantly shifts in phase in the direction of heading angle over time (see Figure 6 below), similar to rotating ring attractors in models by Blair (Blair et al., 2007; Welday et al., 2011). The different temporal phases result in a constant shift in amplitude of synaptic input in all 24 directions across the grid cell plane. Summation of these waves of activity over all 24 different directions results in a circularly symmetric standing wave of synaptic input to the grid cell plane, as illustrated in Figures 1F and 2C,D. However, the model is not proposing cells with circularly symmetric firing fields in medial entorhinal cortex. This is just the pattern of synaptic activation arising from summation across all heading angles of the synaptic input from heading angle cells coding a single spatial phase. This resembles the mechanism used to create synaptic weights in one of the models using continuous attractors (Fuhs and Touretzky, 2006), but the synaptic connectivity used here is not circular but organized in bands. The center of the circle of synaptic output depends upon the spatial phase coded by the active cells in the heading angle population. Thus, the sum of the input from heading angle neurons with the correct phase creates synaptic input that peaks at the center of the circle with coordinates x, y.

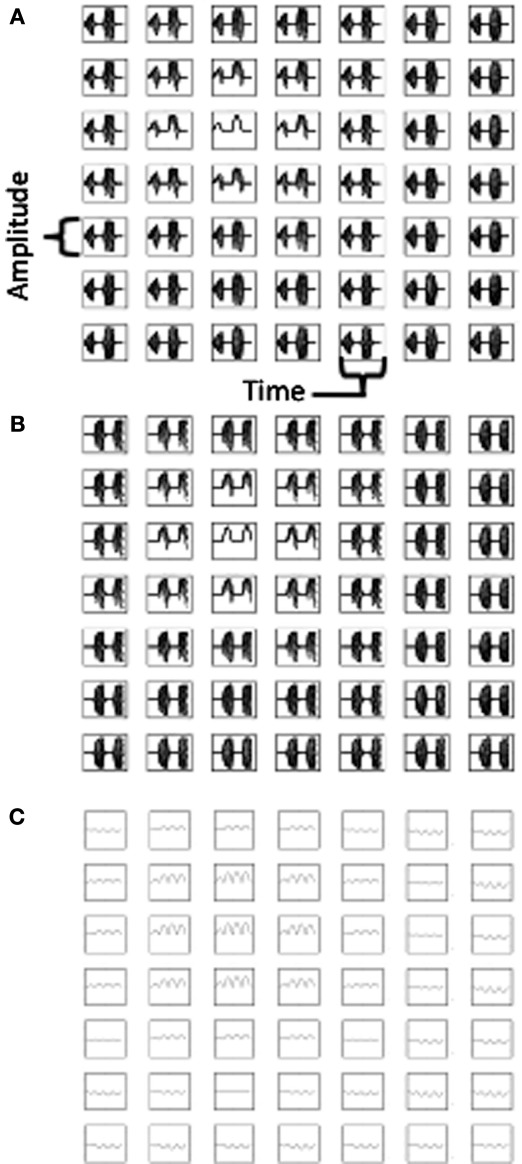
Figure 6.

Temporal dynamics of heading angle cells and synaptic input to grid cells. (A) The synaptic output of heading angle cells coding one spatial phase (px = 15, py = 15) are shown for each of 10 time steps, with each column showing the same 6 headings (18 out of 24 headings are not shown). Note that due to the different temporal phases, the pattern of activity shifts in the direction of the heading angle on each time step. (B) Sum of synaptic input results in a standing wave of oscillations with a circularly symmetric pattern. On timesteps 1–4, the pattern has maximal activity in the center (spatial phase px = 15, py = 15) and has one ring outside the center. On timesteps 5–7, the sum of heading angle outputs results in the opposite pattern. (C) Use of two separate populations of heading angle cells overcomes this problem. On timesteps 1–4, Group (A) shows output activity with a maximum in the center (px = 15, py = 15). On timesteps 5–9, Group (A) is decreased and group (B) is increased in activity to give a similar synaptic input to the grid cell population. (D) With two groups, the synaptic input from the heading angle cells is similar in pattern at most times.

At a single point in time, heading angle synaptic output can have different relative spatial phases as shown in Figures 2B1,B2. Close inspection of the figure will reveal that the bands for each angle have spatial phases that differ between 2B1 (x = 10, y = 15) and 2B2 (x = 20, y = 15). As shown in Figures 2C1,C2, and 2D, when the synaptic outputs for different angles in the heading angle array are summed together they generate input to the grid cell population that appears as concentric circle patterns with different spatial phases. Figure 2C1 is centered on spatial phase x = 10, y = 15, and Figure 2C2 is centered on spatial phase x = 20, y = 15. All the interactions in the model involve summing over both heading angles and spatial phases, but to help understanding of the model the summation over heading angles is shown alone in Figures 1E,F and in Figures 2C,D before the synaptic output is summed over all spatial phases to generate the activity in the grid cell population (e.g., Figure 2E). Each grid cell coding an individual spatial phase x, y then sends feedback that regulates input from the full array of heading angle cells (including all angles and temporal phases) that code that individual spatial phase.

To summarize, at a single point in time, the amplitude of synaptic input from the population of heading angle cells has a band like pattern that may seem analogous to a population of band cells from oscillatory interference models (Burgess et al., 2007). However, this is just at a single point in time. Due to the differences in temporal phases, the activity shifts through spatial phases along the direction of each separate heading angle plane. Thus, these neurons have a specific temporal phase dependent upon their one-dimensional spatial phase, like the cells used in spiking versions of the oscillatory interference model (Burgess, 2008; Hasselmo, 2008) or the ring attractors in models by Blair (Blair et al., 2007; Welday et al., 2011). These waves of temporal phase shifts move simultaneously in the direction of all heading angles. Summation over all heading angles results in standing waves that have the concentric circle pattern shown in Figures 1 and 2. These patterns are then summed across all spatial phases to drive the activity of the grid cell population (e.g., Figure 2E). The grid cell population then sends feedback to regulate the magnitude of input based on the spatial phase.

Results

Generation of grid cell activity

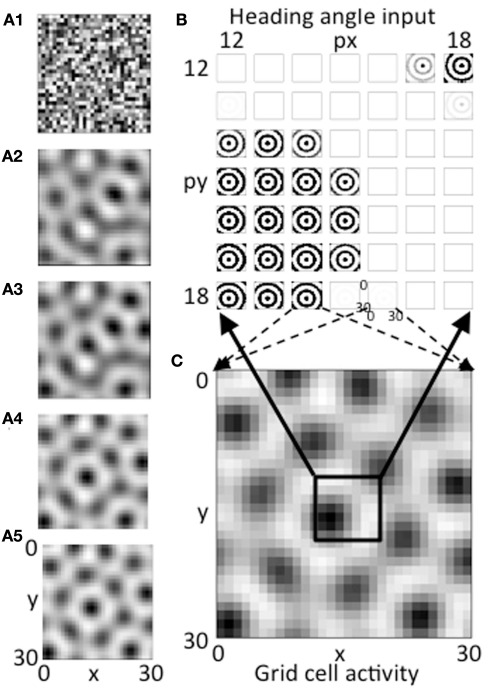
The feedback interaction between the population of heading angle cells and the population of grid cells results in activity in the grid cell plane settling into a pattern resembling the distribution of grid cells. As shown in Figures 3A1–A5, this iterative process results in a gradual evolution of the activity in the grid cell population and heading angle cell from an initial random distribution with regions of higher activity to a regular hexagonal array of active regions. This evolution results from the iterative interaction of the grid cell population with the heading angle cell population. This interaction is similar in effect and mathematical structure to the generation of grid cells in attractor dynamics models, but instead of using circularly symmetric synaptic connectivity, the interaction depends upon feedback to groups of heading angle cells receiving oscillatory input from medial septum that project to the grid cells based on different heading angle preferences. The summation across all heading angles results in circularly symmetric patterns of input to the grid cell population.

Figure 3.

(A1–A5) The evolution of activity in the grid cell plane at different stages during the iterative interaction. The network starts with random activity that then evolves into a hexagonal array of firing fields in a manner similar to continuous attractor dynamics models of grid cells. (B) Example of the magnitude of synaptic input at a single time step at the end of the simulation for a 7 by 7 set of heading angle cell arrays. The full simulation contains 30 spatial phases in the px dimension and 30 in the py dimension, but only a 7 by 7 array of spatial phases from the center is shown (phases 12–18). The input from heading angle cells at a specific spatial phase is determined by feedback from the grid cell plane. (C) The pattern of activity in the full grid cell plane with 30 by 30 spatial phases showing how feedback regulation of the pattern of summed activity from the heading angle plane produces a grid cell firing pattern that is stable. The pattern is stable because the pattern created by summing the 30 by 30 pattern of synaptic input from the 30 by 30 array of spatial phases of heading angles (B) matches the pattern of feedback activation of the heading angle array from active cells in the 30 by 30 array of grid cells (C).

If the network is balanced properly, the activity converges to a stable pattern of activity in the grid cell population (Figure 3C, same as Figure 3A5). This results from a stable pattern of synaptic output from heading angle arrays including the components shown in Figure 3B. In Figure 3B, each pattern that looks like concentric circles shows synaptic output from an array of heading angle cells coding an individual spatial phase, after the vector of temporal phases is multiplied by the synaptic connectivity matrix W_bg and summed across all heading angles. The population of grid cells coding 30 by 30 different spatial phases have different levels of activity that provide feedback to 30 by 30 different groups of heading angle cells representing different spatial phases. For each grid cell that is highly active (e.g., black region in lower left of black box in Figure 3C), the corresponding input to the whole grid cell population from the heading angle array coding that same spatial phase is strong (e.g., black concentric circles in lower left portion of Figure 3B). Thus, the feedback from the grid cells to the heading angle cells causes them to have spatial periodicity similar to the grid cell population.

Figure 3B shows synaptic inputs to the grid cell plane from a 7 by 7 selection of heading angle cell arrays (spatial phases x = 12–18 and y = 12–18) driven by the active grid cells in the 7 by 7 central spatial phases of the 30 by 30 population. This smaller 7 by 7 selection is shown to enhance visibility of the synaptic output arising from each of the heading angle arrays, because this synaptic output projects to the full 30 by 30 population of grid cells (the dashed arrows show this projection for a pair of example phases). The summed synaptic input from the heading angle cells to the grid cells consists of circularly symmetric standing waves that extend across the full population of 900 grid cells. If all heading angle cells are equally active, the input is uniform. But the random initial activity in the grid cell population (Figure 3A1) causes feedback that results in non-uniform activity in heading angle arrays coding different spatial phases. Each input interacts with input from all the other heading angle cells with different phases to generate activity that converges to a hexagonal pattern. The ongoing interaction results in the individual arrays of heading angle cells that code different spatial phases having activity that is strongest when they match the grid cell activity pattern driven by heading angle input summed over different angles and spatial phases. The feedback interaction results in a hexagonal pattern of activity in the grid cell plane (Figures 3A5,C) and results in corresponding patches of activity in the heading angle arrays (shown for the 7 by 7 set of spatial phases in Figure 3B).

The network that generated the simulations shown in Figure 3A was run multiple times with different random initial conditions. The network converged to a grid-like pattern each time and generated grid-like patterns with a range of different spatial phases and orientations, similar to what occurs in continuous attractor dynamic models.

Feedback interaction from grid cell to heading angle cells

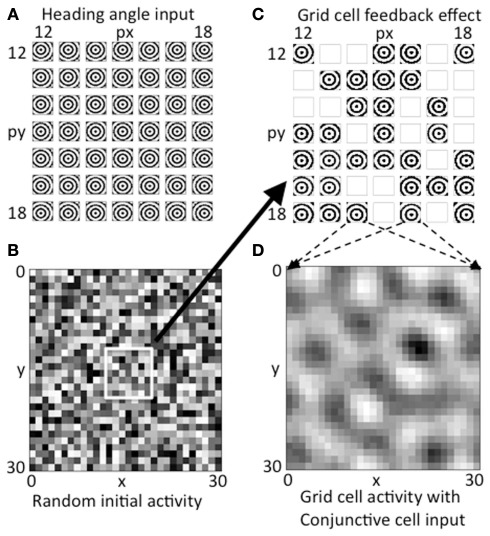
The network involves an interaction between the sum of a wide range of heading angle inputs and the plane of grid cells. As an example in the absence of feedback, the heading angle output with a full array of spatial phases are shown in Figure 4A, illustrating the coding of output starting from a wide range of different spatial phases. Close inspection of the figure will reveal that the concentric circles are centered on different spatial phases (different spatial phases x and y). Figure 4A shows a 7 by 7 array of summed outputs from heading angle groups representing central spatial phases within a larger simulation with a full array of heading angle inputs with 30 different spatial phases in the x dimension and 30 different spatial phases in the y dimension.

Figure 4.

Activity on first two time steps. (A) The array of concentric circles due to summation of synaptic input from all heading angle cells at a 7 by 7 array of heading angle spatial phases. The centers fall at different locations dependent on the different spatial phases of the heading angle cells. (B) Initial random activity in the grid cell population shown for all 30 by 30 spatial phases of grid cells. (C) Feedback from the random grid cell activity in (B) interacts with the corresponding array of heading angle cells at the same spatial phases. Where there is high activity in the grid cell initial random activity, the summation of synaptic input from heading angle planes yields a strong concentric circle input. Where random activity in the grid cells falls below threshold the synaptic input from heading angle cells is absent. (D) The heading angle synaptic input in (C) regulated by random feedback is summed together across the grid cell plane to generate a pattern of activity that already shows peaks of activity falling in a hexagonal pattern due to the overlap of concentric circles.

The grid cell population begins with initial random magnitudes of activity in different spatial locations as shown in Figure 4B. This initial spatially random activity in the plane of grid cell activity has a multiplicative influence on the activity in the heading angle cell populations, as shown by the synaptic input from the 7 by 7 selection of central spatial phases for the heading angle cell arrays shown together in Figure 4C. Multiplicative interactions in neural circuits have been proposed to be mediated by interactions in the dendritic tree involving depolarizing input that activates NMDA receptors (Mel, 1993) or gating of dendritic spike propagation (Jarsky et al., 2005). This could involve input from grid cells that influence the dendritic integration of cells receiving particular heading angle inputs and particular phases of oscillation. Where the magnitude of random activity in the grid cell population is larger, this causes stronger synaptic input from the corresponding set of heading angle cells in Figure 4C (for example, grid cells that appear as active black squares in Figure 4B correspond to stronger concentric standing waves in the heading angle synaptic inputs in Figure 4C). There is a threshold on the feedback from the grid cell plane in Figure 4B, so grid cell units at spatial phases with low magnitude in 4B give a mean output of zero, resulting in the absence of activity (white boxes) for the corresponding spatial phases of heading angle arrays in Figure 4C. Overall, this results in random activation of the heading angle input shown in Figure 4C.

The heading angle planes in Figure 4C are then summed together in Figure 4D. Synaptic output from the entire range of 30 by 30 spatial phases of heading angle arrays are summed up (for visibility only a 7 by 7 subset of summed heading angle inputs to the grid cell population are shown in Figure 4C). The summation across all spatial phases of heading angle arrays yields the distributed pattern of grid cell activity shown in Figure 4D. This already shows elements of a hexagonal distribution of activity due to the properties of interacting heading angle synaptic input. This provides the start of a feedback cycle that involves iterative interaction. On each cycle, the summed activity at each time step in the grid cell population (Figure 4D) is multiplied by the activity at each time step in the corresponding spatial phases of heading angle arrays shown summed across heading angle in Figure 4C, resulting in a varying magnitude of these inputs back to the grid cell plane. This then results in the progression of iterations in grid cell activity shown in Figures 3A1–A5, and ends with the final state of activity in heading angle cells in Figure 3B and in the grid cell population shown in Figure 3C.

Shift in grid cell activity with movement

The network has the capability of representing the influence of movement on the grid cell representation. This was implemented in the model by adding to the amplitude of oscillations in the heading angle cells in proportion to the cosine of the difference between the cell heading angle and the simulated movement heading angle (as shown in Figure 5D). The tuning shown in Figure 5D could represent heading angle cells that have the properties of speed-modulated conjunctive grid-by-head direction cells with baseline activity for all headings. Alternately, this could represent two separate populations of heading angle cells, one of which is active for all heading angles, and the other that would contain neurons that are only active when the rat is moving with non-zero speed in specific heading directions. During movement, the cells with heading angle preference angle ϕ_i closest to the current heading angle ϕ(t) produced the strongest synaptic output to the grid cell plane. Other cells increased their amplitude of oscillation in proportion to the cosine of the angle between their heading angle and the current movement direction of the virtual rat and speed S, as described in the following modified version of Eq. 1.

$$\begin{array}{rcll}{b}_{\varphi ,\phi ,x,y}\left(t\right)& =\tau b\left(t-1\right)+\left(1+Scos\left(\varphi \left(t\right)-{\varphi }_k\right)\right)& & \\ & \times sin\left(2\pi \left(ft+{\phi }_k\right)\right){\left[g_{x,y}\left(t\right)-{\lambda }_g\right]}_{+}∕{max}_{x,y}\left(g\left(t\right)\right)& & \text{(4)}\end{array}$$

The effect of this input on the pattern of activity in the model is shown in Figure 5. This figure shows the effect of sustained movement in the direction West (angle ϕ(t) = π) starting at time step 10 and continuing at constant level (intervals of 5 time steps are shown). As shown in Figure 5A, the grid cell population settles to a pattern of activity corresponding to multiple fields in a hexagonal distribution at time step 10. As the movement input continues, this pattern of grid cell activity progressively shifts to the West over subsequent time steps 15–35. Note that this would result in individual grid cells that increase and decrease in activity similar to experimental data. There was not sufficient space in the figure to show individual time steps, but at the level of single time steps, there is a small scale forward and backward shift on each cycle of the theta rhythm oscillation in the model similar to that observed previously for place cells.

This shift in the pattern of activity is due to the interaction of the grid cell population with the heading angle population, resulting in a progressive Westward shift in the synaptic input from the heading angle cells as shown in Figure 5B. This is driven by an increase in amplitude of a subset of oscillations causing a shift in the synaptic input from heading angle cells to grid cells. There is no change in synaptic connectivity, but the distribution of synaptic input to the grid cells is skewed by the larger amplitude of oscillations in one set of heading angle cells. This shift in the distribution of input is visible in the overall distribution of activity in Figure 5B, time step 30.

To make the shift in synaptic input clearer, the input from one set of heading angle cells across the full set of heading angles is shown in Figure 5C. This shows the circularly symmetric synaptic input from a set of heading angle cells coding an individual spatial phase. On time steps 10–13 in Figure 5C, there is a progressive shift in distribution of the synaptic activity from East to West. This shift is what drives the overall shift in grid cell activity in A that then shifts the magnitude of synaptic input from heading angle cells in B so that the new position is held and movement continues. Note that if the full cycle of oscillation interactions were included, the network would shift back due to oscillations with different temporal phase shifting the activity backward. This is prevented by regulation of activity so that heading angle cells are only active on a specific set of phases, as described below.

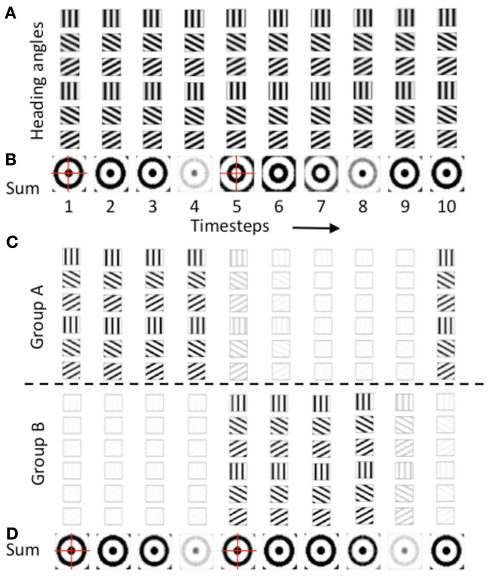
Regulation of phase of heading angle activity

The effective function of the model required regulation of the phase of activity in the heading angle cells providing synaptic input to the grid cell population. There are two reasons this regulation was necessary: (1) to allow oscillations to drive activity in one direction, and (2) to prevent opposite distributions of spatial activity. In the simulations, the regulation of activity took the form of oscillatory gating of input at different phases. This could represent the effects of rhythmic inhibition in the entorhinal cortex. The oscillatory gating depended on a periodic Heaviside step function with timing determined by an oscillation with a phase offset 2π/8 and a threshold λ= 0.24, as follows:

$$\begin{array}{rcll}{b}_{\varphi ,\phi ,x,y}\left(t\right)& =\tau b\left(t-1\right)+\left(1+Scos\left(\varphi \left(t\right)-{\varphi }_k\right)\right)& & \\ & \times {\left[sin\left(2\pi \left(ft+1∕8\right)\right)\right]}_{H}sin\left(2\pi \left(ft+{\phi }_k\right)\right)& & \\ & \times {\left[g_{x,y}\left(t\right)-{\lambda }_g\right]}_{+}∕{max}_{x,y}\left(g\left(t\right)\right)& & \text{(5)}\end{array}$$

The selection of the threshold and phase offset was partly determined by the parameters that allowed effective movement of the grid cell firing fields (reason #1 above). The phase offset meant that oscillations with a particular temporal phase would influence the synaptic output of the network (Figure 5C), without different phases causing a corresponding shift in the opposite direction. Thus, this allowed the network to show effective movement without being counteracted by different oscillatory phases.

As noted above, the second reason for regulation of the phase of heading angle activity was to avoid the opposite pattern of spatial activity. The gate shown above in the equation was used for one population of heading angle cells (Group A) and the same gate offset by an additional phase shift of π was used to gate the activity of a different population of heading angle cells (Group B). The need for this regulation of opposite spatial activity is shown in Figures 6A,B. Figure 6A shows the temporal dynamics of heading angle cells and the synaptic input to grid cells. This shows the synaptic output of heading angle cells coding one spatial phase (x = 15, y = 15). Each column shows the distribution of synaptic output from 6 out of the 24 different heading angles for each of the 10 time steps (the other 18 heading angles are not shown). The spatial frequency is 3, so there are three cycles across the full range of 30 by 30 spatial phases. As the sinewave oscillations of each heading angle cell evolve in time, the difference in temporal phase of the heading angle cells means that the pattern of synaptic input to the grid cell population shifts in the direction of the heading angle on each time step. Figure 6B shows that the progressive shift in all directions of the heading angles causes the sum of synaptic input to the grid cells to be a standing wave of oscillations with a circularly symmetric pattern. On timesteps 1–4, the standing wave pattern has maximal activity in the center (spatial phase x = 15, y = 15) and one ring outside the center. The cross-hairs are there to enhance visibility of the center. On timesteps 5–7, the sum of heading angle outputs results in minimal activity in the center, and a ring just outside of the center, in an opposite pattern from timesteps 1–4. In full simulations, this opposite pattern of activity would disrupt the grid cell firing pattern in the grid cell population.

A number of techniques were tested to overcome this problem, to obtain more stable patterns of activity in the grid cell population. One method that proved effective was used in all of the simulations shown in Figures 3–5. As shown in Figures 6C,D, these simulations all used two separate populations of heading angle cells that are active during opposite phase time periods. During one period, the gating of activity favored output from Group A (on timesteps 1–4), which then shows synaptic output activity with a maximum in the center (px = 15, py = 15). Then on timesteps 5–9, Group A is reduced in activity, and Group B is increased in activity to give a similar synaptic input to the grid cell population. The figure shows that the periodic gating then results in the cycle repeating, as shown in timestep 10. As shown in Figure 6D, this ensures that the pattern of synaptic input from the heading angle cells is essentially equivalent at most times.

Relationship to different cycles of activity

Though the pattern of activity is similar on different timesteps in Figure 6D, it is clearly evident that the amplitude of the inputs increases and decreases in cycles dependent upon the regulation of heading angle cell activity as well as the magnitude of the oscillations at different temporal phases. Figure 6D shows two cycles of periodic changes in activity in the synaptic input to the grid cell population, whereas Figure 6C shows a single cycle in each group of heading angle cells providing input (Group A and Group B). If we consider the changes in overall synaptic input to the grid cells to be at theta rhythm frequency (i.e., 8 Hz), then the activity of each of the two groups providing input to the grid cell population would be at half of that frequency (4 Hz), and would show activity on opposite phases of the theta rhythm oscillation. This pattern of activity resembles recent experimental data from unit recordings in awake behaving animals in our laboratory (Brandon et al., 2011; Brandon et al., in review) as well as previously observed experimental data (King et al., 1998; Deshmukh et al., 2010). In the data, head direction cells and conjunctive grid-by-head direction cells in the medial entorhinal cortex show theta cycle skipping, defined as firing on alternate cycles of the network theta rhythm oscillations.

The activity on alternate theta cycles in the model is illustrated further in Figure 7. The top of Figure 7 shows the pattern of activity in the two different populations of heading angle cells, Group A (Figure 7A) and Group B (Figure 7B). This shows the timecourse of activity during the simulation shown in Figures 3 and 4. Figure 7C shows the time course of the sum of synaptic input to the grid cell population. Note that because the time course of synaptic input includes input from both populations, the frequency of this input is double that of the individual populations. In subsequent discussion, the frequency of the total synaptic input to the grid cell population will be considered as theta rhythm frequency (8 Hz) and the frequency of the individual populations will be considered to be half that frequency (4 Hz).

The two different populations of heading angle cells in Figures 7A,B each show activity on two cycles during the full time period of the simulation. Note that the period of activity of Group B is the opposite of the period of activity of Group A. This means that simultaneous recording of one neuron from Group A and one neuron from Group B would result in non-overlapping spiking activity, that would show up as a low cross-correlation at zero delay between the cell. In contrast, there would be a large cross-correlation at the interval of one theta cycle (i.e., 125 ms) to either side. In contrast, two cells recorded from Group A (or both from Group B) would have a high cross-correlation at zero delay between the cells, with a lower cross-correlation at one theta cycle. In addition, each individual neuron would have an autocorrelation with a peak at two theta cycles rather than a single theta cycle, whereas the grid cells would be expected to have an autocorrelation with a peak at a single theta cycle.

Discussion

The model of grid cell firing presented here was designed to combine the oscillations that are prominent in one set of grid cell models (Burgess et al., 2007; Giocomo et al., 2007; Hasselmo et al., 2007; Blair et al., 2008; Burgess, 2008; Hasselmo, 2008; Hasselmo and Brandon, 2008; Zilli and Hasselmo, 2010; Welday et al., 2011) as well as the attractor dynamics prominent in a different set of grid cell models (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Guanella and Verschure, 2007; Guanella et al., 2007; Burak and Fiete, 2009).

The model uses a population of heading angle cells (Eq. 1) that are motivated by the theory that movement in any given heading could involve transitions between neurons with different temporal phases that code different spatial phases along that heading. This component was inspired by transitions in phase due to frequency modulation of oscillating neurons (Burgess, 2008; Hasselmo, 2008) or oscillating ring attractors (Blair et al., 2007; Welday et al., 2011), but here the transition is triggered by changes in the amplitude of oscillations coding one heading direction rather than changes in frequency.

The population of heading angle cells has synaptic connections with a population of grid cells that are periodic in spatial phase along each heading angle (Eq. 2). Simulations of the model arrays that code 24 different heading angles (see Figure 2B). The synaptic input from the heading angle cells with different temporal phases can be pictured as waves of activity propagating across the grid cell plane in the direction of each heading angle (see Figures 1 and 6). For heading angle cells with a particular spatial phase, the sum of this synaptic input across all angles corresponds to a standing wave of concentric circles centered on the individual spatial phase of that set of heading angle cells in the environment (Figures 1 and 2). Different heading angle cells with different spatial phases will provide standing waves centered on different spatial phases.

The synaptic input influences the activity of a population of grid cells (Eq. 3) that send feedback to the heading angle cells to influence their amplitude of oscillation. The interaction of the synaptic input from heading angle cells with the grid cell activity plane generates grid-like patterns of activity as shown in Figures 3–5. This pattern of activity varies dependent upon initial conditions and spatial frequency of synaptic connectivity. The spatial periodicity of firing occurs in both the grid cell population and across different arrays of heading angle cells. Thus, the heading angle cells would show grid cell periodicity similar to that of conjunctive grid-by-head-direction cells in medial entorhinal cortex (Sargolini et al., 2006; Hafting et al., 2008; Brandon et al., 2011). These same heading angle cells show different amplitudes of activity dependent upon the heading direction of movement (Figure 1C and Figure 5D), similar to the head direction selectivity of conjunctive cells, but with stronger background for all headings.

As shown in Figure 5, the model can shift the locus of firing of the grid cell activity under the influence of head direction input that selectively activates a subset of heading angle cells. This causes an increase in the amplitude of input from one oscillation versus the others. Without any change in synaptic connectivity, this shifts the predominant activity of the grid cells along the direction of movement, thereby shifting the heading angle cell activity in that same direction (Figure 5). The shift in locus of firing depends upon heading angle cells responding to the direction of movement, as shown in Figure 5D. The model is similar to other models using attractor dynamics in that it requires either that there be a set of speed-modulated conjunctive cells that have zero activity when the rat is stationary, or that it have cells that have a uniform baseline response to all heading directions and then increase from this uniform baseline response for the preferred heading angle. Both of these features differ from most head direction cells and conjunctive cells in medial entorhinal cortex (Sargolini et al., 2006; Brandon et al., 2011), which have very low baseline responses to non-preferred headings, but do not reduce to zero activity when the rat is stationary.

The simulations used regulation of heading angle activity on different phases of the theta rhythm oscillations in order to allow the shift in activity with movement. In addition, this regulation of heading angle activity also reduced the disruptive influence of spatial activity during opposite temporal phases, which would cause grid cell activity to activate a mismatching input from the heading angle cells. This problem was avoided by setting up two groups of heading angle cells that were active on different cycles, to allow the grid cells to receive consistent input across all cycles. As shown in Figure 7, the two groups of heading angle cells were active at delta frequencies (e.g., 4 Hz), whereas the total synaptic input to the grid cells showed cycles at twice that frequency (e.g., 8 Hz). This appears to be consistent with neurophysiological data showing theta cycle skipping in a subset of head direction cells and conjunctive grid-by-head direction cells in the medial entorhinal cortex (Deshmukh et al., 2010; Brandon et al., 2011). Theta cycle skipping in the autocorrelogram indicates more inter-spike intervals corresponding to 4 Hz frequencies compared to 8 Hz frequencies.

An alternate mechanism for avoiding the problem of opposite phases could be the resonance properties of medial entorhinal neurons, as shown in a number of studies (Haas and White, 2002; Erchova et al., 2004; Giocomo et al., 2007; Giocomo and Hasselmo, 2009; Boehlen et al., 2010). These resonance properties when implemented in the grid cell population in the model can allow the neurons to be active during one period and then less active (due to decreases in the hyperpolarization activated cation current) on a subsequent period. This prevents the problem of opposite phase input, but results in a pattern of anti-grid firing that has been observed in some preliminary neurophysiological recordings, but not alternating with a grid pattern. The resonance properties of neurons could also contribute to shifts in frequency with depolarization that could alter the phase relationship of grid cells and heading angle cells and contribute to shifting of the grid representation during movement. Experimental data shows that depolarization does shift the resonance frequency of individual medial entorhinal neurons to lower frequencies in a linear manner with depolarization between −70 mV and threshold (Shay et al., 2010).

The model presented here uses interactions of theta-frequency oscillations with attractor dynamics to generate the spatial firing pattern of grid cells. Theta-frequency oscillations have been the primary frequency used in oscillatory interference models (Blair et al., 2007; Burgess et al., 2007; Burgess, 2008; Hasselmo, 2008; Zilli and Hasselmo, 2010). However, another early model showed that lower frequency oscillations can simulate grid cell firing patterns (Hasselmo and Brandon, 2008) based on data showing cyclical changes in bistable persistent spiking (Klink and Alonso, 1997). These spiking phenomenon could occur based on acceleration of spiking due to buildup of calcium activation of the CAN current, and deceleration of spiking due to calcium inactivation of the CAN current or due to the calcium-activated potassium current (AHP). The Hasselmo and Brandon (2008) model can be implemented with the following equations: dV_i/dt = c_i(t)Hv(t), dc_i/dt = −ω²V_i(t)Hv(t), $g(t)={\displaystyle \prod _i{V}_i\left(t\right)}$. Where V represents membrane potential, c represents the net activation of calcium activated currents including both the CAN current and the AHP current, H represents the head direction matrix that transforms the velocity at each time point v(t) into a speed-modulated head direction signal, and the frequency of oscillations depends upon ω². These dynamics generate bands of activity that sum together to create grid cells, showing how slower oscillations based on a different set of cellular mechanisms could generate grid cell firing. This mechanism could use head direction input with preference angles at 60° intervals, or could interact with attractor dynamic properties to generate grid cell firing with head direction input at a wide range of preference angles.

In the model presented here, the use of neurons with oscillatory phase driven by the medial septum resembles features of the oscillatory interference models that code location by relative phase of different velocity controlled oscillators (VCOs; Burgess et al., 2007; Giocomo et al., 2007; Hasselmo et al., 2007; Blair et al., 2008; Burgess, 2008; Hasselmo, 2008; Hasselmo and Brandon, 2008; Zilli and Hasselmo, 2010; Welday et al., 2011). The loss of input from the medial septum would remove this phase signal, thereby blocking the spatial periodicity of grid cells. The loss of grid cell spatial periodicity has been shown during pharmacological inactivation of the medial septum (Brandon et al., 2011; Koenig et al., 2011), and this loss of periodicity could underlie the spatial memory impairments associated with inactivation of the medial septum (Chrobak et al., 1989). The use of an interactive feedback process with circular symmetry resembles features of the continuous attractor dynamic models of grid cells that have the grid cell activity interacting with circularly symmetric synaptic connectivity (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Guanella and Verschure, 2007; Guanella et al., 2007; Burak and Fiete, 2009). The iterative process of interaction of the grid cell plane with the summed heading angle plane is mathematically analogous to the interaction of the grid cell plane with the circularly symmetric synaptic connectivity matrix in attractor dynamic models.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.