Modeling a Cortical Auxin Maximum for Nodulation: Different Signatures of Potential Strategies

Abstract

Lateral organ formation from plant roots typically requires the de novo creation of a meristem, initiated at the location of a localized auxin maximum. Legume roots can form both root nodules and lateral roots. From the basic principles of auxin transport and metabolism only a few mechanisms can be inferred for increasing the local auxin concentration: increased influx, decreased efflux, and (increased) local production. Using computer simulations we investigate the different spatio-temporal patterns resulting from each of these mechanisms in the context of a root model of a generalized legume. We apply all mechanisms to the same group of preselected cells, dubbed the controlled area. We find that each mechanism leaves its own characteristic signature. Local production by itself can not create a strong auxin maximum. An increase of influx, as is observed in lateral root formation, can result in an auxin maximum that is spatially more confined than the controlled area. A decrease of efflux on the other hand leads to a broad maximum, which is more similar to what is observed for nodule primordia. With our prime interest in nodulation, we further investigate the dynamics following a decrease of efflux. We find that with a homogeneous change in the whole cortex, the first auxin accumulation is observed in the inner cortex. The steady state lateral location of this efflux reduced auxin maximum can be shifted by slight changes in the ratio of central to peripheral efflux carriers. We discuss the implications of this finding in the context of determinate and indeterminate nodules, which originate from different cortical positions. The patterns we have found are robust under disruption of the (artificial) tissue layout. The same patterns are therefore likely to occur in many other contexts.

1. Introduction

1.1. Setting

Legume roots can form two kinds of lateral organs: lateral roots and root nodules, the latter in response to Rhizobium-secreted signaling molecules named Nod factors. Although these organs are induced in different ways and their primordia originate from different cell layers, in both cases local accumulation of the hormone auxin coincides with the site of primordium initiation (Larkin et al., 1996; Rolfe et al., 1997; Mathesius et al., 1998; Pacios-Bras et al., 2003; Takanashi et al., 2011). In this light it is not surprising that the number of lateral roots can be increased by exogenous auxin application (Blakely and Evans, 1979; Woodward and Bartel, 2005). For root nodules, however, this is not the case. Auxin’s textbook antagonist, cytokinin, plays an important role in nodulation: a cytokinin receptor is essential for nodulation (Gonzalez-Rizzo et al., 2006; Murray et al., 2007; Tirichine et al., 2007; Plet et al., 2011) and exogenously applied cytokinin can induce nodule-like structures (Cooper and Long, 1994), as can auxin transport blockers (Hirsch et al., 1989). In contrast, cytokinin has an inhibitory effect on lateral root formation (Laplaze et al., 2007), possibly by removing PIN1, an auxin efflux carrier upregulated in lateral root primordia, from the membranes of primordium cells (Marhavý et al., 2011).

This apparent paradox hints at different mechanisms causing the initial auxin accumulation in either case. We hypothesize that the Nod factor activated cytokinin signaling causes the accumulation of auxin in the cortical cell layers of the root that form the nodule primordium. We investigate the possibilities for inducing local auxin accumulation by modeling three conceptually different mechanisms. We start with an unbiased analysis of their generic properties, than continue with the best candidate for nodulation. In the discussion we come back upon the likelihood that cytokinin can activate the proposed mechanism.

1.2. Background

To date lateral root formation is studied most extensively in the model organism Arabidopsis thaliana (Arabidopsis). In this plant the lateral root originates exclusively from a few pericycle cells, called founder cells (Malamy and Benfey, 1997; Casimiro et al., 2003). The first auxin accumulation occurs in these cells (Hirota et al., 2007). Arabidopsis roots contain only a single cortical layer. In model legumes, which all have a multi-layered cortex, the lateral root primordia are also predominantly of pericycle origin (Mallory et al., 1970) and the first auxin accumulation is observed in the pericycle (Larkin et al., 1996; Rolfe et al., 1997).

Nodules can be induced upon contact with a compatible Rhizobium strain, recognized by the plant through the precise chemical structure of the Nod factors the particular Rhizobium species produces (Jones et al., 2007). Two major types of legume nodules exist: indeterminate and determinate, discerned by the presence of a persistent meristem in the former (Hirsch, 1992). The model legume Medicago truncatula (Medicago) makes indeterminate, whereas Lotus japonicus (Lotus), the other model legume, forms determinate nodules. Of special interest is that indeterminate nodules are formed from cell divisions induced in the inner cortical layers, while determinate nodule formation starts with divisions in more outer cortical layers (Hirsch, 1992). Studies in Lotus and white clover have shown local auxin accumulation at the site of the cortical cell divisions (Mathesius et al., 1998; Pacios-Bras et al., 2003; Takanashi et al., 2011) respectively.

In legumes, lateral roots and root nodules originate in approximately the same zone of the root. The zone for nodule induction is called the susceptible zone (Bhuvaneswari et al., 1981). Cortical cells in the susceptible zone have fully differentiated and will de- and redifferentiate in the process of nodule formation. Epidermal cells start developing root hairs from the youngest part of the susceptible zone. In this paper we sometimes refer to the susceptible zone of a legume using DZ (standing for “differentiation zone”) to stress the origin of the parameters we use (see Materials and Methods).

The phytohormone auxin is active in minute concentrations (typical measurements: tens to hundreds pg per mg fresh weight (Ljung et al., 2001; Marchant et al., 2002; Petersson et al., 2009, i.e., 1–10² μmol ml⁻¹) and no methods exist for live monitoring of the actual auxin concentration. All available techniques for auxin detection are either indirect, or kill the plant, or both. This is a key reason why analytical and computational models of auxin transport have become an important tool for studying the implications of auxin related hypotheses with high spatial and temporal resolution (see Kramer, 2008; Grieneisen and Scheres, 2009; Garnett et al., 2010; Jonsson and Krupinski, 2010; for some reviews). The earliest models focused on the propagation of radio-labeled auxin through “linear” tissue (Mitchison, 1980; Goldsmith et al., 1981; Martin et al., 1990). With increasing computer power a plethora of more complex developmental questions came within reach, on topics such as phyllotaxis (Heisler and Jonsson, 2006; Jonsson et al., 2006; Smith et al., 2006; Bainbridge et al., 2008; Stoma et al., 2008), venation (Rolland-Lagan and Prusinkiewicz, 2005; Merks et al., 2007; Bayer et al., 2009; Wabnik et al., 2010), apical dominance (Prusinkiewicz et al., 2009), and root gradients (Swarup et al., 2005; Grieneisen et al., 2007; Laskowski et al., 2008; Jones et al., 2009).

Here, we will use a model of auxin transport and metabolism to investigate different possible scenarios for local auxin accumulation in the root cortex and relate the resulting patterns of auxin accumulation to those observed upon Rhizobium Nod factor induced signaling. To infer the possible scenarios we recapitulate the basics of auxin transport and metabolism. Auxin is a weak acid [the most abundant active natural auxin, indole-3-acetic acid (IAA), has pK_a ≈ 4.8]. Its protonated form is uncharged and can therefore passively cross the cell membrane. The apoplast is mildly acidic and thus contains a fair fraction of protonated auxin (e.g., 24% at pH = 5.3). The cytoplasm, however, is near neutral and thus hardly contains any protonated auxin (e.g., ≈0.4% at pH = 7.2; Jonsson et al., 2006). As only the concentration of protonated auxin matters for the passive influx, the pH difference has the potential to drive a passive auxin influx against the difference in total auxin concentration. Its magnitude is mostly determined by the apoplastic pH as this is closest to the pK_a. Moreover, the influx can be enhanced by more than an order of magnitude by influx carriers such as the AUX1/LAX protein family, that exploit the proton gradient for the import of deprotonated auxin (Swarup et al., 2005). They are usually located homogeneously over the cell membrane, or at higher levels on both apical and basal sides (Swarup et al., 2001, 2004; Kleine-Vehn et al., 2006). Efflux of auxin occurs predominantly by active transport through efflux carriers such as the PIN proteins (Galweiler et al., 1998; Paponov et al., 2005). The membrane PINs often appear concentrated at specific sides of the cells, giving rise to directional auxin transport (Benkova et al., 2003; Blilou et al., 2005). For information about the production of auxin we refer to some reviews (Ljung et al., 2002; Woodward and Bartel, 2005).

1.3. Approach

Reasoning from this overview of auxin transport and metabolism we arrive at three major scenarios for increasing the auxin concentration inside a cell: increasing the amount of influx carriers, decreasing the amount of efflux carriers and (activating) local auxin production. These scenarios we will refer to by (n-fold) Infl↑, Effl↓, and Prod↑, respectively. In this “n-fold” refers to the factor of increase or decrease compared to the starting situation, respectively.

For Infl↑ we specifically focus on the carriers, as changes in the passive influx (such as resulting from changes of the apoplastic pH) will be practically the same on both sides of the wall. As a result the change in the influx capacity will be almost fully compensated by an opposite change in the apoplastic concentration, with hardly any change in the intracellular concentration in either cell (c.f. For the same reason Grieneisen et al., 2007 found no noticeable effect of the, in their case uniform, influx permeability on the intracellular auxin concentrations, despite large variations in the values tested).

We will not consider a decrease of auxin degradation, because this part of the root has to support the passage of auxin from shoot to root tip. To increase the local auxin concentration through a decrease of degradation by any significant degree, a large base degradation rate is required. This is inconsistent with auxin’s function as a long range signal. We will neither consider (the reversible forms of) conjugation and deconjugation of auxin, as this would either complicate the model by having separately to account for the conjugate concentrations, next to active concentrations, or, without this, reduce to a combination of decay and production that need to (almost completely) balance each other on the cell level in order to sustain long range auxin signaling.

Starting from these scenarios we aim to tackle the following questions: which changes in auxin transport/metabolism in the cortex of the DZ can create a sufficiently strong cortical auxin maximum as is observed in root nodule initiation? Furthermore, how do the different scenarios relate to observed patterns of auxin accumulation in nodulation and lateral root formation?

1.4. Key findings

We find that these three scenarios produce clearly different spatial signatures, of which Effl↓ is most compatible with nodulation. The time scales of auxin accumulation under Infl↑ and Effl↓ are comparable and both sufficiently fast to be compatible with the experimentally observed timing of early nodulation events.

We also find that the lateral position of a cortical auxin maximum can be shifted by minor changes in the distribution of cortical PINs. Based on this observation we formulate the tentative hypothesis that differences in the distribution of cortical PINs could determine the lateral position of the early cell divisions in nodulation. This in turn is correlated with the nodule type.

The signatures we have found occur consistently and robustly. We therefore argue that the understanding of these different signatures is of general importance for the area of plant development.

2. Results

2.1. Signatures of increasing influx, decreasing efflux, and local auxin production

Lacking the relevant PIN data for model legumes we have created an in silico DZ root segment based on the Arabidopsis model by Laskowski et al. (2008) by adapting the tissue geometry. The resulting segment has five cortical layers, which is typical for the model legumes Lotus and Medicago (Figure 1A). The PIN layout of the DZ root segment is shown in Figure 1B. This layout results in a strong rootward flux in the stele and a shootward flux in the cortex and epidermis. The equal amount of PINs on the inner and outer sides of the cortical cells, results in a flat transverse auxin concentration profile in the cortex. More details on the creation of the root segment and the verification of the boundary conditions are provided in the Methods section (3).

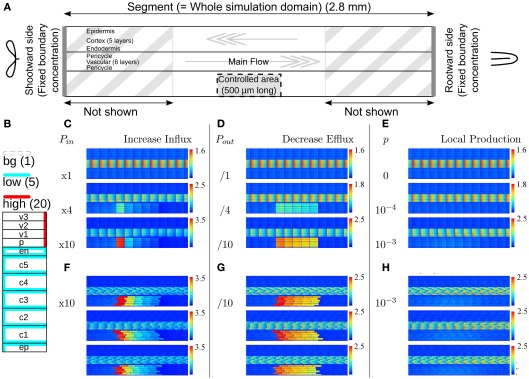
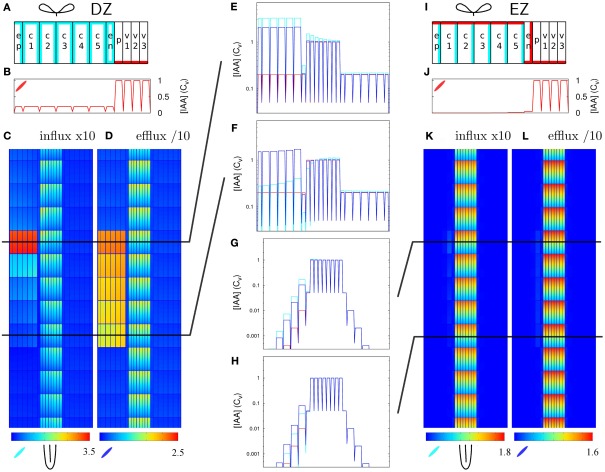
Figure 1.

Effect of single changes in the controlled area on steady state auxin concentrations. (A) Layout of the root segment and the main directions of auxin flow. Throughout the text the word “segment” refers to the whole simulation domain, including the parts not shown in the figures. The same parameter change is applied to all cells in the controlled area (indicated by a gray block). The gray arrows indicate the main flow direction in the stele and cortex. Stylized leaves and root tips are used throughout the manuscript to indicate the orientation of the root segments. (B) Effective efflux permeabilities for each cell from center to periphery. Following Laskowski et al. (2008) we distinguish three levels: high, low, and bg (background). (C,F) Increase of influx permeability (P_in) by an increasing factor (as shown left of the pictures). (D,G) Reduction of all efflux permeabilities (P_out,x). (E,H) Local auxin production with rate p (in C_v s⁻¹ μm⁻³). (F–H) The strongest change from each category was repeated on randomly generated realistic tissue layouts, with an average cell length of 100 μm, normally distributed with σ = 4 μm. The controlled area consists of all cells that fall in the desired area with more than 50% of their volume. (C + F, D + G) Note that with increasing the influx the effect concentrates on the downstream side of the controlled area, whereas the effect of decreasing all efflux with the same factor is much more homogeneous over the controlled area. For maximum information the auxin concentration color gradient is rescaled for each picture. The gradient always starts from 0 and the maximum value is indicated per picture.

From the available knowledge on auxin transport and metabolism we have identified three scenarios that could in theory lead to a local auxin maximum (Infl↑, Effl↓, and Prod↑). To assess whether these scenarios actually are compatible with the events that occur during nodulation we applied each scenario separately to a block of cells on one (lateral) side of the DZ fragment, dubbed the controlled area. It has a length of 500 μm (in the simulations 5 cells long), which corresponds well with the typical length of a nodule primordium. The controlled area includes all cortical layers and the epidermis, as indicated in Figure 1A. For simplicity we assume that the parameter change as a reaction to Nod factor perception is the same for all cells in the controlled area.

In this text, the word segment is reserved for the whole simulation domain (Figure 1A). A segment without any (additional) change in the controlled area is called a reference segment.

We first focused on the steady states of each scenario as obtained from evaluating the model. Although all three scenarios resulted in at least some increase of the local auxin concentration, their effects were remarkably different.

With an increase of the influx permeability, we observed a strong increase of the auxin concentration only in the most shootward cells of the controlled area (Figure 1C). Considering the main flow directions of auxin through the controlled area (i.e., through cortex and epidermis), this corresponds to its downstream side. This strong focus on the most downstream cells inside the controlled area was independent of the length [number of cells in the longitudinal/(y)-direction] of the controlled area (data not shown). This means that the area of the strong(est) auxin accumulation can be much smaller than the area with increased influx activity. A 10-fold (but not a 4-fold) Infl↑ change was sufficient for increasing the cortical auxin concentration above the vascular auxin concentration in the reference segment C_v, which throughout we use as our unit of concentration.

A decrease of the efflux permeability on the other hand resulted in a fairly homogeneous increase throughout the whole controlled area, independent of the reduction factor (Figure 1D). In all cases the auxin accumulation showed a slight maximum on the downstream (shootward) side in the area. This bias, however, was much weaker than with an increase of auxin influx. A 10-fold (but not a 4-fold) Effl↓ change was sufficient for increasing the cortical auxin concentration above the vascular level C_v.

Local auxin production in the controlled area led to a ill confined increase of the local auxin concentration, reaching at most a small fraction of the resting state vascular concentration C_v (Figure 1E), even with what we considered a high production rate (estimated from gas chromatography and mass spectroscopy measurements by Ljung et al., 2001; Marchant et al., 2002). This cannot be contributed to a too low production rate, but happened because the locally produced auxin is transported away and accumulates somewhere else. With the highest production rate tested (p = 10⁻³ C_v μm⁻³ s⁻¹) the absolute increase of the auxin concentration was larger in the vascular tissue rootward from the production site than in the controlled area itself. This is in marked contrast to the other two scenarios, in which the changes of the auxin concentration were limited to the controlled area and a small surrounding region.

In biological tissues the cells are not aligned in a square pattern as in our idealized root segment. We therefore also tested our scenarios on randomly generated root segments without lateral alignment between cell files and with variable cell lengths. All signatures were conserved (Figures 1F–H).

From the three mechanisms tested, only the reduction of the efflux permeabilities (Effl↓) resulted in a strong auxin accumulation that was fairly homogeneous along the length of the controlled area, as is observed in nodulation. Increased influx (x) resulted in a too narrow (single cell wide) maximum and local auxin production alone could not yield a local auxin maximum in the cortex at all. We therefore focused on Effl↓ for the rest of this study.

We next asked how fast auxin accumulates under this scenario, what determines the time scales of auxin accumulation in this case and where the accumulation starts. The final steady state auxin maximum spanned all layers of the cortex, whereas the cell divisions founding a nodule occur either in the inner, or the outer cortex, depending on the legume species. To gain insight into this lateral confinement of the auxin accumulation we looked into both the dynamics of auxin accumulation after a change in the controlled area and the impact of slight changes of the lateral cortical PINs on the lateral position of the steady state auxin maximum.

2.2. Time evolution of auxin accumulation

2.2.1. Auxin accumulation following Effl↓ is sufficiently fast

After studying the steady state patterns the first important question was: is auxin accumulation following reduction of the efflux fast enough to explain the Rhizobium induced cortical cell responses? To be compatible with the formation of a nodule primordium, a scenario should yield a sufficient increase in auxin concentration at least several hours prior to the first cortical cell divisions. For this a time window of at most 20 h is available: cortical cells show cytoskeletal signs of activation for division after 18–24 h after inoculation (Timmers et al., 1999) and no cortical cell divisions are observed within 20 h after inoculation (Yang et al., 1994). The actual time window is probably even shorter, as we start the clock at the moment the cells change with respect to auxin dynamics (which is instantaneously in this model). In reality, the transcription and translation of regulatory genes likely reduces the available time window by a few hours.

We only investigated the dynamics for the strongest (=10-fold) Effl↓ and Infl↑ changes from Figures 1C,D, respectively, because they have the longest adaptation times. With Effl↓, a fairly homogeneous elevated concentration over the whole controlled area was observed within 30 min and almost no further changes occurred after 2 h (Figures 2A,C and Movie S1 in Supplementary Material). Adaptation to a 10-fold Infl↑ was even faster (Figures A1A,B). Both processes happened much faster than strictly required, implying that either our dynamics is too fast, or that the time scales for auxin accumulation are dominated by other processes, such as the induction and buildup of the changes in efflux (or influx) permeabilities that are implemented as instantaneous changes in our simulations.

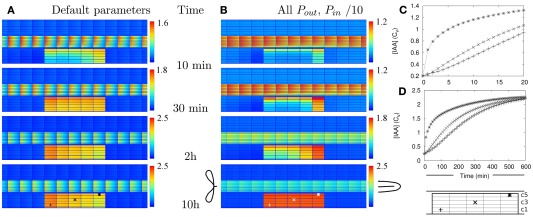
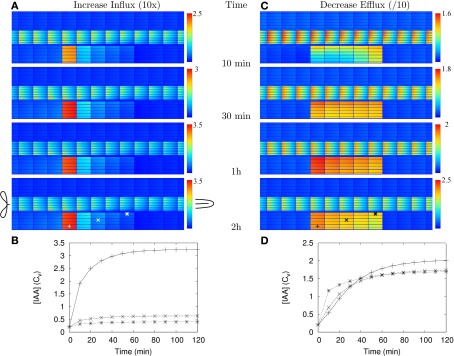
Figure 2.

Auxin accumulation after efflux reduction starts from the inner cortex. The change in the controlled area, a 10-fold reduction of the effective efflux permeabilities (10-fold Effl↓), takes place at T = 0 s. (A,B) Show the auxin concentration at several time points afterward. (A) Default parameters. (B) “Slowed down” parameters: the effective (influx and efflux) permeabilities of the whole root segment are reduced by a factor 10 (the Effl↓-reduction comes on top of this). (C,D) Concentration in the three marked cells during the first 20 min [default parameters (C)] or 10 h [slowed down (D)]. Note how the concentration increases first from the inner cortex and the rootward/upstream side of the controlled area. This corresponds with the locations of possible auxin sources.

We have calculated (wherever possible) or estimated the effective influx and efflux permeabilities used by other authors (Goldsmith et al., 1981; Kramer, 2004; Swarup et al., 2005; Heisler and Jonsson, 2006; Jonsson et al., 2006; Grieneisen et al., 2007; Laskowski et al., 2008; Stoma et al., 2008; Wabnik et al., 2010). We found values ranging over more than two orders of magnitude for both influx and (high) efflux. Our values for (high) effective efflux permeability, P_out,high, and effective influx permeability, P_in, are somewhere in the middle of these ranges. We expected that lower values would slow down the time scales of the response to changes. To assess how much, we also tested the model’s dynamic response in a new reference segment. This was created by reducing all effective permeabilities [influx (P_in) and efflux (P_out,high, P_out,low, and P_out,bg)] by a factor 10. In this case a 10-fold Effl↓ (i.e., a further reduction of the effective efflux permeabilities in the controlled area only) resulted in a fairly homogeneous elevated concentration (>C_v) inside the controlled area within 5 h, the steady state concentration was almost reached at 10 h and hardly any further increase was observed after 20 h (Figures 2B,D and Movie S2 in Supplementary Material).

Even with 10-fold reduced effective permeabilities, auxin accumulation after reduction of the efflux occurred fast enough to be compatible with the observed onset of nodulation. With both parameter sets the accumulation is so fast, that sufficient time is left for the part we did not explicitly consider (i.e., the actual induction of the changes).

2.2.2. Auxin distribution over the controlled area sets the time scale of local auxin accumulation under Effl↓

Given that we do not have perfect knowledge of the PIN layout in the susceptible zone (caricatured by the DZ segment) or the real values of the effective efflux permeabilities, we performed a robustness analysis of the system’s dynamics with respect to the effective efflux permeabilities. To that end we enquired which process was the dynamic bottleneck of auxin accumulation under Effl↓. Was it the supply of auxin to the controlled area, its subsequent distribution over the controlled area, or the total amount accumulated in the whole controlled area?

With the DZ parameters the cortical cells have an effective efflux permeability of P_out,bg on the upstream (rootward) side and of P_out,low on the remaining three sides (Figure 1B). To separate the effects of both we split the effective permeabilities in two groups: “background” (P_out,bg) for the lowest efflux level resulting from mislocalized PINs and “other” [P_out,low, P_out,high, and P_in Figure 1B, equation (2) and Table 1]. We created additional reference segments in which the “other” and “background” permeabilities were reduced by a factor of 1, 10, or 100 independently (reducing “background” at least as much as “other”). The reduction factors are shown in Figure 3F. We applied Effl↓ to this whole set of five reference segments.

Table 1.

Overview of model parameters.

Parameter	(Default) value	Description
DC	300 μm2 s−1	Auxin diffusion constant inside cells (Laskowski et al., 2008)
DW	44 μm2 s−1	Auxin diffusion constant in apoplast (Jones et al., 2009)
Pout,high	20 μm s−1	Effective efflux permeability, high value (Grieneisen et al., 2007; Laskowski et al., 2008)
Pout,low	5 μm s−1	Effective efflux permeability, low value (Grieneisen et al., 2007; Laskowski et al., 2008)
Pout,bg	1 μm s−1	Effective efflux permeability, background value (due to misplaced PINs Grieneisen et al., 2007; Laskowski et al., 2008)
Pin	20 μm s−1	Effective influx permeability (Grieneisen et al., 2007; Laskowski et al., 2008)
Cv	Concentration	The average auxin concentration in the vascular tissue is normalized to 1 Cv. (Strictly speaking, Cv is not a parameter.)
p	0 Cv μm–3 s−1	Auxin production rate; default: no production. Estimates for reasonable rates based on (Ljung et al., 2001), scaled relative to total concentrations (Marchant et al., 2002): order $10^{-4}{C}_v$.
l	100 μm	Cell length
wC	20 μm	Width of cortical cells
wx	10 μm	Width of other cells
dW	0.2 μm	Wall thickness (Jones et al., 2009)
dp	2 μm	Pixel size for the cells’ interior
t	0.5, 1, 2.5 s	Integration time step (dependent on interval between measurements)

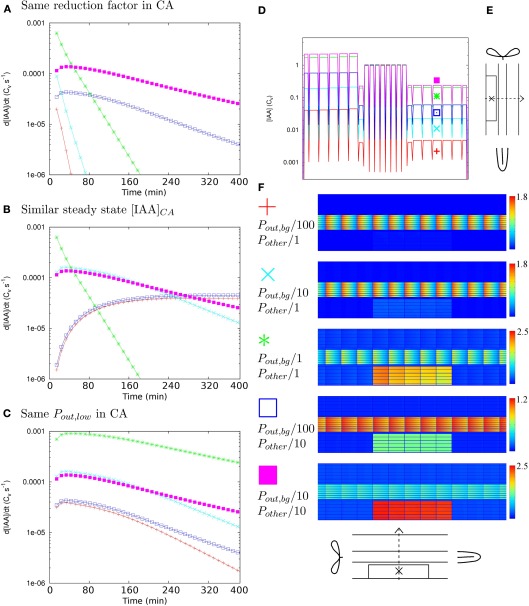
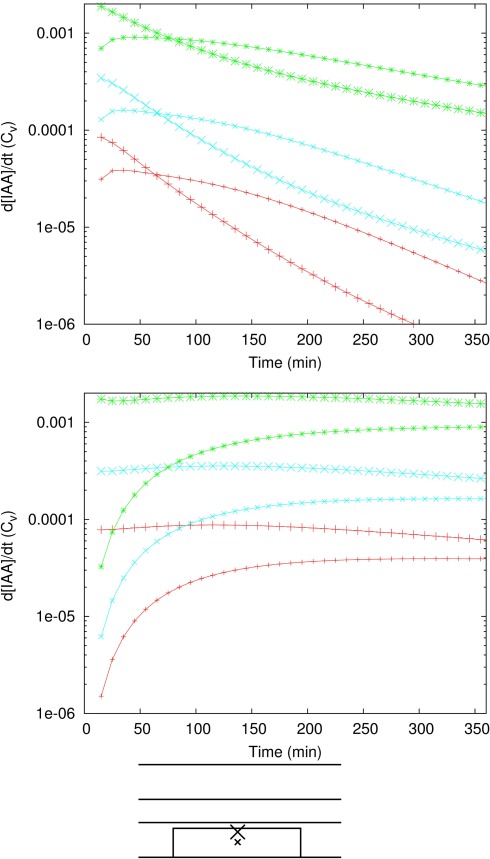
Figure 3.

Determinants of time scales. To determine what factor governs the time scales of auxin accumulation in the controlled area (CA in the scope of this figure) under Effl↓ we followed the changes in the auxin concentration over time in five different reference segments, created by reducing the effective permeabilities with different factors for P_out,bg and all others (P_other = {P_out,low, P_out,high, P_in}). (A–C) Each graph shows simulations that share a common factor. If all five curves have a similar shape, this common factor is the most likely key determinant of the auxin accumulation time scales. (A–C) $\frac{\text{d}\left[\text{IAA}\right]}{\text{d}t}$ In the most central cell of the CA [indicated with “X” in (E)]. (A) Ten-fold (further) reduction of efflux inside the CA. Steady state profiles and overviews matching these curves in (D,F) respectively. (B) Similar steady state [IAA] in the CA: [IAA]_CA ≈ 2–6 C_v. (C) P_out,low = 0.05 μm s⁻¹ inside the CA. (D) Steady state [IAA] profile along the dotted line in (E) for all curves in (A). (F) Legend for all: P_out,bg/100, P_other/1 red pluses, P_out,bg/10, P_other/1 cyan crosses, P_out,bg/1, P_other/1 (original DZ segment) green asterisks, P_out,bg/100, P_other/10 blue open squares, P_out,bg/10, P_other/10 magenta filled squares, next to steady states for the curves in (A). Note that only in (C) all five curves show a similar shape. This implies that the value of P_out,low in the CA, which governs the distribution of auxin over the CA, is the key determinant of the time scales of local auxin accumulation under Effl↓.

To monitor the time scales of this change we calculated the time derivative of the auxin concentration (i.e., the instantaneous change of the auxin concentration) in the most central cell of the controlled area (this cell is indicated in Figure 3E) in all individual simulations. These curves tell how fast the local auxin concentration changes at each moment, making their shape a good proxy for the time scales of the concentration changes. If the course of the time derivatives is similar for the whole set of five, the time scales of auxin concentration changes are dominated by a common feature and conversely, if a certain quantity dominates the time scales, the shape of the time derivatives should be similar in all cases that share the same value of this quantity.

We first applied the same factor, 10-fold, efflux reduction to the set. We found two quite different shapes for the time derivatives, meaning that within the set of five, the auxin concentration in the controlled area increased on different time scales with a change of the same factor (Figure 3A). Additionally, the final concentrations inside the controlled area differed by orders of magnitude (Figures 3D,F). The further the background was reduced relative to the other permeabilities, the lower the steady state concentrations in the controlled area became (Figure 3D). We found an explanation for this effect in the transverse concentration profiles of the reference segments. Actually, in all five cases the cortical concentration in the controlled area increased with a similar factor, but the starting level, or resting state cortical concentration, varied. As we always normalized the vascular concentration to 1 C_v for ease of interpretation (see Materials and Methods), the resting state cortical concentration necessarily differed among these segments. From a 1D calculation along a transverse (x-direction) section with the DZ PIN layout we obtained a first order estimate for the resting state cortical concentration: $\frac{P_{out,bg}}{P_{out,low}}{C}_v.$ Any deviations from this must result from diffusive transport through the apoplast, which is always part of our model. The impact of diffusive transport will be larger for lower (influx) permeabilities, as auxin molecules will then typically remain longer in the apoplast before re-entering a cell.

We also calculated 100 and 1000-fold Effl↓ for the set of five segments and plotted their time derivatives with (Figure 3B) similar steady state concentrations and (Figure 3C) equal P_out,low in the controlled area. Only in the last case, the course of the time derivatives was very similar for all five segments. Revisiting Figures 3A,B with this observation in mind, it became clear that also in the other two cases the curves of root segments with equal P_out,low in the controlled area have a similar shape.

In summary: the amount of auxin available in the cortex determines the level of auxin accumulation with a given degree of efflux reduction. This is a property of the PIN layout of the whole segment, especially its lateral components. The efflux level inside the controlled area (which in this case is mostly set by P_out,low) determines the time scales of auxin accumulation, apparently independent of the supply from outside the controlled area. This implies that the final efflux level in the controlled area (the region of the nodule primordium in biological terms) is important for predicting the time scale of local auxin accumulation, rather than the reduction factor compared to the unaffected root.

2.2.3. Auxin accumulation under Effl↓ starts close to auxin sources

Looking closer at Figure 2 and Movies S1 and S2 in Supplementary Material we observe that despite the homogeneous change in the parameters, the initial auxin accumulation is strongest on two sides of the controlled area: the inner cortex and the rootward (=upstream) side. This is most pronounced in the reference segment with 10-fold reduced parameters (Figures 2B,D). This is particularly interesting, as in legumes forming indeterminate nodules the formation of the primordium occurs predominantly in the inner cortex.

To assess the importance of this transient phenomenon we repeated the analysis from section 2 for the inner cortex (middle of the controlled area; data not shown). We found that also in the inner cortex the time scales are dominated by the efflux level inside the controlled area/P_out,low. The finding that the initial rate of auxin accumulation was faster in the inner cortex than in the central cortex was consistently retrieved in all reference segments and for different reduction factors (Figure A2 in Appendix). The duration of the period with faster auxin accumulation in the inner cortex than in the middle cortex strongly depended on the value of P_out,low in the controlled area, rather than the factor of efflux reduction (compare both parts of Figure A2 in Appendix). The lower P_out,low in the controlled area, the longer this period, so the greater the importance of the inner cortex dominated transient state.

2.3. Precise distribution of cortical PINs can shift the lateral position of the auxin maximum

Determinate and indeterminate nodules differ in the radial position of the root cortical cell divisions from which they originate and (most likely) also in the position of the correlated auxin maximum. The formation of indeterminate nodules starts in the inner cortex, whereas determinate nodule formation occurs in the outer cortex (Libbenga and Harkes, 1973; Mathesius et al., 1998; Timmers et al., 1999; Pacios-Bras et al., 2003; Takanashi et al., 2011). Despite an early increase from the inner cortex (and upstream edge), in our simulations so far the system reached a steady state with a homogeneous increase of the auxin concentration over the full width of the cortex. Coincidentally, the lateral PINs in our DZ reference segment are equally strong on the central and peripheral sides. We wondered if a bias in the lateral PIN positioning in the cortex, either to the periphery or the center, could shift the lateral position of the auxin maximum resulting from Effl↓ and if this would still allow for a sufficiently strong maximum.

To test this we created a set of reference segments based on the original DZ segment but with a varying ratio of inward to outward effective efflux permeability in the lateral walls of the cortical cells. We fixed the inward effective efflux permeability at P_out,low and varied the outward efflux permeability. We then applied a 10-fold Effl↓ to these segments (Figure 4). Indeed the lateral position of the maximum shifted along with the changes of the effective efflux permeability: most auxin accumulated on the side of the controlled area (inner/outer) of the largest effective efflux permeability. In all cases the maximum cortical concentration was well above the vascular level C_v.

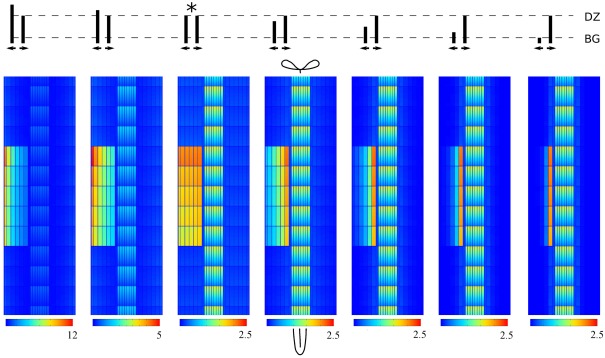
Figure 4.

Shifting the auxin maximum by changing the ratio of lateral PINs in the cortex. All maxima are induced by 10-fold decreased efflux (Effl↓). The cartoon on top shows the ratio of peripheral to central lateral PINs in each cortical cell of the root segment. The original DZ segment is indicated with*. Note that in all cases the highest concentration in the controlled area is well above the vascular concentration C_v.

Our scenario Effl↓ for the reduction of the effective efflux permeability preserves the inward to outward ratio inside the controlled area. As a consequence, changes in this ratio can shift the lateral position of the resulting cortical auxin maximum from inner to outer cortex. This means that the same change of effective efflux permeabilities can result in cortical auxin maxima in different positions, depending on the PIN layout of the root segment concerned. In the discussion we will return to the importance of transient and steady state patterns relative to each other.

2.4. Endodermal PIN layout strongly affects nodulation potential

The DZ PIN layout was the obvious choice for the susceptible zone, but as we did not start from actual legume PIN localization studies in the susceptible zone we asked ourselves if the EZ layout would also allow for the creation of a cortical auxin maximum. If yes, this would imply that the location of the susceptible zone is likely determined independent of the PIN layout (e.g., by the presence of growing root hairs only). If not, we could perhaps identify the feature of the PIN layout responsible for the difference in behavior.

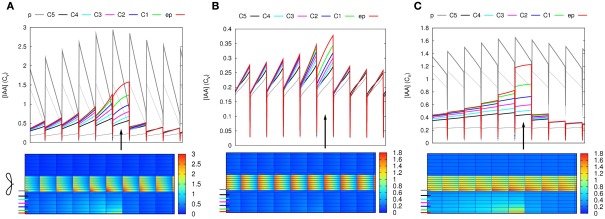
We compared the response to 10-fold Infl↑ and Effl↓ in the DZ and a similarly created EZ segment. To make the EZ root segment we changed the PIN layout (but not the cell sizes) of the DZ root segment, again according to the layout from Laskowski et al. (2008; Figure 5I). This layout differs in two ways from the DZ layout: In the EZ segment the endodermis has a PIN level at the inward and rootward side, rather than ubiquitous and low as in the DZ segment. Additionally, the PIN level at the shootward side of the cortex cells is high in the EZ segment and low in the DZ segment.

Figure 5.

Increased influx and decreased efflux in different zones of the root. The same change in parameters has a different impact with different PIN layouts (but equal tissue geometry). (A–F) DZ, (G–L) EZ parameters. Parameters for the left half of the root (A,I) on top (P_out-levels: red for “high,” cyan for “low,” and white for “bg” as in Figure 1B). The EZ PIN layout results in a much lower auxin concentration in the cortex [compare reference profiles (B,J)]. As a result, the impact of increasing the influx (C,K) or decreasing the efflux (D,L) is hardly visible with the EZ parameters (K,L). (E–H) Show transverse concentration profiles on a logarithmic scale through the middle of the rows of cells indicated in (C,D,K,L) at the shootward and rootward side of the controlled area (Infl↑: cyan, Effl↓: blue). Note how the shape of the profiles in the controlled area largely resembles the shape of the respective reference profiles (in red).

Contrary to the DZ root segment (Figures 5C,D), strongly increasing influx or decreasing efflux in the controlled area of the EZ segment showed little effect (Figures 5K,L). The auxin concentration in the controlled area did increase (Figures 5G,H), but the highest concentration reached was low compared to the vascular auxin concentration C_v (Figures 5K,L).

This can be understood from the (resting state) auxin profiles: they arise as a direct consequence of the segment’s PIN layout (Figures 5A,I). Compared to the DZ segment, the EZ segment contained far less auxin in the cortex and the auxin concentration declined toward the outer cortex (Figures 5G,H,J). The DZ segment, on the other hand, showed a flat transverse cortical profile (Figures 5B,E,F). As in the case with reduced permeabilities (Figure 3D) the profile within the controlled area always resembled the reference profile, apart from a certain offset (Figures 5E–H).

These results show that the creation of a cortical auxin maximum is much harder with the EZ PIN layout than with the DZ PIN layout. As the only difference in PIN layout between the EZ (with little auxin increase upon 10-fold Effl↓) and the rightmost segment in Figure 4 is in the endodermis, this has to be the differentiating element. The transverse concentration profiles show that the difference in the endodermal PINs results in a much lower amount of auxin in the cortex (Figures 5B,E–H,J), explaining the different nodulation potential.

3. Discussion

3.1. Auxin accumulation in nodulation

Our simulations have yielded distinct auxin accumulation signatures for all conceptually different scenarios for creating a local auxin maximum along a root [increasing influx (Infl↑), decreasing efflux (Effl↓), and local auxin production (Prod↑)]. One of these, Effl↓, provides a scenario that is most compatible with Nod factor induced cortical cell divisions, which form the start of nodule formation.

At the start of nodule primordium formation auxin accumulates either in the inner or outer cortex with a homogeneous concentration in a region of several cells long (Pacios-Bras et al., 2003; Takanashi et al., 2011). Of the three simple scenarios Effl↓ is the only one that yields an auxin concentration that is both strong and fairly homogeneous along the length of the root (Figure 1D). Moreover, the lateral location of this position can be shifted by small changes in the lateral PINs in the cortex (Figure 4), allowing for both “Lotus” and “Medicago” locations of the induced auxin maximum. The downregulation of PIN proteins (Effl↓) as the mechanism behind auxin accumulation in the cortical cells that will form a nodule primordium is also compatible with several lines of experimental evidence: The induction of nodule-like structures with auxin transport blocker NPA (Hirsch et al., 1989; Rightmyer and Long, 2011), a decrease of polar auxin transport 24 h after treatment with Rhizobium (van Noorden et al., 2006).

A cytokinin response is observed early in nodulation (Frugier et al., 2008; Plet et al., 2011). A gain of function mutation of a specific cytokinin receptor results in spontaneous pseudonodule formation (Tirichine et al., 2007) and several cytokinin response regulators are induced in nodule primordia (Op den Camp et al., 2011; Plet et al., 2011). Moreover, this key nodulation hormone caused a reduction of PIN expression and/or membrane localization in several Arabidopsis tissues (Dello Ioio et al., 2007, 2008; Pernisova et al., 2009; Ruzicka et al., 2009; Marhavý et al., 2011).

Therefore we argue that cytokinin is a likely candidate for inducing a removal of PIN proteins from the membrane in nodulation, leading to local auxin accumulation.

In our simulations auxin accumulation through efflux reduction was fast enough to be compatible with the known timing of nodulation events (Yang et al., 1994; Timmers et al., 1999). Interestingly, the auxin accumulation started from the inner cortex (Figure 2 and Movies S1 and S2 in Supplementary Material), even though the change (reduction of efflux) occurred simultaneously in all cells of the controlled area. This “head start” for the inner cortex became more pronounced if the effective efflux level in the cortex was reduced to a lower value (Figures 2A,B and Figure A2 in Appendix).

The current view, in which Nod factor signaling induces cytokinin production, which reduces the amount of PIN in the membranes and thus invokes local auxin accumulation, invokes a naive question: why has the pathway evolved such that it includes cytokinin? Is this contingent, or necessary? In other words: would it be possible to create a cortical auxin maximum without a secondary signal such as cytokinin, but with a direct auxin signal?

First thing to note is that such a scenario is similar to our local production scenario (Prod↑). Most of the auxin signal (whether of epidermal or rhizobial origin) would be transported away from the production site and the little local increase will be ill confined (as in Figures 1E,H. Moreover, due to the net shootward flux in the cortex the strongest accumulation will occur longitudinally shifted relative to the production site. These issues are further illustrated in Figure A4 in Appendix. The use of a second signal, that is not transported away like auxin, bypasses this problem. Such a signal could induce local changes in the auxin transport system, which would then result in local auxin accumulation. Indeterminate nodules such as those of Medicago species are also in another way incompatible with a direct auxin signal. These nodules are formed from the inner cortex (Timmers et al., 1999). A direct auxin signal, if effective at all, would always induce divisions starting from the outer cortex. We have observed that under Effl↓, auxin accumulation naturally starts from the sources of auxin, notably the inner cortex (Figure 2).

From this we hypothesize that a secondary signal, in this case cytokinin, is required to induce a cortical auxin maximum in the vicinity of the original epidermal Rhizobium infection.

3.2. The accumulation mechanism affects the dimensions of the primordium

We have observed that in Medicago nodule primordia have a typical width of 5–6 undivided cortical cells which is much broader than a lateral root primordium (data not shown). Could this be a consequence of the mechanism underlying the local auxin accumulation?

Several authors have shown that in Arabidopsis the influx carrier AUX1 is strongly upregulated in the pericycle cells founding the lateral root primordium and their descendants, including the early primordium stages (Marchant et al., 2002; Laskowski et al., 2008). We observed from our simulations that with increased influx a much narrower auxin maximum is formed than with decreasing efflux. This maximum can even be much narrower than the zone of Aux1/Lax expression. Data by Hirota et al. (2007) actually show an auxin maximum that is more focused than the known area of AUX1 expression.

This combination of experimentally observed morphologies and auxin accumulation patterns together with the distinct patterns resulting from different scenarios for auxin accumulation lead to the hypothesis that the mechanism used for local auxin accumulation in a given case affects the dimensions of the emerging organ.

3.3. Steady state vs. transient patterns

We have identified two mechanisms that affect the lateral position of the Effl↓ induced local auxin maximum. A possibility for shifting the steady state maximum toward either the inner or the outer cortex is changing the inward: outward ratio of lateral PINs in the cortex. In that case the steady state maximum will occur on the side of the largest effective efflux permeability (Figure 4). From the dynamics we have observed that without such a lateral bias, the inner cortex accumulates auxin faster than the outer and middle layers (Figures 2 and Figure A2 in Appendix). Specially for strong reductions of the efflux transient patterns could become more important for development than the steady state. How do these two findings interact?

For an auxin maximum in the inner cortex we found two possibilities. The first is a very strong reduction of the efflux, to such a low level that the transient state becomes the only relevant one. The second comprises any reduction that is strong enough to obtain a sufficiently high steady state concentration at the location of the maximum, combined with an inward bias of the lateral cortical PINs. In that case the steady state and transient patterns will be similar, both with the strongest accumulation in the inner cortex. Moreover, with less auxin available in the outer cortex, the vascular tissue will become practically the only auxin source. This would strongly reduce the auxin accumulation from the upstream/rootward side of the controlled area we observed in Figure 2, reducing the dynamical rootward/shootward differences in the process of the local auxin accumulation.

For an auxin maximum in the outer cortex, on the other hand, it seems important that the minimal efflux level in the region of the primordium does not become too low, as that would probably result in a long lived transient maximum in the inner cortex, something that has not been reported in auxin reporter studies in Lotus (Pacios-Bras et al., 2003; Takanashi et al., 2011). Therefore it is more likely that in this case the steady state dominates the development. A slight efflux bias toward the outer side could further increase the auxin accumulation in the outer cortex.

3.4. Are cortical PINs distributed differently for determinate and indeterminate nodules?

A key difference between determinate and indeterminate nodules is the main site of the primordial cell divisions: the outer or the inner cortex respectively. This has also been observed in the location of auxin accumulation (Mathesius et al., 1998; Pacios-Bras et al., 2003; Takanashi et al., 2011). Under the strict, but not necessarily fully true, assumption that the location of auxin accumulation perfectly predicts the division site and this turn perfectly predicts nodule type, we like relate our findings for the formation different nodule types.

The phylogenetic distribution of determinate and indeterminate nodule types within the legumes can not be explained by a single transition from an ancestral to a derived type (Doyle, 1994; Mergaert et al., 2003). From this we conclude that the distinguishing difference must be relatively easy to “invent.” Additionally it has to be root autonomous, as grafting experiments show that the shoot does not affect the nodule type formed (Lohar and VandenBosch, 2005).

We have shown that changing the ratio of inward to outward PINs can be sufficient for shifting the axial position of the Effl↓ auxin maximum. Slight differences in the PIN positioning appear to us as relatively easy changes in an evolutionary sense. Under the assumption that the position of the initial auxin maximum and resulting cell divisions is the key determinant for (in)determinate nodule type, we tentatively hypothesize that the lateral PIN localization in cortex of the DZ could differ between legumes making either nodule type, with a bias toward the center for indeterminate and no bias or a slight bias toward the periphery for determinate nodules.

Phosphorylation and dephosphorylation of PIN proteins by PINOID and PP2A respectively plays an important role in the polar targeting of PIN proteins (Friml et al., 2004; Michniewicz et al., 2007). It has been shown that changes in PINOID activity impact the central/peripheral lateral distribution of PINs in another context (Ding et al., 2011). Differences among legumes in the lateral PIN positioning in the cortex could perhaps result from differential regulation of these players.

3.5. Biological limits of the simple changes

Although in our simulations we are essentially free to give any value to the effective influx- and efflux permeabilities, in reality they are bound by biological constraints. What does this mean for our results?

The increase of influx under Infl↑ must result from a stronger expression of influx carriers. Of course, a plant can and will only produce a certain amount of these proteins. A frequently used value for AUX1 based influx [P_AUX1 = 0.55 μm s⁻¹; Swarup et al., 2005; Heisler and Jonsson, 2006)¹ permeability results in a carrier based influx that is 15 times higher than passive diffusive influx (Swarup et al., 2005). Taking into account the strong upregulation of AUX1 observed in lateral root founder cells (Marchant et al., 2002; Laskowski et al., 2008), a difference between cells of up to two orders of magnitude can be considered reasonable. The model by Laskowski et al. (2008) our starting point, assumes (initially) homogeneous AUX1 expression. Under this assumption the maximum increase we used under Infl↑ is still reasonable, but could be close to the upper bound.

Under Effl↓ the decrease of efflux has to originate from a decrease of PINs or other efflux carriers from the membrane and/or a reduction of their activity. Our implementation of using the same reduction factor for all sides of the cell assumes that the efflux is facilitated by a single type of carrier, or, if it results from multiple types, that these all show the same response to the initial signal. Following current studies on PIN proteins, which show that they can disappear almost completely from the membrane upon addition of large amounts of cytokinin (see e.g., Pernisova et al., 2009), our approach is probably the most reasonable one, barring the explicit consideration of of PIN activity regulation and localization dynamics.

However, a different type of efflux carriers, known as PGP, or ABCB (Noh et al., 2001; Mravec et al., 2008) has been suggested to give rise to a small but significant base efflux permeability even in the absence of PINs (Leyser, 2011). Additionally, some suggestions for a minimal efflux permeability in absence of efflux carriers appear in the literature (Delbarre et al., 1996; Swarup et al., 2005).

The importance of such a minimal efflux permeability will only surface with strong reductions of the efflux carriers. In that case the ratios between P_out,high, P_out,low, and P_out,bg will necessarily change inside the controlled area, resulting in transverse profiles that are flatter than the reference profile. How this affects the auxin accumulation throughout the cortex makes an interesting topic for further research.

3.6. On simple roots

The root segments used in our work are a generalization of PIN layouts measured and modeled in Arabidopsis (Laskowski et al., 2008). Lacking clear PIN layout data of the relevant zones of any legume’s root this starting point is the best we have. It is likely that the rootward flux in the stele and the shootward flux in the cortex, which set the directional bias in the patterns we observe, are conserved. If more precise quantitative predictions are desired, however, actual legume PIN data are needed.

This does not mean that our simple approach is but a poor man’s choice. Its simplicity is also one of its strengths. The first recognition of the typical signature of each scenario is easier with a simple PIN and tissue layout than with a more “realistic” layout. In a next step we checked that they are also well distinguishable on a “realistic” layout (Figures 1F–H). From this we conclude that the signatures we have discovered are general phenomena with a scope well beyond this pseudo-legume.

The way these signatures are affected by certain aspects of the PIN layout sets requirements on the actual PIN layout of diverse legumes. These observations brought us to the tentative hypothesis that differences in the distribution of cortical PINs in the lateral walls might distinguish determinate and indeterminate legumes. We also found a very important role for the endodermal PIN layout on the overall nodulation potential of a stretch of root, as it is pivotal in determining the amount of auxin available in the (inner) cortex.

Our approach is based on the strong link between the positions of auxin carriers and the steady state auxin concentration distribution. We use differences in the patterns resulting from different scenarios (Infl↑, Effl↓, and Prod↑) to address the differential likelihood of these scenarios in a particular situation. This approach may also prove useful in elucidating PIN positioning information from fluorescence data. This data can be hard to interpret, because cell membranes from neighboring cells are usually less than a wavelength apart. When available, information on the auxin accumulation pattern could be used to find the most likely positioning scenario that fits the fluorescence data.

3.7. The next step: A step back

In this work we applied all changes in an all-or-nothing manner to a well defined block of cells (the controlled area). This proved a very powerful approach for recognizing different patterns and their distinguishing features. No plant in its right (absence of) mind, however, will ever show exactly such a precise and all-or-nothing change. This brings forth a very natural follow-up question: how is, upon contact with Rhizobium, such a confined local change in the auxin transport/metabolism induced? What mechanism(s) can spatially confine the response to the signal (likely cytokinin) originating from a single epidermal cell to the correct area? The dynamic localization of PIN proteins (Grunewald and Friml, 2010) will most likely play an important role in the establishment of a local auxin maximum.

4. Materials and Methods

4.1. General approach

We have simulated auxin diffusion and transport on a static root tissue using conventional numerical methods (4.5). We explicitly model intracellular auxin concentrations. This is customary for models describing root tissue (Kramer, 2004; Swarup et al., 2005; Grieneisen et al., 2007; Laskowski et al., 2008; Jones et al., 2009), as, assuming realistic diffusion constants, the relatively long cells give rise to significant concentration differences between the ends of the cell (Kramer, 2008). Following these previous works we also use a static influx/efflux/production parameters within individual simulations (4.2), focusing on the consequences of our different scenarios (4.4). For ease of interpretation we normalize auxin concentrations with the average vascular level (4.6.1) of the respective reference segment (a segment without any change in the controlled area).

4.2. Tissue geometry and PIN layout

Our simulations are carried out on a 2D root segment representing the susceptible zone of a generalized legume. Current model legumes typically have 4–6 cortical layers, so we have created a segment with five cortical layers. Cell sizes were chosen to match the typical length of cortical cells in the susceptible zone, a representative root diameter and the right ratio between cortical and vascular tissue, see Table 1 and Figure 1A.

Lacking good PIN position data for the susceptible zone of model legumes (Medicago or Lotus), we used the DZ part of the Arabidopsis model by Laskowski et al. (2008) as a starting point, as the differentiation zone comes closest to the susceptible zone. Arabidopsis has only a single cortical layer, so we copied the parameters for the cortical layer to four additional layers. All cells of the same type (e.g., cortex, epidermis, vascular) have the same PIN distribution, as in (Laskowski et al., 2008). The resulting PIN layout of the DZ root segment is shown in Figure 1B. We also used the EZ PIN layout from the same paper (shown in Figure 5I).

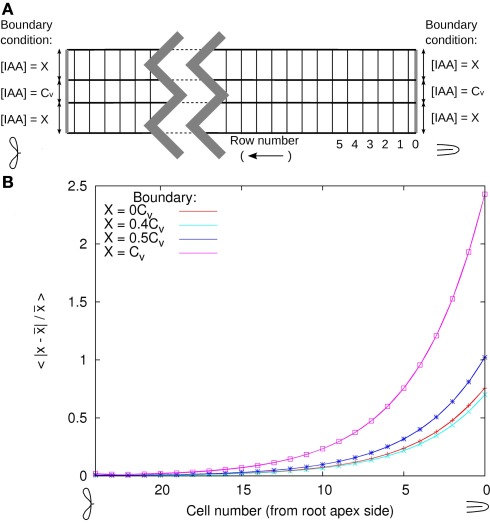
4.3. Boundary conditions

The biological root continues on both (rootward and shootward) ends of the segment (Figure 1A). We modeled these edges with an open boundary consisting of a row of open cells of half the normal length. The concentration at the boundary grid points is fixed. Lateral boundaries have a no-flux boundary condition: no auxin leaves from the epidermis into the surroundings.

The full root simulations from Laskowski et al. show almost no longitudinal gradient within the DZ. Based on this we chose the same concentration profile on both the rootward and shootward side of the segment. In this situation the transverse concentration profile settles at a fixed profile, which is to a very large extent dictated by the PIN layout of the segment. This transverse concentration profile we call “resting state,” because in theory one could create an infinitely long segment with the same concentration profile everywhere along its length by forever repeating the same transverse building blocks (as long as decay is negligible). The rootward and shootward boundaries are fixed at this resting state. Although the concentrations at these boundaries are fixed, a net flux of auxin through the segment does occur.

Considering the whole root, it is conceivable that at the edge of the DZ the resting state is not fully reached yet and the actual concentrations at the boundary are different. A small deviation from the resting state is perhaps far more likely than none at all. For this reason we tested the impact of deviations from the resting state profile at the boundaries of the DZ segment. Looking at a transverse line through the middle of the cells (all at the same distance from the rootward boundary) the resting state profile has the same concentration in all vascular cells including the pericycle. As explained in 1, this level is normalized to 1 C_v. In the DZ fragment all peripheral layers (i.e., epidermis, cortex, and endodermis) have a resting state concentration of 0.2 C_v (Figures 5A,B).

We changed the boundary conditions of the DZ segment by changing the ratio between the vascular and the peripheral auxin concentration (C_v and X in Figure A3A). After equilibration we renormalized the total amount of auxin with the transverse row of cells with a profile closest to the resting state. We found that in the shootward direction the deviation from the resting state transverse profile (integrated over the whole line) decayed exponentially ∼e^−n/4.3 (with n the cell number counted from the rootward edge of the segment). This decay constant implies that the deviation from the resting state is halved every 2.9 cell lengths in the shootward direction (Figure A3B). In the opposite direction deviations decay even faster.

With this we are confident that a segment without a longitudinal gradient, settled at the resting state transverse concentration profile is a very reasonable model of the DZ situation.

4.4. Changes are applied in the “controlled area”

We investigate both dynamic and steady state effects of homogeneous changes of a block of cells situated on one side of the root, dubbed controlled area. It consists of all five cortical layers and the epidermis and is five cells (5 × 100 μm) long (Figure 1A). This corresponds well with the typical length of a nodule primordium. The same change is applied to every cell inthe controlled area:

• (n-fold) Infl↑: increase the effective influx permeability (P_in; n times)

• (n-fold) Effl↓: decrease the effective efflux permeabilities (P_out,bg, P_out,low, and P_out,high; n times)

• Prod↑: local auxin production with the given rate (per volume) in C_v s⁻¹ μm⁻³

4.5. Simulation method

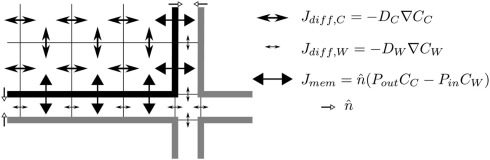
We use in house developed C++ code for simulating the transport and metabolism of auxin. Our simulations are carried out on a 2D longitudinal slice through the center of a generalized root segment, in most cases representing the DZ (Figures 1A,B). We simulate auxin diffusion (in cells and walls separately) and transport (over membranes) with subcellular precision (Figure 6; pixel sizes in Table 1). The apoplast is considered as a separate continuous compartment. Spatial coordinates are denoted with x (transverse) and y (rootward or longitudinal) with coordinates in μm.

Figure 6.

Simulation details. The figure shows the simulation grid of a small corner section of a cell and the surrounding apoplast. Membranes are indicated with thick lines, the grid with thin lines. Different types of arrows indicate the different equations: diffusion inside the cell and within the apoplast (differing only in the value of the diffusion constant) and active + passive transport over the membrane. $\widehat{n}$ Is a unit length vector pointing out of the cell. Note that the apoplast thickness is not drawn to scale.

Within a compartment auxin moves by diffusion, with different diffusion constants for cells (C) and walls (W):

$$J_{diff,CW}\left(x,y\right)=-D_{CW}\nabla C\left(x,y\right)$$ (1)

with C(x, y) the auxin concentration at a given position and D_CW the respective diffusion constant. The combined effects of active transport and passive permeability are grouped into a single parameter for effective efflux permeability P_out and effective influx permeability P_in. In principle P_out can be set for each face of a cell independently, whereas a cell always has a single value of P_in for all four faces. These parameters control the flux over the membrane:

$$J_{mem}\left(x,y\right)=\left(P_{out,xx}{C}_C\left(x,y\right)-P_{in}{C}_W\left(x,y\right)\right)\cdot \widehat{n}$$ (2)

Here P_out,xx is the relevant effective efflux permeability. In the reference segment three different levels are used: high, low, and bg for strong and weak PIN expression and a background level due to ubiquitously expressed PINs respectively. In the choice of three levels we follow (Laskowski et al., 2008). $\widehat{n}$ is a unit length normal vector pointing out of the cell. We follow (Laskowski et al., 2008) in assuming a single value of P_in for the whole reference segment.

These equations are solved using the Alternating Direction Implicit (ADI) algorithm (Peaceman and Rachford, 1955) using a 2D finite volume description of the tissue. We use a rectangular grid topology with different volume sizes within the cell and wall compartments and at junctions. This allows us to use a realistic cell wall width without wasting excessive memory on the cells’ interiors.

The integration time step is chosen depending on the interval between measurements, with typical values of 0.5, 1, and 2.5 s. Results were checked for numerical artifacts and if necessary the time step was adapted.

4.6. Parameters

When thinking of the root segment as a thin 3D slice with unit thickness (1 μm, much thinner than a cell’s diameter) all parameters and quantities can be used in their usual dimensions. For reasons of familiarity we present them as such, although our simulations are carried out on a strictly 2D template.

For an overview of all model parameters, see Table 1.

4.6.1. Normalization of IAA concentration units

By lack of a real 3D volume, concentrations units are arbitrary. This means all concentrations can be multiplied with an arbitrary constant without affecting the model’s behavior. (The only parameter that contains concentration units is the auxin production rate. Thus, this is the only parameter that scales with the actual concentration.) For the ease of interpretation we choose to scale all concentrations such that the average auxin concentration in the center of the vascular cylinder of a reference root segment without a longitudinal gradient is 1 C_v. Without information about the cells’, likely differential, sensitivity to changes in the auxin concentration and/or the absolute concentration it is probably most insightful to compare concentrations to a known level. Nevertheless, it is important to bear in mind that cells could show different responses to the same auxin concentration or change.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Movies S1 and S2 for this article can be found online at http://www.frontiersin.org/Plant_Biophysics_and_Modeling/10.3389/fpls.2012.00096/abstract

Appendix

Figure A1.

Dynamic response to influx and efflux changes compared. At T = 0 s the influx is increased 10-fold [Infl↑ (A,B)] or the efflux is decreased 10× [Effl↓ (C,D)] in the controlled area. The top part shows snapshots of selected time points (A,C). Graphs (B,D) show the auxin concentration in the three indicated cells (see lowest snapshot) over the first 2 h. Note that under Infl↑ the new steady state is reached faster than under flux, but the reverse is true for the most rootward inner cortex cell of the controlled area (marked *).

Figure A2.

Faster auxin accumulation in the inner cortex with Effl↓. Time derivatives of the auxin concentration in two different cells in the (longitudinal) middle of the controlled area: inner cortex (large symbols) and central cortex (small symbols). Colors and symbols as in Figure 3. (For clarity of the graphs the two cases with P_other/10 are omitted. In both cases they are very similar to their respective matches from the lower two pairs of curves, as in Figure 3C.) In all segments, P_out,low in the controlled area is reduced to the same value: P_out,low = 0.05 μm s⁻¹ (top), P_out,low = 0.005 μm s⁻¹ (bottom). In the beginning the auxin concentration increases faster in the inner cortex than in the central cortex, as can be seen from the higher rate of change of the auxin concentration. With a stronger reduction the efflux this period of faster increase in the inner cortex was longer.

Figure A3.

Test of DZ parameters with respect to disturbed boundary conditions. The cortical auxin concentration at both edges is clipped at different values (X) relative to the vascular concentration at the edge, as shown in (A). After equilibration with these boundary conditions and normalization with the central vascular auxin concentration the transverse profile through the center of the cells is compared to the resting state profile for four values of X (B). In the restingstate profile X ≈ 0.2 C_v. For each value of X the deviation form the reference decays exponentially according to e^−n/τ, with τ = 4.3 and n the number of the cell counted from the rootward edge (curves fitted to the data). This means that the deviation from the resting state profile is halved every 2.9 cells.

Figure A4.

Auxin is not suitable as a direct signal. In all three cases auxin is produced in a single epidermal cell (position is indicated with an arrow in the line graphs). For a notable increase of the auxin concentration in some parts of the segment, very high production rates are needed, even with slowed down transport. Moreover, in the inner cortical layers the auxin concentration increases a bit over a wide region and the maximum increase does not occur closest to the production side, but shootward of it (downstream considering the cortical flow direction). The bottom images show steady state auxin concentrations. The graphs on top show the concentrations in the indicated layers (thick lines: pericycle, 5× cortex, and epidermis). The resting state concentrations (i.e., before production started) are plotted in thin black (vascular) and gray (cortex) lines. (A,B) Default parameters (C): “slowed down” parameters from Figure 2B: all effective permeabilities are reduced by a factor 10. Production rates are much higher than in Figures 1E,H, as here only a single cell produces: 0.1 C_v μm^–3 s⁻¹ (A), 0.01 C_v μm^–3 s⁻¹ (B,C). Note that in (A) the producing epidermal cell produces the full amount of auxin present in a vascular cell (both have the same size) of the reference segment every 10 s. The total amount produced per second is slightly more than half of the total in Figure 2E and consequently from several cells rootward of the production site onward the auxin concentration is significantly increased in all cell files. We consider this value (A) absurdly high, but use it because hardly any change is seen with the already high production rate of (B). This is because the auxin is very efficiently transported away from the production site. Reducing the efficiency of this transport by reducing all effective permeabilities of the whole segment [“slowing it down” (C)], a less absurd production rate is enough to support an obvious accumulation, but the issues of ill confined auxin accumulation and a shift of the maximum in the inner cortical layers (C5–C3) remain.

Abbreviations

DZ, Differentiation zone; Effl↓, scenario in which the efflux permeability is decreased in the controlled area (see Figure 1A); EZ, elongation zone; IAA, indole-3-acetic acid (an auxin); Infl↑, scenario in which the influx permeability is increased in the controlled area; Prod↑, Scenario in which all cells of the controlled area produce auxin.