Predicting regional neurodegeneration from the healthy brain functional connectome

Summary

Neurodegenerative diseases target large-scale neural networks. Four competing mechanistic hypotheses have been proposed to explain network-based disease patterning: nodal stress, transneuronal spread, trophic failure, and shared vulnerability. Here, we used task-free fMRI to derive the healthy intrinsic connectivity patterns seeded by brain regions vulnerable to any of five distinct neurodegenerative diseases. These data enabled us to investigate how intrinsic connectivity in health predicts region-by-region vulnerability to disease. For each illness, specific regions emerged as critical network “epicenters” whose normal connectivity profiles most resembled the disease-associated atrophy pattern. Graph theoretical analyses in healthy subjects revealed that regions with higher total connectional flow and, more consistently, shorter functional paths to the epicenters, showed greater disease-related vulnerability. These findings best fit a transneuronal spread model of network-based vulnerability. Molecular pathological approaches may help clarify what makes each epicenter vulnerable to its targeting disease and how toxic protein species travel between networked brain structures.

Introduction

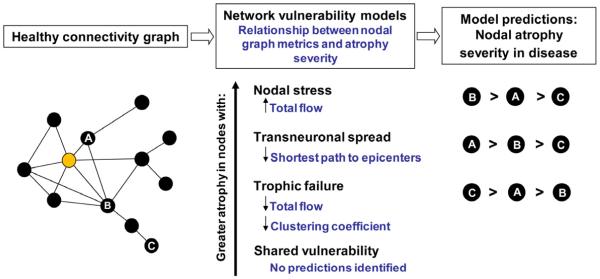
Neurodegenerative diseases have long been linked to neuronal networks by the clinical and anatomical progression observed in patients (Braak and Braak, 1991; Pearson et al., 1985; Saper et al., 1987; Weintraub and Mesulam, 1996). Emerging network-sensitive neuroimaging techniques have allowed researchers to demonstrate that the spatial patterning of each disease relates closely to a distinct functional intrinsic connectivity network (ICN), mapped in the healthy brain with task-free or “resting-state” fMRI (Buckner et al., 2005; Seeley et al., 2009). Collectively, these findings raise mechanistic questions about whether and how connectivity in health predicts regional neurodegeneration severity in disease. In Alzheimer’s disease, increasing evidence suggests that pathology may begin within key vulnerable “hubs”, defined as central nodes within the target network’s architecture (Buckner et al., 2009). Still, open questions remain with regard to why each disease adopts a network-related spatial pattern. At least four disease-general hypotheses have been offered and can be summarized as: (1) “nodal stress”, in which regions subject to heavy network traffic (i.e. “hubs”) undergo activity-related “wear and tear” that gives rise to or worsens disease (Buckner et al., 2009; Saxena and Caroni, 2011); (2) “transneuronal spread”, in which some toxic agent propagates along network connections, perhaps through “prion-like” templated conformational change (Baker et al., 1994; Frost and Diamond, 2010; Frost et al., 2009; Jucker and Walker, 2011; Lee et al., 2010a; Prusiner, 1984; Ridley et al., 2006; Walker et al., 2006); (3) “trophic failure”, in which network connectivity disruption undermines inter-nodal trophic factor support, accelerating disease within nodes lacking collateral trophic sources (Appel, 1981; Salehi et al., 2006); and (4) “shared vulnerability”, in which networked regions feature a common gene or protein expression signature that confers disease-specific susceptibility evenly distributed throughout the network. Although these hypothesized network degeneration mechanisms need not be considered mutually exclusive, they make competing predictions with regard to how healthy network architecture should influence disease-associated regional vulnerability (Figure 1).

Figure 1. Predictions made by network-based degeneration models: effects of healthy intrinsic connectivity graph metrics on atrophy severity in disease.

A simplified healthy connectivity graph is shown (far left) for illustration purposes only; circles represent nodes (brain regions), lines represent edges (a connection between two nodes), and edge lengths represent the connectivity strength between nodes, with shorter edges representing stronger connections. The orange node represents an epicenter. Three nodes, labeled as ‘A’, ‘B’, and ‘C’, feature contrasting graph theoretical properties to illustrate predictions made by the network-based vulnerability models (far right). Listed in the center column are the relationships predicted by each model. For example, the transneuronal spread model predicts that nodes with shorter (↓) paths to the epicenter in health will be associated with greater (↑) atrophy severity in disease. Justification for each model’s prediction set is provided in the main text.

Here, we explored the relationship between healthy functional architecture, as assessed with graph theoretical analyses of task-free fMRI data, and neurodegenerative disease vulnerability, as assessed by quantifying regional atrophy in patients. Our previous work showed that each of five distinct neurodegenerative syndromes featured an atrophy pattern that mirrored the healthy functional ICN seeded by the cortical region most atrophied in patients with that syndrome (Seeley et al., 2009). The present study, in contrast, examined every brain region within the five disease-related atrophy maps to identify the regions whose connectivity pattern in health most resembled the atrophy map seen in each syndrome (see Figure 2 for a methods schematic). The resulting dataset fully specified the node pair connectivity strengths across all regions atrophied in any of the five diseases; collectively, these regions traversed most cerebral cortical and subcortical structures. With this information in hand, we used graph theoretical analyses to test model-based predictions of how network architecture in health relates to disease-associated tissue loss (Figure 1). Although previously described spatial atrophy patterns (Seeley et al., 2009) specified the brain regions interrogated for the current study, all network connectivity analyses were performed on an independent dataset of 16 healthy subjects aged 57 to 70 (8 females, all right-handed and psychoactive medication-free; see Experimental Procedures). The resulting connectivity patterns and graph metrics were used to relate each region’s healthy connectivity profile to that region’s disease-specific vulnerability, defined as its atrophy severity in patients.

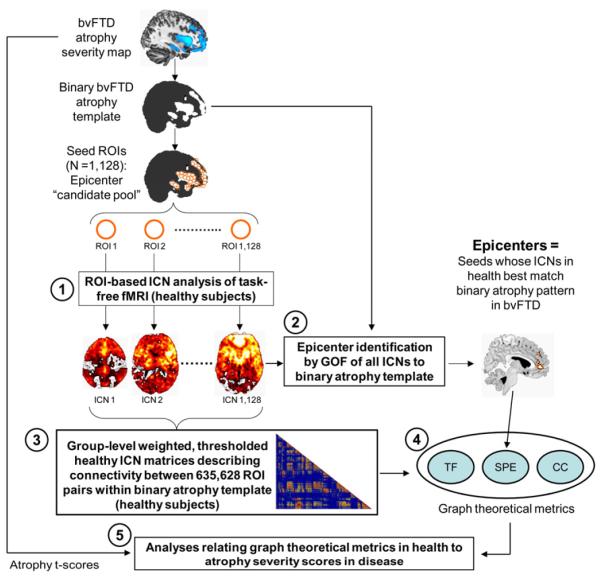
Figure 2. Study design schematic.

Atrophy maps from five neurodegenerative syndromes were delineated in a previous study (Seeley et al., 2009) and binarized to create five sets of 4 mm-radius spherical ROIs representing an epicenter “candidate pool” for each syndrome. Based on these pools, five steps were involved to infer the relationship between healthy intrinsic functional connectivity and atrophy severity in disease: (1) the intrinsic functional connectivity of each ROI was derived with task-free fMRI data from healthy controls, resulting in one whole-brain ICN map for each ROI; (2) regions whose ICNs in health featured significant goodness-of-fit (GOF) to the binarized parent atrophy map were identified as “epicenters” at the group-level; (3) group-level weighted, thresholded healthy ICN matrices were constructed, describing connectivity between all ROI pairs within the binarized atrophy template; (4) three graph theoretical metrics were calculated from the group-level ICN matrices, including shortest functional path to the epicenters (SPE), total flow (TF), and clustering coefficient (CC); (5) correlation and stepwise regression analyses were employed to examine the relationship between the three graph theoretical metrics in health and atrophy t-scores in disease. This process was carried out for each of five syndromic atrophy patterns; for illustration, the steps used for the bvFTD-related analyses are shown here.

Results

Focal epicenters anchor each disease-associated large-scale network

In previous work (Seeley et al., 2009), we identified regional atrophy maxima for five neurodegenerative syndromes: Alzheimer’s disease (AD), behavioral variant frontotemporal dementia (bvFTD), semantic dementia (SD), progressive nonfluent aphasia (PNFA), and corticobasal syndrome (CBS). Then, using healthy subjects scanned with task-free fMRI, we used these five atrophy maxima as “seed” regions to derive five ICNs, representing regions whose blood oxygen level-dependent (BOLD) signal time-series significantly correlated with that of the seed. The atrophy maxima seeded ICNs that resembled the parent atrophy maps, supporting the view that neurodegenerative disease patterns are network-based. By studying only one seed region per atrophy pattern, however, this approach could not determine which regions featured maximal connectivity to the other vulnerable regions. We anticipated that each disease-associated pattern would harbor focal “epicenters,” regions whose connectivity patterns—in the healthy brain—most closely mirrored the disease vulnerability pattern. To seek out these epicenters, here we took a more comprehensive, data-driven approach by studying all regions within each of the five atrophy patterns. For example (Figure 2), we created 1,128 4 mm-radius spherical regions of interest (ROIs) covering the entire bvFTD atrophy pattern and built 1,128 functional ICN maps, one seeded by each ROI, for each of our 16 healthy subjects. We then derived 1,128 group-level ICN maps for comparison to the (binarized) bvFTD atrophy pattern. Applying this general strategy to all five syndromic atrophy patterns, we used group-level goodness-of-fit (GOF) analyses (see Experimental Procedures) to reveal five sets of distinct and focal epicenters (Figure 3 and S1, Table S1), whose large-scale connectivity maps in health showed highest GOF to the binarized syndromic atrophy patterns. Remarkably, although atrophy severity values made no contribution to epicenter identification, the epicenters uncovered here were seated in or near the most atrophic regions identified in our previous work (Seeley et al., 2009) (Figure S1), suggesting that epicenters—in addition to being broadly connected with regions atrophied in a disease—are often among the most atrophied (and perhaps earliest-affected) regions in that disease. Although the terms “epicenter” and “hub” have been used interchangeably to describe transmodal convergence zones within healthy large-scale brain networks (Mesulam, 2011), we chose “epicenter” to describe the regions identified here because (1) “epicenter” carries a pathogenic connotation, describing a region that is often but not necessarily the site of maximal damage and (2) “hub” evokes a brain region with high node centrality (“hub-ness”), as defined within the network science lexicon. Our epicenter identification strategy, however, did not include graph theoretical measures and thus provided no guarantee that the identified epicenters would represent true network hubs.

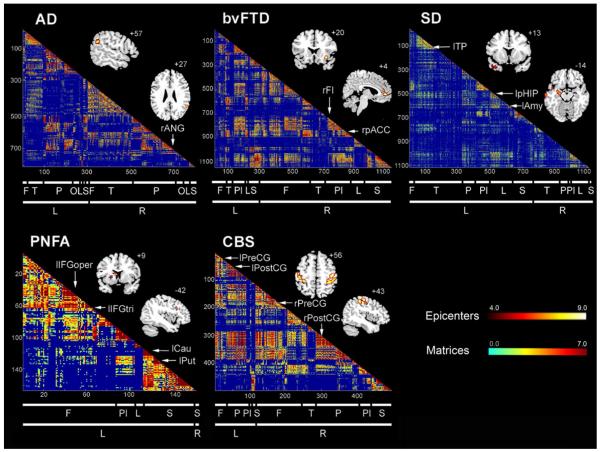
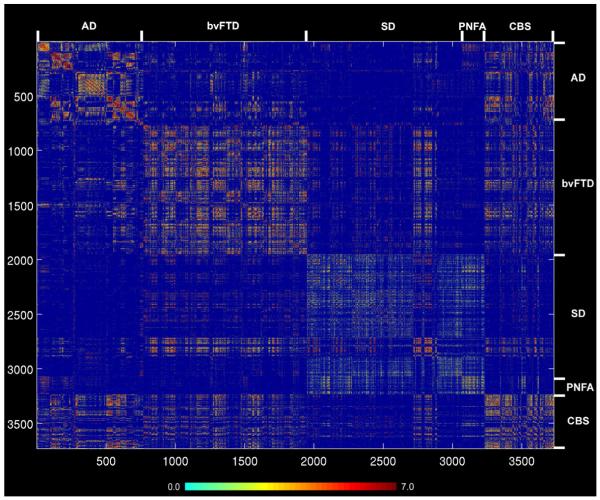
Figure 3. Healthy intrinsic connectivity matrices and network epicenters for each of five neurodegenerative syndrome atrophy patterns.

Regions whose healthy ICN showed significant goodness-of-fit (GOF) to each of the five atrophy maps were identified as epicenters, shown here superimposed on the MNI template brain (see Supplemental Table 1). The red-orange color bar represents the t-scores associated with the group-level significance of the epicenter GOF scores. Matrices representing the group-level node pair-wise connectivity strengths were organized from left to right (and top to bottom) in the order of frontal (F), temporal (T), parietal (P), occipital (O), paralimbic (Pl), limbic (L), and subcortical (S) regions. The blue-red color bar represents the intrinsic connectivity between each node pair, defined as the t-score from the thresholded group-level one-sample t-test (see Experimental Procedures). Subthreshold node pair connectivity strengths were colored dark blue and omitted from the matrices.

Having identified a set of focal epicenters within each atrophy pattern, we next sought to examine where the epicenters fit within their target network’s functional architecture. To this end, we generated five intra-network healthy connectivity matrices covering all ROIs, including the epicenters, contained within the five binary spatial atrophy patterns (Figure 3). Specifically, we first generated unthresholded subject-level intra-network matrices, using ROIs as nodes and connectivity z-scores between ROI pairs as the weights of the undirected edges (see Experimental Procedures). Group-level intra-network healthy connectivity matrices were then derived for each network using one-sample t-tests. Significant edges were determined by thresholding at p < 0.01, false-discovery-rate (FDR) corrected for multiple comparisons across the matrix; non-significant edges were assigned a weight of zero. Examination of these matrices revealed that the epicenters related to each disease showed broad-based connectivity with other nodes in the target network, consistent with the manner in which they were identified (Figure 3). We further questioned whether these epicenters, though defined by their healthy ICN’s resemblance to the (binary) parent atrophy pattern, might also serve as functional hubs, defined as nodes with high weighted degree centrality (total connectional flow) within the target network (Sporns et al., 2007). As shown in Figure S2, although at least some epicenters for each disease ranked among the nodes highest in total intra-network flow, this relationship remained nuanced and varied by disease pattern, and many non-epicenter regions showed equal or greater total flow. These observations indicated that the amount of network traffic experienced by each node may influence but does not determine the network’s disease-critical epicenters. In addition, the dissociation between epicenters and hubs suggested that graph metrics related to these concepts might make dissociable contributions to atrophy severity.

Nodes with higher intra-network centrality and functional proximity to epicenters in health show greater vulnerability to disease

Next, we sought to address how the brain’s healthy connectional architecture, defined in a graph theoretical framework, relates to disease-associated regional vulnerability, defined by atrophy severity in patients. We translated the four major mechanistic models into distinctive sets of connectivity-related predictions (Figure 1). The nodal stress model would predict that metabolic demands or other activity-dependent factors conferred by higher nodal information flow will accelerate vulnerability, worsening nodal atrophy severity. The transneuronal spread hypothesis would predict greatest degeneration in regions connectionally closest to the node of onset, operationally defined here as those regions having the shortest functional path to any of the epicenters. The trophic failure model would predict that eccentric nodes with low total information flow and low clustering coefficients will prove less resilient due to a lack of redundant trophic inputs. The shared vulnerability model, in contrast to all others, predicts no direct impact of intra-network architecture on vulnerability, which is driven instead by a common gene or protein expression profile.

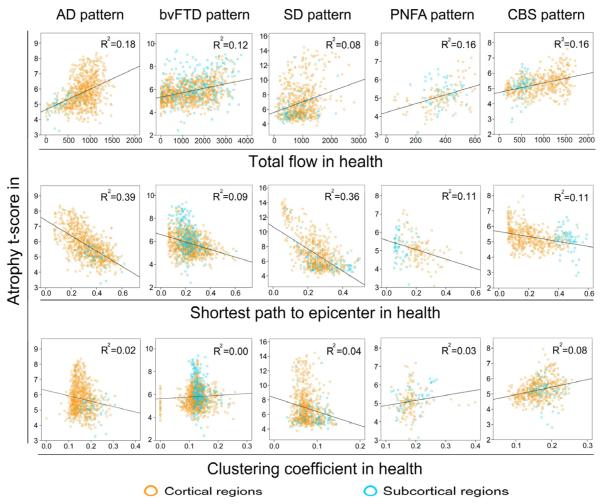
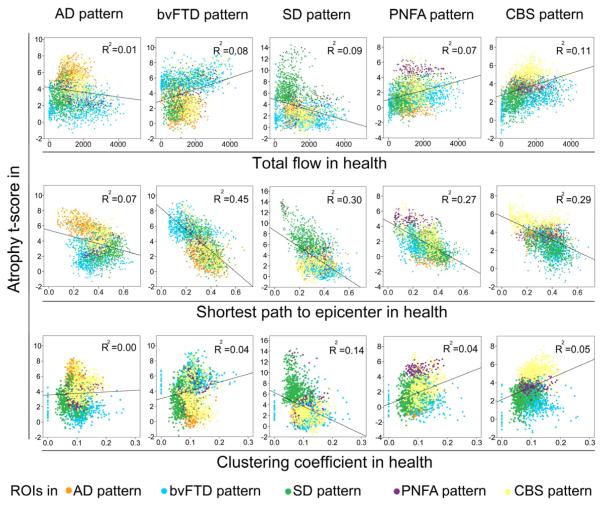
To compare the model-based predictions, we used the healthy intrinsic connectivity matrices (Figure 3) to generate three graph theoretical metrics for each region within each target network: total flow, shortest path to the epicenters, and clustering coefficient (see Experimental Procedures). We then examined the correlation between these nodal metrics, derived from healthy subjects, and nodal atrophy severity in the five neurodegenerative syndromes (Figure 4 and Table S2). A node’s total flow in health showed a positive correlation with disease vulnerability (Figure 4, row 1; p < 0.05 family-wise-error corrected for multiple comparisons) in AD (r = 0.43, p = 8.4e⁻⁴⁰), bvFTD (r = 0.35, p = 4.9e⁻³⁶), SD (r = 0.29, p = 9.9e⁻¹⁵), PNFA (r = 0.40, p = 5.4e⁻⁷), and CBS (r = 0.40, p = 7.9e⁻²¹). A shorter functional path from a node to the disease-related epicenters also predicted greater atrophy severity (Figure 4, row 2; p < 0.05 family-wise-error corrected for multiple comparisons) in all five diseases: AD (r = −0.62, p = 3.2e⁻⁹⁰), bvFTD (r = −0.30, p = 3.1e⁻²⁵), SD (r = −0.60, p = 1.0e⁻⁶⁷), PNFA (r = −0.34, p = 1.2e⁻⁵), CBS (r = −0.33, p = 7.0e⁻¹³), an effect that remained significant after controlling for the Euclidean distance (in Montreal Neurological Institute (MNI) space) from each node to its functionally nearest epicenter. Finally, no consistently significant positive or negative correlations were identified between nodal clustering coefficient and vulnerability across the five diseases (Figure 4, row 3): AD (r = −0.15, p = 2.1e⁻⁵), bvFTD (r = 0.05, p = 0.56), SD (r = −0.20, p = 9.9e⁻⁸), PNFA (r = 0.16, p = 0.03), CBS (r = 0.28, p = 7.7e⁻¹¹)). To reinforce the pairwise correlation findings while considering the influence of all network-based metrics together, we performed stepwise linear regression analyses in which atrophy served as the dependent measure, graph metrics served as independent predictors, and Euclidean distance from node to epicenter and region type (cortical vs. subcortical) were entered as nuisance covariates. These analyses revealed that although total flow accounted for a significant proportion of the variance in atrophy severity for all five syndromes, the shortest functional path to the epicenters explained more of the atrophy variance within the AD and SD patterns (Table S3). Overall, these intra-network findings are compatible with both the nodal stress and transneuronal spread models and suggest that these mechanisms may play differing roles in shaping regional vulnerability across the five syndromes. Predictions derived for the trophic failure and shared vulnerability models were not supported by these experiments.

Figure 4. Intra-network graph theoretical connectivity measures in health predict atrophy severity in disease.

Regions with high total connectional flow (Row 1) and shorter functional paths to the epicenters (Row 2) showed significantly greater disease vulnerability (p < 0.05 family-wise-error corrected for multiple comparisons in AD, bvFTD, SD, PNFA, and CBS), whereas inconsistent weaker or non-significant relationships were observed between clustering coefficient and atrophy (Row 3). Cortical regions = blue circles; subcortical regions = orange circles.

Off-target network nodes with greater functional proximity to epicenters in health show greater vulnerability to disease

Neurodegenerative diseases are known to spread from their initial target network to “off-target” networks in later stages of disease (Forstl and Kurz, 1999; Miller and Boeve, 2009; Seeley et al., 2008). We reasoned that vulnerability within off-target network regions may also be governed by connectional profile. To test this idea, we created a single trans-network connectivity matrix including all ROIs in the five disease-related atrophy maps (Figure 5) and re-calculated the three graph metrics. Nodes within the trans-network connectivity graph having shorter functional paths to the disease-associated epicenters were associated with greater atrophy in patients with that disease (Figure 6, row 2 and Table S2; p < 0.05 family-wise-error corrected for multiple comparisons) across all five diseases: AD (r = −0.27, p = 8.1e⁻⁴⁶), bvFTD (r = −0.65, p < 1e⁻³⁰⁰), SD (r = −0.54, p = 1.5e⁻¹⁹⁸), PNFA (r = −0.52, p = 3.5e⁻¹⁸³), and CBS (r = −0.54, p = 2.1e⁻¹⁹⁷), an effect that remained significant after controlling for the Euclidean distance from each node to its functionally nearest epicenter. Total flow (AD (r = −0.08, p = 1.8e⁻⁵), bvFTD (r = 0.29, p = 6.7e⁻⁵¹), SD (r = −0.30, p = 7.2e⁻⁵⁷), PNFA (r = 0.26, p = 1.2e⁻⁴¹), CBS (r = 0.33, p = 4.6e⁻⁶⁷)) and clustering coefficient (AD (r = −0.0, p = 0.06), bvFTD (r = 0.21, p = 7.8e⁻²⁸), SD (r = −0.38, p = 5.2e⁻⁹¹), PNFA (r = 0.19, p = 1.1e⁻²²), CBS (r = 0.21, p = 1.7e⁻²⁶)), in contrast, exerted a weaker and inconsistent influence on atrophy severity across the five diseases (Figure 6, rows 1 & 3, Table S2). Following the same approach taken for the intra-network analyses, a stepwise linear regression performed at the trans-network level revealed that the shortest functional path to the epicenters stood out as the single strongest graph metric predictor across all five syndromes (Table S3). Similar results were obtained when including Euclidean distance from each node to its functionally nearest epicenter in the model, except that in AD this distance explained a substantial proportion of atrophy variance, reducing the contribution from the shortest path to the epicenters. The strong relationship between functional proximity to the epicenters and atrophy severity emerged from these trans-network analyses even though most nodes contributing to each analysis came from “off-target” networks that made no contribution to epicenter identification. Nonetheless, to eliminate the possibility that node selection bias contributed to the observed relationships, we repeated the trans-network correlation and stepwise regression analyses after removing all ROIs within each target network, thereby examining only how the connectivity of “off-target” network nodes predicts vulnerability. These additional control analyses showed that a node’s shortest functional path to the target network epicenters remained the most robust and consistent predictor of that node’s atrophy in the target disease (Table S4 and S5). Overall, these findings suggest that although both the nodal stress and transneuronal spread models are consistent with the intra-network analysis, incorporating off-target networks provided stronger support for the transneuronal spread hypothesis. Furthermore, the trans-network graph metrics converge with previous studies investigating the relationships between the five neurodegenerative syndromes. For example, consistent with our previous findings that bvFTD and AD feature divergent intrinsic connectivity changes (Zhou et al., 2010), the nodes within the AD and bvFTD patterns featured the most dissimilar healthy connectional profiles and disease-associated atrophy severities (Figure 6). Regions within the bvFTD pattern showed the lowest atrophy in AD and had among the longest paths to the AD-related epicenters and vice versa.

Figure 5. Healthy intrinsic connectivity matrix representing all ROI pairwise interactions across the five neurodegenerative syndrome atrophy patterns.

Matrices representing the group-level node pair-wise connectivity strengths were organized from left to right (and top to bottom) in the order of AD, bvFTD, SD, PNFA, and CBS regions. Ordering of regions within each disease pattern follows the scheme used in Figure 3. The blue-red color bar represents the intrinsic connectivity strength between each node pair, defined as the t-score from the thresholded group-level one-sample t-test (see Experimental Procedures).

Figure 6. Trans-network graph theoretical connectivity measures in health predict atrophy severity in disease.

Row 2: ROIs showing greater disease-related atrophy were those featuring shorter functional paths, in the healthy brain, to the disease-associated epicenters (p < 0.05 family-wise-error corrected for multiple comparisons for AD, bvFTD, SD, PNFA, and CBS). Row 1 and 3: Inconsistent weaker or non-significant relationships were observed between total flow or clustering coefficient and disease-related atrophy.

Discussion

The present results provide new insights regarding how the brain’s functional architecture shapes vulnerability to neurodegenerative disease. We found that each of five neurodegenerative patterns contains focal network epicenters whose healthy brain connectivity profiles strongly resemble the parent atrophy pattern. Although previous studies have demonstrated the similarity between single seed-based healthy ICNs and disease-related atrophy (Buckner et al., 2005; Seeley et al., 2009), the present study used a comprehensive, high dimensional network mapping strategy to seek out those regions with connectivity maps most closely aligned with five patterns of disease-associated vulnerability. We then used graph theoretical approaches to seek disease-general principles governing connectivity-vulnerability interactions, testing predictions made by four proposed models of network-based neurodegeneration. We found that, within each targeted network, a node’s vulnerability was best predicted by greater total connectional flow through that node and by a shorter functional path to the disease-related epicenters. Extending this analysis across all regions contained in any of the five networks revealed that intrinsic functional proximity to the epicenters represents the most potent predictor of disease-related atrophy. Therefore, although both the nodal stress and transneuronal spread model predictions received support from analyses of the individual target networks, incorporating the off-target networks provided strongest support for the notion that neurodegenerative diseases spread from region to region along connectional lines to adopt a network-based spatial pattern.

Exploring the target networks: epicenters and early disease spread

The most mysterious aspect of neurodegenerative disease regards how each disease selects its initial target or targets. Early selective vulnerability, though not the focus of this study, creates a starting point from which disease then spreads. Regions showing greatest atrophy at later stages may or may not represent the sites of initial injury, and even longitudinal imaging studies that follow patients from health to disease may overlook incipient microscopic pathology within small neuronal populations (Braak et al., 2011). Despite these important caveats, our findings converge with our previous work to suggest that the regions most atrophied in each syndrome represent disease-specific network “epicenters”, whose connectivity in health serves as a template for the spatial patterning of disease. These epicenters bear close relationships to the early clinical deficits that define each parent syndrome. In AD, the angular gyrus may serve as the key heteromodal association hub through which information flows from posterior unimodal and polymodal association cortices to modules specialized for the memory, visuospatial, language, and praxis functions lost in patients with AD. Because atrophy in AD is more closely related to tau neurofibrillary than amyloid plaque pathology (Scheinin et al., 2009; Whitwell et al., 2008), we suspect that our connectivity-vulnerability findings in AD largely reflect tau pathology within posterior elements of the large-scale network known as the default mode network (Greicius et al., 2003; Greicius et al., 2004). Nonetheless, the hub-like nature of the angular gyrus may produce activity-dependent “wear and tear” or increases in amyloid production that heighten its early vulnerability to amyloid deposition (Buckner et al., 2009) and incite or compound the neurodegenerative process. Interestingly, numerous frontal regions exhibit striking resistance to AD-related neurodegeneration despite having high fibrillar amyloid-beta deposition (Jack et al., 2008) and, as shown here, short functional paths to the angular gyrus in some instances. This disconnect may reflect the complexity of underlying AD pathology which, in contrast to all other diseases studied here, features two co-occurring major molecular pathologies (amyloid-beta and tau). In bvFTD, the identified epicenters in the right frontoinsula and pregenual anterior cingulate cortex are known for their co-activation during salience processing (Seeley et al., 2007), and both regions harbor a unique class of large, bipolar projection neurons targeted in early-stage bvFTD (Kim et al., 2011; Seeley et al., 2006). The anterior temporal epicenters identified within the SD pattern feature prominent connections to upstream cortices that may converge on the epicenters to foster multimodal semantic integration (Patterson et al., 2007). In PNFA, our epicenter search identified the inferior frontal gyrus (Broca’s area), as well as striatal and thalamic sites that receive robust operculofrontal inputs (Alexander et al., 1986). The CBS epicenters occupy the rolandic and perirolandic cortices involved in skeletomotor planning, control, and execution functions compromised early in the course of typical CBS regardless of the underlying pathology (Lee et al., 2011).

How does disease spread throughout the network once one of its key epicenters is compromised? The present data suggest that at least two major factors influence spread within the target network. First, across all five diseases, network nodes subject to greater intra-network total information flow were found to undergo greater atrophy. This observation raises the possibility that activity-dependent mechanisms, such as oxidative stress, local extracellular milieu fluctuations, or glia-dependent phenomena, influence regional neurodegeneration severity. Furthermore, nodes with shorter connectional paths to an epicenter showed greater vulnerability, suggesting that transneuronal spread represents one of the key factors driving early target network degeneration. In this regard, epicenter infiltration by disease may provide privileged but graded access across the network that determines where the disease will arrive next. Although trophic factor insufficiency or a shared gene or protein expression profile may help to determine sites of initial vulnerability, the present findings are difficult to reconcile with predictions made by these models regarding the graded vulnerability seen within the target networks.

Disease progression into off-target networks: transneuronal spread

Regions exquisitely vulnerable to one neurodegenerative disease are often spared in another. On the other hand, once disease has spread throughout its target network, the process often extends into “neighboring” networks, defined as those with stronger functional relationships to the primary target network (Seeley et al., 2008). We reasoned that these observations might be best explained within a connectivity-based framework. Combining data across all five disease-vulnerable networks into a single connectome (covering 68% of the total cerebral gray matter volume), we found greater atrophy among off-target network regions with shorter functional paths to the target network’s focal epicenters. Combining the intra-network and trans-network findings, these data provide strongest support for the transneuronal spread model, which predicts that the strength of any node’s functional connectivity to an epicenter will determine that node’s ultimate vulnerability to a neurodegeneration once the disease has taken hold. In contrast to the intra-network analysis, we found no consistent evidence for the nodal stress model’s predictions at the trans-network level, perhaps because across a broader brain network space a node’s centrality need not determine its susceptibility to every disease process. As seen at the intra-network level, at the trans-network level we found no consistent evidence supporting predictions derived from the trophic failure or shared vulnerability models.

Limitations and future directions

Several important limitations of this study should be noted. The AD group used to define the anatomical pattern studied here included patients with early age-of-onset AD, which features a more distributed cortical pattern when compared to the hippocampal-predominant pattern seen in late age-of-onset patients (Kim et al., 2005). This factor could account, at least in part, for the identification of the angular gyrus as the lone epicenter within the AD pattern. The present analyses used regional functional connectivity approaches in a healthy older control group to predict neurodegeneration severity in patients. Although the human connectome evolves with aging (Zuo et al., 2010), we chose healthy older subjects to capture the connectome upon which neurodegeneration is most often superimposed. Although we cannot exclude preclinical neurodegeneration in our control sample, each subject was screened with a battery of neuropsychological tests and found to perform within normal limits for age. The ideal approach for predicting neurodegeneration from connectivity data would be to follow individuals from health to disease, exploring connectivity-vulnerability interactions within single subjects. Although this approach may prove challenging for the FTD syndromes studied here, future longitudinal analyses of this type should become feasible for AD through large, ongoing, collaborative longitudinal studies.

Although we used the same five group-level atrophy maps to identify the epicenter “candidate pool” for each disease and to assess connectivity-vulnerability relationships, several key design elements prevented circularity. First, atrophy severity served as the major outcome variable but was not involved in epicenter identification. Second, the healthy network matrices used for calculating graph metrics were epicenter-independent, composed of every region within each binary atrophy map. Third, the trans-network graphs and analyses (Figures 5-6) spanned regions from all five binary atrophy maps. Therefore, most regions used in these analyses were not involved in the identification of any given epicenter, and even limiting the trans-network analyses to off-target network regions produced little change in the major findings.

Our correlation-based intrinsic functional connectivity approaches only measure symmetric (undirected) connections between regions with temporally synchronous BOLD fluctuations. These methods cannot differentiate direct from indirect links or infer causality (direction of information flow). These limitations apply to all current intrinsic functional network analyses in humans because the true graph (determined at the microscopic level by the presence of axonal connections between regions) cannot be determined with existing methods. We attempted to mitigate these concerns by thresholding the graphs at a stringent statistical threshold, leaving only strong edges for calculation of graph metrics, but this approach does not preclude our edges from representing indirect connections within or outside the network. Despite these limitations, the functional information contained in the graphs derived here provides novel and relevant information about how information flows among regions in each network.

Potential implications for cellular-molecular biology of neurodegeneration

Understanding the cellular and molecular basis for network-based disease spread represents an important priority for neurodegenerative disease research. Human intrinsic connectivity data cannot directly inform cellular pathogenesis models, just as simple laboratory models must make assumptions regarding their relevance to human disease. This study sought to bridge these research streams by translating mechanistic network-based neurodegeneration models into simple but rational predictions regarding the relationships between network connectivity and vulnerability. Complementary studies using structural connectivity data could further explore connectivity-vulnerability interactions. The present findings suggest that, overall, a transneuronal spread model best accounts for the network-based vulnerability observed in previous human neuropathological and imaging studies. Several mechanisms of transneuronal spread have been proposed, including axonal transport of undetected viruses or toxins (Hawkes et al., 2007; Saper et al., 1987). Providing a more parsimonious account, growing evidence suggests that prion-like mechanisms may promote the spread of toxic, misfolded, non-prion protein species between interconnected neurons (Baker et al., 1993, 1994; Brundin et al., 2010; Calhoun et al., 1998; Clavaguera et al., 2009; Frost and Diamond, 2010; Frost et al., 2009; Hansen et al., 2011; Jucker and Walker, 2011; Lee et al., 2010b; Li et al., 2008; Ridley et al., 2006; Walker et al., 2006). This notion, that many or all non-infectious neurodegenerative diseases may propagate along networked axons via templated conformational change, has been put forth since the introduction of the prion concept (Prusiner, 1984). Although our data cannot address molecular mechanisms directly or exclude contributions from failed trophism, nodal stress, or shared vulnerability, the present human findings complement the recent tide of cell-based and rodent disease model data to suggest that prion-like transneuronal spreading mechanisms merit further aggressive investigation.

Experimental Procedures

Subjects

Patients with neurodegenerative syndromes who defined the five disease-vulnerable ROI sets were those studied previously as described (Seeley et al., 2009). Clinical diagnostic criteria and clinicopathological correlation data are detailed in the Supplemental Experimental Procedures. In addition, we studied 16 healthy controls (8 females, all right-handed, mean age 65.4 (s.d. 3.2) years, psychoactive medication-free, not included in our previous work (Seeley et al., 2009)) evaluated at the UCSF Memory and Aging Center. All subjects provided informed consent and the procedures were approved by the UCSF Committee on Human Research. Healthy subjects were recruited from the local community through advertisements and underwent a comprehensive neuropsychological assessment and a neurological exam within 180 days of scanning. All controls met the criteria of having a Clinical Dementia Rating scale total score of 0, an Mini-mental state examination score of 28 or higher, no significant history of neurological disease or structural lesions on MRI, and a consensus diagnosis of cognitively normal.

Image acquisition

All subjects underwent an eight-minute task-free or “resting-state” functional magnetic resonance (fMRI) scan after being instructed to remain awake with their eyes closed. Functional and structural images were acquired on a 3 Tesla Siemens MRI scanner at the Neuroscience Imaging Center, University of California, San Francisco. Functional MRI scanning was performed using a standard 12-channel head coil. Thirty-six interleaved axial slices (3 mm-thick with a gap of 0.6 mm) were imaged parallel to the plane connecting the anterior and posterior commissures using a T2*-weighted echo planar sequence [repetition time (TR): 2000 ms; echo time (TE): 27 ms; flip angle (FA): 80°; field of view: 230 × 230 mm²; matrix size: 92 × 92; in-plane voxel size: 2.5 × 2.5 mm]. For coregistration purposes, a volumetric magnetization prepared rapid gradient echo (MPRAGE) MRI sequence was used to obtain a T1-weighted image of the entire brain in sagittal slices in the same session (repetition time, 2300 ms; echo time, 2.98 ms; inversion time, 900 ms; flip angle, 9). The structural images were reconstructed as a 160 × 240 × 256 matrix with 1 mm³ spatial resolution.

Image preprocessing

After discarding the first sixteen seconds to allow for magnetic field stabilization, functional images were realigned and unwarped, slice-time corrected, coregistered to the structural T1-weighted image, normalized, and smoothed with a 4 mm full-width at half-maximum Gaussian kernel using SPM5 (http://www.fil.ion.ucl.ac.uk/spm/), resulting in images with a voxel size of 2 mm³. Coregistration was performed between each subject’s mean T2* image and that subject’s T1-weighted image, and normalization was carried out by calculating the warping parameters between the subject’s T1-weighted image and the Montreal Neurological Institute T1-weighted image template and applying those parameters to all functional images in the sequence.

Seed-based ICN derivation

Previously we delineated the atrophy patterns associated with five neurodegenerative disease syndromes by comparing patients to controls using voxel-based morphometry (VBM) (Seeley et al., 2009). Here, we examined the healthy functional intrinsic connectivity architecture for all ROIs that could be situated within the five previously published atrophy patterns. To this end, we binarized the five atrophy maps and created five sets of 4 mm-radius spherical ROIs for each map (Figure 2, step 1). Preprocessed task-free fMRI data from 16 healthy subjects were then used for ROI-based intrinsic connectivity network (ICN) analyses, seeding all ROIs in each of the five atrophy patterns, resulting in one intrinsic connectivity map for each ROI. The ROI-based ICN analyses followed previous methods (Seeley et al., 2009). That is, the average time series from each ROI within the disease-associated pattern was used as a covariate of interest in a whole-brain regression analysis, and the global signal was entered as a nuisance variable. The voxel-wise z-scores in the resulting subject-level ICN maps described the correlation between each voxel’s spontaneous BOLD signal timeseries and the average timeseries of all voxels within the seed ROI. ICN maps were derived from each ROI in each individual and entered into second-level, random-effects analyses to derive group-level ICN maps for each ROI.

Identification of disease-associated network epicenters

We defined epicenters as regions whose pattern of seed-based intrinsic connectivity in health best fit the disease-related binary atrophy pattern from which the region was taken (Figure 2, step 2). At the level of the individual healthy subjects, we assigned one goodness-of-fit (GOF) score to each ROI based on the similarity between its healthy ICN map and the target binarized atrophy map. The GOF score was calculated by multiplying (i) the average z-score difference between voxels falling within the atrophy map and voxels falling outside the map; and (ii) the difference in the percentage of positive z-score voxels inside and outside the atrophy map (Zhou et al., 2010). In this way, atrophy severity values were omitted from the GOF calculation. For each atrophy pattern, a one-sample t-test on the corresponding GOF maps from the sixteen healthy subjects was used to identify those ROIs (epicenters) with significant GOF scores, stringently thresholded at p < 0.05, family-wise-error corrected for multiple comparisons (Figure 3 and Figure S1) to isolate only the few regions whose connectivity most closely resembled the disease-associated atrophy map. The threshold for the SD GOF map was set to p < 0.0001 (uncorrected) to adjust for signal loss within temporal pole and orbitofrontal regions that make up the SD pattern.

Group-level intra- and trans-network connectivity matrix derivation

To study the healthy intrinsic functional connectome related to each set of disease-vulnerable regions, we derived group-level intra- and trans-network connectivity matrices (Figure 2, step 3). Here, the intra-network matrices represent all ROIs within each target network (defined using the binarized atrophy maps), whereas the trans-network matrix represents all ROIs across the five target networks. These matrices were derived as follows. We first extracted the subject-level intra-network matrices from the seed-based ICN maps of each ROI set, using ROIs as nodes and mean connectivity z-scores between ROI pairs as the weights of the undirected edges (Watts and Strogatz, 1998). Edge weight for every node pair (e.g. nodes A and B) was defined at the subject level as the higher of two connectivity scores (A to B and B to A) for the A-B pair, where A to B connectivity was derived by (1) calculating the mean time-series across all voxels in node A, (2) determining the z-scores for the connectivity of the node A time-series to each voxel within node B, and (3) averaging the resulting z-scores to create a single score. The B to A connectivity score was derived in like manner by reversing A and B in the procedure described above. This procedure made use of the extensive seed-based voxel-wise connectivity data generated for epicenter identification while producing nearly identical node pair connectivity results, in pilot analyses, to those derived by calculating the correlation between the mean time series from nodes A and B. We then generated the group-level intra-network adjacency matrix containing significant connections by performing a one-sample t-test on the group of intra-network matrices, stringently thresholded at p < 0.01, false-discovery-rate (FDR) corrected for multiple comparisons to avoid potentially spurious links introduced by low temporal resolution and hemodynamic blurring in the fMRI signal. The same process was performed for each of the five ROI sets, resulting in five thresholded intra-network healthy functional intrinsic connectivity matrices (Figure 3). A lower statistical threshold of p < 0.05, false discovery rate-corrected for multiple comparisons, was used for the SD pattern to adjust for the fMRI signal loss characteristic of the temporal pole and orbitofrontal regions contained in this network, following previous approaches (Devlin et al., 2000; Seeley et al., 2009). A single healthy trans-network connectivity matrix, including all ROIs across the five atrophy patterns as one network, was constructed in like manner. In the group-level ICN matrices, the pairwise ROI connectivity t-scores resulting from one-sample t-test were used as edge weights.

Graph theoretical analyses

To study how intrinsic network architecture in health relates to disease-associated vulnerability, we examined three graph theoretical metrics for every network node (Figure 2, step 4) in both the intra-network (Figure 3, 4) and trans-network (Figure 5, 6) group-level healthy ICN adjacency matrices, including: (i) total flow – the sum of the magnitudes of the weighted connections passing through each node; (ii) shortest intrinsic functional path to the epicenters – the minimum path length to any of the identified epicenters for the atrophy pattern of interest; and (iii) clustering coefficient -- the ratio of the number of edges between a node’s neighbors to the total possible number of edges between the node’s neighbors (Watts and Strogatz, 1998). Graph theoretical measures were calculated using in-house MATLAB programs based on the publicly available Matlab BGL graph library developed by David Gleich (https://github.com/dgleich/matlab-bgl). Corresponding mathematical notation has been provided (Rubinov and Sporns, 2010). For atrophy patterns featuring multiple epicenters, we chose each ROI’s shortest among the shortest paths to each epicenter in the matrix. For intra-network analyses, graph metrics were based solely on ROIs within each target network pattern, whereas for trans-network analyses we considered ROIs in all five networks together. We limited our analyses to these three metrics because the four prevailing models of network-based neurodegeneration could be used to generate distinguising predictions regarding the relationship between these metrics and disease-associated atrophy severity (Figure 1).

Correlation between healthy network graph metrics and disease-associated atrophy

To test predictions about the relationship between the three graph metrics and disease-associated atrophy severity, we performed five separate intra-network correlation analyses between disease-associated atrophy and the three nodal graph metrics across all ROIs within each of the five disease patterns (Figure 2, step 5; Figure 4). Here, atrophy severity was defined using a previous comparison of patients to age-matched controls (Seeley et al., 2009) and averaging the voxel-wise t-scores from this comparison across each 4 mm-radius spherical ROI used as a node in the present graph theoretical computations. Five similar trans-network correlation analyses (all on the same combined node set) were performed to assess whether the same principles applied to off-target networks (Figure 6). For the intra- and trans-network correlation analyses, statistical significance was set to p < 0.05, family-wise-error corrected for multiple comparisons across three graph metrics, five atrophy patterns, and three node sets (all, cortical only, and sub-cortical only, see Table S2 and Figure 4) for a total of 45 statistical tests. In assessing the relationship between the shortest functional path to the epicenters and atrophy, we used partial correlation to further control for the Euclidean distance between each node and its functionally nearest epicenter. One step further, to take into account the influence of all network-based metrics, we performed stepwise linear regression analyses in which atrophy served as the dependent measure, the three graph metrics served as independent predictors, and cortical versus subcortical (binary membership) and Euclidean distance between each node and its functionally nearest epicenter served as nuisance variables (Table S3). Finally, we repeated the trans-network correlation and stepwise regression analyses for all ROIs within the four off-target networks only, i.e., removing the ROIs in the target network which contributed to epicenter identification (Table S4 and S5).