View-Invariance Learning in Object Recognition by Pigeons Depends on Error-Driven Associative Learning Processes

Abstract

A model hypothesizing that basic mechanisms of associative learning and generalization underlie object categorization in vertebrates can account for a large body of animal and human data. Here, we report two experiments which implicate error-driven associative learning in pigeons’ recognition of objects across changes in viewpoint. Experiment 1 found that object recognition across changes in viewpoint depends on how well each view predicts reward. Analyses of generalization performance, spatial position of pecks to images, and learning curves all showed behavioral patterns analogous to those found in prior studies of relative validity in associative learning. In Experiment 2, pigeons were trained to recognize objects from multiple viewpoints, which usually promotes robust performance at novel views of the trained objects. However, when the objects possessed a salient, informative metric property for solving the task, the pigeons did not show view-invariant recognition of the training objects, a result analogous to the overshadowing effect in associative learning.

1. Introduction

Visually recognizing objects in the environment confers a clear advantage for the survival and reproduction of any animal. Among many functions, object recognition allows the animal to detect food, conspecifics, and predators.

An important computational problem posed by object recognition (Rust & Stocker, 2010) is that of invariance: the same object can project very different images to the retina, depending on such factors as viewpoint, position, scale, clutter, and illumination. The present work focuses on understanding how a biological visual system (i.e., the pigeon) learns to recognize objects across variations in viewpoint.

Several experiments have explored whether pigeons show view-invariant object recognition after being trained with only one object view. These experiments have uniformly found that pigeons do not show one-shot view invariance, regardless of the type of object used to generate the experimental stimuli (Cerella, 1977; Friedman, Spetch, & Ferrey, 2005; Lumsden, 1977; Peissig et al., 1999, 2000; Wasserman et al., 1996). However, pigeons do show above-chance performance with novel views of the training object after training with just one view and they exhibit generalization behavior that is closer to true view invariance as the number of training views is increased (Peissig et al., 1999, 2002; Wasserman et al., 1996).

These and other studies suggest that the pigeon’s recognition of objects from novel viewpoints depends on similarity-based generalization from the training views (Spetch & Friedman, 2003; Spetch, Friedman & Reid, 2001), prompting these questions: Which object properties do pigeons use to generalize performance from training images to novel images? How are such properties extracted from images? How are such properties selected during training to guide performance in a particular task?

Regarding the first question, evidence suggests that pigeons extract view-invariant properties from images and rely heavily on them for object recognition (Gibson, Lazareva, Gosselin, Schyns, & Wasserman, 2007; Lazareva, Wasserman, & Biederman, 2008). For example, Gibson et al. (2007) trained pigeons (and people) to discriminate four simple volumes shown from a single viewpoint in a four-alternative forced-choice task. Once the subjects attained high performance levels in the task, the researchers used the Bubbles technique (Gosselin & Schyns, 2001) to determine which properties of the images the subjects used for recognition. The results showed that pigeons (and people) relied more heavily on properties that are relatively invariant across changes in viewpoint, such as cotermination and other edge properties, than on properties that vary across changes in viewpoint, such as shading.

However, pigeons show pronounced decrements in recognition performance when they are tested with novel object views that retain view-invariant properties (Peissig et al., 1999, 2000, 2002) and with images that have been manipulated only in view-specific properties, such as shading (e.g., Young, Peissig, Wasserman, & Biederman, 2001). In sum, the evidence suggests that pigeons recognize objects from novel viewpoints through a generalization-based mechanism, and that generalization might be based on the extraction of both view-invariant and view-specific shape properties.

We propose that this evidence is best interpreted within the framework of the recently proposed “Common Elements Model” (Soto & Wasserman, 2010a, 2012) of object categorization learning, which is based on the idea that basic mechanisms of associative learning and generalization underlie pigeons’ ability to classify natural objects. Because such basic mechanisms are widespread among vertebrate species, they might also play a role in object categorization by other species, including humans (see Soto & Wasserman, 2010b).

The Common Elements Model proposes that each image in a categorization task is represented by a set of “elements,” which can be interpreted as coding visual properties in a training image. These properties vary widely in the level to which they are repeated across members of the category. In the case of view-invariant object recognition, properties would show varied levels of view invariance, going from relatively view-invariant properties, which are repeated across many views of the same object, to view-specific properties, which are idiosyncratic to a particular object view. Importantly, the model also suggests a mechanism that selects which properties should control the performance of each available response in a recognition task. This selection process is carried out through associative error-driven learning, which selects those properties that are more informative as to whether the response will lead to a reward.

Consider how the Common Elements Model would explain the effect of training with multiple views of an object on the later recognition of novel views. Training with different views of the same object would lead to a “repetition advantage” effect for view-invariant properties. View-invariant properties are often repeated across different training views and they are frequently paired with the correct responses. This repetition gives them an advantage in controlling performance over view-specific properties, which are not common to many views and therefore do not frequently get paired with the correct response. Even if both types of property are informative as to the correct responses in the task, learning continues only until there is no error in the prediction of reward. At this point, view-invariant properties block view-specific properties from acquiring an association with the correct responses. When novel views of the object are presented in testing, these testing views are likely to share some view-invariant properties with the training views, leading to the successful generalization of performance.

Thus, the hypothesis that pigeons extract visual properties with differing levels of view invariance can explain why they show, on the one hand, extremely view-dependent recognition after training with a single view of an object and, on the other hand, they show high sensitivity to view-invariant object properties. Training with a single view of an object leads to the control of behavior by both view-invariant and view-specific properties, because there is no repetition advantage for the former. Even if view-invariant properties are highly salient, behavior must generalize imperfectly to novel views of an object, which do not share the same view-specific properties as the training view.

The present work presents the results of two experiments testing the predictions of the Common Elements Model of view-invariance learning by pigeons. Specifically, these experiments test the assumption that visual properties are selected to control performance in object recognition tasks through an associative learning mechanism driven by reward prediction error. Error-driven learning should lead to competition between view-invariant and view-specific properties for control of performance in object recognition tasks. The experiments show that results analogous to the relative validity effect (Wagner, Logan, Haberlandt, & Price, 1968) and overshadowing (Pavlov, 1927) from the associative learning literature can be found in object recognition experiments. These are two key effects that proved to be central to the development of associative learning theories based on the notion of prediction error. If view-invariance learning in pigeons is driven by reward prediction error, then such experimental designs should reveal competition for behavioral control between view-invariant and view-specific object properties.

2. Experiment 1

A relative validity experiment in Pavlovian conditioning (Wagner et al., 1968; Wasserman, 1974) involves training with two compound stimuli: AX and BX. In the Uncorrelated condition, each compound is reinforced 50% of the time. In the Correlated condition, AX is always reinforced and BX is never reinforced. Even though, in both conditions, X is reinforced 50% of the time—and hence its absolute predictive value is the same—subjects in the Uncorrelated condition respond more to this stimulus than do subjects in the Correlated condition. Thus, conditioning to X depends on the informative value of the other stimuli that are presented in compound with it. When A and B are reliable predictors of the outcome, X does not acquire much associative strength despite its being paired with reinforcement 50% of the time.

The main goal of the present experiment was to investigate an analog of the relative validity effect in view-invariance learning by pigeons, in which the roles of Stimuli A, B, and X were replaced by hypothetical view-specific and view-invariant stimulus properties. The within-subjects design is detailed in Table 1. This design entails two conditions, each trained on a Go/No-Go task involving images of a geon shown from six different viewpoints. Both conditions involve testing novel views of the training geon.

Table 1.

Design of Experiment 5, which tested an analog of the relative validity effect in view-invariant object recognition. “Rf” stands for reinforcement and “NRf” stands for nonreinforcement.

	Training	Generalization Test
		Training trials +
Uncorrelated	Geon 1 - 0° / 50% Rf
	Geon 1 - 120° / 50% Rf	Geon 1 – Rotated around x-axis at 30°, 90°, 150°, 210°, 270°, 330°  / NRf
	Geon 1 - 240° / 50% Rf
	Geon 1 - 60° / 50% Rf
	Geon 1 - 180° / 50% Rf	Geon 1 – Rotated around y-axis at 30°, 90°, 150°, 210°, 270°, 330°  / NRf
	Geon 1 - 300° / 50% Rf
		Training trials +
Correlated	Geon 2 - 0° / Rf
	Geon 2 - 120° / Rf	Geon 2 – Rotated around x-axis at 30°, 90°, 150°, 210°, 270°, 330°  / NRf
	Geon 2 - 240° / Rf
	Geon 2 - 60° / NRf
	Geon 2 - 180° / NRf	Geon 2 – Rotated around y-axis at 30°, 90°, 150°, 210°, 270°, 330°  / NRf
	Geon 2 - 300° / NRf

In the Uncorrelated condition, all of the training views were reinforced and nonreinforced 50% of the time, whereas in the Correlated condition, half of the training views were reinforced 100% of the time and half were nonreinforced 100% of the time. In both cases, the geon itself and properties that were invariant across changes in viewpoint were reinforced and nonreinforced equally often. However, only in the Correlated condition was information specific to each view a perfect predictor of whether responses would be reinforced or nonreinforced.

An error-driven learning rule would predict that properties that are invariant across views and properties that are specific to each view should compete for control of behavior during learning. When view-specific properties are diagnostic of the correct response and view-invariant properties are not, as in the Correlated condition, the view-invariant properties should decrease their control over behavior; hence, generalization to novel views during the Testing phase should be reduced. However, if view-specific and view-invariant properties are equivalent predictors of the correct response, as in the Uncorrelated condition, then view-invariant properties should acquire greater control over behavior, thereby yielding higher generalization of responding to novel views during the Testing phase.

Responding to views that are interpolated between the training views will probably be highly influenced by generalization from the immediately adjacent views. In the Correlated condition, one of the training views should produce responding and the other should not. In the Uncorrelated condition, both training views should produce responding. A higher level of generalization for the interpolated views in the Uncorrelated condition might be the result of generalization from two immediately adjacent training views instead of just one. This possibility would be particularly critical if, with enough training, the level of responding to continuously and partially reinforced stimuli were similar. The same argument cannot be made about novel views from an axis which is orthogonal to that used to generate the training stimuli. Thus, this problem was solved by also testing the pigeons with such novel orthogonal views (Peissig et al., 2002).

The relative validity effect in pigeons can be measured not only by means of generalization tests, but also by directly measuring selective responding to the different elements of a compound discriminative stimulus during training. Wasserman (1974) found that, in a Pavlovian relative validity design, responding directly at the common cue was relatively high in the Uncorrelated condition, but low in the Correlated condition. Responding directly at the distinctive cue that was positively predictive of reinforcement in the Correlated condition was high, whereas responding directly at the corresponding distinctive cue in the Uncorrelated condition was lower than to the common cue. This pattern of results suggests that pigeons preferentially peck stimuli that are more strongly associated with reinforcement.

It has more recently been reported that preferential pecking can be used to identify the features of complex stimuli that pigeons use to solve visual discriminations in Go/No-Go tasks (Dittrich et al., 2010). Because the present experiment used such a Go/No-Go task, the spatial position of pigeons’ pecks directly at the images was recorded for analysis, thereby opening the door to finding an analogous effect to that reported by Wasserman (1974) in Pavlovian conditioning: namely, a higher concentration of pecks to common cues in the Uncorrelated condition and to distinctive cues in the Correlated condition.

A final prediction of the Common Elements Model for this experiment is that responding to both reinforced and nonreinforced stimuli in the Correlated condition should increase early in training, with responding to the nonreinforced stimuli decreasing later, thereby tracing a nonmonotonic learning curve. This prediction holds because, early in training, properties that are common to several training views are repeated often and should acquire control of responding faster than view-specific properties. Only after substantial training can the view-specific properties in each image begin to control responding to allow the discrimination of reinforced and nonreinforced stimuli.

In sum, an account of view-invariance learning based on error-driven associative learning (Soto & Wasserman, 2010a, 2012) predicts that we should find greater generalization of responding to novel views of an object in the Uncorrelated than in the Correlated condition as well as an initial increase in responding to nonreinforced stimuli during training in the Correlated condition. Furthermore, assuming that peck location is a sensitive index of the areas in a visual stimulus that control performance, then pecks should be directed to common spatial locations across all images in the Uncorrelated condition, whereas pecks should be directed to distinctive spatial locations in each of the images in the Correlated condition.

2.1. Method

2.1.2. Subjects and Apparatus

The subjects were four feral pigeons (Columba livia) kept at 85% of their free-feeding weights. The birds had previously participated in unrelated research.

The experiment used four 36- x 36- x 41-cm operant conditioning chambers (see Gibson, Wasserman, Frei, & K. Miller, 2004), located in a dark room with continuous white noise. The stimuli were presented on a 15-in LCD monitor located behind an AccuTouch® resistive touchscreen (Elo TouchSystems, Fremont, CA) which was covered by mylar for durability. A food cup was centered on the rear wall of the chamber. A food dispenser delivered 45-mg food pellets through a vinyl tube into the cup. A houselight on the rear wall of the chamber provided ambient illumination. Each chamber was controlled by an Apple® iMac® computer and the experimental procedure was programmed using Matlab Version 7.9 (© The MathWorks, Inc.) with the Psychophysics Toolbox extensions (Brainard, 1997).

2.1.2. Stimuli

The stimuli were computer renderings of two simple three-dimensional volumes or “geons”: a wedge and a horn, which vary from one another in several properties (e.g., cross-section, curvature of main axis, and tapering). Object models were created using the 3-D graphics software Blender 2.49 (The Blender Foundation, freely available at www.blender.org). The objects were rotated in depth by 30° intervals along their x-axis to yield a total of 12 views, and rotated in depth by 60° intervals within the y-axis of rotation, yielding another 6 testing views. If necessary, the rendering viewpoints were allowed to vary within a margin of plus or minus 10°, to prevent the objects from being shown at accidental views (Biederman, 1987). Stimuli were rendered over a white background, using a camera placed directly in front of the object. Two lights illuminated the object from the front; one slightly to the left of the camera and the other near the top right of the object. The final stimuli were 7.4 × 7.4 cm in size when displayed on each pigeon’s screen during the experiment.

2.1.3. Procedure

Each pigeon was trained on the two conditions shown in Table 1, using a Go/No-Go task. One geon was assigned to each condition, with the assignments counterbalanced across birds.

All of the trials began with the presentation of a white rectangle in the center display area of the screen. A single peck to the rectangle led to the presentation of a stimulus. On a reinforced trial, the stimulus was presented and remained on for 15 s; the first response after this interval turned the display area black and led to the delivery of food. On a nonreinforced trial, the stimulus was presented and remained on for 15 s, after which the display area automatically darkened and the intertrial interval began. On all trials, scored responses were recorded only during the first 15 s of stimulus presentation. The intertrial interval randomly ranged from 6 to 10 s. Reinforcement consisted of 1 to 3 food pellets.

In training, each session consisted of 14 blocks with the 12 trials described in Table 1, for a total of 168 trials per session. In the Correlated condition, three views of one geon were reinforced and three views of the same geon were nonreinforced, whereas in the Uncorrelated condition, all of the views of each geon were reinforced and nonreinforced equally often. To evaluate performance, a discrimination ratio was computed for the stimuli in the Correlated condition by taking the mean response rate to the reinforced stimuli and dividing it by the sum of the mean response rate to the reinforced stimuli plus the mean response rate to the nonreinforced stimuli. Training continued until each bird achieved a ratio higher than 0.85; then, testing ensued.

In each testing session, two warm-up training blocks were followed by two testing blocks. The testing block included one nonreinforced presentation of each of 12 novel views of the two geons, randomly interspersed in four blocks of training trials. The total number of trials in each testing session was 144. Testing continued until the pigeon completed a total of 35 sessions. Across the entire experiment, trials within each testing session were randomized in blocks.

2.2. Results and Discussion

A generalization ratio was computed by taking the mean response rates to each novel stimulus presented during the Testing Phase and dividing it by the mean response rate to all of the reinforced training stimuli in each condition.

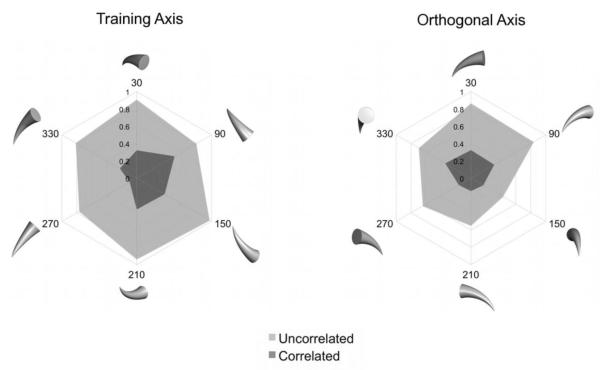
Figure 1 depicts the two polar plots of the mean generalization ratios for all of the testing stimuli. The left plot shows the results with new views of the objects rotated within the same axis used to generate the training views. The right polar plot shows the results with new views of the objects rotated across an axis that was orthogonal to the training axis. The generalization ratios from the Correlated condition are plotted using a darker shade of gray than those from the Uncorrelated condition. It can be seen from the left plot that there was greater generalization of responding in the Uncorrelated condition (M = 0.81, SD = 0.08) than in the Correlated condition (M = 0.31, SD = 0.14) to novel views within the training axis. The right plot shows that there was also greater generalization of responding in the Uncorrelated condition (M = 0.67, SD = 0.05) than in the Correlated condition (M = 0.24, SD = 0.05) for novel views from the orthogonal axis. This pattern of results was observed for each pigeon.

Fig. 1.

Results of the Generalization Test of Experiment 1. Plotted in the polar spikes is the Generalization Ratio for different novel views of the training objects.

To determine the statistical reliability of these results, a 2 (Condition) × 2 (Rotational Axis) × 6 (Degree of Rotation) repeated-measures ANOVA was conducted, with Generalization Ratio as the dependent measure. This analysis yielded a significant main effect of Condition, F(1, 3) = 83.83, p < 0.01, confirming that generalization to novel views was reliably greater in the Uncorrelated condition than in the Correlated condition. The main effect of Rotational Axis was also significant, F(1, 3) = 25.79, p < 0.05, reflecting the greater generalization observed for novel views in the Training Axis than for novel views in the Orthogonal Axis. The main effect of Degree of Rotation was also significant, F(5, 15) = 5.21, p < 0.01, due to the fact that generalization to some views was greater than to other views. None of the interactions were significant.

These results indicate that generalization of responding to novel viewpoints of an object not only depends on how often responses to the object have been reinforced, but also on how well each view of the object predicts food reward. More generalization of a learned response to novel views is observed when individual training views are poor predictors of reinforcement than when individual training views are good predictors of reinforcement. The results in Figure 1 are essentially the same as those previously found in a natural object categorization experiment (Exp. 2 in Soto & Wasserman, 2010), attesting to the generality of the relative validity effect in complex visual shape discriminations.

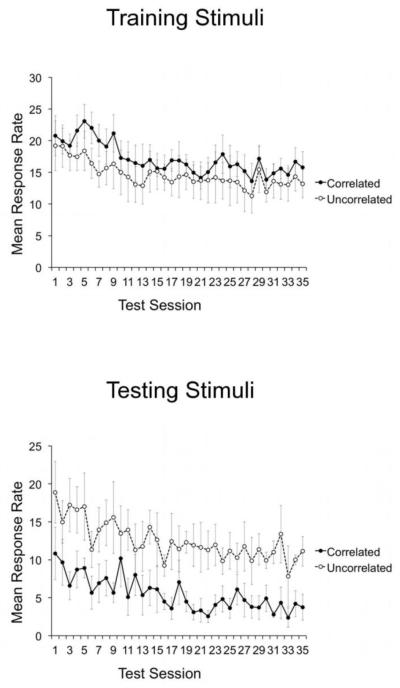
The pattern of results during generalization testing was the same when the raw mean response rates were analyzed. As shown in Figure 2, mean response rate to the testing stimuli in the Uncorrelated condition was higher than in the Correlated condition throughout testing. Furthermore, the opposite result was observed for the mean response rates to reinforced training stimuli (Figure 2, top). Thus, across all testing sessions, the pattern of responding to the testing stimuli cannot be explained by a general tendency to respond more to stimuli in the Uncorrelated condition than in the Correlated condition.

Fig. 2.

Mean response rates to Training and Testing stimuli during the Generalization Test of Experiment 1. Error bars represent standard errors.

The recorded peck locations to the testing stimuli were used to estimate peck densities over the images using kernel density estimation (see Scott, 2004; Scott & Sain, 2005) with a Gaussian kernel and automatic selection of bandwidth according to a “rule of thumb” (Silverman, 1986). This method allows one to obtain a smooth estimate of the areas in an image at which pigeons are pecking and to show graphically which aspects of the stimuli are used to solve the discrimination.

The analysis was focused on those images that were always reinforced in the Correlated condition because: more pecks to these images were recorded, the number of pecks was similar across the two conditions, and pecks to these images were reinforced in both conditions. Thus, any differences between conditions in peck location are likely to be due to differences in the discrimination tasks.

Note that pecks to the selected images were continuously reinforced during training in the Correlated condition, but only partially reinforced during training in the Uncorrelated condition. It has been found that pigeons increase the spatial and temporal variability of their pecks to a discriminative stimulus when the probability of reward decreases, in both instrumental (Stahlman, Roberts, & Blaisdell, 2010) and Pavlovian tasks (Stahlman, Young, & Blaisdell, 2010). Thus, it was expected that the spatial variability of responses would be higher in the Uncorrelated than in the Correlated condition. However, there was no reason to expect reward probability per se to induce a difference between conditions in the areas of the images that attracted more pecks.

Peck densities were estimated from two data sets. The most interesting data set involved peck locations during testing sessions, after learning of the discrimination given in the Correlated condition. The second data set involved peck locations during the first five sessions of training, before learning of the discrimination in the Correlated condition was complete; the absence of learning was corroborated by the observation that none of the pigeons showed a DR higher than 0.6 during these initial training sessions. This data set was included to ensure that any differences between conditions in peck location were not due to stimulus factors alone, but arose as the result of learning in the experiment.

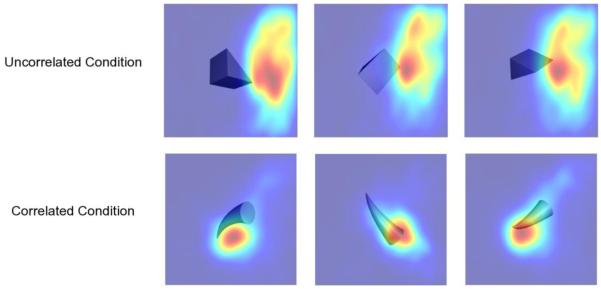
Figure 3 shows the peck densities of a representative pigeon for the reinforced views of the two geons obtained after learning. Warmer colors represent a higher density of pecking. Pecks in the Correlated condition seem to be more focused in a small area of the image, whereas pecks in the Uncorrelated condition seem to be more widespread. Also, peck densities seem to cover a very similar area across images in the Uncorrelated condition, whereas peck densities cover slightly different areas across images in the Correlated condition. Finally, pecks are located on the object itself to a larger extent in the Correlated condition than in the Uncorrelated condition. Similar results were observed for the other three birds.

Fig. 3.

Estimated peck densities for reinforced views of each geon, obtained after learning of the discrimination task of Experiment 1. The data of a single representative pigeon are shown. Warmer colors represent higher peck densities.

To quantitatively evaluate differences between conditions, the peck densities were used to estimate three values for each pigeon. The first value was the average entropy of peck location, which can be regarded as a measure of spatial dispersion of the peck densities, and was measured using a resubstitution estimate (Beirlant, Dudewicz, Gyorfi, & van der Meulen, 1997) given by

$$\widehat{H}=-\frac{1}{N}\sum _{n=1}^N\ln \left(\widehat{p}\left(x_n\right)\right)$$ (1)

, where $\widehat{p}\left(x\right)$ is the kernel density estimate at location x and the sum is over all pecks in the sample, indexed by n.

The second computed value was the average Kullback-Leibler (KL) divergence between pairs of densities from the same condition, which is a measure of how dissimilar the spatial distributions were for pecks to different views of the same object. For a pair of kernel density estimates, $\widehat{p}\left(x\right)$ and $\widehat{q}\left(x\right)$, the KL divergence was estimated by sampling values of x from the density $\widehat{p}\left(x\right)$ and then computing

$${\widehat{D}}_{\mathit{KL}}=\frac{1}{N}\sum _{n=1}^N\ln \left(\widehat{p}\left(x_n\right)\right)-\frac{1}{N}\sum _{n=1}^N\ln \left(\widehat{q}\left(x_n\right)\right).$$ (2)

Since the KL divergence is not symmetric, it was computed twice for each pair of images and the two values were averaged to get a single index of dissimilarity.

The third computed value was the Proportion of Object Pecks, defined as the proportion of the total area in each density that was located in the area occupied by the object.

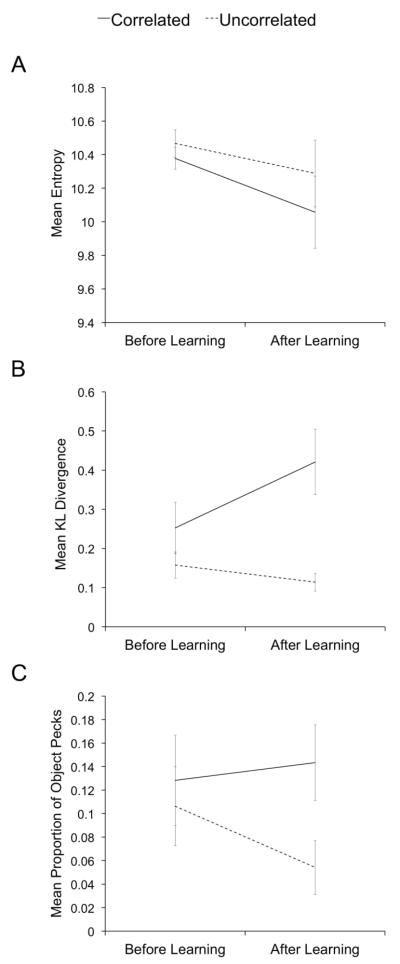
Figure 4A shows the mean entropy measures for both conditions before and after learning of the discrimination task. Although response variability seemed to decrease with learning and was slightly lower in the Correlated condition than in the Uncorrelated condition, both effects were rather small. A 2 (Learning Stage) × 2 (Condition) repeated-measures ANOVA with average entropy as the dependent variable confirmed these observations, with neither the main effects nor the interaction being significant. Thus, this experiment did not find a reliable increase in spatial variability of responses with a decrease in the probability of reward, as reported previously (Stahlman et al., 2010).

Fig. 4.

Results of the analysis of peck densities from Experiment 1. Panel A shows the mean entropy of the peck density estimates. Panel B shows the mean KL divergence of the peck density estimates. Panel C shows the mean proportion of object pecks.

Figure 4B shows the mean KL divergence measures in both conditions before and after learning of the discrimination task. In this case, it is clear that learning had an impact on the distribution of responses. Before learning, the level to which peck densities differed from each other was quite similar between conditions. After learning, differences in peck densities were larger in the Correlated condition than in the Uncorrelated condition. A 2 (Learning Stage) × 2 (Condition) repeated-measures ANOVA with average KL divergence as the dependent variable confirmed these observations. There were significant effects of Condition, F(1, 3) = 11.01, p < 0.05, and the interaction between Condition and Learning Stage, F(1, 3) = 15.177, p < 0.05. Planned comparisons (2-tailed) revealed that the difference between conditions was significant after learning, t(3) = 3.68, p < 0.05, but not before learning, t(3) = 2.21, p > 0.1. The main effect of Learning Stage was not significant.

Figure 4C shows the mean Proportion of Object Pecks for both conditions before and after learning of the discrimination task. This measure also revealed a notable impact of learning on the distribution of responses. Before learning, pecks were located on the object itself to a similar extent in the Correlated and Uncorrelated conditions. After learning, the extent to which pecks were located on the object did not change much in the Correlated condition, but it decreased in the Uncorrelated condition. A 2 (Learning Stage) × 2 (Condition) repeated-measures ANOVA with Proportion of Object Pecks as the dependent variable revealed a significant main effect of Condition, F(1, 3) = 13.16, p < 0.05, but no significant effects of Learning Stage or the interaction between the factors. The main effect of Condition was significant in this comparison instead of the interaction because, as seen in Figure 4C, the Proportion of Object Pecks was already a bit higher in the Correlated than in the Uncorrelated condition before learning. Planned comparisons (2-tailed) revealed that the difference between conditions was significant after learning, t(3) = 4.68, p < 0.05, but not before learning, t(3) = 0.79, p > 0.1.

In sum, when each view of an object was a good predictor of food reward, pigeons selectively pecked different regions of the image across different views, and those regions overlapped with the area occupied by the object. On the other hand, when none of the individual views of an object was a good predictor of food reward, pigeons pecked a common region of the images across different views, which tended to fall outside the area occupied by the object. This pattern of results is analogous to that found by Wasserman (1974) in Pavlovian conditioning. Thus, the relative validity effect found using an object recognition task shares several features with the relative validity effect in simple associative learning tasks, strengthening the idea that birds learn complex visual categorization tasks using error-driven associative learning mechanisms.

There are two things to note about the selective pecking of areas outside the object observed in the Uncorrelated condition. First, allocating pecks outside the object seems to be an effect of learning instead of the default strategy used by the pigeons. As can be seen in Figure 4C, most of the effect of learning over the Proportion of Object Pecks seemed to result from a decrease in the allocation of pecks to the object in the Uncorrelated condition rather than an increase in the allocation of pecks to the object in the Correlated condition. Second, it is possible that when pigeons peck outside the object they might be aiming at properties of the object edges that are common across changes in viewpoint, at least in some cases. For example, in the results shown for the Uncorrelated condition in Figure 3, pecks are concentrated in an area that contained a feature common to all of the training images: a single corner oriented to the right. It is difficult to evaluate whether or not this common feature controlled pigeons’ behavior without a test involving direct manipulation of the image, but the pattern of results was identical in the other pigeon trained with the same stimulus assignment.

Regardless of whether the pigeons in the Uncorrelated condition aim at the white background or at common edge properties in the images, it seems clear that they concentrate their pecks in an area of the images that is similar across viewpoints and that they restrict their pecks to the same area across all views of the same object.

Learning curves for stimuli in the Correlated condition were built using Vincentized Blocks (Kling & Riggs, 1971), which group sessions into a fixed number of blocks for each bird. Figure 5A shows mean response rates across training blocks for both reinforced (solid circles) and nonreinforced (open circles) stimuli in the Correlated condition. Pigeons showed very high levels of responding to all of the stimuli from the inception of training, presumably because of strong generalization of responding from the stimuli rewarded during pretraining (pigeons were pretrained to peck at colored squares on the screen). Thus, although responding was high to nonreinforced stimuli during the early stages of training, it is difficult to determine whether this result was due to generalization from the reinforced stimuli, as predicted by the Common Elements Model, or to generalization from the pretraining stimuli.

Fig. 5.

Learning curves obtained for reinforced and nonreinforced stimuli in the Correlated Condition of Experiment 1. Panel A shows the averaged data, whereas panel B shows the data of each individual pigeon.

The monotonic decrease in mean response rate observed in the group data might be an artifact of averaging. The individual learning curves were considerably more concave than the average curve in Figure 5A, but with large variability in the size and location of the initial concavity across pigeons. Individual learning curves are plotted in Figure 5B. They reveal that for two pigeons (85Y and 60Y) response rate to nonreinforced stimuli rose and stayed high for several training blocks before starting to decrease. For Pigeon 16W, responding increased during the first three blocks, then the bird behaved rather erratically until Block 24; finally, response rate decreased steadily after Block 24. Pigeon 17B also showed an increase in responding at the beginning of training, but it was transient. Note, however, that this pigeon showed the highest initial rate of responding among the birds.

Despite the fact that birds showed high levels of responding to nonreinforced stimuli from the inception of training, it is still possible to test the prediction that, because view-invariant elements acquire control of performance early in training, the pattern of responding should be similar for reinforced and nonreinforced stimuli in the early stages and it should subsequently differ for both stimulus types.

Looking at the correlation between mean response rates for reinforced and nonreinforced stimuli across training might be a sensitive test for changes in the control of performance by view-invariant elements. The Pearson correlation between response rates to reinforced and nonreinforced stimuli was computed for each pigeon in two stages of training: For training Blocks 1-10 and for training Blocks 11-20. If performance is controlled by view-invariant properties early in training, then the correlations for early training blocks should be higher than the correlations for late training blocks. Individual correlation coefficients were converted to Fisher’s z values, which were then averaged, and the result converted back to a correlation coefficient, denoted by r_z (Corey, Dunlap, & Burke, 1998). This average correlation between response rates was higher during Blocks 1-10 (r_z = 0.74) than during Blocks 11-20 (r_z = 0.27), a difference that was statistically significant, z = 2.94, p < 0.01.

To summarize the results regarding learning curves, high response rates to all of the stimuli do not allow one to directly confirm the prediction of a concave learning curve for nonreinforced stimuli in the average group data (Figure 5A). However, some of the individual learning curves did appear to be concave (Figure 5B). Also, evidence from a correlational analysis suggested similar control of behavior by reinforced and nonreinforced stimuli early in training (Blocks 1-10), but not later in training (Blocks 11-20). These results, together with those from the generalization test and the peck density analysis, suggest that error-driven associative learning plays a key role in pigeons’ learning to recognize objects across variations in viewpoint.

An alternative explanation of the results of the present experiment is that pigeons in Go/No-Go tasks learn to respond indiscriminately to all of the stimuli presented on the screen, but to withhold responding to the set of nonrewarded stimuli in the Correlated condition. So, when the birds are presented with new images from the training categories or training objects, they keep responding indiscriminately to all these new stimuli, except those that look similar to the nonrewarded images in the Correlated condition. Because of perceptual similarity, new stimuli in the Correlated condition should be more likely to show this generalized inhibition than new stimuli in the Uncorrelated condition. Thus, the effect shown in Figures 1 and 5 could be explained as the result of differential inhibitory generalization instead of error-driven learning.

This hypothesis does not provide a full account of the data from the peck density analysis. Remember that pigeons displaced their pecks from within the object to outside the object after learning in the Uncorrelated condition. This response pattern could be explained as the outcome of generalization of inhibition, by assuming that nonreinforced objects in the Correlated condition become inhibitory, leading pigeons to avoid pecking at them. The tendency to avoid pecking would then generalize to stimuli in the Uncorrelated condition, if these stimuli are perceptually similar to the directly nonreinforced stimuli. Thus, generalization of inhibition could promote the concentration of pecks outside the objects in the Uncorrelated condition. However, because the reinforced stimuli and the nonreinforced stimuli in the Correlated condition are views of the same object, similarity-based generalization should be stronger in this case than with any stimuli in the Uncorrelated condition, which are views of a completely different object. So, generalization of inhibition should produce more pecks outside the reinforced objects in the Correlated condition than in the Uncorrelated condition. But, the just opposite was found: more pecks were allocated to the object in the Correlated condition than in the Uncorrelated condition. This finding suggests that what birds learn in this task is more complex than simply pecking indiscriminately at all stimuli except those that have become inhibitory by direct training or generalization.

3. Experiment 2

In Pavlovian learning, conditioning to one stimulus is attenuated when it is presented in conjunction with a second stimulus that reliably predicts reinforcement, an effect that Pavlov called “overshadowing” (Pavlov, 1927). The size of this effect depends on the relative salience of the two stimuli, with a more salient component overshadowing a less salient component (Mackintosh, 1976).

An error-driven learning algorithm explains overshadowing as the result of both stimuli acquiring associative strength throughout training until, together, they perfectly predict reinforcement. At that point, learning stops for both stimuli. Thus, each stimulus only acquires part of the total response tendency that it would have acquired if it had been individually paired with reinforcement. The more salient component tends to acquire more associative strength because higher saliency supports a higher learning rate.

As reviewed in Section 1, training with multiple views of an object leads to view-invariance learning in pigeons. However, if view invariance is learned through reward prediction error, then this form of learning can be impaired, even if birds are trained with multiple views of an object. One way to do so is to arrange training conditions in which, together with view-invariant properties, different stimulus properties are repeatedly presented across changes in viewpoint that are also informative as to the response leading to reward on each trial.

The Common Elements Model does not give any special status to view-invariant properties over other image properties, beyond the fact that they get repeated often during multiple-views training. According to the model, if any properties tend to be common to many of the training views, then these properties should acquire control over behavior even if they are view-specific. These common properties should block control of behavior by view-invariant properties, thereby producing an overshadowing effect. The size of the overshadowing effect would depend on such factors as the relative salience of each set of properties and their informative value as to the correct response. If view-specific properties are made especially salient, then view-invariance learning might even be reversed.

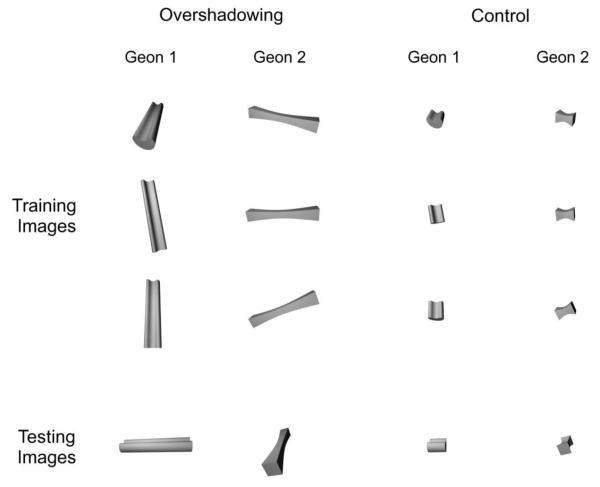
The goal of Experiment 2 was to test the hypothesis that any stimulus properties that are common to several training views of an object, including view-specific properties, will acquire control over pigeons’ behavior. Pigeons were trained in two conditions—Overshadowing and Control—each involving the presentation of ten different views of two objects. One of these objects was shown at viewpoints from which its main axis appeared vertical in the image plane, as exemplified by the renderings of Geon 1 in Figure 6 labeled “Training Images.” The other object was shown at viewpoints from which its main axis appeared horizontal in the image plane, as exemplified by the renderings of Geon 2 in Figure 6 labeled “Training Images.”

Fig. 6.

Examples of the types of stimuli that were used in Experiment 2.

As can be seen from Figure 6, the main difference between the geons included in the Overshadowing and Control conditions was the length of the geon’s main axis. The Overshadowing condition included geons with a long main axis, whereas the Control condition included geons with a short main axis. Note that, in both conditions, the geons can be discriminated on the basis of several properties which are invariant across changes in viewpoint, such as edge parallelism and shape of the cross-section. The geons can also be discriminated on the basis of properties that are variable across changes in viewpoint, such as the orientation of the main axis. A metric which correlates with the orientation of the main axis is the two-dimensional aspect ratio of the object, defined as the width-to-height ratio of the smallest rectangle that can enclose an object (Biederman, 1987). The main difference between the conditions lies in the salience of this metric property. In the Overshadowing condition, the long main axes produce very large differences between the geons in aspect ratio, whereas in the Control condition, the short main axes produce smaller differences in aspect ratio.

Although the geons in Figure 6 can be categorized on the basis of very different properties, which property is actually used has consequences for how well the object will be recognized from novel viewpoints. Properties such as edge parallelism and shape of the cross-section provide information about the three-dimensional structure of the geons, permitting them to be identified from new viewpoints. Properties such as aspect ratio, however, do not provide any information about the three-dimensional structure of the geons and do not permit them to be identified from novel viewpoints.

According to the Common Elements Model, both types of properties should come to control behavior during training. How quickly the birds learn about each property depends on such factors as how salient the differences are between geons along that particular dimension. The difference between geons in aspect ratio is much more salient in the Overshadowing condition than in the Control condition. Thus, aspect ratio should come to control behavior more rapidly during training in the Overshadowing condition, as well as block control by view-invariant properties. In the Control condition, aspect ratio should gain less control over behavior, leading to greater control by view-invariant properties.

The level of control that is acquired by each stimulus property can be assessed by testing with novel views of the training objects (“Testing Images” in Figure 6). The testing image of each geon has an aspect ratio which is the opposite of the aspect ratio that was shown by the geons’ training images. If the pigeons learned to sort the images based on properties such as edge parallelism and shape of the cross-section, then they should correctly identify each object from new viewpoints during the test, exhibiting the same view-invariant behavior previously demonstrated by pigeons trained with multiple views of geons. If, on the other hand, the pigeons learned to sort the images based on their aspect ratio, then they should incorrectly classify the testing images. The birds ought to respond to the new image of Geon 1 with the choice response that was assigned to Geon 2 during training, and they ought to respond to the new image of Geon 2 with the choice response that was assigned to Geon 1 during training.

3.1. Method

3.1.2. Subjects and Apparatus

The subjects were five feral pigeons (Columba livia) kept at 85% of their free-feeding weights. The apparatus was the same as that described in Experiment 1.

3.1.3. Stimuli

The stimuli were renderings of four three-dimensional objects (“geons”). Object models were created using Blender 2.49 (The Blender Foundation; www.blender.org). They were built by swiping four different cross-sections (kidney-shaped, square, circle, and triangle) along a straight main axis, and with the size of the cross-section changing across the main axis in four different ways (constant, contract and expand, expand and contract, expand).

Two versions of each geon were created, one with a short main axis and one with a long main axis (see Figure 6). The long-axis version of each geon had a main axis that was five times longer than the short-axis version of the same geon. For both versions, the length of the main axis was the same across geons and the main axis was always straight. The size of the cross-section, measured by the size of the smallest rectangle that could enclose it, was also the same for all geons. Finally, the length of the main axis was greater than the width of both the short- and the long-axis versions of each geon. The main difference between versions was metric: namely, how much longer the main axis of the geon was compared to its cross-section.

Two-dimensional renderings were generated by placing a camera in front and slightly above the object. Two environmental lights illuminated the object: one positioned in front of the object and below the camera, the other positioned at the top-left of the object. The objects were rotated on their internal axes and rendered on a white background with a size of 256 × 256 pixels. For each object, 49 views were rendered in which the object’s main axis was horizontally oriented and 54 views were rendered in which the object’s main axis was vertically oriented.

From this final pool of stimuli, ten training views were selected by the experimenter. The training views showed the object’s main axis horizontally oriented for Geons 1 and 3 and vertically oriented for Geons 2 and 4. Stimulus sets were grouped by geon. Geons 1 and 2, which differed in a number of structural properties (edge curvature, symmetry of cross-section, tapering of cross-section along main axis) and in the orientation of their main axis, were always grouped together and assigned to the same experimental condition. The same was true for Geons 3 and 4. Thus, the stimuli in both discriminations were highly discriminable on the basis of their structural properties and aspect ratio. The assignment of each pair of geons to the two conditions was counterbalanced across pigeons.

The orientation of the main axis for testing views was the opposite of the orientation of the training views. The selection of testing stimuli was carried out in a three-step process.

First, the pixel-by-pixel dissimilarity in luminosity between the candidate testing stimuli and the training stimuli was computed, with adjustment of position. For a pair of images, the position of the object within one of the displays was shifted several times; each time, the Euclidean distance between the pixel luminosity values of the images was calculated. This dissimilarity measure was computed at each of 10,201 positions and the minimum dissimilarity was kept as the final measure. The large number of positions was the result of the combination of the original position plus 50 translations in upward, downward, leftward, and rightward directions. Translations were done in steps of 2 pixels to reduce computing time.

Second, each testing image was classified as generated by a particular object, according to two criteria: 1) the object with the lowest dissimilarity between a single training image and the testing image, or 2) the object with the lowest mean dissimilarity between all training images and the testing image.

Third, views which were classified in the same way for both the short-axis and the long-axis versions of the object were retained as candidates. From this smaller pool of views, testing views were selected by the experimenter. This selection of testing views ensured that the predicted results could not be explained by the pattern of physical similarity among images.

3.1.4. Procedure

Each pigeon was concurrently trained on both conditions. Four keys (black-and-white icons) were used, each positioned next to one corner of the stimulus. Each condition was trained using a different pair of response keys in a two-alternative forced-choice task (either the two top response keys or the two bottom response keys). The assignment of conditions to pairs of response keys was counterbalanced across pigeons.

The assignment of object pairs to the two conditions was counterbalanced across pigeons. The assignment of objects to response keys was partially counterbalanced, taking care that objects with training views which had the same main axis orientation were assigned to opposite left-right positions on the screen, to prevent the pigeons from learning to respond to one side of the screen whenever an object with a particular orientation was shown.

The stimuli were displayed on a 7.5- × 7.5-cm screen positioned in the middle of the monitor. A trial began with the pigeon being shown a black cross in the center of a white screen. After one peck to the display, an image was shown. The bird had to peck the stimulus a number of times (from 5 to 45, depending on the pigeon’s performance); then, a pair of response keys was shown and the pigeon was required to peck one in order to advance the trial. If the pigeon’s choice was correct, then food was delivered and an intertrial interval followed. If the pigeon’s choice was incorrect, then the house light and the monitor screen darkened and a correction trial followed after a timeout ranging from 5 to 30 s (again, depending on the pigeon’s performance). Correction trials continued to be given until the correct response was made. Only the first report response of each trial was scored in data analysis. Reinforcement consisted of 1 to 3 food pellets.

Training sessions consisted of 4 blocks of 40 trials. Each block consisted on one presentation of each of the training stimuli. Trials were randomized within blocks during this and the following phases. Training continued until the bird met the criterion of 85% accuracy on each of the four response keys; then, a testing session followed.

Testing sessions consisted of 1 warm-up block of 40 training trials plus 1 testing block with 120 trials, for a total of 160 trials per session. The testing block included a single presentation of each of the testing stimuli plus 2 repetitions of each training trial. All presentations of the novel testing stimuli were nondifferentially reinforced. Pigeons continued to be tested as long as they met criterion on the training trials; otherwise, birds were returned to training until criterion was again attained. Each pigeon completed 10 full testing sessions.

3.2. Results and Discussion

It took the birds a mean of 15.6 training sessions to reach criterion for testing, with individual values ranging from 8 to 23 sessions.

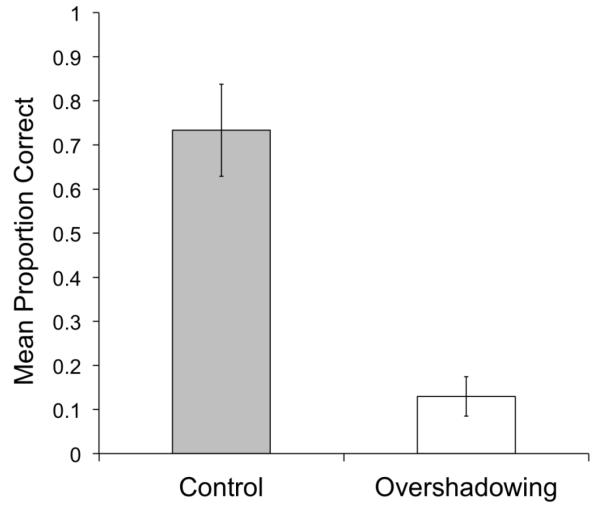
Figure 7 shows the mean proportion of correct choices to testing stimuli in the Control (grey column) and Overshadowing (white column) conditions. Chance performance was 0.5. It can clearly be seen that the pattern of generalization was reversed in the two conditions. Pigeons showed above-chance performance with novel stimuli in the Control condition (M = .73, SD = 0.21). A one-sample t-test indicated that the mean proportion of correct choices in the Control condition was significantly above chance, t(4) = 2.50, p < 0.05. This outcome confirms previous findings indicating that multiple-views training leads to generalization of performance to novel views of the training objects. On the other hand, pigeons showed below-chance performance with novel stimuli in the Overshadowing condition. A one-sample t-test revealed that the mean proportion of correct choices in the Overshadowing condition was significantly below chance, t(4) = 8.69, p < 0.001. This outcome indicates that what came to control performance in the Overshadowing condition was the orientation of the object’s main axis in the image plane, leading the pigeons to misclassify testing views of the objects in which the orientation of their main axis was rotated. A paired-samples t-test revealed that the difference between the Control and Overshadowing conditions was significant, t(4) = 5.82, p < 0.01.

Fig. 7.

Results of the Generalization Test of Experiment 2.

These results suggest that, as predicted by the Common Elements Model, any stimulus properties which are frequently repeated during training with multiple views of an object can acquire control of performance. Usually, properties that enjoy this repetition advantage are view-invariant properties, which are useful to infer the three-dimensional identity of a particular object. However, if conditions are arranged so that both view-invariant and view-specific properties are both frequently repeated across training views and are both informative as to the correct response in a recognition task, then view-invariant properties may not show a selective advantage. In some circumstances, view-specific properties can completely overshadow view-invariant properties, leading to no learning about the identity of the training objects.

Importantly, the results of this experiment cannot be explained in terms of the pattern of image similarities presented in the retinal input. As described in Section 3.1.3, the stimuli were created to explicitly control for this possibility.

4. General Discussion

In the present work, two experiments were reported suggesting that associative error-driven learning is involved in pigeons’ recognition of objects across changes in viewpoint. Experiment 1 found that recognition of an object across changes in viewpoint depends on how well each individual view predicts reward. If reward is well predicted by individual object views, then invariance learning is reduced compared to a condition in which object views are not predictive of reward. This pattern of results is analogous to the relative validity effect in associative learning, a conclusion that was strengthened by analysis of peck location and learning curves, which also exhibited response patterns similar to those found in prior Pavlovian conditioning studies. Experiment 2 found that view-specific and view-invariant object properties compete for control of behavior in object identification. Which properties control performance after training depends on such factors as their saliency and how well they predict reward. We found that, given the right circumstances, training with multiple views of an object results in view-dependent object recognition. This pattern of results is analogous to the overshadowing effect first reported in associative learning experiments.

Our explanation of view-invariance learning by pigeons is predicated on the assumption that their visual system is capable of extracting both view-invariant and view-specific object properties from retinal images. As discussed in Section 1, the available behavioral evidence accords with this assumption. But, an important question remains unanswered: How does the avian visual system build such a representation?

Current thinking suggests that the selectivity and invariance of neurons, at least in the primate visual system, are learned across development through unsupervised exposure to natural images. Several learning algorithms have been proposed that can achieve invariance learning (e.g., Foldiak, 1991; Stringer et al., 2006; Wiskott & Sejnowski, 2002), most of them based on the same general idea: objects in the world tend to remain present for several seconds, but changes in the position of the object and the viewer lead to drastic changes in the images that they project to the retina. Thus, object changes in the real world happen at a slower temporal scale than image changes in the retina. The brain may take advantage of this fact and learn view-invariant object properties from different retinal images that are presented in close temporal contiguity.

Some evidence supports the view that the selectivity of neurons in the primate ventral stream is learned through such unsupervised learning algorithms (Li & DiCarlo, 2008; 2010). However, an interesting possibility is that error-driven learning might play a role in the learning of visual features and not just their selection for performance in specific tasks. Changes in selectivity of visual neurons during perceptual learning has been explained as the result of error-driven learning of representations (Roelfsema & van Ooyen, 2005; Roelfsema et al., 2010). Importantly, the evidence that has been offered in support of unsupervised learning of selectivity and invariance in the primate visual system does not completely eliminate a role for reward prediction error during such learning. This point is explicitly acknowledged by Li and DiCarlo (2010), who note that their data “do not rule out the possibility that [..] top down signals may be required to mediate […] learning. […] These potential top-down signals could include nonspecific reward, attentional, and arousal signals (p. 1073).” The availability of such top-down signals could also explain the results of other monkey studies, which suggest that object discrimination can lead to view-invariance learning in the absence of experience with temporal pairings of object views (Wang et al., 2005; Yamashita et al., 2010).

Learning schemes that can achieve invariance gradually through experience with an object leave open the question as to how invariance is achieved without explicitly experiencing variations in an irrelevant object dimension—the puzzle of initial invariance (Leibo et al., 2010). Such initial invariance, which has been found in people with both natural and artificial objects (e.g., Biederman & Gerhardstein, 1993), could have important value for the adaptation of any species.

One way in which initial invariance can be increased is through the hierarchical processing of visual information (Leibo et al., 2010; Ullman, 2007). In such a framework, object recognition occurs through several stages of visual information processing, with each stage computing a more complex object representation from inputs coming from the previous stage. For example, one stage might extract from the image a number of object parts, whereas the next stage might integrate them into the representation of a whole object. Within this scheme, invariant recognition of a new object can be achieved through invariant recognition of its components. If training with one object leads to invariant representations of its components, then this learning would generalize to the recognition of any new objects which also share those components. Objects from the same natural class, which are very likely to share components, are particularly prone to entail this form of generalized invariance. Although the learning of invariant components is generally implemented through unsupervised mechanisms in hierarchical models, another possibility is that the learning of representations throughout the visual system is gated by a prediction error signal.

Another possibility is that, from all of the visual properties that can be extracted from a single view of an object, the visual system might preferentially process those that are more likely to be repeated from new viewpoints. This selective processing would lead to better performance with novel views of the object than if all of the properties in the original training view were processed to the same extent. Error-driven learning could also play a role in this case. Through experience with many objects, the system could learn to selectively attend to those features that are most diagnostic as to the object’s identity across several irrelevant transformations.

If there is a role for prediction error in attentional learning or the learning of visual representations, then the Common Elements Model could be modified in many ways to provide a better account of invariance learning. The assumptions of the model concerning the conditions that produce learning (i.e., reward prediction error) are independent of its assumptions about the contents of such learning (e.g., associations with responses, object and feature representations, or selective attention).

Another challenge for any model relying on learning through reward prediction error is that object recognition in the natural environment often does not involve situations in which explicit rewards are presented. However, any neutral stimulus can acquire motivational value via Pavlovian conditioning (for a review, see Williams, 1994), thereby becoming rewarding. Furthermore, the same brain substrates that code for reward prediction errors also code for information prediction errors; that is, whether or not surprising information about a possible reward has been presented (Bromberg-Martin & Hikosaka, 2009). Thus, learning through prediction error does not require the presentation of an explicit reward.

An important question regarding object representations is to what extent the representation assumed by the Common Elements Model is related to the representations proposed by structural-description and image-based theories of human object recognition. Structural-description theories (e.g., Biederman, 1987; Marr & Nishihara, 1978) propose that objects are represented as a set of three-dimensional volumetric parts (e.g., a cylinder, a cube, etc.) and their spatial relations. That is, information about the three-dimensional structure of objects is explicitly extracted from images and represented by the visual system. Such extraction of information would be possible thanks to the identification of the volumetric components of an object; edge properties in the two-dimensional image that these volumes project to the retina are likely to arise from similar features in the edges of three-dimensional objects (see Biederman, 1987). On the other hand, image-based models (e.g., Poggio & Edelman, 1990; Tarr & Pinker, 1989; Ullman, 1989) propose that objects are represented as a set of view-dependent images which are stored in memory. These images could be complete templates of a specific view of an object, the metric coordinates of constituent points of the object, or collections of two-dimensional image features. Thus, the stored representation of an object would involve two-dimensional image information acquired through experience, instead of the three-dimensional structure that is proposed by structural-description models.

The Common Elements Model describes the conditions that lead to view-invariance learning, while making minimal assumptions about stimulus representation. Thus, the model does not commit to the kind of representation proposed by either structural-description or image-based models. It only assumes a distributed representation involving object properties with varying levels of invariance across changes in viewpoint. What we have called “view-invariant” properties here can be any properties that are common to many views of an object, which is likely to include properties of the three-dimensional structure of an object, but also two-dimensional image features. Previous research has shown that pigeons rely heavily on three-dimensional shape features to recognize simple geons like those used here (Gibson et al., 2007; Lazareva et al., 2008). However, it might be the case that such features are not available for the recognition of other objects. In that case, two-dimensional image features that are common to adjacent views might play a more important role. Importantly, the model proposes that, regardless of the view-invariant and view-specific properties in a particular set of images, the learning principles by which these properties are selected for performance in a task are always the same.

Here, we have made a distinction between view-invariant and view-specific elements without a more fine-grained distinction involving the degree to which different views of an object share common properties. For example, it could be assumed that the number of properties that are common to two object views increases proportionally to how close they are in terms of rotation. We believe that the validity of this assumption is not guaranteed. There is no reason to think that the distances along the dimension used to create a number of stimuli must be perfectly correlated with the dissimilarities as perceived by the birds. Thus, the Common Elements Model only assumes that views from the same object (or category) are more likely to share common properties than views from different objects. One way in which it might be possible to study graded differences in similarity would be to infer featural representations for individual stimuli from independent data using additive clustering (Navarro & Griffiths, 2008; Shepard & Arabie, 1979), and then using the inferred representations to make more fine-grained predictions about learning and generalization. Although we believe that this is a very promising possibility, it is beyond the scope of the present study.

An important open question is to what extent error-driven learning might play a role in pigeons’ learning to recognize objects across transformations other than viewpoint, such as size and position. Object recognition which is invariant across changes in viewpoint is considered to be a more difficult computational problem than invariance across changes in size and position (Palmeri & Gauthier, 2004; Riesenhuber & Poggio, 2000; Ullman, 1989). However, behavioral evidence from studies with pigeons suggests that their recognition of objects varying in size and translation is similar to their recognition of objects varying in viewpoint.

Several studies have tested pigeons’ recognition of objects varying in size (e.g, Peissig, Kirkpatrick, Young, Wasserman, & Biederman, 2006; Pisacreta, Potter, & Lefave, 1984). The general conclusion from these studies is that pigeons show generalization of performance to familiar objects presented at novel sizes. Nevertheless, pigeons also show a decrement in accuracy to novel sizes compared to the original size. Regarding translation, there is evidence that pigeons generalize their recognition performance only modestly to novel positions on a display screen after training with a single, central position; however, if the birds receive training with as few as four different positions of the object, then they show complete invariance when the object is presented in new positions (Kirkpatrick, 2001).

Thus, the Common Elements Model might offer a good explanation of birds’ recognition of objects across a number of different image transformation, not only viewpoint. Furthermore, we have found (Soto & Wasserman, in preparation) that experience with several affine transformations (scaling, shear, and planar rotation) of a single object view improves view-invariant recognition in pigeons; that is, it improves recognition across a non-affine transformation (rotation in depth), implicating common processing mechanisms for both types of transformation. At least for birds, the distinction between affine and non-affine transformations seems not to be a basic one, as proposed by some theories of object recognition in primates (Riesenhuber & Poggio, 2000). Thus, it is likely that the results of the present experiments will generalize to learning of invariance along other relevant object dimensions, such as size and translation.

A final question is to what extent the results found with birds might tell us something about visual object recognition in other species, particularly people and other primates. Several experimental results suggest that birds and primates use different mechanisms for invariant object recognition. For example, people sometimes exhibit view-invariant recognition when they are tested with the appropriate stimuli (Biederman & Gerhardstein, 1993), whereas pigeons show view-dependent recognition regardless of the type of stimulus with which they are tested (Cerella, 1977; Lumsden, 1977; Peissig et al., 1999, 2000; Spetch et al., 2001; Wasserman et al., 1996). Also, people, but not pigeons, show view-invariant recognition of novel views of an object which are interpolated between experienced views (Spetch & Friedman, 2003) and show view-invariant recognition of bent-paperclip objects when a geon has been added to them (Spetch et al., 2001).

All of these disparities in behavior suggest that there may be a difference between species in the mechanisms that support view-invariant object recognition. However, recent work with a computational model of object recognition indicates that pigeons’ behavior in object recognition tasks is consistent with the principles of visual shape processing discovered in the primate brain (Soto & Wasserman, 2012). Although there may surely be adaptive specializations involved in object recognition by birds and primates, it seems likely that pigeons, people, and other vertebrates share some basic principles of visual representation and associative learning.

It is becoming increasingly accepted among researchers that object categorization in primates results from a two-stage process (e.g., De Baene et al., 2008; DiCarlo & Cox, 2007; Serre et al., 2005), in which high-level visual representations are generated by the visual system and other areas in the brain readout this information to produce category representations and adequate motor responses. What is known about shape processing and representation in the primate brain agrees with the idea that the primate visual system extracts properties with varied levels of view invariance from retinal images, giving origin to a sparse, distributed object representation.

A recent study (Zoccolan et al., 2007) disclosed that both object selectivity and invariance across image transformations range widely in a population of inferotemporal neurons. Although single neurons in high visual areas do not seem to achieve complete invariance, whole populations of neurons can support invariant recognition through readout mechanisms (Leibo et al., 2010). Indeed, it has been found that, if the response of a small population of inferotemporal neurons is used to train a linear classifier in an object recognition task, then the classifier can show invariant recognition across position, scale, and clutter (Hung et al., 2005; Li, Cox, Zoccolan, & DiCarlo, 2009). However, these linear classifiers can read object identity across changes in image transformations only because they are explicitly trained with irrelevant variations across such dimensions (Goris & Op de Beeck, 2009, 2010).

The present work fits nicely into this picture, because it shows that error-driven associative learning is a good candidate for learning how to readout the representations that are generated by the visual system and potentially modify those representations to fit the demands of environmental tasks. The learning mechanism that is proposed by the Common Elements Model provides a similar result to the linear classifiers that have been used in the literature, such as support vector machines and Fisher discriminant analysis (Hung et al., 2005; Li et al., 2009), but with the advantage of being more biologically and evolutionarily plausible. There is evidence that prediction errors are computed in the brains of vertebrates, that they can drive categorization learning in the basal ganglia and other brain areas, and that many of the structures that are involved are homologous in all vertebrates (for a review, see Soto & Wasserman, 2012).

A “general processes” approach to comparative cognition suggests that some basic mechanisms of learning and visual perception, which are known to be present in primates, pigeons, and other vertebrates, are likely to play a role in view-invariance learning across all of these taxa. Although only further comparative research can give a definitive answer, the results presented here suggest that such general processes might play an important role in view-invariance learning by birds.

Highlights.

• - Associative mechanisms underlie view-invariance learning by pigeons.

• - An analog to the relative validity effect was found in object recognition.

• - An analog to the overshadowing effect was found in object recognition.

• - The results were predicted by our model of object categorization learning.