A rule-based seizure prediction method for focal neocortical epilepsy

Abstract

Objective

In the present study, we have developed a novel patient-specific rule-based seizure prediction system for focal neocortical epilepsy.

Methods

Five univariate measures including correlation dimension, correlation entropy, noise level, Lempel-Ziv complexity, and largest Lyapunov exponent as well as one bivariate measure, nonlinear interdependence, were extracted from non-overlapping 10-second segments of intracranial electroencephalogram (iEEG) data recorded using electrodes implanted deep in the brain and/or placed on the cortical surface. The spatio-temporal information was then integrated by using rules established based on patient-specific changes observed in the period prior to a seizure sample for each patient. The system was tested on 316 h of iEEG data containing 49 seizures recorded in eleven patients with medically intractable focal neocortical epilepsy.

Results

For seizure occurrence periods of 30 and 50 min our method showed an average sensitivity of 79.9% and 90.2% with an average false prediction rate of 0.17 and 0.11/h, respectively. In terms of sensitivity and false prediction rate, the system showed superiority to random and periodical predictors.

Conclusions

The nonlinear analysis of iEEG in the period prior to seizures revealed patient-specific spatio-temporal changes that were significantly different from those observed within baselines in the majority of the seizures analyzed in this study.

Significance

The present results suggest that the patient specific rule-based approach may become a potentially useful approach for predicting seizures prior to onset.

1. Introduction

As a chronic neurological disorder, epilepsy is characterized by recurrent unprovoked seizures which are paroxysmal hyper-synchronous electrical discharges of cerebral neurons (Chaovalitwongse et al., 2006). With anincidence of epilepsy estimated at 30 to 50 individuals per 100,000 population (Browne and Holmes, 2008), there remain a significant number of epileptic patients at risk of serious injury or death (Cockerell et al., 1994). The quality of life of epileptic patients would be significantly improved if seizures could be predicted.

To date, many attempts have been made to identify precursors of epileptic seizures by investigating various characteristics of the EEG time series using linear (Gotman and Koffler, 1989; Katz et al., 1991) and nonlinear univariate measures (Iasemidis et al., 1990; Lehnertz and Elger, 1998; Martinerieet al., 1998; Le Van Quyen et al., 2001; van Drongelen et al., 2003; Drury et al., 2003). Among these measures, those taken from the theory of chaotic dynamics, including the correlation dimension (Lehnertz and Elger, 1998), correlation density (Martinerieet al., 1998), largest Lyapunov exponent (Iasemidis et al., 1990), dynamic similarity index (Le Van Quyenet al., 2001), entropy (van Drongelen et al., 2003) and predictability (Drury et al., 2003) have shown higher seizure predictability power in the scalp EEG or iEEG (see Mormann et al. 2006 for review). Seizure prediction using these measures has suggested a transition state with characteristic changes that occur minutes to hours before a seizure. However, no measure has been shown to out-perform a random predictor (Mormann, 2008). Bivariate measures have also been employed for seizure prediction, such as nonlinear interdependence (Arnhold et al., 1999), phase synchronization, and cross correlation (Mormann et al., 2003). In a comparative study, Mormannet al. (2005) compared the performance of univariate and bivariate measures for seizure prediction and found a significant superiority for bivariate over univariate measures.

In general, univariate and bivariate measures can provide different, albeit complementary and relevant, information (Lehnertz et al., 2001). Therefore, for better characterizing preictal states and, consequently, for achieving a clinically acceptable performance across different patients and seizure types, multiple univariate and bivariate features ought to be used for developing seizure prediction tools (Iasemidis and Sackellares, 1996).

In the present study, we have developed a patient-specific method based on integrated univariate and bivariate measures to predict partial seizures using iEEG data. The aim is to improve seizure prediction by combining the predictability power of different measures. We also aim to identify preictal states based on spatio-temporal dynamic characteristics of the iEEG signal. To achieve these goals, the information exploited by using univariate and bivariate measures from iEEG is spatio-temporally integrated with patient-specific rules established using a sample seizure from each patient.

2. Methods

2.1. iEEG data

In this study, iEEG data of patients with medically intractable focal epilepsy were analyzed to test the performance of the developed method. The iEEG data were selected from the Freiburg Seizure Prediction EEG (FSPEEG) database including clinical and subclinical seizures (Maiwald et al., 2004) with authorization, having been recorded by a Neurofile NT digital video-EEG system (IT-Med, Usingen, Germany) with 128 channels, 256 Hz sampling rate, and a 16 bit analog-to-digital converter. Out of a total of 21 patients in the database, we included only the 11 individuals with a neocortical epileptic focus to evaluate our system, because seizure prediction in these patients is typically more challenging (Navarro et al., 2002) due to less inter-patient homogeneity, in terms of clinical manifestations and electrographic characteristics (Lee et al., 2000). It is of interest that almost two-thirds of adult epileptic patients with partial epilepsy suffer from seizures with neocortical onset (Semah et al., 1998).

Grid, strip, and depth electrodes were used to record iEEG data. For each patient in this database, only six contacts were selected by visual inspection of iEEG data by an experienced epileptologist: three near the epileptic focus, and three in remote locations. The extra-focal contacts were located at least more than two contacts distant from the focal contacts. No hyperventilation or photostimulation had been used to provoke seizures.

In total, 316 h of iEEG data containing 49 seizures with at least 50-min pre-ictal data were analyzed. Based on identification of epileptic patterns preceding clinical manifestation of seizures in iEEG recordings, the onset and offset times of seizures had been previously determined by the epileptologist. Table 1 summarizes the details of the iEEG data used in this study.

Table 1.

Patient specific characteristics of the intracranial EEG data

Patient	Sex	Age	Seizure type	Origin	Electrodes	Number of seizures	Average seizure duration (sec)	Interictal seizure-free EEG duration (hour)
1	F	15	SP,CP	Frontal	g,s	4	13.1	24
2	M	14	SP,CP	Frontal	g,s	5	92.7	24
3	F	16	SP,CP,GTC	Frontal	g,s	5	44.9	24
4	F	32	SP,CP	Frontal	g,s	2	163.7	24
5	M	44	CP,GTC	Temporo/Occipital	g,s	5	113.7	24
6	F	10	SP,CP,GTC	Parietal	g,s	4	157.3	24
7	M	28	SP,CP,GTC	Temporal	s	5	86.2	24
8	F	25	SP,CP	Frontal	s	5	13.7	25
9	F	28	SP,CP,GTC	Frontal	s	4	12.5	24.4
10	M	33	SP,CP,GTC	Tempo/Parietal	d,g,s	5	85.7	25.6
11	M	13	SP,CP	Temporal	g,s	5	83.1	24
Total						49		267

SP = simple partial; CP = complex partial; GTC = generalized tonic-clonic; g: grid; s : strip; d : depth.

2.1.1. Optimization and testing subsets

The iEEG data of each patient were split into the optimization and test sets. The optimization set included one randomly selected sample seizure with a preictal period of 50 min and four-hour seizure-free interictal iEEG data distal to any ictal activity, referred to as the reference window or state. The optimization set was used to tune the parameters of the system in a patient-specific way. The testing set containing the remaining seizures and interictal data was used to assess the performance of the system.

2.2. Seizure prediction system

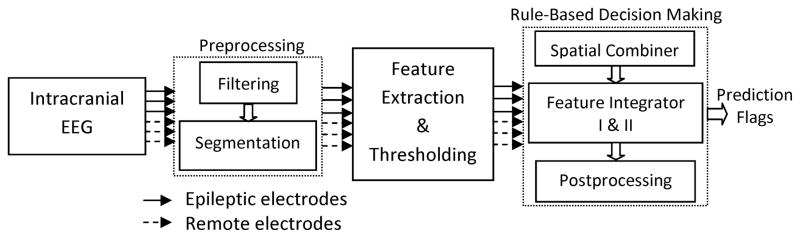
Fig. 1 shows a schematic of the proposed seizure prediction system. It comprises three stages: preprocessing, feature extraction and thresholding, and rule-based decision making.

Fig. 1.

Schematic diagram of the seizure prediction system.

2.2.1. Preprocessing

The purpose of this stage was first to remove both high frequency noise and low frequency activity and subsequently to divide the iEEG signal into quasi-stationary segments. For this two-fold purpose, the iEEG data were band-pass filtered between 0.5 and 100 Hz using a 4th order digital Butterworth filter, and notch filtered to remove 50 Hz power line noise. Then, the filtered iEEG data were partitioned into non-overlapping 10-second segments. The choice of segment length was a trade-off between signal stationarity and having the adequate number of data points required for extracting features from the iEEG data (Mormann et al., 2006).

2.2.2. Feature extraction

This stage aimed at extracting relevant features, which contained specific characteristic properties of iEEG signal, and were suitable for the seizure prediction task. After reviewing the literature, we selected a set of quantitative univariate and bivariate nonlinear features - Correlation Dimension (CD), Correlation ENtropy (CEN), Noise Level (NL), Lempel-Ziv Complexity (LZC), Largest Lyapunov Exponent (LLE), and Nonlinear Interdependence (NI) - to obtain an optimal characterization of the nonlinearities in the iEEG recording as well as in the dynamics of the epileptogenic networks especially in the preictal state. Although these features have been considered to exhibit some value for preictal state identification and have been used separately to investigate the dynamic behavior of the brain, each of these features alone was considered insufficient for depicting the complete ictogenesis process. Therefore, we used a combination of univariate and bivariate nonlinear measures in order to enhance seizure prediction. All these features were extracted from each segment of iEEG. To estimate the time lag and embedding dimension of iEEG signals, we used the methods described by Moon et al. (1995) and Cao (1997), respectively. For each segment of the iEEG data, we also examined synchronies among all 15 possible combinations of the six channels. Further details can be found in the Supplementary Material.

The mutual information method yielded time lag values ranging from 3 to 7 for all patients. Using the method described earlier, an optimal time lag of 5 was found for all patients and used to estimate the optimal value of the embedding dimension using Cao’s method, which obtained embedding dimension values ranging from 8 to 12 for all patients. The value of 12 was considered as the optimal embedding dimension which was then used to reconstruct state space of segments.

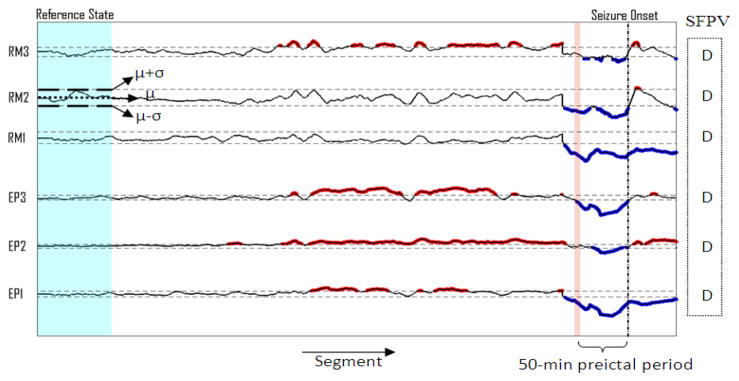
For a practical implementation, a backward-moving-average filter of 5 min was first applied to smooth the time profiles of each feature. Then, a thresholding procedure was applied to the univariate and bivariate feature values extracted from the iEEG segments of each patient separately. For any given feature and channel, the mean (μ) and standard deviation (σ) were calculated over the feature values extracted from the iEEG segments within the reference window. Then, to bring all of the features into the same scale, the feature values were normalized by subtracting the mean (μ) and dividing by the standard deviation (σ) of the reference state for each channel separately. Then, all the feature values of the whole iEEG data were scanned segment by segment and the location and feature value of the segments having values greater than (μ+σ) or lower than (μ−σ) were saved for further analysis (Fig. 2).

Fig. 2.

Thresholding results obtained using the mean (μ) and standard deviation (σ) computed over the feature values within the reference window. Spatial Feature Pattern Vector (SFPV) has been created using the sample seizure. D indicates a decrease in the median of the thresholded feature values within the preictal period with respect to that observed in the reference state. RM: remote channels; EP: epileptic channels.

2.2.3. Rule-based decision making

The rule-based decision making stage included a spatial combiner to integrate the spatial information obtained from the multichannel iEEG data, and feature integrators to combine the information embedded in different features in a way to obtain maximum sensitivity and specificity for seizure prediction (Fig. 3).

Fig. 3.

Schematic diagram of the rule-based decision making stage.

Since the goal of our method was patient-specific seizure prediction, we therefore first needed to determine the spatial behavior of the features in preictal periods with respect to reference periods in iEEG recordings of patients individually. To do so, for each patient, feature values in the 50-min preictal period of the sample seizure were compared to those obtained in the reference state separately for each feature and channel. If the median of the thresholded feature values in the preictal period showed an increase (or a decrease) with respect to the baseline median, then a respective label (I or D) was assigned to the current feature and channel. For the same patient, this procedure was repeated for all features and channels. It should be mentioned that for each of the features, the labels for the epileptic and remote channels were collected in a vector called Spatial Feature Pattern Vector (SFPV) (Fig. 2). This vector was considered as the spatiotemporal profile of the feature characterizing the preictal state of the patient. It should be mentioned that no-change status was included in SFPV for any feature showing no significant changes in comparison with the baseline, but this status was not used in determining seizure precursors. Therefore, for each patient, there were six SFPVs, five for the univariate features and one for the bivariate feature used in this study. All of the SFPVs were saved for further processing required for the other steps of the prediction decision making.

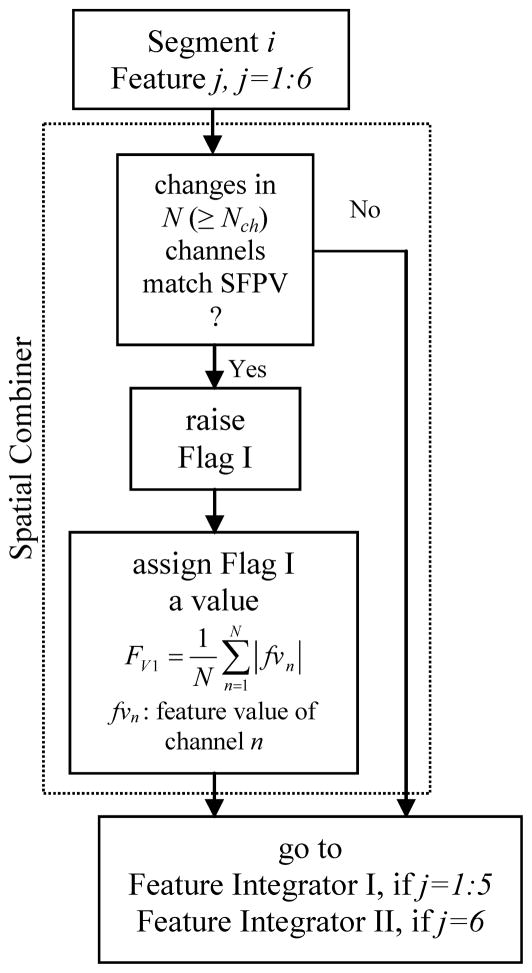
2.2.3.1. Spatial combiner

The spatial combiner included the criteria for spatially combining the information embedded in features values extracted from the iEEG of different channels (Fig. 4). Based on the SFPVs, this component combined feature values previously extracted from the iEEG segments of the channels. The spatial combiner worked on a single feature-multichannel basis. The spatial combiner was applied to each feature separately to identify multichannel seizure precursors.

Fig. 4.

Schematic diagram of the algorithm used in Spatial Combiner.

For a given feature and segment, if N channels (herein, out of 6 for the univariate measures and out of 15 for the bivariate measure) exhibited behaviors like those expected in the SFPV of the feature, and if N was greater than a threshold N_ch, then that segment was temporarily considered as a seizure precursor and a flag, labeled as I, was raised for the segment (Fig. 4). A value was assigned to this flag by averaging the absolute normalized feature values of channels, which showed the same behavior as the one expected in the SFPV. The location and the values of all flag Is at this step were saved and fed into the feature integrator described in the next section. There were six spatial combiners acting on the univariate and bivariate features.

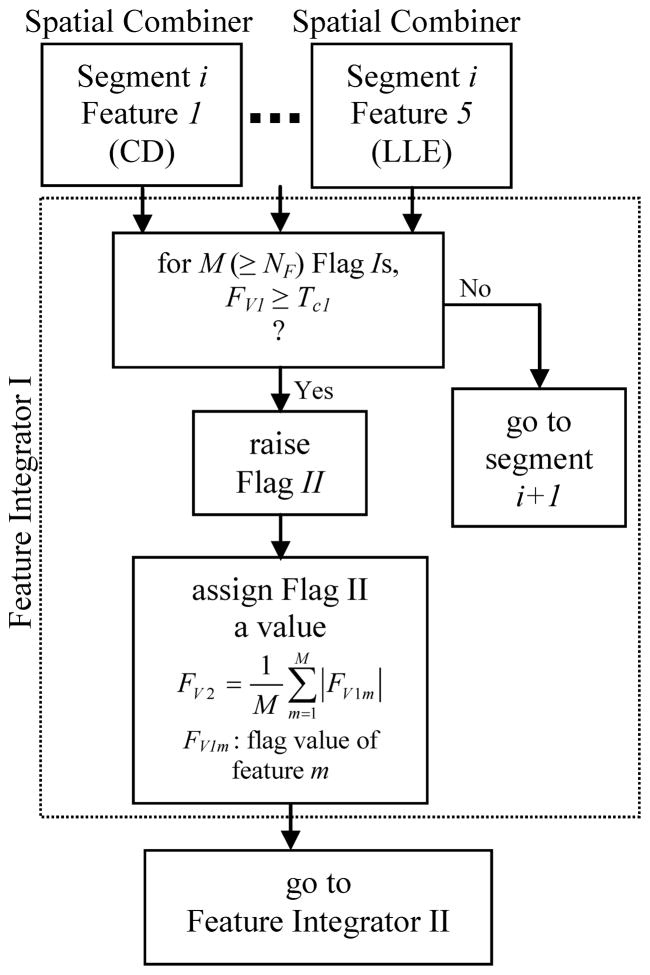
2.2.3.2. Feature integrator I

This feature integrator integrated decisions made for any segment in the previous step to locate seizure precursors (Fig. 5). For any segment, if M flag Is (out of 5) whose values were higher than a significance threshold T_c1 were raised, and if M was greater than a threshold N_F, then a second flag labeled as II was raised for the segment. This flag was given a value by averaging the values of the flag Is taken part in the decision made for that segment (Fig. 5). Flag IIs represented a higher probability of correct seizure prediction for the segment. Flag IIs were fed into the feature integrator II for a higher level decision.

Fig. 5.

Schematic diagram of the algorithm used in Feature Integrator I.

2.2.3.3. Feature integrator II

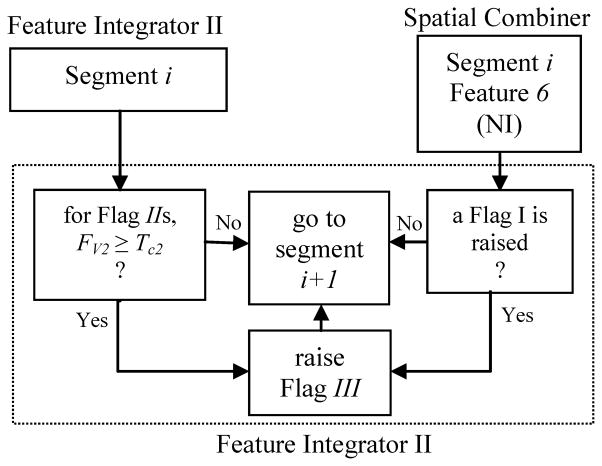
This feature integrator integrated flag Is and flag IIs as shown in Fig. 6. For any segment, if a flag II was raised using the univariate measures while a flag I was also raised using the bivariate measures (provided that their flag values exceeded a significance threshold T_c2), then a flag III, which represented a definitive seizure precursor, was raised for that segment.

Fig. 6.

Schematic diagram of the algorithm used in Feature Integrator II.

2.2.3.4. Postprocessing

In the postprocessing step, any flag IIIs not followed by at least three other flag IIIs were rejected as short false predictions representing precursors whose lengths did not exceed 40 sec. All of the remaining flag IIIs were considered as definite predictions.

2.3. System optimization

Using the optimization subset for each patient (Section 2.1.1), four thresholds - N_ch, N_F, T_c1 and T_c2 - were adjusted in a way to maximize sensitivity and specificity based on characteristic differences between the reference window and the preictal period of the sample seizure selected from each patient. For the optimization purpose we defined the sensitivity and specificity as below. With a given reference state and a sample seizure with a 50-minute preictal period, the sensitivity was calculated as the ratio of the number of prediction flag IIIs to the total number of the segments within the preictal period. Similarly, the specificity was defined as the number of false prediction flag IIIs divided by the total number of segments within the reference period.

To automate the optimization process for each patient, first T_c1 and T_c2 were both set to small values (0.5). This ensured us that T_c1 and T_c2 would not filter out any generated flag IIs and IIIs. Then, N_F was changed from 2 to 5 (maximum number of univariate features). Similarly, N_ch was changed from 2 to 6 (maximum number of intracranial channels) for the univariate features, and from 2 to 15 (maximum number of channel pairs) for the bivariate feature. The system performance was then evaluated on the optimization subset in terms of sensitivity and specificity as defined earlier in this section. The set of N_F and N_ch with which the system achieved maximum sensitivity and specificity were saved as suboptimal values for that reference window and used to optimize T_c1 and T_c2. Using the optimal set of N_F and N_ch, the significance thresholds T_c1 and T_c2 were changed from zero to ten with an increment of 0.1. We found this range of search large enough for the optimizer to search optimal values for T_c1 and T_c2 based on the maximum sensitivity and specificity strategy in all patients. At each round, T_c1 was fixed to a specific value in the range 0 through 15, and by varying T_c2 within the same range, the system performance was evaluated on the optimization subset in terms of sensitivity and specificity. This procedure was repeated for all values of T_c1 at the end of which the so-called receiver operating characteristic (ROC) curve was generated (Zhang et al., 2002). Then the T_c1-T_c2 pair that maximized the sensitivity as well as specificity on the ROC curves was considered as the optimal pair. In practice, a range of T_c1 and T_c2 values provided maximum sensitivity and specificity on the ROC curves. To avoid over-tuning due to the characteristic changes specific to the preictal period of the sample seizure, we did not select the maximum values of T_c1 and T_c2 for each patient. This would effectively decrease the false prediction rate at the expense of a lower sensitivity. Since we used a single seizure for parameter tuning, in order to consider temporal evolution in seizures away from the sample seizure we averaged the upper and lower bounds of the T_c1 and T_c2 value range, which produced the ROC curves with maximum areas to obtain optimal T_c1 and T_c2 values. Finally, the set of thresholds - N_ch, N_F, T_c1 and T_c2 -with which the system obtained maximum sensitivity and specificity using the optimization subset was selected to evaluate the system for the same patient and to assess the system’s performance for further comparison to the work of others.

2.4. System evaluation

The performance of the seizure prediction system was assessed on the seizure-free testing data including the interictal files completely independent from those used for optimizing the system parameters, through the following parameters (Maiwald et al., 2004; Mormannet al., 2006):

• Seizure occurrence period (SOP): after a prediction flag, the time period within which a seizure is expected.

• Seizure prediction horizon (SPH): a time window between any prediction flag and the beginning of SOP. During SPH, no seizure is expected to occur.

• Sensitivity (SEN): a measure of the ability of the system to predict seizures within the PH, quantified as:

  $$\mathit{Sensitivity}=\frac{N_{PS}}{N_{TN}}\times 100$$ (1)

  where N_PS is the number of seizures having at least one flag within the PH, and N_TN is the total number of seizures.

• Specificity (SPE) also called True Negative Rate: A measure of the ability of the system to identify interictal activities, quantified as:

  $$\mathit{Specificity}=\frac{N_{CS}}{N_{TS}}\times 100$$ (2)

  where N_CS is the number of correctly classified interictal segments of length PH, and N_TS is the total number of interictal segments of length PH.

• False prediction rate (FPR): The ratio of number of false positives divided by the duration of the interictal data (preictal periods are excluded). A false positive is defined as a prediction flag not followed by a seizure within the seizure occurrence period.

• Portion of time under false predictions: The duration of the interictal data containing false predictions. In this study, this metric was reported as the percentage of total seizure-free interictal data included in the testing set.

• Mean prediction time (MPT): The average time period between the beginning of SOP and the seizure onset.

We assessed the performance parameters for the seizure occurrence periods of 30 and 50 min and seizure prediction horizon of 10 sec, 5 min and 10 min.

2.4.1. Prospective evaluation

To demonstrate the utility of our system for prospective prediction, the system was first optimized using an optimization subset including a randomly selected sample seizure and the first four-hour seizure-free interictal EEG data selected as the reference state for each patient. Then, the system was run prospectively on the rest of the iEEG recordings of the patient and its performance was reported. Furthermore, to evaluate the predictability power of the individual features, we compared the performance of the system based on single features. For this purpose, our system was tuned up using only one feature at a time by deactivating both the feature integrators I and II. Then, the performance of the single-feature based-system was evaluated using the same reference window as mentioned above and saved for further comparison.

2.4.2. Cross validation

To evaluate the performance of our seizure prediction system for clinical use, we performed a cross validation analysis. At each round of cross-validation, the seizure-free intracranial EEG data for each patient were split into complementary optimization and testing subsets. Then, the system was tuned using the optimization subset and evaluated using the testing set. To reduce variability, multiple rounds of cross-validation were performed using different partitions, and the performance evaluation results were averaged over the rounds.

Towards this objective, we used the repeated random sub-sampling cross-validation method (McLachlan et al., 2004). Using this method, the original 24-hour interictal iEEG data for each patient were partitioned into 24 data files. Then, the optimization subset was constructed by randomly picking out four one-hour interictal data from the interictal data files. The remaining 20 data files were used as testing data. The cross-validation process was then repeated ten times. The results of the system performance evaluation were then averaged to produce single performance estimations.

2.5. Comparison to random and periodical prediction methods

We further compared the system sensitivity with the ones obtained using the random and periodical prediction methods as described by Winterhalderet al. (2003). The sensitivity of the random prediction method based on a Poisson process was obtained from a binomial distribution, with the probability defined as:

$$P=1-e^{-{\mathit{FPR}}_{max}.\mathit{SOP}}$$ (3)

where FPR_max is the maximum false prediction rate..

Similarly, the sensitivity of the periodical prediction method was derived from the following equation:

$$P=\{{\mathit{FPR}}_{max}.\mathit{SOP},100\%\}$$ (4)

2.6. Significance analysis of preictal changes

Using the Mann-Whitney U-test (Mann and Whitney, 1947) for each patient, we further tested the null hypothesis that the feature values within the baseline and the 50-minute preictal period of all of the seizures from the same patient were independent samples from identical distributions with equal medians, or alternatively that they did not have equal medians. A significance level of P<0.05 was set for this step.

To determine the significance of preictal changes of a specific feature for each patient, an extended reference state was first reconstructed by taking the feature values of all ten randomly selected reference windows, as used for cross validation analysis. Then, the feature values within the 50-minute preictal period of the seizures for the same patient were statistically compared to those obtained within the reference state on a channel-by-channel basis for the electrodes within the epileptic zone. We classified the preictal changes into three categories: significant increase, significant decrease, or no-change. The dominant preictal behavior for each feature was determined using the rules listed in Supplementary Table S1. Once the dominant preictal behavior was determined for each seizure, we classified seizures based on increases, decreases, or no-changes. The results from this step were then used to report the percentage of seizures that had preictal periods with similar significant changes for each feature individually, when compared to the reference state.

2.7. Connectivity map

We compared statistically nonlinear interdependence values (S) of preictal periods with those found in the reference state to achieve better insight into interactions between different cerebral regions. First for each iEEG channel pair, the differences between S_X→Y and S_Y→X values were calculated. Then, the difference values within the preictal periods were statistically compared to those obtained within the extended reference state using the Mann-Whitney U-test (Mann and Whitney, 1947). Any significant differences (p<0.05) between the preictal period and the baseline were marked and the ratio between the corresponding medians was computed for all seizures. For all seizures from each patient, the inter-channel connectivity patterns with maximum occurrence rate were used to visualize the connectivity map between different cerebral regions.

3. Results

3.1. Threshold Optimization

Table 2 lists the optimal threshold values computed automatically for each patient (Section 2.3). The optimal values of N_ch, N_F, T_c1, and T_c2 were estimated in a way to simultaneously maximize the sensitivity and specificity. The last two columns show the mean and absolute deviation of the optimal values of T_c1, and T_c2 used for seizure prediction over ten different randomly selected reference windows. In this table, for each patient the increases/decreases in the median values of the nonlinear measures observed in the preictal periods as compared to the one obtained in the reference state have been shown respectively in dark gray and light gray for SOP = 50 min and SPH =10 sec.

Table 2.

Optimal thresholds used for the performance evaluation of the seizure prediction system.

Patient	Nch						NF	Tc1	Tc2
	CD	NL	CEN	LZC	LLE	NI
1	2	2	2	2	2	4	2	1.8 ± 0.4	2.8 ± 0.6
2	3	3	3	3	3	6	2	1.3 ± 0.4	3 ± 0.8
3	2	2	2	2	2	3	3	1 ± 0.3	3 ± 1.1
4	2	2	2	2	2	2	2	1.5 ± 0.3	1.8 ± 0.7
5	3	3	3	3	3	2	2	1.3 ± 0.5	3.6 ± 1
6	3	3	3	3	3	5	4	1.4 ± 0.5	1.2 ± 0.3
7	4	4	4	4	4	4	4	1.6 ± 0.6	3.7 ± 1
8	2	2	2	2	2	2	3	2.4 ± 0.6	3.6 ± 0.5
9	4	4	4	4	4	4	4	1.9 ± 0.4	2.1 ± 0.4
10	2	2	2	2	2	3	2	2.6 ± 0.5	2.8 ± 0.7
11	3	3	3	3	3	4	3	1.6 ± 0.3	2.5 ± 0.9
PSinc (%)	44.9	32.7	36.7	36.7	51	81.6
PSdec (%)	44.9	44.9	49	44.9	36.7	6.2
PSzch (%)	10.2	22.4	14.3	18.4	12. 3	12.2

N_ch: number of channels; N_F: number of features; T_c1 and T_c2: significance thresholds for raising flag IIs and IIIs; CD: correlation dimension; NL: noise level; CEN: correlation entropy; LZC: Lempel-Ziv complexity; LLE: largest Lyapunov exponent ; NI: nonlinear interdependence. PS_inc, PS_dec and PS_zch show the percentage of seizures with significant preictal increase, decrease and no change, respectively. Results are expressed as mean ± absolute deviation. For each patient and feature, the dominant preictal behaviors are shown in dark gray and light gray, which indicate, respectively, increases and decreases in the median of the feature values in the preictal state as compared to that observed in the reference state (see Section 2.6 for details).

For each patient the feature values within the preictal periods were statistically compared with those obtained within the reference state (Section 2.6). For each feature, the last row in Table 2 indicates the percentage of seizures whose preictal states showed a significant decrease, increase, or no change when compared to the reference state, in at least two intracranial electrodes located near the epileptic focus.

The differences between the preictal and reference states in patients 1, 2, 3, 4, 7, 8, 10 and 11 were more pronounced in the remote areas compared to those observed in the epileptogenic zone.

3.2. System performance

3.2.1. Feature significance evaluation

The purpose of this evaluation was to compare the seizure predictive power of different features. To do so, we tested the performance of the single-feature prediction systems using the baseline selected at the beginning of the seizure-free interictal data for each patient (see Section 2.4.1). Table 3 compares the performance of the system using single or multiple features as a function of the seizure occurrence period. The values of the thresholds were adjusted using the method described in the system optimization section. As shown, the contribution of single features in performance improvement is not largely different, but the entire system based on combined features shows the highest mean sensitivity and specificity and the lowest mean false prediction rate for both seizure occurrence periods. Among the single-feature based systems, the CEN-based system obtained relatively lower sensitivities as well as false prediction rates with higher specificities. Supplementary Table S2 lists the detailed results of the system performance evaluation using the single training set for each patient. For SOP = 30 min and SPH = 10 sec, 5 min and 10 min, the average sensitivities and false detection rates are given in Supplementary Table S2. The averaged sensitivities were 77.3, 75 and 62.9%, respectively, for SPH values of 10 sec, 5 min and 10 min.

Table 3.

Average performance of the single-feature based systems as compared to the entire system performance for a seizure prediction horizon of 10 sec.

SOP (min)	System	SEN (%)	SPE (%)	FPR (/hr)	PT (%)	MPT (min)
30	CD-based	68.2 ± 16.5	89.9 ± 5.7	0.38 ± 0.13	10.1 ± 5.8	11.9 ± 7.5
	NL-based	72.7 ± 12.4	91.2 ± 3.9	0.43 ± 0.12	8.8 ± 3.9	11.8 ± 7.5
	CEN-based	57.6 ± 23.7	94.1 ± 3.5	0.3 ± 0.1	6.8 ± 4	11.1 ± 5.9
	LZC-based	61.4 ± 21.9	90.9 ± 6.6	0.34 ± 0.14	9.1 ± 6.6	13.8 ± 11.1
	LLE-based	59.6 ± 20.6	91.2 ± 7	0.29 ± 0.14	8.8 ± 7	13.1 ± 8.8
	NI-based	77.3 ± 12.4	87.7 ± 7.3	0.39 ± 0.15	12.4 ± 7.2	17.4 ± 7.1
	Entire system	77.3 ± 16.5	95.2 ± 4.8	0.15 ± 0.08	3.7 ±3.3	14.5 ± 8.9
50	CD-based	78.8 ± 19.3	89.9 ± 5.7	0.26 ± 0.09	10.1 ± 5.8	28.9 ± 14.
	NL-based	85.6 ± 15.7	91.2 ± 3.9	0.29 ± 0.09	8.8 ± 3.9	19.8 ±15.4
	CEN-based	61.4 ± 24.9	94.1 ± 3.5	0.23 ± 0.09	6.8 ± 4	15 ± 8.4
	LZC-based	68.9 ± 23.7	90.9 ± 6.6	0.24 ± 0.08	9.1 ± 6.6	32.2 ±16.4
	LLE-based	73.5 ± 24.4	91.2 ± 7	0.21 ± 0.09	8.8 ± 7	31.1 ±14.3
	NI-based	84.9 ± 16.5	87.7 ± 7.3	0.26 ± 0.09	12.4 ± 7.2	28.7 ± 14.6
	Entire system	90.2 ± 14.3	95.2 ± 4.8	0.11 ± 0.05	3.7 ± 3.3	31.7 ± 17

The results are averaged across patients. All of the systems have been optimized using the first four-hour seizure-free interictal EEG data selected as the baseline for each patient. CD: correlation dimension; NL: noise level; CEN: correlation entropy; LZC: Lempel-Ziv complexity; LLE: largest Lyapunov exponent; NI: nonlinear interdependence; SOP: maximum seizure occurrence period; SEN: sensitivity; SPE: specificity; FPR: false prediction rate; PT: portion of time under false predictions; MPT: Mean prediction time.

3.2.2. Cross validation results

The performance of the system for seizure occurrence periods of 30 and 50 min for each patient is listed in Table 4. Grand statistics were calculated based on out-of-sample seizure-free interictal data and seizures (see Section 2.4.2).

Table 4.

Overall performance of the seizure prediction system for a seizure prediction horizon of 10 sec.

Patient	SOP (min)	SEN (%)	SPE (%)	FPR (/hr)	PT (%)	MPT (min)
1	30	60 ± 11	99.5 ± 0.5	0.04 ± 0.04	0.6 ± 0.6	7.8 ± 7.7
	50	100 ± 0		0.04 ± 0.04		30.2 ± 20.9
2	30	80 ± 8	98.8 ± 0.6	0.12 ± 0.04	1.7 ± 1.3	2.9 ± 0.8
	50	93 ± 7		0.11 ± 0.03		3.1 ± 0.5
3	30	60 ± 12	92.2 ± 3.1	0.26 ± 0.09	7.8 ± 3.1	22.5 ± 7.8
	50	63 ± 13		0.17 ± 0.05		25.4 ± 14.5
4	30	100 ± 0	99 ± 0.4	0.07 ± 0.03	0.9 ± 0.5	7.7 ± 0.7
	50	100 ± 0		0.07 ± 0.03		7.7 ± 0.7
5	30	93 ± 7	92.8 ± 2	0.23 ± 0.02	7.3 ± 2	15.5 ± 7.5
	50	100 ± 0		0.17 ± 0.03		28.8 ± 6.9
6	30	60 ± 11	99.5 ± 0.4	0.03 ± 0.02	0.6 ± 0.5	13.7 ± 5.5
	50	67 ± 0		0.03 ± 0.02		45.4 ± 6.6
7	30	100 ± 0	91.1 ± 1.6	0.24 ± 0.03	9 ± 1.7	10 ± 3.7
	50	100 ± 0		0.14 ± 0.01		18.7 ± 0.8
8	30	100 ± 0	96.8 ± 2.5	0.12 ± 0.07	3.6 ± 2.7	22.2 ± 4.1
	50	100 ± 0		0.08 ± 0.04		36.8 ± 11.1
9	30	93 ± 7	89.9 ± 2.7	0.43 ± 0.04	9.4 ± 2.5	8.8 ± 2.1
	50	100 ± 0		0.26 ± 0.02		16.6 ± 12.9
10	30	55 ± 8	97.9 ± 1.5	0.17 ± 0.08	1.9 ± 1.5	9.8 ± 1.2
	50	70 ± 16		0.13 ± 0.05		31.5 ± 15.5
11	30	78 ± 5	98.3 ± 0.8	0.12 ± 0.06	1.7 ± 0.8	19.7 ± 4.8
	50	100 ± 0		0.1 ± 0.04		19.7 ± 3.4
Grand Average	30	79.9 ± 17.6	97± 3.6	0.17 ± 0.12	4 ± 3.6	12.8 ± 7.4
	50	90.2 ± 14.1		0.11 ± 0.06		24 ± 15

Mean and absolute deviation (AD) over the performance parameters obtained using the ten reference windows randomly selected for each patient. Results are rounded and expressed as mean ± AD. SOP:maximum seizure occurrence period; SEN: sensitivity; SPE: specificity; FPR: false prediction rate; PT: portion of time under false predictions; MPT: Mean prediction time.

Relatively lower sensitivities were observed in patients 1, 3, 6 and 10 for SOP = 30 min and SPH= 10 sec. Amongst patients, patient 9 showed the highest false prediction rate per hour. On average, a specificity of 97% was observed across patients. The minimum prediction time changed in the order of several minutes using different reference windows for each patient.

3.2.3. Overall performance of the system

The system showed an average sensitivity of 79.9% and 90.2% with an average false prediction rate of 0.17/h and 0.11/h, and an average specificity of 97%, respectively, for SOP= 30 and 50 min and SPH=10 sec. On average, the portion of time under false predictions was approximately 4% of the testing data. The mean minimum prediction time was about 13 and 24 min respectively for SOP = 30 and 50 min. It should be mentioned that the portion of time under false warning was computed based on the definition of specificity (Section 2.4).

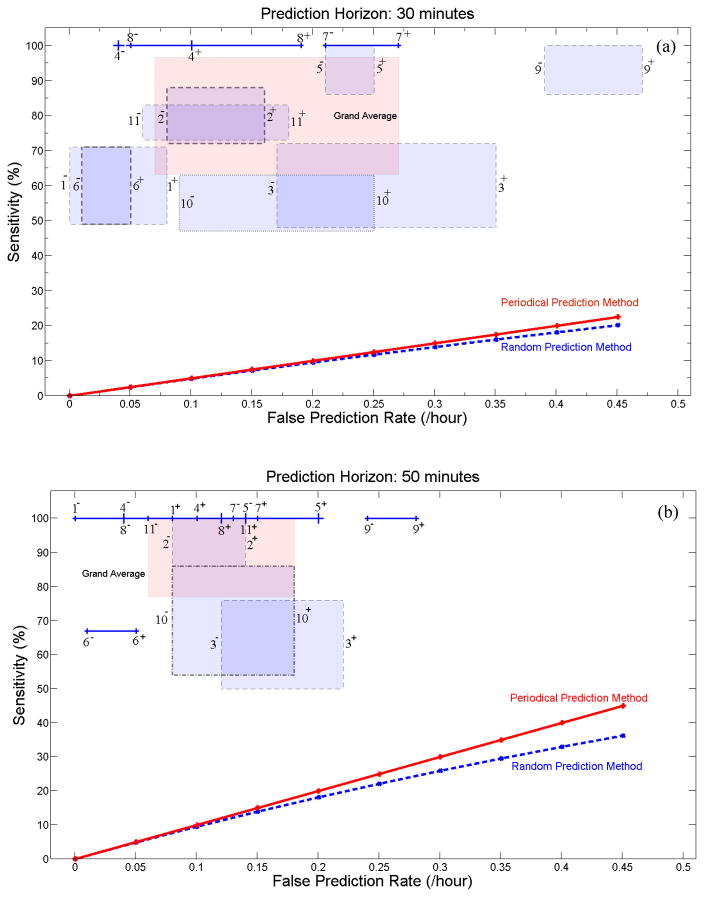
Figs 7a and 7b depict the range of sensitivity variation of the system versus that of the false prediction rate for the seizure occurrence periods of 30 and 50 min for each patient. In both figures, SPH is fixed to 10 sec. These figures were plotted using the results listed in Table 4.

Fig. 7.

Sensitivity versus false prediction rate for each patient (as indicated by patient number seen in Table 1) and for the grand average across patients (labeled in pink as Grand Average) for the seizure occurrence period of (a) 30 and (b) 50 min and SPH=10sec. For each patient, the box or line shows the range of variation of sensitivity versus false prediction rate when different randomly selected reference windows are used. Plus and minus signs used with the patients’ number denote the upper and lower bounds of the corresponding ranges of variation. The performances of the random and periodical prediction methods show values much lower than those found using our system.

3.3. Spatial pattern of nonlinear interdependence

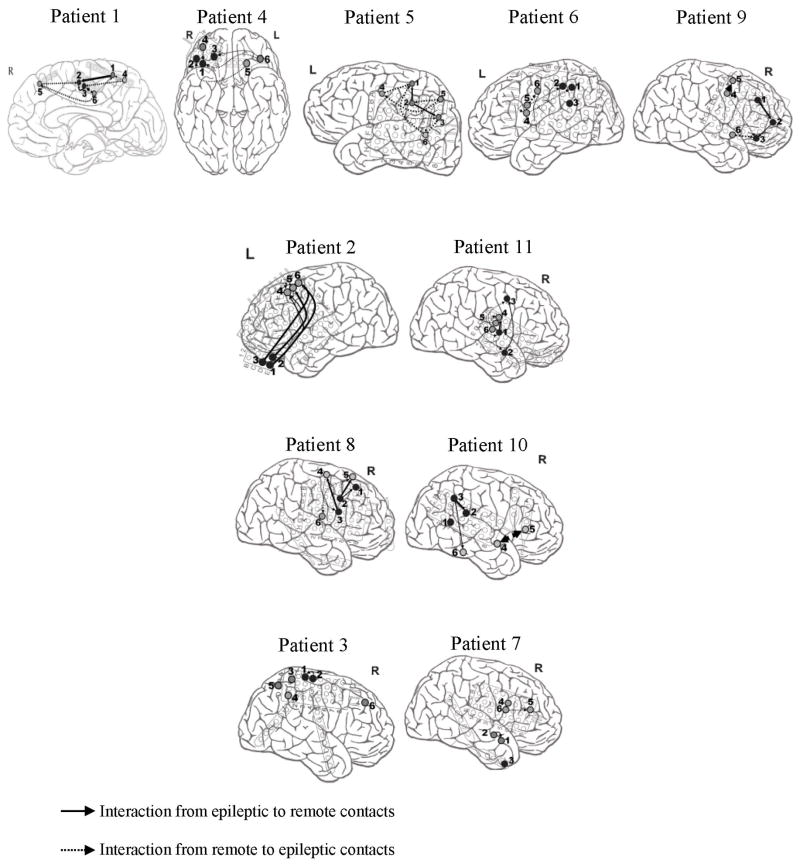
Fig. 8 depicts each patient’s connectivity map between intracranial electrodes within either the epileptogenic zone or remote areas, or between both the epileptogenic zone and remote areas. In this figure, the significant connectivities are illustrated with arrows whose widths indicate the strength of the interactions (Section 2.7). Without indicating the sequence of events over time, the arrows also show the driving-response relationship between epileptic and remote contacts.

Fig. 8.

Connectivity maps characterizing the preictal strength of synchronization and the direction of interaction. The thickness of the arrows reflects the strength of interactions. For the sake of simplicity, we projected all the contacts on the same cross-sectional view. In these maps, numbers 1–3 and 4–6 refer to the electrodes implanted in the epileptogenic zone and remote areas, respectively.

For patients 1, 4, 5, 6, and 9, strong connectivities were observed between epileptic contacts (as driving systems) and remote contacts (as response systems). Conversely in patients 2 and 11, interactions show synchronization between the remote contacts (as driving systems) and the epileptic contacts (as response systems). In patients 8 and 10, strong bidirectional connectivities between the epileptic and remote contacts were observed in the preictal state. As shown, no significant interactions were found between the remote and epileptic contacts in the preictal state for patients 3 and 7.

4. Discussion

In the present study, we have developed a rule-based seizure prediction algorithm, which included extracting univariate and bivariate nonlinear features from iEEG segments, and spatio-temporally integrating these features using the patient-specific rules established from the characteristics of the preictal states. This combinational system helped us to take advantage of the predictability power of individual features and to overcome the shortcomings of certain measures in identifying preictal states. We tested this patient-specific system on blinded long-term iEEG recordings and evaluated it using common performance parameters including sensitivity, specificity, and false prediction rate. Our rule-based seizure prediction system achieved an average sensitivity of 79.9% and 90.2%, an average specificity of 97%, and an average false prediction rate of 0.17/h and 0.11/h, respectively, for seizure occurrence periods of 30 and 50 min and a seizure prediction horizon (SPH) of 10 sec. For most of the patients, the sensitivity of the system showed little dependence on SPH. However, the overall sensitivity of the system decreased when SPH was increased. Our system outperformed the random and periodical prediction methods significantly. This indicates that the spatio-temporal pattern of preictal changes can be captured using univariate and bivariate measures in a patient-specific manner.

4.1. Comparisons to Other Seizure Prediction Methods

To date, considerable attempts have been made to predict epileptic seizures, all with a varying degree of success (see Mormann et al., 2006 and Lehnertz et al., 2003 and the references therein). A few groups have used the FSPEEG database for seizure prediction using nonlinear measures including the correlation dimension (Aschenbrenner-Scheibe et al., 2003), the dynamic similarity index and the mean phase coherence (Schelter et al., 2006), and a phase and a lag synchronization measure (Winterhalder et al., 2006). Maiwald et al. (2004) compared the performance of three different methods including the dynamic similarity index, the accumulated energy, and the effective correlation dimension in a patient-specific way. Table 5 summarizes the performance of different methods in terms of sensitivity and false prediction rate as a function of the seizure occurrence period.

Table 5.

Comparison of the sensitivity statistics of the seizure prediction methods evaluated on iEEG datasets selected from the FSPEEG database.

Authors	Year	Patient-specific	Measure	SOP=30min	SOP=50min
				FPR=0.15/hr	FPR<0.15/hr
Aschenbrenner-Scheibeet al.	2003	Yes	CD	5–25%	8.3–38.3%
Winterhalder et al.,	2003	Yes	DSI	21–42%	32–67%
Maiwaldet al.	2004	Yes	DSI	21–42%	50%
			AE	18–31%	30%
			CD	13–30%	40%
Schelteret al.	2006	No	DSI	82%, for a SOP of 30 min and a FPR of 0.5/h
			MPC
Winterhalderet al.	2006	No	PS	60%	70%
Feldwisch-Drentrup et al.	2010	Yes	MPC (and/or) DSI	35.2% for “OR” combination system 43.2% for “AND” combination system	50% for “OR” combination system 55% for “AND” combination system for SOP of 60 min
Presented system	present	Yes	Combination of five univariate measures and one bivariate measure	79.9%	90.2%

SOP: seizure occurrence period, FPR: false prediction rate. CD: correlation dimension; DSI: dynamical similarity index; AE: accumulated energy; MPC: mean phase coherence; PS: phase synchronization;

In a more recent work, Feldwisch-Drentrup et al. (2010) developed a patient-specific seizure prediction system by combining different seizure prediction algorithms including the mean phase coherence (Mormann et al., 2000) and the dynamic similarity index (Le Van Quyen et al., 1999), for the purpose of improving prediction performances. This group tested two “AND” and the “OR” combinational systems on a database with 182 h of continuous long-term iEEG recordings with an average of 19.1 seizures per patient. For a maximum false prediction rate of 0.15/h, they reported a mean sensitivity of 25% for the individual methods and mean sensitivities of 43.2% and 35.2% respectively for the “AND” and the “OR” combinational systems for a seizure occurrence period of 30 min and a fixed SPH of 10 sec. Our system uses five univariate measures and one bivariate measure, which are combined using a logical “AND” combination rule. Developed under the same concept, our system achieved an average sensitivity of 79.9% with an average false prediction rate of 0.17/h for a seizure occurrence period of 30 min. With FPR_max of 0.11/h,, the sensitivity of the system increased to 90.2% for SOP=50 min and SPH=10 sec.

4.2. Predictability power of univariate and bivariate measures

To date, many groups have investigated the significance of changes in the preictal state with respect to the interictal state through use of univariate nonlinear measures. Such studies have reported significant preictal changes in channels corresponding to the epileptogenic zone (Lehnertzand Elger, 1998; Elger and Lehnertz, 1998; Martinerie et al., 1998; Le Van Quyenet al., 1999; Le Van Quyen et al., 2000; Maiwaldet al., 2004). In a pioneering study in which the correlation dimension was used for seizure prediction, Lehnertz and Elger (1998) reported changes towards low-dimensional system states with a continuous increase in the degree of synchronicity up to 25 min prior to the epileptic seizures from the iEEG of 15 (out of 16) epileptic patients. In the present study, we achieved a sensitivity of 78.8% with a false prediction rate of 0.26/h using the correlation dimension-based seizure prediction system (for SOP= 50 min and SPH=10sec). Only 44.9% of the seizures studied in this paper showed a significant drop in dimension prior to the seizure, while 44.9% showed an increase in the preictal state. Although the ability of the correlation dimension for seizure prediction has been put in doubt by Aschenbrenner-Scheibe et al. (2003) and Harrison et al. (2005), in only 10.2% of the seizures were no significant changes in the values of the correlation dimension observed between the preictal and interictal states. This may be due to the fact that for computing the correlation dimension, we used the method proposed by Yu et al. (2000) which tolerates a certain amount of noise in the dynamics of the system (brain) for estimating the dimension. We also found that in most of the seizures the channels in remote areas showed either stronger preictal changes in dimension or at least the same level as those located in the seizure-onset areas. These findings concur with the findings of other groups (Mormannet al., 2003; D’Alessandro et al., 2003; Mormannet al., 2005; Esteller et al., 2005; Le Van Quyen et al., 2005). At this stage of investigation, we cannot claim with a high certainty that the observed changes in the correlation dimension are reliable evidence of low or high dimensional chaotic states of the brain. Such a conclusion would necessitate a greater analysis using surrogate data. However, this measure can serve as a precursor of ictal activity for epileptic patients, as well as a measure showing the tendency of the epileptic brain progressing from a lower or higher dimensional system, when estimated using the previously mentioned method.

Certain groups have used the largest Lyapunov exponent to represent the degree of chaoticity or unpredictability in the iEEG (Schreiber and Kantz, 1996; Le Van Quyen et al., 2001) for seizure prediction and accordingly, for investigating preictal changes. Iasemidis et al. (2001) showed that the values of the largest Lyapunov exponents of iEEG recorded from electrodes located in the epileptogenic zone converge long before a seizure’s onset. They also observed a significant drop in the values of the largest Lyapunov exponents in the start of seizures at the focal electrode sites. In another study, they used a quadratic optimization technique for the selection of electrodes in the critical brain sites and reported that using the estimated STLmax profiles around a seizure can increase the prediction sensitivity to 91.3% about 91 min prior to the onset of the seizure with one false prediction every 8.27 h (Iasemidis et al., 2005). However, this method was tested in only two patients with 23 seizures. Our largest Lyapunov exponent-based system achieved an average sensitivity of 73.5% with a false prediction rate of 0.21/h for a seizure occurrence period of 50 min across 11 patients. In 51% of the seizures analyzed in this study, a significant preictal drop in the largest Lyapunov exponent values was observed. These findings combined with the positiveness of the values of the largest Lyapunov exponent in the preictal state show that the degree of chaoticity of the iEEG decreases in almost half of the seizures. Yet, in 36.7% of the seizures a significant preictal increase was observed. In the remaining 12.3% of the seizures, no significant changes were observed in the preictal state compared to the interictal state. The changes were observed in electrodes located in both the seizure-onset and remote areas.

In a rather different approach, the Kolmogorov entropy was used by Van Drongelenet al. (2003) for seizure prediction. This method led to a successful seizure prediction in 3 (out of 5) epileptic patients with iEEG recordings. However, no significance analysis was carried out in their study. We used the correlation entropy, a variant of the Kolmogorov entropy, and the Lempel-Ziv complexity for seizure prediction. In 36.7% of the seizures, we found a significant preictal decrease in the values of the Lempel-Ziv complexity, while a significant preictal increase was observed in 44.9% of the seizures. In the remaining 18.4%, no significant changes were observed. Using the correlation entropy, in 36.7%, 49.0% and 14.3% of the seizures, a significant decrease, a significant increase, and no change, respectively, were observed in the values of the preictal state compared to those obtained for the interictal states. Our correlation entropy-based and Lempel-Ziv complexity-based systems achieved an average sensitivity of 61.4% and 68.9%, and an average FPR of 0.23 and 0.24/h, respectively, for a seizure occurrence period of 50 min. The correlation entropy-based system showed a relatively lower sensitivity. This measure also showed high variability prior to the seizures. This may be due to the sensitivity to the segment length and the ergodicity of the signal (Huet al., 2006). Ultimately, from these findings, the Lempel-Ziv complexity showed a better characterization of the iEEG signal.

Bivariate measures have proven to be more appropriate for investigating spatio-temporal dynamics of the brain prior to seizures (Lehnertz et al., 2001; Mormann et al., 2003; Mormann et al., 2005; Le Van Quyen et al., 2005; Iasemidis et al., 2005). Lehnertz et al. (2001) achieved results showing a higher level of interdependence within the primary epileptogenic area and reported a preictal decrease in complexity as measured by the correlation dimension as well as a distinct decrease of interaction between the primary epileptogenic area and remote brain areas. Mormann et al. (2003) also observed a significant decrease in synchronization from several minutes up to a few hours prior to 26 (out of 32) seizures. They observed a drop in synchronization in more distant and even contralateral areas of the brain with an intrahemispheric asymmetry in the spatial dynamics of preictaldesynchronization. In the present study, we obtained a sensitivity of 84.9% with a false prediction rate of 0.26/h (SOP= 50 min). In 81.6% of the seizures analyzed, we observed a significant drop in the nonlinear interdependence values of the preictal state when compared to those obtained in the interictal state. However, in 6.2% of the seizures, a significant preictal increase was observed and in the remaining 12.2% no significant preictal changes were found. These findings are concordant with the findings of Le Van Quyen et al. (2005) who reported that in 36 of the 52 seizures they analyzed, that changes involved both increases and decreases of the synchronization levels, often localized near the primary epileptogenic zone several hours before the seizures. We have also found that the interdependence pattern in each patient’s seizures was almost the same, but the significance level varied from seizure to seizure in a certain range.

In patients 2 and 11, the interactions in the preictal state showed a synchronization in a drive (epileptic contacts) – response (remote contacts) relationship. This may reflect the impact of the epileptic neuronal networks as synchronizers on initiating a seizure. This finding is in agreement with those reported in other studies (Lehnertz and Elger, 1998; Martinerie et al., 1998).

On the contrary, in patients 1, 4, 5, 6 and 9 an inverse relation was observed in the interactions in the preictal state, i.e. the remote areas of the brain behaved as driving systems and the epileptogenic focus as response systems. This may reflect the effect of the nonepileptic brain regions in initiating seizures as described in Mormannet al., (2005).

In patients 8 and 10, connectivities between the epileptic and remote contacts were bidirectional in the preictal state. However, in patients 3 and 7, no significant interactions were found between the remote and epileptic contacts in the preictal state.

4.3. Technical considerations

We have designed a rule-based system from our observations in the preictal state with respect to the reference state. For developing the system, we needed to define and use some thresholds which were tuned using an automatic optimization method in away to achieve maximum sensitivity and specificity, while also being applicable to a sample seizure and 4-hour reference interictal windows for each separate patient. Although the performance of our seizure prediction system depended on the values of the thresholds, in a certain range around the optimal values, the performance showed no changes in obtaining best possible discrimination between interictal and preictal states.

A better sensitivity can usually be obtained at the expense of a decreased specificity. From this point of view, our system showed very good performance. Both of these performance parameters have been investigated in Mormann et al. (2005); however, some investigators have not evaluated the specificity of their methods (Martinerieet al., 1998; Mormann et al., 2006). We also obtained an average FPR of 0.12/h, which is acceptable if the rule-based system is to be considered for clinical use (Maiwaldet al., 2004).

Our analysis has some limitations. First, although the iEEG data analyzed in this study had a high quality, the interictal data were preselected from the patients’ continuous EEG data. This would bias the results due to data preselection by the expert. The channels used in our analysis were also initially preselected from a large pool of channels by the epileptogist. This makes the spatial analysis more difficult, especially when one tries to obtain a detailed connectivity map for the epileptic networks.

We used one sample seizure for each patient to adjust the thresholds and to establish integration algorithms. Using the optimization procedures used in this paper, we found that the performance of the system did not degrade rapidly when thresholds changed slightly around their optimal values.

We hypothesized that the seizures would follow the same behavior in the preictal state for each patient, and the variations in the dynamics of the epileptic networks would differ from patient to patient. Although this was the case for most of patients, it also acts to limit the applicability of the prediction method in patients with different complex seizures. Yet, we believe that the rules can be modified in a way to cover up seizures with different preictal states. In any case, we believe that developing seizure prediction methods needs to be patient-specific.

We randomly selected 4-hour baseline interictal periods in order to reduce the potential bias due to preselection of the reference by visual inspection. We could not find a systematic way accepted by all investigators to select reference data based on predefined criteria including length, and characteristics. However, we found that the performance of the system improved when the reference state was constructed using interictal data randomly selected over different periods of time. Inversely, the performance degraded when the reference state was selected from continuous data in a specific period of time, e.g., from the beginning of the iEEG recordings.

The benefits of our approach in improving seizure prediction performance are multi-fold. First, the method of integrating univariate and bivariate measures assisted the system in including different dynamic aspects of the brain in the search process of preseizure cursors. As we showed, all the features achieved high sensitivities while, interestingly, most of the time they negated false predictions of each other. Second, spatio-temporally integrating the dynamic characteristics exploited from intracranial electrodes in the epileptogenic zones and remote areas in a systematic, rule-based method helped the system to avoid any isolated single-channel seizure precursors, resulting in a reduced false prediction rate. Finally utilizing a sample seizure for establishing rules provided unique signatures for preictal states in a patient-specific way. This also helped the system to include only epochs of iEEG data that resembled the spatio-temporal characteristics of the preictal state.

5. Conclusions

In conclusion, the analysis of dynamic behavior of iEEG prior to seizures has shown that the spatio-temporal pattern of changes in the preictal state is different from that of the reference interictal state in the majority of the seizures analyzed in this study. These patterns contain patient-specific dynamic signatures that can be used for seizure prediction and consequently preictal identification. We also showed that the changes in the dynamics of the epileptic network were not necessarily related to the electrodes located in the epileptogenic zone. High specificity and low time portions under false prediction represented the practical efficiency of the system for seizure prediction. Furthermore, the present results demonstrated the superiority of the system in performance to the random and periodical prediction methods.

Highlights.

• Our rule-based seizure prediction algorithm provided an average sensitivity of >90% and false prediction rate of <0.15/h for a seizure occurrence period of 50 min and a seizure prediction horizon of 10 sec in 11 patients with focal neocortical epilepsy

• Nonlinear analysis of iEEG in the period prior to seizures revealed patient-specific spatio-temporal changes significantly different from those observed within baselines in the majority of the seizures.

• The preictal changes were observed in the electrodes located in the epileptogenic zone as well as in remote areas.