Abstract
Clinical encounters between clinicians and patients begin with an attempt at diagnosis, a foundational element in determining a patient’s ultimate outcome. Diagnosis that is expedient and accurate will result in a treatment that is expedient, appropriate and cost-effective. In essence, evidence-based diagnosis is equally as vital as evidence-based intervention and treatment. If we are committed to making expedient and accurate diagnoses, we must strive to apply diagnostic tests not just for their ease, novelty or availability but for the soundness of evidence behind them.
In the scopes of both aesthetic and reconstructive surgery, advocating evidence driven diagnostic test use is relevant. A pertinent example of how this relates to Plastic Surgery is the United States Food and Drug Administration (FDA) recommendation to screen asymptomatic women with silicone breast implants with MRI 1. For an important recommendation such as this that has tremendous cost implications to patients, sound study design and rigorous evaluation of the accuracy of a MRI as a screening tool has important health policy implications.
We will demonstrate how to determine the accuracy of diagnostic tests and more importantly, we will illustrate the essential qualities of any study to establish the accuracy of a diagnostic test. The United States Food and Drug administration currently recommends screening silicone gel breast implants with magnetic resonance imaging (MRI) 3 years after implantation and then biannually afterwards to diagnose asymptomatic ruptures 1. MRI was recommended because current literature indicates that it has superior accuracy in diagnosing asymptomatic ruptures compared to cheaper imaging modalities 2. However, a recent review of literature found that majority of diagnostic accuracy studies addressing silicone gel breast implant ruptures were done in symptomatic patients 3. MRI performs 14 times better at detecting ruptures in symptomatic patients than asymptomatic patients which means that the reported prevalence of ruptures in these studies is likely higher than what it would be in a sample of asymptomatic patients 3. The implication is that current literature exaggerates the accuracy of MRI in detection of ruptured silicone gel breast implants in asymptomatic patients. Because health policy recommendations like silicone gel implant screening have important implications for patients and society, diagnostic accuracy studies must be properly done to provide unbiased evidence about the efficacy of diagnostic tests.
Keywords: diagnostic accuracy, likelihood ratios, negative predictive value, QUADAS, pretest probability, positive predictive value, posttest probability, precision, reference standard, sensitivity, specificity
DIAGNOSIS AND DIAGNOSTIC ACCURACY STUDIES
Diagnosis is the attempt to classify disease by an established set of criteria using information from patient histories, physical examination, radiographic and laboratory data. In addition to clinical data, a clinician’s experience contributes to the process of diagnosis. For instance, an experienced clinician can draw from years of patient encounters to derive an educated impression that a patient with shortness of breath after a TRAM procedure has pulmonary embolism. But, in addition to his or her experience and clinical signs, the clinician will need diagnostic tests to make this impression more certain before proceeding with treatments that have potential side effects.
Ideally, a diagnostic test should decrease uncertainty about the presence or absence of a clinical condition by altering the pretest probability substantially 4–5. Pretest probability is the probability that a condition is present without input of information from diagnostic tests 6. The prevalence of a clinical condition in the population is commonly used as an estimate of pretest probability 7. Posttest probability is product of pretest probability that has been altered by applying results of diagnostic tests 6,8. This explains why unbiased diagnostic accuracy results are important; to ensure reliable posttest probability estimates.
A diagnostic accuracy study compares a diagnostic test of interest to a reference standard in the same sample of patients. A reference standard is the “gold” standard for diagnosing the condition of interest and ideally can distinguish patients with disease from those without perfectly 9. Hence, the accuracy of a diagnostic test is proportional to its agreement with the reference standard 9. The advent of evidence-based medicine has produced several guidelines from study experts about ways to ensure high quality evidence in various study types. Examples of these guidelines include; Quality of Reporting of Meta-analyses (QUORUM), and the Consolidated Standards of Reporting Trials (CONSORT) statement for randomized control trials 10. The Quality Assessment of Diagnostic Accuracy Studies (QUADAS) 11 provides quality guidelines for diagnostic accuracy studies (Table 1).
Table 1.
Quality Assessment of Studies of Diagnostic Accuracy (QUADAS) guidelines 11 on the three vitals elements of diagnostic accuracy studies: the reference standard, the diagnostic test and the study design
| Guidelines | Biases | |
|---|---|---|
| Reference Standard | Applicability to condition of interest | |
| A universal application of the reference standard | Partial verification bias | |
| A uniform application of the reference standard | Differential verification bias | |
| Independence from the diagnostic test | Incorporation bias | |
| Sufficient detail to permit exact re-do | ||
| Results interpreted blinded to diagnostic test results | Reference standard review bias | |
| Diagnostic Test (Test being studied) | Sufficient detail to permit exact re-do | |
| Results interpreted blinded to reference standard results | Diagnostic test review bias | |
| Study Design/Execution | A representative spectrum of patients | Spectrum bias |
| Outlined selection criteria | ||
| Interval between tests (short: to ensure target condition did not change) | Disease progression bias | |
| Availability of relevant clinical information for diagnosis | Clinical review bias | |
| All results reported; including in-determinable | ||
| Explanation of withdrawals |
OBJECTIVES
Our goal is to illustrate how to evaluate the strength of evidence in diagnostic accuracy studies and secondly to describe statistical analysis and interpretation of diagnostic accuracy study results.
CLINICAL SCENARIO
Let us consider a hypothetical Ms. Jones. She is a 48-years-old woman who presents with a 12 months history of intermittent achy pain over her wrist radiating along her right thumb, index and long finger and distal forearm. She experiences intermittent paresthesias affecting the same fingers that resolve when she shakes her hand. She is frequently awoken from sleep by these symptoms. Sensation in the median nerve distribution of her right hand is normal. Her grip strength is less for the affected hand, but there is no notable thenar wasting. Provocative tests such as Phalen and Hoffman-Tinel tests are negative. Her physician suspects carpal tunnel syndrome (CTS) but her symptoms and physical examination findings are not fully suggestive of CTS. What diagnostic test will we use to confirm her diagnosis? How accurate is our diagnostic test of choice?
DISCUSSION
The diagnosis of CTS is made on clinical grounds 12, however, current recommendations are to obtain a confirmatory test when surgical intervention is being considered 13. Electrodiagnostic studies are the most widely used confirmatory tests for CTS 13, but they can have false positive and false negative findings, depending on the populations used for evaluating the accuracy of the tests 14. This has engendered interest in finding more diagnostically accurate alternatives and sonography is one of the tests of interest 12,15–22. We randomly selected 5 studies evaluating the diagnostic accuracy of sonography as a confirmatory test for CTS to use as illustrative examples (table 2) 15–19. We will apply guidelines from the Quality Assessment of Diagnostic Accuracy Studies (QUADAS) 11 to these 5 selected studies to illustrate how to judge the soundness of evidence in diagnostic accuracy studies.
Table 2.
Characteristics of 5 selected studies on diagnostic accuracy of sonography as a confirmatory test for carpal tunnel syndrome
| Study type | Index test cut off value (median nerve CSA)† | Reference standard (clinical exam diagnosis criteria) | |
|---|---|---|---|
| Kwon et al.15 | Prospective case-control | 10.7 mm2: at carpal tunnel inlet (level of pisiform) | Paraesthesias, pain and Phalen’s test |
| Pastare et al.16 | Prospective case-control | 9.0 mm2: at proximal entry of carpal tunnel | Paraesthesias |
| Altinok et al.17 | Prospective case-control | 9.0 mm2: at the level of pisiform | Pain, numbness, sensory disturbance and Tinel’s or Phalen’s test |
| Kele et al.18 | Prospective case-control | 11 mm2: at proximal edge of carpal tunnel (level of pisiform) | Paraesthesias, decrease in fine touch sensitivity, motor weakness and thenar atrophy |
| El Mediany et al.19 | Prospective case-control | 10.03 mm2: at carpal tunnel inlet | Paraesthesia, pain, swelling, weakness, clumsiness, sensory deficit, thenar atrophy and Phalen’s test |
CSA: cross-sectional area
How do we statistically measure diagnostic accuracy?
Table 3 is a 2 × 2 table typically used to summarize the results of a diagnostic accuracy study comparing a diagnostic test to a reference standard. Positive and negative reference standard results identify patients with and without the condition of interest respectively. True positive (A), false positive (B), false negative (C) and true negative (D) represent diagnostic test results verified against the reference standard. Table 4 shows statistical calculations for examining the results of a diagnostic accuracy study using the parameters displayed in Table 3.
Table 3.
Comparison of reference standard results and diagnostic test results
| Reference standard positive† | Reference standard negative† | |
|---|---|---|
| Diagnostic test positive | True positive results A |
False positive results B |
| Diagnostic test negative | False negative results C |
True negative results D |
Correctness of the diagnostic test result is judged by agreement with the reference standard.
Table 4.
Statistics used in evaluating diagnostic accuracy study results
| Statistic | Definition | Formula † |
|---|---|---|
| Overall accuracy | Proportion of correct test results | (A + D)/(A + B + C + D) |
| Sensitivity | Probability of a positive test result in an individual with the condition | A/(A + C) |
| Specificity | Probability of a negative test result in an individual without the condition | D/(B + D) |
| Positive predictive value | The probability of having the condition when the test result is positive | A/(A + B) |
| Negative predictive value | The probability of not having the condition when the test result is negative | D/(C + D) |
| Positive likelihood ratio | Increase in odds favoring the condition when the test result is positive | Sensitivity/(1−specificity) |
| Negative likelihood ratio | Decrease in odds favoring the condition when the test result is negative | (1−sensitivity)/specificity |
Formulas are based on parameters in table 3
Overall accuracy: what is the percentage of test results that are correct?
Overall accuracy is the percentage of individuals tested who have correct results. It addresses true positives and true negatives but it does not distinguish false positives from false negatives 23. Differentiating false positives from false negatives is clinically important and also necessary for a better diagnostic accuracy determination. Hence, this is not a useful measure of diagnostic accuracy 23.
Sensitivity and Specificity: what is the probability that this test will be correct whether or not the condition is present?
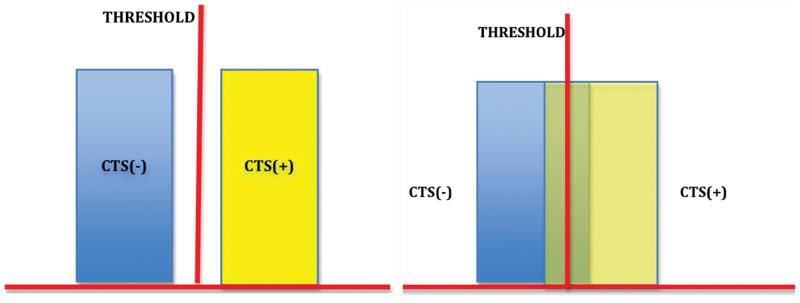
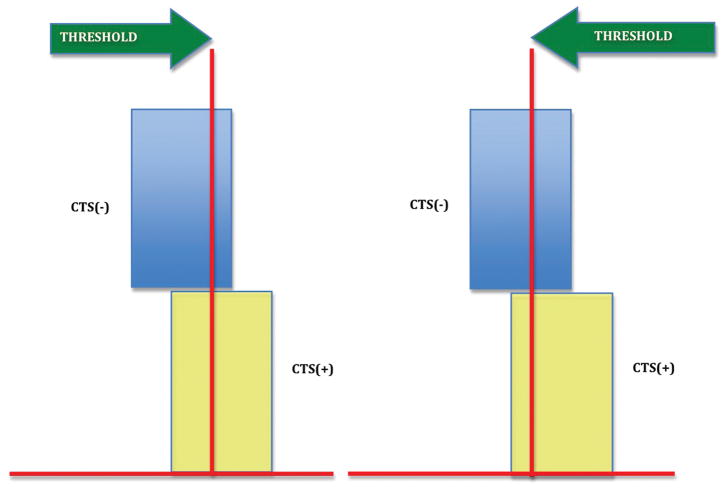
Sensitivity is the proportion of individuals with the condition who have a positive test result and specificity is the proportion of individuals without the condition who have a negative test result23. Sensitivity and specificity directly address the accuracy of a diagnostic test because they infer the probability of correct diagnostic test results 23. They are a direct measure of the performance of the diagnostic test in comparison to the benchmark reference standard. Figures 1a–d demonstrate the relationship between reference standards and diagnostic tests through sensitivity and specificity. The threshold in the figures differentiates a positive from a negative diagnostic test result. In figure 1a, there is no overlap between presence and absence of disease; this is akin to an ideal reference standard and a perfectly accurate diagnostic test with 100% sensitivity and specificity (that is, every patient with the condition tests positive and every patient without tests negative). If however as shown in figure 1b there is overlap of patients with and without disease around the threshold, neither sensitivity nor specificity is 100% hence the test is not perfectly accurate. The overlap region represents the 2 forms of inaccurate results, false positives and false negatives in varying proportions depending on where the threshold is set (figs. 1c and d). The width of the overlap region in fig 1b is inversely proportional to the accuracy of a diagnostic test. That is, the more false positives and false negatives there are, the less accurate the diagnostic test is. In summary, sensitivity and specificity estimate the accuracy of a diagnostic test because they provide more detail about how well it matches a reference standard by distinguishing false negatives, false positives, true positives and true negatives. However, telling us the probability that the test result is correct does not tell us anything about the patient’s probability of having the condition of interest. Sensitivity and specificity answer the question of diagnostic test accuracy but not how test results change a patient’s probability 23,24,25.
Figure 1.
Figure 1a
CTS(−): carpal tunnel syndrome absent
CTS(+): carpal tunnel syndrome present
This schematic shows a test with sensitivity and specificity of 100% respectively. There are no false positive or false negatives. There is a threshold value that perfectly delineates patients with CTS from patients without. This is akin to an ideal reference standard and a perfectly accurate diagnostic test.
Figure 1b
CTS (−): carpal tunnel syndrome is absent
CTS (+): carpal tunnel syndrome is present
This shows a test with values that overlap within a certain range for patients who are CTS (+) and CTS (−). This is imperfect when compared to the test in 1a. Sensitivity and specificity do not equal 1, the test is not perfectly accurate.
The width of the overlap area (false positives and false negatives) is inversely proportional to its accuracy. The narrower the overlap area, the easier it is to find a threshold that can approximate the performance of the reference standard (better accuracy). The converse is true for wider areas of overlap.
Figure 1c
CTS (−): carpal tunnel syndrome is absent
CTS (+): carpal tunnel syndrome is present
Everyone to the right of the threshold is CTS (+).
If the threshold is moved to the right, we eliminate CTS (−) patients (decrease false positives; increase specificity) but we also miss a substantial number of CTS (+) patients (increase false negatives: decrease sensitivity)
If the area of overlap is narrow, the percentage of CTS (−) patients we had in the overlap region was small to begin with and the percentage of CTS (+) patients we miss by moving the threshold right will be small hence, the accuracy of the test will be close to that demonstrated in fig. 1a. If the overlap area is wide, we would have to move the threshold farther right to eliminate most false positives. And as you can see we would also have to sacrifice a larger percentage of our true positives. Compared to fig. 1a, the accuracy would be significantly inferior.
Figure 1d
CTS (−): carpal tunnel syndrome is absent
CTS (+): carpal tunnel syndrome is present Every one to the right of the threshold is CTS (+).
If the threshold is moved to the left, we capture most CTS (+) patients (decrease false negatives; increase sensitivity) but we also capture a substantial number of CTS (−) patients (increase false positives: decrease specificity). The width of overlap area applies here as well. As you can see, the width of the overlap area gives us its sensitivity and specificity values relative to the reference standard.
Likelihood ratios (positive and negative): how much more likely is it that the condition is present or absent?
Likelihood ratios quantify the change in odds favoring the presence of a condition when diagnostic test results are known. A positive likelihood ratio quantifies the increase in odds favoring a condition when the test result is positive and a negative likelihood ratio quantifies the decrease in odds favoring a condition when the test result is negative 23–25. Figure 2 shows the formula used to calculate likelihood ratios. The positive likelihood ratio formula translates to;
Figure 2.
Formulas for the calculation of posttest probability from likelihood ratios.
| (probability of the test being positive in a patient with disease)/(probability of the test being positive in a patient without disease). |
From that formula we can see that the higher the numerator (true positive rate) the more significant the positive likelihood ratio (table 5) 23,25. The negative likelihood ratio formula translates to;
Table 5.
Effect of positive and negative likelihood ratio values on pretest probability†
| Positive likelihood ratio | Negative likelihood ratio | Effect on pretest probability |
|---|---|---|
| > 10 | < 0.1 | Pretest probability almost always convincingly changed |
| 5–10 | 0.1–0.2 | Pretest probability is moderately changed |
| 2–5 | 0.2–0.5 | Change in pretest probability is small but can be useful |
| 1–2 | 0.5–1 | Change in pretest probability is very small and usually not useful |
Adapted from Fritz 23.
| (probability of the test being negative in a patient with disease)/(probability of the test being negative in a patient without disease). |
Here, the larger the denominator (true negative rate), the more significant the negative likelihood ratio (table 5) 23,25. Likelihood ratios are clinically informative because they directionally quantify the change in odds that a patient has a condition of interest 23,25. This change in odds is applied to the pretest probability to obtain a posttest probability that improves the degree of certainty 25.
Consider that Ms. Jones is found to have a median nerve CSA of 10.5 mm 2 by sonography. According to Kele et al.’s 18 criteria displayed on table 2, the test is positive and her positive likelihood ratio is 37 (table 6). If we assume her pretest probability is 0.40 or 40% (table 6) 20, after applying the positive likelihood ratio using the formulas shown in figure 2, the posttest probability is 0.96 or 96%. She went from a baseline 40% probability of having CTS based on her symptoms at presentation to 96% probability after a positive result. Notice table 6 shows that Pastare et al. 16 and El Mediany et al. 19 have positive likelihood ratios of infinity. If we apply their estimates of sonographic accuracy for CTS diagnosis, a positive sonography test for CTS is infinitely accurate and hence never wrong.
Table 6.
Statistical determination of pretest probability revision in 5 selected studies on diagnostic accuracy of sonography as a confirmatory test for carpal tunnel syndrome
| Pretest probability (prevalence)† | Sensitivity | Specificity | Positive likelihood ratio | Negative likelihood ratio | Posttest probability†† | ||
|---|---|---|---|---|---|---|---|
| Kwon et al.22 | 0.40 | 0.66 | 0.63 | 1.78 | 0.54 | 0.54 | 0.27 |
| Pastare et al.23 | 0.40 | 0.62 | 1.0 | Inf* | 0.38 | Inf** | 0.20 |
| Altinok et al.24 | 0.40 | 0.65 | 0.92 | 8.13 | 0.38 | 0.85 | 0.20 |
| Kele et al.25 | 0.40 | 0.74 | 0.98 | 37 | 0.26 | 0.96 | 0.15 |
| El Mediany et al.26 | 0.40 | 0.98 | 1.0 | Inf* | 0.02 | Inf** | 0.01 |
We assumed a pretest probability of 0.40 because estimates from population studies suggest this is the approximate prevalence of CTS amongst patients that present to a primary care setting with the symptoms in the clinical scenario 20
The grayscale column represents posttest probability if the index test is positive and the clear column represents probability of absence of disease if the index test result is negative.
These studies reported specificities of 1. The positive likelihood ratio formula is; sensitivity/1−specificity, if the specificity is 1, the denominator is 0 which = infinity.
Multiplication by infinity = infinity.
Predictive values (positive and negative): if the test result is positive or negative, what is the probability that the condition is present or absent respectively?
Positive and negative predictive values represent the proportion of individuals with diagnostic test results that are correct. Positive predictive value (PPV) represents the proportion of individuals with a correct positive test result and negative predictive value (NPV) represents the proportion of individuals with a correct negative test result 23,25. Compared to sensitivity and specificity, predictive values answer a more clinically relevant question: if a patient’s diagnostic test result is positive or negative, what is the probability that the condition is present or absent respectively? 23 However, the shortcoming of predictive values is their dependence on prevalence of the condition being tested. If prevalence is low, PPV will be low and NPV high, the converse is also true 23,25. Sensitivity and specificity are less sensitive to prevalence hence they are more reliable measures of diagnostic accuracy.
Precision: how confident are we in our estimates of diagnostic accuracy?
Sensitivity, specificity and likelihood ratios derived from a diagnostic accuracy study sample are estimates of values that would be found if the diagnostic test were applied to the general population 23,25. The precision of these estimates is represented in 95% confidence intervals (CI). The CI is a predicted range within which sensitivity, specificity and likelihood ratio values would lie 95% of the time if the diagnostic test were applied to the general population. The narrower the range of values, the more precise the study accuracy estimate, the converse is also true.
How well was the diagnostic accuracy study designed and executed? (Quality assessments of the diagnostic test, the reference standard and study execution using QUADAS 11)
Tables 7a–c show examples of how diagnostic accuracy studies are evaluated using the QUADAS guidelines. A clinically useful diagnostic test is one that can be generalized to an appropriate clinical population 26. The ability to generalize estimates of diagnostic accuracy depends on the spectrum of disease severity represented in the study 27,28. If patients with more severe disease are over-represented in the study, it is easier for a diagnostic test to identify patients with disease than would otherwise be in the general population 4,28. This was illustrated in our example of MRI screening for asymptomatic silicone breast implant ruptures. The accuracy of MRI in detecting asymptomatic ruptures is likely exaggerated because symptomatic patients are over-represented in majority of existing studies creating a spectrum bias 4. By a similar logic, case-control design in a diagnostic accuracy study is problematic because subjects with milder manifestations tend to be left out and this also creates spectrum bias 23,28. Additionally, study design must include blinding test administrators to test results to avoid the bias introduced if knowledge of one set of results influences the interpretation of the other test results 28,29. Knowledge of the reference standard results can and do influence interpretation of the diagnostic test results and vice versa. Lastly, relevant clinical data that are readily available in practice (such as age and sex) can impact the performance of a diagnostic test and should be available when study test results are interpreted 11,28.
Table 7a.
Evaluation of the reference standard in 5 selected studies on the diagnostic accuracy of sonography as a confirmatory test for carpal tunnel syndrome using QUADAS guidelines 11
| Classifies condition | Partial verification bias | Differential verification bias | Incorporation bias | Execution of reference standard†† | Review bias | |
|---|---|---|---|---|---|---|
| Kwon et al. 15 | Y | Y | Y | N/A† | Y | Y |
| Pastare et al. 16 | Y | Y | Y | N/A† | Y | Y |
| Altinok et al. 17 | Y | Y | Y | N/A† | Y | Y |
| Kele et al. 18 | Y | Y | Y | N/A† | U | Y |
| El Mediany et al. 19 | Y | Y | Y | N/A† | Y | Y |
Y: yes (followed guideline)
N: no (did not follow guideline)
U: unclear (insufficient information to determine if guideline was followed)
Incorporation bias is not applicable. This guideline is evaluated if the reference standard is a composite of 2 or more tests, e.g. clinical exam and electrodiagnostic tests for CTS diagnosis 20.
“U” in this column indicates that it was unclear if all details of the reference standard execution were included.
Table 7c.
Evaluation of study design and execution in 5 studies on diagnostic accuracy of sonography as confirmatory test for carpal tunnel syndrome using QUADAS guidelines 11
| Spectrum bias† | Selection criteria | Disease progression bias†† | Clinical review bias | Indeterm.‡ results explained | Withdrawals explained††† | |
|---|---|---|---|---|---|---|
| Kwon et al. 15 | N | Y | U | Y | Y | Y |
| Pastare et al. 16 | N | Y | Y | Y | Y | N |
| Altinok et al. 17 | N | Y | U | Y | Y | Y |
| Kele et al. 18 | N | Y | U | Y | Y | Y |
| El Mediany et al. 19 | N | Y | U | Y | Y | Y |
Y: yes (followed guideline)
N: no (did not follow guideline)
U: unclear (insufficient information to determine if guideline was followed)
Spectrum bias in all studies is due to the case-control design. The recommended study design is a prospective blinded comparison of the diagnostic test and reference standard in consecutive patients 23
“U” in this column indicates that the interval between the diagnostic test and reference standard test was unclear. The interval must be short enough to be reasonably sure that the diagnostic test and reference standard detect the same condition
Abbreviation for indeterminate
“U” in this column indicates that withdrawals from the study were not analyzed for characteristics.
Using an appropriate reference standard is critical because it is the benchmark for evaluating the diagnostic test of interest 9. A reference standard with poor sensitivity and specificity is not a sound benchmark by which to compare a new test to estimate the accuracy of the new test 27,28. Additionally, a reference standard that is not directly relevant to the condition of interest is also not appropriate 27,28. Glycosylated hemoglobin is a good measure of diabetes control but will do poorly as a benchmark for diagnosing lower extremity osteomyelitis in diabetic wounds. When conducting diagnostic accuracy studies in conditions with no sound reference standard, as is the case with CTS 15, investigators may use a composite of diagnostic tests as the reference standard to improve sensitivity and specificity and thus provide a better benchmark 30. For instance, Ziswiler et al. 20 in their study were able to improve sensitivity and specificity of their reference standard by combining electrodiagnostic studies and clinical parameters of CTS instead of using clinical parameters alone. When using a composite reference standard, the diagnostic test should not be a component of the composite reference standard 11,23. The reason is that the agreement between the diagnostic test and the composite reference standard may become exaggerated because both will be influenced by the characteristics of the diagnostic test.
Reference standards are used as a benchmark to verify results of diagnostic tests being studied and hence, the reference standard should be applied uniformly 28,31–32. If the reference standard is not applied to all study subjects, partial verification bias is introduced 28,33–34. When partial verification occurs, it is usually biased in favor of patients with more robust manifestation of the condition of interest who are likely easier to diagnose 4. Asymptomatic patients and those with milder manifestations of the condition of interest are the most likely to be exempted from verification. This can happen if the reference standard is cost-prohibitive, invasive or causes significant discomfort to the patient. The implication is that the estimated accuracy is biased in favor of the diagnostic test. Differential verification bias results from another form of nonuniform reference standard verification 28,33–34. In this case, two different reference standards are used with one having inferior (accuracy) sensitivity and or specificity 23,28. The inferior reference standard is usually the less invasive or less costly option used to verify patients who had negative diagnostic tests. These subjects may have tested negative because the diagnostic test was not sensitive enough to identify them as actually having the condition of interest. Verifying the incorrect diagnostic test results using the inferior reference standard with a comparatively lower sensitivity might in the end not identify them as a false negative. Instead, they will be verified as true negative and that exaggerates the accuracy of the diagnostic test 33–34.
Variations in execution of either diagnostic tests or reference standards have implications for diagnostic accuracy estimates 23. If for instance the measurement of median nerve cross-sectional area is performed with inconsistent application of pressure from the transducer, it calls to question the reliability of individual test results and the estimates of diagnostic accuracy calculated from those results. Hence, it is vital to provide exact details of test administration to ensure it is replicable within the study and in other settings as well 11,23. Additionally, study withdrawals should always be reported because this can be a source of bias if withdrawals skew the sample of subjects in either direction (individuals with or without disease) 11,28,31.
Finally, one might look at table 6 and rightly ask why likelihood ratios and posttest probabilities from studies on the same diagnostic test using the same reference standard differ so widely? Table 2 shows the characteristics of all 5 studies and evidently there are numerous variations amongst them 15–19. For instance, the threshold for a positive median nerve CSA varies from 9 mm 2 to 11 mm 2. The methodological rigor within each study might be sound, as tables 7a–c demonstrate however, pooling data across studies for a systematic review is problematic because the data are not uniformly defined. It is best if investigators of the accuracy of any particular diagnostic test agree on crucial components like selection criteria, representative disease spectrum and so on to ensure consistency of results.
CONCLUSION
Evaluating the evidence in a diagnostic accuracy study is a means to verify that the accuracy claimed was well earned by standardized methods of analyses. The stake is high, because inaccurate diagnostic test accuracy will lead to ill-conceived policy recommendations that affect many patients and could lead to more invasive procedures based on biased data.
Table 7b.
Evaluation of the diagnostic test in 5 selected studies on diagnostic accuracy of sonography as a confirmatory test for carpal tunnel syndrome using QUADAS guidelines 11
| Execution of diagnostic test† | Review bias†† | |
|---|---|---|
| Kwon et al. 15 | Y | Y |
| Pastare et al. 16 | Y | Y |
| Altinok et al. 17 | Y | Y |
| Kele et al. 18 | U | U |
| El Mediany et al. 19 | U | Y |
Y: yes (followed guideline)
N: no (did not follow guideline)
U: unclear (insufficient information to determine if guideline was followed)
“U” in this column indicates that it was unclear if all details of the diagnostic test execution were included
“U” in this column indicates that it was unclear if diagnostic test results were interpreted without knowledge of reference standard results
Acknowledgments
Supported in part by a Midcareer Investigator Award in Patient-Oriented Research (K24AR053120) and 2R01AR047328 - 06A2 from the National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS), and R01AR062066 from NIAMS and the National Institute on Aging (to Dr. Kevin C. Chung).
Footnotes
Disclosures: None of the authors has a financial interest in any of the products, devices, or drugs mentioned in this manuscript.
References
- 1.U.S. Food and Drug Administration. [Assessed September 6, 2011];Medical devices: Silicone-gel filled breast implants. Available at: http://www.fda.gov/MedicalDevices/ProductsandMedicalProcedures/ImplantsandProsthetics/BreastImplants/ucm063871.htm.
- 2.Berg WA, Soo MS, Pennello G. MR imaging of extracapsular silicone from breast implants: Diagnostic pitfalls. AJR Am J Roentgenol. 2002;178:465–472. doi: 10.2214/ajr.178.2.1780465. [DOI] [PubMed] [Google Scholar]
- 3.Song JW, Kim HM, Bellfi LT, Chung KC. The effect of study design biases on the diagnostic accuracy of magnetic resonance imaging for detecting silicone breast implant ruptures: A meta-analysis. Plast Reconstr Surg. 2011;127:1029–1044. doi: 10.1097/PRS.0b013e3182043630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sackett DL. A primer on the precision and accuracy of the clinical examination. JAMA. 1992;267:2638–2644. [PubMed] [Google Scholar]
- 5.Sox HC., Jr Probability theory in the use of diagnostic tests: An introduction to critical study of the literature. Ann Intern Med. 1986;104:60–66. doi: 10.7326/0003-4819-104-1-60. [DOI] [PubMed] [Google Scholar]
- 6.Richardson WS, Wilson MC, Guyatt GH, Cook DJ, Nishikawa J. Users’ guides to the medical literature: XV. How to use an article about disease probability for differential diagnosis. Evidence-Based Medicine Working Group. JAMA. 1999;281:1214–1219. doi: 10.1001/jama.281.13.1214. [DOI] [PubMed] [Google Scholar]
- 7.Bernstein J. Decision analysis. J Bone Joint Surg Am. 1997;79:1404–1414. doi: 10.2106/00004623-199709000-00018. [DOI] [PubMed] [Google Scholar]
- 8.Dujardin B, Van den Ende J, Van Gompel A, Unger JP, Van der Stuyft Likelihood ratios: A real improvement for clinical decision making? Eur J Epidemiol. 1994;10:29–36. doi: 10.1007/BF01717448. [DOI] [PubMed] [Google Scholar]
- 9.Jaeschke RZ, Meade MO, Guyatt GH, Keenan SP, Cook DJ. How to use diagnostic test articles in the intensive care unit: Diagnosing weanability using f/Vt. Crit Care Med. 1997;25:1514–1521. doi: 10.1097/00003246-199709000-00018. [DOI] [PubMed] [Google Scholar]
- 10.Bent S, Shijania KG, Saint S. The use of systematic reviews and meta-analyses in infection control and hospital epidemiology. Am J Infection Cont. 2004;32:246–254. doi: 10.1016/j.ajic.2003.10.004. [DOI] [PubMed] [Google Scholar]
- 11.Whiting P, Rutjes AW, Reitsma JB, Bossuyt PM, Kleijnen J. The development of QUADAS: A tool for the quality assessment of studies of diagnostic accuracy included in systematic reviews. BMC Med Res Methodol. 2003;3:25. doi: 10.1186/1471-2288-3-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pinilla I, Martín-Hervás C, Sordo G, Santiago S. The usefulness of ultrasonography in the diagnosis of carpal tunnel syndrome. J Hand Surg Eur Vol. 2008;33:435–439. doi: 10.1177/1753193408090396. [DOI] [PubMed] [Google Scholar]
- 13.Keith MW, Masear V, Chung KC, et al. American Academy of Orthopaedic Surgeons clinical practice guideline on diagnosis of carpal tunnel syndrome. J Bone Joint Surg Am. 2009;91:2478–2479. doi: 10.2106/JBJS.I.00643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jablecki CK, Andary MT, Floeter MK, et al. American Association of Electrodiagnostic Medicine; American Academy of Neurology; American Academy of Physical Medicine and Rehabilitation. Practice parameter: Electrodiagnostic studies in carpal tunnel syndrome report of the American Association of Electrodiagnostic Medicine, American Academy of Neurology, and the American Academy of Physical Medicine and Rehabilitation. Neurology. 2002;58:1589–1592. doi: 10.1212/wnl.58.11.1589. [DOI] [PubMed] [Google Scholar]
- 15.Kwon BC, Jung KI, Baek GH. Comparison of sonography and electrodiagnostic testing in the diagnosis of carpal tunnel syndrome. J Hand Surg Am. 2008;33:65–71. doi: 10.1016/j.jhsa.2007.10.014. [DOI] [PubMed] [Google Scholar]
- 16.Pastare D, Therimadasamy AK, Lee E, Wilder-Smith EP. Sonography versus nerve conduction studies in patients referred with a clinical diagnosis of carpal tunnel syndrome. J Clin Ultrasound. 2009;37:389–393. doi: 10.1002/jcu.20601. [DOI] [PubMed] [Google Scholar]
- 17.Altinok T, Baysal O, Karakas HM, et al. Ultrasonographic assessment of mild and moderate idiopathic carpal tunnel syndrome. Clin Radiol. 2004;59:916–925. doi: 10.1016/j.crad.2004.03.019. [DOI] [PubMed] [Google Scholar]
- 18.Kele H, Verheggen R, Bittermann HJ, Reimers CD. The potential value of ultrasonography in the evaluation of carpal tunnel syndrome. Neurology. 2003;61:389–391. doi: 10.1212/01.wnl.0000073101.04845.22. [DOI] [PubMed] [Google Scholar]
- 19.El Miedany YM, Aty SA, Ashour S. Ultrasonography versus nerve conduction study in patients with carpal tunnel syndrome: Substantive or complementary tests? Rheumatology (Oxford) 2004;43:887–895. doi: 10.1093/rheumatology/keh190. [DOI] [PubMed] [Google Scholar]
- 20.Ziswiler HR, Reichenbach S, Vogelin E, Bachmann LM, Villiger PM, Juni P. Diagnostic value of sonography in patients with suspected carpal tunnel syndrome: A prospective study. Arthritis Rheum. 2005;52:304–311. doi: 10.1002/art.20723. [DOI] [PubMed] [Google Scholar]
- 21.Buchberger W, Judmaier W, Birbamer G, Lener M, Schmidauer C. Carpal tunnel syndrome: Diagnosis with high-resolution sonography. AJR Am J Roentgenol. 1992;159:793–798. doi: 10.2214/ajr.159.4.1529845. [DOI] [PubMed] [Google Scholar]
- 22.Hammer HB, Haavardsholm EA, Kvien TK. Ultrasonography shows increased cross-sectional area of the median nerve in patients with arthritis and carpal tunnel syndrome. Rheumatology (Oxford) 2006;45:584–588. doi: 10.1093/rheumatology/kei218. [DOI] [PubMed] [Google Scholar]
- 23.Fritz JM, Wainner RS. Examining diagnostic tests: An evidence based perspective. Phys Ther. 2001;81:1546–1564. doi: 10.1093/ptj/81.9.1546. [DOI] [PubMed] [Google Scholar]
- 24.Hawkins RC. The evidence based medicine approach to diagnostic testing: Practicalities and limitations. Clin Biochem Rev. 2005;26:7–18. [PMC free article] [PubMed] [Google Scholar]
- 25.Simel DL, Samsa GP, Matchar DB. Likelihood ratios with confidence: Sample size estimation for diagnostic test results. J Clin Epidemiol. 1991;44:763–770. doi: 10.1016/0895-4356(91)90128-v. [DOI] [PubMed] [Google Scholar]
- 26.Reid MC, Lachs MS, Feinstein AR. Use of methodological standards in diagnostic test research: Getting better but still not good. JAMA. 1995;274:645–651. [PubMed] [Google Scholar]
- 27.Jaeschke R, Guyatt G, Sackett DL. Users’ guides to the medical literature, III: how to use an article about a diagnostic test, A: Are the results of the study valid? JAMA. 1994;271:389–391. doi: 10.1001/jama.271.5.389. [DOI] [PubMed] [Google Scholar]
- 28.Begg CB. Biases in the assessment of diagnostic tests. Stat Med. 1987;6:411–423. doi: 10.1002/sim.4780060402. [DOI] [PubMed] [Google Scholar]
- 29.Greenhalgh T. How to read a paper: Papers that report diagnostic or screening tests. BMJ. 1997;315:540–543. doi: 10.1136/bmj.315.7107.540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Alonzo TA, Pepe MS. Using a combination of reference tests to assess the accuracy of a new diagnostic test. Stat Med. 1999;18:2987–3003. doi: 10.1002/(sici)1097-0258(19991130)18:22<2987::aid-sim205>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 31.Lijmer JG, Mol BW, Heisterkamp S, et al. Empirical evidence of design-related bias in studies of diagnostic tests. JAMA. 1999;282:1061–1066. doi: 10.1001/jama.282.11.1061. [DOI] [PubMed] [Google Scholar]
- 32.Mulrow CD, Linn WD, Gaul MK, Pugh JA. Assessing quality of diagnostic test evaluation. J Gen Intern Med. 1989;4:288–295. doi: 10.1007/BF02597398. [DOI] [PubMed] [Google Scholar]
- 33.Panzer RJ, Suchman AL, Griner PF. Workup bias in prediction research. Med Decis Making. 1987;7:115–119. doi: 10.1177/0272989X8700700209. [DOI] [PubMed] [Google Scholar]
- 34.Irwig L, Tosteson ANA, Gatsonis C, et al. Guidelines for meta-analyses evaluating diagnostic tests. Ann Intern Med. 1994;120:667–676. doi: 10.7326/0003-4819-120-8-199404150-00008. [DOI] [PubMed] [Google Scholar]