Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 May 29;2:429. doi: 10.1038/srep00429

Computer-assisted and fractal-based morphometric assessment of microvascularity in histological specimens of gliomas

Antonio Di Ieva 1,2,a, Emiliano Bruner 3, Georg Widhalm 4, Georgi Minchev 4, Manfred Tschabitscher 5, Fabio Grizzi 6
PMCID: PMC3361706  PMID: 22645645

Abstract

Fractal analysis is widely applied to investigate the vascular system in physiological as well as pathological states. We propose and examine a computer-aided and fractal-based image analysis technique to quantify the microvascularity in histological specimens of WHO grade II and III gliomas. A computer-aided and fractal-based analysis was used to describe the microvessels and to quantify their geometrical complexity in histological specimens collected from 17 patients. The statistical analysis showed that the fractal-based indexes are the most discriminant parameters to describe the microvessels. The computer-aided quantitative analysis also showed that grade III gliomas are generally more vascularized than grade II gliomas. The fractal parameters are reliable quantitative indicators of the neoplastic microvasculature, making them potential surrogate biomarkers. The qualitative evaluation currently performed by the neuropathologist can be combined with the computer-assisted quantitative analysis of the microvascularity to improve the diagnosis and optimize the treatment of patients with brain cancer.

Since Brem et al. introduced the idea to quantify the neoplastic microvasculature in histological specimens in 19721, several investigators have studied the microvascular spatial pattern as a biomarker to predict the patient prognosis and response to anti-angiogenic drugs2,3,4. However, there are no still available methods that have been validated for routine use in clinical practice5. The histopathological diagnosis and grading of brain tumors have important implications in designing improved therapeutic strategies. Notwithstanding the existence of advanced genetic, biochemical, radiologic and nuclear imaging tools, the gold standard for typing and grading brain tumors is the evaluation of histological specimens performed by the neuropathologist. However, the assignment of a glioma to a specific grade can be challenging, particularly in grade II versus grade III gliomas, according to the World Health Organization (WHO) classification system6. The inter-observer variability and the erroneous perception of the tumor histology can results in a patient being over- or under-treated7. Therefore, additional criteria and appropriate tools are required in tumor grading.

Morphometrics is an integrative tool to study the microvasculature of brain tumors. Computer-assisted image analysis can improve the analyses of histological entities by generating continuous variables that can be used for statistical comparisons. An index of the microvascularity should be: a) capable of quantitatively describing what the human eye visually observes and describes under the microscope in qualitative terms or by a semi-quantitative score; b) objective, i.e., not affected by intra- and/or inter-observer variability, and c) clinically meaningful, i.e., having potential prognostic and/or predictive value. The last point cannot prescind from the other two points, because no method can be translated into clinical application without validation and standardization of the methodology.

Fractal geometry8 has been accepted as a valid approach in the field of quantitative microscopy and histopathology9,10,11,12,13. As “Fractals are an attractive framework to try and resolve a variety of problems involving the assessment of structural complexity and irregularity”11, fractal-based analysis has been increasingly used to investigate the vascular system in physiological as well as pathological states5.

As microvascularity has been shown as an alternative feature for differentiating astrocytic cancers of different grades3,14,15,16,17, we explored a computer-assisted and fractal-based approach to objectively quantify the histological microvascular pattern configuration to establish a method that can be translated into clinical practice to appropriately describe and categorize gliomas.

Results

We characterized the microvascularity of WHO grade II (diffuse) and III (anaplastic) gliomas by means of a set of morphological variables summarized in Table 1 that were automatically obtained using a computer-assisted image analysis system (for the explanation of each variable, see Methods). The morphometric variables were compared to: a) the semi-quantitative scores assigned by the neuropathologist to categorize the microvasculature patterns (“angioscore”); and b) the histological grade of the tumor (grade II, diffuse, versus grade III, anaplastic, according to the WHO classification). In addition, a proliferation index expressed as the percent of Ki-67/MIB-1-immunopositive tumor cells was estimated as an independent parameter to compare between the groups.

Table 1. Morphometric parameters used to quantify the microvascular pattern identified in histological specimens of grade II and III gliomas.

Angioarchitectural Morphometric Parameters
ATum Area covered by the specimen of brain tumor on the histological section
TVA Total Vascular Area, the area of the microvessels of the whole specimen
A% Ratio between TVA and ATum
MVs/mm2 Microvascular density expressed as the mean number of microvessels per mm2
Hot-Spot 1 mm2-area of the specimen having the highest local A(%)
local A(%) The % vascular area in the hot-spot
mvFD Microvascular Fractal Dimension: monofractal dimension of the microvascular pattern of the whole specimen (scaling window: εmin = 50 µm; εmax = 2 mm)
loc mvFD Local mvFD: monofractal dimension of the microvascular pattern expressed in the hot-spot area (scaling window: εmin = 1 micron; εmax = 100 micron)
loc bcD Local Box-Counting Dimension: value of fractal dimension estimated by the box-counting method in a non-monofractal range (scaling window: εmin = 1 micron; εmax = 1000 micron)
Open in a new tab

Correlations and covariation structure

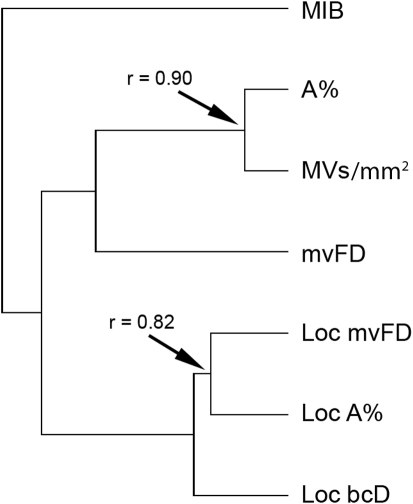
The correlation matrix (Table 2) and cluster analysis of the values (Figure 1) showed scarce relationships among some of the variables, suggesting multifactorial components associated with these metrics. One group of variables was formed by the local percent covering surface (loc A%), microvascular fractal dimension (mvFD), and local box-counting dimension (loc bcD) and displayed high correlation coefficients (r = 0.75−0.82). A second group was formed by loc A% and the density of microvessels expressed as the mean number of microvessels per mm2 (MVs/mm2) and showed the highest value of correlation in the matrix (r = 0.90). The mvFD showed very small correlation with the first group of variables (r = 0.22−0.29) and moderate correlation with the second (r = 0.54−0.56). Similarly, tumor proliferation showed very low correlation with the first group and mvFD (r = 0.21−0.27) and moderate correlation with the second (r = 0.49−0.53).

Table 2. Correlation matrix of the values (mvFD: Microvascular Fractal Dimension; Loc mvFD: Local mvFD; Loc A%: The % vascular area in the hot-spot; Loc bcD: Local box-counting dimension; A%: Ratio between the Total Vascular Area and the area covered by the specimen of brain tumor on the histological section (TVA/ATum); MVs/mm2: Microvascular density expressed as the mean number of microvessels per mm2; MIB-1: antibody against Ki-67 (a protein expressed in proliferating cells).

  mvFD Loc mvFD Loc A% Loc bcD A% MVs
mvFD            
Loc mvFD 0.22          
Loc A% 0.29 0.82        
Loc bcD 0.23 0.81 0.75      
A% 0.56 0.59 0.71 0.55    
MVs/mm2 0.54 0.36 0.52 0.34 0.90  
MIB-1 0.21 0.22 0.27 0.27 0.49 0.53
Open in a new tab

(in bold, values with p < 0.05).

Figure 1. Hierarchical clustering of the angiomorphometric parameters by means of the un-weighted pair group method with arithmetic mean (UPGMA), according to their correlation coefficients (co-phenetic correlation coefficient for the whole set: 0.81).

Figure 1

Open in a new tab

Variables are clustered according to their degree of correlation. The coefficients of correlation for the most correlated variables are shown as indicative references. (For the list of abbreviations, see Table 1).

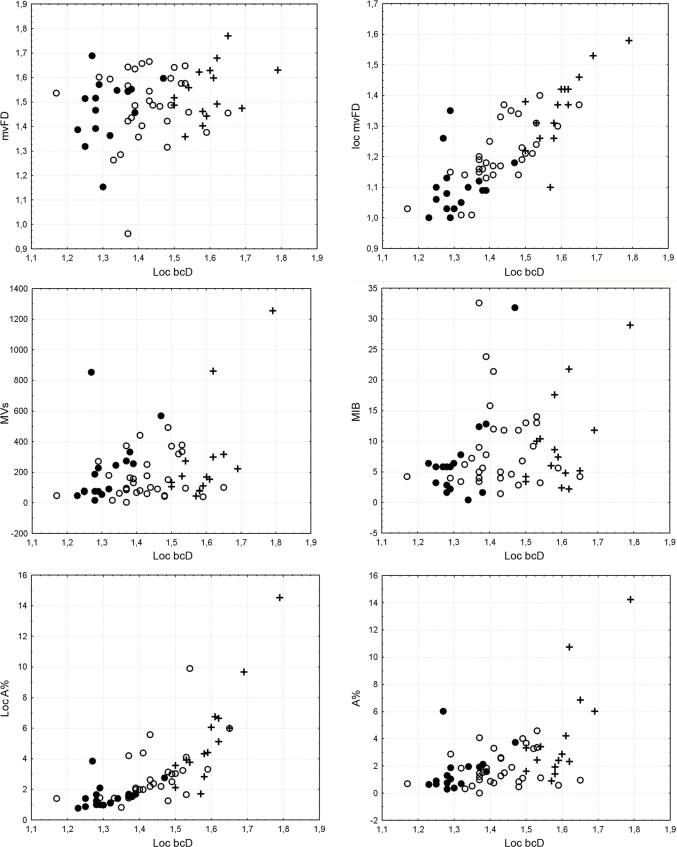
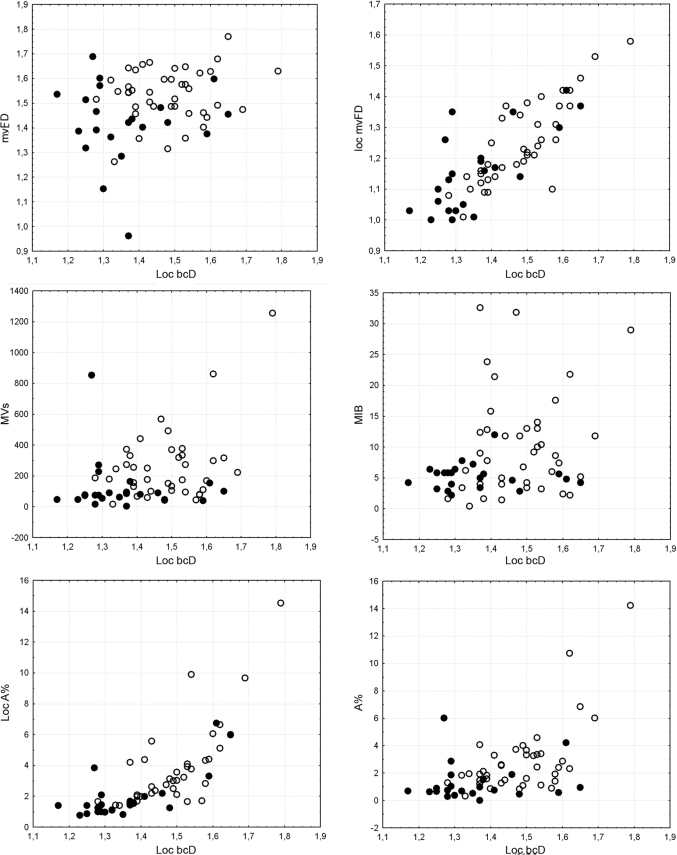
Bivariate plots showed the relationships between loc bcD and the other variables according to the microvascular patterns (Figure 2) and histological grade (Figure 3). The correlation with mvFD was very low, while the relationship with loc mvFD and loc A% was tighter, even if it was non-linear in the latter case. The relationships with loc A%, MVs/mm2, and MIB were almost absent, and spurious minor correlations were probably caused by dispersion of the values and outliers at the higher values of the range. Taking into account the distribution of microvascular patterns and histological grade, it was apparent that the increase in the dispersion of values was associated with an increase in pathological conditions (microvascular pattern 0 and 1 and most of all histological grade II). Thus, the most advanced gliomas departed from a homogeneous situation, which increased the dispersion of the values without fixed patterns in association with a high loc bcD value.

Figure 2. Bivariate plots showing the relationships between loc bcD and the other variables, according to the microvascular pattern (black circle, angioscore 0; white circle, angioscore 1; cross, angioscore 2).

Figure 2

Open in a new tab

Figure 3. Bivariate plots showing the relationships between loc bcD and the other variables, according to the histological grade (black circle, grade II tumors, according to the WHO classification system; white circle, grade III tumors).

Figure 3

Open in a new tab

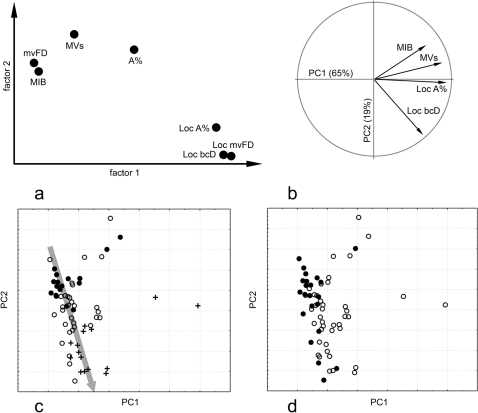
A factor analysis on the whole set of variables with varimax rotation (Figure 4a) further demonstrated the structure of variation, with the first axis associated with an increase in mvFD, loc bcD, and loc A% and the second axis associated with an increase in MVs/mm2, loc A%, mvFD, and MIB, respectively (in decreasing order of relevance). The principal component analysis was computed on a subset of the variables (loc bcD, loc A%, MVs/mm2, and MIB) using only loc bcD as the morphometric value to demonstrate the role of this component in the overall variation (Figure 4b). The multivariate space was largely polarized along the first principal component and explained 65% of the total variance. This component was associated with an increase in all of the variables at the same time (most of all loc A% and MVs/mm2). In contrast, the second component explained 19% of the variance and was associated with an increase in MIB (and a minor increase in the MVs/mm2) and a decrease in loc bcD. Plotting these two components together (thus considering 84% of the whole variation) and demonstrating microvascular patterns (Figure 4c) and the histological grade (Figure 4d), it could be easily recognized that in the first case, specimens were disposed along a trajectory of increasing loc bcD and increasing severity of the pathological malignancy (Figure 5). Few gliomas departing (orthogonally) from this homogeneous trajectory generated most of the dispersion along the first axis independently from the pathological assignment but always because of excess of values (MIB, MVs/mm2, loc A%) and never by defect. In sum, apart from a few specimens that were characterized by extreme values, the rest of the sample continued along a homogeneous trajectory of increasing expression of the pathological indexes and increasing loc bcD.

Figure 4.

Figure 4

Open in a new tab

(a) Factor analysis with varimax rotation of the axes on all of the variables (the loadings for each of the variables are plotted on the first and second factors). (b) Principal component (PC) analysis on the subset using only loc bcD as a geometric variable (vectors show the contribution of each variables along the first and second components). Sample distribution according to the microvascular pattern (c) and histological grade (d) is shown on the same PC1-PC2 subspace, with the large arrow showing a general trajectory of increasing pathological conditions (symbols as in figures 3 and 4, respectively).

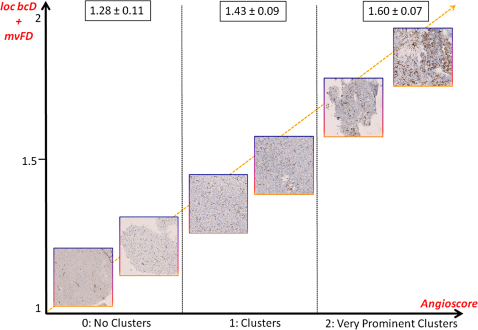
Figure 5. Correlation between the fractal angiomorphometric parameters and the level of clustering of the microvessels.

Figure 5

Open in a new tab

Schema showing the correlation between the angioscore assigned by the neuropathologist to each specimen and the fractal-based variables [local box-counting dimension (loc bcD) and microvascular Fractal Dimension (mvFD)]. The value reported for each angio-architectural group is the mean value of loc bcD ± standard deviation. The yellow line indicates the increasing grade of malignancy of the tumor. The fractal parameters assigned nearly 75% of the gliomas to the correct histological grade and angioscore.

Discriminant analysis

Table 3 summarizes the main results combining different factors for the discriminant analysis, which measured the percentage of gliomas correctly assigned to the pathologist's scores with each combination of variables. Figure 6 shows non-parametric boxplots (median, interquartile, and range) for the variables involved, according to the pathological scoring.

Table 3. Percentage of cases correctly classified using different combinations of morphometric variables after Discriminant Analysis.

Microvascular pattern %
Loc A% 52
Loc mvFD 62
Loc bcD 73
Loc bcD+MVs/mm2+A% 86
Open in a new tab

Figure 6. Box plots showing differences between the microvascular (upper row) and histological (lower row) classes for loc bcD, mvFD, and MIB-1 (median, interquartile, range; outliers are excluded).

Figure 6

Open in a new tab

A, angioscore; G, histological grade.

Microvascular patterns

A Kruskal-Wallis test demonstrated significant differences among three microvascular patterns for loc bcD (p < 0.0001) but not for MIB (p = 0.38) or mvFD (p = 0.47). Loc bcD alone correctly classified 73% of the specimens. Classifications with loc A% or mvFD were significant (p < 0.001) but scarcely effective (52% and 62%, respectively). Discriminant analyses with MIB or mvFD were not significant. The best classification (86%) was obtained by integrating loc bcD, loc A%, and MVs/mm2. Other combinations did not increase the percentage of correct matching between the discriminant values and the pathological assignment.

Histological grade

A Mann-Whitney test showed significant differences between histological grade II and III for loc bcD (p < 0.0001) but also for MIB (p = 0.0143) and mvFD (p = 0.0028); mvFD correctly classified 71% of the specimens (p < 0.0018). Classifications with loc A% and loc mvFD were significant (p < 0.01) but scarcely effective (62% each). Loc A% and MVs/mm2 did not add efficiency to the classifications. Loc bcD and MIB correctly classified 70% and 67% of the specimens, respectively. Together, these two variables achieved a percentage of 73% of correct classifications. By integrating loc bcD and mvFD, 75% of the specimens correctly matched the pathological scoring; other combinations did not increase this percentage.

Discussion

The predictive role of the WHO grading system for defining the outcome of patients with brain tumors and their response to therapy6 claims additional indexes for the assignment of the most appropriate grade to a tumor.

It is well known that a peculiar vascular network supports the development and evolution of brain tumors18,19, and as the vascularity can be detected in histological specimens by immunohistochemistry, this indication has been proposed as a histopathological biomarker for grading the tumor and as a potential prognostic factor. The lack of objective and validated quantitative parameters has, however, led the actual histopathological classifications that ignore the microvascular assessment to differentiate grade II from grade III gliomas. The WHO classification system defines the low-grade (grade II) diffuse astrocytoma as characterized by a high degree of cellular differentiation, slow growth, cellularity moderately increased and occasional nuclear atypia, with not mitotic activity, while distinct nuclear atypia, increased cellularity and significant proliferative activity characterize the anaplastic astrocytoma (grade III)6. Necrosis and/or microvascular proliferation are considered peculiar features for grade IV brain tumors6.

In recent years, computer-assisted fractal-based analysis has been proposed as a valid tool to quantify irregularly shaped objects, including microvascularity5. The most applied fractal index in biomedicine is the so-called fractal dimension, which estimates the space-filling properties of an irregular object9,20. This index is usually obtained using the box-counting algorithm that determines the minimum number of differently sized boxes necessary to entirely cover the object10,21. If the concept of self-similarity is applicable to mathematical fractals in which the level of geometrical complexity is retained at each magnification, natural forms retain a constant level of complexity in a limited range of scales, i.e. “scaling window”, that normally range in two to three orders of magnitude12,22,23,24. Microvascularity, similar to other natural fractals, are random fractals, which mean that they are characterized by a statistical, non-geometrical self-similarity.

A number of methods have been proposed to quantify the geometrical complexity of entities showing “non-ideal” fractal behavior24,25. The mvFD quantifies the space-filling properties of the microvasculature. The higher the value of mvFD (with a value ranging between 0 and 2 in the two-dimensional plane), the higher the geometrical complexity shown by the microvessels, i.e., they fill more of the surrounding tissue in which they are embedded.

Here, we carry out a computer-assisted quantification of microvascularity using a set of Euclidean parameters, including the vascular area and the mean density of microvessels, and fractal indexes, i.e., mvFD, local mvFD and local bcD, and show that a combination of different morphometric variables correctly graded 75% of the analyzed gliomas.

A critical consideration of the employed method is that the mvFD of the whole histological section was not always specifically related to a particular configuration of the microvasculature because it represented all co-existing vascular patterns as a whole, as already shown in specimens of glioblastoma multiforme26. This could underestimate the correlation of the morphometric parameter with the evaluation performed by the neuropathologist. To overcome this limitation, assuming that a tissue specimen is randomly sampled, we considered as fundamental the choice of a “hot-spot”, which was classified as a surface area “statistically representative” of the whole tumor. To avoid the high variability underlying the MVD (microvessel density)27 according to the described methods28,29, we standardized an automatic computer-aided procedure to extract a square box 1 mm to a side that had the highest microvascular immunoreactive surface (Figure 7). We analyzed several scaling windows and found a monofractal behavior of the microvasculature on a scale of magnitude ranging from 1 to 100 micron. However, to include in the evaluation the cluster of microvessels with a superior order of magnitude, we extended the analysis to the scaling window that ranged between 1 and 1000 micron. The curve obtained in the log-log graph did not show typical monofractal behavior. Even if we considered different approaches to evaluate the nonlinearity of log-log relations (i.e., multifractal functions, Hill's plots; for review, see Landini, 2011)11, for simplicity we estimated the slope of the straight line interpolating the points and considered it as a statistical mean value that expressed the space-filling properties of the microvessels. This value was indicated as the local box-counting dimension (local bcD) that, even if intrinsically approximate from the mathematical point of view, it was considered a reliable parameter to quantify the main geometrical characteristic (space-filling properties) of the microvessels in a representative area (hot-spot) of the tumor area. Considering all of the analyzed variables, the local bcD was found to be the most robust index to discriminate the microvascular configuration. These data suggest that this parameter was significantly correlated to the angiostructures showed by the tumor; gliomas showing higher degrees of vascularization and vessel clusterization had a higher value of loc bcD, as represented in Figure 5. Exploring the variables in a multivariate analysis, a higher level of discrimination (86%) was found using a set of morphometric indexes that included the loc bcD, MVs/mm2 and local vascular A%. A less discriminative combination of variables to identify the degree of vascularization was offered by the set that included MIB, MVs/mm2 and the local vascular A%. Conversely, when the single variables were compared to the grade, the microvascular mvFD of the whole specimen was found equally discriminative to the local bcD (70%), meaning that the monofractal value of the microvasculature shown on the whole specimen is well-correlated to the grade. Anaplastic tumors show higher values of mvFD, loc mvFD and loc bcD. Considering only a single variable, anaplastic gliomas have higher values of loc bcD than grade II gliomas. The combination of two fractal indexes in the multivariate analysis, the mvFD and the loc bcD, can assign the glioma to the correct histological grade in 75% of the cases; the addition of the MIB value does not improve the discrimination.

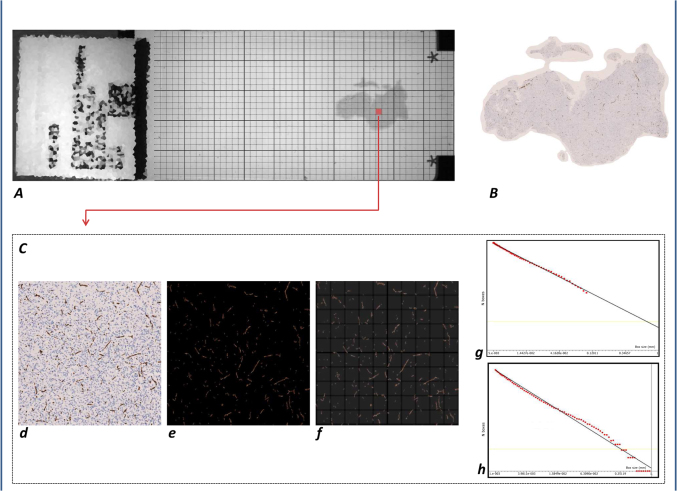
Figure 7. Computer-aided technique for fractal analysis of the microvasculature in histological specimens.

Figure 7

Open in a new tab

Estimation of the morphometric fractal parameter in the whole section and in the hot-spot region of specimens of brain gliomas; detection of microvessels using antibodies raised against CD34. The extraction of the whole specimen and the segmentation of the immunoreactive vessels (A) and (B) allow the automatic measurement of the morphometric parameters listed in Table 1. Moreover, a grid of boxes measuring 1 mm to a side length is superimposed on the whole histological section. For each box, the ratio between the local vascular area and the local neoplastic area was calculated [local A(%)]; the box with the highest local A(%) was automatically selected and extracted to be used as the “hot-spot” representative of the whole specimen (C). (d) Hot-spot of the specimen, automatically extracted. (e) Selection of the RGB threshold to automatically extract the CD34+ vessels. (f) Box-counting method: superimposition on the image of grids with boxes of different lengths, from a minimum size (εmin) to a maximum size (εmax), in the preselected scaling window. (g) A monofractal behavior was found by limiting the scaling window to a range of two orders of magnitude (εmin = 1 µm − εmax = 100 µm). The slope of the obtained curve is the microvascular fractal dimension (mvFD) [Axes of the log-log graph (box-counting method): X-axis = Box size (mm); Y-axis = N Boxes]. (h) Considering that a maximum size of the box of 100 µm does not cover the complete hot-spot, not considering the clusters of distant microvessels (the relationships of the microvessels located in the upper right corner of the specimen with the ones located in the lower left corner, for example), a wider scaling window was also applied.

It is obvious that a histological specimen has intrinsic limitations related to its sampling variability and its bi-dimensionality, which could not reflect the real three-dimensional microvascular architecture of the tumor. However, histopathological evaluation is still a standard method of diagnosis in clinical practice7. By hypothesizing that the increased appreciation for the morphological diversity of the microvascular patterns of astrocytomas can improve the diagnosis, this study confirmed that the histological assessment of the microvasculature in brain tumor specimens could aid the discrimination between WHO grade II and III gliomas. In addition, our findings suggest that the local box-counting dimension can be used as a valid index to quantify the microvascular pattern that can improve the diagnostic process when combined with other indexes in a multivariate analysis.

Fractal-based approaches represent a quantitative and robust method for reliable parameters to quantify the neoplastic microvascular patterns. The combination of different morphometric variables can be a valid additional tool to help pathologists corroborate the assignment of a tumor to the correct histological grade. Computer-aided fractal-based morphometric analyses can be extended to the quantification of the neoangiogenic microvessels (e.g., by means of immunohistochemistry with CD31 and/or CD105 antibodies) and/or to the study of the microvascular patterns of brain tumors in vivo by means of high- and ultra-high fields in magnetic resonance imaging30.

The clinical importance of these findings demands further studies to confirm these results on a larger series of patients and to identify new estimators or sets of variables that strengthen the discrimination between brain tumors with different grades or to be correlated with some biological aspect of the tumor and/or epidemiological characteristics of patients.

Methods

Specimens and vascular staining

A total of 70 histological specimens which were collected from 17 patients affected by diffusely infiltrating gliomas, previously described31, were analyzed. All patients underwent surgical resection at the Department of Neurosurgery of the Medical University of Vienna, Austria, and signed a written informed consent form for the use of their biological materials for diagnostic and research purposes. The local ethics committee approved the study (Ethics committee of the Medical University of Vienna and of the General Hospital of Vienna, EK Nr. 245/2010). Before the intervention, none of the patients had received chemo- or radiotherapy. Table 4 summarizes the main characteristics of the patients. The specimens (1-8 samples for each patient with an average of 4 samples per patient), which were collected according to the method previously described31, were formalin-fixed, paraffin-embedded and processed for conventional histopathology. The final diagnosis was made according to the specimen with the highest tumor grade in each patient. Immunohistochemistry was performed to specifically identify vessels using antibodies raised against CD34. Microvascularity was scored (angioscore) by an expert neuropathologist who was blind to the computer-assisted morphometric parameters and results by assigning the score of 0 to the specimens without clusters of vessels, a score of 1 when clusters of vessels appeared, and a score of 2 when very prominent clusters of vessels were found. According to this scoring system, sixteen specimens scored 0, thirty-two scored 1 and fifteen scored 2. Because of the presence of artifacts or weakly immunoreactive microvessels, 7 specimens were excluded from the analysis. A mitotic index was estimated for each specimen as the percent of Ki-67/MIB-1-immunopositive tumor cells, as previously described31.

Table 4. Patients' Characteristics.

Characteristics Number
Number of patients 17
Gender, women:men 1:1.125
Median age (years), range 44, 25–65
WHO grade and subtype  
Grade II 8
Astrocytoma 4
Mixed oligoastrocytoma 3
Oligodendroglioma 1
Grade III 9
Astrocytoma 4
Mixed oligoastrocytoma 1
Oligodendroglioma 4
Open in a new tab

Specimen digitalization

The histological sections were digitized using a computer suite for virtual microscopy (NanoZoomer Digital Pathology, Hamamatsu, Hamamatsu City, Japan) at 20x magnification with a fixed light intensity and resolution (pixel size: 0.46 microns, ∼ 55,000 dpi). To manage these data sets, we used custom-made software developed in Visual C++ language. Red-green-blue (RGB) thresholding was applied to convert the images into binary data and extract the CD34+ vessels (Figure 7), as previously described26. The threshold was defined to automatically and specifically select the immunopositive vascular entities (i.e., brown-stained microvessels). The same threshold was applied to all 63 specimens.

Assessment of Euclidean parameters

For each specimen, the following parameters were automatically measured: a) the surface covered by the whole histological section (ATum); b) the surface covered by the total vascular area (TVA); c) the percent covering surface (A%, the ratio between TVA and ATum); and d) the density of microvessels expressed as the mean number of microvessels per mm2 (MVs/mm2).

Because of the heterogeneous distribution pattern of vascular vessels in two-dimensional sections, we additionally identified a “hot-spot” area that was defined as the portion of the histological specimen with the highest percentage of microvascular area in which the morphometric analysis was applied. The “hot spot” area was identified as follows: a) a grid of boxes 1 mm to a side that was superimposed on the whole histological section; b) for each box, the ratio between the local vascular area and the local neoplastic area was calculated [local A(%)]; and c) the box with the highest local A(%) was automatically selected and extracted to be used as the “hot-spot” representative of the whole specimen (Figure 7).

Assessment of the microvascular fractal dimension

The space filled by the microvessels recognized in the whole section was estimated using the box-counting method, which considers the number of boxes of a given size required to completely cover the analyzed objects. It applies the equation: 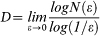Inline graphic, where D is the box-counting fractal dimension of the cross-sectional area of the immunostained vessels, ε is the side length of the box, and N(ε) is the smallest number of contiguous and non-overlapping boxes of side ε required to completely cover the objects (i.e., the immunoreactive vessels). As the zero limit cannot be applied to biological images, D was estimated by means of the slope of the graph of log [N(ε)] against log (1/ ε). D represents the microvascular fractal dimension, and as the histological image is a two-dimensional plane, D is a fractional number somewhere between the Euclidean dimensions 0 and 2. The self-similarity of natural, including biological, objects (i.e., the microvascularity) is maintained in a “scaling window” of two orders of magnitude12,22,23,24. As previously reported26, the self-similar behavior of neoplastic microvascularity in histological samples of glioblastoma multiforme was found in a scaling window between εmin = 50 µm and εmax = 2 mm. This range was applied to the entire analysis, and the value obtained using the box-counting method was defined as the microvascular fractal dimension (mvFD).

Assessment of the fractal parameters in the “hot-spot” area

The box-counting method was subsequently applied to the “hot-spot” area (Figure 7). Different scaling windows were tested, and a monofractal behavior was found in the range εmin = 1 µm and εmax = 100 µm. This index was indicated as the local microvascular fractal dimension (local mvFD). Assuming an average diameter of the microvessel between 5 and 10 micron, this range considers the smallest features of the microvessels, i.e., the rough outline (at the magnitude of 1 micron), as well as the agglomerate of micro-clusters of vessels (at the magnitude of 100 micron). This led to our hypothesizing the insufficiency to cover the whole histopathological characteristics of the microvessels, such as the macro-agglomerates in large clusters because the box with the maximum size of 100 micron could underestimate the real complexity of the distribution of the microvessels in the space. A scale window ranging between 1 µm and 1 mm, i.e., 3 orders of magnitude, was considered significant to cover all of the mean histopathological characteristics of the microvessels, including the intrinsic morphologic features and their clustering property. When the box-counting algorithm was applied in this range of scales, a monofractal behavior was not confirmed (see the trend of the obtained curve, Figure 7h). Several power-laws were found, demonstrating that microvascularity exhibits different degrees of geometrical complexity when observed at various scales of magnification. The goodness-of-fits, reported as the R2 of the regression analysis, represents the distribution of the points on the log-log graph. Although more complex and accurate methods are available to measure the slope of the curve11, for simplicity, we considered the slope of the straight line interpolating the points on the log-log graph as statistically representative of the space-filling properties of the vessels in the hot-spot. However, a similar trend was found in all the specimens. Even if no more self-similar, the obtained slope of the straight line interpolating the curve was considered as the mean value expressing the space-filling properties of the microvessels and was indicated as the local box-counting dimension (local bcD).

Both mvFD and local bcD express by a single number the property of the microvessels to fill the space in which they are embedded, which is a characteristic intrinsically correlated to their number, magnitude, shape and distribution pattern. Figure 7 summarizes the method used for estimating the local bcD.

Statistical Analysis

A correlation analysis was computed to evaluate the relationships among all the metric variables used in this study. Data were neither normalized nor adjusted by logarithm to assess the actual relationships between factors. Even if the relationships were shown to not always be linear, the outliers found in each bivariate plot were always considered to analyze the real distribution of the scores. The correlation coefficients matrix was also used as a similarity matrix to perform a cluster analysis based on the un-weighted pair group method with arithmetic mean (UPGMA) to visualize the main association between variables (Figure 1). Bivariate approaches were used to assess the relationships between loc bcD and the other variables, taking into consideration both the microvascular patterns and histological grade. The structure of the variation was also analyzed through factor analysis and principal component analysis based onto correlation matrix of the raw values. The efficiency of the different variables to characterize the microvascular patterns and histological grade was assessed using non-parametric comparisons (Mann-Whitney and Kruskal-Wallis test) as well as discriminant analysis to quantify the percentage of correct classifications for different combination of variables. The statistics were computed with Statistica 7.0.

Author Contributions

ADI planned the whole study and designed and performed the morphometric analysis of the histological specimens. FG contributed to computer-assisted analysis and to the development of the software. EB performed the statistical analysis and essentially wrote the results section. GW and GM contributed to the immunostaining of the specimens and to the assessment of the angioscore and MIB. They also contributed to the editing of the final drafts of the manuscript, which was essentially written by ADI and FG. MT contributed to the preparation of the manuscript, supervised the project and provided the logistics facilities.

Acknowledgments

We would like to thank Dr. Johannes Hainfellner for the histopathological evaluation of the whole series of glioma specimens and for his continuous scientific and logistic support. We would also like to thank Dr. Matthias Preusser for his comments on the manuscript, and Andreas Jurkowitsch for the digitalization of the samples. This study was performed in the context of the doctoral program (PhD in Clinical Neurosciences) at the Medical University of Vienna, Vienna, Austria (CLINS N790, coordinator: Prof. Dr. Johannes A. Hainfellner). The first author is a recipient of a grant from the SINch (Italian Society of Neurosurgery). The authors also wish to thank the FMEA (Society for the Promotion of Research in Microsurgical and Endoscopic Anatomy) for paying the costs related to the production of the article. Special thanks are also addressed to the Virtual Fractal Lab Team (www.fractal-lab.org) for the development of the software and for their continued technical support beyond the image and fractal analysis.

References

  1. Brem S., Cotran R. & Folkman J. Tumor angiogenesis: a quantitative method for histologic grading. J. Natl. Cancer. Inst. 48, 347–356 (1972). [PubMed] [Google Scholar]
  2. Folkerth R. D. Descriptive analysis and quantification of angiogenesis in human brain tumors. J. Neurooncol. 50, 165–172 (2000). [DOI] [PubMed] [Google Scholar]
  3. Leon S. P., Folkerth R. D. & Black P. M. Microvessel density is a prognostic indicator for patients with astroglial brain tumors. Cancer 77, 362–372 (1996). [DOI] [PubMed] [Google Scholar]
  4. Wesseling P., van der Laak J. A., Link M., Teepen H. L. & Ruiter D. J. Quantitative analysis of microvascular changes in diffuse astrocytic neoplasms with increasing grade of malignancy. Hum. Pathol. 29, 352–358 (1998). [DOI] [PubMed] [Google Scholar]
  5. Di Ieva A. Angioarchitectural morphometrics of brain tumors: are there any potential histopathological biomarkers? Microvasc. Res. 80, 522–533 (2010). [DOI] [PubMed] [Google Scholar]
  6. Louis D. N., Ohgaki H., Wiestlet O. D. & Cavenee W. K. WHO Classification of Tumours of the Central Nervous System. IARC, Lyon (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Van den Bent M. J. Intraobserver variation of the histopathological diagnosis in clinical trials on gliomas: a clinician's perspective. Acta Neuropathol. 120, 297–304 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Mandelbrot B. B. The Fractal Geometry of Nature. Freeman, San Francisco (1982). [Google Scholar]
  9. Baish J. W. & Jain R. K. Fractals and cancer. Cancer Res. 60, 3683–3688 (2000). [PubMed] [Google Scholar]
  10. Cross S. S. Fractals in pathology. J. Pathol. 182, 1–8 (1997). [DOI] [PubMed] [Google Scholar]
  11. Landini G. Fractals in microscopy. J. Microsc. 241, 1–8 (2011). [DOI] [PubMed] [Google Scholar]
  12. Losa G. A. The fractal geometry of life. Riv. Biol. 102, 29–60 (2009). [PubMed] [Google Scholar]
  13. Vakoc B. J. et al. Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging. Nat. Med. 10, 1219–1223 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Assimakopoulou M., Sotiropoulou-Bonikou G., Maraziotis T., Papadakis N. & Varakis I. Microvessel density in brain tumors. Anticancer Res. 17, 4747–4753 (1997). [PubMed] [Google Scholar]
  15. Bian X. W., Wang Q. L., Xiao H. L. & Wang J. M. Tumor microvascular architecture phenotype (T-MAP) as a new concept for studies of angiogenesis and oncology. J. Neurooncol. 80, 211–213 (2006). [DOI] [PubMed] [Google Scholar]
  16. Sharma S., Sharma M. C., Gupta D. K. & Sarkar C. Angiogenic patterns and their quantitation in high grade astrocytic tumors. J Neurooncol 79, 19–30 (2006). [DOI] [PubMed] [Google Scholar]
  17. Selby D. M., Woodard C. A., Henry M. L. & Bernestein J. J. Are endothelial cell patterns of astrocytomas indicative of grade? In Vivo 11, 371–375 (1997). [PubMed] [Google Scholar]
  18. Jain R. K. Normalization of tumor vasculature: an emerging concept in antiangiogenic therapy. Science 307, 58–62 (2005). [DOI] [PubMed] [Google Scholar]
  19. Jain R. K. et al. Angiogenesis in brain tumours. Nat. Rev. Neurosci. 8, 610–622 (2007). [DOI] [PubMed] [Google Scholar]
  20. Goldberger A. L. & West B. J. Fractals in physiology and medicine. Yale J. Biol. Med. 60, 421–435 (1987). [PMC free article] [PubMed] [Google Scholar]
  21. Feder J. Fractals. Planum Press, New York, NY (1988). [Google Scholar]
  22. Losa G. A. & Nonnenmacher T. F. Self-similarity and fractal irregularity in pathologic tissues. Mod. Pathol. 9, 174–182 (1996). [PubMed] [Google Scholar]
  23. Paumgartner D., Losa G. & Weibel E. R. Resolution effect on the stereological estimation of surface and volume and its interpretation in terms of fractal dimensions. J. Microsc. 121, 51–63 (1981). [DOI] [PubMed] [Google Scholar]
  24. Rigaut J. P. An empirical formulation relating boundary lengths to resolution in specimens showing “non-ideally fractal” dimensions. J. Microsc. 133, 41–54 (1984). [Google Scholar]
  25. Landini G. & Rigaut J. P. A method for estimating the dimension of asymptomatic fractal sets. Bioimaging 2, 65–70 (1997). [Google Scholar]
  26. Di Ieva A., Grizzi F., Sherif C., Matula C. & Tschabitscher M. Angioarchitectural heterogeneity in human glioblastoma multiforme: a fractal-based histopathological assessment. Microvasc. Res. 81, 222–230 (2011). [DOI] [PubMed] [Google Scholar]
  27. Preusser M. et al. Histopathologic assessment of hot-spot microvessel density and vascular patterns in glioblastoma: poor observer agreement limits clinical utility as prognostic factors. Cancer 107, 162–170 (2006). [DOI] [PubMed] [Google Scholar]
  28. Weidner N., Semple J. P., Welch W. R. & Folkman J. Tumor angiogenesis and metastasis: correlation in invasive breast carcinoma. N. Engl. J. Med. 324, 1–8 (1991). [DOI] [PubMed] [Google Scholar]
  29. Fox S. B. et al. Quantification and prognostic value of breast cancer angiogenesis: comparison of microvessel density, Chalkley count, and computer image analysis. J. Pathol. 177, 275–283 (1995). [DOI] [PubMed] [Google Scholar]
  30. Di Ieva A. Fractal analysis of microvascular networks in malignant brain tumors. Clin Neuropathol (in Press, DOI 10.5414/NP300485). [DOI] [PubMed] [Google Scholar]
  31. Widhalm G. et al. 5-Aminolevulinic acid is a promising marker for detection of anaplastic foci in diffusely infiltrating gliomas with nonsignificant contrast enhancement. Cancer 15, 1545–1552 (2010). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES