Cardiac Position Sensitivity Study in the Electrocardiographic Forward Problem Using Stochastic Collocation and Boundary Element Methods

Abstract

The electrocardiogram (ECG) is ubiquitously employed as a diagnostic and monitoring tool for patients experiencing cardiac distress and/or disease. It is widely known that changes in heart position resulting from, for example, posture of the patient (sitting, standing, lying) and respiration significantly affect the body-surface potentials; however, few studies have quantitatively and systematically evaluated the effects of heart displacement on the ECG. The goal of this study was to evaluate the impact of positional changes of the heart on the ECG in the specific clinical setting of myocardial ischemia. To carry out the necessary comprehensive sensitivity analysis, we applied a relatively novel and highly efficient statistical approach, the generalized polynomial chaos-stochastic collocation method, to a boundary element formulation of the electrocardiographic forward problem, and we drove these simulations with measured epicardial potentials from whole-heart experiments. Results of the analysis identified regions on the body-surface where the potentials were especially sensitive to realistic heart motion. The standard deviation (STD) of ST-segment voltage changes caused by the apex of a normal heart, swinging forward and backward or side-to-side was approximately 0.2 mV. Variations were even larger, 0.3 mV, for a heart exhibiting elevated ischemic potentials. These variations could be large enough to mask or to mimic signs of ischemia in the ECG. Our results suggest possible modifications to ECG protocols that could reduce the diagnostic error related to postural changes in patients possibly suffering from myocardial ischemia.

INTRODUCTION

The standard electrocardiogram (ECG) records body-surface potentials at the limbs and precordial area of the chest and provides remote measurements of the electrical activity of the heart. It is a powerful diagnostic and monitoring tool for patients exhibiting cardiac pathophysiologies such as rhythm disturbances, acute myocardial ischemia, and infarction. Despite its utility, a fundamental weakness of the ECG is the fact that it is a remote measurement, capturing cardiac electrical activity at the body surface. As a result, a number of factors that are not related to intrinsic cardiac activity can affect the signals recorded at the body-surface lead positions and thus induce errors in clinical evaluation.^1,2,12 The goal of our research was to capture and quantify those factors and their influence on the clinical use of the ECG.

In a healthy heart, the ST segment represents the time between complete ventricular depolarization and the beginning of repolarization. During this time interval, the myocardium is relatively isopotential, with potential differences that are small compared to those that arise during activation and repolarization. In a heart experiencing myocardial ischemia, there is at least one region of underperfused tissue that has decreased action potential amplitude and an increased resting membrane potential. The resulting potential difference between the healthy and ischemic tissue during the ST segment causes injury currents, which are then detected on the body surface as ST elevations or depressions.^6,11,18,21 During movement of the heart due, for example, to changes in posture, the position of these electrical sources also changes, thus changing the amplitude and orientation of the associated body-surface potentials. Our results suggest that such changes can potentially mask the injury currents. Conversely, even in a healthy heart, there are small spatial variations in action potential amplitude during the plateau phase that generate cardiac currents and body-surface potentials usually below clinically meaningful thresholds. To account for variations in ST potentials across patients and improve sensitivity of the ECG during patient monitoring, it is common clinical practice to use a baseline recording to set patient specific thresholds against which subsequent variations are compared.^2,11,26,30

Positional changes of the heart with posture and respiration can alter ECG signal amplitude and morphology in ways that influence clinical decision making. Though the heart is anchored at its base by relatively rigid tissue, the apical end of the heart can shift position significantly within the torso due to simple movements of the patient, e.g., lying down or rolling over. In the clinical context, such positional shifts can affect the ST-segment and R-wave amplitude ²²; however, these parameters are also common indicators of myocardial ischemic injury.^6,11,18,21 Postural changes can be minimized and controlled during ECG recording for diagnostic and acute evaluation purposes, but not during continuous patient monitoring. Even seemingly insignificant movements during such monitoring can result in deviations from the baseline ECG pattern that are sufficient to unnecessarily trigger patient distress alarms.^2,11,26,30

In ECG interpretation, one can identify two types of errors that result from these heart and body position changes. The first category includes errors that mimic disease induced changes, i.e., that create false positive results.¹¹ The second category includes factors that hide underlying disease or deteriorating cardiac function and thus precipitate false negative results, a situation known as “electrocardiographically silent ischemia”.^8,22 Silent ischemia is much more difficult to detect and is also of greater clinical concern as failure to detect a true injury has such a high impact on patient well being. The settings in which such errors are of the greatest concern include the emergency room and intensive care units, where patient monitoring is constant and the consequences of hesitation can be costly.

Previous research has described the effects of heart position on torso-surface potentials but has lacked comprehensive statistical quantification. MacLeod et al. used a realistically human-shaped, electrolytic torso tank to measure the body-surface and epicardial potentials from healthy canine hearts located at various positions along three orthogonal directions within the tank.²⁴ They concluded that changes in heart position of only a few centimeters were sufficient to produce changes in ST-segment potentials that could mimic acute myocardial ischemic injury. In a separate study using the same approach but with a heart experiencing acute myocardial ischemia, the group showed that simple rotation of the heart position produced ECG waveforms without the characteristic features of ischemic injury and proposed a possible mechanism for clinically silent ischemia.²² Both these studies also included simulation of geometric models derived from the torso tank to predict torso potentials from epicardial sources measured during the experiments. A limitation of these studies was that they included only on a small number of specific instances, i.e., the heart was placed in a series of fixed locations. Complete sensitivity analyses, by contrast, should include a comprehensive statistical description of the dependence of the outcome on variations of all parameters of interest. Such a study based on experiments would be prohibitively expensive and plagued with methodological challenges. Even simulation, which provides a more tractable framework for sensitivity analysis, can become prohibitive in computational cost if each test requires more than a few seconds to complete.

Many methods exist for simulation based assessment of sensitivity and their utility depends on the complexity of the underlying system. The best known and simplest is the Monte Carlo approach, which samples the entire parameter space and often results in prohibitive computational cost. A simplification of this approach known as “brute-force” methods reply on highly under-sampling the parameter space and interpolating between the results.²⁹ Another variation is that what is known as “range finding” experiments, in which the outer extremes of the parameter limits are evaluated and assumed to represent the total variation across the parameter range. As we will show, variation of the ECG with heart position is not linear and the maximum impacts do not occur at the extremes of the parameters, thus precluding range finding and undermining bruteforce approaches. A more sophisticated variation, known as the “generalized polynomial chaos-stochastic collocation” (gPC-SC) method^33,34 is effectively a sampling method which exploits assumptions concerning the mathematical nature of the stochastic field or process of interest—assumptions which are often justified mathematically—to minimize the number of samples that are needed for the computation of accurate statistics. This approach has formed the basis of previous studies by our group^15,16 and of the results described here.

In this study, we carried out a mathematically robust sensitivity evaluation using gPC-SC to predict the effects of changes in heart location and orientation on body-surface electrocardiographic potentials have gone beyond simple case-study strategies to a systematic and quantitative approach that provides a statistical metric of parameter sensitivity which could lead to clinical improvements for ECG based diagnosis and monitoring. The findings support and enhance previously reported results from torso tank experiments by MacLeod et al.^22,24

METHODS

The electrocardiographic forward problem solves for body-surface potentials given a set of known cardiac sources and the shape and conductivity of the intervening volume conductor.¹⁹ Of the possible source models, arguably the most complete and most unique representation of cardiac activity is the time sequence of epicardial voltages,⁵ which leads to a quasi-static approximation of Maxwell’s equations expressed as the following classic Laplace problem:

$$\begin{array}{l}\nabla ·(\sigma (\mathit{x})\nabla u(\mathit{x}))=0,\mathit{x}\in \mathrm{\Omega }\\ u(\mathit{x})=u_0(\mathit{x}),\mathit{x}\in {\mathrm{\Gamma }}_H\\ \overrightarrow{n}·\sigma (\mathit{x})\nabla u(\mathit{x})=0,\mathit{x}\in {\mathrm{\Gamma }}_T,\end{array}$$ (1)

where Ω denotes the torso domain, consisting of the volume internal to the torso surface, Γ_T, and external to the heart surface, Γ_H. u(x) is the potential, which obeys Dirichlet boundary conditions, u₀(x), on the heart surface and a Neumann zero-flux condition on Γ_T. The electrical conductivity, σ(x), is that of the volume conductor, assumed homogeneous in the experiments with the electrolytic torso tank. The outward facing normal with respect to the torso is denoted n⃗.

Geometric Model

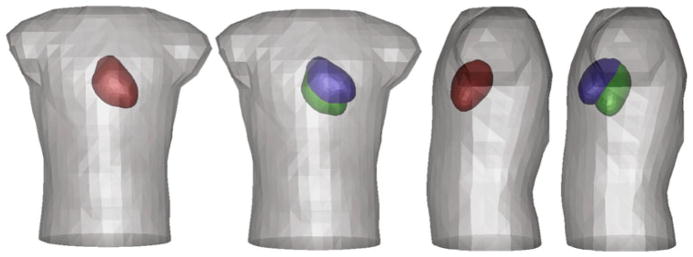
The geometric model consisted of triangular elements that represented the heart and torso tank surfaces, as depicted in Fig. 1. The heart surface contained 670 points, of which 247 were the locations of electrodes that recorded cardiac electrical potentials in canine experiments of acute ischemia. A surface Laplacian interpolation was used to reconstruct the values for the remaining points.²⁸ The tank surface consisted of 771 nodes and 1538 triangular elements. Figure 1 shows the relative position of the reference heart location within the torso tank, as well as the coordinate axes of the geometry. An MRI of a healthy adult was used as a reference for the placement of the heart in the torso. The conductivity of the torso was modeled after the experimental setup of MacLeod et al.^22,24,25 with a homogeneous value of 500 Ω·cm, approximating the average conductivity of the torso. The coordinate system was set so that the x-axis corresponded to the lateral (left/right) direction, the y-axis to the dorsal/ventral direction, and the z-axis to the cranial/caudal direction.

FIGURE 1.

Extremes of motion of the torso tank and cardiac sources. The torso surface is grey and the epicardial surface red in the most central location. The cardiac location extremes are shown in green and blue for a pivoting motion in both x and y directions around a vector centered at the base of the heart.

Numerical Methods

To solve Eq. (1) we used the well known boundary element method (BEM),⁷ which has been successfully applied to a range of electrocardiographic problems. ^4,10,23,32 The result is a transformation operator, 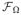: ν_H → ν_T, that links epicardial to torso potentials, u_T ∈ ν_T : 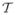(Γ_T) → ℝ. In order to evaluate variations in torso potential resulting from uncertainties in the position of the heart, we sought solutions to the forward problem for various positions of Γ_H within Ω. We assumed linear variation of the potential over the elements that make up both surfaces¹³ so that the transformation operator 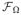was a matrix that transformed the heart potentials, u_H, to the torso-surface potentials, u_T. The BEM requires computation of weighted solid angles between each collocation point and every triangular element in all surfaces and we employed the analytical formulas for solid angles given by de Munck¹⁰ and the transform matrix construction scheme presented by Barr et al.⁵ Because the solid angles change in response to affine transformations of the heart surface, the transformation operator, 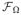, must be recomputed for each unique coordinate transformation resulting from a new heart surface location.

Experimental Methods

All experimental data were taken from previous studies that had the approval from the Institutional Animal Care and Use Committee at the University of Utah and conformed to Guide for the Care and Use of Laboratory Animals (NIH Pub. No 85–23, Revised 1996). Epicardial potentials used in the simulations were taken directly from experiments of isolated, instrumented canine hearts suspended in the human-shaped torso tank. Variable degrees of ischemia were induced by restriction of blood flow through the left anterior descending coronary artery and the epicardial potentials were recorded using 247 electrodes covering the ventricles.^24,25 We used epicardial potentials from the ST segment of the ECG during representative beats under both control and ischemic conditions.

Imaging of Cardiac Position

It was essential for these studies to set the variation of spatial parameters—heart motion arising from respiration and changes in posture—to physiologically realistic values. We obtained magnetic resonance images (MRIs) for a test subject during normal respiration in three positions; supine, prone, and lying on the right side. One set of data contained images that were cardiac gated and acquired during breath holds. To quantify a respiration induced cardiac motion, a second set of scans recorded ungated, cine MRI in supine and the right side positions. The scans were registered together in order to measure the changes in heart orientation.

From these images, we derived the following constraints: (1) apical motion in the axial plane restricted to a maximum end-to-end deviation of 6 cm, achieved through a pendulum-like swinging motion about a point near the center of the base of the heart; (2) vertical translation limited to a deviation of 2 cm; (3) rotational pivoting of the heart about a vertical axis, limited to a deviation of 20°. A final assumption was that all positions have an approximately equal likelihood so that we could assume uniform probability density functions for each parameter of motion. This assumption implies that, within physiological ranges, all values of swing, rotation, and vertical translation are equally likely to occur. It does not suggest that the time the heart spends in each position is equal, just that there is no a priori knowledge of which positions the heart is likely to assume within the specific constraints.

Modeling Uncertainty in Heart Position

To carry out a comprehensive and quantitative sensitivity analysis of the role of heart position on the ECG requires a combination of simulation to compute body-surface potentials from cardiac sources, as well as an efficient strategy to capture statistical variation in the model variables. The simulation model, described below, is a solution to the forward problem of electrocardiography based on source potentials on the outer (epicardial) surface of the heart.⁵ Implemented as a boundary element discrete model, this approach allows efficient movement in heart position, which is the parameter space to explore. To capture the statistical variation, we employed the gPC-SC method for its efficiency and appropriate assumptions about the underlying system.

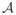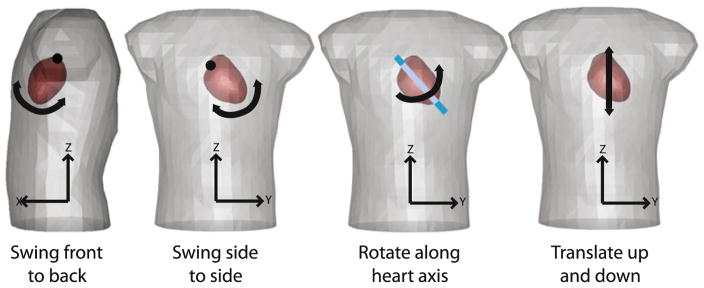
To formalize this process mathematically, we let (χ, , μ) be a complete continuous probability space that expresses variation in the heart position, where χ is the event space consisting of outcomes corresponding to heart position, 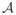⊂ 2^χ is the σ-algebra used to define measurable events, and μ is the probability measure expressing the distribution from which outcomes are drawn. We can now express the heart position as a function of four uniform independent random variables ξ⃗ = (ξ₁, ξ₂, ξ₃, ξ₄), which correspond to swing about x-axis, swing about y-axis, rotation about the long axis of the heart, and translation along the z-axis, respectively, as seen in Fig. 2. The term swing refers to the pendulum type of movement made by the heart as it pivots around its base. The random field of interest (and in particular, its statistical characterization) in this study is the torso-surface potential. The heart position can be completely expressed in terms of ξ⃗, and because the torso-surface potential is a direct consequence of heart position, the torso potential can also be expressed as a function of ξ⃗. We can denote the torso potential by f(ξ⃗). We are interested in computing statistics on the random field f(ξ⃗) with the mean of the field given by mean(f) = 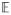[f(ξ⃗)] and the variance by var(f) = 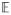[(f(ξ⃗) ] mean(f))²].

FIGURE 2.

Modes of motion. ξ₁ = swing front to back, ξ₂ = swing side to side, ξ₃ = rotation along the long axis of the heart, and ξ₄ = translation along the z-axis.

The stochastic collocation approach selects a collection of sample points for the random field and applies a set of corresponding weights that account for the probability density function characteristics of the set from which the points (or outcomes) are drawn. In this case, each collocation point, ξ⃗_j, represented a particular heart position selected from the outcome set. At each collocation point we computed the torso potential field, f(ξ⃗_j), by traditional ECG forward solution techniques (described above). Unlike traditional Monte Carlo, in which very large numbers of collocation points are required to compute accurate statistics, only a limited number of samples are necessary by utilizing the smoothness assumption to select points and weights without loss of accuracy (achieving as much as 400 times speed-up in test simulations).

Statistical Analysis

Once solutions (torso potentials) were computed for each heart position dictated by the collocation sampling, the statistics of these solutions were given by the following expressions:

$$\begin{array}{l}\text{mean}(f)=\mathbb{E}[f(\overrightarrow{\xi })]\approx \sum _{j=1}^q{w}_{j}f({\overrightarrow{\xi }}_j)\\ var(f)=\mathbb{E}[{(f(\overrightarrow{\xi })-\text{mean}(f))}^2]\\ \approx \sum _{j=1}^q{w}_j{(f({\overrightarrow{\xi }}_j)-\text{mean}(f))}^2,\end{array}$$ (2)

variable, and w_j denotes the weights. For this study, we utilized second-order Smolyak collocation points and weights for independent and uncorrelated uniform distributions, which required q = 5 points for a single random dimension, q = 13 points for two, q = 25 points for three, and q = 41 points for four random dimensions.^31,33,35 The points and weights were based on Smolyak’s first algorithm and more details are available elsewhere,³⁶ including discussion of further statistics that can be computed beyond mean and variance using the collocation approach. As in other applications, larger values of standard deviation (STD) at particular points on the torso surface indicated a larger sensitivity of the ECG at those points to variations in the associated modes of cardiac swing, rotation, or translation.

Range Finding Evaluation

Stochastic Collocation methods are an effective tool for a specific class of numerical problems because the gPC-SC relies on the underlying probability distribution being continuous. Moreover, if variations within the parameter space produce nearly linear results, then the added complexity of the collocation methods may not be justified and a range finding approach may be sufficient. To evaluate the utility of the range finding approach to sensitivity analysis in this problem, we carried out simulations of the ECG at lead V₄ for different ranges of cardiac motion constrained as described above. For each of 20 positions uniformly spaced between the extremes, we computed a forward transform matrix and applied epicardial potentials from the ST segment. The results were plotted to demonstrate the response of the system for one sample parameter.

RESULTS

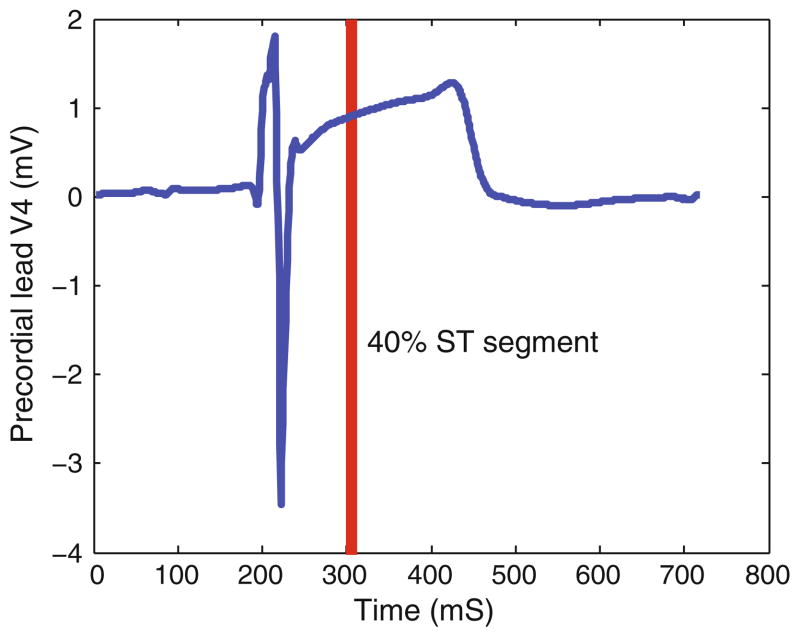
Figure 3 shows a reconstructed ECG from the V₄ location from epicardial potentials recorded during conditions that produced ischemia. The resulting elevation of the ST segment is obvious, as is the large amplitude of the ECG (approximately 5 mV peak to peak for the QRS complex). The amplitude of ECGs from the experimental preparation was determined by the conductivity of the electrolyte tank in which the heart was placed, and they could not perfectly replicate the conditions in humans. The figure also shows the time point used to capture ST-segment shifts (40% of the time between the QRS and T waves) based on the root mean square (RMS) curve of the measured electrograms. All subsequent displays of body-surface potentials maps were based on the value recorded at this time point. The ECG also shows the typical, shifted ischemic ST segments relative to a TQ segment that was adjusted for each beat to define a flat baseline, as is customary with ECG recordings.

FIGURE 3.

Reconstructed ECG for precordial lead V₄. The ECG signal was reconstructed using the BEM from epicardial potentials captured during the late phase of a 180-s episode of elevated heart rate and reduced coronary blood flow. The red line indicates the time of 40% of the ST segment, the time instant used for all subsequent displays of body surface- potential maps below.

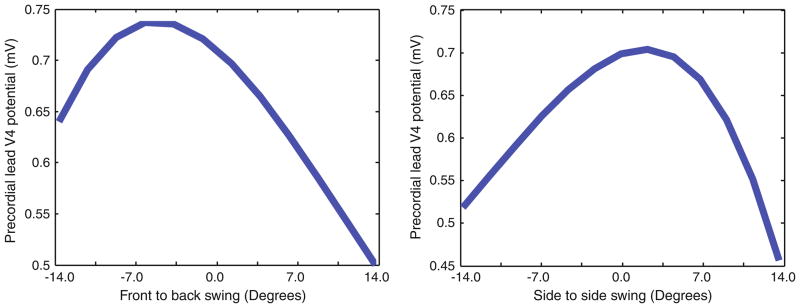
Figure 4 contains the results of the range finding evaluation for the V₄ position and heart swing in two orthogonal directions. The shape of the resulting curves shows that variation of ECG amplitude is neither linear nor monotonic over the range of motion. Moreover, the peak variations do not arise at either extreme of motion, but somewhere in the middle of the range. These results suggest that simple schemes like range finding or brute force will capture only part of the true variation and that a comprehensive sensitivity analysis is justified.

FIGURE 4.

Sampling of the front-to-back swing and the side-to-side swing on the recordings of precordial lead V4. The left figure shows the effects of 20 sample points for front-to-back heart with a maximum value at −6.5°. At right, the figure demonstrates the case of side-to-side cardiac swinging motion. Both figures illustrate the nonlinear nature of the parameter space.

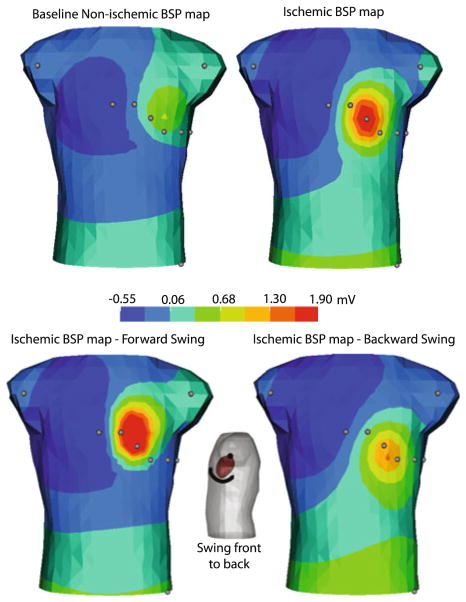
Figure 5 depicts an example of ST-segment torso potentials computed from measured epicardial potentials. The baseline map represents the torso potentials computed from epicardial potentials during control conditions, i.e., without induced ischemic injury. The ischemic tank potentials show the obvious changes that arise from using measured heart potentials recorded during an episode of induced acute ischemia. The lower row of the figure contains computed tank potentials from ischemic epicardial potentials, for the two extreme positions of one mode of heart motion: front/back swing (±17.5°) as seen in Fig. 1. The torso potentials, computed at maximum backswing, would be difficult to distinguish from those computed from control conditions shown at top left panel—a case that could result in a false negative diagnosis.

FIGURE 5.

Effect of heart position shift on ST segments during ischemic injury. The top left panel depicts the torso potentials for the baseline condition obtained from the epicardial potentials with normal blood flow. Top right panel shows the torso potentials obtained from epicardial potentials recorded during acute ischemia. The bottom row shows the torso potentials in response to the ischemic heart swinging forward and backward to reasonable physiological limits, ±17.5°.

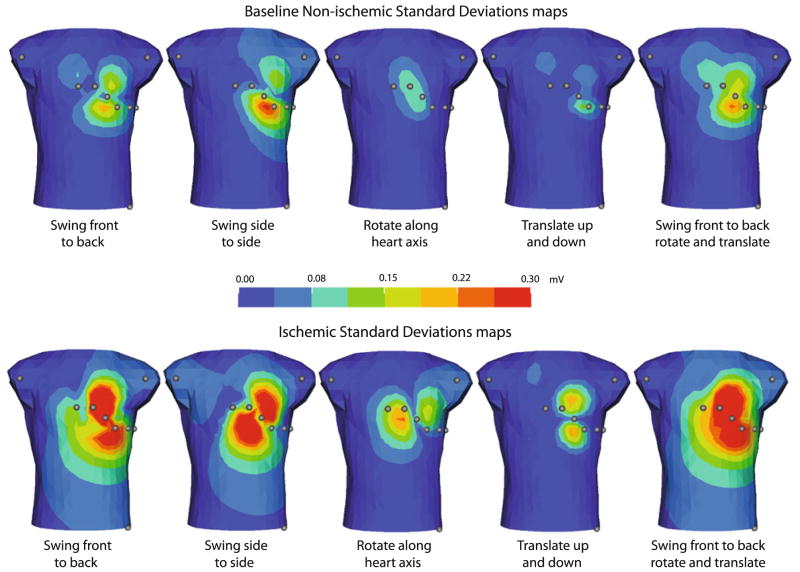
While Fig. 5 shows torso potentials from the extreme positions of a single mode of motion, the STD maps shown in Fig. 6 provide a more comprehensive report of the sensitivity throughout the entire range of motion for all parameters. For example, the SD map for swinging front-to-back in the case of ischemia shows large STDs for leads V₂, V₃, and V₄ with values of 0.40, 0.37, and 0.29 mV, respectively, and only moderate SD values for V₁ and V₅ at 0.11 and 0.17 mV. Figure 6 also contains the quantitative results for each of the modes of motion and for both ischemic and nonischemic epicardial potentials.

FIGURE 6.

Standard deviation of tank-surface potentials resulting from heart position shift during ischemia. The top row shows the SD from the motion of a heart with control epicardial potentials. The bottom row shows the SD of tank surface potentials from the motion of a heart with ischemic epicardial potentials. Colored dots indicate locations of standard limb and precordial leads.

Observations from this figure summarize general findings about the effect of heart position on the ECG. For example, the precordial areas—and hence the precordial electrodes (V₁–V₆)—would be specifically sensitive to swinging around either of the x or y-axes, i.e., antero-posterior or lateral movement of the apex. Moreover, combinations of antero-posterior swing and vertical translation caused some of the largest STDs, indicating very high sensitivities to this type of motion. Such motion would occur when a patient rolls over in bed or sits up and then lies back down. Translation in the vertical (z) axis, perhaps as expected, produced changes above and below the precordial areas and thus would be better detected in the limb leads. This type of motion was evident during respiration but produced very low STDs. Pivoting motions around the long axis of the heart produced similarly low variations in tank-surface potentials. Thus, it appears particularly unlikely that pivoting of the heart about the long axis or translations along the z-direction would be sufficient to produce significant errors in the ECG during ischemia. However, the STDs of the torso potentials due to swinging motions were large enough at 0.3 mV or more, that it would be possible to measure substantial ST-segment elevations in leads V₃ and V₄, even for the case of nonischemic epicardial potentials (upper row of Fig. 5). Such a result suggests the possibility of a false positive detection of ischemic injury.

DISCUSSION

The goal of the study was to evaluate the role of positional changes of the heart in the setting of acute myocardial ischemia through statistical sensitivity analysis using the gPC-SC methodology. This approach provides advantages over other methods reported in the setting of electrocardiography.^3,9,20 We have also shown that the parameter sensitivity of the problem is neither linear nor monotonic, thus justifying the need for an unbiased statistical approach like the gPC-SC. Statistical methods provide detailed quantitative results, including the spatial maps of STD for any distribution of parameter variation, examples of which appear in Fig. 6. Our results both support and refine previously reported clinical findings and suggest specific heart motions that are likely to cause substantial errors in ECG monitoring and diagnosis.

The results summarized in Figs. 5 and 6 illustrate both the power of the gPC-SC approach and its utility in quantifying complex relationships. We evaluated the twin hypotheses that shifts in heart position can cause (a) false positive or (b) false negative monitoring errors and could predict which ECG leads would be most susceptible to such errors. No previous studies have provided this level of spatial detail or a probabilistic metric of the error possible from such a variation in system parameters. The STD maps are a novel means to summarize parameter sensitivity in electrocardiography. They represent the spatial extent and magnitude of possible shifts in potentials induced by variation in one or more modes of heart movement. Just as one often assigns two or three times the STD (for a Gaussian distribution) to encompass the full extent of variation that is likely in a single random variable, one can picture two or three times the absolute values of the standard-deviation torso maps as the approximate range of absolute variation possible for a given set of cardiac potentials and mode(s) of motion.

The results of the sensitivity study indicate that some modes of heart motion are capable of both obscuring ST elevations as well as mimicking them. Rotation around the long axis of the heart is a component of normal cardiac contraction; translation up and down mimics a major component of respiratory motion. Neither mode of motion produced significant variations in the ECG, with STD less than 0.1 mV, suggesting that if such findings came from a realistic, patient based model, they need not be of concern to clinicians. In contrast, the motions of swinging front-to- back and side-to-side both produced STDs of more than 0.3 mV, larger than the ST shifts of 0.2 mV that are considered clinically significant. Such swinging occurs, for example, when a subject lies down, sits up, or leans forward. And while postural changes can readily be controlled in an emergency room or other acute setting, they represent a more elusive problem for critical care, in which monitoring continues over hours or days and patient motion is common. With knowledge of the specific results of postural changes, one could imagine clinical tests in which a patient were articulated in ways that could increase the sensitivity to ischemia; thus the test sensitivity and specificity might be improved. Conversely, mechanical sensors on a critically ill patient could record postural changes and adjust ECG monitoring to account for the associated changes in ECG sensitivity and reduce the incidence of false positives, as other have proposed.²⁷

In order for cardiac motion to create false positive findings of ST-segment shifts in the ECG, it is necessary that there exist during the plateau phase of the action potential at least small cardiac potential differences that project to the torso surface. Even during the nominally isopotential period of the plateau phase, there exist differences in voltage across the heart because of variations in action potential amplitude and timing. Such differences create currents that are small but detectable on the cardiac surface and the body surface, as reflected by the need to set thresholds for clinically meaningful ST-segment potentials.¹⁷

The STD represents a statistical expectation of the possible range of the quantity of interest, in this case ECG potentials. It does not indicate which specific values of the system parameters, in this case heart motion, will generate extremes of that range. In some cases, basic biophysical relationships will provide the necessary intuition to explain, for example, enhancement of anterior body-surface potentials when the heart moves closer to the front of the chest. But for others (e.g., the swinging motion we have explored), the maximum deviation of the body-surface potentials occurs not at the extremes of motion, but somewhere in the midrange. The SD maps indicate the extent of possible variations but further exploration is necessary to identify the actual parameter values (heart position) that would create such variations.

We have assumed a uniform distribution of the input parameters of the simulation, the heart-motion values, because there is no data available to suggest otherwise. The uniform distribution assumes that any particular value of heart rotation, swing, or translation is equally likely to occur, but not that the heart spends equal time in each position. One notable feature of the gPC-SC method is that it supports any assumed probability density function. If data became available or one wished to test other assumptions about the distribution of heart positions, this information could be included by using the appropriate probability density function.

Our approach does not account for the impact of variations in heart position and orientation upon the epicardial potentials because these potentials are assumed to be constant regardless of the heart position, an assumption supported by previous experimental studies from members of our group.²⁴ The gPC-SC approach presented here could, however, be easily modified to include such changes in the source potentials. Our formulation also did not account for consequences of the deformation of the heart during postural changes. However, such effects would likely increase the variability of the system, and our conclusions would become a conservative estimate of the variation caused by positional changes.

The primary objectives of this study were to describe a quantitative sensitivity approach that has not been reported previously for this problem and then carry out a study using cardiac potentials measured from a torso tank experiment in order to augment previous qualitative analyses.²⁴ The advantages of this approach compared to one based on artificial or estimated cardiac sources embedded in a realistic or patient specific human torso model are twofold. First, the cardiac sources available from experiments, although from an animal model, are highly realistic and capture normal and ischemic conditions that arise during physiologically realistic conditions. Secondly, the volume conductor in these simulations was based on a very accurate (within 5 mm) measurement of a rigid electrolytic tank and the heart position in the tank, thus preserving a geometric accuracy rarely achievable even from medical imaging of a human subject. Moreover, the conductivity of the volume conductor in such an experimental preparation can be set very precisely, removing an additional source of ambiguity that arises in a patient specific model.

This approach also presents limitations to interpreting the results of such a study, especially when extrapolating to the clinical domain. The model of the electrolytic tank is homogeneous and thus the effects of organs or other variations in tissue conductivity cannot be evaluated. Similarly, changes in the shape of both the internal organs and the torso as a whole due to respiration or changes in posture are not included in a model based on a rigid, homogeneous torso tank. A model that did include all these variations would also depend on many approximations, e.g., conductivity values and distortions of soft tissue shape during cardiac and respiratory motion and postural changes. A quantitative and statistical parameter sensitivity evaluation under such conditions would require a sophistication of model construction and variation that would likely be prohibitive. There are very few reports of cardiac simulations that even include cardiac contraction and none to our knowledge that include respiration and postural changes. No matter which modeling paradigm or level of realism one wishes to pursue, the framework of gPC-SC can accommodate and provide a method for quantitative sensitivity analysis as long as boundaries among the heart and other organs in the thorax are respected.

One indication of the physiological reasonableness of our results comes from a comparison with previously reported experiments,²⁴ in which a canine heart was suspended in the same, human shaped, electrolytic tank. Variations in due to positional changes heart position 6 cm side-to-side.²⁴ The gPC-SC method computed similar results with STDs of up to 0.25 mV, as shown in Fig. 5. A different study by Garcia et al. measured ST₆₀ and T-wave amplitude as a function of body position and found large variations among patients.¹⁴ The maximum variation of torso potentials after a positional change from the left side to supine, was 188 μV for the ST segment and 686 μV during the T wave. The results simulated for the gPC-SC method, 350 μV STD for the T wave and 250 μV STD for the ST₆₀ amplitude, were well within this range for the T-wave amplitude, and just outside their extremes for ST₆₀. It is reasonable to expect that our modeling approach would correlate better with the tank experiments, which make the same assumptions of geometry and tissue conductivity, than with the results of patient studies.

These results and our previous studies of the effects of variations in tissue conductivities¹⁵ support the further use of the gPC-SC technique—and parameter sensitivity studies in general—for this problem domain. There is a clear need to improve the diagnostic robustness of the ECG, especially in the setting of emergency and critical care medicine, and our results point to sources of variation that are large enough to explain at least some of the errors that arise in clinical practice. These findings also suggest some possible means of adjusting current practice to accommodate for heart motion, or even to use explicit movements to reveal otherwise subthreshold abnormalities in ECG metrics.