Biaxial vasoactivity of porcine coronary artery

Abstract

The passive mechanical properties of blood vessel mainly stem from the interaction of collagen and elastin fibers, but vessel constriction is attributed to smooth muscle cell (SMC) contraction. Although the passive properties of coronary arteries have been well characterized, the active biaxial stress-strain relationship is not known. Here, we carry out biaxial (inflation and axial extension) mechanical tests in right coronary arteries that provide the active coronary stress-strain relationship in circumferential and axial directions. Based on the measurements, a biaxial active strain energy function is proposed to quantify the constitutive stress-strain relationship in the physiological range of loading. The strain energy is expressed as a Gauss error function in the physiological pressure range. In K⁺-induced vasoconstriction, the mean ± SE values of outer diameters at transmural pressure of 80 mmHg were 3.41 ± 0.17 and 3.28 ± 0.24 mm at axial stretch ratios of 1.3 and 1.5, respectively, which were significantly smaller than those in Ca²⁺-free-induced vasodilated state (i.e., 4.01 ± 0.16 and 3.75 ± 0.20 mm, respectively). The mean ± SE values of the inner and outer diameters in no-load state and the opening angles in zero-stress state were 1.69 ± 0.04 mm and 2.25 ± 0.08 mm and 126 ± 22°, respectively. The active stresses have a maximal value at the passive pressure of 80–100 mmHg and at the active pressure of 140–160 mmHg. Moreover, a mechanical analysis shows a significant reduction of mean stress and strain (averaged through the vessel wall). These findings have important implications for understanding SMC mechanics.

vasoactivity of large epicardial coronary arteries is affected by cardiovascular diseases such as diabetes (14, 15), hypertension (14, 20), atherosclerosis (11), vasospasm (10, 32), and aneurysm (26), which are major risk factors for angina pectoris or myocardial infarction in patients. The constitutive passive and active stress-strain relationships can characterize the vasoactivity and are fundamental for understanding the mechanical behaviors of vascular smooth muscle cell (SMC) in health and disease (5). The strain energy function has been widely used to characterize the passive mechanical properties of blood vessels (5, 8). For large epicardial coronary arteries, extensive mechanical measurements and analysis were carried out in the passive state (18, 19, 23, 30, 33, 34).

The active mechanical properties of coronary arteries are much known. To date, there are only uniaxial active constitutive length-tension relationships in the circumferential direction of coronary arteries (1, 2, 24, 31). Although some multi-axial active models have been proposed, those have been of theoretical forms not rooted in experimental measurements (25, 36). Clearly, there is a need for multi-axial active mechanical measurements and experimentally determined multi-dimensional active strain energy functions for coronary arteries.

The objective of the study is to determine the active biaxial (circumferential and axial) stress-strain relationship and to quantify the experimental data in the form of a strain energy function in the physiological range of loading. Hence, the biaxial coronary artery loading and deformation were simultaneously measured in passive and active states, based on which a Gauss error function was proposed as the biaxial active strain energy function in the physiological loading range. A limited memory quasi-Newton method for large-scale optimization (L-BFGS method) (13) was performed for determination of the passive and active material parameters of the strain energy functions. The limitations and significance of the study are discussed accordingly.

MATERIALS AND METHODS

Animal preparation and vessel harvest.

Six farm pigs weighing 28 ± 5 kg were used in the study. The animal preparation was similar to that described previously (7, 35). All animal experiments were performed in accordance with national and local ethical guidelines, including the Institute of Laboratory Animal Research Guide, Public Health Service policy, Animal Welfare Act, and IUPUI (Indiana University-Purdue University, Indianapolis) polices regarding the use of animals in research and received institutional approval.

Briefly, surgical anesthesia was induced with TKX (Telaxol 500 mg, Ketamine 250 mg, Xylazine 250 mg) and maintained with 2% isoflurane. The animal was intubated and ventilated with room air and oxygen by a respiratory pump. After a midline sternotomy was performed, the animal was euthanized by an injection of pentobarbital sodium (300 mg/kg). The heart was harvested and placed in an ice-cold saline bath. A fresh right coronary artery (RCA) of ∼2.5 cm was dissected free of fat and connective tissue, and the branches were ligated with suture under dissection microscope in 4°C HEPES PSS (physiological saline solution) (16, 17).

Active test.

The RCA was cannulated on both ends with connectors in an organ bath containing HEPES PSS at room temperature and aerated with 95% O₂-5% CO₂. The PSS was perfused through the vessel for several seconds to ensure the lumen was completely filled. The temperature in bath was gradually increased to 37°C in 10 min. The vessel was stretched to the in vivo length [axial stretch ratio (λ_z) equals to 1.3], and the intravascular pressure was set at 15 mmHg to allow the vessel to equilibrate for 45 min. The intravascular pressure was then increased to 80 mmHg, the 37°C PSS in bath was replaced by the 60 mM K⁺ PSS at the same temperature, and the vessel was equilibrated for 15 min to attain full vasoconstriction. The vessel was preconditioned several times to obtain reproducible mechanical data (19). The transmural pressure was varied from 20 to 200 mmHg by an increment of 20 mmHg. The image of the vessel was displayed on screen with a CCD camera mounted on a stereo microscope, and the diameter changes were measured with dimensional analysis software (DIAMTRAK 3+). The axial force changes were measured by a force transducer (Fort100, <0.01 g, World Precision Instruments) fixed with a connector on one end of the vessel. Microbeads (60 μm in diameter) were dispersed on the outer surface of the vessel and videotaped during testing to measure the axial displacement. The pressure transducer, diameter tracings, and force transducer were interfaced into a computer by a Biopac system (MP100, Biopac Systems), which can monitor transient changes of pressure, diameter, and force. The loading and deformation measurements were then repeated for λ_z = 1.5. Since the vessel was connected to a pressurized container during the entire experimental procedure, the data were determined by a pressure myograph.

Passive test.

After the active test, the organ bath was filled with Ca²⁺-free Krebs solution to relax the RCA. After removal of vasoactivity, the passive pressure-diameter-axial force relation of the vessel was determined. Pressure ranges were varied between 20 and 200 mmHg by a step increase of 20 mmHg for λ_z =1.3 and λ_z =1.5, similar to the active protocol. Finally, the vessel was disconnected from the organ bath, and three rings (3-mm length) were cut from the vessel. The cross section was photographed in the no-load state, and each ring was then cut radially by a scissor at the anterior position (labeled with microbeads). The ring opened into a sector and gradually approached a constant opening angle defined as the angle subtended by two radii connecting the midpoint of the inner wall. The cross section of each sector was photographed 30 min after the radial cut taken as the zero-stress state. The morphological measurements of inner and outer circumference, wall thickness, and area in the no-load and zero-stress states were made from the images with a morphometric analysis system (ImageJ).

Theoretical model.

The mathematical derivation is described in the appendix. Briefly, in Fung's two-dimensional model without shear deformation, the passive strain energy function is given by:

$$\begin{array}{ccc}{W}_{\text{passive}}=\frac{C_1}{2}[\exp (Q)-1]& \text{with}& Q=a_1{E}_{\theta \theta }^2+a_2{E}_{\text{zz}}^2+2a_4{E}_{\theta \theta }{E}_{\text{zz}}\end{array}$$ 1

where C₁, a₁, a₂, and a₄ are material constants and E_θθ and E_zz are circumferential and axial Green strains, respectively. An active strain energy function induced by K⁺-induced SMC contraction is proposed as:

$$W_{\text{active}}=C_2\left[\text{Erf}\left(\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_{\text{z}}}{b_2}-b^{\prime }\right)-1\right]$$ 2

where C₂, b₁, b₂, and b′ are material constants, λ_θ and λ_z are the circumferential and axial stretch ratios, respectively, and Erf(X) is the Gauss error function. Since Gauss error function is the integral of Gaussian distribution, an interaction term of λ_θ and λ_z has been incorporated into Eq. 2 (see Eq. A11 in appendix). The total strain energy of K⁺-induced active vessel can be written as the sum of passive and active contributions (W_total = W_passive + W_active). The passive and active stresses can be determined as the derivatives of the respective strain energy functions. The total stress was determined from measurements of K⁺-induced vasoconstriction, whereas the passive stress was obtained from Ca²⁺-free measurements (active stress = total stress − passive stress).

Determination of material constants.

The material constants were determined by minimizing the square of difference between the theoretical and experimental values of passive circumferential and axial first Piola-Kirchhoff stresses (i.e., T_{θθ passive} and T_{zz passive}, respectively) as:

$$\text{Error}={\displaystyle {\sum }_{n=1}^N\left[{\left({T_{\theta \theta }}_{\text{passive}}^{\text{therapy}}-{T_{\theta \theta }}_{\text{passive}}^{\text{experiment}}\right)}^2+{\left({T_{zz}}_{\text{passive}}^{\text{therapy}}-{T_{zz}}_{\text{passive}}^{\text{experiment}}\right)}^2\right]}$$ 3

where T_{θθ passive}^theory and T_{zz passive}^theory were computed by Eq. A7 in the appendix; and T_{θθ passive}^experiment = Pr_i/hλ_θ [P is the pressure; $r_{\text{i}}=\sqrt{r_{\text{o}}^2-\frac{A_0}{\pi {\lambda }_{\text{z}}}}$ is the inner radius in loaded state; r_o is the outer radius in loaded state; A₀ is the wall area in no-load state; h = r_o − r_i is the wall thickness in loaded state] and $T_{\text{zz passive}}^{\text{experiment}}=\frac{1}{{\lambda }_{\text{z}}}\left[\frac{F}{\pi (r_{\text{o}}^{\text{2}}-r_{\text{i}}^{\text{2}})}+\frac{{\mathrm{Pr}}_{\text{i}}^{\text{2}}}{h\text{(}{r}_{\text{o}}+r_{\text{i}})}\right]$ (F is the axial force) were obtained from the passive experimental measurements; and N is the total number of experimental points.

Similar to the passive Eq. 3, the square of difference between the theoretical and experimental values of active circumferential and axial first Piola-Kirchhoff stresses (i.e., T_{θθ active} and T_{zz active}, respectively) is given as:

$$\text{Error}={\displaystyle {\sum }_{n=1}^N\left[{\left({T_{\theta \theta }}_{\text{active}}^{\text{therapy}}-{T_{\theta \theta }}_{\text{active}}^{\text{experiment}}\right)}^2+{\left({T_{zz}}_{\text{active}}^{\text{therapy}}-{T_{zz}}_{\text{active}}^{\text{experiment}}\right)}^2\right]}$$ 4

where T_{θθ active}^theory and T_{zz active}^theory were computed by Eq. A11 in the appendix; and ${T_{zz}}_{\text{active}}^{\text{experiment}}={\left[\frac{F}{{\lambda }_{\text{z}}\pi (r_{\text{o}}^{\text{2}}-r_{\text{i}}^{\text{2}})}+\frac{{\mathrm{Pr}}_{\text{i}}^{\text{2}}}{{\lambda }_{\text{z}}h\text{(}{r}_{\text{o}}+r_{\text{i}})}\right]}_{\text{total}}-{\left[\frac{F}{{\lambda }_{\text{z}}\pi (r_{\text{o}}^{\text{2}}-r_{\text{i}}^{\text{2}})}+\frac{{\mathrm{Pr}}_{\text{i}}^{\text{2}}}{{\lambda }_{\text{z}}h\text{(}{r}_{\text{o}}+r_{\text{i}})}\right]}_{\text{passive}}$ and ${T_{\theta \theta }}_{\text{active}}^{\text{experiment}}={\left(\frac{{\mathrm{Pr}}_{\text{i}}}{h{\lambda }_{\theta }}\right)}_{\text{total}}-{\left(\frac{{\mathrm{Pr}}_{\text{i}}}{h{\lambda }_{\theta }}\right)}_{\text{passive}}$ were obtained from active and passive experimental measurements.

A limited-memory quasi-Newton method for large-scale optimization (L-BFGS method) (13) was performed to minimize the error function as expressed by Eqs. 3 and 4. A FORTRAN program was developed to implement the L-BFGS method to identify material parameters C₁, a₁, a₂, and a₄ for passive strain energy function (Eq. 1) and C₂, b₁, b₂, and b′ for active strain energy functions (Eq. 2).

Statistical analysis.

The means ± SE for the six hearts were presented. ANOVA (SigmaStat 3.5) was used to compare passive and active experimental measurements in six hearts, where P < 0.05 represented statistically significant differences.

RESULTS

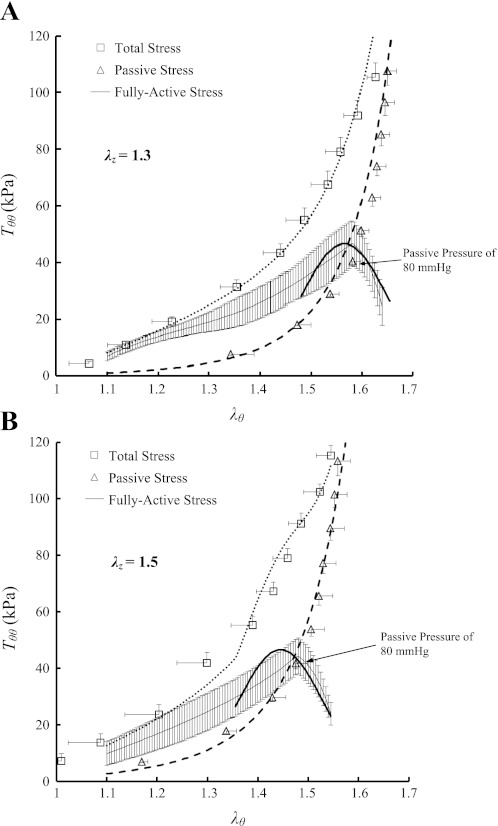
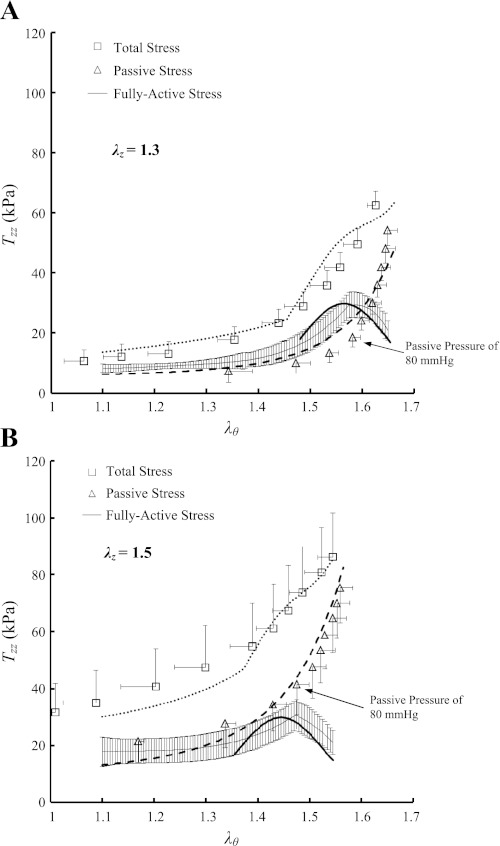
ANOVA showed no statistically significant differences of the measured outer diameters and axial forces (P >> 0.05) between the six RCAs in the transmural pressure range of 20–200 mmHg. Hence, the data were grouped together and expressed as means ± SE (averaged over six hearts). Figure 1, A and B, shows the data for the circumferential first Piola-Kirchhoff stresses (T_θθ) as a function of the circumferential stretch ratios (λ_θ) at λ_z of 1.3 and 1.5, respectively. Figure 2, A and B, shows the axial first Piola-Kirchhoff stresses (T_zz) as a function of λ_θ at λ_z of 1.3 and 1.5 in correspondence with Fig. 1, A and B. The square markers, triangle markers, and thin solid line with error bars of SE values in Figs. 1 and 2 represent the experimental total, passive, and active stresses, respectively, whereas the thick dot, dash, and solid lines refer to the theoretical values accordingly.

Fig. 1.

Circumferential first Piola-Kirchhoff stress (T_θθ) as a function of circumferential stretch ratio (λ_θ) at λ_z of 1.3 (A) and 1.5 (B) measured at K⁺-induced vasoconstriction and Ca²⁺-free-induced vasodilation. Total stress (□): ${\left(\frac{{\mathit{Pr}}_{\text{i}}}{h{\lambda }_{\theta }}\right)}_{\text{total}}$ at vasoconstriction; passive stress (▵): ${\left(\frac{{\mathrm{Pr}}_{\text{i}}}{h{\lambda }_{\theta }}\right)}_{\text{passive}}$ at vasodilation; and active stress (thin solid line) = ${\left(\frac{{\mathrm{Pr}}_{\text{i}}}{h{\lambda }_{\theta }}\right)}_{\text{total}}-{\left(\frac{{\mathrm{Pr}}_{\text{i}}}{h{\lambda }_{\theta }}\right)}_{\text{passive}}$. The thick dot, dash, and solid lines refer to the theoretical total, passive, and active stresses, respectively.

Fig. 2.

Axial first Piola-Kirchhoff stress (T_zz) as a function of circumferential stretch ratio (λ_θ) at λ_z of 1.3 (A) and 1.5 (B) measured at K⁺-induced vasoconstriction and Ca²⁺-free-induced vasodilation. Total stress (□): ${\left[\frac{F}{{\lambda }_{\text{z}}\pi (r_{\text{o}}^2-r_{\text{i}}^2)}+\frac{{\mathrm{Pr}}_{\text{i}}^2}{{\lambda }_{\text{z}}h(r_{\text{o}}+r_{\text{i}})}\right]}_{\text{total}}$ at vasoconstriction; passive stress (▵): ${\left[\frac{F}{{\lambda }_{\text{z}}\pi (r_{\text{o}}^2-r_{\text{i}}^2)}+\frac{{\mathrm{Pr}}_{\text{i}}^2}{{\lambda }_{\text{z}}h(r_{\text{o}}+r_{\text{i}})}\right]}_{\text{passive}}$ at vasodilation; and active stress (thin solid line) = ${\left[\frac{F}{{\lambda }_{\text{z}}\pi (r_{\text{o}}^2-r_{\text{i}}^2)}+\frac{{\mathrm{Pr}}_{\text{i}}^2}{{\lambda }_{\text{z}}h(r_{\text{o}}+r_{\text{i}})}\right]}_{\text{total}}-{\left[\frac{F}{{\lambda }_{\text{z}}\pi (r_{\text{o}}^2-r_{\text{i}}^2)}+\frac{{\mathrm{Pr}}_{\text{i}}^2}{{\lambda }_{\text{z}}h(r_{\text{o}}+r_{\text{i}})}\right]}_{\text{passive}}$. The thick dot, dash, and solid lines refer to the theoretical total, passive, and active stresses, respectively.

Table 1 summarizes material constants of the passive energy function (Eq. 1), whereas Table 2 lists material constants of the K⁺-induced active strain energy function (Eq. 2) for the six RCAs. The mean ± SE values of the outer diameters at transmural pressure of 80 mmHg in the active state were 3.41 ± 0.17 and 3.28 ± 0.24 mm at λ_z of 1.3 and 1.5, respectively, which were smaller than those in the passive state (i.e., 4.01 ± 0.16, P < 0.05; and 3.75 ± 0.20 mm, P = 0.16, respectively). Moreover, the mean ± SE values of the inner and outer diameters in no-load state are 1.69 ± 0.04 mm and 2.25 ± 0.08 mm, respectively, whereas the opening angles in zero-stress state have values of 126 ± 22°. At λ_z of 1.3 and pressure of 80 mmHg, the mean circumferential stress and strain (averaged through the wall) were 40.3 kPa and 0.80 in passive state and 35.9 kPa and 0.58 in active state, respectively. Given the decreased inner diameter and increased wall thickness, the isobaric constriction significantly decreased mean circumferential stress and strain.

Table 1.

Material constants of Fung's passive strain energy function

Animal No.	C1, kPa	a1	a2	a4	R2 for Tθθ passive	R2 for Tzz passive
Heart 1	1.27	2.61	1.59	0.6	0.94	0.73
Heart 2	0.94	2.86	2.09	1.14	0.90	0.94
Heart 3	0.87	3.39	3.91	0.42	0.94	0.94
Heart 4	1.51	2.89	3.29	0.43	0.74	0.90
Heart 5	0.89	3.18	2.82	0.75	0.72	0.74
Heart 6	1.25	2.59	1.55	0.59	0.96	0.94
Fit of all experimental data of hearts 1–6	1.33	3.08	2.48	0.49	0.96	0.90
Mean ± SE for hearts 1–6	1.12 ± 0.11	2.92 ± 0.13	2.54 ± 0.39	0.66 ± 0.11
CV	23.0%	10.8%	37.7%	40.8%

Material constants C₁, a₁, a₂, and a₄ are obtained from experimental measurements of right coronary artery using the L-BFGS method. R², correlation coefficient; T_θθ, circumferential first Piola-Kirchhoff stress; T_zz, axial first Piola-Kirchhoff stress; CV, coefficient of variation [(SD/mean) × 100].

Table 2.

Material constants of K⁺-induced active strain energy function (Eq. A11) in the pressure range of 60–200 mmHg

Animal No.	C2, kPa	b1	b2	b′	R2 for Tθθ active	R2 for Tzz active
Heart 1	3.80	0.109	0.212	21.2	0.78	0.83
Heart 2	3.00	0.105	0.185	21.9	0.55	0.79
Heart 3	6.24	0.156	0.297	14.0	0.57	0.61
Heart 4	2.49	0.112	0.127	24.2	0.66	0.74
Heart 5	6.78	0.110	0.209	20.1	0.64	0.74
Heart 6	3.52	0.108	0.21	21.3	0.73	0.85
Fit of all experimental data of hearts 1–6	4.18	0.120	0.182	20.3	0.71	0.78
Mean ± SE for hearts 1–6	4.31 ± 0.73	0.117 ± 0.008	0.207 ± 0.022	20.5 ± 1.4
CV	41.3%	16.6%	26.5%	16.8%

Material constants, C₂, b₁, b₂, and b′, are obtained from experimental measurements of right coronary artery using the L-BFGS method.

DISCUSSION

Active strain energy function.

A good fit of experimental measurements in Ca²⁺-free-induced vasodilation was obtained from Fung's passive model (W_passive in Eq. 1), as shown in Table 1 consistent with previous studies (23, 30). Unlike the passive strain energy function (5), the major obstacle for an active strain energy function at basal vessel tone is that one strain can sometimes correspond to more than one stress (12). The K⁺-induced vasoconstriction overcomes this issue and shows similar pseudoelastic properties to the vasodilated state (3, 4, 21). Hence, we proposed an active strain energy function of K⁺-induced SMC contraction in the circumferential and axial directions (W_active in Eq. 2), which was curve fitted to the biaxial mechanical measurements in RCAs. The biaxial experiment results in good fit to Eq. 2 in physiological pressure range, as shown in Table 2.

As the transmural pressure increases in physiological pressure range, the active stress-strain relationship is expressed as the Gaussian (normal) distribution, which has a maximal value when the passive and active pressures are in the range of 80–100 and 140–160 mmHg, respectively, as shown in Figs. 1 and 2. This relationship is consistent with the sliding actin-myosin molecules, where the number of active cross bridges is proportional to the active stress (5, 21). Although SMC contraction shows an in vitro optimal point at the passive pressure of 80–100 mmHg and at the active pressure of 140–160 mmHg, the in vivo optimal point for SMC contraction in coronary arteries needs further study.

The second derivative of the active strain energy function with respect to strain needs to be positive definite, i.e., $\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_{\text{z}}}{b_2}$ < b′ for Eq. 2, to satisfy the physical requirements of hyperelasticity (22). $\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_{\text{z}}}{b_2}$ < b′ for Eq. 2 is achievable as λ_θ < 1.64 at λ_z = 1.3 or λ_θ < 1.54 at λ_z = 1.5 (see material constants in Table 2). Hence, the proposed active strain energy function is convex and ensures physically meaningful mechanical behavior. The Fung's two-dimensional passive strain energy function is also found to be convex because material constants C₁ > 0, a₁ > 0, a₂ > 0, and a₁a₂ > a₄², as shown in Table 1.

Comparison with other active constitutive models.

In the physiological range of loading, parabolic function (6, 24, 36) and Gaussian (normal) distribution (1, 2, 28) were used to account for the active length-tension relationship of chemically induced SMC contraction only in the circumferential direction and did not consider the axial direction. In the circumferential direction, a combination of the passive tension and active tension multiplied by various sigmoidal regulation curves was assumed to predict the vasomotion at baseline (1, 2, 9). Experimental measurements, however, have shown that SMC contraction can generate active stresses in both circumferential and axial directions (27). Hence, multi-dimensional active constitutive relationships are required to capture the experimental measurements. Based on a biaxial mechanical test for basilar and carotid arteries, Wagner and Humphrey proposed two separate Gaussian relationships for T_θθ − λ_θ and T_zz − λ_z but did not consider the interaction of stresses and strains in different directions (29).

The proposed active strain energy function (Eq. 2) accounts for both circumferential and axial deformation and stress (Eq. A11) caused by K⁺-induced SMC contraction. The study not only extends the empirical active length-tension relationship from the circumferential direction (1, 2, 28) to the axial direction but also considered the interaction between different directions. A comparison of the stresses between λ_z = 1.3 and λ_z = 1.5 (Fig. 1A vs. Fig. 1B) shows the important effect of λ_z on T_θθ. Therefore, a combination of Fung's passive and present active strain energy functions can quantify the vessel vasoactivity more accurately than previous models.

Critique of method.

There are some limitations to the study. First, we only considered the K⁺-induced vasoconstriction and Ca²⁺-free-induced vasodilation in the present study. The prediction of the stress-strain relationship in basal tone requires further experimental studies. Second, the two-dimensional active strain energy function should be extended to three dimensions to include all normal and shear directions. Third, studies in smaller vessels are needed for comparison and for understanding of autoregulation of coronary circulation. Finally, these studies should be extended to diseased vessels.

In summary, to our knowledge, this study presents the first biaxial active mechanical properties of the coronary arteries. In conjunction, a biaxial active strain energy function was used to characterize K⁺-induced SMC contraction, which was expressed as a Gauss error function in the pressure range of 60–200 mmHg. The material constants were determined by the L-BFGS method to minimize the residuals between the theory and biaxial mechanical measurements. The active stresses have a maximal value when the passive pressure is in the range of 80–100 mmHg and the active pressure is in the range of 140–160 mmHg. Moreover, SMC contraction resulted in a reduction of overall mean stress and strain compared with the passive state.

APPENDIX

Biomechanical principles.

The blood vessel is assumed to be a thin-walled elastic tube deformed in the circumferential (θ) and axial (z) directions. Green strains are defined as:

$$E_{\theta \theta }=\frac{1}{2}({\lambda }_{\theta }^2-1)\text{and}{E}_{\text{zz}}=\frac{1}{2}({\lambda }_{\text{z}}^2-1)$$ A1

where λ_θ = D/D₀ and λ_z = L/L₀ are the circumferential and axial stretch ratios, respectively; D and D₀ are diameters in loaded and zero-stress states, respectively; and L and L₀ are axial lengths in loaded and no-load states, respectively. If the densities of vessel wall are identical in loaded and no-load state, first Piola-Kirchhoff and Cauchy stresses can be written as:

$$\begin{array}{ccc}\{\begin{array}{c}{T}_{\theta \theta }={\lambda }_{\theta }{S}_{\theta \theta }\\ T_{\text{zz}}={\lambda }_{\text{z}}{S}_{\text{zz}}\end{array}& \text{and}& \{\begin{array}{c}{\sigma }_{\theta \theta }={\lambda }_{\theta }^2{S}_{\theta \theta }\\ {\sigma }_{\text{zz}}={\lambda }_{\text{z}}^2{S}_{\text{zz}}\end{array}\end{array}$$ A2

where S_θθ and S_zz are the circumferential and axial second Piola-Kirchhoff stresses, respectively.

Strain energy function.

Fung's passive exponential-type pseudoelastic strain energy function (5) has been widely used to model the highly nonlinear and anisotropic behavior of blood vessels. Here, a K⁺-induced strain energy function is proposed as:

$$W_{\text{total}}=W_{\text{passive}}+W_{\text{active}}$$ A3

where W_passive is the strain energy of passive vessel; W_active is the active strain energy caused by the K⁺-induced smooth muscle contraction; and W_total is the total strain energy of the K⁺-induced active vessel.

Passive strain energy function.

In Fung's two-dimensional model without shear deformation, the strain energy per unit volume (W_passive) is given by:

$$W_{\text{passive}}=\frac{C_1}{2}[\exp (Q)-1]$$ A4

and

$$Q=a_1{E}_{\theta \theta }^2+a_2{E}_{\text{zz}}^2+2a_4{E}_{\theta \theta }{E}_{\text{zz}}$$ A5

where C₁, a₁, a₂, and a₄ are constants. The passive second Piola-Kirchhoff stresses are obtained by differentiating the strain energy with respect to the corresponding Green strains as:

$$\{\begin{array}{c}{S}_{\theta {\theta }_{\text{passive}}}=\frac{\partial W_{\text{passive}}}{\partial E_{\theta \theta }}=C_1(a_1{E}_{\theta \theta }+a_4{E}_{\text{zz}})\exp (Q)\\ S_{{\text{zz}}_{\text{passive}}}=\frac{\partial W_{\text{passive}}}{\partial E_{\text{zz}}}=C_1(a_1{E}_{\text{zz}}+a_4{E}_{\theta \theta })\exp (Q)\end{array}$$ A6

The passive first Piola-Kirchhoff stresses can be written as:

$$\{\begin{array}{c}{T}_{\theta {\theta }_{\text{passive}}}=C_1(a_1{E}_{\theta \theta }+a_4{E}_{\text{zz}})\sqrt{2E_{\theta \theta }+1}\exp (Q)\\ T_{{\text{zz}}_{\text{passive}}}=C_1(a_1{E}_{\text{zz}}+a_4{E}_{\theta \theta })\sqrt{2E_{\text{zz}}+1}\exp (Q)\end{array}$$ A7

where C₁, a₁, a₂, and a₄ for coronary arteries were determined by experimental measurements.

Active strain energy function.

The active strain energy function caused by the K⁺-induced SMC contraction is proposed as:

$$\begin{array}{c}{W}_{\text{active}}=C_2\left[\text{Erf}\left(\frac{\sqrt{2E_{\theta \theta }+1}-b_3}{b_1}+\frac{\sqrt{2E_{\text{zz}}+1}-b_4}{b_2}\right)-1\right]\\ =C_2\left(\text{Erf}\left(\frac{{\lambda }_{\theta }-b_3}{b_1}+\frac{{\lambda }_{\text{z}}-b_4}{b_2}\right)-1\right)\end{array}$$ A8

where C₂, b₁, b₂, b₃, and b₄ are constants, and Erf(X) is the Gauss error function. If we define b′ = $\frac{b_3}{b_1}+\frac{b_{\text{4}}}{b_2}$, Eq. A8 can be simplified as:

$$W_{\text{active}}=C_2\left[\text{Erf}\left(\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_{\text{z}}}{b_2}-b^{\prime }\right)-1\right]$$ A9

Equation A9 has four unknown parameters instead of five in Eq. A8. The active second Piola-Kirchhoff stresses are obtained by differentiating the strain energy with respect to the corresponding Green strains as:

$$\{\begin{array}{c}{S}_{\theta {\theta }_{\text{active}}}=\frac{\partial W_{\text{active}}}{\partial E_{\theta \theta }}=\frac{2C_2}{b_1\sqrt{\pi }}\frac{1}{\sqrt{2E_{\theta \theta }+1}}\exp \left[-{\left(\frac{\sqrt{2E_{\theta \theta }+1}}{b_1}+\frac{\sqrt{2E_{\text{zz}}+1}}{b_2}-b^{\prime }\right)}^2\right]\\ S_{{\text{zz}}_{\text{active}}}=\frac{\partial W_{\text{active}}}{\partial E_{\text{zz}}}=\frac{2C_2}{b_2\sqrt{\pi }}\frac{1}{\sqrt{2E_{\text{zz}}+1}}\exp \left[-{\left(\frac{\sqrt{2E_{\theta \theta }+1}}{b_1}+\frac{\sqrt{2E_{\text{zz}}+1}}{b_2}-b^{\prime }\right)}^2\right]\end{array}$$ A10

The active first Piola-Kirchhoff stresses are obtained by differentiating the strain energy with respect to the corresponding stretch ratios as:

$$\begin{array}{c}\{\begin{array}{c}{T}_{\theta {\theta }_{\text{active}}}=\frac{2C_2}{b_1\sqrt{\pi }}\exp (-Q^{\prime })\\ T_{{\text{zz}}_{\text{active}}}=\frac{2C_2}{b_2\sqrt{\pi }}\exp (-Q^{\prime })\end{array}\end{array}\text{with}{Q}^{\prime }={\left(\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_{\text{z}}}{b_2}-b^{\prime }\right)}^2={\left(\frac{{\lambda }_{\theta }}{b_1}\right)}^2+{\left(\frac{{\lambda }_{\text{z}}}{b_2}\right)}^2+2\frac{{\lambda }_{\theta }}{b_1}\frac{{\lambda }_{\text{z}}}{b_2}-2\left(\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_{\text{z}}}{b_2}\right)b^{\prime }+{(b^{\prime })}^2$$ A11

The material constants in Eq. A11 were determined by biaxial experimental measurements for coronary arteries.

GRANTS

This research was supported in part by National Heart, Lung, and Blood Institute Grants HL-087235 and HL-086400 (G. S. Kassab) and American Heart Association Scientist Development Grant 0830181N (Y. Huo).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: Y.H., Y.C., X.Z., X.L., and G.S.K. conception and design of research; Y.H., Y.C., and X.L. performed experiments; Y.H., Y.C., X.Z., X.L., and G.S.K. analyzed data; Y.H., Y.C., X.Z., X.L., and G.S.K. interpreted results of experiments; Y.H., Y.C., and X.L. prepared figures; Y.H., Y.C., and G.S.K. drafted the manuscript; Y.H., Y.C., X.L., and G.S.K. edited and revised the manuscript; Y.H., Y.C., X.Z., X.L., and G.S.K. approved the final version of the manuscript.