Permeation properties of the hair cell mechanotransducer channel provide insight into its molecular structure

Abstract

Mechanoelectric transducer (MET) channels, located near stereocilia tips, are opened by deflecting the hair bundle of sensory hair cells. Defects in this process result in deafness. Despite this critical function, the molecular identity of MET channels remains a mystery. Inherent channel properties, particularly those associated with permeation, provide the backbone for the molecular identification of ion channels. Here, a novel channel rectification mechanism is identified, resulting in a reduced pore size at positive potentials. The apparent difference in pore dimensions results from Ca²⁺ binding within the pore, occluding permeation. Driving force for permeation at hyperpolarized potentials is increased because Ca²⁺ can more easily be removed from binding within the pore due to the presence of an electronegative external vestibule that dehydrates and concentrates permeating ions. Alterations in Ca²⁺ binding may underlie tonotopic and Ca²⁺-dependent variations in channel conductance. This Ca²⁺-dependent rectification provides targets for identifying the molecular components of the MET channel.

the molecular identity of the hair cell mechanoelectric transduction (MET) channel remains unknown. Intrinsic, native channel properties will yield important clues as to its molecular nature and are required for validating any potential candidate channel. A fundamental difficulty in the biophysical characterization of the MET channel is delineating which properties are ascribed to the channel proper and which to underlying cytoarchitecture and accessory proteins. MET channels are located near the tips of actin-filled stereocilia that comprise the sensory hair bundle (Beurg et al. 2009). Deflection of the sensory hair bundle creates tension in a tip-link element that spans stereocilia of different heights. This tension is translated either directly or indirectly to MET channels, modulating their open probability. Tip-link tension is modulated by multiple adaptive processes such that MET channel kinetics are at least in part dictated by hair bundle mechanics (Ricci et al. 2005; Vollrath et al. 2007; Wu et al. 1999) and can be modulated by accessory proteins such as harmonin that are found at a distance from the channel (Grillet et al. 2009; Ricci et al. 2006). Thus pore properties such as rectification, ionic permeability, and binding sites within the pore are the most likely candidates to provide direct information about the molecular makeup of the MET channel.

MET channels are nonspecific cation channels (Corey and Hudspeth 1979; Ohmori 1985; Ricci and Fettiplace 1998) previously thought to exhibit little rectification or voltage dependence (Crawford et al. 1989; Farris et al. 2004; Kros et al. 1992; Ohmori 1985). Permeation follows a cation order inversely proportional to hydration energy, suggesting a highly electronegative outer face (Farris et al. 2004; Ohmori 1985). A large external vestibule is deduced from pharmacological data and sensitivity to changes in ionic strength (Beurg et al. 2006; Farris et al. 2004). Single-channel data indicate a large, nonspecific cation channel whose conductance varies tonotopically (Beurg et al. 2006; Crawford et al. 1991; Kros et al. 1992; Ricci et al. 2003). The tonotopic variation suggests heterogeneity in the molecular structure of the MET channel. Measured conductances also increased with lowered external Ca²⁺ concentration but did not vary with depolarization, a phenomenon whose mechanism remains to be elucidated (Ricci et al. 2003).

MET channels are highly permeable to Ca²⁺ (Beurg et al. 2006; Crawford et al. 1991; Denk et al. 1995; Lumpkin et al. 1997; Ohmori 1985; Ricci and Fettiplace 1998). Ca²⁺ blocks the MET channel with a half-block concentration (K_d) of 1 mM (Ricci and Fettiplace 1998). Monovalent and divalent ions interact within the pore such that permeation and block are a function of the monovalent ion present (Lumpkin et al. 1997; Ricci and Fettiplace 1998). Ca²⁺ binds within the channel pore at a distance about midway through the membrane electric field (Farris et al. 2004; Kros et al. 1992).

The present work extends our knowledge regarding permeation of the MET channel, focusing on the intracellular face of the channel. It provides insight into the mechanisms of several anomalous findings, including a single-channel conductance that varies with external Ca²⁺ concentration and the finding that permeant channel blockers are ineffective from the inner face of the channel. Data demonstrate that the MET channel is inwardly rectified under symmetrical ionic conditions. A unifying theory is presented to account for these findings as well as to potentially provide a mechanism for tonotopic variations in conductance. This theory posits binding sites within the pore for divalent ions. Binding to these sites obstructs permeation through the channel. The driving force for permeation is greater from the external face due to a large electronegative vestibule that concentrates ions, creating a rectified response under uniform ionic environments. Variations in binding affinity or in the electronegativity of the vestibule may be responsible for tonotopic differences in MET channel properties.

METHODS

Tissue preparation.

Auditory papillae were prepared as previously described (Farris et al. 2006; Ricci and Fettiplace 1997). Red-eared sliders (Trachemys scripta elegans), carapace length 3–5,″ were decapitated and the inner ear organs removed using procedures approved by the Institutional Animal Care and Use Committee at Stanford University and standards established by National Institutes of Health guidelines. The inner ear organs were placed into external solution containing (in mM) 125 NaCl, 0.5 KCl, 2.8 CaCl₂, 2.2 MgCl₂, 2 pyruvate, 2 creatine, 2 lactate, 2 ascorbate, 6 glucose, and 10 HEPES. The solution was buffered to pH 7.6 and had a final osmolality of 275 mosmol/kgH₂O. The tissue was pinned to the bottom of a Sylgard-coated dish, and the tectorial membrane was exposed to a solution containing 50 mM sucrose and 10 mM CaCl₂ for 15 min. The tectorial membrane was removed with an etched tungsten wire; the papilla was trimmed, placed into a recording chamber, and held in place with three single strands of dental floss. The recording chamber was perfused at 0.5–1 ml/min with external solution supplemented with 100 nM apamin (Calbiochem) to block the Cs⁺-permeable small-conductance Ca²⁺-activated K⁺ current (Tucker and Fettiplace 1996). A peristaltic pump (Gilson, Middleton, WI) was used for both bath and apical perfusions.

Drug application.

Drugs were applied to the apical surface through a 2-mm-diameter pipette whose tip was pulled to an external diameter of ∼75 μm. The pipette was placed about 100 μm away from the papilla. Flow was perpendicular to the sensitive axis of the hair bundle (Ricci and Fettiplace 1997), and flow rate was controlled using a Gilson peristaltic pump coupled through miniature solenoid valves (Lee Valves). Complete exchange of the apical fluid took ∼1.5 min. Drugs were purchased from Fisher, Calbiochem, and Sigma when necessary. Drugs were also applied using a picospritzer placed next to the bundle of choice. Here, the perfusion pipette had a tip diameter of 3–7 μm and complete exchange took seconds.

Recording procedures.

A large blunt pipette, filled with extracellular solution, was advanced into the papilla from the abneural edge while pressure was applied to the back end of the pipette to make a hole from which one to three cells could be removed to ensure good access. The location of the hole (d) is the relative position measured from the papilla apex. Unless otherwise stated, measurements were made from a high-frequency location (n = 226, d = 0.60 ± 0.02). An Axopatch 200b (Axon Instruments) was used for all recordings. The standard internal solution contained (in mM) 110 CsCl, 3 MgATP, 5 creatine phosphate, 1 BAPTA, 10 HEPES, and 2 ascorbate; pH was 7.2. Monovalent ions were substituted for Cs⁺ in a manner to maintain osmolality of ∼250 mosmol/kgH₂O. Series resistances averaged 15 ± 5 MΩ (n = 226) before compensation. Cell capacitance was 13 ± 2 pF (n = 186), giving voltage-clamp speeds of ∼138 μs. Junction potentials were measured and corrected offline, as was any residual series resistance. Cells with leak currents >50 pA, measured as nonmechanically gated inward current at −80 mV, were excluded. Cells were excluded if series resistance varied by >25% during the recording. All experiments were performed between 19 and 22°C.

Mechanical stimulation.

Hair bundles were stimulated with an acid-cleaned stiff glass probe attached to a piezoelectric stack (Physika Instruments) (Ricci et al. 2005). The voltage step to the piezo was filtered, with an 8-pole Bessel filter, at either 2 or 5 kHz. The glass probe, 10 μm in diameter, was placed near the bottom third of the bundle on the short stereocilia side so that the bundle was effectively pushed to open channels and pulled to close channels. When necessary, the probe could be placed on the back end of the hair bundle to push the bundle into the off position, thus ensuring reproducible movements that were not dependent on probe adherence. Activation protocols were driven by JClamp software.

Imaging.

Two-photon (2P) imaging was used to demonstrate access of large molecules into the stereocilia. The Ultima system (Prairie Technologies, Middlefield, WI) was used for the imaging with the Chameleon laser (Coherent). Two-photon microscopy reduces out-of-focus fluorescence, allowing for a reduced z volume. A ×100, 1.0-NA objective allowed for high-resolution imaging of the stereocilia. Dextrans (3,000 and 10,000 MW) coupled to AlexaFluor 488 were used to demonstrate diffusional access into the stereocilia. Prairieview software was used for data collection. Adobe Photoshop and Illustrator were used for data analysis.

Data analysis.

All data are means ± SD unless otherwise stated. The number of cells (n) is given with each set of data. Unless otherwise stated, current traces illustrated were averages of 16 sweeps for activation protocols and 4 sweeps for depolarization protocols. Data were collected with JClamp software and exported to Origin (Microcal) for analysis. Origin uses the Levenberg-Marquardt algorithm for fitting. Where appropriate, correlation coefficients are given as r² values. Unless otherwise stated, Student's two-tailed t-tests were used to assess statistical significance (P < 0.01).

Maximal currents were obtained by adding the current amplitudes measured from saturating positive and negative hair bundle displacements. Responses were determined to be saturating by fitting the peak current plotted against stimulus amplitude with the equation for a double Boltzmann function (Ricci and Fettiplace 1997):

$$I/I_{\max }=1/\left\{1+{\exp }^{\left(a_1{x}_1-a_{2}x\right)}\times \left[1+{\exp }^{\left(a_2{x}_2-a_{2}x\right)}\right]\right\}$$ (1)

where a₁ and a₂ determine the steepness and x_1,2 determines the position along the displacement axis for both processes. Generating a full activation curve ensured saturating stimuli. The current-voltage plots used only a single large positive and negative step, the amplitude predetermined from an activation curve generated at a holding potential of −80 mV.

Molecular dimensions.

The dimensions of the amine compounds were determined by building Corey-Pauling-Koltun (CPK) space-filling models (Adams et al. 1980; Farris et al. 2004). The orientation of the models was first determined using energy minimalization in Chem3D software (CambridgeSoft, Cambridge, MA). For the amine derivatives, the diameter was measured as the diameter of the smallest circle that the molecule could pass through.

A single-site blocking model was fit to current-voltage data obtained in the presence of different antagonists and n-alkyl-amine compounds of the form

$$I/I_{\max }=k\left[\exp \left\{\left[\left(1-\delta \right)\left(V-V_{\text{r}}\right)/V_{\text{s}}\right]-\exp \left[-\delta \left(V-V_{\text{r}}\right)/V_{\text{s}}\right]\right\}\right]$$ (2)

where k is a proportionality constant, δ is the fractional distance through the membrane electric field of the binding site, V_r is the reversal potential, and V_s reflects the steepness of rectification (Farris et al. 2004; Gale et al. 2001; Rusch et al. 1994; Woodhull 1973).

RESULTS

Pharmacology.

MET channel pharmacology is nonspecific, with blockers from a variety of chemical classes and channel types having similar efficacies (Farris et al. 2004; Kroese et al. 1989; Marcotti et al. 2005). Most blockers are either permeable blockers like FM1-43 and methylene blue (MB) (Farris et al. 2004; Gale et al. 2001; Meyers et al. 2003) or open channel blockers like curare (Farris et al. 2004; Glowatzki et al. 1997; Ricci et al. 2002; Rusch et al. 1994). Only amiloride and its derivatives bind to the MET channel at some external site (Lane et al. 1993; Rusch et al. 1994). Inexplicably, permeable blockers, thought to completely traverse the channel pore, like dihydrostreptomycin and FM1-43 are ineffective blockers from the inner face of the channel (Marcotti et al. 2005).

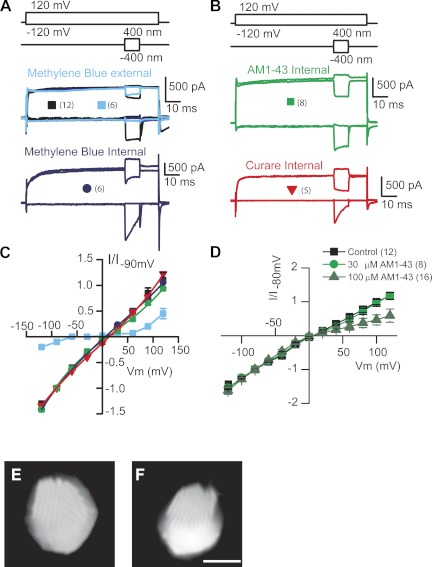
The goal of the present work was to characterize the inner face of the MET channel, identifying unique channel features that might shed light onto its unusual pharmacology and also its molecular underpinnings. Current-voltage plots were obtained by stepping the membrane potential between −120 and 120 mV in 20-mV increments and maximally mechanically stimulating the hair bundle during the voltage pulses. Figure 1 presents results from the permeable MET blocker MB (Farris et al. 2004). The protocol used for these experiments first steps the membrane potential and then elicits maximal positive and negative hair bundle deflections (Fig. 1A). The net current change is considered that elicited by MET channels. Depolarizations typically reduce the driving force for Ca²⁺ entry, and so the MET channels open as adaptation compensates for the reduced Ca²⁺. Thus at positive potentials, MET channels are largely being closed, whereas at hyperpolarized potentials, channels are largely being opened (Fig. 1, B–D). Control data, presented in black, illustrate comparable inward and outward MET currents at −120 and 120 mV. External application of 1 mM MB abolishes most of the inward current while having little effect on the outward current (Fig. 1A). The voltage dependence of external application of MB is described in Fig. 1C, where it presents as a classic permeable channel blocker. MET current is abolished at all but extreme voltages where driving force either allows MB to carry current (negative potentials) or else repels the compound from the channel (positive potentials). Previous data also demonstrated that MB loaded the hair cells rapidly, supporting the permeable block mechanism (Farris et al. 2004). Surprisingly, when applied intracellularly at comparable (1 mM) concentrations, MB had no effect (Fig. 1, B and E), despite its ability to traverse the channel.

Fig. 1.

Permeable channel blockers are ineffective from the internal face of the mechanoelectric transducer (MET) channel. A: protocol (top) shows the electrical (upper) and mechanical (lower) stimuli used to generate current-voltage plots for the MET channel. Middle traces show MET currents elicited in the absence (black) and presence (blue) of methylene blue (MB; 1 mM) externally. Bottom traces show another cell recorded with MB internally (1 mM). B: stimuli (top) and MET currents recorded with AM1-43 (middle) or curare (bottom) included in the recording pipette, showing no effect on MET currents. Symbols in A and B are key for the plots in C; number of recorded cells is presented in parentheses. C: summary of the current-voltage plots for A and B demonstrating no effect with intracellular blockers. Data are fit with a single-site binding model equation. Also included is extracellular MB application demonstrating a classic pattern for a permeant blocker with escape from block achieved at both depolarizing and hyperpolarizing potentials (Farris et al. 2004). D: current-voltage plots for higher concentrations of intracellular AM1-43 showing that at concentrations 30 times that of the extracellular K_d, there is a partial block of the current. Again, fits are to the single-site binding equation. Error bars are SE. E and F: 2-photon imaging of Alexa 488-conjugated dextrans (3,000 MW dextran in E, 10,000 MW dextran in F) demonstrates that large molecules can enter the stereocilia. Scale bar is 5 μm for both panels. Images show hair bundles from a top down (E) and a more side view (F) to show stereo cilia are loaded. I/I, normalized current; V_m, voltage potential.

Similar results were obtained with intracellular 30 μM AM1-43, a known permeable blocker of the channel (Fig. 1D) (Gale et al. 2001), and curare, an open channel blocker (Fig. 1B) (Farris et al. 2004). Doses greater than 10 times the K_d for AM1-43 were applied intracellularly with little effect. Partial block, ∼50% at +120 mV, could be obtained (Fig. 1D summarizes data for intracellular AM1-43) at intracellular concentrations of 30 and 100 μM (∼30 times Kd for extracellular block).

What might be responsible for these unusual results? One possibility is that the compounds cannot gain access to the stereocilia in high enough concentrations to affect a channel block when applied intracellularly. That is, a diffusion barrier might limit compound access to the channel. To test this possibility, fluorescently tagged (Alexa 488) dextrans of 3,000 and 10,000 MW were introduced via the patch pipette and the time course of diffusion into the stereocilia was monitored (Fig. 1, G and H). Two-photon microscopy was used for imaging because it allowed for the optical isolation of the upper portion of the hair bundle. Hair bundles were rapidly filled with both dyes, suggesting access was not an issue, and fill time ranged from 5 to 15 min, most closely correlating with access resistance of the patch pipette. The time course of access varied considerably between cells and was independent of access resistance (as long as <10 MΩ). Because of the variation, we did not quantify the time course of entry; however, hair bundles were typically filled (at an apparent steady state) by 20 min after breakthrough. Because the dextran sizes were much larger than any of the tested compounds, all experiments with intracellular compounds were not begun until at least 15 min after whole cell mode was reached.

Estimating the pore size.

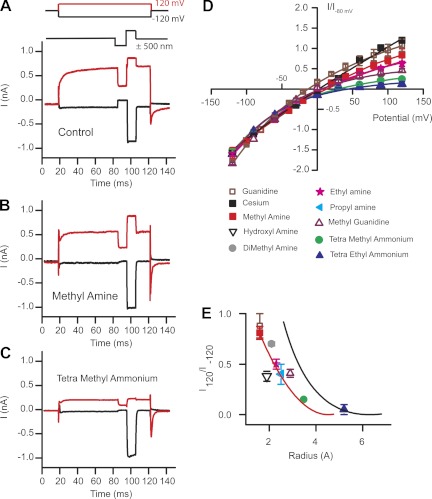
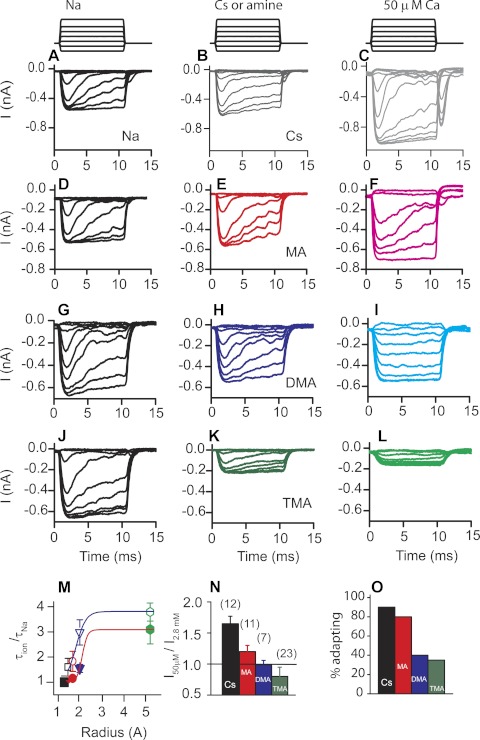
Given that these compounds have access to the channels, what other possibilities might explain the lack of effectiveness as intracellular channel blockers? Perhaps the pore size is larger at hyperpolarized potentials compared with depolarized potentials, thus allowing larger molecules to permeate. Given that the channel was believed to be nonrectified, this hypothesis initially suggested a difference between permeation and conductance, much like that found for gap junction channels (Gong and Nicholson 2001). To address this hypothesis, experiments were performed to estimate the MET channel pore size using small amine molecules. This approach was pioneered for sodium and nicotinic acetylcholine channels (Dwyer et al. 1980; Hille and Schwarz 1978) and was previously used to estimate hair cell MET channel pore dimensions from the external face (Farris et al. 2004). Internal solutions were made with monovalent amines of different sizes, with size estimated as previously described from CPK models (Adams et al. 1980). To assess permeation at the internal face, current-voltage plots were generated and relative currents compared at the +120-mV membrane potentials. An immediate observation was that compounds previously reported as permeable from the external face were not permeable from the internal side (Farris et al. 2004). For example, trimethylammonium carried >40% of the current compared with that carried by sodium from the outside but carried <20% when applied intracellularly, and larger amines were not permeable at all. Thus smaller sized amines were used and corresponding current-voltage plots created (Fig. 2). From these data a plot of amine radius vs. relative current at +120 mV was generated and plotted in Fig. 2E. Fitting this plot empirically to

$$I_x/I_{\text{Cs}}=A\left(1-a/r^2\right)$$ (3)

where a is the radius of the amines, r is the radius of the channel, and A is a scaling factor (Adams et al. 1980; Farris et al. 2004; Sun et al. 1997) revealed a pore diameter of 0.6 ± 0.2 nm (red line is fit to data), a value one-half that measured when amines were applied externally and estimates made at −120 mV (black solid line represents estimates made with external amines, Fig. 2E) (Farris et al. 2004).

Fig. 2.

Estimates of the pore size from the inner face produce a smaller value than when probed from the external face. A: stimulus protocol shows voltage steps (top) and mechanical stimulation (bottom; red indicates positive potential). Control currents were recorded with Cs⁺ internal and Na⁺ external. B: methylamine used as the internal charge carrier with Na⁺ external. C: tetramethylammonium used internally with Na⁺ external. D: current-voltage plots normalized to the −80-mV current level for various internal amine compounds. Data are fit with single-site binding equation for each compound. E: current obtained at +120 mV normalized to that at −120 mV plotted against radius of the intracellular amine as determined from Corey-Pauling-Koltun (CPK) space-filling models (Adams et al. 1980; Farris et al. 2004). The solid black line represents estimates of pore size made previously by varying external charge carrier (Farris et al. 2004). Fits to the data using Eq. 2 (solid red line) gave a pore radius of 0.6 ± 0.2 nm. All error bars are SE; n values of at least 5 cells were obtained for each compound tested.

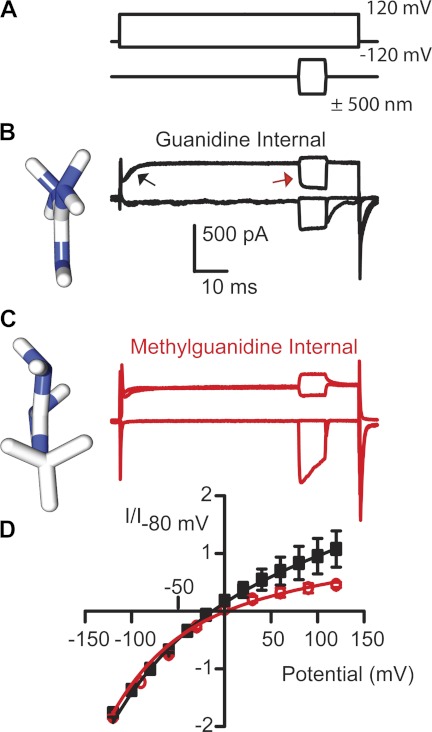
While exploring smaller amine permeations, we observed a difference between guanidine and methyl guanidine (Fig. 3). Guanidine is a planar molecule (see molecular models in Fig. 3, B and C), so selecting a dimension for the plot in Fig. 2 depends on the orientation of the molecule when entering the pore. Methyl guanidine is not planar but actually geometrically symmetrical, so equal permeabilities of the two guanidines would suggest permeation was independent of orientation, whereas methyl guanidine being less permeable would suggest the pore is asymmetric and that guanidine access is via its short axis (Dwyer et al. 1980). Figure 3 shows a clear difference in permeation between guanidine and methyl guanidine, thus supporting the argument that the pore shape is not uniform. An unexpected and inexplicable finding was that 40% of the cells with methyl guanidine as the major internal cation showed a loss of adaptation. Depolarization leads to MET channel activation due to the reduction in Ca²⁺ entry and can be seen as a shift in resting open probability (see Figs. 1 and 3). Figure 3B illustrates this process in two ways: MET currents first activate when the cell is depolarized (see black arrow) and secondly from the relative current that is turned on or off by the mechanical stimulation (also indicated by red arrow). When guanidine was used as the monovalent ion, there was little MET current activated when the cell was depolarized. This difference was also reflected in the response to mechanical stimulation where most current needed to be turned on, similar to that at hyperpolarized potentials.

Fig. 3.

Comparisons of guanidine and methyl guanidine demonstrate the MET channel pore is asymmetrical. A: stimulus protocol with voltage steps (top) and mechanical stimulation (bottom). Guanidine (B) and methyl guanidine (C) were used as the internal charge carrier. Molecular models, obtained from PubChem and oriented in Chimera (UCSF software), are displayed at left next to the current responses to illustrate the planar orientation of guanidine compared with methyl guanidine. D: current-voltage plots demonstrate a rectification with methyl guanidine, not apparent with guanidine (n = 6 for each). Data were fit with the single-site binding equation. Error bars are SE.

A role for hydration energy.

Because current amplitude through an ion channel might be expected to be proportional to pore size (although there are exceptions), observing a different pore diameter at depolarized potentials compared with hyperpolarized potentials was surprising. Figure 2 clearly shows that the functional pore size at positive potentials is about one-half that previously estimated at hyperpolarized potentials (Farris et al. 2004). Given that the channel is considered neither rectified, that is, current flow is considered similar inwardly as well as outwardly, nor voltage dependent, where conformational changes might be predicted to alter pore properties, how might the channel diameter be regulated assuming no voltage-dependent conformational change? It is possible that the channel shows some rectification, meaning that it passes current better in one direction than the other; in this case, inward current is predicted to be carried better than outward current because of the different pore size. A candidate mechanism for this rectification is the presence of an electronegative external pore that is able to concentrate ions, thus increasing driving force and current flow through the channel. The MET channel is posited to have such an electronegative external vestibule (Beurg et al. 2006; Farris et al. 2004).

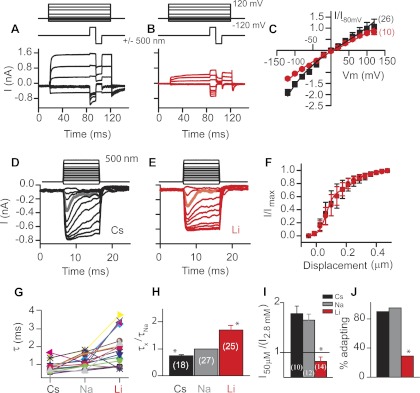
To test this hypothesis, currents were compared between ions with different hydration energies, because hydration energy will dictate the ions' sensitivity to this external pore. The electronegative nature of the external channel face would predict that ions with lower hydration energies would pass through the channel more readily from the outside than from the inside (assuming the internal face of the channel was not equally electronegative). As ions move through an ion channel, their hydration shell will be stripped based on the hydration energy of the ion and the electronegativity of the pore. Comparisons between Cs⁺ (low hydration energy) and Li⁺ (high hydration energy) are given in Fig. 4, A–C, where both current-voltage plots and current-displacement plots are analyzed. Currents were larger at negative potentials for Cs⁺ than for Li⁺, whereas there was no difference in current amplitudes at positive potentials (data were normalized to currents obtained with Na⁺ as the monovalent ion at −80 mV). Inward Cs⁺ current flow was about twice that of outward current flow, consistent with the apparent difference in pore diameter, creating a channel rectification. These data support the idea that ion flow through the MET channel is augmented by the electronegative external vestibule and indicate that previous arguments for a nonrectified channel were confounded by comparisons made under asymmetrical ionic environments. These data demonstrate that the MET channel is inwardly rectified, an important characteristic when identifying the molecular components of this channel.

Fig. 4.

Comparisons of molecules with different hydration energies suggest inward current was influenced by hydration whereas outward current was not. A–C: MET currents with either Cs⁺ (black, A) or Li⁺ (red, B) as internal and external charge carriers in response to maximal bundle deflections used to generate current-voltage plots (C). Current-voltage plots generated from A and B were fit with the equation for a single-site binding model (n shown in parentheses). Cs⁺ shows greater inward current than Li⁺ but no difference in outward current. D–F: mechanical activation curves (stimulus protocol shown at top) for cells with Cs⁺ (black, D) and Li⁺ (red, E) as the monovalent ion present extracellularly. Currents are larger and adaptation faster with Cs⁺ as the charge carrier. Gray trace in D and orange trace in E highlight the change in adaptation rate. Normalized current-displacement plots (F) show no significant difference between Cs⁺ and Li⁺ (n = 7 for Li⁺ and 6 for Cs⁺). Plots were normalized to account for reduced current with Li⁺ as the charge carrier. Current-displacement plots were fit to the equation for a double Boltzmann plot. Adaptation time constants (τ) were measured by fitting a single exponential to the current decay in response to a stimulus evoking <50% of the maximal current. Individual cell responses (G) and average values (H) show the time constant varies depending on the monovalent ion present. I: comparisons between different monovalent ions in current amplitude when extracellular Ca²⁺ was lowered to 50 μM. Values are averages (n shown in parentheses). J: plots of the percentage of cells retaining adaptation when extracellular Ca²⁺ was lowered for cells with differing extracellular monovalent ions. *P < 0.01.

Ca²⁺ binding in the pore.

Unmasking rectification based on hydration energy supports a functional significance to the external vestibule and also provides data for how driving force for current flow is increased for inward current but does not directly explain the mechanism underlying the different pore size estimates. Because previous data have demonstrated that Ca²⁺ permeates and blocks the MET channel, one possibility is that the enhanced driving force described above facilitates the removal of the Ca²⁺ block, thus enhancing current flow and altering the apparent pore size. Given that the MET channel is a multi-ion pore where ion interaction within the pore dictates permeation, it is hypothesized that the properties of the monovalent ion present will dictate its ability to remove Ca²⁺ from the channel pore. Thus the hypothesis is that the difference in pore estimates may be related to pore size varying when Ca²⁺ is bound compared with when it is unbound.

Adaptation manifests itself as a decrease in current amplitude during constant stimulation and is a Ca²⁺-dependent process (Eatock et al. 1987; Ricci and Fettiplace 1998). Therefore, adaptation can be used as an indicator of Ca²⁺ permeation through the channel. Adaptation rates, as measured from single-exponential fits to stimuli that activate <50% of the maximal current, were faster when Cs⁺ was used extracellularly than when either Na⁺ or Li⁺ were used, suggesting the monovalent ions were altering Ca²⁺ permeation. Individual cell results are plotted in Fig. 4G as well as summary data (Fig. 4H) to demonstrate that all but one cell showed adaptation getting faster in Cs⁺ compared with Li⁺. The picture emerging from these data is one where ions are concentrated at the external vestibule of the channel, increasing driving force; this enhanced driving force allowed for more efficient current passing through the channel pore. The augmented driving force promoted current flow in part by promoting the ability of the monovalent ion to drive Ca²⁺ away from its pore binding site into the cell; thus adaptation got faster. Further insight into the mechanism of the rectification is gained by comparing the effects of altering external Ca²⁺ concentrations on the change in current amplitude. Lowering external Ca²⁺ has long been known to increase the MET current by alleviating a Ca²⁺ pore block (Crawford et al. 1991; Ricci and Fettiplace 1998). A comparison of the change in current amplitude, plotted as the ratio of peak current in 50 μM Ca²⁺ to that in 2.8 mM, reveals a larger ratio in Cs⁺ than in Na⁺ and that Li⁺ as the major monovalent ion does not result in a current increase but actually causes a reduction in current amplitude (Fig. 4I). Similarly, the ability to maintain adaptation in low external Ca²⁺ is also a function of the monovalent ion (Fig. 4J). These data indicate that the channel rectification may be established by the ability of the monovalent ion to remove Ca²⁺ from its binding site, an ability that is at least in part dictated by the hydration energy of the ion. It is postulated that the ability to move ions inward was augmented by the external vestibule increasing driving force compared with when current is outward and no vestibule is present to concentrate ions.

Ionic size matters for permeation.

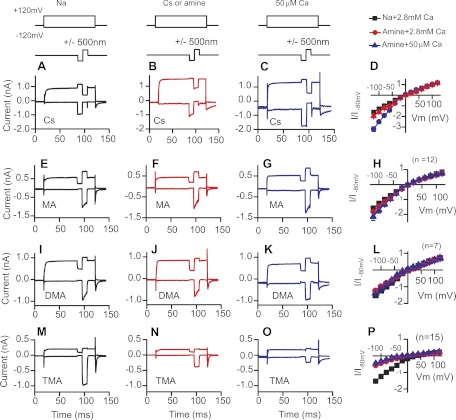
To this point, data demonstrate that the hydration energy of the monovalent ion alters Ca²⁺ permeation and that this enhances channel rectification. How significant is ionic size in this process? To better investigate the role of steric hindrance in regulating channel permeation, amine molecules of similar and larger sizes (1.5 to 3 times the size of Na⁺) than Na⁺ were used and external Ca²⁺ concentration was varied. Since Ca²⁺ blocks permeation, lowering Ca²⁺ reduces the blocking ability and provides a better estimate of monovalent ion permeation. Comparisons between external Ca²⁺ concentrations are a convenient way of assessing the efficacy of the block. In addition, because internal Ca²⁺ concentration is quite low, lowering external Ca²⁺ provides the most symmetrical ionic conditions from which to investigate channel rectification. Current-voltage plots were created as previously described under conditions where the intracellular ion was varied from Cs⁺ to methylamine (MA) to dimethylamine (DMA) to tetramethylamine (TMA). Similarly, the external ion was varied to match the internal ion, and external Ca²⁺ was lowered from 2.8 mM to 0.05 mM as described above (Fig. 5). Experiments with Cs⁺ demonstrate that Cs⁺ was more permeant than Na⁺ and that lowering external Ca²⁺ increased the inward current even further (Fig. 5, A–D). Under the most equivalent ionic conditions technically possible with internal and external Cs⁺ and low extracellular Ca²⁺, the MET channel was inwardly rectified, passing inward current three times better than outward current, supporting the finding that the pore size appears different when probed from the inside compared with the outside. MA replacement gave qualitatively similar results as experiments with Cs⁺, but changes were not as dramatic such that in low Ca²⁺ the rectification was about twofold (Fig. 5, E–H), indicating that MA was not as efficient at removing the Ca²⁺ block from the channel. With DMA, no rectification was observed and the current magnitude did not change when external Ca²⁺ was lowered, indicating that Ca²⁺ pore block remained (Fig. 5, I–L).Thus the driving force for DMA was the same internally and externally, suggesting DMA was not concentrated in the vestibule to the point of providing enough energy to remove Ca²⁺ from its binding site. This is critically important as it supports the conclusion that the rectification is provided by Ca²⁺ binding and not by a conformational change in the channel. Increasing the amine size further (TMA) reduced current flow significantly, and again, lowering Ca²⁺ further reduced current amplitudes (Fig. 5, M–P). The reduction in current when Ca²⁺ was lowered is likely due to the majority of current in TMA being carried by Ca²⁺ so that when its concentration is reduced, the concomitant reduction in driving force reduces current flow. Together these data suggest that permeation through the channel was critically dependent on the ability to remove the Ca²⁺ channel block. It supports the hypothesis that the size as well as the hydration energy of the monovalent ion is important for regulating Ca²⁺ permeation and channel rectification.

Fig. 5.

Size of the extracellular monovalent ion dictates rectification of the MET channel. Currents are shown with Cs⁺ (A–C), methylamine (MA) (E–G), dimethylamine (DMA) (I–K), and TMA (M–O) as the intracellular and extracellular cation. Stimulus protocol is given above responses. A, E, I, and M show control data with Na⁺ as the extracellular ion but with different intracellular monovalents. B, F, J, and N show these cells with their corresponding monovalent ion extracellularly and intracellularly. C, G, K, and O show these same cells with lowered external Ca²⁺ (0.05 mM) and the same intracellular and extracellular monovalent ion. D, H, L, and P: current-voltage plots summarizing the changes observed in their respective rows.

Effects of these amines on Ca²⁺ permeation were further investigated by comparing adaptation in the presence of these different-sized amines and at high and low Ca²⁺ concentrations. In this case, inward current flowing through the external channel face was probed. Figure 6 provides examples and summarizes these data. Similar to Cs⁺, responses with MA showed rapid adaptation that slowed when Ca²⁺ was lowered. Current magnitude increased when external Ca²⁺ was lowered but to a lesser extent than with Cs⁺. When DMA was used, adaptation slowed in high Ca²⁺, indicating reduced Ca²⁺ permeation. When external Ca²⁺ was lowered, adaptation was eliminated, further suggesting Ca²⁺ permeation was limited with DMA as the external ion. Current amplitude with external DMA and lowered Ca²⁺ did not change (Fig. 6N), supporting the argument that Ca²⁺ block was not removed so that Ca²⁺ was not permeating. TMA reduced current amplitude in high Ca²⁺ and also when Ca²⁺ was lowered, suggesting the Ca²⁺ block was enhanced by TMA compared with Na⁺ and that lowering Ca²⁺ did not alleviate the block. Plotting the relative change in adaptation against monovalent ion radius showed a strong correlation, suggesting that Ca²⁺ permeation was regulated by the size of the external monovalent ion (Fig. 6M). A similar plot existed for the data collected in lowered Ca²⁺; the plot was simply shifted leftward. Similarly, relative currents obtained for each monovalent ion as a function of Ca²⁺ also decreased with the size of the monovalent ion (Fig. 6N). And finally, the proportion of cells having time-dependent adaptation was reduced with the size of the monovalent ion, again indicative of a response where monovalent ions were regulating divalent Ca²⁺ entry. Together these data provide further support that channel rectification was provided by Ca²⁺ blocking the channel pore. The difference in driving force as dictated in part by the external vestibule's electronegativity served to better remove Ca²⁺ from its binding site, enhancing permeation from the external side compared with the internal side.

Fig. 6.

Size of the monovalent ion regulates Ca²⁺ permeation of the MET channel. Similar to Fig. 5, examples of cells recorded with different monovalent ions intracellularly and extracellularly and in the presence of lowered extracellular 0.05 mM Ca²⁺ are shown for Cs⁺ (A–C), MA (D–F), DMA (G–I), and TMA (J–L). Stimulus protocol is given above responses. A, D, G, and J show control traces with extracellular Na⁺ and different intracellular cations as indicated. B, E, H, and K show these same cells with their corresponding monovalent presented extracellularly as well. C, F, I, and L show these same cells with their corresponding monovalent ion and lowered external Ca²⁺ (50 μM). Adaptation slows as the monovalent ion gets larger, indicating a reduced Ca²⁺ entry. A summary of the changes in adaptation time constant is represented in M as the ratio of time constants measured with the various monovalents referenced to the control Na⁺ external solution (filled circles). Open circles similarly represent the change in time constant for data obtained when Ca²⁺ was lowered. Color coding is consistent throughout: Cs⁺, black; MA, red; DMA, blue; and TMA, green. The ability of Ca²⁺ to block the MET channel is assessed in N where the current ratio for the various ions is compared in response to lowering external Ca²⁺. Na⁺ and TMA were statistically different from each compound; MA and DMA were not different from each other (n is given in parentheses and is the same for M–O). O shows the fraction of cells adapting when external Ca²⁺ was lowered to 0.05 mM.

DISCUSSION

Data presented here provide new insight into the molecular underpinnings of the MET channel by characterizing the internal face of the pore and reevaluating ion permeation. These new data allow for a unifying hypothesis to be presented regarding ionic permeation of the MET channel that accounts for all known channel properties. It also provides predictions as to molecular components of the channel that can be used to probe the identity of candidate channels.

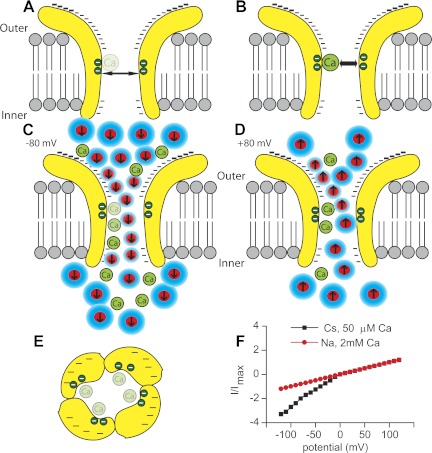
The MET channel has long been considered a nonrectifying channel based on a very linear current-voltage response when measured in asymmetrical ionic environments (Beurg et al. 2006; Farris et al. 2004; Kros et al. 1992; Ohmori 1985). Data presented here come closest to providing a symmetrical environment by using Cs⁺ both intracellularly and extracellularly and lowering extracellular Ca²⁺ to 50 μM. Further lowering of Ca²⁺ is difficult due to the sensitivity of the tip link to Ca²⁺. Under these conditions, inwardly flowing current at −120 mV was more than three times greater than that measured at 120 mV, clearly demonstrating the channel's rectifying properties (Fig. 7), suggesting that previous estimates were confounded by the use of asymmetrical ionic environments.

Fig. 7.

Schematic representation of the MET channel depicts a hypothesis as to how channel rectification occurs and the role of Ca²⁺ in channel permeation. A illustrates the channel in low external Ca²⁺ so that the internal Ca²⁺ binding site is empty and the pore diameter is larger, whereas B presents high external Ca²⁺ where the binding site is filled, creating a smaller pore diameter. Minus signs indicate electronegativity on the external vestibule. C depicts ion permeation at negative potentials where dehydration (shown as the reduction in water, blue) associated with the ions increases driving force and electrostatic repulsion of Ca²⁺ from its binding site, whereas D shows permeation at positive potentials where flow is reduced because there is less energy to move Ca²⁺ from its binding site. E presents a topdown view with the potential binding sites on each subunit shown as the green circles and the electronegative external vestibule depicted by minus signs. The asymmetrical pore is based on the guanidine data. F presents channel rectification under symmetrical ionic conditions (black) compared with previous nonrectified responses under asymmetrical conditions (red). In this depiction, Cs⁺ is also the internal ion.

Support for the conclusion of a rectifying channel arises from the estimated inner face pore size. The obtained pore diameter on the inner face is about one-half that estimated for the external face of the channel (Farris et al. 2004). It is posited here that the difference in pore size estimates arises from the ability of Ca²⁺ to bind to a site on the channel within the electric field and that binding occludes the pore (Fig. 7). Ca²⁺ is driven from this site electrostatically by monovalent ions permeating the channel. Thus no conformational change of the channel is necessary to explain the difference in pore size. The energy associated with removal of the Ca²⁺ block derives from the driving force for the monovalent ion and the electrostatic repulsion created as the monovalent ion approaches the Ca²⁺. Data presented here, however, cannot clearly delineate between these two energy sources, and likely both are relevant. A hypothesis to explain the observations would be that more energy is available at the external face of the channel than from its inner face. Ca²⁺ is thus more easily driven into the cell than out of the cell, resulting in rectified current flow. Figure 7 illustrates this hypothesis, incorporating known properties of the channel, and is consistent with present and existing data.

The energy difference is posited to arise from a greater driving force for monovalent ion entry at negative potentials compared with positive. This difference is predicted to arise from the highly electronegative external channel vestibule (Beurg et al. 2006; Farris et al. 2004; Ohmori 1985), dehydrating and concentrating the ions, thus increasing their driving force. Dehydration from the external face and not the inner face of the channel may also allow the ions closer access to the bound Ca²⁺ such that electrostatic repulsive forces are greater (Fig. 7). The reduced access to the bound Ca²⁺ could also explain the ineffectiveness of permeable channel blockers placed in the intracellular solution, because the effective concentration is reduced and the Ca²⁺ access limited. Dihydrostreptomycin is one of these permeable blockers shown to be ineffective from the inner face (Marcotti et al. 2005). A two-energy barrier model was presented for this data where the energy barrier for entry from the external face was lower compared with the energy barrier for access from the inner channel face. This model and these data are consistent with the hypothesis proposed here. In our hypothesis, the difference in energy barriers derives from the strong electronegative external vestibule creating a larger driving force for displacing Ca²⁺ at negative potentials compared with positive potentials.

Present data can also explain the unusual finding that the single-channel conductance increases with lowered extracellular Ca²⁺ (Ricci et al. 2003). Data presented here suggest that Ca²⁺ may physically occlude the pore at negative potentials and that Ca²⁺ removal results in a larger pore and thus a larger conductance. Depolarizations, which also increase the channel open time, do not result in an increased conductance because Ca²⁺ is not removed from its binding site. The driving force at positive potentials is not large enough to remove the Ca²⁺ block, so conductance does not change.

Previous work demonstrated a tonotopic variation in single-channel conductance (Ricci et al. 2003) that is thought to originate from different combinations of channel subunits. Data provided here may provide insight into how this happens. A simple possibility is that the number of Ca²⁺ binding sites varies between tonotopic locations such that not all MET channel subunits have equal binding sites. However, this possibility predicts the relative Ca²⁺ block to be tonotopic as well. This might be expected to be observable as a greater block at low-frequency locations, which does not appear to be the case (Beurg et al. 2006; Ricci 2002). Another possibility remaining to be explored is that a change of Ca²⁺ affinity varies the time the channel spends in the bound, lower conductance state. This effect could lead to altered permeation due to Ca²⁺ without the requisite change in absolute block. Difficult experiments, titrating Ca²⁺, are required to evaluate this hypothesis. A third possibility is that there are tonotopic differences in electronegativity of the vestibule resulting in reduced driving force for current flow in low-frequency channels. A corollary might be that the vestibule size varies; however, a lack of difference in affinity of channel blockers between frequency locations likely precludes this possibility as well (Farris et al. 2004; Ricci 2002).

Similar to the tonotopic differences described and the possible mechanisms that might underlie these variations are the possible differences in channel properties between end organs and species. Data presented here are from turtle auditory papilla, largely at a characteristic frequency range of 400 Hz. Hair cells are required to operate at an amazingly broad range of frequencies, and it is unlikely that a single channel type or subunit is going to operate across the orders of magnitude of frequency range covered between vestibular and auditory organs. However, given the strong similarities between permeation properties across species, it is likely that similar channel subtypes are involved with subtle changes responsible for differences in conductance and permeability. From this perspective all hair cell models are valid for characterizing MET properties, and turtle provides an excellent example because of the ease with which the MET current can be separated from other currents across potentials with minimal pharmacological interventions.

Divalent binding sites within ion channel pores have been investigated in a variety of channel types such as Ca²⁺ channels, NMDA channels, cyclic nucleotide-gated channels, and transient receptor potential channels (TRPs) (Corry et al. 2001; McCleskey 1999; Owsianik et al. 2006; Sather et al. 1994; Zarei and Dani 1994). These binding sites can effect permeation of monovalent ions as well as dictate selectivity through the channel. A ring of glutamate residues in the pore-forming region of these channels is often critical for determining ion selectivity as well as providing drug binding sites and altering relative permeation. We postulate a similar mechanism in the MET channel such that mutations of these residues should have dramatic effects on permeation that could be used to unequivocally identify the molecular nature of the channel. Consistent with this hypothesis are previous investigations of Ca²⁺ permeation suggesting a two-binding site model for the MET channel (Fig. 7) (Ricci and Fettiplace 1998). Although potentially useful for determining the molecular identity of the MET channel, binding sites within the channel pore are relatively common and so do not in and of themselves point to a particular channel class as a candidate.

Many channels also have vestibules, some internal, some external, and these often play a role in ion selectivity (Roux et al. 2004). Here, too, negatively charged residues within the vestibule often have large effects on channel permeation, again offering a site for intervention when identifying the channel (Corry et al. 2000; Jogini and Roux 2005). For example, 5HT3A receptor channels have aspartate residues in their outer vestibule that alter inward but not outward permeation (Livesey et al. 2008, 2011). NMDA receptors also have external vestibules where charged residues dictate Ca²⁺ permeation (Watanabe et al. 2002). The ubiquitous nature of channel vestibules, however, does not direct attention to any particular class of ion channels. However, the similarity in mechanism of generating charged vestibules provides a means of probing candidate MET channels by altering potentially significant amino acids to influence Ca²⁺ permeation and conductance, thus validating their role in mechanosensitivity.

The molecular identity of the MET channel has long been sought but largely has been limited technically by the paucity of channels available in the native tissue. Although in the big picture this channel is one protein of many that is critical to the proper functioning of sensory hair cells, identification of this molecule is an important question in that it will provide a means to investigate the mechanisms of mechanosensitivity and adaptation as well as the physiological relevance of the process. To date, a variety of potential candidates have been identified, but none have stood the test of time. Amiloride sensitivity, mechanosensitivity in Caenorhabditis elegans, and localization based on immunogold labeling at stereocilia tops have implicated channels of epithelial Na⁺ channel (ENaC) class (Furness et al. 1996; Goodman and Schwarz 2003; Hackney et al. 1992; Jorgensen and Ohmori 1988; Rusch et al. 1994). However, variations in conductance, lack of expression in sensory hair cells, and normal hearing and mechanotransduction in knockout animals of the α-subunit have made this family less of a focus (Corey 2006; Corey and Garcia-Anoveros 1996; Rusch and Hummler 1999). TRP channels have also received considerable attention, largely based on them being a mechanosensitive component in Drosophila and zebrafish (Atiba-Davies and Noben-Trauth 2007; Castiglioni et al. 2011; Grimm et al. 2007; Nagata et al. 2008; Sidi et al. 2003; Takumida and Anniko 2009; van Aken et al. 2008; Walker et al. 2000). TRPA1 was also a short-lived candidate for the mechanotransducer channel, discounted by knockout data having no phenotype (Bautista et al. 2006; Corey et al. 2004; Kwan et al. 2006; Nagata et al. 2005; Prober et al. 2008). TRP channels remain a highly investigated class of channels despite little evidence supporting a role in hair cell mechanotransduction. To date, biophysical evidence of similarities between candidate channels and the hair cell native channel have not been used to support or negate potential candidacy, with none of the above candidates having biophysical properties similar to the native hair cell (either previously known data or those presented herein). Single-channel data suggest the hair cell MET channel has multiple subtypes such that homomeric expression systems used for comparing biophysical properties of potential candidate channels may not provide data similar to those for the native channel despite the tested component being a channel subunit (Beurg et al. 2006; Ricci et al. 2003). The most recent candidates are not TRP channels; TMC1 and 2 (Kawashima et al. 2011) are viable channel candidates despite the lack of evidence to support their ability to act as ion channels. Recent data have also identified a novel class of ion channels, Piezo 1 and 2, which comprise a distinct class of mechanically sensitive channels (Coste et al. 2010). The initial properties of these channels make them similar to but distinct from the native hair cell channel, but whether additional variants exist that alter properties remains to be determined. Given the complexity of defining unequivocally the molecular nature of the MET channel, it is clear that a combination of targeted molecular, genetic, and electrophysiological tools is needed. Existing data regarding the native MET channels provide a template from which molecular and genetic experiments can be designed to identify and test potential candidate proteins. Perhaps more subtle experiments altering channel permeation, rather than knocking down a subunit completely, are needed to directly implicate a protein as the MET channel proper.

In summary, the data presented demonstrate that the hair cell MET channel is inwardly rectified. The rectification derives from the ability to drive Ca²⁺ from a binding site within the pore. The driving force for current flow is greater from the external face because of a large external vestibule that is highly electronegative compared with the inner face of the channel pore. The difference in driving force leads to apparent changes in channel pore size. These channel properties are most likely intrinsic to the channel and may serve as sites for modification when identifying the molecular nature of the MET channel.

GRANTS

This work was supported by National Institutes of Health (NIH) Grant R01 003896 (to A. J. Ricci) and NIH Core Grant P30 44992.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: B.P., J.W., M.E.S., C.L., and A.J.R. performed experiments; B.P., J.W., M.E.S., C.L., and A.J.R. analyzed data; B.P., J.W., M.E.S., and C.L. edited and revised manuscript; B.P., J.W., M.E.S., C.L., and A.J.R. approved final version of manuscript; A.J.R. conception and design of research; A.J.R. interpreted results of experiments; A.J.R. prepared figures; A.J.R. drafted manuscript.