Efficient generation of reciprocal signals by inhibition

Abstract

Reciprocal activity between populations of neurons has been widely observed in the brain and is essential for neuronal computation. The different mechanisms by which reciprocal neuronal activity is generated remain to be established. A common motif in neuronal circuits is the presence of afferents that provide excitation to one set of principal neurons and, via interneurons, inhibition to a second set of principal neurons. This circuitry can be the substrate for generation of reciprocal signals. Here we demonstrate that this equivalent circuit in the cerebellar cortex enables the reciprocal firing rates of Purkinje cells to be efficiently generated from a common set of mossy fiber inputs. The activity of a mossy fiber is relayed to Purkinje cells positioned immediately above it by excitatory granule cells. The firing rates of these Purkinje cells increase as a linear function of mossy fiber, and thus granule cell, activity. In addition to exciting Purkinje cells positioned immediately above it, the activity of a mossy fiber is relayed to laterally positioned Purkinje cells by a disynaptic granule cell → molecular layer interneuron pathway. Here we show in acutely prepared cerebellar slices that the input-output relationship of these laterally positioned Purkinje cells is linear and reciprocal to the first set. A similar linear input-output relationship between decreases in Purkinje cell firing and strength of stimulation of laterally positioned granule cells was also observed in vivo. Use of interneurons to generate reciprocal firing rates may be a common mechanism by which the brain generates reciprocal signals.

reciprocal activity between populations of neurons has been commonly observed in neuronal circuitry. In neural regions where sensory information is encoded, the reciprocal activity of different sets of neurons has been postulated to be a basis behind contrast enhancement. Visual, auditory, chemical, and tactile distinguishability has been attributed to the enhanced activity of one set of neurons relative to the suppressed activity of another set of neurons (Calford and Semple 1995; Mastronarde 1983; Moore and Nelson 1998; Priebe and Ferster 2008; Wilson and Mainen 2006). For neural regions that coordinate motor behavior, the reciprocal activity of different populations of neurons plays roles in representing motor actions and coordinating muscle force (Allen and Tsukahara 1974; Georgopoulos et al. 1986).

Given the ubiquity of reciprocal signals, it is essential to understand how these signals are generated. On the one hand, reciprocal activity in two populations of neurons may be the effect of two inversely correlated inputs. As one set of inputs provides increased excitation to one set of neurons, another set of inputs provides reduced excitation to a second set of neurons. Alternatively, a more efficient and precise method of generating reciprocal activity in neurons may be through lateral inhibition (Andersen et al. 1964). By scaling the strength of inhibition with excitation and targeting specific populations of neurons, lateral inhibition could in principle decrease the activity of one set of neurons in proportion to the increased activity of another set of neurons. While efficient, this method of reciprocal signal generation requires that inhibition has an equal yet opposite effect to that of excitation despite the many differences between how excitation and inhibition are transmitted to and integrated in neurons.

To determine whether lateral inhibition can generate reciprocal signals in populations of principal neurons, we first found a brain region that has a circuitry representative of many regions but is amenable to investigation. The cerebellar cortex has an anatomical center-excitation surround-inhibition circuitry similar to other brain regions, but one that is highly stereotypic. Mossy fibers provide sensory and cortical inputs to granule cells, which have ascending axons and parallel fibers that form direct excitatory inputs to only a restricted set of Purkinje cells in the sagittal plane. Molecular layer interneurons also receive excitation from granule cells and inhibit Purkinje cells lateral to the activated population of Purkinje cells (Dizon and Khodakhah 2011; Gao et al. 2006) (Fig. 1A). Thus a common set of granule cells could in principle generate reciprocal simple spike activity in two populations of Purkinje cells. Indeed, recordings from awake behaving animals routinely demonstrate populations of Purkinje cells with reciprocal simple spike firing rates, each of which encodes movement-related variables (Frysinger et al. 1984; Lisberger and Fuchs 1978; Mano and Yamamoto 1980; Medina and Lisberger 2008).

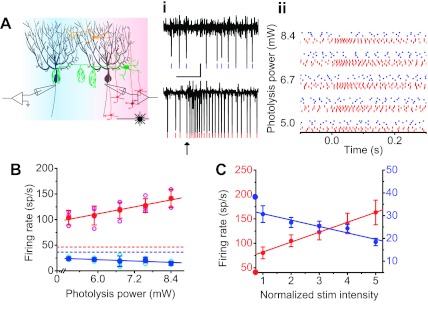
Fig. 1.

Activity of single patches of granule cells can drive the reciprocal firing rates of laterally positioned Purkinje cells. A: direct input from a single patch of granule cells (depicted as red cells) provides net excitation (red zone) to Purkinje cells (depicted in black). Feedforward inhibition by interneurons (green and yellow cells) also allows the same patch of granule cells to inhibit a second group of Purkinje cells (blue zone). i: A pair of Purkinje cells were monitored extracellularly in response to photorelease of glutamate on a single patch of granule cells. ii: Raster plot of the activity of the same 2 cells in response to varying stimulus strengths. B: maximum and minimum instantaneous firing rates (each trial: open circles; mean ± SD: filled circles) of the Purkinje cell pair recorded in A as a function of stimulation strength (photolysis power). Solid line represents the linear regression (red: R = 0.68, P = 0.002; blue: R = −0.41, P = 0.088). Dashed lines: baseline firing rate of each cell = 46.4 sp/s and 36.4 sp/s. C: average (±SE) minimum instantaneous firing rate of all 5 Purkinje cells examined as a function of photolysis power. Solid line represents the linear regression (red: R = 0.99, P < 0.001; blue: R = −0.94, P = 0.018). The position of the symbols on the y-axis indicates the average baseline firing rate of cells receiving excitation (41.9 ± 2.1 sp/s) and inhibition (38.5 ± 0.7 sp/s) (unpaired t-test: P = 0.24).

Here we show that the strength of a single set of granule cell inputs is reciprocally encoded in the complementary firing rates of two groups of Purkinje cells. This efficient method of signal generation is made possible by individual components that linearly propagate activity within the granule cell → molecular layer interneuron → Purkinje cell disynaptic pathway.

EXPERIMENTAL PROCEDURES

All experiments were reviewed and approved by the Albert Einstein College of Medicine Institutional Animal Care and Use Committee (IACUC).

Cerebellar slice preparation.

Wistar rats aged P13–P22 were decapitated under halothane anesthesia. Despite anatomical and synaptic development (McKay and Turner 2005; Pouzat and Hestrin 1997) and granule cell migration (Fujita 1967) throughout this age range, no differences were observed in the experimental results. Brains were quickly removed and placed in ice-cold artificial cerebrospinal fluid (aCSF) containing (in mM) 125 NaCl, 2.5 KCl, 26 NaHCO₃, 1.25 NaH₂PO₄, 1 MgCl₂, 2 CaCl₂, and 11 glucose (pH 7.4 with 95% O₂-5% CO₂). Three hundred-micrometer sagittal slices of the cerebellar vermis were made with a modified Oxford vibratome. Slices were kept in aCSF warmed to 35°C for 1 h and then kept for up to 4 h at room temperature until use.

In vitro electrophysiological recordings.

Slices were placed in a chamber perfused with aCSF at a rate of ∼1.5 ml/min; aCSF was warmed to 35 ± 1°C and bubbled with 95% O₂-5% CO₂. Previous work has shown that these conditions are equivalent to experiments with a flow rate of 5 ml/min (Walter and Khodakhah 2006). For photolysis experiments, aCSF was preequilibrated with ∼250 μM MNI-caged glutamate. Cerebellar neurons were visualized with an upright BX61WI Olympus (Tokyo, Japan) or an upright Zeiss microscope with ×40, 0.8 NA water-immersion objectives using infrared optics.

Single-unit extracellular recordings were made from cerebellar neurons from all vermal lobules with a homemade differential amplifier and glass pipettes filled with aCSF. Purkinje cells were identified by their large somata (∼20 μm) and placement between the granule and molecular layers. Molecular layer interneurons were identified by their round somata of 5–10 μm and placement in the molecular layer. Basket cells were defined as cells in the inner one-third of the molecular layer and stellate cells in the outer two-thirds. Recording electrodes were placed near the axon hillock of Purkinje cells, resulting in spike heights of ∼400 μV. Recording electrodes were placed near the somata of molecular layer interneurons, resulting in spike heights of 75–200 μV. For dual recordings the average tip-to-tip distance between the two electrodes was ≈320 μm.

Whole cell recordings were made with a Cairn Optopatch amplifier (Faversham, UK). Electrodes were made from borosilicate glass and pulled to a resistance of 1–3 MΩ when filled with internal solution. The internal solution contained (in mM) 130 Cs-gluconate, 10 CsCl, 10 HEPES, and 3 MgATP (pH 7.2 with CsOH), and Purkinje cells were clamped at a command voltage (V_cmd) of 0 mV. Series resistance (typically 6.5–8 MΩ) was compensated by 50–60%. For any one cell, the voltage-clamp error between any set of stimulus intensities was typically ≪10%. The recorded currents were blocked by bath application of GABA_A and GABA_B blockers picrotoxin (Sigma, St. Louis, MO) and CGP55845 (Tocris, Ellisville, MO), respectively.

Photostimulation with glutamate photolysis.

Slices were preequilibrated with ∼250 μM MNI-caged glutamate (Tocris), which is neither an agonist nor an antagonist for glutamate receptors (Canepari et al. 2001). Ultraviolet light from a continuous multiline krypton ion laser (Innova 300C; Coherent, Santa Clara, CA) was set at 500–600 mW. An acousto-optical modulator (Neos) scaled the intensity (0–100%) and gated the light to 1 ms. The laser light was transmitted to the microscope through a fiber-optic cable, collimated, and positioned via a pair of galvos (Cambridge Technology, Cambridge, MA). This was all driven by custom-written software. The laser light was focused to a 40-μm-diameter spot on the granule cell layer. A power meter positioned at the end of the objective measured the maximum power of this spot to be ∼1.4% of the source laser light power (Walter et al. 2009). For each cell, stimulation occurred at 20- or 10-s intervals, with ∼10 trials for every photolysis power. Stimulation intensities were randomly administered. In none of the experiments did the baseline firing rate of the cells change appreciably from the beginning to the end of the experiment (paired t-test: Purkinje cells P = 0.13; interneurons P = 0.25). Moreover, for each neuron, the averaged evoked response from the first set of trials was comparable to the average response from the last set of trials (paired t-test: Purkinje cells P = 0.12; interneurons P = 0.13), indicating that there were no time-dependent changes in the responses of neurons. Photostimulation of a patch of granule cells results in their asynchronous activation such that the resulting excitatory postsynaptic currents (EPSCs) recorded in the target Purkinje cells are noisy and clearly composed of individual synaptic events, take 10–15 ms to peak, and are severalfold longer in duration than EPSCs evoked by electrical stimulation of granule cells (Walter and Khodakhah 2006, 2009). The time course of asynchronous activity of granule cells achieved with photostimulation is very comparable to that seen in vivo after their activation by mossy fibers with a discrete sensory input (Chadderton et al. 2004; Jaeger and Bower 1994).

The cerebellar cortex incorporates inhibition from Golgi cells and feedforward excitation from unipolar brush cells (UBCs). To determine whether lateral inhibition was sufficient in generating reciprocal signals, our investigation focused on inhibition from molecular layer interneurons. In our preparation photolysis of glutamate primarily activated granule cells and not UBCs because of the paucity of UBCs in our vermal slices and also the lower excitability of the UBC relative to the granule cell (Takacs et al. 1999) (for details see Walter et al. 2009). The short action of glutamate photolysis also resulted in minimal effects of Golgi cells. Indeed, it has been demonstrated previously that under our experimental conditions selective blockade of Golgi-mediated inhibition of granule cells minimally affects the excitatory or inhibitory responses of Purkinje cells (Dizon and Khodakhah 2011).

Both extracellular and whole cell data were acquired at 10 kHz with an analog-to-digital converter (PCI-MIO-16XE-10; National Instruments, Austin, TX), using custom software written in LabVIEW (National Instruments).

In vivo electrophysiological recordings.

Single-unit extracellular recordings were made from Purkinje cells in 8- to 12-wk-old C57BL/6 mice under 1–3% isoflurane anesthesia. For these recordings, a 1.5-mm-diameter hole was drilled through the skull at −6 mm from bregma and ±1 mm from midline. Great care was taken to leave the surface of the cerebellum untouched for surface recordings. Recordings were made in lobules 4 and 5. Purkinje cells were identified by electrode depth and the presence of complex spikes and pauses. Only Purkinje cells located ∼250 μm deep from the surface of the cerebellum were recorded. These arrangements allowed for accurate placement of the stimulation electrode in the granular layer and for effective blockade of GABA_A receptors by topical application of 2 mM SR95531.

Individual units were acquired with a multitrode with gold cores (0.7–2 MΩ; Thomas Recording) or with platinum-quartz electrodes (2–3 MΩ; Thomas Recording) and a homemade amplifier. To target the underlying granular layer, stimulation was 100–200 μm deeper than the recording site, either through one of the multitrode's sites or with a separate tungsten wire positioned ≈350 μm lateral to the recording site in the sagittal plane. Data were filtered (80–500 Hz high pass, 10 kHz low pass) and sampled at 20 kHz. Spikes were sorted with Offline Sorter software (Plexon, Dallas, TX) using principal component analysis and consideration of additional parameters such as spike shape and peak and valley amplitudes and half-width. Only sorted spikes that could be reasonably unambiguously identified to be from one neuron were included in the analysis.

Data analysis.

The data acquisition and analysis software was written with LabVIEW, and, when needed, further analysis was performed in MATLAB (MathWorks, Natick, MA) and Origin (OriginLab, Northampton, MA). Maximum and minimum instantaneous firing rates were determined as the inverse of the briefest and longest interspike intervals after stimulus, respectively. The interspike intervals considered as part of the response were the intervals that started from the first spike before the stimulus to 1 s later, well beyond the longest conductance recordings (see Fig. 4E). For Purkinje cells, the baseline firing rate was calculated by averaging 24 instantaneous firing rates before the response. For interneurons, because of their slow firing rate, 15–24 prestimulus instantaneous firing rates were averaged to obtain the baseline firing rate. The change in the number of spikes was quantified as the number of spikes 500 ms before the stimulus (i.e., baseline firing rate multiplied by 500 ms) subtracted from the number of spikes during 500 ms after the stimulus. Poststimulus time histograms (PSTHs) were made by dividing the average number of spikes per trial over a bin size of 20 ms. The duration of the response was determined from the PSTHs and was from the time of stimulus to the first instance when the firing rate returned to or below the mean baseline rate. The number of interneuron spikes in the response was the integral of this response duration. For conductance measurements, currents were divided by the 65-mV driving force (determined by the subtracting the calculated E_Cl from V_cmd). Conductance areas were the integral from the time of stimulus to 500 ms later.

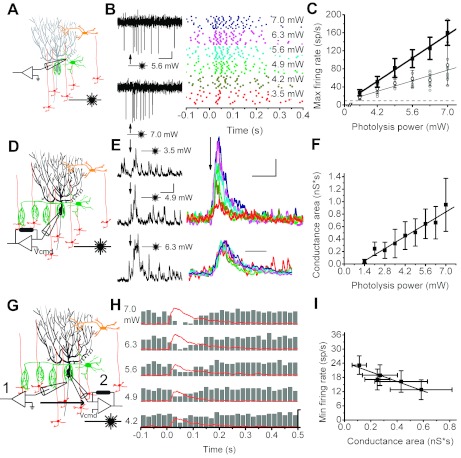
Fig. 4.

Feedforward inhibition is mediated by linear input-output components. A and B: a patch of granule cells positioned immediately underneath an interneuron was photoactivated while the activity of the target interneuron was monitored extracellularly. The concentration of photoreleased glutamate was varied by altering the laser power to change the strength of granule cell inputs. Raw data scale bar: 100 ms, 50 μV. In the raster plots the stimulus was delivered at t = 0. C: maximum firing rate of the interneuron recorded in B (gray circles; mean ± SD: black circles) and average data from 10 interneurons (mean ± SE: black squares) Solid lines: linear regression. Dashed line: average baseline firing rate (9.69 ± 2.13 sp/s). D and E: synaptically evoked GABAergic changes produced by photolytic activation of a patch of granule cells were measured in a voltage-clamped Purkinje cell [command voltage (V_cmd) = 0 mV]. Black traces show the single-trial GABAergic conductances, whereas top set of colored traces show averaged conductances at photolysis powers indicated in B. Scale bar: 100 ms and 2 nS. Bottom set of colored traces is normalized to allow comparison of their kinetics (scale bar: 50 ms). F: average (±SE) of GABAergic conductance areas plotted as a function of photolysis power. Solid line: linear regression. G: response of the same Purkinje cell to varying strengths of activation of a patch of granule cells was first recorded extracellularly and then under voltage clamp (V_cmd = 0 mV). H: poststimulus time histogram of a cell examined as detailed in G to varying strength of granule cell input with its corresponding GABA conductance traces overlaid. Stimulus was delivered at t = 0. Y-scale: 65 sp/s and 18 nS. I: average Purkinje cell minimum firing rate as a function of the average GABA conductance area (n = 5 cells) obtained from experiments outlined in G and H.

Behavioral studies.

To explore the consequences of acute pharmacological blockade of cerebellar cortical GABA_A receptors on motor function, behavioral experiments were performed on adult C57BL mice. Under isoflurane anesthesia four 1.5-mm-wide holes were drilled in the skull at positions corresponding to paravermal and lateral lobes of the cerebellum (−6.9 mm from bregma ± 0.750 mm from midline and −6.9 mm from bregma ± 1.7–2 mm from midline) (the average length of time taken was <5 min for the first surgery and <2 min for the second surgery). To expose the cerebellar cortex to drugs, the holes were filled with Gelfoam sponges (Pfizer) (Marshall and Lang 2009) soaked in 10–25 mM SR95531 or its vehicle. Animals were sutured with the Gelfoam sponges left inside the holes, allowed to fully recover from anesthesia for at least 15 min, and tested on the balance beam and observed in an open field. The average duration of time that each animal was able to maintain its balance on the beam (1-cm diameter) was determined from 10 consecutive trials. Each animal served as its own control, as it received vehicle-soaked Gelfoams first and then the vehicle-soaked Gelfoams were removed and replaced by SR95531-soaked Gelfoams. The approximate time between the application of vehicle- and SR95531-soaked Gelfoams was 1 h. In separate experiments we found that application of SR95531 without prior exposure of the animal to vehicle produced comparable motor dysfunction, suggesting that exposure to vehicle first did not worsen the symptoms by producing additional damage. However, we did not include these experiments in our analysis because SR95531 does not readily wash out within our experimental time frame, and therefore it was not possible to use the same animal as its own control. The SR95531 solution also contained 0.01% methylene blue, which allowed postmortem confirmation of the location of holes and the approximate depth of the cerebellar cortex exposed to the drugs. The dye diffused less than ≈500 μm into the cerebellum, making it extremely unlikely that any GABA receptors in the deep cerebellar nuclei were affected by the blocker.

Statistical analyses were performed with Origin software. To examine the linearity of the data, we calculated the Pearson's correlation coefficient (R). P values were acquired based on R and the degrees of freedom. To determine these parameters, raw data were used for individual cells and mean and standard error of the mean for averaged data. Linear regressions were also determined from these data. For statistical significant differences, we used two-sample independent and paired t-tests.

RESULTS

A common granule cell input can generate reciprocal signals.

For the two reciprocal cerebellar signals to be complementary to one another, they must encode the strength of granule cell inputs with similar but mirroring functions. While other features such as excitation-induced pauses (Steuber et al. 2007) or the pattern of activity of Purkinje cells (Shin et al. 2007) have been proposed to encode cerebellar information, studies in awake behaving animals have shown only changes in the firing rate of Purkinje cells to be correlated with movement-related parameters (Lisberger and Fuchs 1978; Mano and Yamamoto 1980; Medina and Lisberger 2007, 2008; Pasalar et al. 2006; Thach 1970; Yamamoto et al. 2007). For direct excitation it has been demonstrated that the firing rate of Purkinje cells is a linear function of the input strength of granule cells (Walter and Khodakhah 2006). Thus as a test of the hypothesis that a single set of granule cell inputs can generate both of the reciprocal Purkinje cell firing rates, we determined whether the input strength of granule cells is concurrently encoded in two sets of Purkinje cells as increases and decreases in firing rate (Fig. 1A).

We simultaneously recorded the spontaneous firing (Llinas and Sugimori 1980; Raman and Bean 1999) of two Purkinje cells in vitro in cerebellar slices and activated a 40-μm patch of granule cells by photoreleasing glutamate. This stimulation paradigm results in the asynchronous activity of granule cells with a time course (Walter et al. 2009; Walter and Khodakhah 2006) comparable to that seen in vivo after the activation by mossy fibers with a discrete sensory input (Chadderton et al. 2004; Jaeger and Bower 1994). The size of the photolysis spot was chosen to be comparable to the spatial extent of synapses formed by a single (or a few) mossy fiber branch. The location of the activated patch of granule cells was selected to be immediately below one of the recorded Purkinje cells and ≈200–300 μm lateral to the other (Fig. 1A). Earlier studies have shown that with such an arrangement the Purkinje cells positioned above the activated patch of granule cells are excited by the granule cells whereas those located laterally are inhibited by disynaptic inhibition (Dizon and Khodakhah 2011; Gao et al. 2006). The experimental conditions ensured that the concentration of photolyzed glutamate was a linear function of the photolysis power such that the input strength of the patch of granule cells was a linear function of the photolysis power (Walter et al. 2009; Walter and Khodakhah 2006). We estimate that the range of photolysis powers used corresponds to asynchronous activation of 200–650 granule cells with each pulse (Walter and Khodakhah 2006, 2009). As expected, asynchronous activation of a patch of granule cells promptly increased the firing of the Purkinje cell directly above the site of photolysis and decreased the firing rate of the Purkinje cell positioned laterally (Fig. 1Ai). With stronger photolysis powers, greater changes in firing rate were observed in each of the two cells (Fig. 1Aii). Since the instantaneous firing rate of Purkinje cells is a linear function of movement-related variables in diverse behavioral tasks (Lisberger and Pavelko 1986), we used this parameter to quantify the responses. For the Purkinje cell receiving direct excitation, the maximum instantaneous firing rate increased as a linear function of the strength of granule cell inputs (Walter and Khodakhah 2006) (Fig. 1B, R = 0.68, P = 0.002). For the Purkinje cell receiving disynaptic inhibition, the minimum instantaneous firing rate decreased as a linear function of the strength of granule inputs (Fig. 1B, R = −0.41, P = 0.088). Naturally, the two reciprocal firing rates in this cell were linear functions of each other (data not shown, R = −0.89, P = 0.045). In the average of all cell pairs examined (n = 5), both maximum and minimum instantaneous firing rates were each linear functions of the strength of granule cell inputs (average, Fig. 1C: R = 0.99, P < 0.001; R = −0.94, P = 0.018, respectively) and to each other (average: R = −0.95, P = 0.011).

In vivo recordings show that the firing rate of Purkinje cells is modulated during behavior within a range as high as ≈250 spikes per second (sp/s) and as low as ≈5 sp/s (Lisberger and Fuchs 1978). For increases in firing rate, the physiologically relevant dynamic range is thus from a baseline firing of ∼50 sp/s to ∼250 sp/s. On the other hand, the dynamic range for decreases in activity spans from baseline to ∼5 sp/s. We found that the reciprocal Purkinje cell firing rates generated by stimulation of a patch of granule cells were sufficient to smoothly alter the firing rates of the two populations of Purkinje cells to levels somewhat comparable to those observed during behavioral tasks (Frysinger et al. 1984; Lisberger and Fuchs 1978; Thach 1970). However, while activity of a patch of granule cells comparably changed the firing rate of the complementary Purkinje cells within their respective dynamic range, the absolute ranges were fourfold different. When we examined the efficacy with which a single patch of granule cells reciprocally modulated the activity of Purkinje cells, we found that the slopes of increases and decreases in activity as a function of input strength were largely reflections of each other (Fig. 1C; slope of each function within its respective range: excitation 20.3 ± 5.6; inhibition −14.1 ± 3.6). Thus our experiments show that direct excitation and disynaptic inhibition provide the requisite circuitry for the cerebellum to encode the strength of the same granule cell inputs as two sets of reciprocal Purkinje cell firing rates. Within the context of cerebellar motor coordination, the reduced range of the reciprocal decrease in the Purkinje cell firing rate may appropriately match the asymmetric properties of muscles during relaxation compared with contraction (Todorov 2000), although it is likely that these signals are further fine-tuned by gain modifications by downstream neurons.

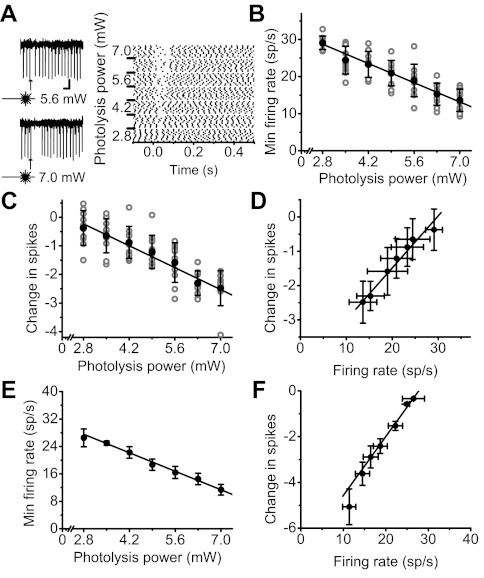
To scrutinize the relationship between granule cell input strength and decreases in Purkinje cell activity in more detail, we recorded from 14 additional Purkinje cells while activating lateral granule cell patches throughout a larger range of photolysis powers and with a larger number of repetitions at each input strength. Within this range, the minimum poststimulus instantaneous firing rate of the Purkinje cell shown in Fig. 2 decreased linearly as a function of the strength of granule cell inputs (Fig. 2, A and B; R = −0.83, P < 0.0001). Compared with its baseline spontaneous rate, inhibition transiently reduced the number of action potentials fired by the Purkinje cell after the stimulus. In the cell shown, we found that the change in the number of spikes after stimulus (for a 500-ms period) was also a linear function of the strength of granule cell inputs (Fig. 2C; R = −0.79, P < 0.0001) and was directly correlated with the minimum instantaneous firing rate (Fig. 2D; R = 0.98, P < 0.0001). The average minimum instantaneous firing rate and the change in the number of spikes fired after stimulus of all 14 Purkinje cells examined was linearly correlated with the input strength of granule cells (Fig. 2, E and F; R = −0.99, P < 0.0001 and R = 0.98, P < 0.0001, respectively). Thus Purkinje cells linearly encode the strength of inhibitory inputs both in their minimum instantaneous firing rate and also as a reduction in the number of spikes after inhibition.

Fig. 2.

Feedforward inhibition enables Purkinje cells to linearly encode the strength of granule cell inputs in their firing rate. A, left: response of an extracellularly monitored Purkinje cell to photoactivation of a patch of granule cells by glutamate photolysis at 2 different laser powers. The location of the activated patch of granule cells was chosen to inhibit the activity of the target Purkinje cell. Scale bar: 50 ms, 100 μV. Right: raster plot of responses of the same cell to varying stimulation strengths (at t = 0). B: minimum instantaneous firing rate (each trial: gray circles; mean ± SD: black circles) of the Purkinje cell recorded in A as a function of photolysis power. Solid line represents the linear regression. Baseline firing rate = 37.0 sp/s. C: change in the postresponse number of spikes (each trial: gray circles; mean ± SD: black circles) of the Purkinje cell recorded in A as a function of photolysis power. Solid line represents the linear regression. D: reduction in the number of spikes fired by the cell after activation of a patch of granule cells as a linear function of its minimum instantaneous firing rate (mean ± SD). Solid line: linear regression (R = 0.98, P < 0.0001). E: average (±SE) minimum instantaneous firing rate of all 14 Purkinje cells examined as a function of photolysis power. Solid line represents the linear regression. Average baseline firing rate = 40.4 ± 2.1 sp/s. F: average change (n = 14 cells) in the number of spikes fired after stimulus by Purkinje cells as a linear function of the average minimum instantaneous firing rate in the same cells (mean ± SE). Solid line: linear regression (R = 0.98, P < 0.0001).

Firing rate of Purkinje cells decreases as a linear function of granule cell inputs strength in vivo.

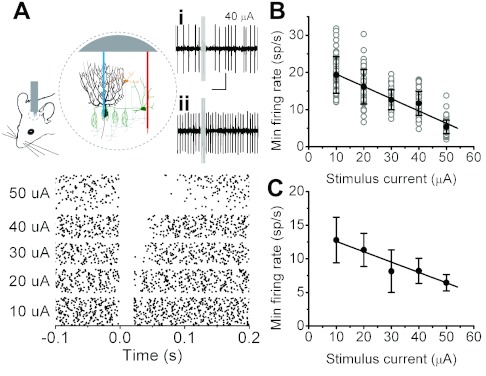
To determine whether the linearity of the disynaptic granule cell → molecular layer inhibition to Purkinje cells is maintained in vivo under background parallel fiber and interneuron activity, we monitored the discharge rate of single Purkinje cells in isoflurane-anesthetized mice and, as in the experiments in brain slices, stimulated granule cells positioned laterally in the same sagittal plane. Electrical activation of granule cells resulted in immediate decreases in the firing rate of the target Purkinje cell (Fig. 3Ai). Similar to that seen in cerebellar slices in vitro, the minimum poststimulus instantaneous firing rate of Purkinje cells was a linear function of the stimulus intensity (Fig. 3B; R = −0.80, P < 0.0001), a consistent finding in all cells examined (Fig. 3C; R = −0.98, P = 0.003; n = 5). No inhibitory responses were detected when GABA_A receptors were pharmacologically blocked (Fig. 3Aii) (n = 5), suggesting that, under our experimental conditions, fast GABAergic synaptic transmission was the sole mediator of decreases in Purkinje cell firing rate. In agreement with prior work demonstrating a critical role for cerebellar cortical GABA_A receptors in generating motor coordination signals (Wisden et al. 2009), their acute pharmacological blockade in awake behaving mice resulted in ataxia and impaired balance (average time on a balance beam reduced from 234.5 ± 38.1 s under control conditions to 26.8 ± 8.0 s when GABA receptors were blocked; P = 0.02, n = 4).

Fig. 3.

Purkinje cell firing rate linearly encodes the strength of granule cell inputs via inhibition in vivo. A, top: response of an extracellularly recorded Purkinje cell in vivo to electrical stimulation of a lateral patch of granule cells (3 stimuli at 100 Hz, each consisting of a 200-μs, 40-μA pulse stimulus denoted by gray rectangle) in the absence (i) and presence (ii) of a GABA_A blocker. Scale bar: 100 ms, 200 μV. Bottom: raster plots of the same cell at various stimulus strengths. B: minimum instantaneous firing rate (each trial: gray circles; mean ± SD: black circles) of the Purkinje cell recorded in A as a function of the stimulus intensity. Solid line represents the linear regression (R = −0.80, P < 0.0001). Baseline firing rate = 35.2 sp/s. C: average (±SE) minimum instantaneous firing rate of all 5 Purkinje cells examined as a function of photolysis power. Solid line represents the linear regression (R = −0.98, P = 0.003). Average baseline firing rate = 50.6 ± 4.6 sp/s.

Series of linear input-output relationships determines overall linearity.

Although conceptually straightforward, the implementation of monosynaptic glutamatergic excitation and disynaptic GABAergic inhibition to generate reciprocal firing rates is not trivial. In this case, to generate complementary firing rates, the input-output relationship of monosynaptic excitation and the disynaptic inhibition must both be linear. For disynaptic inhibition, this linearity may be achieved through a series of linear components, which is perhaps the simplest functional organization. To test whether the disynaptic granule cell → molecular layer interneuron → Purkinje cell pathway is linear because of linear input-output components, we first examined whether interneurons linearly encode the strength of granule cell inputs in their firing rate. Consistent with earlier findings (Eccles et al. 1966), stimulation of an underlying patch of granule cells increased the firing rate of the target interneuron from its baseline spontaneous rate (Fig. 4A) (the average spontaneous firing rate of basket cells was 11.9 ± 0.1 sp/s and that of the stellate cells was 7.2 ± 0.4 sp/s). Additionally, stronger activation of granule cells yielded greater increases in the firing rate of the interneuron (Fig. 4B). Similar to that seen in Purkinje cells (Walter and Khodakhah 2006), these increases were a linear function of the strength of granule cell inputs (Fig. 4C, for cell shown in 4B, R = 0.70, P < 0.0001). A linear input-output function was observed in all molecular layer interneurons examined (Fig. 4C, R = 0.99, n = 10, P < 0.0001). When basket and stellate cells were examined in isolation, the response of each class was also linear (data not shown; basket cells: R = 0.99, n = 5, P < 0.0001; stellate cells: R = 0.99, n = 5, P < 0.0001), although basket cells had a slightly steeper input-output function compared with stellate cells (ratio ≈1.3).

Considering that interneurons linearly encode the strength of granule cell inputs as increases in firing rate, we next examined whether the changes in their firing rate are also linearly transmitted to Purkinje cells as changes in GABA conductance (Fig. 4D). Photolytic activation of granule cells evoked inhibitory postsynaptic currents (IPSCs) in the target Purkinje cell, which became progressively larger and more distinguishable from background with increasing input strengths (Fig. 4E). Examination of the average IPSCs revealed that the IPSCs increased with stimulus power, principally by increasing their peak amplitude and without appreciably changing kinetics (Fig. 4E). The 10–90% rise time and the decay time constant of the average evoked GABA conductances were comparable at all granule cell activation strengths (10–90% rise time range 11.1 ± 4.0 to 22.5 ± 7.9 ms, linear correlation R = −0.19, P = 0.72; decay time constant range 46.1 ± 19 - 74.6 ± 30.6 ms, R = 0.41, P = 0.43; n = 4). In all four cells examined there was a linear relationship between the area of GABAergic conductance and the input strength of granule cells (Fig. 4F; R = 0.98, P < 0.0001). In these same cells the maximum GABA conductance was also linearly correlated with the strength of granule cell input (R = 0.95, P = 0.004). Based on the photolysis power used to activate the patches of granule cells, we correlated the data reported in Fig. 4, A–C, with those in Fig. 4, D–F. We explored whether the maximum average peak GABA conductance evoked in Purkinje cells when a patch of granule cells was activated was a linear function of the maximum instantaneous firing rate of interneurons. We found this to be the case with a linear regression line closely fitting the data (R = 0.95, P = 0.003). Similarly, we found that the duration of the GABA conductance evoked in Purkinje cells when the granule cells were activated was a linear function of the duration of the increase in the firing rate of interneurons (R = 0.94, P = 0.006).

The data presented so far demonstrate that interneurons linearly encode and transmit the input strength of granule cells to Purkinje cells. We next examined whether Purkinje cell pacemaking is also linearly regulated by the strength of inhibition from molecular layer interneurons. To do so we first recorded the changes in the firing rate of a Purkinje cell in response to activation of granule cells positioned laterally to it. We then voltage-clamped the same cell and measured the GABAergic conductances produced by the same granule cell stimuli. The peristimulus time histogram in Fig. 4H shows that the temporal changes in the firing rate of the Purkinje cell largely mirrored that of the GABA conductance. In all five Purkinje cells examined similarly, there was a clear inverse correlation between the minimum instantaneous firing rate and the GABAergic conductance (Fig. 4I; R = −0.95, P = 0.01). This finding is consistent with previous reports of a linear relationship between the amplitude of the outward current injected into the soma of Purkinje cells and decreases in their firing rate (Mittmann and Hausser 2007).

At least five interneurons mediate the observed decreases in the firing rate of Purkinje cells.

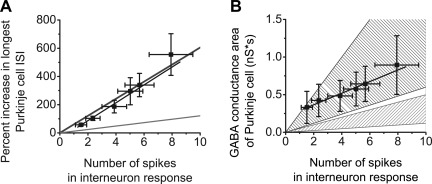
We sought to estimate the number of interneurons that were activated by granule cell stimulations that drove the decreases in the firing rate of Purkinje cells reported above. With the first approach we took advantage of the finding that each individual spike fired by a single interneuron increases the Purkinje cell interspike interval by ∼12% (Hausser and Clark 1997) and linearly extrapolated the impact of multiple spikes on the increase in the interspike interval of a Purkinje cell. We found that if we assumed that five interneurons were activated by the patch of granule cells, thus inhibiting the Purkinje cell five times as much, we could reconcile the pauses produced in the activity of Purkinje cells reported here with the average number of spikes fired by interneurons (Fig. 5A; R = 0.99, P < 0.001). It should be noted that this analysis did not take into consideration the failure rate (Pouzat and Hestrin 1997) or synaptic depression (Bao et al. 2010; Sakaba 2008) at the molecular layer interneuron → Purkinje cell synapse, and therefore the number of interneurons thus obtained is likely to be an underestimate.

Fig. 5.

The GABA conductance evoked in Purkinje cells by activation of a patch of granule cells is composed of the concerted activity of ∼5 interneurons. A: estimated number of interneurons activated by photorelease of glutamate, which contributed to inhibition of Purkinje cells under our experimental conditions. The number of interneurons was estimated by extrapolating data from Hausser and Clark (1997), which demonstrated that a single interneuron prolongs the interspike interval (ISI) of Purkinje cells by ∼12% (see text for specifics on the method used for extrapolation). B: estimated number of interneurons activated under our experimental conditions using data from 2 published works. Vincent et al. (1992) and Pouzat and Hestrin (1997) characterized the interneuron-Purkinje cell inhibitory postsynaptic current (IPSC). The number of interneurons was approximated by the parameters of the IPSCs found in these 2 investigations (see text for specifics on the method of extrapolation).

We also used a second complementary approach to estimate the number of interneurons that contribute to reducing the firing rate of Purkinje cells when a patch of granule cells is activated. With this approach we compared the GABAergic conductance produced by activity of single interneurons in Purkinje cells with that obtained in our recordings. Based on the published literature, single spikes from single interneurons yield IPSCs of 80–330 pA (conductance peaks of 1.33–5.5 nS) in Purkinje cells of comparable-age animals (Pouzat and Hestrin 1997). These IPSCs decay with a single exponential decay constant of 9.3 ms (Vincent et al. 1992). Using these parameters, we estimate that single spikes from an interneuron produce a GABA conductance area of 0.012–0.050 nS·s (integrated from the peak to 500 ms later). Again assuming no synaptic failure or depression and similar to that estimated based on our first approach, comparison of our data with the published work suggests that concerted activity of approximately five interneurons is needed to produce the responses seen in our experiments (Fig. 5B).

DISCUSSION

By noninvasively monitoring the activity of Purkinje cells, here we demonstrated that a common granule cell input can generate two reciprocal firing rates in two populations of Purkinje cells. This is possible through two complementary linear input-output relationships that originate in the granule cell layer and end on Purkinje cells. Granule cells form direct excitatory inputs onto Purkinje cells, and it was previously shown that increases in the firing rate of Purkinje cells are a linear function of the input strength of these direct granule cell inputs (Walter and Khodakhah 2006). Here we showed, both in cerebellar slices in vitro and in anesthetized mice in vivo, that the disynaptic granule cell → molecular layer interneuron → Purkinje cell pathway also decreases the firing rate of Purkinje cells as a linear function of the input strength of granule cells. As each component of this pathway is linear, disynaptic inhibition is the equal but opposite counterpart to monosynaptic excitation. Thus in the intact animal these two pathways should allow single mossy fiber inputs to simultaneously generate reciprocal signals. More generally, our data demonstrate the utility and efficiency of the use of lateral inhibition for generation of reciprocal signals in the brain from a common set of inputs.

Reciprocal Purkinje cell signals and the cerebellum.

The anatomy of the cerebellar cortex is composed of repeated motifs that provide the requisite circuitry for reciprocal Purkinje cell signals to be generated throughout regions of the cerebellum. Indeed, functional studies demonstrate that a center-excitation surround-inhibition format exists throughout the cerebellum (Dizon and Khodakhah 2011; Gao et al. 2006). Indeed, reciprocal firing rates of Purkinje cells are found in large parts of the cerebellum in cats, rabbits, and even primates (Chan et al. 1982; Eccles 1973; Frysinger et al. 1984; Lisberger and Fuchs 1978; Mano and Yamamoto 1980; Medina and Lisberger 2008; Miyashita and Nagao 1984; Yamamoto et al. 2007). While the functional significance of reciprocal signals is better understood in brain regions involved in processing of sensory information, the role of these signals in the cerebellum remains to be established. As discussed below, one potential role of reciprocal signals in the cerebellum and other motor-related brain regions may be generation of the signals required for simultaneous reciprocal control of agonist and antagonist muscles.

Experimental ablation of the cerebellum in animals and examinations of patients with cerebellar lesions have collectively established that the cerebellum is involved in motor coordination (Manni and Dow 1963; Robinson and Fuchs 2001). It is thought that the cerebellum performs its function by generating a set of signals that, in one form or another, orchestrate the precise timing and contraction of muscles. In support of this notion, a tight correlation between the firing rate of Purkinje cells and specific motor variables has been observed for simple tasks such as movements of the arm and eye. For movements of the arm, for example, the firing rates of Purkinje cells are correlated with both static (Frysinger et al. 1984) and dynamic (Yamamoto et al. 2007) force. For movements of the eye, the instantaneous firing rate of floccular Purkinje cells can be quantitatively accounted for by the linear weighted sum of acceleration, velocity, and position of the eyes (Shidara et al. 1993).

While many movements require the contraction of an agonist set of muscles and the simultaneous relaxation of an antagonist set, there are tasks in which cocontraction of agonist and antagonist muscles are desirable, such as when the cocontraction of the opposing muscles is employed as a means to stiffen a limb. Thus while within the spinal cord there are known mechanisms in place that in part generate the reciprocal signals required for contraction and relaxation of corresponding muscles, higher-order task-dependent coordination is indispensable (De Luca and Mambrito 1987). The cerebellar cortex is an optimal structure for coordinating the signals required for control of antagonist pair muscle activity. In support of this notion, in vivo recordings from cerebellar Purkinje cells during motor tasks have demonstrated the presence of Purkinje cells whose activity are reciprocal to each other, some of which change polarity as the direction of movement is reversed (Frysinger et al. 1984; Lisberger and Fuchs 1978; Mano and Yamamoto 1980; Thach 1970). This latter finding is expected because movement in the reverse direction often requires the opposite action of the same group of muscles and thus the opposite control signal. These complementary Purkinje cell firing rates could very well be the mechanism by which the cerebellum coordinates the activity of agonist and antagonist muscle pairs. The reciprocal firing rates generated by cerebellar cortical interneurons reported here might be one of the substrates with which the cerebellum generates these complementary signals. In this context, the stereotypic functional circuitry of the cerebellar cortex in the sagittal plane (Dizon and Khodakhah 2011) provides for a simple substrate by which reciprocal activity of a complementary pair of Purkinje cells can be converted to one during which both Purkinje cells endorse the cocontraction of the muscle pairs. Dynamically, when cocontraction of agonist and antagonist muscle pairs is required, activation of mossy fibers located immediately underneath both Purkinje cell pairs can ensure that the firing rates of both are increased concurrently.

It is worth emphasizing that the presence of the anatomical substrate for the generation of reciprocal signals does not necessarily mandate the presence of reciprocal signals under all conditions. For example, reciprocally firing Purkinje cells are rarely found in the flocculus, uvula, and nodulus of mice and rabbit cerebella even though these regions have a similar cortical structure (Barmack and Yakhnitsa 2008; De Zeeuw et al. 1995). The presence of neighboring Purkinje cells without reciprocal firing rates despite the presence of the anatomical substrate for generation of reciprocal circuitry suggests that the firing rate of one set of Purkinje cells is not always obligatorily coupled to decreases in the firing rate of another set of Purkinje cells. Dynamic or permanent changes in the spatial organization of active inputs or plasticity could modify the functional output of the circuitry. For example, within the regions mentioned the granule cell layer accommodates numerous UBCs. These neurons directly receive mossy fiber inputs and excite laterally positioned granule cells (Takacs et al. 1999), thereby providing a mechanism for overriding the automatic generation of Purkinje cell reciprocal firing rates. Additionally, climbing fiber-mediated plasticity of both excitatory (Ito 2001) and inhibitory (Mittmann and Hausser 2007) inputs may silence the inputs to one set of Purkinje cells to effectively spare only one type of Purkinje cell response.

Clearly, the hypothesis that the reciprocal firing of groups of Purkinje cells controls contraction of antagonist muscle pairs requires substantiation with experiments that simultaneously record EMG signals from agonist and antagonist muscles while simultaneously recording the activity of related Purkinje neurons. Moreover, while for the purposes of this discussion we have specifically considered cerebellar reciprocal signals within the context of coordination of agonist and antagonist muscles, our findings on a mechanism for generation of these complementary signals are equally relevant to kinematic-based (Pasalar et al. 2006) models of cerebellar function. This is because in these models increases in the firing rate of one set of Purkinje cells coupled to the decrease of another set of Purkinje cells collectively encode the population vector that predicts a limb's movement (Fortier et al. 1989).

As an additional mechanism to that described here, decreases in the firing rate of Purkinje cells may also be mediated through the action of climbing fibers on Purkinje cells (Davie et al. 2008; Mathy et al. 2009) or interneurons (Barmack and Yakhnitsa 2008). While these mechanisms may act in concert with the granule cell → interneuron inhibitory pathway to decrease the firing rate of Purkinje cells, they are not necessary for the decreases to occur (Ke et al. 2009; Yakusheva et al. 2010).

The balance between excitation and inhibition in many brain regions may be the common underpinning that endows inhibition with the ability to perform multiple functions. For a single neuron, the balance but fixed delay between these two inputs dictates time windows for synaptic integration enabling the precise output of spikes (Mittmann et al. 2005; Pouille and Scanziani 2001; Wehr and Zador 2003). Moreover, inhibition prevents aberrant activity such as runaway excitation (Silberberg and Markram 2007). Between neurons, excitation and inhibition shape the output of neurons located within specific regions of networks (Adesnik and Scanziani 2010; Dizon and Khodakhah 2011). Here, we have demonstrated that within these networks inhibition can scale appropriately with excitation. Thus this canonical circuit may also mediate the generation of reciprocal activity for other brain regions such as motor control areas that also operate as linear systems (Bagnall et al. 2008; Ethier et al. 2006; Todorov 2000; Townsend et al. 2006).

GRANTS

This work was supported by grants from the National Institutes of Health.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.-m.P., E.T., and K.K. conception and design of research; S.-m.P. and E.T. performed experiments; S.-m.P. and E.T. analyzed data; S.-m.P. and K.K. interpreted results of experiments; S.-m.P. prepared figures; S.-m.P. drafted manuscript; S.-m.P., E.T., and K.K. edited and revised manuscript; S.-m.P., E.T., and K.K. approved final version of manuscript.