1. INTRODUCTION
Analysis of quadrupedal and bipedal gait data generally requires temporal segmentation into stride cycles with further division into stance and swing phases (Philippson, 1905). This involves detection of such time events as stance onset and offset. The ‘gold standard’ for determining these events is commonly based on a specified ground reaction force (GRF) value recorded from forceplates. However, the disadvantages of using forceplates are that they can be installed only in specialized laboratories, and few labs possess more than two, thereby limiting the number of strides available for analysis. An alternative method to estimate event timings is through application of event detection algorithms to kinematic data (Table 1). In quadrupeds, whose anatomy and gait differ from humans, there have been limited comparisons of gait timing events determined by kinematically based algorithms and forceplates (Peham et al., 1999). Instead, observation of video frames is a commonly used method (Barriere et al., 2010, Thota et al., 2005).
Table 1.
Selected previous studies determining kinematically derived gait events
| De Witt (2010) | Kiss (2010) | Zeni (2008) | O’Connor (2007) | Ghoussayni (2004) | Hreljac & Marshall(2000) | Peham (1999) | |
|---|---|---|---|---|---|---|---|
| Treadmill/ Overground | Treadmill | Treadmill | Treadmill & Overground | Overground | Overground | Overground | Overground |
| Subject group and Number | Adults (12) | Adults (45) | Healthy Adults (7) Adults-MS (7) Adults -Stroke (4) |
Children (54) SP (3) |
Adults (12) | Adults (2) | Horses (4) |
| Number of cycles analysed | 100 | N/A | 382 (healthy) 494 (MS) 110 (stroke) |
126 (healthy) 6 (SP) |
144 | 12 | 416 |
| Speed | Walking 1.3 ms−1 Running 3.1 ms−1 |
Slow-1.2 ms−1 Mod-1.5 ms−1 Fast-1.8 ms−1 |
Walking | Walking | Slow Normal |
Slow Medium Fast |
1.48 ms−1 |
| GRF threshold for stance onset / offset | <1000 N s−1 while GRF<100N | >19.8 N (mean) for 40 ms | <20 N (onset) or >20 N (offset) for 67 ms | 10N (onset) 5N (offset) |
10N | 10N | 50N (1.5% max GRF) |
| Sampling frequency of kinematic data | 60Hz | 100Hz | 60 Hz | 60 Hz (healthy) 120 Hz (SP) |
60Hz | 60Hz | 240 Hz |
| AXIS/ PLANE* | X (onset) X & Z (offset) |
X | X | Z (onset) X & Z (offset) |
X-Z | Z (onset) X (offset) |
X |
| Digital filter | 4th order Butterworth | N/A | N/A | 4th order Butterworth | 4th order Butterworth | 4th order Butterworth | N/A |
| Method-stance onset |
|
Max (heel-ASIS) displacement |
|
|
Velocity-threshold 100 mms−1 (shod) 50 mms−1 (barefoot) |
Maximum acceleration Heel marker | Velocity threshold (maximum frequency in histogram) |
| Method–stance offset |
|
Min (heel-ASIS) displacement |
|
|
Velocity-threshold 100 mms−1 (shod) 50 mms−1 (barefoot) |
Maximum acceleration Toe marker | Velocity threshold (maximum frequency in histogram) |
| Stance-onset systematic error† |
|
+6.9 ms (4.1) (slow) +3.2 ms (3.3) (moderate) −2.3 ms (0.9) (fast) |
TREADMILL
|
|
< 25 ms | 4.7 ms | −4.5ms |
| Stance-offset systematic error† |
|
+3.6 ms (0.9) (slow) +1.7 ms (3.1) (moderate) +1.6 ms (3.2) (fast) |
TREADMILL
|
|
<117 ms (Shod) <175 ms (Barefoot) |
5.6 ms | +6.3 ms |
Notes:
x is forwards direction. z is upwards;
- estimated before GRF estimated event. and +estimated after GRF estimated event.
MS-multiple sclerosis. SP-spastic diplegia. N/A – not available.
Table does not present an exhaustive list of studies; additional studies include, for example, Desailly et al., 2009, Karcnik, 2003, Mickelborough et al., 2000, Stanhope et al., 1990.
The accuracy of estimating contact times using observation of limb kinematics may be impacted by surface slope (Damavandi et al., 2010, Gregor et al., 2006), differences between healthy and pathological gait (Barriere et al., 2010, Maas et al., 2007) and inter-individual differences in gait kinematics.
This study aimed at determining systematic errors and variability of paw-contact (PC) and paw-off (PO) timings found by different kinematic algorithms during quadrupedal gait, specifically feline gait. The following hypothesis was tested: the accuracy of gait event detection depends on locomotor conditions (slope), stage of recovery after peripheral nerve injury, subjects and event detection method.
Preliminary results of this work have previously been published in abstract form (Pantall and Prilutsky, 2011).
2. METHODS
All experimental and surgical procedures were consistent with US Public Health Service Policy on Humane Care and Use of Laboratory Animals and approved by the Institutional Animal Care and Use Committee. In this study, four female adult cats (mass 2.9 kg – 4.1 kg) were investigated.
2.1. Data collection
Each cat was trained to walk along a level, upslope (+27°) and downslope (−27°) walkway covered with nonslip rubberized material with embedded forceplates (Bertec Corporation, Columbus, OH, USA) recording at 360 Hz (Gregor et al., 2006, Maas et al., 2007, Prilutsky et al., 2011). Prior to recordings, small retroreflective markers were placed on the greater trochanter (GT) and the 5th metatarsophalangeal (MTP) joint of the right hindlimb. A 6-camera motion capture system Vicon (Vicon Motion Systems, UK) recorded marker positions at a sampling rate of 120 Hz. As part of a larger study, the four cats had nerves supplying two right ankle extensors cut and repaired (Maas et al., 2007, Prilutsky et al., 2011). Each cat had multiple walking trials recorded several times a week, from 2–4 weeks before to 12 weeks after nerve injury and repair.
2.2. Data processing
Trials prior to surgery, 2 weeks post-surgery, 6 weeks post-surgery and 12 weeks post-surgery were analyzed. All analysis was carried out in the Matlab environment (Natick, MA, USA). Firstly, ‘gold standard’ timings for PC and PO were identified using a vertical GRF threshold value of 0.5 N (1.5 % of mean cats’ weight) (Figure 1). Secondly, recorded marker displacement data were filtered using a low-pass, fourth order, zero lag critically damped digital filter with 10 Hz cut-off frequency (Robertson and Dowling, 2003). Finally, the five kinematic methods for detection of PC and PO were applied to the filtered kinematic data (Figure 1). These detection methods were adapted from previously applied kinematic methods as outlined below.
Figure 1.
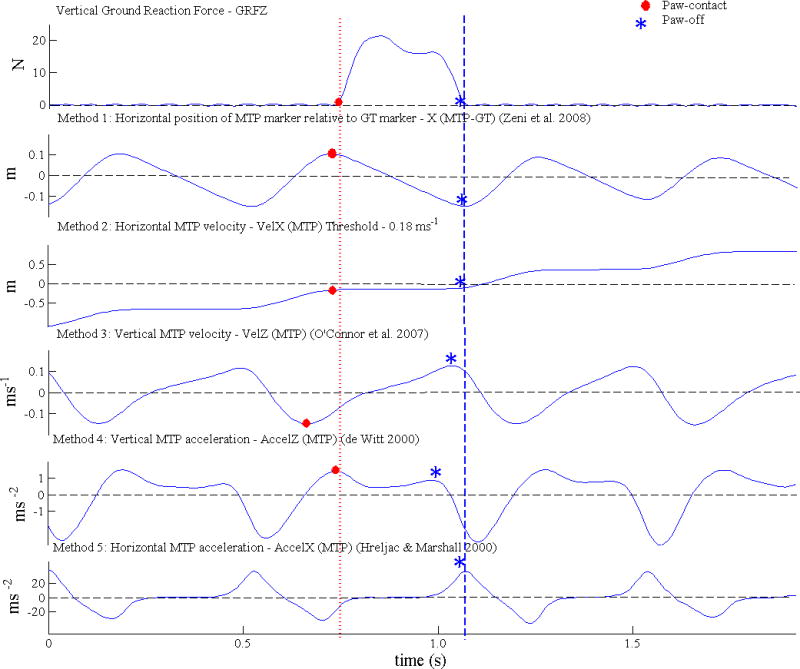
Paw-contact and Paw-off timings determined by vertical ground reaction force and five kinematic methods for a typical trial. See text for explanations of kinematic methods.
Method 1
Time of maximum and minimum anterior-posterior (AP) displacement of MTP relative to GT (X(MTP-GT)) corresponding to PC and PO, respectively. This method was modified from Zeni et al. (2008) who tracked heel and sacral markers.
Method 2
Time of first frame when change in MTP displacement in AP direction (VelX(MTP)) fell below (PC) or rose above (PO) 1.5 mm between successive frames, equivalent to a velocity of 0.18 m s−1. A similar method was applied to kinematic data in the sagittal plane by Ghoussayni et al. (2004) although their selected threshold was lower at 0.05 m s−1.
Method 3
Time of minimum and maximum vertical MTP velocity (VelZ(MTP)), corresponding to PC and PO, respectively modified from O’Connor et al. (2007). Modifications involved tracking the MTP marker rather than the midpoint of the heel and 2nd metatarsal head. Furthermore, we did not apply time windows of 0.8 s and 0.08 s to automatically determine major peaks and troughs of the foot marker trajectories.
Method 4
Time of first and second local maxima in vertical MTP acceleration (AccelZ(MTP)) during gait cycle, corresponding to PC and PO, respectively modified from Hreljac and Marshall (2000) for PC and De Witt (2010) for PO. Hreljac and Marshall used the heel marker to determine heelstrike and De Witt tracked the toe to determine toe-off. Contrary to these studies we did not apply interpolation to calculate between frame timings.
Method 5
Time of maximum AP acceleration of MTP (AccelX(MTP)), corresponding to PO. As opposed to Hreljac and Marshall (2000), we used the MTP marker rather than the toe marker to detect stance offset.
Further details on methods are contained in Supplementary Material.
Finally, the systematic error was calculated as the difference in timing between the value calculated by one of the methods described above and the GRF determined timing, with a positive value indicating that the timing occurred later than the value obtained from the GRF. Random error was the standard deviation of the systematic error.
2.3. Statistical analysis
Since systematic errors of PC and PO detection were not normally distributed (see Supplementary Material), nonparametric repeated measures Friedman ANOVAs were applied to the systematic errors of PC and PO obtained from all walking cycles, walking conditions and cats, with kinematic detection method as the independent variable. Nonparametric Kruskal-Wallis ANOVAs were applied to mean systematic error values for combinations of slope, timing and cat to determine whether there was a significant effect of slope (3 levels), recovery times (4 levels), and cats (4 levels) on systematic errors of PC and PO. Nonparametric Dunn’s post hoc tests were applied to all datasets following a significant ANOVA result. Levene’s test was applied to test for difference in variance of PC and PO (random error) between kinematic methods and experimental conditions. Statistical significance was set at p<0.05 for all tests. Statistical analyses were performed using Statistica 7 (Statsoft, Tulsa, Ok, USA) and Matlab (Natick. MA, USA).
3. RESULTS
A total of 963 step cycles were analyzed.
3.1 Mean systematic and random errors
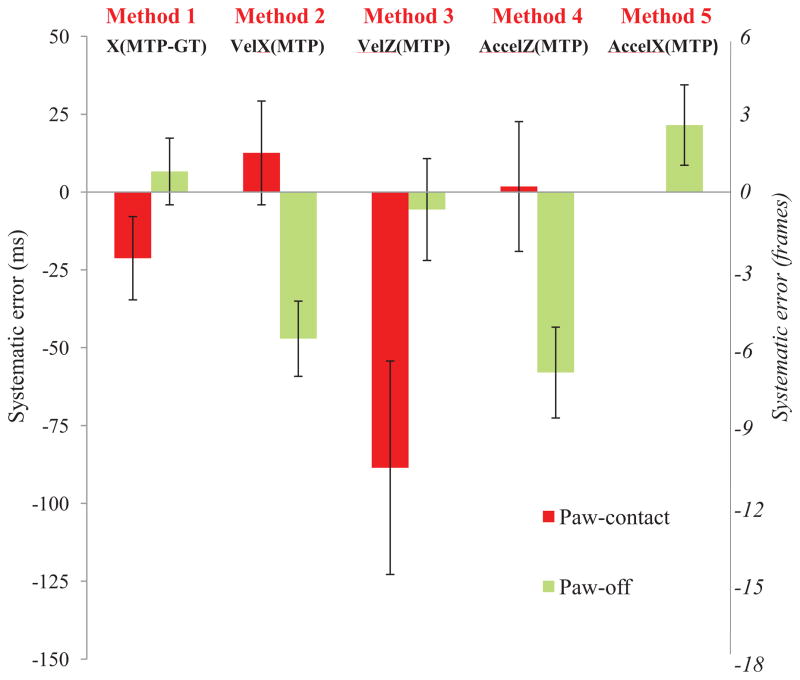
Across all slope conditions, times and cats there was a significant difference in systematic error between methods for PC and PO detection (p<0.05) (Figure 2). Dunn’s post-hoc tests revealed significant differences between all pairs of systematic errors (p<0.05) for both PC and PO. For PC, the smallest absolute systematic error was 1.8 ms (Method 4) whereas the largest was −88.5 ms (Method 3). However, for PO, Method 3 produced the smallest absolute systematic error of −5.6 ms whereas Method 4 resulted in the greatest absolute value of −58.0 ms. The statistical tests conducted on the averaged PC and PO systematic errors for individual slopes, recovery times and cats revealed similar results (Fig. A2 in the Supplemental Materials).
Figure 2.
Mean systematic error and random error (± SD) for paw-contact and paw-off times across all slope conditions, recovery times and cats determined by comparing the kinematic methods with the GRF method. n=963. Significant differences between all pairs of systematic error for paw-contact and paw-off (p<0.05) were found.
Levene’s test indicated significant difference in random error for both PC and PO timings with Method 1 producing the smallest (13.4 ms and 10.7 ms respectively) and Method 3 the greatest random errors (34.3 ms and 16.4 ms respectively).
3.2 Slope conditions
Comparison of systematic errors of each method between slope conditions showed that slope had a significant effect on PC timing of Method 2 only with the lowest error in upslope and the largest in downslope condition (p<0.05, Table 2). For PO, slope had a significant effect on timing determined by Method 1 with differences in timings between level and upslope (p<0.05). Slope had significant effects on random errors of PC and PO timing for all Methods, with level and upslope conditions yielding significantly smaller random errors compared to downslope (Table 2).
Table 2.
Systematic Error (S. E.) (shaded columns) and Random Error (R.E.) in ms calculated by 5 kinematic methods for paw-contact and paw-off timing for 3 different slope conditions, 4 recovery times and 4 subjects.
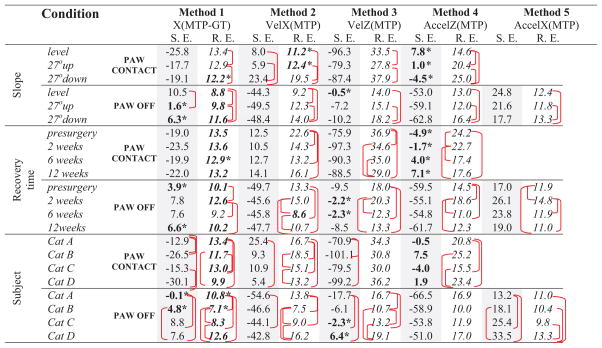 |
 – significant difference between timings for a specific condition (p<0.05).
– significant difference between timings for a specific condition (p<0.05).
Highlighted values indicate lowest absolute error between methods for a specific condition.
significant difference between methods (p<0.05).
3.3 Recovery time
Recovery time after peripheral nerve injury had no significant effect on the systematic error of PC and PO timing determined by any kinematic method (p30.05, Table 2). Recovery time however significantly affected the random error of PC (determined by Methods 2–4) and PO for all methods (p<0.05, Table 2). For example, the PC random error was significantly greater at pre-nerve injury than the lowest random errors at 6 or 12 weeks for methods 2–4.
3.4 Subject
The factor subject (cats) significantly influenced the PC and PO systematic errors for all methods except Method 4; the latter demonstrated the lowest PC and the highest PO systematic errors across all cats (Table 2). The random PC and PO errors were also dependent significantly on the cats for all methods except Method 3 (PC) and Method 4 (PO) (Table 2).
4. DISCUSSION
The goal of the study was to determine differences in timing of PC and PO through the application of five kinematic methods and examine the effects of slope condition, recovery time, subjects and kinematic methods on derived timings. In summary, the systematic errors between the kinematic methods differed significantly. Effects of slope and subject on the systematic errors were significant, whereas effects of recovery time after nerve injury were not. Selection of the ‘best’ method for determining PC and PO timing is based on two considerations, namely the minimum systematic error and the minimum random error. Results indicated that the ‘best’ method differed between PC and PO. For PC, Method 4, based on the MTP vertical acceleration, resulted in the smallest absolute systematic error and Method 3, based on the MTP vertical velocity, resulted in the greatest error. Results for PO were reversed. Thus, Methods 4 and 3 can be considered best for minimizing systematic error of PC and PO timing detection, respectively. However, Method 1 (MTP horizontal displacement of MTP relative to hip marker) would be preferable for both event timings if the aim is to minimize random error (SD). Overall, the least favourable method to determine PC timing is Method 3. As the aim of locomotion is to propel the body forwards one would anticipate lowest variability to be along the direction of progression (x-axis). The smallest random error (SD) of Method 1 could also be explained by the fact that it does not involve any differentiation as lower levels of differentiation and simple kinematic trajectories with clearly defined minima and maxima have been suggested as preferable for determining gait time events (O’Connor et al. 2007). The lowest mean systematic error for PC, 1.8 ms, calculated by Method 4 was similar to the 4.7 ms for stance onset reported for human adults during walking by Hreljac and Marshall (2000) (Table 1). Likewise, the systematic error of −5.6 ms (± 16.4) determined by Method 3 for PO was similar to −6 ms (± 26) reported by O’Connor (2007) for stance offset in children with spastic diplegia (Table 1).
The effect of slope on timings was only significant for Method 2 for PC and Method 1 for PO, both methods involving horizontal gait parameters. The finding that both PC and PO systematic errors were statistically no different at any tested period after nerve injury compared to pre-nerve injury suggests that this specific pathology does not affect kinematically derived PC and PO timing. The effect of subject on PC and PO timing was significant for all the methods except Method 4 (MTP vertical acceleration). Studies usually combine subjects’ timing data to obtain a mean (Table 1). However, this practice, given significant inter-individual differences, may produce inaccurate results.
Supplementary Material
Acknowledgments
This research was supported by NIH grants HD032571, NS048844 and EB 012855 and by the Center for Human Movement Studies at Georgia Tech. Thank-you to Dr. Huub Maas, Dr. Margarita Bulgakova and Mr. Brad Farrell for assistance with data collection. We also thank Dr. Guay-haur Shue for his technical assistance.
Footnotes
CONFLICT OF INTEREST STATEMENT
The authors, Annette Pantall, Robert J. Gregor and Boris I. Prilutsky declare no conflict of interest. None of the authors have any financial or personal relationship with other people or organizations that could inappropriately bias their work.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Barriere G, Frigon A, Leblond H, Provencher J, Rossignol S. Dual spinal lesion paradigm in the cat: evolution of the kinematic locomotor pattern. Journal of Neurophysiology. 2010;104:1119–1133. doi: 10.1152/jn.00255.2010. [DOI] [PubMed] [Google Scholar]
- Damavandi M, Dixon PC, Pearsall DJ. Kinematic adaptations of the hindfoot, forefoot, and hallux during cross-slope walking. Gait & Posture. 2010;32:411–415. doi: 10.1016/j.gaitpost.2010.07.004. [DOI] [PubMed] [Google Scholar]
- De Witt JK. Determination of toe-off event time during treadmill locomotion using kinematic data. Journal of Biomechanics. 2010;43:3067–3069. doi: 10.1016/j.jbiomech.2010.07.009. [DOI] [PubMed] [Google Scholar]
- Desailly E, Daniel Y, Sardain P, Lacouture P. Foot contact event detection using kinematic data in cerebral palsy children and normal adults gait. Gait & Posture. 2009;29:76–80. doi: 10.1016/j.gaitpost.2008.06.009. [DOI] [PubMed] [Google Scholar]
- Ghoussayni S, Stevens C, Durham S, Ewins D. Assessment and validation of a simple automated method for the detection of gait events and intervals. Gait Posture. 2004;20:266–272. doi: 10.1016/j.gaitpost.2003.10.001. [DOI] [PubMed] [Google Scholar]
- Gregor RJ, Smith DW, Prilutsky BI. Mechanics of slope walking in the cat: quantification of muscle load, length change, and ankle extensor EMG patterns. Journal of Neurophysiology. 2006;95:1397–1409. doi: 10.1152/jn.01300.2004. [DOI] [PubMed] [Google Scholar]
- Kiss RM. Comparison between kinematic and ground reaction force techniques for determining gait events during treadmill walking at different walking speeds. Medical Engineering & Physics. 2010;32:662–667. doi: 10.1016/j.medengphy.2010.02.012. [DOI] [PubMed] [Google Scholar]
- Hreljac A, Marshall RN. Algorithms to determine event timing during normal walking using kinematic data. Journal of Biomechanics. 2000;33:783–786. doi: 10.1016/s0021-9290(00)00014-2. [DOI] [PubMed] [Google Scholar]
- Karcnik T. Using Motion Analysis Data for Foot - Floor Contacted Detection. 2003. Medical and Biological Engineering and Computing. 41:509–512. doi: 10.1007/BF02345310. [DOI] [PubMed] [Google Scholar]
- Maas H, Prilutsky BI, Nichols TR, Gregor RJ. The effects of self-reinnervation of cat medial and lateral gastrocnemius muscles on hindlimb kinematics in slope walking. Experimental Brain Research. 2007;181:377–393. doi: 10.1007/s00221-007-0938-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mickelborough J, van der Linden ML, Richards J, Ennos AR. Validity and reliability of a kinematic protocol for determining foot contact events. 2000. Gait and Posture. 11:32–37. doi: 10.1016/s0966-6362(99)00050-8. [DOI] [PubMed] [Google Scholar]
- O’Connor CM, Thorpe SK, O’Malley MJ, Vaughan CL. Automatic detection of gait events using kinematic data. Gait & Posture. 2007;25:469–474. doi: 10.1016/j.gaitpost.2006.05.016. [DOI] [PubMed] [Google Scholar]
- Pantall A, Prilutsky BI. Kinematic methods for determining gait events during level and slope walking in the cat. American Society of Biomechanics Annual Meeting; August 10–13; Long Beach, CA. 2011. [Google Scholar]
- Peham C, Scheidl M, Licka T. Limb locomotion--speed distribution analysis as a new method for stance phase detection. Journal of Biomechanics. 1999;32:1119–1124. doi: 10.1016/s0021-9290(99)00102-5. [DOI] [PubMed] [Google Scholar]
- Philippson M. L’autonomie et la centralisation dans le système nerveux des animaux. Travaux de Laboratoire d’Institut Physiologie Solvay (Bruxelles); 1905. pp. 1–208. [Google Scholar]
- Prilutsky BI, Maas H, Bulgakova M, Hodson-Tole EF, Gregor RJ. Short-term motor compensations to denervation of feline soleus and lateral gastrocnemius result in preservation of ankle mechanical output during locomotion. Cells Tissues Organs. 2011;193:310–324. doi: 10.1159/000323678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson DG, Dowling JJ. Design and responses of Butterworth and critically damped digital filters. J Electromyogr Kinesiol. 2003;13(6):569–573. doi: 10.1016/s1050-6411(03)00080-4. [DOI] [PubMed] [Google Scholar]
- Stanhope SJ, Kepple TM, McGuire DA, Roman NL. Kinematic-Based Technique for Event Time Determination during Gait. Medical and Biological Engineering and Computing. 1990;28:355–60. doi: 10.1007/BF02446154. [DOI] [PubMed] [Google Scholar]
- Thota AK, Watson SC, Knapp E, Thompson B, Jung R. Neuromechanical control of locomotion in the rat. Journal of Neurotrauma. 2005;22:442–465. doi: 10.1089/neu.2005.22.442. [DOI] [PubMed] [Google Scholar]
- Zeni JA, Jr, Richards JG, Higginson JS. Two simple methods for determining gait events during treadmill and overground walking using kinematic data. Gait & Posture. 2008;27:710–714. doi: 10.1016/j.gaitpost.2007.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.