Impact of the Partitioning Scheme on Divergence Times Inferred from Mammalian Genomic Data Sets

Abstract

Data partitioning has long been regarded as an important parameter for phylogenetic inference. The division of heterogeneous multigene data sets into partitions with similar substitution patterns is known to increase the performance of probabilistic phylogenetic methods. However, the effect of the partitioning scheme on divergence time estimates has generally been ignored. To investigate the impact of data partitioning on the estimation of divergence times, we have constructed two genomic data sets. The first one with 15 nuclear genes comprising 50,928 bp were selected from the OrthoMam database; the second set was composed of complete mitochondrial genomes. We studied two partitioning schemes: concatenated supermatrices and partitioned gene analysis. We have also measured the impact of taxonomic sampling on the estimates. After drawing divergence time inferences using the uncorrelated relaxed clock in BEAST, we have compared the age estimates between the partitioning schemes. Our results show that, in general, both schemes resulted in similar chronological estimates, however the concatenated data sets were more efficient than the partitioned ones in attaining suitable effective sample sizes.

Introduction

Divergence time estimation has been revolutionized by the application of models that relax the assumption of the strict molecular clock by decomposing branch lengths into absolute times and evolutionary rates.^1,2 Such an approach has been successfully implemented in a Bayesian framework in which complex models of evolutionary rate evolution may be feasibly used because the marginal distributions of divergence times are obtained via a Markov chain Monte Carlo method.³ Although this approach is widely used, several aspects of molecular dating by such relaxed clock methods require detailed scrutiny. For example, it is still unclear which modeling strategy for describing the change in rates along lineages is more appropriate for biological data.^4,5 Another unsolved issue is the possible impact of taxonomic sampling on the estimates of evolutionary rates.^6–8

In addition to the modeling of evolutionary rates and taxonomic sampling, the effect of the data-partitioning scheme on the estimation of divergence times has attracted relatively little attention. Curiously, this issue has been addressed frequently over the past decade in the context of topological estimation only, mainly because of the increased availability of multigene data sets.^9–12 Researchers may study multigene data sets as a single concatenated supermatrix or may set a predefined number of partitions. Evidently, the estimation of the optimal number of partitions to be used in phylogenetic analysis is a subject of theoretical interest.^13,14 Although the effect of data partitioning on the estimation of divergence time has rarely been investigated, the few existing studies show that divergence times are influenced by the partitioning scheme used in multigene data sets.¹¹

In this sense, evaluations of the effects of data partitioning on divergence time inference are needed. Ideally, such analyses must be conducted via simulation or by the analysis of biological data in which there exists considerable empirical evidence of the values of the parametric estimates. The advantage of the latter approach is that the complexity of the evolutionary process is captured. Mammalian timescales have been intensively investigated,^15–17 and the availability of molecular data for the lineage is unrivalled among vertebrates because of the hundreds of mitochondrial genomes that have been sequenced and the more than 30 nuclear genomes that are being assembled (http://www.ensembl.org). In addition, the rich fossil record of mammals provides several sources of calibration information that can be used in molecular dating analyses.¹⁸

In this paper, we compared the impact on divergence time estimation of concatenated and partitioned schemes using nuclear and mitochondrial data sets of mammals with the relaxed molecular clock. Our analyses showed that, although both of the partitioning schemes yielded similar divergence time estimates, the concatenated data were more efficient than the partitioned scheme because the former allowed effective sample sizes to increase more rapidly. This finding indicates that the concatenated data yielded parametric estimates with better mixing of the Markov chain. The effectiveness of concatenated data is probably due to the smaller number of model parameters, which facilitates exploration of the parametric space by the MCMC sampler.

Materials and Methods

Sequences, alignments and tree topologies

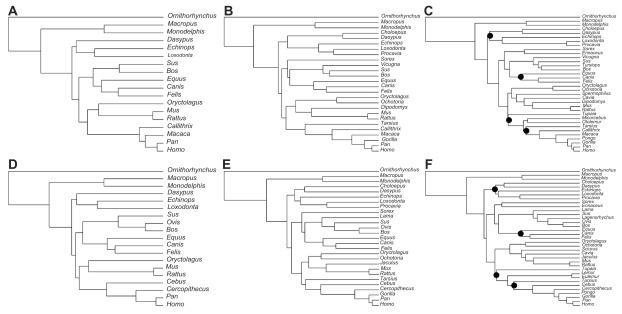
We have constructed two phylogenomic data sets to investigate the impact of data partitioning on mammalian divergence times. In each data set, chronological inferences were obtained by concatenating all of the genes in a single supermatrix or by allowing the partitions to have independent evolutionary parameters. To evaluate the behavior of the chronological estimates with increasing taxonomic sampling, we have studied three species compositions with increasing numbers of terminals in each data set (Fig. 1).

Figure 1.

Phylogenies used in this study. Topologies (A–C) refer to the taxonomic compositions 1 (A), 2 (B) and 3 (C) of the nuclear data set. Topologies (D–F) refer to the taxonomic compositions 1 (C), 2 (D) and 3 (F) of the mitochondrial data set. Phylogenies (C and F) were inferred in PhyML.

Note: Black circles indicate nodes in which aLRT value was lower than 0.9, otherwise aLRT statistics = 1.

The first data set was composed of 15 nuclear genes that were selected from the OrthoMam database.¹⁹ Genes were selected according to their relative rates (varying from 0.25 to 1.25), calculated following the approach of Criscuolo et al.²⁰ The 15 genes were sampled in order to obtain an alignment with approximately 50,000 nucleotides (Table 1), which is close to the total sequence length used in recent mammalian phylogenomic studies.^21,22 Only genes with the full species sampling were selected. The final concatenated supermatrix contained 50,928 nucleotides, and the corresponding taxonomic compositions included 18, 26 and 34 species (Fig. 1).

Table 1.

Orthologous gene groups downloaded from the OrthoMam database used to compose the nuclear dataset.

Ensembl code	Gene name (OrthoMam)
ENSG00000070961	ATP2B1
ENSG00000144290	SLC4A10
ENSG00000160551	TAOK1
ENSG00000163939	PBRM1
ENSG00000198408	MGEA5
ENSG00000071794	HLTF
ENSG00000102385	DRP2
ENSG00000115839	RAB3GAP1
ENSG00000157680	DGKI
ENSG00000166387	PPFIBP2
ENSG00000075856	SART3
ENSG00000122025	FLT3
ENSG00000127463	KIAA0090
ENSG00000143924	EML4
ENSG00000157404	KIT

The second data set was composed of mitochondrial genomes of the same lineages present in the nuclear data set. When the genome of the same species was not available, we used a close sister taxa. For instance, Callithrix was used in the nuclear data set and Cebus was used in the mitochondrial data set. The taxonomic compositions contained 19, 27 and 35 species respectively (Fig. 1). We used all 13 mitochondrial coding genes, resulting in a supermatrix of 11,763 nucleotides. Mitochondrial genes were partitioned into three classes containing first, second and third codon positions, as opposed to the nuclear. This is the partitioning scheme commonly applied to mitochondrial data and is intended to reduce evolutionary rate variability within the partitions studied.²³ Accession numbers of the mitochondrial genomes of the species shown in Figure 1D–F are available in Table 2.

Table 2.

Accession numbers of the mitochondrial genomes used in this study.

Taxon	Accession
Bos	NC_006853
Canis	NC_002008
Cavia	NC_000884
Cebus	NC_002763
Cercopithecus	NC_007009
Choleopus	NC_006924
Dasypus	NC_001821
Echinops	NC_002631
Equus	NC_001640
Erinaceus	NC_002080
Eulemur	NC_012771
Felis	NC_001700
Gorilla	NC_001645
Homo	NC_012920
Jaculus	NC_005314
Lagenorhynchus	NC_005278
Lama	NC_012102
Lemur	NC_004025
Loxodonta	NC_000934
Macropus	NC_001794
Monodelphis	NC_006299
Mus	NC_005089
Ochotona	NC_003033
Ornithorhynchus	NC_000891
Oryctolagus	NC_001913
Ovis	NC_001941
Pan	NC_001643
Pongo	NC_002083
Procavia	NC_004919
Rattus	NC_012374
Sciurus	NC_002369
Sorex	NC_005435
Sus	NC_000845
Tarsius	NC_012774
Tupaia	NC_002521

The genes were aligned individually in PRANK under default parametric settings.²⁴ The phylogenetic inference was performed with supermatrices of the nuclear and mitochondrial data sets under the taxonomically richer species composition (Fig. 1C and F). These trees were then pruned to obtain the topologies of the compositions with reduced numbers of terminals. Maximum likelihood tree topology search was performed in PhyML 3²⁵ under the GTR + Γ4 + I model of sequence evolution. Branch support was measured with the aLRT statistics.²⁶ The tree topologies shown in Figure 1 were fixed throughout the analyses to eliminate topological variance of the inferred divergence times.

Divergence time analysis

Divergence times were estimated in BEAST 1.6.2³ using the uncorrelated lognormal model of evolutionary rate evolution. In all of the analyses, the Yule process was used as the tree topology prior, and the GTR + Γ4 + I model of evolution was applied to each partition independently. We have chosen a parameter-rich model to incorporate the complexity of the substitution process of the sequences. Posterior distributions of node ages was achieved by Markov chain Monte Carlo (MCMC) using 2 × 27,000 samples obtained by visiting two independent chains every 1,000nd cycle for 3 × 10⁷ generations and discarding 10% of the collected trees from each chain as burn-in.

The calibration information was obtained from Benton and Donoghue.¹⁸ Sixteen normal priors for the age of selected nodes were used (Table 3). The means of the normal distributions were calculated by averaging the minimum of the maximum recommended values for the age of the splits according to that study. We have set the standard deviations so that the minimum and maximum boundary values delimited the 95% highest probability interval (HPD) of the prior.

Table 3.

Calibration information used as divergence time priors.

Divergence	Normal prior mean	Normal prior SD
Homo/Pan	8.3	0.9
Mus/Rattus	11.7	0.4
Bovinae/Antilopinae	23.4	2.6
Hominoidea/Cercopithecoidea	28.5	2.8
Ruminantia/Tylopoda–Suiformes	50.9	1.3
Caniformia/Feliformia	53.3	2.6
Ameridelphia/Australidelphia	66.4	2.5
Carnivora/Perissodactyla	66.8	2.2
Afrosoricida/Tubulidentata–Paenungulata	80.7	16.5
Glires	81.0	10.0
Archonta/Glires	81.0	10.0
Ferungulata	104.2	4.5
Euarchontoglires/Laurasiatheria	104.2	4.5
Boreoeutheria/Xenarthra	104.2	4.5
Eutheria/Metatheria	131.5	3.5
Theriimorpha/Australosphenida	176.8	7.3

Note: For each divergence represented in the first column, a normal prior distribution was assigned with the respective mean and standard deviation (SD).

As commonly used in molecular dating, the effective sample size (ESS) of parameters was used to examine the mixing of the chains. The convergence of the MCMC algorithm was checked by calculating the potential scale reduction factor statistics²⁷ and the Heidelberger and Welch test,²⁸ all MCMC output analyses were implemented in the CODA package of the R programming environment (http://www.r-project.org).

Comparison procedure

Empirical studies of methods present limitations that do not arise during classical simulation analysis. Because the true mammalian timescale is unknown, one cannot calculate the accuracy of the age estimates. However, empirical data offer the advantage of studying methods with realistic data sets. In this study, the comparison between the partitioning schemes was implemented to investigate whether the schemes yield the same chronological estimates. Therefore, our analyses were guided by the following four key questions: Do both partitioning schemes yield the same divergence estimates of nodes? In which scheme do the posterior estimates depart more from the priors? Which scheme yields estimates with greater precision? Which partitioning scheme more rapidly reaches ESS values suitable for analysis? To answer the first three questions, we have estimated the correlation coefficients and fitted a simple linear regression model, without variable transformation, to the estimates of the cases to be compared, whereas the fourth question was addressed using a cumulative sliding-window strategy. According to this strategy, the size of the sample analyzed increased by units of 100 MCMC samples. For each new window, ESSs were calculated for all of the parameters and then averaged; the average ESS was then used to monitor the cumulative increase of the effective sample size.

Results

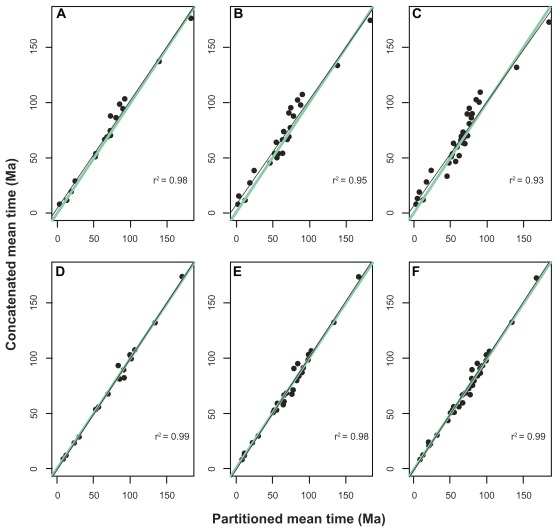
The means of the posterior distributions of the divergence times were similar in the concatenated and partitioned schemes for both nuclear and mitochondrial data sets (Fig. 2). The chronological estimates of the partitioning schemes from the nuclear set were significantly correlated, and all of the node ages were similar (Fig. 2A–C). The slopes of the regression lines varied from 0.98 to 0.95 for the smaller and larger taxonomic compositions, respectively. In the first taxonomic arrangement of the nuclear set, the greatest difference between the concatenated and partitioned schemes was found for the (Bos, Sus)/(Equus, (Canis, Felis)) split (15.1 Ma). In the second nuclear arrangement, the greatest difference was found for the separation of Sorex from other laurasiatherians (19.6 Ma). Lastly, in the third nuclear taxon composition, the basal Laurasiatheria split, the divergence of (Sorex, Erinaceus) from other laurasiatherians was also inferred to present the greatest difference between the partitioning schemes (19.3 Ma).

Figure 2.

Linear regressions between the means of the posterior distributions of the node ages of the phylogenies in Figure 1.

Notes: The solid green lines represent the regressions with a slope equal to 1. The solid black lines represent the regressions between the concatenated and partitioned schemes. Regression coefficients (r²) are all significant at P < 0.001.

In the mitochondrial data set, the posterior distributions of the divergence times of the concatenated and partitioned schemes were also significantly correlated (a product-moment correlation greater than 0.98) (Fig. 2D–F), and were statistically identical because the slope of the regression line was estimated to be 1.0 in all of the taxonomic compositions. In general, the age estimates obtained from both schemes using the mitochondrial set were more similar to each other than those inferred using the nuclear genes. For instance, the greatest discrepancy between the posterior means of the schemes in the first taxonomic arrangement was 10.1 Ma, which was also inferred for the separation between (Bos, Sus) and (Equus, (Canis, Felis)). In contrast to the result for the nuclear data set, the increased taxonomic sampling did not significantly affect the difference between the posterior distributions of the divergence times. Although the same evolutionary split continued to show the greatest difference between the schemes, namely, the Cetartiodactyla/(Carnivora, Perissodactyla) separation, the magnitude of the discrepancy remained constant: 11.1 and 10.5 Ma for the second and third taxonomic arrangements, respectively.

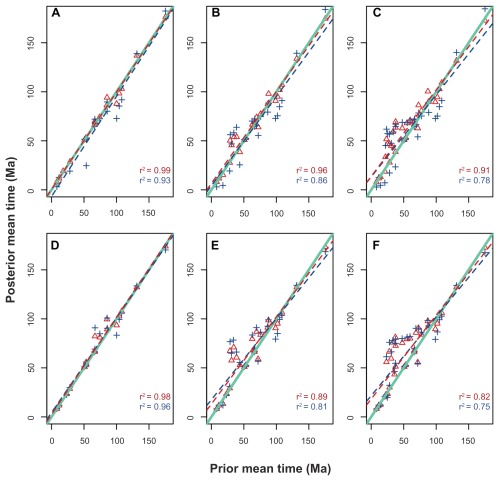
In the nuclear data sets, the comparison between the prior and posterior distributions revealed strong correlations between the estimates (Fig. 3A–C). However, as taxon sampling increased, the difference between the prior and posterior means of the chronological estimates became larger. For example, under the smallest taxonomic arrangement, the means of the posterior distributions of the concatenated scheme were more similar to their priors than to the posterior means of the partitioned scheme. The same was true for the comparison between the priors and posteriors of the partitioned scheme (Fig. 3A). However, when comparing the slopes of the regression lines in the second nuclear taxonomic composition, the posterior divergence time means of both of the partitioning schemes were more similar to each other than to their respective priors (Fig. 3B). This scenario was intensified in the more species-rich nuclear arrangement (Fig. 3C).

Figure 3.

Linear regressions between the means of the prior and posterior distributions of the node ages of the phylogenies in Figure 1.

Notes: The solid green lines represent the regressions with a slope equal to 1. The dashed blue lines represent the regression between the prior and posterior under the partitioned scheme, whereas the dashed red lines represent the regression between the prior and posterior under the concatenated scheme. Regression coefficients (r²) are all significant at P < 0.001.

The assessment of the difference between the prior and posterior distributions in the mitochondrial set showed that the posterior distribution of the divergence time estimates diverged considerably from the priors in the mitochondrial set (Fig. 3D–F). Moreover, the extent of the departure from the prior increased on larger taxonomic sampling.

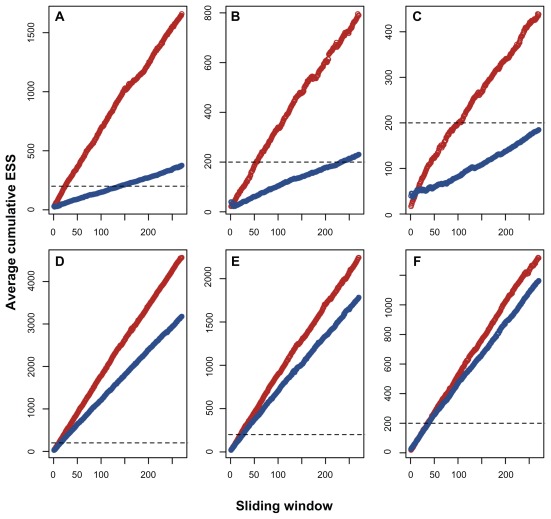
The evaluation of the average cumulative ESS clearly showed that, for all the cases studied, in the concatenated scheme, the average ESS increased at a faster rate than the partitioned scheme estimates (Fig. 4). However, the nuclear and mitochondrial sets showed very different rates of ESS increase. In the nuclear data set, only the concatenated scheme was similarly efficient, and the average ESS of the nuclear partitioned data increased very slowly and required more than 15,000 MCMC samples to reach 200 in the first and second taxonomic arrangements (Fig. 4A and B). In the third nuclear taxonomic composition, the partitioned scheme only approached 200 after 30,000 MCMC samples (Fig. 4C). On the other hand, all of the mitochondrial taxonomic compositions yielded an average ESS of 200, with fewer than 5,000 MCMC samples, independent of the partitioning scheme (Fig. 4D–F).

Figure 4.

Plot of the average cumulative ESS along the sliding window of the MCMC samples.

Notes: The red points represent the concatenated data sets, and the blue points represent the partitioned analysis.

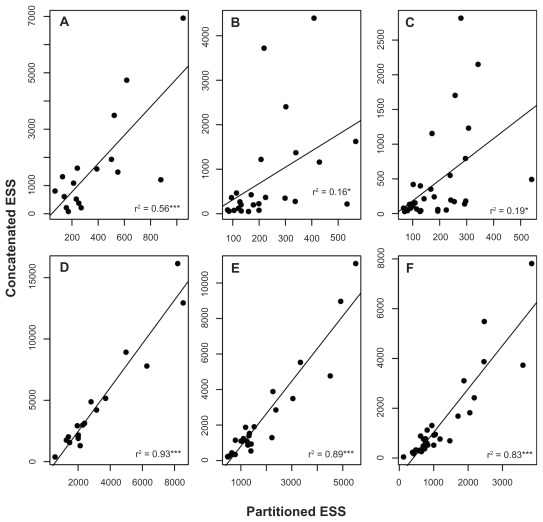
The efficiency of the concatenated scheme is confirmed by the comparison of the ESSs of each divergence time estimate between the concatenated and partitioned schemes (Fig. 5). Although the correlation coefficients were significant and the slopes of the regression lines were greater than 3.0 in the nuclear set, the coefficients were low (varying from 0.58 to 0.16). These findings indicate that the increased slopes were influenced by a few age estimates (points above the regression line) for which the discrepancy between the ESSs of the partitioned and concatenated schemes was large (Fig. 5A–C). Generally, the individual ESSs of node ages are higher in the concatenated schemes, and this tendency is more clearly observed in the mitochondrial data set (Fig. 5D–F) in which the correlation coefficients were greater than 0.8 and the slopes of the regression lines were greater than 1.0.

Figure 5.

Linear regressions between the effective sample sizes of the node age estimates based on the concatenated and partitioned schemes.

Notes: (r²) regression coefficients. Asterisks represent statistical significance at P < 0.001 (***), 0.01 (**) and 0.5 (*) respectively.

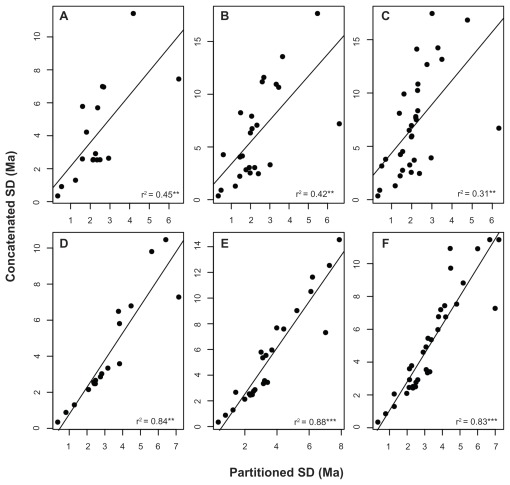
We have also examined the behavior of the precision of the posterior distribution of the divergence times, as measured by the standard deviation of the samples collected during the MCMC analysis. In general, the standard deviations of the posterior distributions of the node ages were significantly correlated between the concatenated and partitioned schemes. However, although the product-moment correlation coefficients were significant, they were not high in the nuclear data set and ranged between 0.43 and 0.76; conversely, the correlations varied from 0.91 to 0.97 for the mitochondrial data set (Fig. 6). Nevertheless, an overall tendency was evident: in both mitochondrial and nuclear data sets, independent of the taxonomic composition, the standard deviations of the posterior distributions of the concatenated supermatrices were greater than those calculated for the partitioned data sets.

Figure 6.

Linear regressions between the standard deviations of the posterior distributions of the node age estimates of the concatenated and partitioned schemes.

Notes: (r²) regression coefficients. Asterisks represent statistical significance at P < 0.001 (***), 0.01 (**) and 0.5 (*) respectively.

Discussion

In this study, we have demonstrated several features of the partitioning scheme applied to nuclear and mitochondrial data sets and its consequence to mammalian divergence time estimates. Essentially, our results showed that the effect of the data partitioning was, on average, statistically negligible, even though the concatenated supematrices were more efficient than the partitioned analysis.

It might be argued that all data sets would eventually converge to the same estimates of divergence times if the Markov chains were run long enough. The differences among data sets observed in this study were, therefore, temporary. However, we think that, realistically, this is exactly the main argument to be considered. Bayesian divergence time inference using relaxed clock methods is computationally demanding, thus, if both partitioning schemes yielded similar estimates, we should assume that the simpler composition, ie, the concatenated scheme, was more efficient.

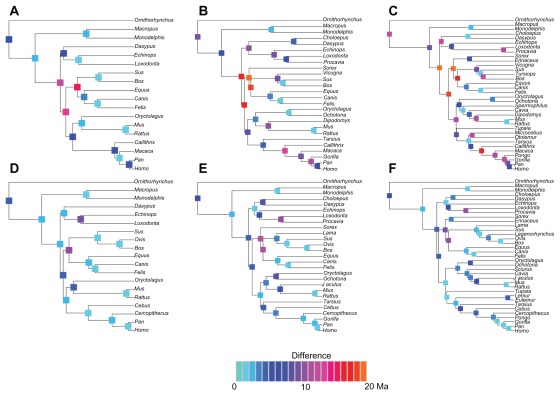
Nodes with large difference between partitioning schemes

One of our findings was that the greatest difference between the partitioning schemes occurred for the nodes that were close to the basal Laurasiatheria split. In the nuclear data set, these nodes were the Atlantogenata/ Boreoeutheria separation, the basal Boreoeutheria divergence, the split between insectivores and Ferungulata (basal Laurasiatheria), and the basal Ferungulata divergence (Fig. 7). The basal Ferungulata split was also dated at discrepant ages by both of the schemes for the mitochondrial data set (Fig. 7). One of the reasons for the lower efficiency of the nuclear data set for these nodes might be associated with the large variation commonly found in the coalescence times of nuclear genes.²⁹ Actually, the resolution of the phylogenetic branching between the superorders of Mammalia and the early evolution of Laurasiatheria are the most difficult problems in mammalian phylogenomics.^16,17,30

Figure 7.

Phylogenies used in this study.

Notes: The magnitude of the difference between the node ages from the concatenated and partitioned schemes is represented in each node using the color scale shown at the bottom of the figure.

In this sense, if the reason for the difference found between the partitioning schemes in the age of these splits is associated with deep coalescence events, we would expect a large standard deviation of the posterior distributions of the partitioned data sets. However, as shown in Figure 6, the standard deviation of divergence time estimates of the partitioned scheme were actually smaller than those obtained from the concatenated analysis. Thus, it appears that the difference might be simply associated with low ESSs values on these nodes found particularly on the partitioned analysis (all bellow 200). This could be caused by the inability of the MCMC algorithm to efficiently explore the parametric space and would lead to spuriously low standard deviations. For instance, in the nuclear data set, the ESS estimated for the age of the Atlantogenata/Boreoeutheria split using the concatenated supermatrix was 419.8, whereas it decreased to 101.9 under the partitioned scheme. The standard deviations of the posterior distributions of this parameter were 3.7 and 2.1 Ma for the concatenated and partitioned schemes, respectively. Not surprisingly, the autocorrelation of the Markov chain was higher in the partitioned scheme (0.68 vs. 0.41 using the concatenated sequence), which indicates a poor mixing of the chain.

Efficiency of mitochondrial data

In our analysis, divergence time estimates based on the mitochondrial coding genes were robust to taxonomic sampling and were also efficient. On average, the ESS of the age estimates rapidly increased along the MCMC run, particularly when genes were concatenated in a single supermatrix. The robustness to the partitioning scheme of the estimates obtained from the mitochondrial data might be a consequence of the smaller number of partitions used in the partitioned data set, which reduced the number of parameters of the model and facilitated MCMC convergence. The robustness of mitochondrial estimates, however, does not indicate that mitochondrial estimates were accurate.

Unfortunately, accuracy cannot be easily accessed on analysis of empirical data. Thus, it is meaningful to ask whether the mitochondrial and nuclear age estimates were similar, because is unlikely that two independent data sets yield the same incorrect estimate. We have calculated the differences between the nuclear and mitochondrial concatenated sets and between the nuclear and mitochondrial partitioned sets for the nodes for which the estimates showed greater irregularity in our results (Table 4). Such an examination demonstrated that the nuclear concatenated age estimates were close to the mitochondrial concatenated estimates. The differences between the concatenated analyses ranged from 0.0 to 5.6 Ma (Table 4); in contrast, the partitioned estimates from the nuclear and mitochondrial genes ranged from 9.4 to 14.6 Ma (Table 4).

Table 4.

Differences between nuclear and mitochondrial divergence time estimates of selected nodes.

Basal divergence*	Concatenated			Partitioned
	C1§	C2	C3	C1	C2	C3
Placentalia	4.7	0.6	3.1	14.0	12.5	11.8
Boreoeutheria	4.2	1.3	0.1	13.9	14.6	14.3
Laurasiatheria	5.6	0.0	0.7	10.6	9.4	11.5
Ferungulata	NA	0.2	0.0	NA	6.5	6.3

Notes: Comparisons were performed by calculating the absolute value of the difference between the nuclear and mitochondrial concatenated schemes and between the nuclear and mitochondrial partitioned schemes.

^*The nodes analyzed consisted of the basal split of the lineages in the column;

^§Refers to the taxonomic compositions. C1 is the taxon-poorer taxonomic arrangement, and C3 is the species-richer composition.

NA = Not applicable because the basal Laurasiatheria and Ferungulata nodes were the same after eliminating the insectivores.

Efficiency of nuclear data and other statistical issues

The nuclear divergence times inferred using the concatenated scheme are closer to the ages estimated from the mitochondrial data than they are to the nuclear partitioned set. This finding demonstrates that the nuclear partitioned set yielded the most deviant divergence times. As we have previously suggested, the partitioned analysis of the nuclear data presented small standard deviations (Fig. 6), possibly as a result of poor exploration of the parametric space. It is worth mentioning, however, that the Gelman and Rubin’s²⁷ statistic was close to 1.0 for all divergence times estimated from the three nuclear partitioned data sets. MCMC runs also passed the Heidelberger and Welch’s²⁸ test. Therefore, although the use of a large number of model parameters in the partitioned nuclear data did not permit an exhaustive evaluation of the parametric space, the results would be considered satisfactory by the methods of evaluation of MCMC runs usually available in Bayesian software.

Because we have not conducted a simulation study, our results offer limited power to evaluate the performance of the partitioning schemes. In practical terms, however, when analyzing biological data, researchers generally check for convergence by calculating the ESS of parameters. With respect to ESS, concatenated data sets were superior. Researchers should consider though that the use of concatenated data is biologically meaningless if partitions share different evolutionary histories.³¹ However, this is not the case of mammalian mitochondrial genomes.

In conclusion, our study showed that, in general, the age estimates of both of the partitioning schemes attained similar values, with the exception of the divergence times of the nodes associated with the basal diversification of placentals, Boreoeutheria, Laurasiatheria and Ferungulata. The posterior distributions of the divergence times based on the partitioned scheme presented smaller standard deviations (they were more precise). This observation, however, might be associated with the poor mixing of the Markov chains. Therefore, in both mammalian genome data sets analyzed, given the same number of MCMC generations, the simpler modeling of the evolutionary process implemented by concatenating genes in supermatrices reached divergence time estimates similar to those inferred from partitioned data sets. Moreover, the MCMC samples obtained from concatenated data sets presented greater ESS and lower autocorrelation.