Signal transduction in a compliant thick ascending limb

Abstract

In several previous studies, we used a mathematical model of the thick ascending limb (TAL) to investigate nonlinearities in the tubuloglomerular feedback (TGF) loop. That model, which represents the TAL as a rigid tube, predicts that TGF signal transduction by the TAL is a generator of nonlinearities: if a sinusoidal oscillation is added to constant intratubular fluid flow, the time interval required for an element of tubular fluid to traverse the TAL, as a function of time, is oscillatory and periodic but not sinusoidal. As a consequence, NaCl concentration in tubular fluid alongside the macula densa will be nonsinusoidal and thus contain harmonics of the original sinusoidal frequency. We hypothesized that the complexity found in power spectra based on in vivo time series of key TGF variables arises in part from those harmonics and that nonlinearities in TGF-mediated oscillations may result in increased NaCl delivery to the distal nephron. To investigate the possibility that a more realistic model of the TAL would damp the harmonics, we have conducted new studies in a model TAL that has compliant walls and thus a tubular radius that depends on transmural pressure. These studies predict that compliant TAL walls do not damp, but instead intensify, the harmonics. In addition, our results predict that mean TAL flow strongly influences the shape of the NaCl concentration waveform at the macula densa. This is a consequence of the inverse relationship between flow speed and transit time, which produces asymmetry between up- and downslopes of the oscillation, and the nonlinearity of TAL NaCl absorption at low flow rates, which broadens the trough of the oscillation relative to the peak. The dependence of waveform shape on mean TAL flow may be the source of the variable degree of distortion, relative to a sine wave, seen in experimental recordings of TGF-mediated oscillations.

in a series of studies we have used a mathematical model of the tubuloglomerular feedback (TGF) loop to propose plausible explanations for phenomena that have been reported in experimental studies and to predict phenomena that might be found in new experimental studies (23, 24, 28, 29, 30, 31, 32, 34, 36). Our mathematical model consists of simple components that have been individually well characterized in our publications. The thick ascending limb (TAL) is represented by a rigid tube with plug flow that carries only the chloride ion, which is believed to be the principal species sensed by the macula densa (MD; Ref. 39). The time delay in the TGF signal transmission from the tubular fluid chloride concentration alongside the MD to the action of the smooth muscle cells in the distal portion of the afferent arteriole is represented by either a discrete time delay (28) or by a discrete time delay followed by a delay that is distributed over a few seconds (4, 31, 35). The TGF response relationship is represented by a scaled hyperbolic tangent function that closely represents the experimental response that has been documented extensively in experimental studies (2, 39). The actions of the proximal tubule and descending limb of a short-looped nephron are modeled by a linear function that represents glomerular-tubular balance in the proximal tubule and water absorption from the descending limb (28). Thus, with the exception of the TAL, we have modeled the components of the TGF loop by means of simple, phenomenological representations.

In the case of the TAL, however, we have used a more detailed representation (28), because our model investigations have indicated that the transduction process in the TAL, in which changes in tubular fluid flow rate are transformed into chloride concentration variation in tubular fluid alongside the MD, exhibits a number of features that may help explain phenomena found in regular and irregular oscillations that are mediated by TGF (23, 30, 31). In particular, a sinusoidal tubular fluid flow in the TAL is transformed into a nonsinusoidal chloride concentration waveform alongside the MD. Thus the transduction process can be characterized as “nonlinear” in the sense that the chloride concentration waveform is not a linear function of the tubular fluid flow waveform.

Hydrodynamic pressure drives tubular fluid flow and oscillations in fluid flow, through the tubules of the kidney, including the TAL. Marsh and colleagues (15, 38, 49) developed a mathematical model of the nephron that represents hydrodynamic pressure and compliant tubular walls; simulations from that model predict that a compliant renal tubule will tend to function as a low-pass filter with respect to flow oscillations (see Fig. 7 in Ref. 38). In our rigid tubule model, flow rate in the TAL is prescribed as a function of predicted single nephron glomerular filtration rate (27): we do not compute hydrodynamic pressure. Thus one might wonder whether the nonlinearity exhibited by our model is an artifact of the rigid tubule formulation and if our model, instead of using a rigid tubule, represented pressure-driven flow in a more realistic TAL model having compliant walls, then some of our model's predictions might be rendered null and void.

To address this concern, we have analyzed, in the present study, a mathematical model of the TAL that includes pressure-driven flow and compliant walls. We found that this more inclusive model exhibits essentially the same nonlinear phenomena as the rigid tubule model; moreover, some of these phenomena are more marked in the compliant tubule model than in the rigid tubule model. Thus the present study appears to vindicate our use of the rigid tubule model, which has advantages of conceptual and computational simplicity and which permits the derivation of useful analytical results, e.g., model solutions obtained by means of the method of characteristics (30, 37) and characteristic equations derived from linearized formulations of the model (12, 18, 28, 31, 35, 36, 37).

Moreover, the model results predict that mean TAL flow strongly influences the shape of the NaCl waveform at the MD. This influence is a consequence of the inverse relationship between flow and transit time, which produces asymmetry between up- and downslopes of the oscillation, and the nonlinearity of TAL transport at low flow rates, which broadens the trough of the oscillation relative to the peak. These findings provide an explanation for the varying degrees of waveform distortion found in experimental recordings of TGF-mediated oscillations. This suggests that the degree of distortion, relative to a sinusoidal oscillation, may provide insight into TAL function, including, e.g., fractional Na⁺ and Cl⁻ reabsorption in the TAL.

MATHEMATICAL MODEL

Formulation: compliant tubule model.

To study the signal transduction properties of the TAL, we used a mathematical model of a compliant tubule that predicts tubular fluid flow, fluid pressure, and tubular radius as functions of space and time. However, TAL tubular fluid pressure at the MD is not well characterized. Therefore, to estimate approximate fluid pressure at the MD, the model represents the TAL and distal tubule segments of a short-looped nephron and a contiguous and composite collecting duct that extends in space from x = 0 (the bend of the Henle's loop) to x = L₀ at the end of the collecting duct, where fluid pressure is better characterized. In rat, the pressure at the end of the collecting duct can be inferred to be ∼1–3 mmHg, based on measurements in the interstitia, the vessels, and the pelvic space (1, 10, 11). The walls of the model tubule were assumed to be compliant, and the walls were assumed to have a radius that depends on the transmural pressure gradient. To investigate the effects of tubular wall motion on TGF signal transduction, we represented the chloride ion concentration ([Cl⁻]) in the TAL tubular fluid; the concentration of that ion alongside the MD is believed to be the principal tubular fluid signal for the TGF response (39). The chloride concentration was represented only along the TAL, which extends in space from x = 0 at the bend of Henle's loop to x = L at the MD. A schematic diagram for the model TAL is given by Fig. 1.

Fig. 1.

Schematic representation of model thick ascending limb (TAL). Hydrodynamic pressure P(0, t) drives flow into TAL entrance (x = 0) at time t. Oscillations in pressure result in oscillations in TAL flow Q(x, t), radius R(x, t), fluid transit time T(x, t) to position x, and tubular fluid chloride concentration C(x, t).

Fluid motion along the model tubule segments was modeled as the flow of an incompressible fluid within a compliant tubule that is long relative to its radius. Intratubular fluid flow and pressure were described by two coupled partial differential equations:

$$\frac{\partial }{\partial x}P\left(x,t\right)=-\frac{8\mu }{\pi R^4\left(x,t\right)}Q\left(x,t\right),$$ (1)

and

$$\frac{\partial }{\partial x}Q\left(x,t\right)=-\left\{2\pi R\left(P\left(x,t\right)\right)\left(\frac{\partial R}{\partial P}\left(x,t\right)\right)\right\}\frac{\partial }{\partial t}P\left(x,t\right),$$ (2)

where x is axial position along the represented tubular segments, t is time, P(x, t) is the tubular fluid pressure, Q(x, t) is the tubular volume flow rate, and R(P(x, t)) is the tubular radius, which is a function of pressure (see below). Equation 1 represents Poiseuille flow, which is driven by the axial pressure gradient. Equation 2 represents fluid incompressibility and conservation. Equations 1 and 2 are justified in appendix a. The inflow pressure P₀(t) = P(0, t) was assumed to be given as a function of time t, and the outflow pressure P₁ = P(L₀, t) was considered to be a constant.

Conservation of Cl⁻ in TAL tubular fluid was represented by a hyperbolic partial differential equation that is similar to our previous formulations (3, 23) but that here included the effects of a time-varying radius R:

$$\pi R^2\left[P\left(x,t\right)\right]\frac{\partial }{\partial t}C\left(x,t\right)=-2\pi R\left(P\left(x,t\right)\right)C\left(x,t\right)\frac{\partial }{\partial t}R\left(P\left(x,t\right)\right)-\frac{\partial }{\partial x}\left[Q\left(x,t\right)C\left(x,t\right)\right]-2\pi R_o\left\{\frac{V_{\max }C\left(x,t\right)}{K_M+C\left(x,t\right)}+P_M\left[C\left(x,t\right)-C_e\left(x\right)\right]\right\},$$ (3)

where C(x, t) is TAL tubular fluid chloride concentration, C_e(x) is the extratubular (interstitial) chloride concentration, and R_o is a constant reference radius that represents the area available for transmural solute transport. The two terms inside the braces correspond to active solute transport characterized by Michaelis-Menten-like kinetics (with maximum Cl⁻ transport rate V_max and Michaelis constant K_m) and transepithelial Cl⁻ diffusion (with backleak permeability P_M). For the transport terms in Eq. 3, the radius was considered fixed at R_o, because the number of transport proteins was assumed to be time-independent. Also, the [Cl⁻] at the TAL entrance was assumed known: C(0, t) = C_o.

To represent a compliant tube, the tubular luminal radius was assumed to vary as a linear function of transmural pressure difference (15); thus

$$R\left(P\left(x,t\right)\right)=\alpha \left[P\left(x,t\right)-P_e\left(x\right)\right]+\beta \left(x\right),$$ (4)

where P_e(x) is the extratubular (interstitial) pressure, α specifies the degree of tubular compliance, and β(x) is the tubular radius when the transmural pressure difference is zero (see below). The radius changes instantaneously as P(x, t) changes because tissue viscosity was not represented.

Parameters.

Base-case values for the model parameters are given in Table 1. The luminal radius parameter β(x) (in μm) for an unpressurized model tubule is a piecewise-defined function given by

$$\beta \left(x\right)=\{\begin{array}{ll}{\beta }_0\left(x\right),\hfill & 0\le x\le L\hfill \\ {\beta }_1,\hfill & L<x\le a_d\hfill \\ {\beta }_2\left(x\right),\hfill & a_d<x\le 3L\hfill \\ {\beta }_3,\hfill & 3L<x\le L_0,\hfill \end{array}$$ (5)

where a_d = 1.5 × L; β₀(x) is the cubic polynomial such that β₀(0) = β₀,₀, β₀(x = L) = β₁, β₀^′(0) = 0, and β₀₀^′(L) = 0 [the prime symbol (′) indicates differentiation]. Similarly, β₂(x) is the cubic polynomial such that β₂(1.5L) = β₁, β₂ (3L) = β₃, and β₂^′(1.5L) = β₂^′(3L) = 0. The parameters β_0,0, β₁, and β₃ (4.8, 9.9, and 7.4, respectively) were chosen so that in the time-independent steady state (when Q is constant in time and space), the mean radius was ∼5.5 µm at the bend of Henle's loop and 10 μm at the MD (19) and so that the TAL tubular fluid pressure was ∼7 mmHg at the MD (i.e., x = L; Ref. 14) and ∼2 mmHg at the end of the model tubule (i.e., x = L₀).

Table 1.

Base-case parameter values

Independent Parameters	Dimensional Value
α	1.33 × 10−5 cm/mmHg
ad	1.5 × L
β0,0	4.8 μm
β1	9.9 μm
β3	7.4 μm
Co	275 mM
Km	70.0 mM
L0	2.00 cm
L	0.500 cm
μ	7.2 × 10−3 g·cm−1·s−1
Pe	5.00 mmHg
P̄0	10.00 mmHg
P1	2.00 mmHg
Pp	1.50 mmHg
PM	1.50 × 10−5 cm/s
Qo	6 nl/min
Ro	10.0 μm
to	8.83 s
Vmax	14.5 nmol·cm−2·s−1

See glossary for definitions.

Extratubular [Cl⁻] was specified by C_e(x) = C_o{A₁ exp[−A₃(x/L)] + A₂}, where A₁ = [1 − C_e(L)/C_o] = [1 − exp(−A₃)], A₂ = 1 − A₁, and A₃ = 2, and where C_e(L) corresponds to a cortical interstitial concentration of 150 mM. A graph for C_e(x) was given in Fig. 1 of Ref. 28.

Numerical methods.

To compute an approximation for tubular fluid motion, we first recast Eqs. 1 and 2 as a single equation. That was achieved by taking the spatial derivative of Eq. 1 and using the resulting equation to eliminate ∂Q(x, t)/∂x the fluid flow gradient, from Eq. 2. The result is an advection-diffusion equation for the pressure P(x, t),

$$\frac{\partial }{\partial t}P\left(x,t\right)-\frac{R^2\left(x,t\right)}{4\mu \left[\frac{\partial R}{\partial P}\left(x,t\right)\right]}\frac{\partial }{\partial x}R\left(P\left(x,t\right)\right)\frac{\partial }{\partial x}P\left(x,t\right)=\frac{R^3\left(x,t\right)}{16\mu \left[\frac{\partial R}{\partial P}\left(x,t\right)\right]}\frac{{\partial }^2}{\partial x^2}P\left(x,t\right),$$ (6)

which is subject to the boundary conditions P(0, t) = P₀(t) and P(L0, t) = P1. The numerical procedure by which Eq. 6 was solved to advance P(x, t) in time is described in appendix b.

Numerical solutions to the solute conservation equation (Eq. 3) were found as previously described (26, 31): an ENO method that is second-order in space was used in conjunction with Heun's method to obtain a method that is second-order in both space and time. The time step used was Δt = 1/320 = 0.003125 s; the spatial grid was assumed to have 1,280 subintervals, which yields a space step of Δx = 1.5625 × 10⁻³ cm.

RESULTS

To investigate the effect of tubular compliance on the propagation of perturbations in fluid flow, fluid pressure, and fluid [Cl⁻], we compared the predictions of a base-case model (having compliance α = 1.33 × 10⁻⁵ cm/mmHg; Ref. 15) with two other models. One is a “rigid-tubule model,” in which the tubular walls are noncompliant. In that model, the tubular radius is constant; i.e., α = 0 and β(x) = [5.5 + 4.5(x/L)] μm. Consequently, fluid flow is constant in space at each time t, but flow may vary as a function of time. A second model is a “more-compliant model,” in which the compliance is twice the base-case value; i.e., α = 2.66 × 10⁻⁵ cm/mmHg. In this model, the radius parameters β_0,0, β₁, and β₃ were set to 4.3, 9.8, and 7.4 μm, respectively.

Steady-state behavior.

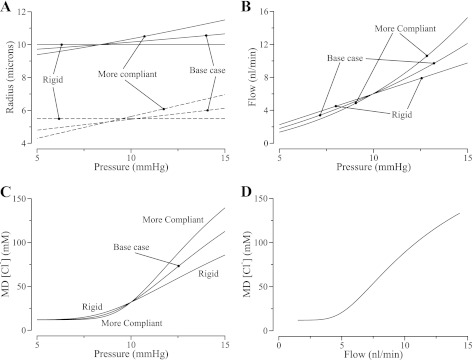
We first examined the effects of TAL compliance on luminal [Cl⁻] under conditions of steady flow established by a specified input pressure. Figure 2A illustrates the effects of input pressure on TAL radius at the beginning (dashed lines) and end of the segment (solid lines). The radius at the TAL entrance is smaller than at the exit, despite the drop in pressure, because the baseline radius has been found to be larger towards the MD (19). Figure 2B illustrates that compliance increased the sensitivity of flow to changes in input pressure because of the reduction in segmental resistance as the tubule dilated in response to increased luminal pressure. Because TAL Cl⁻ reabsorption depends on tubular fluid transit time (which is a variable that decreases as flow increases), the compliant TAL model also exhibited higher sensitivity of [Cl⁻] at the MD to input pressure than the rigid tubule model, as illustrated in Fig. 2C. However, the enhanced sensitivity of MD [Cl⁻] to input pressure in the compliant and more compliant model TAL segments arises solely from the heightened sensitivity of flow to pressure. This is illustrated in Fig. 2D, where the flow and MD [Cl⁻] pairs for all three cases from Fig. 2, B and C, superimpose. Although this result is expected because the model assumes that the [Cl⁻] transport characteristics of the TAL are independent of variation in tubular radius (see Eq. 3), the exact superposition of the computed curves nevertheless provides an informative test and confirmation of our numerical procedures.

Fig. 2.

Steady-state TAL luminal radius (A), tubular flow rate (B), and macula densa (MD) chloride ion concentration ([Cl⁻]; C) as functions of TAL entrance pressure, for the rigidtubule case, base case, and the more-compliant case. A: radii at the TAL entrance and MD are shown in dashed and solid lines, respectively. D: monotonic relationship between TAL flow and MD [Cl⁻] as defined by the values for the 3 cases plotted in B and C; note that the curves superimpose.

Responses to a step perturbation.

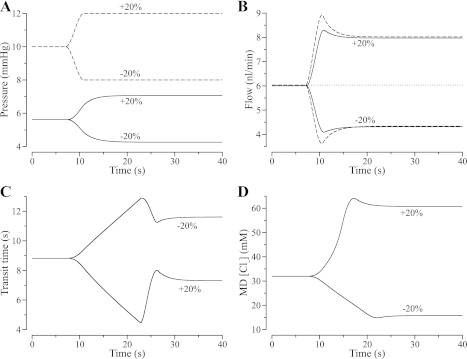
To better understand the characteristics of our model, we simulated the responses of flow, transit time, and MD [Cl⁻] to a rapid, step-like, increase or decrease in input pressure. To avoid numerical errors that may arise from using a centered, finite-difference method to compute the derivatives of a step function, we approximated the true step change in pressure by a smooth rise having a duration of 3.75 s. Figure 3A shows the imposed changes in the input pressure (dashed lines) and the resulting changes in outflow pressure (solid lines) for the TAL model with base-case compliance. Figure 3B shows the resulting changes in TAL inflow (dashed lines) and outflow (solid lines), relative to the initial flow (dotted line). The over- and undershoots in flow during the transitions in pressure arise from adjustments in tubular radius (and hence volume) during the time interval when luminal pressure is rapidly changing.

Fig. 3.

Model responses to a rapid, step-like 20% increase or 20% decrease in TAL entrance pressure (A, dashed lines) on TAL outflow pressure (A, solid lines), TAL inflow (B, dashed lines) and outflow (B, solid lines), TAL transit time (C), and MD [Cl⁻] (Panel D). Model predicts rapid changes in flow rate (B), whereas the changes in TAL transit time (C) and MD [Cl⁻] (D) are slower, more complex, and asymmetric.

These transient changes in flow and tubular radius result in a complex pattern of changes in transit time of the fluid reaching the MD. The transit time at time t, denoted T(t), is the time required by a fluid particle that is initially at the TAL entrance to reach the MD at time t. The transit time T(t) is defined implicitly by

$$L={\displaystyle {\int }_{t-T\left(t\right)}^t}v\left(x\left(s\right),s\right)ds,$$ (7)

where v(x(s), s) denotes the axial speed of the TAL tubular fluid at time s and location x(s). Under appropriate simplifying assumptions, it can be shown that the change in [Cl⁻] in a small fluid element flowing up the model TAL depends only on the time that transepithelial transport has acted on that element (the transit time) and not on its changing speeds along the TAL. The simplifying assumptions are that the TAL is rigid, the concentration is fixed at the TAL entrance, and the transepithelial transport depends only on the interior TAL concentration (30). If the assumptions are only approximated, then the transit time provides an approximation of concentration change along the TAL. The initial slow rise or fall in transit time that begins when pressure first changes reflects the fact that the interval of time that any fluid element has spent in the tubule depends on its location within the TAL at the time the pressure perturbation is applied. Hence, the effects on transit time of the transient changes in flow at the entrance to the TAL (Fig. 3C) are fully developed after a time delay that is approximately equal to the mean transit time at the new level of pressure. At those points in time, the effect of the overshoot and undershoot in flow are evident.

Figure 3D illustrates the changes in MD [Cl⁻], which depend on both the transit time and the transport characteristics of the TAL. The +20% pressure perturbation results in an approximately linear rise followed by a small overshoot before settling at the higher concentration. In this case, the MD [Cl⁻] curve is similar in shape to the transit time curve in Fig. 3C except that the MD [Cl⁻] curve is inverted and scaled. This similarity arises because the flow changes over a range where the TAL transport curve is quasilinear (see Fig. 2D). The shape of the MD [Cl⁻] response is similar to NaCl conductivity measurements during step-wise variations in perfusion rate reported by Mason et al. (33). The model response is also similar to that obtained in a rigid TAL in a previous study (see Fig. 4B, right-hand column, in Ref. 29), except that there was no concentration overshoot in the rigid tubule. In contrast, the MD [Cl⁻] response to the 20% reduction in input pressure was smaller, and the large peak in transit time had little effect on MD [Cl⁻]. In this case, flow was reduced into the range where MD [Cl⁻] approaches the static-head limit, the limit in which tubular fluid [Cl⁻] reaches a minimum value (along the terminal portion of the TAL) because Cl⁻ backleak balances TAL transepithelial absorption. Hence, at low flow, the response of MD [Cl⁻] is determined by both transit time and the inability of the TAL epithelium to further reduce luminal [Cl⁻].

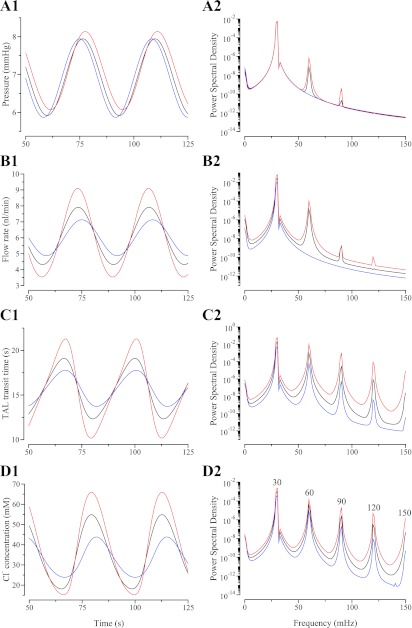
Fig. 4.

A1, B1, C1, and D1: oscillations, as functions of time, in key model variables when a sinusoidal perturbation is applied to input pressure, for the rigid-tubule case (blue), base case (black), and the more-compliant case (red). A2, B2, C2, and D2: corresponding power spectra. Sinusoidal or approximately sinusoidal oscillations were obtained for outflow pressure (A1 and A2) and tubular flow rate (B1 and B2). Nonsinusoidal oscillations were obtained for TAL transit time (C1 and C2), and MD [Cl⁻] (D1 and D2).

Responses to sinusoidal perturbations.

To study the characteristics of the transduction of oscillations in tubular fluid pressure into oscillations in TAL tubular [Cl⁻] concentration, we superimposed a sinusoidal perturbation onto the steady-state inflow pressure at the TAL entrance (x = 0): we applied a pressure of

$$P_0\left(t\right)={\overline{P}}_0+P_p\sin \left(2\pi ft\right),$$ (8)

where P̄₀ = 10 mmHg, P_p = 1.5 mmHg, and f = 30 mHz. The resulting oscillations in TAL tubular fluid pressure, tubular fluid flow, TAL transit time, and Cl⁻ concentration at the MD are illustrated in Fig. 4 for the rigid-tubule case (blue), the base case (black), and the more-compliant case (red).

Results in Fig. 4A1 show that a sinusoidal oscillations in inflow fluid pressure result in almost sinusoidal oscillations in fluid pressure alongside the MD, with time delays (assessed as peak-to-peak time offsets) of 0, ∼0.4, and ∼1.6 s for the rigid-tubule case, the base case, and the more-compliant case, respectively. These results indicate that the pressure wave speed decreases with increasing compliance, which results in progressively larger phase differences in the pressure oscillations at the entrance and exit of the TAL. This result can be explained by a consideration of the pressure equation (Eq. 6): a more compliant tubule results in a larger value of $\frac{\partial R}{\partial P}\left(x,t\right)$, which, taken in isolation, means that advection speed of the pressure wave, given within the second term on the left-hand side of Eq. 6 by $\frac{R^2\left(x,t\right)}{4\mu \left(\frac{\partial R}{\partial P}\left(x,t\right)\right)}\frac{\partial }{\partial x}R\left(x,t\right)$, will decrease. In the compliant cases, luminal radius is assumed to be a linear function of pressure; hence, the radius profiles differ from corresponding pressure profiles by a constant scaling (results not shown).

The model also predicts that oscillations in tubular fluid flow are nearly sinusoidal. The magnitude of the fluid flow oscillations increases with increased compliance. Tubular fluid flow oscillations alongside the MD have smaller amplitudes than do oscillations at the TAL entrance: amplitude along the model TAL decreases by ∼9.55% in the base case and ∼19.6% in the more compliant case. Flow oscillations at the TAL entrance lead flow oscillations at the MD by ∼0.6 s in the base case and by ∼1.2 s in the more-compliant case.

The nonlinear characteristics of the transduction of pressure oscillations into oscillations in tubular fluid [Cl⁻] are exhibited as a function of time. Figure 4C1 shows the TAL transit time of a fluid particle that reaches the MD at time t; the results in Fig. 4D1 show the tubular fluid [Cl⁻] at the MD. As previously noted, given the same pressure oscillations, the amplitude of the tubular fluid flow oscillations is larger in a more compliant tubule. This results in larger oscillations in TAL transit times, as can be seen by comparing the three curves in Fig. 4C1: the oscillation amplitude in the compliant case is increased relative to the rigid case by a factor of ∼2, and the amplitude in the more-compliant case is increased by a factor of ∼4 relative to the rigid case. The larger oscillations in transit time, relative to the rigid case, result in larger oscillations in [Cl⁻] concentration alongside the MD and in more pronounced harmonics in those oscillations (see below).

A comparison of the tubular fluid flow records (Fig. 4B1) with the MD Cl⁻ concentration records (Fig. 4D1) reveals that oscillations in fluid flow are nearly sinusoidal and their extrema are nearly symmetric around the steady-state value (6 nl/min), whereas oscillations in Cl⁻ concentration are markedly nonsinusoidal: they have extrema that are not symmetric around their steady-state value (32 mM) but that are shifted up from that value. Moreover, the oscillations have sharp crests, relative to their troughs. Thus a sinusoidal tubular fluid flow waveform can generate a highly nonlinear [Cl⁻] waveform at the MD. Furthermore, because of the dependence of MD [Cl⁻] on transit time, the Cl⁻ concentration waveforms are phase-shifted relative to fluid flow waveforms.

As we have previously reported (32), a consequence of the highly nonlinear Cl⁻ concentration waveform is increased Cl⁻ delivery to the MD relative to the case of steady (constant) TAL flow. The increased delivery arises from the asymmetry of the waveform relative to the case of steady flow; the asymmetry arises from both transit-time asymmetry and the limitation that NaCl backleak places on the capability of the cortical TAL to reduce tubular fluid [Cl⁻]. For fixed pressure, and thus steady water inflow at the TAL entrance, Cl⁻ delivery is 191.8 pmol/min in all three cases. For the sinusoidal pressure at the TAL entrance used in Fig. 4, resulting Cl⁻ delivery to the TAL is 198.7, 212.3, and 214.5 pmol/min for the rigid, base, and more-compliant cases, respectively. Thus, in the rigid, base, and more compliant cases, delivery is increased by 3.60, 10.69, and 11.84%, respectively. As we have previously noted (30, 31), the distinct nonlinear characteristics in the [Cl⁻] oscillations can be attributed, in part, to variations in TAL fluid transit time. As can be observed via a careful comparison of the transit time and [Cl⁻] waveforms, an increasing flow velocity (or decreasing TAL transit time) produces a rapid rise to a narrow crest in concentration, relative to the trough, whereas decreasing flow velocity (or increasing transit time) produces a slower decrease to a wide trough. The wide trough results from the excursion of flow into a regime where TAL Cl⁻ backleak increases to match TAL cell Cl⁻ absorption. Consequently, a more compliant tubule, which exhibits larger amplitude fluid flow and transit time oscillations, generates a more nonlinear [Cl⁻] waveform at the MD, relative to a more nearly rigid tubule. This result can be observed in Fig. 4, A2, B2, C2, and D2, where the power spectra corresponding to pressure, fluid flow rate, TAL transit time, and [Cl⁻] oscillations, all measured at the MD, are shown: the harmonics, which correspond to the peaks at frequencies above the fundamental frequency of 30 mHz, are stronger in the TAL transit times and MD [Cl⁻] (Fig. 4, C2 and D2) than in the tubular fluid pressures and fluid flows (Fig. 4, A2 and B2). Moreover, for each dependent variable, the spectral peaks of the harmonics are strongest in the more compliant model and weakest in the rigid-tubule model.

The preceding results predict that TAL compliance, by increasing the amplitude of transit time oscillations, intensifies, rather than damps, the nonlinearities and harmonics associated with the transduction of pressure oscillations at the TAL entrance into [Cl⁻] oscillations at the MD. The accentuation of nonlinearities is a result of the slower pressure wave speed in a compliant TAL, which introduces a phase lag between inflow and outflow pressure oscillations and which therefore results in a larger pressure gradient along the TAL and thus larger amplitude oscillations in tubular fluid flow and transit time.

Oscillation profiles.

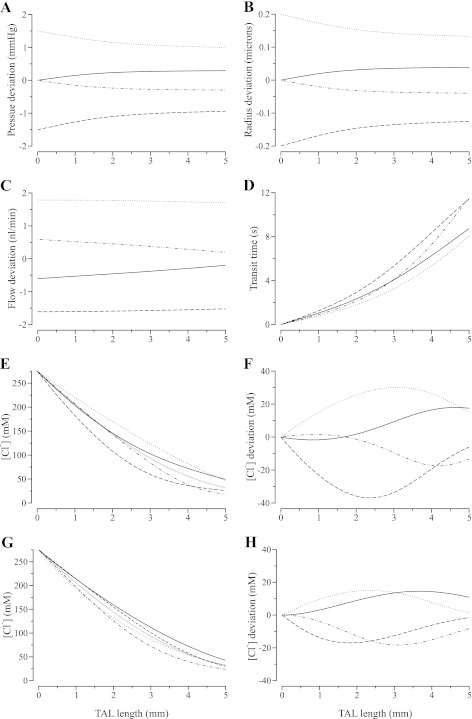
To elucidate the spatial characteristics of the oscillations established by sinusoidal pressure perturbations, in Fig. 5 we exhibit base-case axial TAL tubular fluid pressure, luminal radius, tubular fluid flow rate, transit time, and tubular fluid [Cl⁻] profiles. Some of the profiles are given and labeled as deviations from the respective steady-state profiles (i.e., in each case the steady-state profile was subtracted from the dynamic profile). The profiles were obtained at four equally spaced times within the period of the sinusoidal pressure perturbation: t_n = np/4, for n = 0, 1, 2, 3, and p = 1/f, where f is frequency.

Fig. 5.

Base-case axial profiles along TAL in tubular fluid pressure deviation from steady state (A), tubular radius deviation (B), tubular flow rate deviation (C), transit time (D), and tubular fluid [Cl⁻] (E and F) in response to a sinusoidal pressure perturbation applied to the TAL entrance. Profiles are shown as deviations from nonoscillatory steady-state profiles at 4 time instances, p/4, p/2, 3p/4, and p within an oscillatory period of p = 33.33 s. Dashes, p/4 = 8.33 s; dots-dashes, p/2 = 16.66 s; dots, 3p/4 = 24.00 s; solid, p = 33.33 s. Analogous axial profiles along a rigid-tube TAL in tubular fluid [Cl⁻] (G) and corresponding deviations from steady-state profile (H).

The pressure and radius deviation profiles in Fig. 5, A and B, tend to approximate straight lines, which means that, as the inflow pressure fluctuates, the entire model TAL expands and contracts almost simultaneously (although there are phase delays between different portions of the TAL; see below). This result suggests that, for physiologic values of tubular compliance, the pressure wave does not travel along the TAL as a bolus.

The flow deviation profiles (Fig. 5C) illustrate the attenuation of the amplitude of the flow oscillation along the TAL. Note that although the pressure and radius are in phase, flow is phase shifted with respect to pressure, and thus the flow deviation profiles, at the points in time displayed, do not reflect the extremes of the oscillation, even at the TAL entrance.

The difference between the transit time profiles (Fig. 5D) and the profiles of radius and flow (Fig. 5, B and C) is striking: the transit time profiles are significantly more complex, the deviations from the steady-flow profile are no longer monotonic along the TAL, and the amplitude of fluctuations in transit time increases as tubular compliance increases (results not shown).

Figure 5, E and F, corresponds to MD [Cl⁻] profiles and the deviations from the steady-flow profile. As in the case of tubular fluid flow and transit time oscillations, the [Cl⁻] oscillations have the largest amplitude in the more compliant case (not shown), and the smallest amplitude in the rigid-tubule case (Fig. 5, G and H). The prescribed pressure oscillations produced standing waves with substantial oscillations in [Cl⁻] along the entire TAL, relative to the steady-state profiles, except at the TAL entrance. For the prescribed frequency (f = 30 mHz), the only node in the oscillation profile is the TAL entrance (x = 0), where the [Cl⁻]was fixed as a boundary condition. As the perturbation frequency increases, the wavelength of the standing wave decreases, and additional nodes begin to emerge (results not shown; see Refs. 3, 30 for results in a rigid-tube TAL model). The response of the model TAL to differing perturbation frequencies is further investigated below, where we show that approximate nodes in luminal [Cl⁻] emerge alongside the MD for specific frequencies.

TAL frequency response.

We (30, 31) have shown in previous studies that used our rigid-tubule TAL model that the transduction process from flow oscillations to [Cl⁻] oscillations acts as a lowpass filter: for flow oscillations of uniform amplitude, oscillations of sufficiently low frequency result in [Cl⁻] oscillations that have a large amplitude relative to those that arise from flow oscillations of higher frequencies. Also, we (30) have previously shown in a rigid tubule model that when a sinusoidal perturbation of sufficiently large amplitude is added to the steady-state TAL flow, the resulting tubular [Cl⁻] oscillations alongside the MD have a bounded amplitude range and that the amplitude range decreases, although not monotonically, as a function of increasing frequency.

In the present study, we conducted simulations to assess the effect of TAL compliance on the oscillation amplitude range envelope. We used pressure perturbations given by Eq. 8, with P_p = P̄₀ /10, and with frequencies ranging from 0 to 5/t₀, where t₀ denotes the steadystate TAL transit time for the base case. We recorded MD [Cl⁻] oscillation extrema for 200 equally spaced frequency values. The resulting range envelope is shown in Fig. 6A1. The amplitude of the range envelope increases when TAL tubular compliance increases (results not shown).

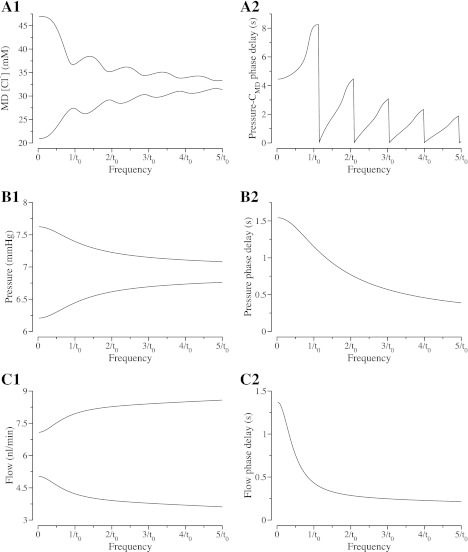
Fig. 6.

TAL frequency base-case response arising from sustained, sinusoidal oscillations in tubular fluid pressure for a range of frequencies. A1: range of tubular fluid [Cl⁻] at the MD as a function of tubular fluid pressure frequency. Top and bottom bounds of the range reveal a nodal structure in the frequency response. Steady-state TAL transit time, denoted by t₀, is 8.83 s; therefore, 1/t_o = 113 mHz; 2/t_o = 227 mHz; 3/t_o = 340 mHz; 4/t_o = 453 mHz; and 5/t_o = 566 mHz. A2: phase delay between oscillations in TAL inflow pressure and [Cl⁻] oscillations alongside the MD. B1: range of tubular fluid pressure alongside the MD as a function of tubular fluid pressure frequency. B2: phase delay between oscillations in pressure at the TAL entrance and alongside the MD. C1: range of tubular fluid flow alongside the MD as a function of tubular fluid pressure frequency. C2: phase delay between tubular fluid flow oscillations at the TAL entrance and alongside the MD.

Approximate nodes are found at frequencies of approximately n/t₀, for n = 1, 2, 3, 4, and 5. At these approximate nodes, the MD [Cl⁻] excursion amplitudes have local minima. Indeed, if backleak permeability P is set to 0 in a rigid tubule, the [Cl⁻] excursion amplitudes at the nodal frequencies are zero. The zero amplitudes occur because, in this case, the [Cl⁻] depends only on TAL transit time (30). Thus, when that transit time equals t₀, or its integer multiples, as is the case for the nodal frequencies, the MD [Cl⁻]remains constant at its steady-state value. In the case of nonzero [Cl⁻] backleak, the nodes become approximate (30). As tubular compliance increases, the amplitudes of the [Cl⁻] excursions increase at the nodal frequencies, and the nodal frequencies increase, albeit only slightly, owing to a small reduction in TAL transit time (results not shown).

A comparison of the waveform plots in Fig. 4A1 with those in Fig. 4D1 reveals that [Cl⁻] oscillations at the MD lag corresponding TAL inflow pressure oscillations. The TAL inflow pressure-C_MD phase delay and the effect of forcing frequency on that delay are shown in Fig. 6A2. The phase delay has a striking nodal structure in which the delay decreases sharply as the forcing frequency reaches a nodal value. The first decrease in the phase delay occurs when a node is established at the MD at a frequency of ∼1/t₀; then the phase delay increases as frequency increases until another node at the MD develops at f = ∼2/t₀. At this frequency, the standing wave in [Cl⁻] has one node within the TAL and one node at the MD (see Fig. 2 in Ref. 30). At multiples of the frequency ∼1/t₀, additional nodes are formed within the TAL. The decrease in the height of the series of peaks in phase delay as frequency increases occurs because the delay cannot be greater than the period of time required for the fluid to travel a distance equal to the half-wavelength of the standing wave in [Cl⁻] within the tubular lumen; at the higher frequencies, this distance is much less than the length of the TAL.

Figure 6B1 shows the pressure amplitude range at the MD (x = L) as a function of pressure oscillation frequency at the TAL entrance (x = 0). This plot illustrates that, with compliant walls, the TAL acts as a low-pass filter for pressure wave propagation. Again, the amplitude of the range envelope increases when TAL tubular compliance increases (results not shown).

In Fig. 6B2, the phase delay between tubular fluid pressure at the TAL entrance and alongside the MD is shown for the base case: the phase delay decreases as frequency increases. For a rigid tubule, the pressure wave travels at infinite speed; thus, there is no phase delay between the two pressure oscillations. As the tubular compliance increases, the phase delay increases for a given frequency (results not shown). Unlike the pressure-C_MD phase delay exhibited in Fig. 6A2, the pressure-pressure phase delay does not exhibit nodal structure, because fluid is conserved within the TAL, and pressure propagation does not depend on transit time.

Figure 6C1 shows the amplitude range for tubular fluid volume flow at the MD as a function of pressure oscillation frequency at the TAL entrance. Unlike the results for MD [Cl⁻] and for MD tubular fluid pressure, which suggest that the TAL acts as a low-pass filter, the results in Fig. 6C1 suggest that lower frequency oscillations in tubular fluid flow are damped to a larger extent than are higher frequency oscillations. We attribute this somewhat surprising result to the pressure gradient-driven nature of the model fluid flow (see Eq. 1). Because the pressure signal travels at a finite speed along a compliant tube, when the inflow pressure oscillations frequency increases, the magnitude of the pressure gradient becomes larger along the TAL. As a result, larger magnitude extrema in tubular fluid flow are predicted.

Figure 6C2 shows the phase delay between TAL inflow and outflow oscillations: the compliant model TAL exhibits a phase delay that diminishes as frequency increases. These results are qualitatively similar to those for the phase delay in pressure (Fig. 6B2). Note, however, that at each frequency the phase delay in flow is shorter than the phase delay in pressure. The phase delay between pressure oscillations at the TAL entrance and tubular fluid flow oscillations alongside the MD (results not shown) is qualitatively similar to the phase delays shown in Fig. 6, B2 and C2.

Effect of distal tubule and collecting duct representation.

To avoid the need to specify pressure at the end of the TAL, the model represents a tubule longer than the TAL; this tube represents not only the TAL but also both the distal tubule and the contiguous collecting duct system. The unpressurized luminal radius β(x) along that distal portion of the model tubule is chosen so that the hydrostatic pressure at x = L₀ is ∼2 mmHg. In vivo, however, water is absorbed along the distal tubules and, in antidiuresis, along the collecting duct system; also, in the inner medulla, the collecting ducts undergo successive coalescences. Both processes likely have a substantial impact on the pressure profile along the distal tubule and the collecting duct system, but neither process is represented in the model. Therefore, in a set of parameter studies, we assessed the effects of variations in the pressure profile of the distal portion of the model tubule on the dynamic behaviors of the model.

We varied the parameter a_d, which is the location at which the unpressurized luminal radius β(x) begins to decrease (see Eq. 5). We obtained model results for a_d = 1.25 × L, 1.75 × L, and 2.0 × L (in the base case, a_d = 1.5 × L). Additionally, we conducted simulations for which the unpressurized luminal radius β(x) exhibits an exponential decrease in the terminal 5 mm of the distal model tube to approximate the faster decrease in hydrostatic pressure owing to the faster fluid flow caused by the coalescences of the collecting duct system. For the exponential-decrease case, we set

$$\beta \left(x\right)=\{\begin{array}{ll}{\beta }_0\left(x\right),\hfill & 0\le x\le L,\hfill \\ {\beta }_1,\hfill & L<x\le a_d,\hfill \\ {\beta }_2\left(x\right),\hfill & a_d<x\le L_0-L_{\text{IM}},\hfill \\ {\beta }_1\left(x\right)e^{\left(L_0-x-L_{\text{IM}}\right)/L_{\text{IM}}},\hfill & L_0-L_{\text{IM}}<x\le L_0,\hfill \end{array}$$ (9)

where L_IM is taken to be 5 mm, the thickness of a rat inner medulla. For all cases, β_0,0, β₁, and β₃ were chosen to yield a target steady-state TAL luminal radius and to produce P(L₀) = 2.0 mmHg.

The four alternative cases generate pressure profiles that differ significantly from the base case of the distal model tubule. Nonetheless, the dynamic behaviors of the model appear to be nearly insensitive to the shape of the distal pressure profile. For instance, for base case compliance, the MD [Cl⁻] profiles are qualitatively similar in all cases, with relative differences of <5%. The effects on other model predictions, and on results obtained for TAL compliance twice that of the base case, are similarly small, and all cases yielded the prediction that compliance in TAL walls amplifies the nonlinearity of oscillations in [Cl⁻] at the MD.

Mean TAL flow affects TGF waveform distortion.

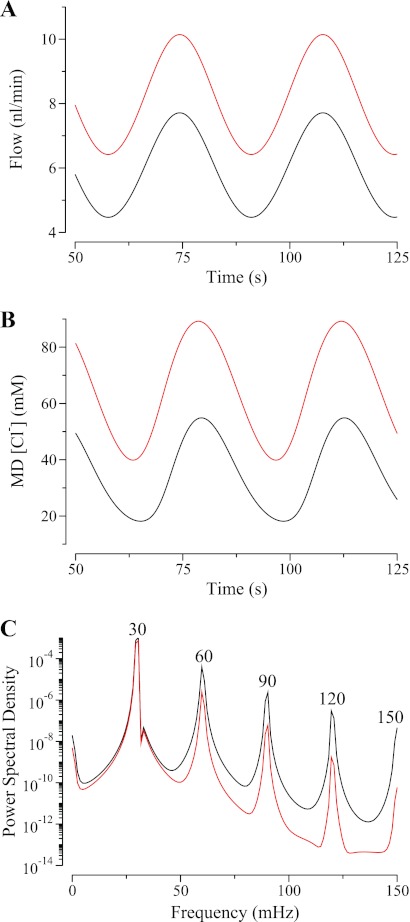
We conclude this study with simulations designed to characterize the influence of mean TAL flow on the strength of the nonlinearities in the transduction process that produces a nonlinear waveform in [Cl⁻] at the MD in response to a sinusoidal variation in TAL input pressure or flow. The motivation for the simulations is the observation that the nonlinear features of [Cl⁻] waveforms at the MD predicted by our compliant TAL model appear to be more prominent (see Fig. 4D1) than those obtained by Holstein-Rathlou and Marsh (15) with a model TAL that is, in most respects, similar to ours. Close examination of Fig. 2 in Holstein-Rathlou and Marsh reveals a modest slope asymmetry in the [Cl⁻] oscillation, which is a consequence of the nonlinearity of the transit time oscillation produced by a sinusoidal oscillation in flow, but the waveform does not exhibit a noticeably widened trough relative to the peak. We hypothesize that these differences in waveform shape are a consequence of the higher baseline TAL flow used by Holstein-Rathlou and Marsh (8.6 vs. 6.0 nl/min in our study). With oscillations of similar amplitude, a higher mean flow would result in less waveform distortion because the fractional changes in flow during the oscillation are less than in the case of a lower mean flow. Further, because of the inverse relationship between flow and transit time (transit time becomes infinite as flow approaches zero), the case where the mean flow is lower should exhibit larger, more asymmetric, swings in transit time, leading to a stronger slope asymmetry. Finally, with high baseline flow, the flow excursion along the TAL reabsorption curve (see Fig. 2D) remains well above the low flow rates where the curve flattens, owing to NaCl backleak in the distal TAL. Thus high baseline flow will tend to minimize the formation of a broad trough.

The results of our simulation are shown in Fig. 7. Inflow pressure was adjusted to yield inflow rates similar to the input flows in each model. Inflow pressure oscillations were applied in each case so that the amplitudes of the resulting inflow waves are approximately equal. Figure 7B shows the resultant [Cl⁻] waveforms. Although the mean [Cl⁻] for the high-flow case (shown in red) is somewhat higher than in the model by Holstein-Rathlou and Marsh (because we chose to retain our TAL transport parameters rather than adopt the somewhat different values used by Holstein-Rathlou and Marsh), the waveform in the high flow case is not strikingly distorted relative to a sine wave. In contrast, in the low-flow case, the [Cl⁻] waveform is clearly nonsinusoidal: it has marked slope asymmetry and a broad trough relative to the peak. That this waveform is nonsinusoidal is verified by the power spectra presented in Fig. 7C, where the low-flow oscillation in MD [Cl⁻] has substantially stronger harmonics than the high-flow waveform. In addition to providing a means to reconcile our results with those of Holstein-Rathlou and Marsh, this result is of interest in that it suggests that the waveshape of TGF-mediated oscillations may provide qualitative insight into the balance between tubular fluid flow and NaCl reabsorption from the TAL.

Fig. 7.

Effect of mean TAL flow on the [Cl⁻] waveform at the MD. A: outflow for high (red) and low (black) mean TAL flow. B: oscillations in MD [Cl⁻]; at high mean flow, oscillation is more nearly sinusoidal than at low mean TAL flow. C: power spectra for the [Cl⁻] oscillations in B; the harmonics are much more pronounced in the high-flow case than in the low-flow case (note that the ordinate is logarithmic).

DISCUSSION

Model predictions.

In this study we have sought to determine whether TAL compliance would reduce the degree of nonlinearity exhibited in tubular fluid Cl⁻ oscillations alongside the MD. The results show, instead, that compliance in our model TAL amplifies the nonlinearity of [Cl⁻] oscillations at the MD. Hence, these results validate our use of a rigid-tube TAL model, in that the rigid-tube model captures the essence of the major nonlinearities in the TGF signal transduction process in the TAL, although it underestimates the strength of nonlinearities relative to a compliant TAL. Nevertheless, this study supports the concept that a model TAL that has rigid walls can be used to make meaningful and reliable predictions about in vivo dynamic phenomena (i.e., MD [Cl⁻] oscillations) mediated by TGF. This conclusion is based on the following findings.

Our model simulations predict that when pressure at the TAL entrance is sinusoidal in time, a compliant TAL will not have oscillatory pressure profiles as a function of axial position along the TAL; rather, pressure profiles along the TAL will be nearly linear along the axis of the TAL lumen at any given time (Fig. 5A1). Nonetheless, these same simulations show that the resulting flow of tubular fluid is nearly sinusoidal in time at all individual points along the TAL (Fig. 4B1), whereas the TAL transit time arising from the sinusoidal pressure oscillation has a nonsinusoidal waveform (Fig. 4C1); that waveform results in a tubular fluid [Cl⁻] waveform at the MD that is nonsinusoidal (Fig. 4D1).

Our model simulations predict that pressure oscillations introduced at the entrance of the TAL are reduced in amplitude along the course of the TAL and that this reduction in amplitude increases as a function of increasing frequency (Fig. 6B1). Thus our model acts as a low-pass filter with respect to pressure, as does the compliant model of the proximal nephron and TAL developed by Marsh and colleagues (15, 38).

Although our model simulations predict that a compliant TAL acts as a low-pass filter for pressure oscillations, the model also predicts that the amplitude of flow oscillations increases as the frequency of pressure oscillations at the TAL entrance increase (Fig. 6C1). Consequently, the model predicts that harmonics of periodic nonsinusoidal flow oscillations are substantially preserved along the TAL, and, moreover, the model predicts that compliant TALs will introduce more nonlinearity into the [Cl⁻] oscillations than will rigid tubules, provided that transmural pressure differences are sufficiently large to produce significant variations in radius along the TAL.

Our model simulations predict that TGF signal transduction from pressure changes at the TAL entrance, to intratubular TAL fluid flow, to NaCl concentration at the TAL exit depends strongly on the transit time of intratubular fluid flow (Fig. 4C1). This finding is in agreement with our mathematical analysis based on the method of characteristics (as in Refs. 30 and 37) and with numerical studies that used a rigid-tube TAL model (30, 31).

Our model predicts a second source of nonlinearity that arises from the flattening of the slope of the TAL transport curve at low flows where the TAL cells reach the limit of their capability to dilute tubular fluid. This waveform distortion, which broadens the trough of the oscillation relative to the peak, is a consequence of the inverse relationship between flow and transit time and the nonlinearity of TAL transport at low flow rates. The degree of MD [Cl⁻] waveform distortion (relative to the pressure waveform at the TAL entrance) that is attributable to this nonlinearity is strongly dependent on baseline TAL flow.

Comparison with experimental measurements.

Our model predicts that, in response to sinusoidal perturbations in inflow pressure, tubular fluid flow and MD [Cl⁻] exhibit oscillations with significant phase differences. Specifically, MD [Cl⁻] oscillations lag behind inflow pressure (Fig. 6A2), outflow pressure lags inflow pressure (Fig. 6B2), and MD tubular fluid flow oscillations leads inflow pressure (Fig. 6D). These results are consistent with measurements by Holstein-Rathlou and Marsh (14), who reported that distal Cl⁻ activity followed the proximal tubular pressure and that the distal tubular pressure followed the proximal tubular pressure, and that late proximal flow led pressure oscillations.

The waveform distortion predicted by our model, in which the asymmetric MD [Cl⁻] oscillations exhibit broader troughs than crests, is evident in most, but not all, experimental recordings of TGF-mediated oscillations (see Table 3 in Ref. 31 for a summary). The fact that the characteristic wave shape predicted by our model was not observed in some of the experimental records may be explained by the relation between waveform distortion and baseline TAL flow: with oscillations of similar amplitude, waveform distortion is small with a higher mean flow because of the fractional changes in flow during the oscillations.

Comparison with previous modeling studies.

The results of this study are consistent with the model study of Sakai et al. (38), who also appear to have found that the TAL acts as a lowpass filter for pressure (their Fig. 4), and with the studies by Holstein-Rathlou and Marsh that found only a brief phase lag in pressure transmission along the TAL arising from compliance (14) and that therefore predicted a modest value for TAL compliance relative to reported compliance values for the proximal tubule (15). However, the study by Sakai et al. (38) appears to have found that the nephron (which includes the TAL) acts as a low-pass filter for fluid oscillations (their Figs. 4 and 7), whereas our results suggest that, in compliant model TALs, high frequency flow components are intensified. The discrepancy between the findings of Sakai et al. and our study may be attributed to the different perturbations applied to the inflow. In Sakai et al. the forcing was applied to flow, whereas in our model, inflow pressure, not the flow itself, was perturbed. The increasing flow variation amplitude as a function of frequency arises from the observation that faster pressure oscillations result in larger inflow variations, and despite more attenuation along the TAL, larger flow oscillations were observed at the MD. A theoretical study by Jung et al. (17) on valveless pumping suggests that flow rate is sensitive to a number of factors, including forcing frequency, amplitude, and elastic properties of the tube.

A significant difference between our studies and the results of Holstein-Rathlou and Marsh (15) is related to the ability of our model analyses to explain the shape of waveforms in measurements of TGF-mediated limit-cycle oscillations (LCO). We (see Table 3 in Ref. 31) have previously pointed out that the waveshape of TGF-mediated LCO, which are consistent with measurements of proximal intratubular pressure, exhibits characteristics similar to the predictions of our TAL model.

In contrast, nonlinearity in TGF transduction was not noted in Ref. 15, and it was concluded that tubular delays and damping of pressure waves limited the frequency response of TGF in the context of renal autoregulation. However, a careful examination of Fig. 1 in that study reveals that the NaCl oscillations at the MD have asymmetric up- and downslopes and, hence, are nonsinusoidal, although the distortion, relative to a sinusoidal waveform, is more subtle than seen in our model at our baseline conditions.

The simulations shown in Fig. 7 provide a means to reconcile this apparent conflict, and they provide a mechanistic explanation for the range of waveform distortion seen in recordings of TGF-mediated LCO. Specifically, the findings suggest that differences in TAL fractional Na⁺ absorption and TAL flow may provide a sufficient explanation. In our model, the rate of TAL flow and TAL transport parameters were set so that the TAL effluent [Cl⁻] concentration is ∼30 mM at a steady flow of 6 nl/min, values based on a study in Munich- Froemter rats by Vallon et al. (45). In this study, micropuncture samples were taken just downstream from the MD in nephrons with superficial glomeruli. In contrast, in Holstein-Rathlou and Marsh (15) transport parameters were selected to yield a TAL flow of ∼8.6 nl/min with a mean [Cl⁻] of ∼45 mM, values typical of measurements in the early distal tubule in Sprague-Dawley rats. As shown in Fig. 7, our TAL model predicts that these relatively minor differences (relative to our values) are sufficient to reduce the degree of waveform distortion to the level predicted in Ref. (15). This suggests that the extent of TGF waveform distortion may well depend on the fluid and electrolyte status of the animal. TGF waveforms, either of early distal [Cl⁻], single nephron glomerular filtration rate, or proximal intratubular pressure, where the waveform has a markedly broadened crest relative the peak and marked slope asymmetry are predicted by our model to be associated with low distal fluid delivery and near maximal TAL Na⁺ fractional reabsorption, as expected in hydropenic rats. Lesser distortion is predicted by our model to occur in euvolemic or extracellular volume expanded rats.

Model limitations.

Our mathematical model for fluid dynamics in the TAL, although based on the Navier-Stokes equations, involves simplifying assumptions that reduce the model to one spatial variable, viz., the axial location along the TAL. Although the model is based on sound principles of dimensional analysis, some error is introduced relative to a fully developed three-dimensional formulation: nonetheless, we believe that the error is negligible (the one-dimensional formulation has been used by others in renal models; Refs. 15, 38, 49). Solute advection along the tubule also depends only on the spatial variable along the TAL, and both axial and radial diffusion are ignored. These assumptions, which have been standard for sufficiently long tubular segments, have been previously justified (25). Also, as in other modeling efforts by us (28) and by others (15), we have assumed that transepithelial transport rates respond to variations in tubular fluid NaCl concentration instantaneously. This assumption merits further investigation in a fully developed model of the TAL epithelium, as delay in the TAL cell response could introduce additional dynamics into the TGF signal transduction process.

The in situ compliance of the TAL is a difficult quantity to assess, as it depends not only on the inherent elasticity of the TAL epithelium but also on possible tethering to other tubules via the interstitial matrix. On a larger scale, the expression of tubular compliance in the medulla may be limited by the renal capsule: this thin, fibrous sheath that contains the kidney may place limits on the distension of tubules and vessels. Regardless of how compliant the TAL is in situ, our results suggest that the nonlinearities in TGF signal transduction should influence the wave shape of TGF-mediated MD [Cl⁻] oscillations, with the degree of distortion increasing with TAL compliance.

The model assumes a fixed Na⁺ concentration of 275 mM at the entrance of the TAL. As the fluid flow rate along the proximal tubule and descending limb oscillates, the loop-bend Na⁺ concentration oscillates as well. However, a previous modeling study (21) predicted that the amplitude of the loop-bend Na⁺ concentration oscillations is small, compared with MD Na⁺ concentration oscillations. In that study, the TGF signal transduction along a short loop nephron was investigated using a mathematical model that combines a simple representation of the renal cortex with a highly detailed representation of tubular transport in the outer medulla (22). The amplitude of the loop-bend Na⁺ oscillations was predicted to be <1 mM. Unlike the TAL tubular fluid Na⁺ concentration, which changes as Na⁺ is actively transported out of TAL, tubular fluid Na⁺ concentration along the short descending limb changes, in large part, because of water absorption along the proximal tubule. Because the oscillations in the interstitial fluid osmolality are predicted to be small (see Ref. 21 for details), the oscillations in water reabsorption rate, and thus oscillations in loop-bend Na⁺ concentration, are also small.

Significance of our findings.

The findings presented in this study are important for at least four reasons: 1) our findings help explain peaks found in power spectra of time series that were collected in experiments intended to elucidate both normal and pathophysiologic renal hemodynamics in rats; 2) our findings provide an explanation for the differing degrees to which TGF-mediated approximate sine waves; 3) our findings are consistent with the hypothesis that distortions (relative to sine waveshapes) in TGF-mediated [Cl⁻] oscillations can increase NaCl delivery to the distal nephron; and 4) our findings of marked nonlinearities in TGF transduction that arise from compliant TALs suggest the hypothesis that such nonlinearities may significantly affect the stability of TGF systems and thus have an impact on renal hemodynamic control or contribute to renal hemodynamic dysregulation. We briefly consider each of these below.

1) Power spectra have been widely used, both in physiologic experiments and in mathematical models, as an aid to understanding the factors that contribute to both normal and disordered hemodynamic control (7, 8, 9, 23, 31, 40, 46). Power spectra have contributed to the understanding of limit-cycle oscillations mediated by TGF (13, 14, 50); to the role of interacting oscillations arising from both the myogenic mechanism of the afferent arteriole and TGF (5, 6, 16, 48); and to investigations of the origin and nature of chaos-like TGF-mediated oscillations found in spontaneously hypertensive rats (13, 23, 47). Although feedback-mediated oscillations are not considered in this study, the present results lend support to previous studies by us (e.g., Refs. 3, 23, 31) that indicate that some of the complexity observed in power spectra emerges from harmonics arising in TGF signal transduction in the TAL.

2) We have previously noted that the degree of waveshape distortion, relative to sine waves, observed in experimental records of TGF oscillations exhibits substantial variability (31). The findings of the present study suggest that waveshape variability is related to variability in the mean tubular flow rate through the TAL and the resulting effects on the degree of dilution, via NaCl absorption, that is attained in tubular fluid alongside the MD.

3) We (32) have previously used our rigid-tube TAL model to predict that the emergence of LCO is associated with an increase in NaCl delivery to the distal nephron. This natriuretic effect is a consequence of the distortion of the [Cl⁻] waveform, such that timeaveraged [Cl⁻] of the LCO is greater than the [Cl⁻] at a steady flow that is equal to the time averaged oscillating TAL flow. The underlying mechanism is that the TAL cells have a limited ability to reduce the effluent tubular fluid [NaCl] when flow decreases, whereas there is no similar limitation on the rise in [NaCl] when TAL flow increases. The present study extends and refines this concept. First, compliant TAL segments have much larger swings in [Cl⁻] than in a rigid tubule model, but the increase in [Cl⁻] excursion is mainly to higher concentration levels, which leads to enhanced Na⁺ delivery to the distal tubule. Hence, the natriuretic effect of LCO emergence is predicted to be substantially greater in a compliant TAL. However, this natriuretic action would be reduced in nephrons in which the TGF operating point is reset to higher TAL flow and effluent [Cl⁻] where our model predicts less distortion of the LCO waveform. Because the TGF system exhibits adaptive long- and short-term resetting consequent to changes in physiological state and with the onset of several diseases (41, 42, 43, 44), the interactions among hemodynamic regulation, TAL transport, and TGF system resetting merit careful study.

4) Finally, TAL compliance markedly increases the strength of the nonlinearities in the TGF signal transduction process; thus compliance may also have a significant effect on the stability of the TGF system. Previously, we have used our rigid TAL model as part of a model of the TGF system, which we used to investigate the nonlinear dynamics of the TGF system. We (23, 24) found that small numbers of coupled nephrons can exhibit complex dynamics, including LCO and multistability, within a physiologically reasonable range of parameters. Because these complex behaviors are consequences of the nonlinearity of the TGF system, it is likely that a TGF model with a compliant TAL will exhibit even more complex dynamics or that complex behavior will emerge at a broader range of TGF parameters. These intriguing possibilities also merit further study.

The predictions of this study, and their implications for physiologic function, could be investigated by means of sufficiently well-designed laboratory experiments that reveal the relationship between periodic perturbations in proximal flow and resulting oscillations in distal tubular flow and [Cl⁻]. A comparison of experimental results with model predictions would help us evaluate our understanding of TAL signal transduction.

GRANTS

This research was supported by the National Science Foundation Grant DMS-0715021 (to A. T. Layton) and National Institute of Diabetes and Digestive and Kidney Diseases Grants DK-42091 (to H. E. Layton) and DK-89066 (to A. T. Layton).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

APPENDIX A: DERIVATION OF THE FLUID EQUATIONS

The model TAL and contiguous resistance tubule is represented as a cylindrical, compliant tube. Fluid flow within the tube is assumed to be laminar flow. Because the Reynolds number for the model tubule is sufficiently low, tubular flow can be approximated by Poiseuille flow (49), which describes the laminar flow of a viscous, incompressible, Newtonian fluid through a cylindrical tube:

$$\frac{\partial }{\partial x}P\left(x,t\right)=-\frac{8\mu }{\pi R^4\left(x,t\right)}Q\left(x,t\right).$$ (A1)

(In this equation, the nature of the dependence of R on space and time remains unspecified.) To maintain mass conservation, the radial and axial fluid velocities, denoted V_r and V_x, respectively, are related (20) by

$$\frac{1}{r}\frac{\partial }{\partial r}\left[r{V}_r\left(r,x,t\right)\right]+\frac{\partial }{\partial x}{V}_x\left(r,x,t\right)=0.$$ (A2)

Because we assume cylindrical symmetry, V_r and V_x do not depend on the angular coordinate θ. To relate Eq. A2 to fluid pressure P and volumetric flow Q, we observe that Q(x, t) = A(x, t) V̄_x(r, x, t), where A(x, t) = πR²(x, t) is the cross-sectional area of the tubule, and V̄_x(x, t) is the axial velocity averaged over that cross-sectional area, i.e.,

$${\overline{V}}_x\left(x,t\right)=\frac{1}{A\left(x,t\right)}{\displaystyle {\int }_0^{2\pi }}{\displaystyle {\int }_0^{R\left(x,t\right)}}{V}_x\left(r,x,t\right)rdrd\theta .$$ (A3)

By integrating Eq. A2 over the cross-sectional area, one obtains

$$2\pi R\left(x,t\right)V_r\left(R,x,t\right)+\frac{\partial }{\partial x}Q\left(x,t\right)=0.$$ (A4)

At r = R, V_r is the rate at which the tubular radius R changes, i.e.,

$$V_r\left(R,x,t\right)=\frac{\partial }{\partial t}R\left(x,t\right).$$ (A5)

Because the radius R(x, t) is assumed in our model to be a function of tubular fluid pressure P(x,t) {i.e., R(x, t) = F(P(x,t)), for an appropriate F; see Eq. 4}, we replace the notation R(x, t) with R(P(x, t)), so that the dependence of R on x and t is made explicit through Eq. 4. By means of the chain rule, we can write

$$\frac{\partial }{\partial t}R\left(P\left(x,t\right)\right)=\left[\frac{\partial R}{\partial P}\left(x,t\right)\right]\left[\frac{\partial }{\partial t}P\left(x,t\right)\right].$$ (A6)

Therefore, Eq. A4 can be expressed as

$$2\pi R\left(x,t\right)=\left[\frac{\partial R}{\partial P}\left(x,t\right)\right]\left[\frac{\partial }{\partial t}P\left(x,t\right)\right]+\frac{\partial }{\partial x}Q\left(x,t\right)=0,$$ (A7)

which is equivalent to Eq. 2.

APPENDIX B: NUMERICAL METHOD

The advection-diffusion equation (Eq. 6) that describes the changes in pressure P was integrated in time by means of a numerical method that is second order in space and time. Let Δx denote the spatial mesh interval, and let Δt denote the time step interval. Then we denote P(jΔx, nΔt) by P_jⁿ; analogous notation is used for other functions of x and t. Then to advance P by one time step, we discretized Eq. 6, and we solved for P_j^{n + 1}.

The discretized version of Eq. 6, was given by

$$\left(\frac{P_j^{n+1}+P_j^{n-1}}{2\Delta t}\right)-\left[\frac{{\left(R_j^n\right)}^2}{4\mu \alpha }\right]\left(\frac{R_{j+1}^n-R_{j-1}^n}{2\Delta x}\right)\times \left[\frac{\left(P_{j+1}^n+\Delta P_{j+1}^n\right)-\left(P_j^n+\Delta P_j^n\right)}{\Delta x}\right]=\frac{{\left(R_j^n\right)}^3}{2\cdot 16\mu \alpha }\times \left[\frac{P_{j+1}^{n+1}-2P_j^{n+1}+P_{j-1}^{n+1}}{{\left(\Delta x\right)}^2}+\frac{P_{j+1}^{n-1}-2P_j^{n-1}+P_{j-1}^{n-1}}{{\left(\Delta x\right)}^2}s\right],$$ (B1)

where

$$\Delta P_j^n=\frac{1}{2}\left[\text{sign}\left(P_{j+1}^n-P_j^n\right)+\text{sign}\left(P_j^n-P_{j-1}^n\right)\right]\times \frac{1}{2}\min \left(\left|P_{j+1}^n-P_j^n\right|,\left|P_j^n-P_{j-1}^n\right|\right)$$ (B2)

with sign(x) defined by

$$\text{sign}\left(x\right)=\{\begin{array}{ll}0,\hfill & \text{if}x\le 0,\hfill \\ 1,\hfill & \text{otherwise};\hfill \end{array}$$ (B3)

with min(x, y) defined as the smalller of x or y; and where $\frac{\partial R}{\partial P}$ in Eq. 6 was replaced by α (from Eq. 4). Equations 6 and B3 yield a system of coupled linear equations, which were solved at each time step n.

Glossary

Parameters

α

TAL compliance (cm/mmHg)

a_d

Beginning location for β₁(x) (mm)

β_0,0, β₁, β₃

Parameters for TAL radius (μm)

C_o

Cl⁻ concentration at TAL entrance (mM)

K_m

Michaelis constant (mM)

L₀

Length of model tubule (cm)

L

Length of TAL (cm)

P_e

Extratubular (steady-state) pressure (mmHg)

P₁

Pressure at end of tubule (mmHg)

P_p

Amplitude of sinusoidal pressure perturbation (mmHg)

P_M

TAL chloride permeability (cm/s)

Q_o

Base-case TAL flow (nl/min)

R_o

TAL reference radius (μm)

t_o

Base-case steady-state TAL transit time (s)

V_max

Maximum transport rate of chloride (nmol·cm⁻²·s⁻¹)

μ

Fluid viscosity (cm/s)

Independent Variables

t

Time (s)

x

Axial position along tubule (cm)

Specified Functions

β(x)

Unpressurized TAL radius (μm)

β₀(x), β₂ (x)

Cubic polynomial portions of unpressurized TAL radius (μm)

C_e(x)

Extratubular Cl⁻ concentration (mM)

P₀(t)

Pressure at loop bend (mmHg)

P_e(x)

Extratubular pressure (mmHg)

Dependent Variables

C(x, t)

TAL Cl⁻ concentration (mM)

P(x, t)

Tubular fluid pressure (mmHg)

Q(x, t)

Tubular fluid flow (nl/min)

R(x, t)

Luminal radius (μm)