HIGH DIMENSIONAL COVARIANCE MATRIX ESTIMATION IN APPROXIMATE FACTOR MODELS

Abstract

The variance covariance matrix plays a central role in the inferential theories of high dimensional factor models in finance and economics. Popular regularization methods of directly exploiting sparsity are not directly applicable to many financial problems. Classical methods of estimating the covariance matrices are based on the strict factor models, assuming independent idiosyncratic components. This assumption, however, is restrictive in practical applications. By assuming sparse error covariance matrix, we allow the presence of the cross-sectional correlation even after taking out common factors, and it enables us to combine the merits of both methods. We estimate the sparse covariance using the adaptive thresholding technique as in Cai and Liu (2011), taking into account the fact that direct observations of the idiosyncratic components are unavailable. The impact of high dimensionality on the covariance matrix estimation based on the factor structure is then studied.

1. Introduction

We consider a factor model defined as follows:

$$y_{\mathit{\text{it}}}={\mathbf{b}}_i^{\prime }{\mathbf{f}}_t+u_{\mathit{\text{it}}},$$ (1.1)

where y_it is the observed datum for the ith (i = 1, …, p) asset at time t = 1, …, T; b_i is a K × 1 vector of factor loadings; f_t is a K × 1 vector of common factors, and u_it is the idiosyncratic error component of y_it. Classical factor analysis assumes that both p and K are fixed, while T is allowed to grow. However, in the recent decades, both economic and financial applications have encountered very large data sets which contain high dimensional variables. For example, the World Bank has data for about two-hundred countries over forty years; in portfolio allocation, the number of stocks can be in thousands and be larger or of the same order of the sample size. In modeling housing prices in each zip code, the number of regions can be of order thousands, yet the sample size can be 240 months or twenty years. The covariance matrix of order several thousands is critical for understanding the co-movement of housing prices indices over these zip codes.

Inferential theory of factor analysis relies on estimating Σ_u, the variance-covariance matrix of the error term, and Σ, the variance-covariance matrix of y_t = (y_1t, …, y_pt)′. In the literature, Σ = cov(y_t) was traditionally estimated by the sample covariance matrix of y_t:

$${\mathbf{\Sigma }}_{\mathit{\text{sam}}}=\frac{1}{T-1}{\displaystyle \sum _{t=1}^T}({\mathbf{y}}_t-\overline{\mathbf{y}})({\mathbf{y}}_t-\overline{\mathbf{y}})\prime ,$$

which was always assumed to be pointwise root-T consistent. However, the sample covariance matrix is an inappropriate estimator in high dimensional settings. For example, when p is larger than T, Σ_sam becomes singular while Σ is always strictly positive definite. Even if p < T, Fan, Fan and Lv (2008) showed that this estimator has a very slow convergence rate under the Frobenius norm. Realizing the limitation of the sample covariance estimator in high dimensional factor models, Fan, Fan and Lv (2008) considered more refined estimation of Σ, by incorporating the common factor structure. One of the key assumptions they made was the cross-sectional independence among the idiosyncratic components, which results in a diagonal matrix ${\mathbf{\Sigma }}_u=E{\mathbf{u}}_t{\mathbf{u}}_t^{\prime }$. The cross-sectional independence, however, is restrictive in many applications, as it rules out the approximate factor structure as in Chamberlain and Rothschild (1983). In this paper, we relax this assumption, and investigate the impact of the cross-sectional correlations of idiosyncratic noises on the estimation of Σ and Σ_u, when both p and T are allowed to diverge. We show that the estimated covariance matrices are still invertible with probability approaching one, even if p > T. In particular, when estimating Σ⁻¹ and ${\mathbf{\Sigma }}_u^{-1}$, we allow p to increase much faster than T, say, p = O (exp(T^α)), for some α ∈ (0, 1).

Sparsity is one of the commonly used assumptions in the estimation of high dimensional covariance matrices, which assumes that many entries of the off diagonal elements are zero, and the number of nonzero off-diagonal entries is restricted to grow slowly. Imposing the sparsity assumption directly on the covariance of y_t, however, is inappropriate for many applications of finance and economics. In this paper we use the factor model and assume that Σ_u is sparse, and estimate both Σ_u and ${\mathbf{\Sigma }}_u^{-1}$ using the thresholding method (Bickel and Levina (2008a), Cai and Liu (2011)) based on the estimated residuals in the factor model. It is assumed that the factors f_t are observable, as in Fama and French (1992), Fan, Fan and Lv (2008), and many other empirical applications. We derive the convergence rates of both estimated Σ and its inverse respectively under various norms which are to be defined later. In addition, we achieve better convergence rates than those in Fan, Fan and Lv (2008).

Various approaches have been proposed to estimate a large covariance matrix: Bickel and Levina (2008a, 2008b) constructed the estimators based on regularization and thresholding respectively. Rothman, Levina and Zhou (2009) considered thresholding the sample covariance matrix with more general thresholding functions. Lam and Fan (2009) proposed penalized quasi-likelihood method to achieve both the consistency and sparsistency of the estimation. More recently, Cai and Zhou (2010) derived the minimax rate for sparse matrix estimation, and showed that the thresholding estimator attains this optimal rate under the operator norm. Cai and Liu (2011) proposed a thresholding procedure which is adaptive to the variability of individual entries, and unveiled its improved rate of convergence.

The rest of the paper is organized as follows. Section 2 provides the asymptotic theory for estimating the error covariance matrix and its inverse. Section 3 considers estimating the covariance matrix of y_t. Section 4 extends the results to the seemingly unrelated regression model, a set of linear equations with correlated error terms in which the covariates are different across equations. Section 5 reports the simulation results. Finally, Section 6 concludes with discussions. All proofs are given in the appendix. Throughout the paper, we use λ_min(A) and λ_max(A) to denote the minimum and maximum eigenvalues of a matrix A. We also denote by ‖A‖_F, ‖A‖ and ‖A‖_∞ the Frobenius norm, operator norm and elementwise norm of a matrix A respectively, defined respectively as ‖A‖_F = tr^1/2(A′A), $\Vert \mathbf{A}\Vert ={\lambda }_{\text{max}}^{1/2}(\mathbf{A}\prime \mathbf{A})$, and ‖A‖_∞ = max_i,j |A_ij|. Note that, when A is a vector, both ‖A‖ and ‖A‖_F are equal to the Euclidean norm.

2. Estimation of Error Covariance Matrix

2.1. Adaptive thresholding

Consider the following approximate factor model, in which the cross-sectional correlation among the idiosyncratic error components is allowed:

$$y_{\mathit{\text{it}}}={\mathbf{b}}_i^{\prime }{\mathbf{f}}_t+u_{\mathit{\text{it}}},$$ (2.1)

where i = 1, ‥, , p and t = 1, …, T; b_i is a K × 1 vector of factor loadings; f_t is a K × 1 vector of observable common factors, uncorrelated with u_it. Write

$$\mathbf{B}=({\mathbf{b}}_1,\dots ,{\mathbf{b}}_p)\prime ,{\mathbf{y}}_t=(y_{1t},\dots ,y_{\mathit{\text{pt}}})\prime ,{\mathbf{u}}_t=(u_{1t},\dots ,u_{\mathit{\text{pt}}})\prime ,$$

then model (2.1) can be written in a more compact form:

$${\mathbf{y}}_t={\mathbf{\text{Bf}}}_t+{\mathbf{u}}_t,$$ (2.2)

with E(u_t|f_t) = 0.

In practical applications, p can be thought of as the number of assets or stocks, or number of regions in spatial and temporal problems such as home price indices or sales of drugs, and in practice can be of the same order as, or even larger than T. For example, an asset pricing model may contain hundreds of assets while the sample size on daily returns is less than several hundreds. In the estimation of the optimal portfolio allocation, it was observed by Fan, Fan and Lv (2008) that the effect of large p on the convergence rate can be quite severe. In contrast, the number of common factors, K, can be much smaller. For example, the rank theory of consumer demand systems implies no more than three factors (e.g., Gorman (1981) and Lewbel (1991)).

The error covariance matrix

$${\mathbf{\Sigma }}_u=\text{cov}({\mathbf{u}}_t),$$

itself is of interest for the inferential theory of factor models. For example, the asymptotic covariance of the least square estimator of B depends on ${\mathbf{\Sigma }}_u^{-1}$, and in simulating home price indices over a certain time horizon for mortgage based securities, a good estimate of Σ_u is needed. When p is close to or larger than T, estimating Σ_u is very challenging. Therefore, following the literature of high dimensional covariance matrix estimation, we assume it is sparse, i.e., many of its off-diagonal entries are zeros. Specifically, let Σ_u = (σ_ij)_p×p. Define

$$m_T=\underset{i\le p}{\text{max}}{\displaystyle \sum _{j\le p}}I({\sigma }_{\mathit{\text{ij}}}\ne 0).$$ (2.3)

The sparsity assumption puts an upper bound restriction on m_T. Specifically, we assume:

$$m_T^2=o\left(\frac{T}{K^2\text{ log}p}\right).$$ (2.4)

In this formulation, we even allow the number of factors K to be large, possibly growing with T.

A more general treatment (e.g., Bickel and Levina (2008a) and Cai and Liu (2011)) is to assume that the l_q norm of the row vectors of Σ_u are uniformly bounded across rows by a slowly growing sequence, for some q ∈ [0, 1). In contrast, the assumption we make in this paper, i.e., q = 0, has clearer economic interpretation. For example, the firm returns can be modeled by the factor model, where u_it represents a firm’s individual shock at time t. Driven by the industry-specific components, these shocks are correlated among the firms in the same industry, but can be assumed to be uncorrelated across industries, since the industry-specific components are not pervasive for the whole economy (Connor and Korajczyk (1993)).

We estimate Σ_u using the thresholding technique introduced and studied by Bickel and Levina (2008a), Rothman, Levina and Zhu (2009), Cai and Liu (2011), etc, which is summarized as follows: Suppose we observe data (X₁, …, X_T) of a p × 1 vector X, which follows a multivariate Gaussian distribution N (0, Σ_X). The sample covariance matrix of X is thus given by:

$${\mathbf{S}}_X=\frac{1}{T}{\displaystyle \sum _{i=1}^T}({\mathbf{X}}_i-\overline{\mathbf{X}})({\mathbf{X}}_i-\overline{\mathbf{X}})\prime ={(s_{\mathit{\text{ij}}})}_{p\times p}.$$

Define the thresholding operator by 𝒯_t(M) = (M_ijI (|M_ij| ≥ t)) for any symmetric matrix M. Then 𝒯_t preserves the symmetry of M. Let ${\hat{\mathbf{\Sigma }}}_X^{𝒯}={𝒯}_{{\omega }_T}({\mathbf{S}}_X),\text{ where }{\omega }_T=O(\sqrt{\text{log }p/T})$. Bickel and Levina (2008a) then showed that:

$$\Vert {\hat{\mathbf{\Sigma }}}_X^{𝒯}-{\mathbf{\Sigma }}_X\Vert =O_p({\omega }_T{m}_T).$$

In the factor models, however, we do not observe the error term directly. Hence when estimating the error covariance matrix of a factor model, we need to construct a sample covariance matrix based on the residuals û_it before thresholding. The residuals are obtained using the plug-in method, by estimating the factor loadings first. Let b̂_i be the ordinary least square (OLS) estimator of b_i, and

$${\mathit{û}}_{\mathit{\text{it}}}=y_{\mathit{\text{it}}}-{\hat{\mathbf{b}}}_i^{\prime }{\mathbf{f}}_t.$$

Denote by û_t = (û_1t, …, û_pt)′. We then construct the residual covariance matrix as:

$${\hat{\mathbf{\Sigma }}}_u=\frac{1}{T}{\displaystyle \sum _{t=1}^T}{\mathbf{û}}_t{\mathbf{û}}_t^{\prime }=({\hat{\sigma }}_{\mathit{\text{ij}}}).$$

Note that the thresholding value ${\omega }_T=O(\sqrt{\text{log }p/T})$ in Bickel and Levina (2008a) is in fact obtained from the rate of convergence of max_ij |s_ij − Σ_X,ij |. This rate changes when s_ij is replaced with the residual û_ij, which will be slower if the number of common factors K increases with T. Therefore, the thresholding value ω_T used in this paper is adjusted to account for the effect of the estimation of the residuals.

2.2. Asymptotic properties of the thresholding estimator

Bickel and Levina (2008a) used a universal constant as the thresholding value. As pointed out by Rothman, Levina and Zhu (2009) and Cai and Liu (2011), when the variances of the entries of the sample covariance matrix vary over a wide range, it is more desirable to use thresholds that capture the variability of individual estimation. For this purpose, in this paper, we apply the adaptive thresholding estimator (Cai and Liu (2011)) to estimate the error covariance matrix, which is given by

$$\begin{array}{c}\hfill {\hat{\mathbf{\Sigma }}}_u^{𝒯}=({\hat{\sigma }}_{\mathit{\text{ij}}}^{𝒯}),{\hat{\sigma }}_{\mathit{\text{ij}}}^{𝒯}={\hat{\sigma }}_{\mathit{\text{ij}}}I(|{\hat{\sigma }}_{\mathit{\text{ij}}}|\ge \sqrt{{\hat{\theta }}_{\mathit{\text{ij}}}}{\omega }_T)\\ \hfill {\hat{\theta }}_{\mathit{\text{ij}}}=\frac{1}{T}{\displaystyle \sum _{t=1}^T}{({\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-{\hat{\sigma }}_{\mathit{\text{ij}}})}^2,\end{array}$$ (2.5)

for some ω_T to be specified later.

We impose the following assumptions:

Assumption 2.1. (i) {u_t}_t≥1 is stationary and ergodic such that each u_t has zero mean vector and covariance matrix Σ_u. In addition, the strong mixing condition in Assumption 3.2 holds.

(ii) There exist constants c₁, c₂ > 0 such that c₁ < λ_min(Σ_u) ≤ λ_max(Σ_u) < c₂, and c₁ < var(u_itu_jt) < c₂ for all i ≤ p, j ≤ p.

(iii) There exist r₁ > 0 and b₁ > 0, such that for any s > 0 and i ≤ p,

$$P(|u_{\mathit{\text{it}}}|>s)\le \text{exp}(-{(s/b_1)}^{r_1}).$$ (2.6)

Condition (i) allows the idiosyncratic components to be weakly dependent. We will formally present the strong mixing condition in the next section. In order for the main results in this section to hold, it suffices to impose the strong mixing condition marginally on u_t only. Roughly speaking, we require the mixing coefficient

$$\alpha (T)=\underset{A\in {ℱ}_{-\mathrm{\infty }}^0,B\in {ℱ}_T^{\mathrm{\infty }}}{\text{sup}}|P(A)P(B)-P(A\cap B)|$$

to decrease exponentially fast as T → ∞, where (${ℱ}_{-\mathrm{\infty }}^0,{ℱ}_T^{\mathrm{\infty }}$) are the σ-algebras generated by ${\{{\mathbf{u}}_t\}}_{t=-\mathrm{\infty }}^0\text{ and }{\{{\mathbf{u}}_t\}}_{t=T}^{\mathrm{\infty }}$ respectively.

Condition (ii) requires the nonsingularity of Σ_u. Note that Cai and Liu (2011) allowed max_j σ_jj to diverse when direct observations are available. Condition (ii), however, requires that σ_jj should be uniformly bounded. In factor models, a uniform upper bound on the variance of u_it is needed when we estimate the covariance matrix of y_t later. This assumption is satisfied by most of the applications of factor models. Condition (iii) requires the distributions of (u_1t, …, u_pt) to have exponential-type tails, which allows us to apply the large deviation theory to $\frac{1}{T}{\displaystyle {\sum }_{t=1}^T}{u}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}}$.

Assumption 2.2. There exist positive sequences κ₁(p, T) = o(1), κ₂(p, T) = o(1) and a_T = o(1), and a constant M > 0, such that for all C > M,

$$\begin{array}{c}P(\underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}|u_{\mathit{\text{it}}}-{\mathit{û}}_{\mathit{\text{it}}}{|}^2>{\mathit{\text{Ca}}}_T^2)\le O({\kappa }_1(p,T)),\hfill \\ P(\underset{i\le p,t\le T}{\text{max}}|u_{\mathit{\text{it}}}-{\mathit{û}}_{\mathit{\text{it}}}|>C)\le O({\kappa }_2(p,T)).\hfill \end{array}$$

This assumption allows us to apply thresholding to the estimated error covariance matrix when direct observations are not available, without introducing too much extra estimation error. Note that it permits a general case when the original “data” is contaminated, including any type of estimate of the data when direct observations are not available, as well as the case when data is subject to measurement of errors. We will show in the next section that in a linear factor model when {u_it}_i≤p,t≤T are estimated using the OLS estimator, the rate of convergence $a_T^2=(K^2\text{log }p)/T$.

The following theorem establishes the asymptotic properties of the thresholding estimator ${\hat{\mathbf{\Sigma }}}_u^{𝒯}$, based on observations with estimation errors. Let ${\gamma }^{-1}=3r_1^{-1}+r_2^{-1}$, where r₁ and r₂ are defined in Assumptions 2.1, 3.2 respectively.

Theorem 2.1. Suppose γ < 1 and (log p)^6/γ−1 = o(T). Then under Assumptions 2.1 and 2.2, there exist C₁ > 0 and C₂ > 0 such that for ${\hat{\mathbf{\Sigma }}}_u^{𝒯}$ defined in (2.5) with

$${\omega }_T=C_1(\sqrt{\frac{\text{log }p}{T}}+a_T),$$

we have,

$$P(\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert \le C_2{\omega }_T{m}_T)\ge 1-O(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T)).$$ (2.7)

In addition, if ω_Tm_T = o(1), then with probability at least $1-O(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T))$,

$${\lambda }_{\text{min}}({\hat{\mathbf{\Sigma }}}_u^{𝒯})\ge 0.5{\lambda }_{\text{min}}({\mathbf{\Sigma }}_u),$$

and

$$\Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}\Vert \le C_2{\omega }_T{m}_T.$$

Note that we derive the result (2.7) without assuming the sparsity on Σ_u, i.e., no restriction is imposed on m_T. When ω_Tm_T ≠ o(1), (2.7) still holds, but $\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert$ does not converge to zero in probability. On the other hand, the condition ω_Tm_T = o(1) is required to preserve the nonsingularity of ${\hat{\mathbf{\Sigma }}}_u^{𝒯}$ asymptotically and to consistently estimate ${\mathbf{\Sigma }}_u^{-1}$.

The rate of convergence also depends on the averaged estimation error of the residual terms. We will see in the next section that when the number of common factors K increases slowly, the convergence rate in Theorem 2.1 is close to the minimax optimal rate as in Cai and Zhou (2010).

3. Estimation of Covariance Matrix Using Factors

We now investigate the estimation of the covariance matrix Σ in the approximate factor model:

$${\mathbf{y}}_t={\mathbf{\text{Bf}}}_t+{\mathbf{u}}_t,$$

where Σ = cov(y_t). This covariance matrix is particularly of interest in many applications of factor models as well as corresponding inferential theories. When estimating a large dimensional covariance matrix, sparsity and banding are two commonly used assumptions for regularization (e.g., Bickel and Levina (2008a, 2008b)). In most of the applications in finance and economics, however, these two assumptions are inappropriate for Σ. For instance, the US housing prices in the county level are generally associated with a few national indices, and there is no natural ordering among the counties. Hence neither the sparsity nor banding is realistic for such a problem. On the other hand, it is natural to assume Σ_u sparse, after controling the common factors. Therefore, our approach combines the merits of both the sparsity and factor structures.

Note that

$$\mathbf{\Sigma }=\mathbf{B}\text{cov}({\mathbf{f}}_t)\mathbf{B}\prime +{\mathbf{\Sigma }}_u.$$

By the Sherman-Morrison-Woodbury formula,

$${\mathbf{\Sigma }}^{-1}={\mathbf{\Sigma }}_u^{-1}-{\mathbf{\Sigma }}_u^{-1}\mathbf{B}{[\text{cov}{({\mathbf{f}}_t)}^{-1}+\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B}]}^{-1}\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}.$$

When the factors are observable, one can estimate B by the least squares method: B̂ = (b̂₁, …, b̂_p)′, where,

$${\hat{\mathbf{b}}}_i=\text{arg }\underset{{\mathbf{b}}_i}{\text{min}}\frac{1}{\mathit{\text{Tp}}}{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^p}{(y_{\mathit{\text{it}}}-{\mathbf{b}}_i^{\prime }{\mathbf{f}}_t)}^2.$$

The covariance matrix cov(f_t) can be estimated by the sample covariance matrix

$$\widehat{\text{cov}}({\mathbf{f}}_t)=T^{-1}\mathbf{\text{XX}}\prime -T^{-2}\mathbf{X}\mathbf{11}\prime \mathbf{X}\prime ,$$

where X = (f₁, …, f_T), and 1 is a T-dimensional column vector of ones. Therefore, by employing the thresholding estimator ${\hat{\mathbf{\Sigma }}}_u^{𝒯}$ in (2.5), we obtain substitution estimators

$${\hat{\mathbf{\Sigma }}}^{𝒯}=\hat{\mathbf{B}}\widehat{\text{cov}}({\mathbf{f}}_t)\hat{\mathbf{B}}\prime +{\hat{\mathbf{\Sigma }}}_u^{𝒯},$$ (3.1)

and

$${({\hat{\mathbf{\Sigma }}}^{𝒯})}^{-1}={({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}{[\widehat{\text{cov}}{({\mathbf{f}}_t)}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}.$$ (3.2)

In practice, one may apply a common thresholding λ to the correlation matrix of Σ̂_u, and then use the substitution estimator similar to (3.1). When λ = 0 (no thresholding), the resulting estimator is the sample covariance, whereas when λ = 1 (all off-diagonals are thresholded), the resulting estimator is an estimator based on the strict factor model (Fan, Fan and Lv (2008)). Thus we have created a path (indexed by λ) which connects the nonparametric estimate of covariance matrix to the parametric estimate.

The following assumptions are made.

Assumption 3.1. (i) {f_t}_t≥1 is stationary and ergodic.

(ii) {u_t}_t≥1 and {f_t}_t≥1 are independent.

In addition to the conditions above, we introduce the strong mixing conditions to conduct asymptotic analysis of the least square estimates. Let ${ℱ}_{-\mathrm{\infty }}^0,\text{ and }{ℱ}_T^{\mathrm{\infty }}$ denote the σ-algebras generated by {(f_t, u_t) : −∞ ≤ t ≤ 0} and {(f_t, u_t) : T ≤ t ≤ ∞} respectively. In addition, define the mixing coefficient

$$\alpha (T)=\underset{A\in {ℱ}_{-\mathrm{\infty }}^0,B\in {ℱ}_T^{\mathrm{\infty }}}{\text{sup}}|P(A)P(B)-P(\mathit{\text{AB}})|.$$

The following strong mixing assumption enables us to apply the Bernstein’s inequality in the technical proofs.

Assumption 3.2. There exist positive constants r₂ and C such that for all t ∈ ℤ⁺,

$$\alpha (t)\le \text{exp}(-{\mathit{\text{Ct}}}^{r_2}).$$

In addition, we impose the following regularity conditions.

Assumption 3.3. (i) There exists a constant M > 0 such that for all i, j and t, ${\mathit{\text{Ey}}}_{\mathit{\text{it}}}^2<M,{\mathit{\text{E f}}}_{\mathit{\text{it}}}^2<M$, and |b_ij| < M.

(ii) There exists a constant r₃ > 0 with $3r_3^{-1}+r_2^{-1}>1$, and b₂ > 0 such that for any s > 0 and i ≤ K,

$$P(|f_{\mathit{\text{it}}}|>s)\le \text{exp}(-{(s/b_2)}^{r_3}).$$ (3.3)

Condition (ii) allows us to apply the Bernstein type inequality for the weakly dependent data.

Assumption 3.4. There exists a constant C > 0 such that λ_min(cov(f_t)) > C.

Assumptions 3.4 and 2.1 ensure that both λ_min(cov(f_t)) and λ_min(Σ) are bounded away from zero, which is needed to derive the convergence rate of ‖(Σ̂^𝒯)⁻¹ − Σ⁻¹‖ below.

The following lemma verifies Assumption 2.2, which derives the rate of convergence of the OLS estimator as well as the estimated residuals.

Let ${\gamma }_2^{-1}=1.5r_1^{-1}+1.5r_3^{-1}+r_2^{-1}$.

Lemma 3.1. Suppose K = o(p), K⁴(log p)² = o(T) and (log p)^2/γ₂−1 = o(T). Then under the assumptions of Theorem 2.1 and Assumptions 3.1–3.4, there exists C > 0, such that

1. $$P(\underset{i\le p}{\text{max}}\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert >C\sqrt{\frac{K\text{ log }p}{T}})=O(\frac{1}{p^2}+\frac{1}{T^2}),$$
2. $$P(\underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}|u_{\mathit{\text{it}}}-{\mathit{û}}_{\mathit{\text{it}}}{|}^2>\frac{{\mathit{\text{CK}}}^2\text{ log }p}{T})=O(\frac{1}{p^2}+\frac{1}{T^2}),$$
3. $$P(\underset{i\le p,t\le T}{\text{max}}|u_{\mathit{\text{it}}}-{\mathit{û}}_{\mathit{\text{it}}}|>\mathit{\text{CK}}{(\text{log}T)}^{1/r_3}\sqrt{\frac{\text{log }p}{T}})=O(\frac{1}{p^2}+\frac{1}{T^2}).$$

By Lemma 3.1 and Assumption 2.2, $a_T=K\sqrt{(\text{log }p)/T}$, and κ₁(p, T) = κ₂(p, T) = p⁻² + T⁻². Therefore in the linear approximate factor model, the thresholding parameter ω_T defined in Theorem 2.1 is simplified to: for some positive constant $C_1^{\prime }$,

$${\omega }_T=C_1^{\prime }K\sqrt{\frac{\text{log}p}{T}}.$$ (3.4)

Now we can apply Theorem 2.1 to obtain the following theorem:

Theorem 3.1. Under the Assumptions of Lemma 3.1, there exist $C_1^{\prime }>0\mathit{\text{ and }}{C}_2^{\prime }>0$ such that the adaptive thresholding estimator defined in (2.5) with ${\omega }_T^2=C_1^{\prime }\frac{K^2\text{log }p}{T}$ satisfies

1. $$P(\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert \le C_2^{\prime }{m}_{T}K\sqrt{\frac{\text{log }p}{T}})=1-O(\frac{1}{p^2}+\frac{1}{T^2}).$$
2. If $m_{T}K\sqrt{\frac{\text{log }p}{T}}=o(1)$, then with probability at least $1-O(\frac{1}{p^2}+\frac{1}{T^2})$,

   $${\lambda }_{\text{min}}({\hat{\mathbf{\Sigma }}}_u^{𝒯})\ge 0.5{\lambda }_{\text{min}}({\mathbf{\Sigma }}_u),$$

   and

   $$\Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}\Vert \le C_2^{\prime }{m}_{T}K\sqrt{\frac{\text{log }p}{T}}.$$

Remark 3.1. We briefly comment on the terms in the convergence rate above.

1. The term K appears as an effect of using the estimated residuals to construct the thresholding covariance estimator, which is typically small compared to p and T in many applications. For instance, the famous Fama-French three-factor model shows that K = 3 factors are adequate for the US equity market. In an empirical study on asset returns, Bai and Ng (2002) used the monthly data which contains the returns of 4883 stocks for sixty months. For their data set, T = 60, p = 4883. Bai and Ng (2002) determined K = 2 common factors.

2. As in Bickel and Levina (2008a) and Cai and Liu (2011), m_T, the maximum number of nonzero components across the rows of Σ_u, also plays a role in the convergence rate. Note that when K is bounded, the convergence rate reduces to $O_p\left(m_T\sqrt{(\text{log }p)/T}\right)$, the same as the minimax rate derived by Cai and Zhou (2010).

One of our main objectives is to estimate Σ, which is the p × p dimensional covarinace matrix of y_t, assumed to be time invariant. We can achieve a better accuracy in estimating both Σ and Σ⁻¹ by incorporating the factor structure than using the sample covariance matrix, as shown by Fan et al (2008) in the strict factor model case. When the cross sectional correlations among the idiosyncratic components (u_1t, …, u_pt) are in presence, we can still take advantage of the factor structure. This is particularly essential when direct sparsity assumption on Σ is inapproriate.

Assumption 3.5. ‖p⁻¹B′B−Ω‖ = o(1) for some K × K symmetric positive definite matrix Ω such that λ_min(Ω) is bounded away from zero.

Assumption 3.5 requires that the factors should be pervasive, i.e., impact every individual time series (Harding (2009)). It was imposed by Fan et al.(2008) only when they tried to establish the asymptotic normality of the covariance estimator. However, it turns out to be also helpful to obtain a good upper bound of ‖(Σ̂^𝒯)⁻¹ − Σ⁻¹‖, as it ensures that λ_max((B′Σ⁻¹B)⁻¹) = O(p⁻¹).

Fan et al. (2008) obtained an upper bound of ‖Σ̂^𝒯 − Σ‖_F under the Frobenius norm when Σ_u is diagonal, i.e., there was no cross-sectional correlation among the idiosyncratic errors. In order for their upper bound to decrease to zero, p² < T is required. Even with this restrictive assumption, they showed that the convergence rate is the same as the usual sample covariance matrix of y_t, though the latter does not take the factor structure into account. Alternatively, they considered the entropy loss norm, proposed by James and Stein (1961):

$${\Vert {\hat{\mathbf{\Sigma }}}^{𝒯}-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma }}={(p^{-1}\text{tr}[{({\hat{\mathbf{\Sigma }}}^{𝒯}{\mathbf{\Sigma }}^{-1}-I)}^2])}^{1/2}=p^{-1/2}{\Vert {\mathbf{\Sigma }}^{-1/2}({\hat{\mathbf{\Sigma }}}^{𝒯}-\mathbf{\Sigma }){\mathbf{\Sigma }}^{-1/2}\Vert }_F.$$

Here the factor p^−1/2 is used for normalization, such that ‖Σ‖_Σ = 1. Under this norm, Fan et al. (2008) showed that the substitution estimator has a better convergence rate than the usual sample covariance matrix. Note that the normalization factor p^−1/2 in the definition results in an averaged estimation error, which also cancels out the diverging dimensionality introduced by p. In addition, for any two p × p matrices A₁ and A₂:

$$\begin{array}{cc}{\Vert {\mathbf{A}}_1-{\mathbf{A}}_2\Vert }_{\mathrm{\Sigma }}\hfill & =p^{-1/2}{\Vert {\mathbf{\Sigma }}^{-1/2}({\mathbf{A}}_1-{\mathbf{A}}_2){\mathbf{\Sigma }}^{-1/2}\Vert }_F.\hfill \\ \hfill & \le \Vert {\mathbf{\Sigma }}^{-1/2}({\mathbf{A}}_1-{\mathbf{A}}_2){\mathbf{\Sigma }}^{-1/2}\Vert \hfill \\ \hfill & \le \Vert {\mathbf{A}}_1-{\mathbf{A}}_2\Vert ·{\lambda }_{\text{max }}({\mathbf{\Sigma }}^{-1}).\hfill \end{array}$$

Combining with the estimated low-rank matrix Bcov(f_t)B′, Theorem 3.1 implies the main theorem in this section:

Theorem 3.2. Suppose log T = o(p). Under the assumptions of Theorem 3.1 and Assumption 3.5, we have

1. $$\begin{array}{c}P({\Vert {\hat{\mathbf{\Sigma }}}^{𝒯}-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma }}^2\le \frac{{\mathit{\text{CpK}}}^2{(\text{log }p)}^2}{T^2}+\frac{{\mathit{\text{Cm}}}_T^2{K}^2\text{ log }p}{T})=1-O(\frac{1}{p^2}+\frac{1}{T^2}),\hfill \\ P({\Vert {\hat{\mathbf{\Sigma }}}^{𝒯}-\mathbf{\Sigma }\Vert }_{\mathrm{\infty }}^2\le \frac{{\mathit{\text{CK}}}^2\text{ log }p+{\mathit{\text{CK}}}^4\mathrm{ log }T}{T})=1-O(\frac{1}{p^2}+\frac{1}{T^2}).\hfill \end{array}$$
2. If $m_{T}K\sqrt{\frac{\text{log }p}{T}}=o(1)$, with probability at least $1-O(\frac{1}{p^2}+\frac{1}{T^2})$,

   $${\lambda }_{\text{min}}({\hat{\mathbf{\Sigma }}}^{𝒯})\ge 0.5{\lambda }_{\text{min}}({\mathbf{\Sigma }}_u),$$

   and

   $$\Vert {({\hat{\mathbf{\Sigma }}}^{𝒯})}^{-1}-{\mathbf{\Sigma }}^{-1}\Vert \le {\mathit{\text{Cm}}}_{T}K\sqrt{\frac{\text{log }p}{T}}$$

Note that we have derived a better convergence rate of (Σ̂^𝒯)⁻¹ than that in Fan et al.(2008). When the operator norm is considered, p is allowed to grow exponentially fast in T in order for (Σ̂^𝒯)⁻¹ to be consistent.

We have also derived the maximum elementwise estimation ‖Σ̂^𝒯 − Σ‖_∞. This quantity appears in risk assessment as in Fan, Zhang and Yu (2008). For any portfolio with allocation vector w, the true portfolio variance and the estimated one are given by w′Σw and w′Σ̂^𝒯 w respectively. The estimation error is bounded by

$$|\mathbf{w}\prime {\hat{\mathbf{\Sigma }}}^{𝒯}\mathbf{w}-\mathbf{w}\prime \mathbf{\Sigma }\mathbf{w}|\le {\Vert {\hat{\mathbf{\Sigma }}}^{𝒯}-\mathbf{\Sigma }\Vert }_{\mathrm{\infty }}{\Vert \mathbf{w}\Vert }_1^2,$$

where ‖w‖₁, the l₁ norm of w, is the gross exposure of the portfolio.

4. Extension: Seemingly Unrelated Regression

A seemingly unrelated regression model (Kmenta and Gilbert (1970)) is a set of linear equations in which the disturbances are correlated across equations. Specifically, we have

$$y_{\mathit{\text{it}}}={\mathbf{b}}_i^{\prime }{\mathbf{f}}_{\mathit{\text{it}}}+u_{\mathit{\text{it}}},i\le p,t\le T,$$ (4.1)

where b_i and f_it are both K_i × 1 vectors. The p linear equations (4.1) are related because their error terms u_it are correlated, i.e., the covariance matrix

$${\mathbf{\Sigma }}_u={({\mathit{\text{Eu}}}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})}_{p\times p}$$

is not diagonal.

Model (4.1) allows each variable y_it to have its own factors. This is important for many applications. In financial applications, the returns of individual stock depend on common market factors and sector-specific factors. In housing price index modeling, housing price appreciations depend on both national factors and local economy. When f_it = f_t for each i ≤ p, model (4.1) reduces to the approximate factor model (1.1) with common factors f_t.

Under mild conditions, running OLS on each equation produces unbiased and consistent estimator of b_i separately. However, since OLS does not take into account the cross sectional correlation among the noises, it is not efficient. Instead, statisticians obtain the best linear unbiased estimator (BLUE) via generalized least square (GLS). Write

$$\begin{array}{c}\hfill {\mathbf{y}}_i=(y_{i1},\dots ,y_{\mathit{\text{iT}}})\prime ,T\times 1,{\mathbf{X}}_i=({\mathbf{f}}_{i1},\dots ,{\mathbf{f}}_{\mathit{\text{iT}}})\prime ,T\times K_i,i\le p,\hfill \\ \hfill \mathbf{y}=\left(\begin{array}{c}\hfill {\mathbf{y}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{y}}_p\hfill \end{array}\right),\mathbf{X}=\left(\begin{array}{ccc}\hfill {\mathbf{X}}_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathbf{X}}_p\hfill \end{array}\right),\mathbf{B}=\left(\begin{array}{c}\hfill {\mathbf{b}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{b}}_p\hfill \end{array}\right).\hfill \end{array}$$

The GLS estimator of B is given by Zellner (1962):

$${\hat{\mathbf{B}}}_{\mathit{\text{GLS}}}={[\mathbf{X}\prime {({\hat{\mathbf{\Sigma }}}_u^{-1}\otimes I_T)}^{-1}\mathbf{X}]}^{-1}[\mathbf{X}\prime {({\hat{\mathbf{\Sigma }}}_u^{-1}\otimes I_T)}^{-1}\mathbf{y}],$$ (4.2)

where I_T denotes a T × T identity matrix, ⊗ represents the Kronecker product operation, and Σ̂_u is a consistent estimator of Σ_u.

In classical seemingly unrelated regression in which p does not grow with T, Σ_u is estimated by a two-stage procedure: (Kmenta and Gilbert (1970)): On the first stage, estimate B via OLS, and obtain residuals

$${\mathit{û}}_{\mathit{\text{it}}}=y_{\mathit{\text{it}}}-{\hat{\mathbf{b}}}_i^{\prime }{\mathbf{f}}_{\mathit{\text{it}}}.$$ (4.3)

On the second stage, estimate Σ_u by

$${\hat{\mathbf{\Sigma }}}_u=({\hat{\sigma }}_{\mathit{\text{ij}}})={(\frac{1}{T}{\displaystyle \sum _{t=1}^T}{\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}})}_{p\times p}.$$ (4.4)

In high dimensional seemingly unrelated regression in which p > T, however, Σ̂_u is not invertible, and hence the GLS estimator (4.2) is infeasible.

By the sparsity assumption of Σ_u, we can deal with this singularity problem by using the adaptive thresholding estimator, and produce a consistent nonsingular estimator of Σ_u:

$${\hat{\mathbf{\Sigma }}}_u^{𝒯}=({\hat{\sigma }}_{\mathit{\text{ij}}}I(|{\hat{\sigma }}_{\mathit{\text{ij}}}|>\sqrt{{\hat{\theta }}_{\mathit{\text{ij}}}}{\omega }_T)),{\hat{\theta }}_{\mathit{\text{ij}}}=\frac{1}{T}{\displaystyle \sum _{t=1}^T}{({\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-{\hat{\sigma }}_{\mathit{\text{ij}}})}^2.$$ (4.5)

To pursue this goal, we impose the following assumptions:

Assumption 4.1. For each i ≤ p,

1. {f_it}_t≥1 is stationary and ergodic.

2. {u_t}_t≥1 and {f_it}_t≥1 are independent.

Assumption 4.2. There exists positive constants C and r₂ such that for each i ≤ p, the strong mixing condition

$$\alpha (t)\le \text{exp}(-{\mathit{\text{Ct}}}^{r_2})$$

is satisfied by (f_it, u_t):

Assumption 4.3. There exist constants M and C > 0 such that for all i ≤ p, j ≤ K_i, t ≤ T

1. ${\mathit{\text{Ey}}}_{\mathit{\text{it}}}^2<M$, |b_ij| < M, and ${\mathit{\text{E f}}}_{\mathit{\text{it}},j}^2<M$.

2. min_i≤p λ_min(cov(f_it)) > C.

Assumption 4.4. There exists a constant r₄ > 0 with $3r_4^{-1}+r_2^{-1}>1$, and b₃ > 0 such that for any s > 0 and i, j,

$$P(|f_{\mathit{\text{it}},j}|>s)\le \text{exp}(-{(s/b_3)}^{r_4}).$$

These assumptions are similar to those made in Section 3, except that here they are imposed on the sector-specific factors. The main theorem in this section is a direct application of Theorem 2.1, which shows that the adaptive thresholding produces a consistent nonsingular estimator of Σ̂_u.

Theorem 4.1. Let K = max_i≤p K_i and ${\gamma }_3^{-1}=1.5r_1^{-1}+1.5r_4^{-1}+r_2^{-1}$; suppose K = o(p), K⁴(log p)² = o(T) and (log p)^2/γ₃−1 = o(T). Under Assumptions 2.1, 4.1–4.4, there exist constants C₁ > 0 and C₂ > 0 such that the adaptive thresholding estimator defined in (4.5) with ${\omega }_T^2=C_1\frac{K^2\text{log }p}{T}$ satisfies

1. $$P(\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert \le C_2{m}_{T}K\sqrt{\frac{\text{log }p}{T}})=1-O(\frac{1}{p^2}+\frac{1}{T^2}).$$
2. If $m_{T}K\sqrt{\frac{\text{log }p}{T}}=o(1)$, then with probability at least $1-O(\frac{1}{p^2}+\frac{1}{T^2})$,

   $${\lambda }_{\text{min}}({\hat{\mathbf{\Sigma }}}_u^{𝒯})\ge 0.5{\lambda }_{\text{min}}({\mathbf{\Sigma }}_u),$$

   and

   $$\Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}\Vert \le C_2{m}_{T}K\sqrt{\frac{\text{log }p}{T}}.$$

Therefore, in the case when p > T, Theorem 4.1 enables us to efficiently estimate B via feasible GLS:

$${\hat{\mathbf{B}}}_{\mathit{\text{GLS}}}^{𝒯}={[\mathbf{X}\prime {({({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\otimes I_T)}^{-1}\mathbf{X}]}^{-1}{[\mathbf{X}\prime ({({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\otimes I_T)}^{-1}\mathbf{y}].$$

5. Monte Carlo Experiments

In this section, we use simulation to demonstrate the rates of convergence of the estimators Σ̂^𝒯 and (Σ̂^𝒯)⁻¹ that we have obtained so far. The simulation model is a modified version of the Fama-French three-factor model described in Fan, Fan, Lv (2008). We fix the number of factors, K = 3 and the length of time, T = 500, and let the dimensionality p gradually increase.

The Fama-French three-factor model (Fama and French (1992)) is given by

$$y_{\mathit{\text{it}}}=b_{i1}{f}_{1t}+b_{i2}{f}_{2t}+b_{i3}{f}_{3t}+u_{\mathit{\text{it}}},$$

which models the excess return (real rate of return minus risk-free rate) of the ith stock of a portfolio, y_it, with respect to 3 factors. The first factor is the excess return of the whole stock market, and the weighted excess return on all NASDAQ, AMEX and NYSE stocks is a commonly used proxy. It extends the capital assets pricing model (CAPM) by adding two new factors- SMB (“small minus big” cap) and HML (“high minus low” book/price). These two were added to the model after the observation that two types of stocks - small caps, and high book value to price ratio, tend to outperform the stock market as a whole.

We separate this section into three parts, calibration, simulation and results. Similar to Section 5 of Fan, Fan and Lv (2008), in the calibration part we want to calculate realistic multivariate distributions from which we can generate the factor loadings B, idiosyncratic noises ${\{{\mathbf{u}}_t\}}_{t=1}^T$ and the observable factors ${\{{\mathbf{f}}_t\}}_{t=1}^T$. The data was obtained from the data library of Kenneth French’s website.

5.1. Calibration

To estimate the parameters in the Fama-French model, we will use the two-year daily data (ỹ_t, f̃_t) from Jan 1^st, 2009 to Dec 31^st, 2010 (T=500) of 30 industry portfolios.

1. Calculate the least squares estimator B̃ of ỹ_t = Bf̃_t + u_t, and take the rows of B̃, namely b̃₁ = (b₁₁, b₁₂, b₁₃), …, b̃₃₀ = (b_30,1, b_30,2, b_30,3), to calculate the sample mean vector μ_B and sample covariance matrix Σ_B. The results are depicted in Table 1. We then create a mutlivariate normal distribution N₃(μ_B, Σ_B), from which the factor loadings ${\{{\mathbf{b}}_i\}}_{i=1}^p$ are drawn.

2. For each fixed p, create the sparse matrix ${\mathbf{\Sigma }}_u=\mathbf{D}+\mathbf{\text{ss}}\prime -\text{diag}\{s_1^2,\dots ,s_p^2\}$ in the following way. Let û_t = ỹ_t − B̃f̃_t. For i = 1, …, 30, let σ̂_i denote the standard deviation of the residuals of the ith portfolio. We find min(σ̂_i) = 0.3533, max(σ̂_i) = 1.5222, and calculate the mean and the standard deviation of the σ̂_i’s, namely σ̄ = 0.6055 and σ_SD = 0.2621.

   Let $\mathbf{D}=\text{diag}\{{\sigma }_1^2,\dots ,{\sigma }_p^2\}$, where σ₁, …, σ_p are generated independently from the Gamma distribution G(α, β), with mean αβ and standard deviation α^1/2β. We match these values to σ̄ = 0.6055 and σ_SD = 0.2621, to get α = 5.6840 and β = 0.1503. Further, we create a loop that only accepts the value of σ_i if it is between min(σ̂_i) = 0.3533 and max(σ̂_i) = 1.5222.

   Create s = (s₁, …, s_p)′ to be a sparse vector. We set each s_i ~ N(0, 1) with probability $\frac{0.2}{\sqrt{p}\text{ log }p}$, and s_i = 0 otherwise. This leads to an average of $\frac{0.2\sqrt{p}}{\text{log }p}$ nonzero elements per each row of the error covariance matrix.

   Create a loop that generates Σ_u multiple times until it is positive definite.

3. Assume the factors follow the vector autoregressive (VAR(1)) model f_t = μ + Φf_t−1 + ε_t for some 3 × 3 matrix Φ, where ε_t’s are i.i.d. N₃(0, Σ_ε). We estimate Φ, μ and Σ_ε from the data, and obtain cov(f_t). They are summarized in Table 2.

Table 1.

Mean and covariance matrix used to generate b

μB	ΣB
1.0641	0.0475	0.0218	0.0488
0.1233	0.0218	0.0945	0.0215
−0.0119	0.0488	0.0215	0.1261

Table 2.

Parameters of f_t generating process

μ	cov(ft)			Φ
0.1074	2.2540	0.2735	0.9197	−0.1149	0.0024	0.0776
0.0357	0.2735	0.3767	0.0430	0.0016	−0.0162	0.0387
0.0033	0.9197	0.0430	0.6822	−0.0399	0.0218	0.0351

5.2. Simulation

For each fixed p, we generate (b₁, …, b_p) independently from N₃(μ_B, Σ_B), and generate ${\{{\mathbf{f}}_t\}}_{t=1}^T\text{ and }{\{{\mathbf{u}}_t\}}_{t=1}^T$ independently. We keep T = 500 fixed, and gradually increase p from 20 to 600 in multiples of 20 to illustrate the rates of convergence when the number of variables diverges with respect to the sample size.

Repeat the following steps N = 200 times for each fixed p:

1. Generate ${\{{\mathbf{b}}_i\}}_{i=1}^p$ independently from N₃(μ_B, Σ_B), and set B = (b₁, …, b_p)′.

2. Generate ${\{{\mathbf{u}}_t\}}_{t=1}^T$ independently from N_p(0, Σ_u).

3. Generate ${\{{\mathbf{f}}_t\}}_{t=1}^T$ independently from the VAR(1) model f_t = μ + Φf_t−1 + ε_t.

4. Calculate y_t = Bf_t + u_t for t = 1, …, T.

5. Set ${\omega }_T=0.10K\sqrt{\text{log }p/T}$ to obtain the thresholding estimator (2.5) ${\hat{\mathbf{\Sigma }}}_u^{𝒯}$ and the sample covariance matrices $\widehat{\text{cov}}({\mathbf{f}}_t),{\hat{\mathbf{\Sigma }}}_y=\frac{1}{T-1}{\displaystyle {\sum }_{t=1}^T}({\mathbf{y}}_t-\overline{\mathbf{y}}){({\mathbf{y}}_t-\overline{\mathbf{y}})}^T$.

We graph the convergence of Σ̂^𝒯 and Σ̂_y to Σ, the covariance matrix of y, under the entropy-loss norm ‖·‖_Σ and the elementwise norm ‖·‖_∞. We also graph the convergence of the inverses (Σ̂^𝒯)⁻¹ and ${\hat{\mathbf{\Sigma }}}_y^{-1}$ to Σ⁻¹ under the operator norm. Note that we graph that only for p from 20 to 300. Since T = 500, for p > 500 the sample covariance matrix is singular. Also, for p close to 500, Σ̂_y is nearly singular, which leads to abnormally large values of the operator norm. Lastly, we record the standard deviations of these norms.

5.3. Results

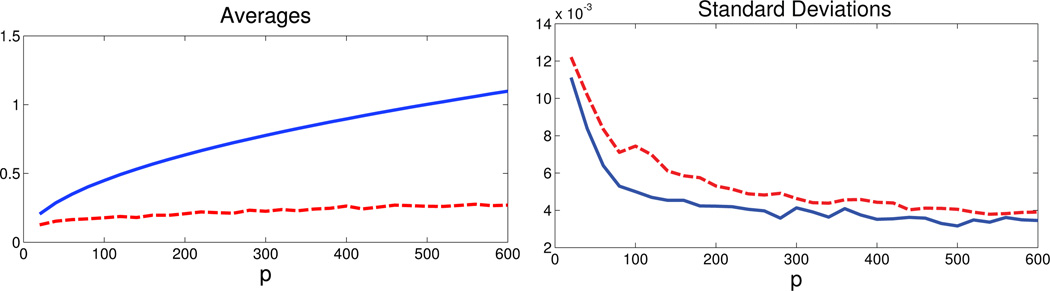
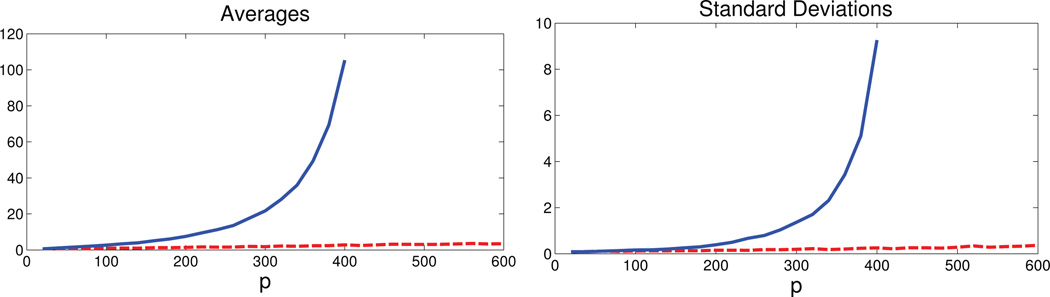
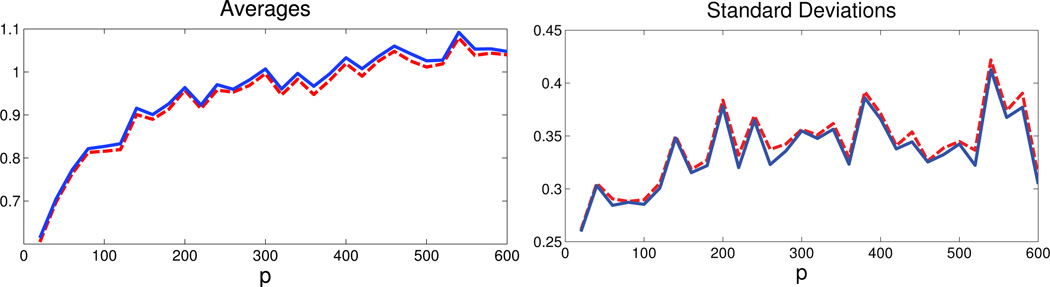
In Figures 1–3, the dashed curves correspond to Σ̂^𝒯 and the solid curves correspond to the sample covariance matrix Σ̂_y. Figure 1 and 2 present the averages and standard deviations of the estimation error of both of these matrices with respect to the Σ-norm and infinity norm, respectively. Figure 3 presents the averages and estimation errors of the inverses with respect to the operator norm. Based on the simulation results, we can make the following observations:

1. The standard deviations of the norms are negligible when compared to their corresponding averages.

2. Under the ‖·‖_Σ, our estimate of the covariance matrix of y, Σ̂^𝒯 performs much better than the sample covaraince matrix Σ̂_y. Note that, in the proof of Theorem 2 in Fan, Fan, Lv(2008), it was shown that:

   $${\Vert {\hat{\mathbf{\Sigma }}}_y-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma }}^2=O_p\left(\frac{K^3}{\mathit{\text{Tp}}}\right)+O_p\left(\frac{p}{T}\right)+O_p\left(\frac{K^{3/2}}{T}\right).$$ (5.1)

   For a small fixed value of K, such as K = 3, the dominating term in (5.1) is $O\left(\frac{p}{T}\right)$. From Theorem 4.1, and given that m_T = o(p^1/4), the dominating term in the convergence of ${\Vert {\hat{\mathbf{\Sigma }}}^{𝒯}-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma }}^2\text{ is }{O}_p(\frac{p}{T^2}+\frac{m_T^2\text{log }p}{T})$. So, we would expect our estimator to perform better, and the simulation results are consistent with the theory.

3. Under the infinity norm, both estimators perform roughly the same. This is to be expected, given that the thresholding affects mainly the elements of the covariance matrix that are closest to 0, and the infinity norm depicts the magnitude of the largest elementwise absolute error.

4. Under the operator norm, the inverse of our estimator, (Σ̂^𝒯)⁻¹ also performs significantly better than the inverse of the sample covariance matrix.

5. Finally, when p > 500, the thresholding estimators ${\hat{\mathbf{\Sigma }}}_u^{𝒯}$ and Σ̂^𝒯 are still nonsingular.

Fig 1.

Averages and standard deviations of ‖Σ̂^𝒯 − Σ‖_Σ (dashed curve) and ‖Σ̂_y − Σ‖_Σ (solid curve) over N = 200 iterations, as a function of the dimensionality p.

Fig 3.

Averages and standard deviations of ‖(Σ̂^𝒯)⁻¹ − Σ⁻¹‖ (dashed curve) and $\Vert {\hat{\mathbf{\Sigma }}}_y^{-1}-{\mathbf{\Sigma }}^{-1}\Vert$ (solid curve) over N = 200 iterations, as a function of the dimensionality p.

Fig 2.

Averages and standard deviations of ‖Σ̂^𝒯 − Σ‖_∞ (dashed curve) and ‖Σ̂_y − Σ‖_∞ (solid curve) over N = 200 iterations, as a function of the dimensionality p.

In conclusion, even after imposing less restrictive assumptions on the error covariance matrix, we still reach an estimator Σ̂^𝒯 that significantly outperforms the standard sample covariance matrix.

6. Conclusions and Discussions

We studied the rate of convergence of high dimensional covariance matrix of approximate factor models under various norms. By assuming sparse error covariance matrix, we allow for the presence of the cross-sectional correlation even after taking out common factors. Since direct observations of the noises are not available, we constructed the error sample covariance matrix first based on the estimation residuals, and then estimate the error covariance matrix using the adaptive thresholding method.We then constructed the covariance matrix of y_t using the factor model, assuming that the factors follow a stationary and ergodic process, but can be weakly-dependent. It was shown that after thresholding, the estimated covariance matrices are still invertible even if p > T, and the rate of convergence of (Σ̂^𝒯)⁻¹ and ${({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}$ is of order $O_p({\mathit{\text{Km}}}_T\sqrt{\text{log }p/T})$, where K comes from the impact of estimating the unobservable noise terms. This demonstrates when estimating the inverse covariance matrix, p is allowed to be much larger than T.

In fact, the rate of convergence in Theorem 2.1 reflects the impact of unobservable idiosyncratic components on the thresholding method. Generally, whether it is the minimax rate when direct observations are not available but have to be estimated is an important question, which is left as a research direction in the future.

Moreover, this paper uses the hard-thresholding technique, which takes the form of σ̂_ij(σ_ij) = σ_ijI(|σ_ij| > θ_ij) for some pre-determined threshold θ_ij. Recently, Rothman et al (2009) and Cai and Liu (2011) studied a more general thresholding function of Antoniadis and Fan (2001), which admits the form σ̂_ij(θ_ij) = s(σ_ij), and also allows for soft-thresholding. It is easy to apply the more general thresholding here as well, and the rate of convergence of the resulting covariance matrix estimators should be straightforward to derive.

Finally, we considered the case when common factors are observable, as in Fama and French (1992). In some applications, the common factors are unobservable and need to be estimated (Bai (2003)). In that case, it is still possible to consistently estimate the covariance matrices using similar techniques as those in this paper. However, the impact of high dimensionality on the rate of convergence comes also from the estimation error of the unobservable factors. We plan to address this problem in a separate paper.

APPENDIX A: PROOFS FOR SECTION 2

A.1. Lemmas. The following lemmas are useful to be proved first, in which we consider the operator norm ‖A‖² = λ_max(A′A).

Lemma A.1. Let A be an m × m random matrix, B be an m × m deterministic matrix, and both A and B are semi-positive definite. If there exists a positive sequence ${\{c_T\}}_{T=1}^{\mathrm{\infty }}$ such that for all large enough T, λ_min(B) > c_T. Then

$$\begin{array}{c}\hfill P({\lambda }_{\text{min}}(\mathbf{A})\ge 0.5c_T)\ge P(\Vert \mathbf{A}-\mathbf{B}\Vert \le 0.5c_T),\mathit{\text{and}}\hfill \\ \hfill P(\Vert {\mathbf{A}}^{-1}-{\mathbf{B}}^{-1}\Vert \le \frac{2}{c_T^2}\Vert \mathbf{A}-\mathbf{B}\Vert )\ge P(\Vert \mathbf{A}-\mathbf{B}\Vert \le 0.5c_T).\hfill \end{array}$$

Proof. For any v ∈ ℝ^m such that ‖v‖ = 1, under the event ‖A − B‖ ≤ 0.5c_T,

$$\begin{array}{cc}\mathbf{v}\prime \mathbf{\text{Av}}\hfill & =\mathbf{v}\prime \mathbf{\text{Bv}}-\mathbf{v}\prime (\mathbf{B}-\mathbf{A})\mathbf{v}\ge {\lambda }_{\text{min}}(\mathbf{B})-\Vert \mathbf{A}-\mathbf{B}\Vert \hfill \\ \hfill & \ge 0.5c_T\hfill \end{array}$$

Hence λ_min(A) ≥ 0.5c_T.

In addition, still under the event ‖A − B‖ ≤ 0.5c_T,

$$\begin{array}{cc}\Vert {\mathbf{A}}^{-1}-{\mathbf{B}}^{-1}\Vert \hfill & =\Vert {\mathbf{A}}^{-1}(\mathbf{B}-\mathbf{A}){\mathbf{B}}^{-1}\Vert \hfill \\ \hfill & \le {\lambda }_{\text{min}}{(\mathbf{A})}^{-1}\Vert \mathbf{A}-\mathbf{B}\Vert {\lambda }_{\text{min}}{(\mathbf{B})}^{-1}\hfill \\ \hfill & =2c_T^{-1}\Vert \mathbf{A}-\mathbf{B}\Vert .\hfill \end{array}$$

Q.E.D.

Lemma A.2. Suppose that the random variables Z₁, Z₂ both satisfy the exponential-type tail condition: There exist r₁, r₂ ∈ (0, 1) and b₁, b₂ > 0, such that ∀s > 0,

$$P(|Z_i|>s)\le \text{exp}(1-{(s/b_i)}^{r_i}),i=1,2.$$

Then for some r₃ and b₃ > 0, and any s > 0,

$$P(|Z_1{Z}_2|>s)\le \text{exp}(1-{(s/b_3)}^{r_3}).$$ (A.1)

Proof. We have, for any s > 0, $M={({\mathit{\text{sb}}}_2^{r_2/r_1}/b_1)}^{r_1/(r_1+r_2)}$, b = b₁b₂, and r = r₁r₂/(r₁ + r₂),

$$\begin{array}{cc}P(|Z_1{Z}_2|>s)\hfill & \le P(M|Z_1|>s)+P(|Z_2|>M)\hfill \\ \hfill & \le \text{exp}(1-{(s/b_{1}M)}^{r_1})+\text{exp}(1-{(M/b_2)}^{r_2})\hfill \\ \hfill & =2\text{ exp}(1-{(s/b)}^r).\hfill \end{array}$$

Pick up an r₃ ∈ (0, r), and b₃ > max{(r₃/r)^1/rb, (1 + log 2)^1/rb}, then it can be shown that F(s) = (s/b)^r − (s/b₃)^r₃ is increasing when s > b₃. Hence F(s) > F(b₃) > log 2 when s > b₃, which implies when s > b₃,

$$P(|Z_1{Z}_2|>s)\le 2\text{exp}(1-{(s/b)}^r)\le \text{exp}(1-{(s/b_3)}^{r_3}).$$

When s ≤ b₃,

$$P(|Z_1{Z}_2|>s)\le 1\le \text{exp}(1-{(s/b_3)}^{r_3}).$$

Q.E.D.

Lemma A.3. Under the Assumptions of Theorem 2.1, there exists a constant C_r > 0 that does not depend on (p, T), such that when C > C_r,

1. $$P(\underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}}|>C\sqrt{\frac{\text{log }p}{T}})=O\left(\frac{1}{p^2}\right),$$
2. $$P(\underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}({\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}|>{\mathit{\text{Ca}}}_T)=O(\frac{1}{p^2}+{\kappa }_1(p,T)),$$
3. $$P(\underset{i,j\le p}{\text{max}}|{\hat{\sigma }}_{\mathit{\text{ij}}}-{\sigma }_{\mathit{\text{ij}}}|>C(\sqrt{\frac{\text{log }p}{T}}+a_T))=O(\frac{1}{p^2}+{\kappa }_1(p,T)).$$

Proof. (i) By Assumption 2.1 and Lemma A.2, u_itu_jt satisfies the exponential tail condition, with parameter r₁/3 as shown in the proof of Lemma A.2. Therefore by the Bernstein’s inequality (Theorem 1 of Merlevède (2009)), there exist constants C₁, C₂, C₃, C₄ and C₅ > 0 that only depend on b₁, r₁ and r₂ such that for any i, j ≤ p, and ${\gamma }^{-1}=3r_1^{-1}+r_2^{-1}$,

$$P(|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}}|\ge s)\le T\text{ exp }(-\frac{{(\mathit{\text{T s}})}^{\gamma }}{C_1})+\text{exp }(-\frac{T^2{s}^2}{C_2(1+{\mathit{\text{TC}}}_3)})+\text{exp }(-\frac{{(\mathit{\text{T s}})}^2}{C_{4}T}\text{exp }(\frac{{(\mathit{\text{T s}})}^{\gamma (1-\gamma )}}{C_5{(\text{log}\mathit{\text{T s}})}^{\gamma }}\left)\right).$$

Using Bonferroni’s method, we have

$$P(\underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}}|>s)\le p^2\underset{i,j\le p}{\text{max}}P(|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}}|>s).$$

Let $s=C\sqrt{(\text{log }p)/T}$ for some C > 0. It is not hard to check that when (log p)^2/γ−1 = o(T) (by assumption), for large enough C,

$$p^{2}T\text{ exp }(-\frac{{(\mathit{\text{T s}})}^{\gamma }}{C_1})+p^2\text{exp }(-\frac{{(\mathit{\text{T s}})}^2}{C_{4}T}\text{exp }(\frac{{(\mathit{\text{T s}})}^{\gamma (1-\gamma )}}{C_5{(\text{log}\mathit{\text{T s}})}^{\gamma }}\left)\right)=o\left(\frac{1}{p^2}\right),$$

and

$$p^2\text{exp }(-\frac{T^2{s}^2}{C_2(1+{\mathit{\text{TC}}}_3)})=O\left(\frac{1}{p^2}\right).$$

This proves (i).

(ii) For some $C_1^{\prime }>0$ such that

$$P(\underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}{({\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}})}^2>C_1^{\prime }{a}_T^2)=O({\kappa }_1(p,T)),$$ (A.2)

under the event $\{{\text{max}}_{i\le p}|\frac{1}{T}{\displaystyle {\sum }_{t=1}^T}{u}_{\mathit{\text{it}}}^2-{\sigma }_{\mathit{\text{ii}}}|\le {\text{max}}_{i\le p}{\sigma }_{\mathit{\text{ii}}}/4\}\cap \{{\text{max}}_{i\le p}\frac{1}{T}{\displaystyle {\sum }_{t=1}^T}{({\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}})}^2\le C_1^{\prime }{a}_T^2\}$, by Cauchy-Schwarz inequality,

$$\begin{array}{cc}Z\hfill & \equiv \underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}({\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})|\hfill \\ \hfill & \le \underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}({\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}})({\mathit{û}}_{\mathit{\text{jt}}}-u_{\mathit{\text{jt}}})|+2\underset{i,j\le p}{\text{ max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}({\mathit{û}}_{\mathit{\text{jt}}}-u_{\mathit{\text{jt}}})|\hfill \\ \hfill & \le \underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}{({\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}})}^2+2\sqrt{\underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}^2}\sqrt{\underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}{({\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}})}^2}\hfill \\ \hfill & \le C_1^{\prime }{a}_T^2+2\sqrt{\frac{5}{4}\underset{i\le p}{\text{max}}{\sigma }_{\mathit{\text{ii}}}}\sqrt{C_1^{\prime }{a}_T^2}.\hfill \end{array}$$

Since a_T = o(1), when $C>3\sqrt{C_1^{\prime }{\text{max}}_{i\le p}{\sigma }_{\mathit{\text{ii}}}}$, we have, for all large T,

$${\mathit{\text{Ca}}}_T>C_1^{\prime }{a}_T^2+2\sqrt{\frac{5}{4}\underset{i\le p}{\text{max}}{\sigma }_{\mathit{\text{ii}}}}\sqrt{C_1^{\prime }{a}_T^2},$$

and

$$P(Z\le {\mathit{\text{Ca}}}_T)\ge 1-P(\underset{i\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}^2-{\sigma }_{\mathit{\text{ii}}}|>\underset{i\le p}{\text{max}}{\sigma }_{\mathit{\text{ii}}}/4)-P(\underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}{({\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}})}^2>C_1^{\prime }{a}_T^2).$$

By part (i) and (A.2), P(Z ≤ Ca_T) ≥ 1 − O(p⁻² + κ₁(p, T)).

(iii) By (i) and (ii), there exists C_r > 0, when C > C_r, the displayed inequalities in (i) and (ii) hold. Under the event $\{{\text{max}}_{i,j\le p}|\frac{1}{T}{\displaystyle {\sum }_{t=1}^T}{u}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}}|\le C\sqrt{(\text{log }p)/T}\}\cap \{{\text{max}}_{i,j\le p}|\frac{1}{T}{\displaystyle {\sum }_{t=1}^T}{\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}|\le {\mathit{\text{Ca}}}_T\}$, by the triangular inequality,

$$\begin{array}{cc}\underset{i,j\le p}{\text{max}}|{\hat{\sigma }}_{\mathit{\text{ij}}}-{\sigma }_{\mathit{\text{ij}}}|\hfill & \le \underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}}|+\underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}|\hfill \\ \hfill & \le C(\sqrt{\frac{\text{log }p}{T}}+a_T).\hfill \end{array}$$

Hence the desired result follows from part (i) and part (ii) of the lemma.

Q.E.D.

Lemma A.4. Under Assumptions 2.1, 2.2,

$$P(C_L\le \underset{ij}{\text{min}}{\hat{\theta }}_{\mathit{\text{ij}}}\le \underset{ij}{\text{max}}{\hat{\theta }}_{\mathit{\text{ij}}}\le C_U)\ge 1-O\left(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T)\right),$$

where

$$\begin{array}{c}{C}_L=\frac{1}{45}\underset{ij}{\text{min}}\text{var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})\hfill \\ C_U=3\underset{i\le p}{\text{max}}{\sigma }_{\mathit{\text{ii}}}+4\underset{\mathit{\text{ij}}}{\text{max}}\text{var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}).\hfill \end{array}$$

Proof. (i) Using Bernstein’s inequality and the same argument as in the proof of Lemma A.3(i), we have, there exists $C_r^{\prime }>0,\text{when }C>C_r^{\prime }$, and (log p)^6/γ−1 = o(T),

$$P\left(\underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}})}^2-\text{var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})|>C\sqrt{\frac{\text{log }p}{T}}\right)=O\left(\frac{1}{p^2}\right).$$

For some C > 0, under the event ${\cap }_{i=1}^4{A}_i$, where

$$\begin{array}{c}{A}_1=\{\underset{i,j\le p}{\text{max}}|{\sigma }_{\mathit{\text{ij}}}-{\hat{\sigma }}_{\mathit{\text{ij}}}|\le C(\sqrt{\frac{\text{log }p}{T}}+a_T)\}\hfill \\ A_2=\{\underset{i\le p,t\le T}{\text{max}}|{\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}}|\le \text{min}\{\frac{1}{2},\sqrt{{(20\underset{i}{\text{ max }}{\sigma }_{\mathit{\text{ii}}})}^{-1}\underset{ij}{\text{min}}\text{ var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})}\}\}\hfill \\ A_3=\{\underset{i\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{u}_{\mathit{\text{it}}}^2-{\sigma }_{\mathit{\text{ii}}}|\le C\sqrt{\frac{\text{log }p}{T}}\}\hfill \\ A_4=\{\underset{i,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}})}^2-\text{var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})|\le C\sqrt{\frac{\text{log }p}{T}}\},\hfill \end{array}$$

we have, for any i, j, by adding and subtracting terms,

$$\begin{array}{cc}{\hat{\theta }}_{i,j}\hfill & =\frac{1}{T}{\displaystyle \sum _t}{({\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-{\hat{\sigma }}_{\mathit{\text{ij}}})}^2\hfill \\ \hfill & \le \frac{2}{T}{\displaystyle \sum _t}{({\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}})}^2+2\underset{i,j}{\text{max}}{({\sigma }_{\mathit{\text{ij}}}-{\hat{\sigma }}_{\mathit{\text{ij}}})}^2\hfill \\ \hfill & \le \frac{4}{T}{\displaystyle \sum _t}{({\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}})}^2{\mathit{û}}_{\mathit{\text{jt}}}^2+\frac{4}{T}{\displaystyle \sum _t}{({\mathit{û}}_{\mathit{\text{jt}}}-u_{\mathit{\text{jt}}})}^2{u}_{\mathit{\text{it}}}^2+\frac{4}{T}{\displaystyle \sum _t}{(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}})}^2+O(\frac{\text{log }p}{T}+a_T^2)\hfill \\ \hfill & \le 4\underset{\mathit{\text{it}}}{\text{max}}|{\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}}{|}^2(\underset{i}{\text{max}}{\hat{\sigma }}_{\mathit{\text{ii}}}+\underset{i}{\text{max}}\frac{1}{T}{\displaystyle \sum _t}{u}_{\mathit{\text{it}}}^2)+4\text{var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})+O(\sqrt{\frac{\text{log }p}{T}}+\frac{\text{log }p}{T}+a_T^2)\hfill \\ \hfill & \le (2C\sqrt{\frac{\text{log }p}{T}}+{\mathit{\text{Ca}}}_T+2\underset{i}{\text{max}}{\sigma }_{\mathit{\text{ii}}})+4\text{var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})+o(1),\hfill \end{array}$$

where the O(.) and o(.) terms are uniformly in p an T. Hence under ${\cap }_{i=1}^4{A}_i$, for all large enough T, p, uniformly in i, j, we have

$${\hat{\theta }}_{i,j}\le 3\underset{i\le p}{\text{max}}{\sigma }_{\mathit{\text{ii}}}+4\underset{\mathit{\text{ij}}}{\text{max}}\text{ var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}).$$

Still by adding and subtracting terms, we obtain

$$\begin{array}{c}\frac{1}{T}{\displaystyle \sum _t}{(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\sigma }_{\mathit{\text{ij}}})}^2\hfill \\ \le \frac{4}{T}{\displaystyle \sum _t}{(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}-{\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}})}^2+\frac{4}{T}{\displaystyle \sum _t}{({\mathit{û}}_{\mathit{\text{it}}}{\mathit{û}}_{\mathit{\text{jt}}}-{\hat{\sigma }}_{\mathit{\text{ij}}})}^2+4{({\sigma }_{\mathit{\text{ij}}}-{\hat{\sigma }}_{\mathit{\text{ij}}})}^2\hfill \\ \le \frac{8}{T}{\displaystyle \sum _t}{u}_{\mathit{\text{it}}}^2{(u_{\mathit{\text{jt}}}-{\mathit{û}}_{\mathit{\text{jt}}})}^2+\frac{8}{T}{\displaystyle \sum _t}{\mathit{û}}_{\mathit{\text{jt}}}^2{(u_{\mathit{\text{it}}}-{\mathit{û}}_{\mathit{\text{it}}})}^2+4{\hat{\theta }}_{\mathit{\text{ij}}}+O(\frac{\text{log }p}{T}+a_T^2)\hfill \\ \le 8\underset{\mathit{\text{it}}}{\text{ max}}|{\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}}{|}^2(\underset{i}{\text{max}}{\hat{\sigma }}_{\mathit{\text{ii}}}+\underset{j}{\text{max}}\frac{1}{T}{\displaystyle \sum _t}{u}_{\mathit{\text{jt}}}^2)+4{\hat{\theta }}_{\mathit{\text{ij}}}+o(1).\hfill \end{array}$$

Under the event ${\cap }_{i=1}^4{A}_i$, we have

$$\begin{array}{cc}4{\hat{\theta }}_{\mathit{\text{ij}}}+o(1)\hfill & \ge \underset{\mathit{\text{ij}}}{\text{min}}\text{ var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}})-C\sqrt{\frac{\text{log }p}{T}}-8\underset{\mathit{\text{it}}}{\text{max}}|{\mathit{û}}_{\mathit{\text{it}}}-u_{\mathit{\text{it}}}{|}^2[2C\sqrt{\frac{\text{log }p}{T}}+{\mathit{\text{Ca}}}_T+2\underset{i}{\text{max}}{\sigma }_{\mathit{\text{ii}}}]\hfill \\ \hfill & \ge \frac{1}{10}\underset{\mathit{\text{ij}}}{\text{min}}\text{ var}(u_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}).\hfill \end{array}$$

Hence for all large T, p, uniformly in i, j, we have ${\hat{\theta }}_{\mathit{\text{ij}}}\ge \frac{1}{45}$ min_ij var(u_itu_jt).

Finally, by Lemma A.3 and Assumption 2.2,

$$P({\displaystyle {\cap }_{i=1}^4}{A}_i)\ge 1-O(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T)),$$

which completes the proof.

Q.E.D.

A.2. Proof of Theorem 2.1.

Proof. (i) For the operator norm, we have

$$\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert \le \underset{i\le p}{\text{max}}{\displaystyle \sum _{j=1}^p}|{\hat{\sigma }}_{\mathit{\text{ij}}}I(|{\hat{\sigma }}_{\mathit{\text{ij}}}|\ge {\omega }_T{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2})-{\sigma }_{\mathit{\text{ij}}}|$$

By Lemma A.3 (iii), there exists C₁ > 0 such that the event

$$A_1^{\prime }=\{\underset{i,j\le p}{\text{max}}|{\hat{\sigma }}_{\mathit{\text{ij}}}-{\sigma }_{\mathit{\text{ij}}}|\le C_1(\sqrt{\frac{\text{log }p}{T}}+a_T)\}$$

occurs with probability $P(A_1^{\prime })\ge 1-O(\frac{1}{p^2}+{\kappa }_1(p,T))$. Let C > 0 be such that $C\sqrt{C_L}>2C_1$, where C_L is defined in Lemma A.4. Let ${\omega }_T=C(\sqrt{\frac{\text{log }p}{T}}+a_T),b_T=C_1(\sqrt{\frac{\text{log }p}{T}}+a_T),\text{ then }\sqrt{C_L}{\omega }_T>2b_T$, and by Lemma A.4,

$$\begin{array}{cc}P(\underset{\mathit{\text{ij}}}{\text{min}}{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2}{\omega }_T>2b_T)\hfill & \ge P(\underset{\mathit{\text{ij}}}{\text{min}}{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2}>\sqrt{C_L})\hfill \\ \hfill & \ge 1-O\left(\frac{1}{p}+{\kappa }_1(p,T)+{\kappa }_2(p,T)\right).\hfill \end{array}$$

Define the following events

$$\begin{array}{c}{A}_2^{\prime }=\{\underset{\mathit{\text{ij}}}{\text{min}}{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2}{\omega }_T>2b_T\}\hfill \\ A_3^{\prime }=\{\underset{\mathit{\text{ij}}}{\text{max}}{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2}\le C_U^{1/2}\},\hfill \end{array}$$

where C_U is defined in Lemma A.4. Under ${\cap }_{i=1}^3{A}_i^{\prime }$, the event $|{\hat{\sigma }}_{\mathit{\text{ij}}}|\ge {\omega }_T{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2}$ implies |σ_ij| ≥ b_T, and the event $|{\hat{\sigma }}_{\mathit{\text{ij}}}|<{\omega }_T{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2}$ implies $|{\sigma }_{\mathit{\text{ij}}}|<b_T+\sqrt{C_U}{\omega }_T$. We thus have, uniformly in i ≤ p, under ${\cap }_{i=1}^3{A}_i^{\prime }$,

$$\begin{array}{cc}\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert \hfill & \le {\displaystyle \sum _{j=1}^p}|{\hat{\sigma }}_{\mathit{\text{ij}}}I(|{\hat{\sigma }}_{\mathit{\text{ij}}}|\ge {\omega }_T{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2})-{\sigma }_{\mathit{\text{ij}}}|\hfill \\ \hfill & \le {\displaystyle \sum _{j=1}^p}|{\hat{\sigma }}_{\mathit{\text{ij}}}-{\sigma }_{\mathit{\text{ij}}}|I(|{\hat{\sigma }}_{\mathit{\text{ij}}}|\ge {\omega }_T{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2})+{\displaystyle \sum _{j=1}^p}|{\sigma }_{\mathit{\text{ij}}}|I(|{\hat{\sigma }}_{\mathit{\text{ij}}}|<{\omega }_T{\hat{\theta }}_{\mathit{\text{ij}}}^{1/2})\hfill \\ \hfill & \le {\displaystyle \sum _{j=1}^p}|{\hat{\sigma }}_{\mathit{\text{ij}}}-{\sigma }_{\mathit{\text{ij}}}|I(|{\sigma }_{\mathit{\text{ij}}}|\ge b_T)+{\displaystyle \sum _{j=1}^p}|{\sigma }_{\mathit{\text{ij}}}|I(|{\sigma }_{\mathit{\text{ij}}}|<b_T+\sqrt{C_U}{\omega }_T)\hfill \\ \hfill & \le b_T{m}_T+(b_T+\sqrt{C_U}{\omega }_T)m_T\hfill \\ \hfill & \le (\sqrt{C_L}+\sqrt{C_U}){\omega }_T{m}_T.\hfill \end{array}$$

By Lemmas A.3(iii) and A.4, $P({\cap }_{i=1}^3{A}_i^{\prime })\ge 1-O(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T))$, which proves the result. Q.E.D.

(ii) By part (i) of the theorem, there exists some C > 0,

$$P(\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert >C{\omega }_T{m}_T)=O\left(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T)\right).$$

By Lemma A.1,

$$\begin{array}{cc}P\left({\lambda }_{\text{min}}({\hat{\mathbf{\Sigma }}}_u^{𝒯})\ge 0.5{\lambda }_{\text{min}}({\mathbf{\Sigma }}_u)\right)\hfill & \ge P(\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert \le 0.5{\lambda }_{\text{min}}({\mathbf{\Sigma }}_u))\hfill \\ \hfill & \ge 1-O(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T)).\hfill \end{array}$$

In addition, when ω_Tm_T = o(1),

$$\begin{array}{c}P(\Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}\Vert \le 2\Vert {\mathbf{\Sigma }}_u^{-1}\Vert C{\omega }_T{m}_T)\hfill \\ \ge P(\Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}\Vert \le 2\Vert {\mathbf{\Sigma }}_u^{-1}\Vert ·\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert ,\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert \le C{\omega }_T{m}_T)\hfill \\ \ge P(\Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}\Vert \le 2\Vert {\mathbf{\Sigma }}_u^{-1}\Vert ·\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert )-P(\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert >C{\omega }_T{m}_T)\hfill \\ \ge P(\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert \le 0.5{\lambda }_{\text{min}}({\mathbf{\Sigma }}_u))-O(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T))\hfill \\ \ge 1-O\left(\frac{1}{p^2}+{\kappa }_1(p,T)+{\kappa }_2(p,T)\right),\hfill \end{array}$$

where the third inequality follows from Lemma A.1 as well.

Q.E.D.

APPENDIX B: PROOFS FOR SECTION 3

B.1. Proof of Theorem 3.1.

Lemma B.1. There exists C₁ > 0 such that,

1. $$P\left(\underset{i,j\le K}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{it}}}{f}_{\mathit{\text{jt}}}-{\mathit{\text{E f}}}_{\mathit{\text{it}}}{f}_{\mathit{\text{jt}}}|>C_1\sqrt{\frac{\text{log }T}{T}}\right)=O\left(\frac{1}{T^2}\right),$$
2. $$P\left(\underset{k\le K,i\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{kt}}}{u}_{\mathit{\text{it}}}|>C_1\sqrt{\frac{\text{log }p}{T}}\right)=O\left(\frac{1}{p^2}\right).$$

Proof. (i) Let $Z_{\mathit{\text{ij}}}=\frac{1}{T}{\displaystyle {\sum }_{t=1}^T}(f_{\mathit{\text{it}}}{f}_{\mathit{\text{jt}}}-E{f}_{\mathit{\text{it}}}{f}_{\mathit{\text{jt}}})$. We bound max_ij |Z_ij| using Bernstein type inequality. Lemma A.2 implies that for any i and j ≤ K, f_itf_jt satisfies the exponential tail condition (3.3) with parameter r₃/3. Let $r_4^{-1}=3r_3^{-1}+r_2^{-1}$, where r₂ > 0 is the parameter in the strong mixing condition. By Assumption 3.3, r₄ < 1, and by the Bernstein inequality for weakly dependent data in Merlevède (2009, Theorem 1), there exist C_i > 0, i = 1, …, 5, for any s > 0

$$\underset{i,j}{\text{max}}P(|Z_{\mathit{\text{ij}}}|>s)\le T\text{ exp }\left(-\frac{{(\mathit{\text{T s}})}^{r_4}}{C_1}\right)+\text{exp }\left(-\frac{T^2{s}^2}{C_2(1+{\mathit{\text{TC}}}_3)}\right)+\text{exp }\left(-\frac{{(\mathit{\text{T s}})}^2}{C_{4}T}\text{exp }\left(\frac{{(\mathit{\text{T s}})}^{r_4(1-r_4)}}{C_5{(\text{log}\mathit{\text{T s}})}^{r_4}}\right)\right).$$ (B.1)

Using the Bonferroni inequality,

$$P(\underset{i\le K,j\le K}{\text{max}}|Z_{\mathit{\text{ij}}}|>s)\le K^2\underset{i,j}{\text{max}}P(|Z_{\mathit{\text{ij}}}|>s).$$

Let $s=C\sqrt{(\text{log }T)/T}$. For all large enough C, since K² = o(T),

$$\begin{array}{c}{\mathit{\text{TK}}}^2\text{ exp }\left(-\frac{{(\mathit{\text{T s}})}^{r_4}}{C_1}\right)+K^2\text{ exp }(-\frac{{(\mathit{\text{T s}})}^2}{C_{4}T}\text{exp }\left(\frac{{(\mathit{\text{T s}})}^{r_4(1-r_4)}}{C_5{(\text{log}\mathit{\text{T s}})}^{r_4}}\right))=o\left(\frac{1}{T^2}\right),\hfill \\ \hfill K^2\text{ exp }\left(-\frac{T^2{s}^2}{C_2(1+{\mathit{\text{TC}}}_3)}\right)=O\left(\frac{1}{T^2}\right).\hfill \end{array}$$

This proves part (i).

(ii) By Lemma A.2, and Assumptions 2.1(iii) and 3.3(ii), $Z_{\mathit{\text{ki}},t}^{\prime }\equiv f_{\mathit{\text{kt}}}{u}_{\mathit{\text{it}}}$ satisfies the exponential tail condition (2.6) for the tail parameter 2r₁r₃/(3r₁ + 3r₃), as well as the strong mixing condition with parameter r₂. Hence again we can apply the Bernstein inequality for weakly dependent data in Merlevède (2009, Theorem 1) and the Bonferroni’s method on $Z_{\mathit{\text{ki}},t}^{\prime }$ similar to (B.1) with the parameter ${\gamma }_2^{-1}=1.5r_1^{-1}+1.5r_3^{-1}+r_2^{-1}$. It follows from $3r_1^{-1}+r_2^{-1}>1\text{ and }3r_3^{-1}+r_2^{-1}>1$ that γ₂ < 1. Thus when $s=C\sqrt{(\text{log }p)/T}$ for large enough C, the term

$$\mathit{\text{pK}}\text{exp }\left(-\frac{T^2{s}^2}{C_2(1+{\mathit{\text{TC}}}_3)}\right)\le p^{-2},$$

and the rest terms on the right hand side of the inequality, multiplied by pK are of order o(p⁻²). Hence when (log p)^2/γ₂−1 = o(T) (which is implied by the Theorem’s assumption), and K = o(p), there exists C′ > 0,

$$P\left(\underset{k\le K,i\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{kt}}}{u}_{\mathit{\text{it}}}|>C\prime \sqrt{\frac{\text{log }p}{T}}\right)=O\left(\frac{1}{p^2}\right).$$ (B.2)

Q.E.D.

Proof of Lemma 3.1

1. Since $K\sqrt{\text{log }T}=o(\sqrt{T}),\text{ and }{\lambda }_{\text{min}}(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime })$ is bounded away from zero, for large enough T, by Lemma B.1(i),

   $$\begin{array}{cc}\hfill & P(\Vert \frac{1}{T}\mathbf{\text{XX}}\prime -E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime }\Vert \le 0.5{\lambda }_{\text{min}}(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime }))\hfill \\ \ge \hfill & P\left(K\underset{i\le K,j\le K}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{it}}}{f}_{\mathit{\text{jt}}}-{\mathit{\text{E f}}}_{\mathit{\text{it}}}{f}_{\mathit{\text{jt}}}|\le 0.5{\lambda }_{\text{min}}(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime })\right)\hfill \\ \ge \hfill & 1-O\left(\frac{1}{T^2}\right).\hfill \end{array}$$ (B.3)
   Hence by Lemma A.1,

   $$P({\lambda }_{\text{min}}(T^{-1}\mathbf{\text{XX}}\prime )\ge 0.5{\lambda }_{\text{min}}(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime }))\ge 1-O\left(\frac{1}{T^2}\right).$$ (B.4)
   As b̂_i − b_i = (XX′)⁻¹Xu_i, we have ${\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert }^2={\mathbf{u}}_i^{\prime }\mathbf{X}\prime {(\mathbf{\text{XX}}\prime )}^{-2}{\mathbf{\text{Xu}}}_i$. For C′ > 0 such that (B.2) holds, under the event

   $$A\equiv \{\underset{k\le K,i\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{kt}}}{u}_{\mathit{\text{it}}}|\le C\prime \sqrt{\frac{\text{log }p}{T}}\}\cap \{{\lambda }_{\text{min}}(T^{-1}\mathbf{\text{XX}}\prime )\ge 0.5{\lambda }_{\text{min}}(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime })\},$$

   we have

   $$\begin{array}{cc}{\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert }^2\hfill & \le \frac{4}{{\lambda }_{\text{min}}{(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime })}^2}{\displaystyle \sum _{k=1}^K}{(\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{kt}}}{u}_{\mathit{\text{it}}})}^2\hfill \\ \hfill & \le \frac{4K}{{\lambda }_{\text{min}}{(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime })}^2}\underset{k\le K,i\le p}{\text{max}}{(\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{kt}}}{u}_{\mathit{\text{it}}})}^2\hfill \\ \hfill & \le \frac{4\mathit{\text{KC}}{\prime }^2\text{log }p}{{\lambda }_{\text{min}}{(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime })}^{2}T}.\hfill \end{array}$$

   The desired result then follows from that $P(A)\ge 1-O(\frac{1}{T^2}+\frac{1}{p^2})$.

2. For C > max_i≤K ${\mathit{\text{E f}}}_{\mathit{\text{it}}}^2$, we have, by Lemma B.1(i),

   $$P(\frac{1}{T}{\displaystyle \sum _t}{\Vert {\mathbf{f}}_t\Vert }^2>\mathit{\text{CK}})\le P\left(K\underset{k\le K}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{kt}}}^2-{\mathit{\text{E f}}}_{\mathit{\text{kt}}}^2|+K\underset{k\le K}{\text{max}}{\mathit{\text{ Ef}}}_{\mathit{\text{kt}}}^2>\mathit{\text{CK}}\right)=O\left(\frac{1}{T^2}\right).$$
   The result then follows from

   $$\underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}|u_{\mathit{\text{it}}}-{\mathit{û}}_{\mathit{\text{it}}}{|}^2\le \underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _t}{\Vert {\mathbf{f}}_t\Vert }^2{\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert }^2$$

   and part(i).
3. By Assumption 3.3, for any s > 0,

   $$\begin{array}{cc}P(\underset{t\le T}{\text{max}}\Vert {\mathbf{f}}_t\Vert >s)\hfill & \le \mathit{\text{TP}}(\Vert {\mathbf{f}}_t\Vert >s)\le \mathit{\text{TK }}\underset{k\le K}{\text{max }}P(f_{\mathit{\text{kt}}}^2>s^2/K)\hfill \\ \hfill & \le \mathit{\text{TK}}\text{exp }(-{\left(\frac{s}{b_2\sqrt{K}}\right)}^{r_3}).\hfill \end{array}$$
   When $s\ge C\sqrt{K}{(\text{log }T)}^{1/r_3}$ for large enough C, i.e., $C^{r_3}>4b_2^{r_3}$,

   $$P(\underset{t\le T}{\text{max}}\Vert {\mathbf{f}}_t\Vert >C\sqrt{K}{(\text{log }T)}^{1/r_3})\le T^{-2}.$$
   The result then follows from

   $$\underset{t\le T,i\le p}{\text{max}}|u_{\mathit{\text{it}}}-{\mathit{û}}_{\mathit{\text{it}}}|=\underset{t\le T,i\le p}{\text{max}}|({\hat{\mathbf{b}}}_i-{\mathbf{b}}_i)\prime {\mathbf{f}}_t|\le \underset{i}{\text{max}}\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert \underset{t}{\text{max}}\Vert {\mathbf{f}}_t\Vert ,$$

   and Lemma 3.1(i). Q.E.D.

Proof of Theorem 3.1 Theorem 3.1 follows immediately from Theorem 2.1 and Lemma 3.1. Q.E.D.

B.2. Proof of Theorem 3.2 Part (i). Define

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbf{D}}_T=\widehat{\text{cov}}({\mathbf{f}}_t)-\text{cov}({\mathbf{f}}_t),\hfill & \hfill {\mathbf{C}}_T=\hat{\mathbf{B}}-\mathbf{B},\hfill \end{array}\hfill \\ \hfill \mathbf{E}=({\mathbf{u}}_1,\dots ,{\mathbf{u}}_T).\hfill \end{array}$$

We have,

$${\Vert {\hat{\mathbf{\Sigma }}}^{𝒯}-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma }}^2\le 4{\Vert {\mathbf{\text{BD}}}_T\mathbf{B}\prime \Vert }_{\mathrm{\Sigma }}^2+24{\Vert \mathbf{B}\widehat{\text{cov}}(\mathbf{f}){\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2+16{\Vert {\mathbf{C}}_T\widehat{\text{cov}}(\mathbf{f}){\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2+2{\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert }_{\mathrm{\Sigma }}^2.$$ (B.5)

We bound the terms on the right hand side in the following lemmas.

Lemma B.2. There exists C > 0, such that

1. $$P\left({\Vert {\mathbf{D}}_T\Vert }_F^2>\frac{{\mathit{\text{CK}}}^2\text{log }T}{T}\right)=O(T^{-2});$$
2. $$P\left({\Vert {\mathbf{C}}_T\Vert }_F^2>\frac{\mathit{\text{CKp}}\text{log }p}{T}\right)=O(T^{-2}+p^{-2}).$$

Proof. (i) Similar to the proof of Lemma B.1(i), it can be shown that there exists C₁ > 0,

$$P\left(\underset{i\le K}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{it}}}-{\mathit{\text{E f}}}_{\mathit{\text{it}}}|>C_1\sqrt{\frac{\text{log }T}{T}}\right)=O(T^{-2}).$$

Hence sup_K max_i≤K E|f_it| < ∞ implies that there exists C > 0 such that

$$P\left(\underset{i,j\le K}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{it}}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{jt}}}-{\mathit{\text{E f}}}_{\mathit{\text{it}}}{\mathit{\text{E f}}}_{\mathit{\text{jt}}}|>C\sqrt{\frac{\text{log }T}{T}}\right)=O(T^{-2}).$$

The result then follows from Lemma B.1(i) and that

$${\Vert {\mathbf{D}}_T\Vert }_F^2\le K^2\left(\underset{i,j\le K}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{it}}}{f}_{\mathit{\text{jt}}}-{\mathit{\text{E f}}}_{\mathit{\text{it}}}{f}_{\mathit{\text{jt}}}{|}^2+\underset{i,j\le K}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{it}}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{jt}}}-{\mathit{\text{E f}}}_{\mathit{\text{it}}}{\mathit{\text{E f}}}_{\mathit{\text{jt}}}{|}^2\right).$$

(ii) We have C_T = EX′(XX′)⁻¹. By Lemma B.1 (ii), there exists C′ > 0 such that

$$P\left(\underset{k,i}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{kt}}}{u}_{\mathit{\text{it}}}|>C\prime \sqrt{\frac{\text{log }p}{T}}\right)=O(p^{-2}).$$

Under the event

$$A=\{\underset{k,i}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{kt}}}{u}_{\mathit{\text{it}}}|\le C\prime \sqrt{\frac{\text{log }p}{T}}\}\cap \{{\lambda }_{\text{min}}(T^{-1}\mathbf{\text{XX}}\prime )\ge 0.5{\lambda }_{\text{min}}(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime })\},$$

${\Vert {\mathbf{C}}_T\Vert }_F^2\le 4{\lambda }_{\text{min}}^{-2}(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime }){C\prime }^{2}pK(\text{log }p)/T$, which proves the result since ${\lambda }_{\text{min}}(E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime })$ is bounded away from zero and P(A) ≥ 1 − O (T⁻² + p⁻²) due to (B.4).

Q.E.D.

Lemma B.3. There exists C > 0 such that

1. $$P\left({\Vert {\mathbf{\text{BD}}}_T\mathbf{B}\prime \Vert }_{\mathrm{\Sigma }}^2+{\Vert \mathbf{B}\widehat{\text{cov}}({\mathbf{f}}_t){\mathbf{C}}_T^{\prime }\Vert }_{\mathrm{\Sigma }}^2>\frac{\mathit{\text{CK}}\text{log }p}{T}+\frac{{\mathit{\text{CK}}}^2\text{log }T}{\mathit{\text{Tp}}}\right)=O(T^{-2}+p^{-2});$$
2. $$P\left({\Vert {\mathbf{C}}_T\widehat{\text{cov}}(\mathbf{f}){\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2>\frac{{\mathit{\text{CpK}}}^2{(\text{log }p)}^2}{T^2}\right)=O(T^{-2}+p^{-2}).$$

Proof. (i) The same argument in Fan, Fan and Lv (2008), proof of Theorem 2 implies that

$$\Vert \mathbf{B}\prime {\mathbf{\Sigma }}^{-1}\mathbf{B}\Vert \le 2\Vert \text{cov}{({\mathbf{f}}_t)}^{-1}\Vert =O(1).$$

Hence

$$\begin{array}{cc}{\Vert {\mathbf{\text{BD}}}_T\mathbf{B}\prime \Vert }_{\mathrm{\Sigma }}^2\hfill & =p^{-1}\text{tr}({\mathbf{\Sigma }}^{-1/2}{\mathbf{\text{BD}}}_T\mathbf{B}\prime {\mathbf{\Sigma }}^{-1}{\mathbf{\text{BD}}}_T\mathbf{B}\prime {\mathbf{\Sigma }}^{-1/2})\hfill \\ \hfill & =p^{-1}\text{tr}({\mathbf{D}}_T\mathbf{B}\prime {\mathbf{\Sigma }}^{-1}{\mathbf{\text{BD}}}_T\mathbf{B}\prime {\mathbf{\Sigma }}^{-1}\mathbf{B})\hfill \\ \hfill & \le p^{-1}{\Vert {\mathbf{D}}_T\mathbf{B}\prime {\mathbf{\Sigma }}^{-1}\mathbf{B}\Vert }_F^2\hfill \\ \hfill & \le O(p^{-1}){\Vert {\mathbf{D}}_T\Vert }_F^2.\hfill \end{array}$$ (B.6)

On the other hand,

$${\Vert \mathbf{B}\widehat{\text{cov}}(\mathbf{f}){\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2\le 8T^{-2}{\Vert \mathbf{\text{BXX}}\prime {\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2+8T^{-4}{\Vert \mathbf{\text{BX}}\mathbf{11}\prime \mathbf{X}\prime {\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2.$$ (B.7)

Respectively,

$${\begin{array}{cc}\hfill {\Vert \mathbf{\text{BXX}}\prime {\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2& \le p^{-1}{\Vert \mathbf{\text{XX}}\prime {\mathbf{C}}_T^{\prime }{\mathbf{\Sigma }}^{-1}\Vert }_F{\Vert {\mathbf{C}}_T\mathbf{\text{XX}}\prime \mathbf{B}\prime {\mathbf{\Sigma }}^{-1}\mathbf{B}\Vert }_F\hfill \\ \hfill {\Vert \mathbf{\text{BX}}\mathbf{11}\prime \mathbf{X}\prime {\mathbf{C}}_T^{\prime }\Vert }_{\mathrm{\Sigma }}^2& \le p^{-1}{\Vert \mathbf{X}\mathbf{11}\prime \mathbf{X}\prime {\mathbf{C}}_T^{\prime }{\mathbf{\Sigma }}^{-1}\Vert }_F\Vert {\mathbf{C}}_T\mathbf{X}\mathbf{11}\prime \mathbf{X}\prime \mathbf{B}\prime {\mathbf{\Sigma }}^{-1}\mathbf{B}\Vert \hfill \end{array}}_F.$$ (B.8)

By Lemma B.1(i), and $E{\mathbf{f}}_t{\mathbf{f}}_t^{\prime }<\mathrm{\infty }$, P(‖XX′‖ > TC) = O(T⁻²) for some C > 0. Hence, Lemma B.2 (ii) implies

$$P({\Vert \mathbf{\text{BXX}}\prime {\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2>C\prime \mathit{\text{TK}}\text{log }p)=O(T^{-2}+p^{-2})$$ (B.9)

for some C′ > 0. In addition, the eigenvalues of $\widehat{\text{cov}}({\mathbf{f}}_t)=T^{-1}\mathbf{\text{XX}}\prime -T^{-2}\mathbf{X}\mathbf{11}\prime \mathbf{X}\prime$ are all bounded away from both zero and infinity with probability at least 1 − O(T⁻²) (implied by Lemmas B.1(i), A.1, and Assumption 3.4). Hence for some C₁ > 0, with probability ast least 1 − O(T⁻²),

$$\begin{array}{cc}\hfill \Vert \mathbf{X}\mathbf{11}\prime \mathbf{X}\prime \Vert & \le \Vert T\mathbf{\text{XX}}\prime \Vert \le T^2{C}_1,\hfill \\ \hfill {\Vert \mathbf{\text{BX}}\mathbf{11}\prime \mathbf{X}\prime {\mathbf{C}}_T^{\prime }\Vert }_{\mathrm{\Sigma }}^2& \le O(p^{-1}){\Vert \mathbf{X}\mathbf{11}\prime \mathbf{X}\prime \Vert }^2{\Vert {\mathbf{C}}_T\Vert }_F^2.\hfill \end{array}$$ (B.10)

The result then follows from the combination of (B.6)–(B.10), and Lemma B.2.

(ii) Straightforward calculation yields:

$$\begin{array}{cc}p{\Vert {\mathbf{C}}_T\widehat{\text{cov}}(\mathbf{f}){\mathbf{C}}_T\prime \Vert }_{\mathrm{\Sigma }}^2\hfill & =\text{tr}({\mathbf{C}}_T\widehat{\text{cov}}(\mathbf{f}){\mathbf{C}}_T\prime {\mathbf{\Sigma }}^{-1}{\mathbf{C}}_T\widehat{\text{cov}}(\mathbf{f}){\mathbf{C}}_T\prime {\mathbf{\Sigma }}^{-1})\hfill \\ \hfill & \le {\Vert {\mathbf{C}}_T\widehat{\text{cov}}(\mathbf{f}){\mathbf{C}}_T\prime {\mathbf{\Sigma }}^{-1}\Vert }_F^2\hfill \\ \hfill & \le {\lambda }_{\text{max}}^2({\mathbf{\Sigma }}^{-1}){\lambda }_{\text{max}}^2(\widehat{\text{cov}}({\mathbf{f}}_t)){\Vert {\mathbf{C}}_T\Vert }_F^4.\hfill \end{array}$$

Since ‖cov(f_t)‖ is bounded, by Lemma B.1(i), ${\lambda }_{\text{max}}^2(\widehat{\text{cov}}({\mathbf{f}}_t))$ is bounded with probability at least 1 − O(T⁻²). The result again follows from Lemma B.2(ii).

Proof of Theorem 3.2 Part (i)

1. We have

   $$\begin{array}{cc}{\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert }_{\mathrm{\Sigma }}\hfill & =p^{-1/2}{\Vert {\mathbf{\Sigma }}^{-1/2}({\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u){\mathbf{\Sigma }}^{-1/2}\Vert }_F\hfill \\ \hfill & \le \Vert {\mathbf{\Sigma }}^{-1/2}({\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u){\mathbf{\Sigma }}^{-1/2}\Vert \hfill \\ \hfill & \le \Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert ·{\lambda }_{\text{max}}({\mathbf{\Sigma }}^{-1}).\hfill \end{array}$$ (B.11)
   Therefore, (B.5), (B.11), Theorem 3.1 and Lemmas B.2, B.3 yield the result, with the fact that (assuming log T = o(p))

   $$\frac{K\text{ log }p}{T}+\frac{K^2\text{ log }T}{\mathit{\text{Tp}}}+\frac{p{K}^2{(\text{log }p)}^2}{T^2}+\frac{m_T^2{K}^2\text{ log }p}{T}=O(\frac{p{K}^2{(\text{log }p)}^2}{T^2}+\frac{m_T^2{K}^2\text{ log }p}{T}).$$
2. For the infinity norm, it is straightforward to find that

   $${\Vert {\hat{\mathbf{\Sigma }}}^{𝒯}-\mathbf{\Sigma }\Vert }_{\mathrm{\infty }}\le {\Vert 2{\mathbf{C}}_T\text{cov}({\mathbf{f}}_t)\mathbf{B}\prime \Vert }_{\mathrm{\infty }}+{\Vert {\mathbf{\text{BD}}}_T\mathbf{B}\prime \Vert }_{\mathrm{\infty }}+{\Vert {\mathbf{C}}_T\text{cov}({\mathbf{f}}_t){\mathbf{C}}_T^{\prime }\Vert }_{\mathrm{\infty }}+{\Vert 2{\mathbf{\text{BD}}}_T{\mathbf{C}}_T^{\prime }\Vert }_{\mathrm{\infty }}+{\Vert {\mathbf{C}}_T{\mathbf{D}}_T{\mathbf{C}}_T^{\prime }\Vert }_{\mathrm{\infty }}+{\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert }_{\mathrm{\infty }}.$$ (B.12)

By Assumption, both ‖B‖_∞ and ‖cov(f_t)‖_∞ are bounded uniformly in (p, K, T). In addition, let e_i be a p-dimensional column vector whose ith component is one with the remaining components being zeros. Then under the events ${\Vert {\mathbf{D}}_T\Vert }_{\mathrm{\infty }}\le C\sqrt{(\text{log }T)/T},{\text{max}}_{i\le K,j\le p}|\frac{1}{T}{\displaystyle {\sum }_{t=1}^T}{f}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}|\le C\sqrt{(\text{log }p)/T},\Vert \frac{1}{T}\mathbf{\text{XX}}\prime \Vert \le C,{\text{and max}}_{i\le p}\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert \le C\sqrt{K(\text{log }p)/T}$, we have, for some C′ > 0,

$$\begin{array}{cc}{\Vert 2{\mathbf{C}}_T^{\prime }\text{cov}({\mathbf{f}}_t)\mathbf{B}\Vert }_{\mathrm{\infty }}\hfill & \le 2\underset{i,j\le p}{\text{max}}\Vert {\mathbf{e}}_i^{\prime }{\mathbf{C}}_T^{\prime }\text{cov}({\mathbf{f}}_t){\mathbf{\text{Be}}}_j\Vert \hfill \\ \hfill & \le 2\underset{i\le p}{\text{max}}\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert \Vert \text{cov}({\mathbf{f}}_t)\Vert \underset{j\le p}{\text{max}}\Vert {\mathbf{b}}_j\Vert \hfill \\ \hfill & \le C\prime K\sqrt{\frac{\text{log }p}{T}},\hfill \end{array}$$ (B.13)

$$\begin{array}{cc}{\Vert {\mathbf{C}}_T\Vert }_{\mathrm{\infty }}\hfill & =\underset{i,j\le p}{\text{max}}|{\mathbf{e}}_i^{\prime }\frac{1}{T}\mathbf{\text{EX}}\prime {(\frac{1}{T}\mathbf{\text{XX}}\prime )}^{-1}{\mathbf{e}}_j|\le \underset{i\le p}{\text{max}}\Vert {\mathbf{e}}_i^{\prime }\frac{1}{T}\mathbf{\text{EX}}\prime \Vert ·\Vert {(\frac{1}{T}\mathbf{\text{XX}}\prime )}^{-1}\Vert \hfill \\ \hfill & \le \sqrt{K}\underset{i\le K,j\le p}{\text{max}}|\frac{1}{T}{\displaystyle \sum _{t=1}^T}{f}_{\mathit{\text{it}}}{u}_{\mathit{\text{jt}}}|·\Vert {(\frac{1}{T}\mathbf{\text{XX}}\prime )}^{-1}\Vert \hfill \\ \hfill & \le C\prime \sqrt{K(\text{log }p)/T},\hfill \end{array}$$ (B.14)

$${\Vert \mathbf{B}\prime {\mathbf{D}}_T\mathbf{B}\Vert }_{\mathrm{\infty }}\le K^2{\Vert \mathbf{B}\Vert }_{\mathrm{\infty }}^2{\Vert {\mathbf{D}}_T\Vert }_F\le C\prime K^2\sqrt{\frac{\text{log }T}{T}},$$ (B.15)

$$\begin{array}{cc}{\Vert {\mathbf{C}}_T^{\prime }\text{cov}({\mathbf{f}}_t){\mathbf{C}}_T\Vert }_{\mathrm{\infty }}\hfill & \le \underset{i,j\le p}{\mathbf{\text{max}}}\Vert {\mathbf{e}}_i^{\prime }{\mathbf{C}}_T^{\prime }\text{cov}({\mathbf{f}}_t){\mathbf{C}}_T{\mathbf{e}}_j\Vert \hfill \\ \hfill & \le \underset{i\le p}{\text{max}}{\Vert {\mathbf{e}}_i^{\prime }{\mathbf{C}}_T^{\prime }\Vert }^2\Vert \text{cov}({\mathbf{f}}_t)\Vert \le \frac{C\prime K^2\text{log }p}{T},\hfill \end{array}$$ (B.16)

$$\begin{array}{cc}{\Vert 2\mathbf{B}\prime {\mathbf{D}}_T{\mathbf{C}}_T\Vert }_{\mathrm{\infty }}\hfill & \le 2K^2{\Vert \mathbf{B}\Vert }_{\mathrm{\infty }}{\Vert {\mathbf{D}}_T\Vert }_{\mathrm{\infty }}{\Vert {\mathbf{C}}_T\Vert }_{\mathrm{\infty }}\hfill \\ \hfill & =o\left(K^2\sqrt{\frac{\text{log }T}{T}}\right),\hfill \end{array}$$ (B.17)

and

$${\Vert {\mathbf{C}}_T^{\prime }{\mathbf{D}}_T{\mathbf{C}}_T\Vert }_{\mathrm{\infty }}\le K^2{\Vert {\mathbf{D}}_T\Vert }_{\mathrm{\infty }}{\Vert {\mathbf{C}}_T\Vert }_{\mathrm{\infty }}^2=o\left(K^2\sqrt{\frac{\text{log }T}{T}}\right).$$ (B.18)

Moreover, the (i, j)th entry of ${\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u$ is given by

$${\hat{\sigma }}_{\mathit{\text{ij}}}I(|{\hat{\sigma }}_{\mathit{\text{ij}}}|\ge {\omega }_T\sqrt{{\hat{\theta }}_{\mathit{\text{ij}}}})-{\sigma }_{\mathit{\text{ij}}}=\{\begin{array}{cc}-{\sigma }_{\mathit{\text{ij}}},\hfill & \text{if}|{\hat{\sigma }}_{\mathit{\text{ij}}}|<{\omega }_T\sqrt{{\hat{\theta }}_{\mathit{\text{ij}}}}\hfill \\ {\hat{\sigma }}_{\mathit{\text{ij}}}-{\sigma }_{\mathit{\text{ij}}},\hfill & \mathrm{o}.\mathrm{w}.\hfill \end{array}$$

Hence ${\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert }_{\mathrm{\infty }}\le {\text{max}}_{i,j\le p}|{\sigma }_{\mathit{\text{ij}}}-{\hat{\sigma }}_{\mathit{\text{ij}}}|+{\omega }_T{\text{max}}_{i,j\le p}\sqrt{{\hat{\theta }}_{\mathit{\text{ij}}}}$, which implies that with probability at least 1 − O(p⁻² + T⁻²),

$${\Vert {\hat{\mathbf{\Sigma }}}_u^{𝒯}-{\mathbf{\Sigma }}_u\Vert }_{\mathrm{\infty }}\le C\prime K\sqrt{\frac{\text{log }p}{T}}.$$ (B.19)

The result then follows from the combination of (B.12)–(B.19), (B.4), and Lemmas 3.1,B.1.

Q.E.D.

B.3. Proof of Theorem 3.2 Part (ii). We first prove two technical lemmas to be used below.

Lemma B.4. (i) ${\lambda }_{\text{min}}(\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B})\ge \mathit{\text{cp}}$ for some c > 0.

(ii) $\Vert {[\text{cov}{(\mathbf{f})}^{-1}+\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B}]}^{-1}\Vert =O(p^{-1})$.

Proof. (i) We have

$${\lambda }_{\text{min}}(\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B})\ge {\lambda }_{\text{min}}({\mathbf{\Sigma }}_u^{-1}){\lambda }_{\text{min}}(\mathbf{B}\prime \mathbf{B}).$$

It then follows from Assumption 3.5 that λ_min(B′B) > cp for some c > 0 and all large p. The result follows since ‖Σ_u‖ is bounded away from infinity.

(ii) It follows immediately from

$${\lambda }_{\text{min}}(\text{cov}{({\mathbf{f}}_t)}^{-1}+\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B})\ge {\lambda }_{\text{min}}(\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B}).$$

Q.E.D.

Lemma B.5. There exists C > 0 such that,

1. $$P(\Vert \hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}-\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B}\Vert >{\mathit{\text{Cpm}}}_{T}K\sqrt{\frac{\text{log }p}{T}})=O(\frac{1}{p^2}+\frac{1}{T^2});$$
2. $$P(\Vert {[\widehat{\text{cov}}{(\mathbf{f})}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}\Vert >\frac{C}{p})=O(\frac{1}{p^2}+\frac{1}{T^2});$$
3. for $G={[\widehat{\text{cov}}{(\mathbf{f})}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}$,

   $$P(\Vert \hat{\mathbf{B}}G\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\Vert >C)=O(\frac{1}{p^2}+\frac{1}{T^2}).$$

Proof. (i) Let $H=\Vert \hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}-\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B}\Vert$.

$$H\le 2\Vert {\mathbf{C}}_T^{\prime }{\mathbf{\Sigma }}_u^{-1}\mathbf{B}\Vert +2\Vert {\mathbf{C}}_T^{\prime }({({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1})\mathbf{B}\Vert +\Vert \mathbf{B}″({({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1})\mathbf{B}\Vert +\Vert {\mathbf{C}}_T^{\prime }{\mathbf{\Sigma }}_u^{-1}{\mathbf{C}}_T\Vert +\Vert {\mathbf{C}}_T^{\prime }({({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}){\mathbf{C}}_T\Vert .$$

The same argument of Fan, Fan and Lv (2008) (eq. 14) implies that ${\Vert \mathbf{B}\Vert }_F=O(\sqrt{p})$. Therefore, by Theorem 3.1 and Lemma B.2(ii), it is straightforward to verify the result.

(ii) Since ‖D_T ‖_F ≥ ‖D_T‖, according to Lemma B.2(i), there exists C′ > 0 such that with probability ast least 1 − O(T⁻²), $\Vert {\mathbf{D}}_T\Vert <C\prime K\sqrt{(\text{log }T)/T}$. Thus by Lemma A.1, for some C″ > 0,

$$P(\Vert \widehat{\text{cov}}{({\mathbf{f}}_t)}^{-1}-\text{cov}{({\mathbf{f}}_t)}^{-1}\Vert <C″\Vert {\mathbf{D}}_T\Vert )\ge P(\Vert {\mathbf{D}}_T\Vert <C\prime K\sqrt{\frac{\text{log }T}{T}})\ge 1-O(T^{-2}),$$

which implies

$$P(\Vert \widehat{\text{cov}}{({\mathbf{f}}_t)}^{-1}-\text{cov}{({\mathbf{f}}_t)}^{-1}\Vert <C″C\prime K\sqrt{\frac{\text{log }T}{T}})\ge 1-O(T^{-2}).$$ (B.20)

Now let $\hat{\mathbf{A}}=\widehat{\text{cov}}{({\mathbf{f}}_t)}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}},\text{and }\mathbf{A}=\text{cov}{({\mathbf{f}}_t)}^{-1}+\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B}$. Then part (i) and (B.20) imply

$$P(\Vert \hat{\mathbf{A}}-\mathbf{A}\Vert <C″C\prime K\sqrt{\frac{\text{log }T}{T}}+{\mathit{\text{Cpm}}}_{T}K\sqrt{\frac{\text{log }p}{T}})\ge 1-O(\frac{1}{p^2}+\frac{1}{T^2}).$$ (B.21)

In addition, $m_{T}K\sqrt{(\text{log }p)/T}=o(1)$. Hence by Lemmas A.1, B.4(ii), for some C > 0,

$$P({\lambda }_{\text{min}}(\hat{\mathbf{A}})\ge Cp)\ge P(\Vert \hat{\mathbf{A}}-\mathbf{A}\Vert <Cp)\ge 1-O(\frac{1}{p^2}+\frac{1}{T^2}),$$

which implies the desired result.

(iii) By the triangular inequality, ${\Vert \hat{\mathbf{B}}\Vert }_F\le {\Vert {\mathbf{C}}_T\Vert }_F+O(\sqrt{p})$. Hence Lemma B.2(ii) implies, for some C > 0,

$$P({\Vert \hat{\mathbf{B}}\Vert }_F\le C\sqrt{p})\ge 1-O(T^{-2}+p^{-2}).$$ (B.22)

In addition, since $\Vert {\mathbf{\Sigma }}_u^{-1}\Vert$ is bounded, it then follows from Theorem 3.1 that $\Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\Vert$ is bounded with probability at least 1 − O(p⁻²+T⁻²). The result then follows from the fact that

$$P(\Vert G\Vert >{\mathit{\text{Cp}}}^{-1})=O(\frac{1}{p^2}+\frac{1}{T^2}),$$

which is shown in part (ii).

Q.E.D.

To complete the proof of Theorem 3.2 Part (ii), we follow similar lines of proof as in Fan, Fan and Lv (2008). Using the Sherman-Morrison-Woodbury formula, we have

$$\Vert {({\hat{\mathbf{\Sigma }}}^{𝒯})}^{-1}-{\mathbf{\Sigma }}^{-1}\Vert =\Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}\Vert +\Vert ({({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1})\hat{\mathbf{B}}{[\widehat{\text{cov}}{(\mathbf{f})}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\Vert +\Vert ({({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1})\hat{\mathbf{B}}{[\widehat{\text{cov}}{(\mathbf{f})}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}\hat{\mathbf{B}}\prime {\mathbf{\Sigma }}_u^{-1}\Vert +\Vert {\mathbf{\Sigma }}_u^{-1}(\hat{\mathbf{B}}-\mathbf{B}){[\widehat{\text{cov}}{(\mathbf{f})}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}\hat{\mathbf{B}}\prime {\mathbf{\Sigma }}_u^{-1}\Vert +\Vert {\mathbf{\Sigma }}_u^{-1}(\hat{\mathbf{B}}-\mathbf{B}){[\widehat{\text{cov}}{(\mathbf{f})}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\Vert +\Vert {\mathbf{\Sigma }}_u^{-1}\mathbf{B}({[\widehat{\text{cov}}{(\mathbf{f})}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}-{[\text{cov}{(\mathbf{f})}^{-1}+\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\mathbf{B}]}^{-1})\mathbf{B}\prime {\mathbf{\Sigma }}_u^{-1}\Vert =L_1+L_2+L_3+L_4+L_5+L_6.$$ (B.23)

The bound of L₁ is given in Theorem 3.1.

For $G={[\widehat{\text{cov}}{(\mathbf{f})}^{-1}+\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\hat{\mathbf{B}}]}^{-1}$, then

$$L_2\le \Vert {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}-{\mathbf{\Sigma }}_u^{-1}\Vert ·\Vert \hat{\mathbf{B}}G\hat{\mathbf{B}}\prime {({\hat{\mathbf{\Sigma }}}_u^{𝒯})}^{-1}\Vert .$$ (B.24)

It follows from Theorem 3.1 and Lemma B.5(iii) that

$$P(L_2\le {\mathit{\text{Cm}}}_{T}K\sqrt{\frac{\text{log }p}{T}})\ge 1-O(\frac{1}{p^2}+\frac{1}{T^2}).$$

The same bound can be achieved in a same way for L₃. For L₄, we have

$$L_4\le {\Vert {\mathbf{\Sigma }}_u^{-1}\Vert }^2·\Vert \hat{\mathbf{B}}-\mathbf{B}\Vert ·\Vert \hat{\mathbf{B}}\Vert ·\Vert G\Vert .$$

It follows from Lemmas B.2, B.5(ii), and inequality (B.22) that

$$P(L_4\le C\sqrt{\frac{K\text{ log }p}{T}})\ge 1-O(\frac{1}{p^2}+\frac{1}{T^2}).$$

The same bound also applies to L₅. Finally,

$$L_6\le {\Vert \mathbf{B}\Vert }^2{\Vert {\mathbf{\Sigma }}_u^{-1}\Vert }^2\Vert {\hat{\mathbf{A}}}^{-1}-{\mathbf{A}}^{-1}\Vert \le {\Vert \mathbf{B}\Vert }^2{\Vert {\mathbf{\Sigma }}_u^{-1}\Vert }^2\Vert \hat{\mathbf{A}}-\mathbf{A}\Vert ·\Vert {\hat{\mathbf{A}}}^{-1}\Vert ·\Vert {\mathbf{A}}^{-1}\Vert ,$$

where both  and A are defined after inequality (B.20). By Lemma B.4(ii), ‖A⁻¹‖ = O(p⁻¹). Lemma B.5(ii) implies P(‖Â⁻¹ ‖ > Cp⁻¹) = O(p⁻² + T⁻²). Combining with (B.21), we obtain

$$P(L_6\le {\mathit{\text{Cm}}}_{T}K\sqrt{\frac{\text{log }p}{T}})\ge 1-O(\frac{1}{p^2}+\frac{1}{T^2}).$$

The proof is completed by combining L₁ ~ L₆. Q.E.D.

APPENDIX C: PROOFS FOR SECTION 4

The proof is similar to that of Lemma 3.1. Thus we sketch it very briefly. The OLS is given by

$${\hat{\mathbf{b}}}_i={({\mathbf{X}}_i^{\prime }{\mathbf{X}}_i)}^{-1}{\mathbf{X}}_i^{\prime }{\mathbf{y}}_i,i\le p.$$

The same arguments in the proof of Lemma B.1 can yield, for large enough C > 0,

$$P(\underset{i\le p}{\text{max}}\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert >C\sqrt{\frac{K\text{ log }p}{T}})=O(\frac{1}{p^2}+\frac{1}{T^2}),$$

which then implies the rate of

$$\underset{i\le p}{\text{max}}\frac{1}{T}{\displaystyle \sum _{t=1}^T}{(u_{\mathit{\text{it}}}-{\mathit{û}}_{\mathit{\text{it}}})}^2\le \underset{i\le p}{\text{max}}{\Vert {\hat{\mathbf{b}}}_i-{\mathbf{b}}_i\Vert }^2\frac{1}{T}{\displaystyle \sum _{t=1}^T}{\Vert {\mathbf{f}}_{\mathit{\text{it}}}\Vert }^2.$$

The result then follows from a straightforward application of Theorem 2.1. Q.E.D.