Abstract
In his pioneering work, Alan Turing showed that de novo pattern formation is possible if two substances interact that differ in their diffusion range. Since then, we have shown that pattern formation is possible if, and only if, a self-enhancing reaction is coupled with an antagonistic process of longer range. Knowing this crucial condition has enabled us to include nonlinear interactions, which are required to design molecularly realistic interactions. Different reaction schemes and their relation to Turing's proposal are discussed and compared with more recent observations on the molecular–genetic level. The antagonistic reaction may be accomplished by an inhibitor that is produced in the activated region or by a depletion of a component that is used up during the self-enhancing reaction. The autocatalysis may be realized by an inhibition of an inhibition. Activating molecules can be processed into molecules that have an inhibiting function; patterning of the Wnt pathway is proposed to depend on such a mechanism. Three-component systems, as discussed in Turing's paper, are shown to play a major role in the generation of highly dynamic patterns that never reach a stable state.
Keywords: pattern formation, Turing's theory, morphogenesis, activator–inhibitor systems, Wnt pathway
1. The problem of pattern formation
A most fascinating aspect in biology is the generation of a complex organism starting with a single cell, the fertilized egg. The final complexity of the organism is generated during development under the influence of the genetic information. However, this genetic information is the same in all cells. The structures certainly do not pre-exist in a hidden form within the egg cell. In many cases, a fragment taken from an early embryo can give rise to a normal animal. Such pattern regulation indicates that a communication exists between different parts. The removal of some parts is detected in the remaining organism and the missing structures become replaced. A most spectacular demonstration that pattern formation can occur from an initially homogeneous situation has been provided with the small freshwater polyp hydra. After dissociation into individual cells and re-aggregation, the resulting clumps of cells can form viable organisms [1] (see below). Classical experiments have revealed that during development certain small specialized regions are formed that play a decisive role in the overall organization of the developing organism. Such organizers are local sources of signalling molecules and direct pattern formation in the surrounding tissue. Classical examples are the gastric opening of the hydra mentioned earlier [2,3] and the dorsal lip of an amphibian embryo [4,5].
In his pioneering paper with the provocative title ‘The chemical basis of morphogenesis’, Turing [6] showed that pattern formation can be accomplished by the interaction of two substances that spread at different rates. He demonstrated that, in certain such systems, a homogeneous steady state is unstable, and any small local deviation from this steady state is sufficient to trigger the onset of pattern formation. Turing provided the following model equation as an example [6, p. 42]. Assumed is that Y is highly diffusible while X acts local,
| 1.1a |
and
| 1.1b |
For this interaction, there is a homogeneous steady state at X = 1 and Y = 1, but this state is unstable. In a row of cells, a small local elevation of X above the homogeneous steady state will grow further. A simulation using Turing's equation is given in figure 1.
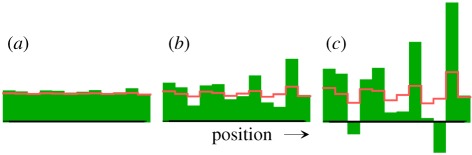
Figure 1.
Pattern formation using Turing's [6] example equation (1.1). The initial (a) and two later distributions (b,c) are shown (green bars, X-concentrations; red lines, Y-concentrations). Since the removal of X in equation (1.1a) is independent of the number of X molecules, X molecules can be removed even if no X molecules are left. This can lead to negative concentrations. Without a cut-off of negative concentrations, there is no final stable steady state. The repair of this problem requires nonlinear reactions. An example is given in equation (2.1).
This mechanism has an essential drawback: its molecular basis is not reasonable. According to equation (1.1), the number of X molecules disappearing per time unit is assumed to be proportional to the number of Y molecules and thus independent of the number of X molecules. Thus, X molecules can disappear even when all X molecules are gone. This can lead to negative concentrations (figure 1). Without cutting off negative concentrations, the system described by equation (1.1) will not reach a patterned steady state; positive concentrations become even higher and negative concentrations become even more negative. Turing saw this problem and proposed to ignore negative concentrations.
For interactions of this type, Turing introduced the term ‘reaction–diffusion systems’, which is now generally in use. However, it is sometimes overlooked that most of these systems are unable to form any pattern, even if substances are involved that diffuse with drastically different rates. For instance, if, in the reaction described by equation (1.1), X instead of Y is diffusible, pattern formation would be impossible, although it would be clearly a reaction–diffusion system. Thus, ‘reaction–diffusion systems’ require specifications as to which of these systems do have pattern-forming capabilities.
Turing's paper was initially not regarded as a breakthrough. One reason could be that the paper is hard to understand by non-mathematicians. Even those biologists who were willing to consider mathematics based models were sceptical. Waddington [7], for instance, did not regard Turing's model as the solution to the problem. Since pattern formation was assumed to be initiated by random fluctuations, Waddington expected that the resulting pattern should also have some degree of randomness, which seems to be in contrast to the astonishing reproducibility observed in development. The finding that even the periodic pattern of Drosophila segmentation is not based on a Turing-like process involving de novo patterning gave rise to further doubts as to whether Turing's mechanism plays a role in development [8]. Early patterning in Drosophila turned out to be based on localized maternal determinants and a hierarchical transmission of this pattern by downstream gene activation.
In contrast to these notions of early scepticism, in the first part of this paper I will show that the fundamental discovery of Turing that patterns can be generated by conventional interactions of molecules that move with different rates is highly relevant for the understanding of essential steps in development and regeneration. However, this requires introducing into the theory of pattern formation the condition of self-enhancement and long-ranging inhibition, which is not inherent in Turing's original paper. Knowing these conditions allowed us to distinguish which types of reactions lead to patterns and which do not, to handle nonlinear interactions that are required to generate stable patterns, to introduce interactions that are in accordance with molecular biology and to account for the striking self-regulatory features of developing organisms. In the final part of the paper, I will focus on two subjects in Turing's original paper of 1952, the periodic arrangement of tentacles in hydra and the most interesting, highly dynamic, three-component systems.
2. Pattern formation requires local self-enhancement and long-range inhibition
In 1972, Alfred Gierer and I published a paper in which we showed that pattern formation is possible if, and only if, a local self-enhancing reaction is coupled with an antagonistic reaction of long range [9]. When we submitted our paper, we were not aware of Turing's work; we only became aware when a reader drew our attention to his paper. In retrospect, it is easy to see that Turing's equation (1.1) satisfies our condition: X has a positive feedback on itself and catalyses the substance Y. In turn, Y acts antagonistically by removing X. Thus, although the equations (1.1a,b) look almost identical, their pattern-forming capability resides in the self-enhancement of X and in the role of Y as the long-ranging antagonist. However, these conditions, local self-enhancement and long-ranging inhibition, are not formulated in Turing's paper. Although Turing did not mention anything such as ‘inhibition’ or the like in his paper, it seems that he later suspected something like this. In unpublished notes found after his death the following sentence was found: ‘The amplitude of the waves is largely controlled by the concentration V of “poison” ’ (see [10, p. 494]). A more extensive proof of the equivalence of Turing's and our theory can be found in Gierer [11].
The following interaction between an autocatalytic activator a and a rapidly diffusing inhibitor b is a straightforward realization of the mechanism we envisaged (figure 2; [9])
| 2.1a |
and
| 2.1b |
where t is time and x is the spatial coordinate. The activator a has a nonlinear positive feedback on its own production. This condition is satisfied if two activator molecules have to form a complex in order to accomplish the feedback—a prediction that meanwhile found experimental support (see below). The activator production is slowed down by the inhibitor b. The diffusion rates of a and b are Da and Db; the removal rates are μa and μb. The source density or competence ρ describes the ability of the cells to perform the autocatalysis; ρ is usually set to μa to obtain absolute concentrations around 1. Superimposed small fluctuations (±1%) in ρ are sufficient to trigger the onset of pattern formation. As will be shown below, by further interactions the competence ρ can obtain a graded distribution, which is a key process in the maintenance of a polar axial organization. A small baseline activator production, ρa, can initiate the patterning at low activator concentrations. In terms of biological pattern formation, it is required for regeneration, for the insertion of new maxima during growth and for sustained oscillations. In contrast, a small baseline inhibitor production, ρb, can sustain a homogeneous stable state at low activator concentrations: the system can be ‘asleep’ until an external trigger occurs, for instance, by an influx of activator from a neighbouring activated cell or by a cross reaction exerted by a previously generated pattern-forming system as a means to link several systems in a reproducible way. If the autocatalysis saturates at high activator concentrations (replacing a2 by a2/(1+κa2)), the activated regions can obtain the geometry of stripes (figure 3).
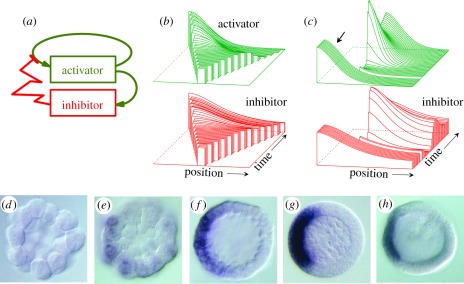
Figure 2.
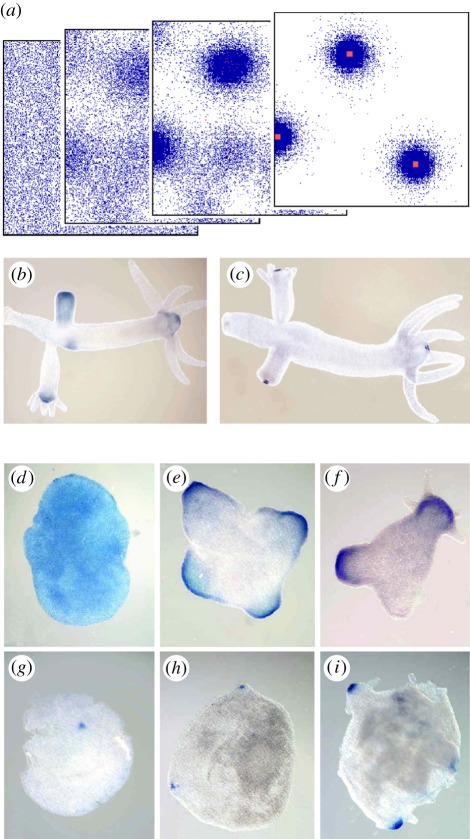
Pattern formation by an activator–inhibitor interaction. (a) Reaction scheme: the activator catalyses its own production and that of its rapidly spreading antagonist, the inhibitor [9,12]. (b) Simulation in a growing chain of cells using equation (2.1). Whenever a certain size is exceeded, random fluctuations are sufficient to initiate pattern formation. A high concentration appears at a marginal position. Thus, although the genetic information is the same in all cells, such a system is able to generate a reproducible polar pattern, appropriate to accomplish space-dependent cell differentiation and the generation of an embryonic axis. (c) Regeneration: after removal of the activated region, the remnant inhibitor fades away until a new activation is triggered. The graded profiles are restored as long as the remaining fragment is large enough. (d–g) A biological example: the emerging Nodal gradient in the sea urchin embryo [13] that is responsible for the formation of the oral field. (h) Antivin (or Lefty2) acts as inhibitor [13,14] and is, as predicted, produced at the same position as the activator. (Figures d–h kindly provided by Dr Thierry Lepage, see [13]; with permission from Dev. Cell.)
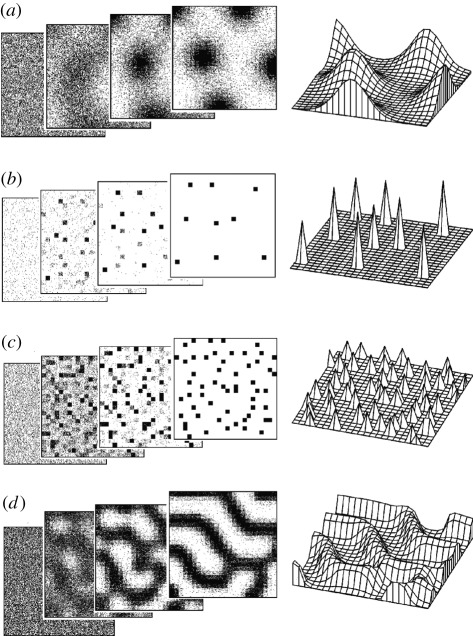
Figure 3.
Periodic patterns. Several maxima appear if the field size is larger than the range of the antagonist. For the simulations, an activator–inhibitor mechanism was used (equation (2.1)). (a) With a substantial spread of the activator, e.g. by diffusion, the peaks are smooth. (b) If the the self-enhancement is cell local, only isolated activated cells remain. Some initially activated cells lose their activity. (c) If the self-enhancement is cell local and the activator production has an upper limit owing to saturation, many activated cells remain in a scattered arrangement. Owing to the limitation in the activator production, the inhibitor production is also limited and an activated cell has to tolerate an activated neighbour. More activated cells remain, with an activation at a lower level. (d) With saturation and some diffusion of the activator, stripe-like patterns can emerge. Diffusion causes activated cells to have the tendency to appear in coherent patches. In stripes, activated cells have activated neighbours along the stripe and non-activated cells are close by, into which the inhibitor can be dumped. The initial, two intermediate and the final stable distributions are shown. For initiation, small random fluctuations in the factor ρ (equation (2.1a)) were assumed.
At the time this mechanism was proposed, possible molecular realizations were virtually unknown. Meanwhile, several interactions were discovered that exhibit the basic function of autocatalytic activation and long-range inhibition [12]. An example is the Nodal/Lefty2 interaction. In vertebrates, it is involved in mesoderm and midline formation; at later stages in the left/right patterning [14–16]. In sea urchins, Nodal/Lefty2 is involved in the formation of the oral field (figure 2) [13]. Nodal is a secreted factor that positively feeds back on its own production. For signalling, Nodal has to form dimers, in agreement with the theoretically expected nonlinearity of the autocatalysis. Lefty2 is under the same control as Nodal and acts as an inhibitor. In agreement with the theoretical expectation for an inhibitor, Lefty2 diffuses much faster than Nodal [17,18]. Most remarkable is that, in this and in other systems [19], the inhibitor interrupts the self-enhancement by blocking the receptor that is required for activation. Thus, the inhibitory action occurs outside the cell. Transmission of an inhibitory signal into the cell would require time, and this may render the system susceptible for becoming oscillating [20]. With blocking the self-activation in the extracellular space, the danger of entering into an oscillating mode is much reduced.
A most important feature of activator–inhibitor systems is that in growing fields the first pattern that can appear is a graded distribution (figure 2); a high concentration forms at one side and a low concentration at the opposide. In other words, such a reaction is appropriate to generate an embryonic axis and polarity. In contrast to the expectation of Waddington mentioned earlier, this pattern is by no means random, although it could be initiated by random fluctuations. In small fields, i.e. in fields comparable to the range of the activator, a graded distribution is the only pattern that can emerge. This pattern is surprisingly robust against perturbations. For instance, after removal of the activated region, a new one regenerates (figure 2c). Other elementary patterns such as periodic patches or stripe-like arrangements emerge if the ranges of the components are smaller than the field size (figure 3).
3. The activator-depleted substrate mechanism
Another possible realization of our general scheme is that the antagonistic effect results from the consumption and depletion of a substrate b that is produced everywhere; b is a prerequisite for the self-enhancing reaction and is consumed during activator production [9],
| 3.1a |
and
| 3.1b |
Again, the production rate of the activator has to be nonlinear; the autocatalysis is proportional to the substrate concentration b; b molecules are removed at the same rate at which new a molecules are produced; the substrate b is produced everywhere with the rate ρb.
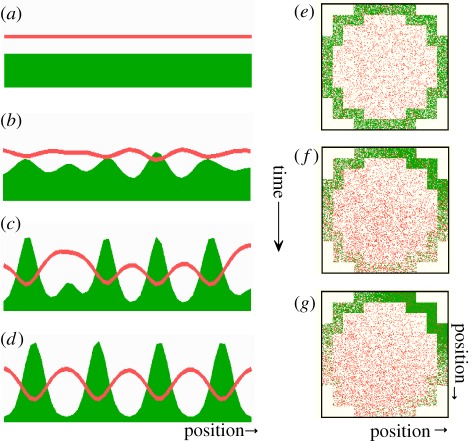
This mechanism has turned out to be especially appropriate to describe pattern formation within a cell where local concentration maxima emerge at the inner side of the cell membrane. At this position, however, nothing is produced; also, there is no inhibitor that could keep the activated area localized. According to the model, activation can occur by a cooperative aggregation of molecules at the cell cortex, i.e. aggregation proceeds more rapidly at positions where some of these molecules are already present. This aggregation is antagonized by the depletion of unbound molecules that diffuse in the cytoplasm (figure 4). Because diffusion in the membrane is slow while diffusion in the cytoplasm is usually more rapid, the condition for different ranges is automatically satisfied. In intracellular patterning, ‘long range’ denotes a communication over the entire cell while ‘short range’ indicates a cooperative process that covers only a part of the cell cortex. This model was used to model the pole-to-pole oscillation of MinD in the Escherichia coli bacterium to find the centre of the cell to initiate the cell division at the correct position [23] (see below). The proposed mechanism has been meanwhile confirmed by the reproduction of this pattern-forming reaction in vitro [24]. Another example for a corresponding intracellular pattern-forming reaction is the generation of Cdc42 maxima in budding yeast [21].
Figure 4.
Pattern formation by an activator–depletion mechanism. (a–d) The development of a pattern in which the self-enhancing reaction proceeds at the expense of a rapidly spreading substrate or cofactor (equation (3.1)) [9]. The concentration of the antagonist is lowest in regions of high activator concentration, in contrast to the situation in an activator–inhibitor system (figure 2). (e–g) Such a system is appropriate for intracellular pattern formation. In this simulation, the self-enhancing reaction is assumed to proceed by a cooperative aggregation of molecules (green) at the membrane. This aggregation proceeds at the expense of freely diffusible monomers that can spread rapidly in the cytoplasm (red). Local high concentrations emerge at a particular part of the cell membrane. Corresponding mechanisms are discussed for the yeast [21], in Dictyostelium discoideum [22] and is part of the centre-finding mechanism in E. coli (figure 7; [23]).
4. The self-enhancement can be realized by an inhibition of an inhibition
By knowing the crucial condition, it was straightforward not only to include nonlinear interactions but also to realize the pattern-forming capabilities in reactions that look overtly very different. For instance, in equation (4.1) only inhibitions are involved. The famous Spemann organizer of the amphibian embryo is proposed to be generated in this way.
| 4.1a |
| 4.1b |
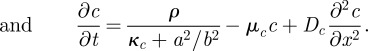 |
4.1c |
The two substances, a and c, inhibit each other's production. On their own, they form a switching system in which one of the substances becomes fully activated. The rapidly diffusing substance b is required for pattern formation. It is produced under control of a and undermines the inhibition of the c production by the a molecules. It acts, therefore, as an inhibitor. The constants κa and κc are Michaelis–Menten-type constants that limit the maximum production rates if a or c become very low. In this way, they determine the maximum concentration the substances may reach, functioning as a sort of saturation term.
Experimentally, it has been found that the two key components of the Spemann organizer, Chordin and BMP, inhibit each other [5,25], which provides, according to the model, the necessary self-enhancement by an inhibition of an inhibition (corresponding to a and c in equation (4.1)). The anti-dorsalizing morphogenetic protein acts as the longer ranging antagonist (b). It is produced under the same control as Chordin and undermines the inhibitory action of Chordin on BMP (reviewed in De Robertis [5] and Niehrs [25]; for modelling see [12,26]).
5. A strong team: the tight coupling of two pattern-forming systems with different wavelength
If the range of the activator corresponds to a substantial fraction of the field size, the resulting maxima are relatively smooth. Such systems are appropriate to integrate information over a larger part of the tissue to find the best place for activation, including that peak formation takes place preferentially at a marginal position (figure 2). In contrast, if the activator has a short range or is cell local, very sharp maxima appear, which are appropriate to initiate a very localized structure. Under this condition, several maxima may appear initially in a larger field, some may disappear later on and the surviving one may not be localized at the appropriate position (figure 3b). An analysis of head formation in the small freshwater polyp hydra revealed that Nature found an elegant way to combine the advantages of both modes by using a system with two feedback loops of different ranges. By sharing a common component, these two systems are strongly coupled such that both maxima always appear precisely at the same position. The long-ranging system allows an optimized general localization. At the maxima of the first system, the second system is triggered, delivering a very sharp signal ([27]; figure 5).
Figure 5.
Two coupled pattern-forming systems with different wavelengths. (a) Simulation using equations (6.1). A first loop includes components that show substantial diffusion; the corresponding peaks (blue) are relatively smooth such that their place of activation can be better optimized. Assumed is that by processing Wnt molecules become converted from short-ranging activators to long-ranging inhibitors [27]. A second loop (red) is cell-local. The resulting maxima are sharp, allowing the determination of very localized structures (figure 3b). Owing to a common component, both loops appear superimposed in a centred way. (b–h) Observations in the small freshwater polyp hydra [28]: Tcf (b) (and β-catenin) have a more shallow distribution around the opening of the gastric column, while Wnt3 expression (c) is more localized. (d–h) After dissociation of hydra tissue into individual cells and and subsequent re-aggregation, complete and viable animals can be formed [1], one of the most impressive examples of de novo pattern formation. During re-aggregation, Tcf/β-catenin appear first in a more cloudy pattern (d–f), as is theoretically expected. In contrast, Wnt3 expression (g–i) appears directly in sharp peaks. (Figures (b–i) kindly supplied by Bert Hobmayer and Thomas Holstein [28], with permission from Nature.)
6. The Wnt pathway: the conversion of an activator into an inhibitor
For the Wnt pathway mentioned earlier, good evidence became available for the predicted involvement of autoregulation [29]. In contrast, no convincing candidates for long-ranging molecules with inhibitory functions have been found. Those that have been assigned for this function such as Dkk are not produced in the activated region [30,31] and fail, therefore, to satisfy the criterion. Recent observations have revealed that, after processing, Wnt molecules obtain a very different range (for review, see [32–34]). As Wnt molecules are first secreted, they are attached to lipids, which allow only a very limited diffusion. Later, these molecules are taken up by the cells again, become associated with lipid particles and are secreted again. In this form, the Wnt molecules are much more mobile. Although it has not yet been shown that the differently processed Wnt molecules have different functions, from our model we would expect that the slowly diffusing variety is involved in the self-enhancement while the long-ranging variety undermines this self-enhancement [27]. The following set of equations describes a highly simplified version of this reaction scheme. It incorporates the activator-to-inhibitor conversion, the coupling of a long-ranging and a short-ranging loop by employment of a common element (a) and the very special mode of autoregulation by slowing down a high destruction rate of one component (β-catenin, equation (6.1c)),
| 6.1a |
| 6.1b |
| 6.1c |
| 6.1d |
| 6.1e |
The simulation in figure 5 shows that this set of equations describes essential observations. The component a describes the transcription of the Wnt3 molecules, which is assumed to depend on β-catenin (c) and Brachyury (e). Wnt3 molecules are secreted into the intercellular space (b). They diffuse only slowly owing to binding to lipids and attachment to the cell surfaces. After stimulation of the Wnt receptors at the cell surface by the b molecules and signalling into the cell, the degradation rate of β-catenin, c, is drastically reduced (−νcc/b). This reflects another speciality of the patterning by the Wnt pathway: the self-enhancement is not achieved by a positive feedback on the production rate but by a block of an otherwise rapid destruction. Thus, more a (Wnt3 transcription) leads to more c (β-catenin) by c stabilization, which, in turn, is assumed to have a nonlinear feedback on a. For the inhibitor production, it is assumed that the slowly diffusible Wnt3 molecules b become converted into a rapidly diffusing variety d by association with lipid particles [34] that undermine the reception of the b molecules, counteracting in this way the stabilization of c. Therefore, d acts as an inhibitor. This is achieved by an undermining effect of the rapidly diffusing d on the slowly diffusing Wnt signal b on the stabilization of β-catenin (νcc/(b/d), equation (6.1c)). For simulations in two-dimensional fields as given in figure 5a, the corresponding diffusion terms are used.
To account for the sharp Wnt3 peaks, a second positive loop is assumed that is cell local [27]. It may employ another transcription factor e such as Brachyury [35]. The observed delay between the appearance of β-catenin and Wnt3 peaks during regeneration indicates that this second loop a → e → a is triggered only when the first loop has reached a certain threshold. The threshold results from the term γe in equation (6.1e). Both loops are tightly coupled because both employ the Wnt transcripts a as a common element. Although this loop is cell local, several cells can remain activated owing to a saturation in the self-enhancement (κe in equation (6.1e)).
7. A third wavelength: feedback on the competence as a means to maintain a polar pattern
The involvement of two components with different wavelength has been mentioned earlier (figure 5). In hydra, a third component is involved in the positive loops that has an even longer range, the competence (ρ in terms of equation (2.1)). Owing to this feedback, the competence obtains a graded distribution over the body column [36] (see the blue curve in figure 6a). The competence (corresponding to the ambiguous notion of ‘head activation gradient’ that is frequently used in the hydra literature) provides a measure for the ability of the tissue to perform the pattern-forming reaction. The competence has been determined by classical transplantation experiments. A tissue fragment derived from a position closer to the head of a donor hydra has a higher chance of triggering a new head after transplantation into the body column of another hydra. In terms of the model, the graded competence provides a bias; it is decisive where the activation will occur during regeneration. Because the organizing region is small (the tip of the hypostome) but the competence is a smoothly graded tissue property over the body column, it is expected that a long-ranging signal spreads from the organizer that causes an increase in the ability to perform the pattern-forming reaction [36,39]. Thus, with increasing distance from an existing maximum, not only the inhibitor concentration but also the competence decreases. The cells become less and less able to establish a new centre, especially while the primary organizer is present. This stabilizes the polar character of the axial pattern during growth by suppressing the trigger of secondary organizing regions. The inhibitor may have a double function: inhibiting the formation of other maxima and establishing this graded competence. It is crucial that the competence has a much longer time constant; it remains almost unchanged during the decisive early steps in regeneration, providing in this way a sort of memory for the polarity of the tissue. It causes regeneration to occur with a predictable polarity. In contrast, the actual pattern formation is a self-regulating process. Foot formation occurs at the lowest level of head competence and reduces the head competence further (figure 6). Thus, the foot signal appears at the largest possible distance from the head signal and contributes to suppressing the formation of a second head signal [27,36]. As discussed later, the graded competence also plays a crucial role in the positioning of the tentacles. The molecular realization of the competence in hydra is not yet clear.
Figure 6.
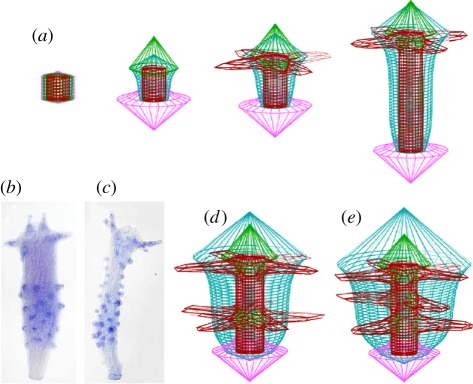
Already considered by Turing: tentacle patterning in hydra as an example of a periodic pattern on a ring. (a) Model for hydra patterning: the signals for head (green), foot (pink) and tentacle formation (brown) are assumed to be accomplished by activator–inhibitor systems [36]. These systems are coupled via the competence (blue). The head signal inhibits locally the tentacle signal but generates on longer range the high competence that is required for tentacle formation. Therefore, tentacles are formed only next to the head. (b,c) After treatment with a drug (alsterpaullone), tentacles are formed all over the body column [37], Wnt5 marks the tip of the tentacles (b), Wnt8 their base (c) [38]. The drug stabilizes β-catenin; all cells of the body column obtain a high competence [37]. (d,e) Model: owing to the generally elevated competence (blue), the position next to the head is no longer privileged; tentacles appear first at some distance from the existing tentacles (d), as observed (b), and later all over with a similar spacing that is normally only observed in the tentacle ring, in agreement with the observations [37,38]. (Photographs were kindly provided by Isabelle Philipp and Bert Hobmayer; see Philipp et al. [38]; with permission from Proc. Natl Acad. Sci. USA.)
Taken together, by coupling positive-acting elements of different ranges, the polarity can be maintained over a large range of sizes and very localized signals are available nevertheless. The expected generation of multiple peaks in situations where only a single peak should occur was used as an argument against Turing's mechanism. As shown earlier, this ‘wavelength problem’, inherent in simple pattern-forming systems, can be solved by the superposition of several patterning systems with different wavelengths.
8. Tentacle formation in hydra: a system that Turing was considering as an example of a periodic pattern on a circle
The ring of tentacles around the opening of the gastric column in hydra was mentioned explicitly by Turing as an example of a periodic pattern on a ring. As the primary axial pattern, the tentacle pattern is also restored during regeneration and during pattern formation in re-aggregating cells (figure 5). A second look at this pattern, however, shows that its generation is not so simple. Tentacles emerge close to each other around the circumference but no tentacles are formed further down along the body column. Tentacle formation is an example of a type of pattern that is frequently encountered in development: two structures emerge close to each other but not somewhere else. Such a controlled neighbourhood of structures is enforced if one structure activates the other on a medium range but excludes it locally [40,41]. Tentacle formation can be explained under the assumption that the primary patterning system that generates the head—or, more precisely, the hypostome—generates on a longer range the precondition to form the tentacles. Locally, however, the tentacle system is suppressed by the hypostome system. Therefore, tentacles can only appear next to the hypostome. Owing to the inhibition produced by the tentacles formed at the privileged position, tentacle formation is suppressed further down the body column. Even further down, around the budding zone, tentacle formation is impossible since the competence is too low. This model [36] has recently found support from molecular investigations. By treatment with the drug alsterpaullone that stabilizes β-catenin, it was possible to obtain a high competence everywhere in the body column [37], allowing tentacle formation everywhere (figure 6). As observed, the first supernumerary tentacles appear at some distance from the normal tentacles because there their inhibitory influence is the lowest.
9. An almost forgotten part of Turing's paper: highly dynamic three-component systems
In his famous paper Turing discussed not only two-component systems, which can generate stable patterns. He showed that three-component systems can lead to the spontaneous generations of travelling waves and to out-of-phase oscillations. Turing wrote
… but with three or more morphogens it is possible to have travelling waves. With a ring there would be two sets of waves, one travelling clockwise and the other anticlockwise. There is a natural chemical wave-length and wave frequency in this case as well as a wave-length; no attempt was made to develop formulae for these … (Turing [6, p. 67])
The absence of a model equation and a biological example is presumably the reason why this part of his paper became largely forgotten.
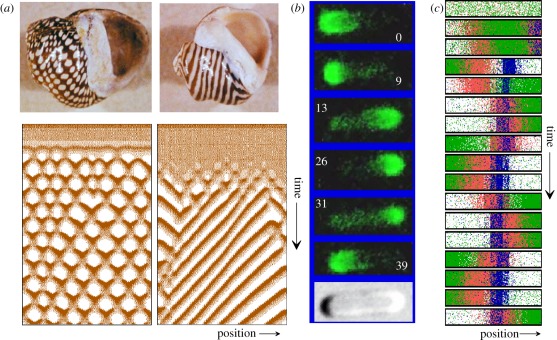
By searching for mechanisms that account for the pigment pattern on tropical sea shells, we came across a reaction type that is able to generate highly dynamic patterns that never reach a steady state [42–44]. The basic idea was that concentration maxima, generated by a conventional two-component system, become destabilized by an additional antagonist that locally quenches the once established maxima. Maxima can disappear and re-appear at displaced positions or they are permanently shifted into an adjacent position, causing spontaneously travelling waves. Owing to the long-ranging inhibition involved, their initiation does not require a special pacemaker region. Thus, our three-component systems have essentially the same properties as those discussed by Turing. Whether both mechanisms are also mathematically equivalent is not yet clear. Meanwhile, several biological pattern-forming systems are known that require the presence of a local destabilization to understand their behaviour [43–45]. Examples are given in figure 7.
Figure 7.
Pattern formation by three-component systems. As Turing mentioned already in his paper, three-component systems can generate spontaneous travelling waves and out-of-phase oscillations. Modelling has shown that these patterns emerge if, in addition to the long-ranging antagonist, a local-acting but long-lasting antagonist is involved. The latter quenches a maximum shortly after it appeared [42–44]. (a) Two patterns on shells of the same species and their simulations. Shell patterns are natural space–time plots since new pattern elements are added only at the growing edge. Minor changes in the parameter decide whether out-of-phase oscillations or travelling waves occur. These patterns emerge spontaneously and do not need a pacemaker. (b) The pole-to-pole oscillation of MinD in E. coli is used to localize the division plane. The division can only be initiated at positions where, on average, the MinD concentration (green) is at the lowest, i.e. at the centre of the cell. The numbers indicate seconds, a full cycle requires about 50 s [46]. (c) Simulation [23]: MinD (green) associates with the membrane. A second component, MinE (red), generates a local maximum that needs MinD to bind to the membrane but removes MinD with this binding. Thus, a MinE maximum permanently destabilizes itself by removing MinD, causing the back-and-forth shift of MinE maxima around the centre and the periodic breakdown of MinD maxima at the poles. High MinD levels appear at the poles in an alternating sequence while the centre remains free. This allows the initiation of a further patterning system, FtsZ (blue). These tubulin-like molecules initiate cell division by a constriction at the cell centre. (Photographs kindly provided by (a) Rainer Willman and (b) Piet de Boer [46].)
10. Conclusion
Molecular interactions that allow de novo pattern formation during development as envisaged by Turing are now well documented in the literature. As we have shown, the driving force behind these is a local self-enhancement combined with a long-ranging inhibition. This pattern formation may take place between or within the cells. Diffusion is presumably the driving force but other mechanisms are conceivable as well—for instance, direct cell contact of distant cells by long protrusions. Even if initiated by random fluctuations, the resulting patterns can be highly reproducible because, at small scales, only well-defined polar patterns are possible. Subsequent patterning is reproducible too because any pattern generated at a particular step introduces a strong bias for the next. The reproducible initiation of tentacles in hydra was used to illustrate this point. Owing to the required communication between cells, e.g. by diffusion, these de novo patterning processes are only possible at small extensions, as given at early stages of development or in animals that remain small anyway. Modelling has turned out to be an appropriate tool to understand complex networks of interactions. The models outlined earlier are minimum models. For instance, the signalling by components of the Wnt pathway is certainly much more complex than described. However, the models reveal what is required at least to perform a particular developmental step, make the underlying logic comprehensible despite the complexity and allow firm predictions. We expect that also in the future mathematically-based modelling will contribute to a better understanding of how a complex organism can emerge from a single cell.
Acknowledgements
The author expresses his sincere thanks to Prof. Alfred Gierer. Much of the basic work described in this paper emerged from a fruitful collaboration over many years. He also provided helpful comments on this paper.
References
- 1.Gierer A., Berking S., Bode H., David C. N., Flick K., Hansmann G., Schaller H., Trenkner E. 1972. Regeneration of hydra from reaggregated cells. Nat. New Biol. 239, 98–101. [DOI] [PubMed] [Google Scholar]
- 2.Browne E. N. 1909. The production of new hydrants in Hydra by insertion of small grafts. J. Exp. Zool. 7, 1–23. 10.1002/jez.1400070102 ( 10.1002/jez.1400070102) [DOI] [Google Scholar]
- 3.Broun M., Bode H. R. 2002. Characterization of the head organizer in hydra. Development 129, 875–884. [DOI] [PubMed] [Google Scholar]
- 4.Spemann H., Mangold H. 1924. Über Induktion von Embryonalanlagen durch Implantation artfremder Organisatoren. Wilhelm Roux' Arch. Entw. Mech. Org. 100, 599–638. [Google Scholar]
- 5.De Robertis E. M. 2009. Spemann's organizer and the selfregulation of embryonic fields. Mech. Dev. 126, 925–941. 10.1016/j.mod.2009.08.004 ( 10.1016/j.mod.2009.08.004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Turing A. 1952. The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B 237, 37–72. 10.1098/rstb.1952.0012 ( 10.1098/rstb.1952.0012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Waddington C. H. 1956. Principles of embryology. London, UK: Georg Allen and Unwin Ltd; 10.5962/bhl.title.7217 ( 10.5962/bhl.title.7217) [DOI] [Google Scholar]
- 8.Wolpert L. 1989. Positional information revisited. Development (Supplement) 107, 3–12. [DOI] [PubMed] [Google Scholar]
- 9.Gierer A., Meinhardt H. 1972. A theory of biological pattern formation. Kybernetik 12, 30–39. 10.1007/BF00289234 ( 10.1007/BF00289234) [DOI] [PubMed] [Google Scholar]
- 10.Hodges A. 1983. Alan Turing: the enigma. New York, NY: Simon and Schuster. [Google Scholar]
- 11.Gierer A. 1981. Generation of biological patterns and form: some physical, mathematical, and logical aspects. Prog. Biophys. Mol. Biol. 37, 1–47. 10.1016/0079-6107(82)90019-0 ( 10.1016/0079-6107(82)90019-0) [DOI] [PubMed] [Google Scholar]
- 12.Meinhardt H. 2008. Models of biological pattern formation: from elementary steps to the organization of embryonic axes. Curr. Top. Dev. Biol. 81, 1–63. 10.1016/S0070-2153(07)81001-5 ( 10.1016/S0070-2153(07)81001-5) [DOI] [PubMed] [Google Scholar]
- 13.Duboc V., Rottinger E., Besnardeau L., Lepage T. 2004. Nodal and BMP2/4 signaling organizes the oral–aboral axis of the sea urchin embryo. Dev. Cell 6, 397–410. 10.1016/S1534-5807(04)00056-5 ( 10.1016/S1534-5807(04)00056-5) [DOI] [PubMed] [Google Scholar]
- 14.Chen Y., Schier A. F. 2002. lefty proteins are long-range inhibitors of squint-mediated nodal signaling. Curr. Biol. 12, 2124–2128. 10.1016/S0960-9822(02)01362-3 ( 10.1016/S0960-9822(02)01362-3) [DOI] [PubMed] [Google Scholar]
- 15.Bisgrove B. W., Essner J. J., Yost H. J. 1999. Regulation of midline development by antagonism of lefty and nodal. Development 126, 3253–3262. [DOI] [PubMed] [Google Scholar]
- 16.Nakamura T., Mine N., Nakaguchi E., Mochizuki A., Yamamoto M., Yashiro K., Meno C., Hamada M. 2006. Generation of robust left-right asymmetry in the mouse embryo requires a self-enhancement and lateral-inhibition system. Dev. Cell 11, 495–504. 10.1016/j.devcel.2006.08.002 ( 10.1016/j.devcel.2006.08.002) [DOI] [PubMed] [Google Scholar]
- 17.Sakuma R., et al. 2002. Inhibition of nodal signalling by lefty mediated through interaction with common receptors and efficient diffusion. Genes Cells 7, 401–412. 10.1046/j.1365-2443.2002.00528.x ( 10.1046/j.1365-2443.2002.00528.x) [DOI] [PubMed] [Google Scholar]
- 18.Marjoram L., Wright C. 2011. Rapid differential transport of nodal and lefty on sulfated proteoglycan-rich extracellular matrix regulates left–right asymmetry in Xenopus. Development 138, 475–485. 10.1242/dev.056010 ( 10.1242/dev.056010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rentzsch F., Fritzenwanker J. H., Jens H., Scholz C. B., Technau U. 2008. FGF signalling controls formation of the apical sensory organ in the cnidarian Nematostella vectensis. Development 135, 1761–1769. 10.1242/dev.020784 ( 10.1242/dev.020784) [DOI] [PubMed] [Google Scholar]
- 20.Lee S. S., Gaffney E. A., Monk N. A. M. 2010. The influence of gene expression time delays on Gierer–Meinhardt pattern formation systems. Bull. Math. Biol. 72, 2139–2160. 10.1007/s11538-010-9532-5 ( 10.1007/s11538-010-9532-5) [DOI] [PubMed] [Google Scholar]
- 21.Irazoqui J. E., Gladfelter A. S., Lew D. J. 2003. Scaffold-mediated symmetry breaking by Cdc42p. Nat. Cell Biol. 5, 1062–1070. 10.1038/ncb1068 ( 10.1038/ncb1068) [DOI] [PubMed] [Google Scholar]
- 22.Charest P. G., Firtel R. A. 2006. Feedback signaling controls leading-edge formation during chemotaxis. Curr. Opin. Gen. Dev. 16, 339–347. 10.1016/j.gde.2006.06.016 ( 10.1016/j.gde.2006.06.016) [DOI] [PubMed] [Google Scholar]
- 23.Meinhardt H., de Boer P. A. J. 2001. Pattern formation in E. coli: a model for the pole-to-pole oscillations of Min proteins and the localization of the division site. Proc. Natl Acad. Sci. USA 98, 14 202–14 207. 10.1073/pnas.251216598 ( 10.1073/pnas.251216598) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Loose M., Fischer-Friedrich E., Ries J., Kruse K., Schwille P. 2008. Spatial regulators for bacterial cell division self-organize into surface waves in vitro. Science 320, 789–792. 10.1126/science.1154413 ( 10.1126/science.1154413) [DOI] [PubMed] [Google Scholar]
- 25.Niehrs C. 2004. Regionally specific induction by the Spemann–Mangold organizer. Nat. Rev. Genet. 5, 425–434. 10.1038/nrg1347 ( 10.1038/nrg1347) [DOI] [PubMed] [Google Scholar]
- 26.Meinhardt H. 2006. Primary body axes of vertebrates: generation of a near-Cartesian coordinate system and the role of Spemann-type organizer. Dev. Dyn. 235, 2907–2919. 10.1002/dvdy.20952 ( 10.1002/dvdy.20952) [DOI] [PubMed] [Google Scholar]
- 27.Meinhardt H. 2012. Modeling pattern formation in hydra—a route to understand essential steps in development. Int. J. Dev. Biol. ( 10.1387/ijdb.113483hm) [DOI] [PubMed] [Google Scholar]
- 28.Hobmayer B., Rentzsch F., Kuhn K., Happel C. M., Cramer von Laue C., Snyder P., Rothbacher U., Holstein T. W. 2000. Wnt signalling molecules act in axis formation in the diploblastic metazoan hydra. Nature 407, 186–189. 10.1038/35025063 ( 10.1038/35025063) [DOI] [PubMed] [Google Scholar]
- 29.Nakamura Y., Tsiairis C. D., Ozbek S., Holstein T. W. 2011. Autoregulatory and repressive inputs localize hydra wnt3 to the head organizer. Proc. Natl Acad. Sci. USA 108, 9137–9142. 10.1073/pnas.1018109108 ( 10.1073/pnas.1018109108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Guder C., Pinho S., Nacak T. G., Schmidt H. A., Hobmayer B., Niehrs C., Holstein T. W. 2006. An ancient Wnt-Dickkopf antagonism in hydra. Development 133, 901–911. 10.1242/dev.02265 ( 10.1242/dev.02265) [DOI] [PubMed] [Google Scholar]
- 31.Augustin R., Franke A., Khalturin K., Kiko R., Siebert S., Hemmrich G., Bosch T. C. G. 2006. Dickkopf related genes are components of the positional value gradient in hydra. Dev. Biol. 296, 62–70. 10.1016/j.ydbio.2006.04.003 ( 10.1016/j.ydbio.2006.04.003) [DOI] [PubMed] [Google Scholar]
- 32.Port F., Basler K. 2010. Wnt trafficking: new insights into wnt maturation, secretion and spreading. Traffic 11, 1265–1271. 10.1111/j.1600-0854.2010.01076.x ( 10.1111/j.1600-0854.2010.01076.x) [DOI] [PubMed] [Google Scholar]
- 33.Lorenowicz M. J., Korswagen H. C. 2009. Sailing with the Wnt: charting the Wnt processing and secretion route. Exp. Cell Res. 315, 2683–2689. 10.1016/j.yexcr.2009.06.015 ( 10.1016/j.yexcr.2009.06.015) [DOI] [PubMed] [Google Scholar]
- 34.Bartscherer K., Boutros M. 2008. Regulation of Wnt protein secretion and its role in gradient formation. EMBO Rep. 9, 977–982. 10.1038/embor.2008.167 ( 10.1038/embor.2008.167) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Technau U., Bode H. R. 1999. HyBra1, a brachyury homologue, acts during head formation in Hydra. Development 126, 999–1010. [DOI] [PubMed] [Google Scholar]
- 36.Meinhardt H. 1993. A model for pattern-formation of hypostome, tentacles, and foot in hydra: how to form structures close to each other, how to form them at a distance. Dev. Biol. 157, 321–333. 10.1006/dbio.1993.1138 ( 10.1006/dbio.1993.1138) [DOI] [PubMed] [Google Scholar]
- 37.Broun M., Gee L., Reinhardt B., Bode H. R. 2005. Formation of the head organizer in hydra involves the canonical wnt pathway. Development 132, 2907–2916. 10.1242/dev.01848 ( 10.1242/dev.01848) [DOI] [PubMed] [Google Scholar]
- 38.Philipp I., Aufschnaiter R., Ozbek S., Pontasch S., Jenewein M., Watanabe H., Rentzsch F., Holstein T.W., Hobmayer B. 2009. wnt/beta-catenin and noncanonical wnt signaling interact in tissue evagination in the simple eumetazoan hydra. Proc. Natl Acad. Sci. USA 106, 4290–4295. 10.1073/pnas.0812847106 ( 10.1073/pnas.0812847106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Meinhardt H. 2009. Models for the generation and interpretation of gradients. Cold Spring Harb. Perspect. Biol. 1, a001362. 10.1101/cshperspect.a001362 ( 10.1101/cshperspect.a001362) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Meinhardt H., Gierer A. 1980. Generation and regeneration of sequences of structures during morphogenesis. J. Theor. Biol. 85, 429–450. 10.1016/0022-5193(80)90318-5 ( 10.1016/0022-5193(80)90318-5) [DOI] [PubMed] [Google Scholar]
- 41.Meinhardt H. 1982. Models of biological pattern formation. London, UK: Academic Press; See http://www.eb.tuebingen.mpg.de/meinhardt. [Google Scholar]
- 42.Meinhardt H., Klingler M. 1987. A model for pattern formation on the shells of molluscs. J. Theor. Biol 126, 63–89. 10.1016/S0022-5193(87)80101-7 ( 10.1016/S0022-5193(87)80101-7) [DOI] [Google Scholar]
- 43.Meinhardt H. 2009. The algorithmic beauty of sea shells, 4th edn Heidelberg, Germany: Springer. [Google Scholar]
- 44.Meinhardt H. 2004. Out-of-phase oscillations and traveling waves with unusual properties: the use of three-component systems in biology. Physica D 199, 264–277. 10.1016/j.physd.2004.08.018 ( 10.1016/j.physd.2004.08.018) [DOI] [Google Scholar]
- 45.Harris M. P., Williamson S., Fallon J. F., Meinhardt H., Prum R. O. 2005. Molecular evidence for an activator–inhibitor mechanism in development of embryonic feather branching. Proc. Natl Acad. Sci. USA 102, 11 734–11 739. 10.1073/pnas.0500781102 ( 10.1073/pnas.0500781102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Raskin D. M., de Boer P. A. J. 1999. Rapid pole-to-pole oscillation of a protein required for directing division to the middle of Escherichia coli. Proc. Natl Acad. Sci. USA 96, 4971–4976. 10.1073/pnas.96.9.4971 ( 10.1073/pnas.96.9.4971) [DOI] [PMC free article] [PubMed] [Google Scholar]