Wing vein patterns of the Hemiptera insect Orosanga japonicus differ among individuals

Abstract

Although Turing's reaction–diffusion model (RD model) has been gradually accepted among biologists, application of the model is still limited. Accumulated experimental studies have shown that the morphogen gradient model can explain most patterning phenomena in embryogenesis. These experiments have been performed only in a few model animals. Therefore, it is not clear whether the discovered principle of the mechanism is generally applicable. The wing venation pattern of Drosophila melanogaster is largely determined by the morphogen gradient mechanism. We found that the gradient model cannot be applied to some other species. In the Hemiptera insect Orosanga japonicus, each individual has a unique pattern. Veins of O. japonicus extend radially from the proximal region and bifurcate to add the veins in the distal region. Interestingly, the bifurcation points are almost random and the vein number at the wing edge differs with wing size. However, the spacing between the veins is maintained evenly. Computer simulation of the RD model showed these properties do not fit the morphogen gradient model, but perfectly fit the RD model. This result suggests that the RD model may explain phenomena to which the morphogen gradient mechanism is currently believed to apply.

1. Turing's reaction–diffusion model

Turing's legendary paper entitled ‘The chimerical basis of morphogenesis’ was published in 1952 [1]. In the paper, Turing proved mathematically that a combination of known physical processes—chemical reaction and diffusion—generates a kind of spatial pattern (Turing pattern), and proposed that the mechanism (reaction–diffusion (RD) mechanism) may serve as the basis of pattern formation during morphogenesis. The most impactful element of the hypothesis is that it can generate stable positional information without any pre-pattern [2,3]. Although the animal egg possesses a substantial amount of preset positional information, it is much less than the complex structure of an adult animal. Therefore, an autonomous mechanism must mediate the development of all species [4]. Simulation studies of the model later performed by mathematical biologists [5,6] showed that the mechanism can replicate a variety of biological spatial patterns, which led to acceptance of the RD model as one of the standard mathematical theories of biological pattern formation. Recent papers have presented compelling evidence that the RD mechanism underlies developmental phenomena such as skin colour patterns in fish [7], feather patterns in chicks [8] and hair patterns in rodents [9].

However, the RD model has yet to gain wide acceptance among experimental biologists [4]. Most developmental biologists rely on the simpler morphogen gradient model [10]. The morphogen gradient model does not have the property of autonomous pattern formation because the ‘gradient’ is completely dependent on the preset position (pre-pattern) of the morphogen in the egg. Experimental studies of Drosophila melanogaster have shown that there are many specifically localized molecules in the egg that behave precisely as predicted by the morphogen gradient model [11,12]. With such strong experimental support, the gradient model is now recognized by experimental biologists as the most fundamental mechanism of biological pattern formation.

Recent molecular genetic studies in developmental biology have concentrated on several model animals. This strategy has enabled common use of genetic methods and remarkable progress in our understanding of the molecular basis of morphogenesis. However, we need to be aware of the fact that a mechanistic principle found in a model animal is not always applicable to other species. For example, homologues of Drosophila segmentation genes that operate upstream of the homeotic genes can be isolated across phyla, and the gene expression patterns of these homologues, and presumably their functions, are not always conserved, even within the insects [13].

2. Archetype of insect venation pattern is difficult to be made by the gradient mechanism

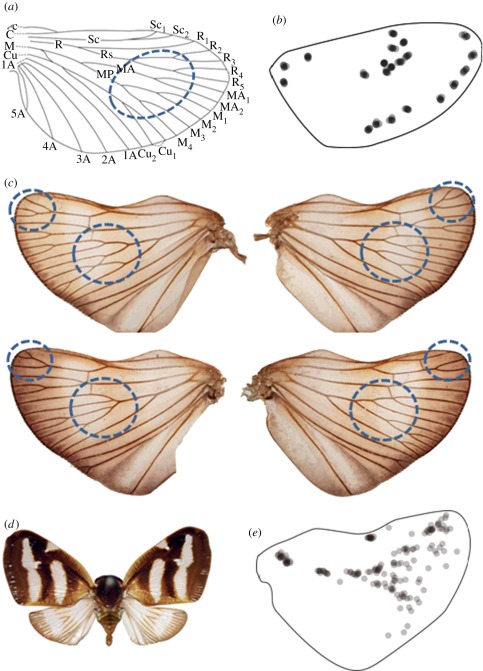
Insect wing venation is a popular model system for studying biological pattern formation. Extensive experimental studies in D. melanogaster have indicated that the position of a vein is determined by a gradient of the morphogen molecule Dpp [11,12], a property thought to apply to all insects [14–17]. However, it is unclear whether this gradient mechanism is universal to all complicated venation patterns in insects. The venation pattern of D. melanogaster is much simpler than that of many other insect species; figure 1a shows the archetype [14,15] of insect venation patterns deduced from the fossil record. Many insects share similar characteristics [14,15]. Archetypical veins bifurcate repeatedly while maintaining constant spacing between neighbouring veins, and branch out extensively at the wing edge. The morphogen gradient mechanism is not well suited for explaining such bifurcations. Additionally, the number of veins at the distal edge in the archetype wing is much greater than four. To specify the positions of so many veins using the gradient mechanism requires complementing it with an extremely complex downstream network [18]. Therefore, for a simpler description of the complex venation patterns in the archetype and other insects, an alternative mechanism should be considered.

Figure 1.

Wing venation patterns of archetype and Orosanga japonicus. (a) Wing pattern archetype deduced from fossil records. (b) Branch points of 10 Cryptotympana facialis individuals show fixed positions. Most insect species show a similar profile. (c) Two pairs of hind wings from O. japonicus. (d) Orosanga japonicus. (e) Branch points of 10 O. japonicus individuals superimposed in the shape of a hind wing. In the distal region, the positions of the branches are almost random.

3. Archetype wing venation pattern suggests the involvement of a self-regulating mechanism

The properties of the venation pattern discussed earlier indicate that the archetype has the autonomous property of even spacing. Many hypothetical mechanisms have been proposed for the autonomous generation of evenly spaced stripes, the best known being the RD mechanism [7]. In this mechanism, evenly spaced stripes with bifurcations emerge as nonlinear waves without any pre-existing positional information [3,5]. However, one drawback of this mechanism is that the generated pattern fluctuates substantially because the absolute position of each stripe cannot be determined. An example of such fluctuations is seen in the pigment pattern of the tropical fish Pomacanthus imperator [7], for which the RD mechanism works well. The stripes on the body of this fish contain bifurcations similar to the insect wing pattern archetype but the positions differ among individuals [7]. In contrast, insect venation patterns are believed to be strictly identical, almost similar to photocopies of one another (figure 1b), suggesting that the RD mechanism does not apply. However, it can still be argued the RD mechanism is relevant if one considers that later evolved mechanisms may mitigate its inherent randomness [6,19]. If this is true, then certain evolutionally primitive insects should express fluctuating vein patterns analogous to the skin pattern of P. imperator that can be explained by the RD mechanism.

4. Wing venation pattern of orosanga japonicus looks random, but the spacing between the veins is kept even

Using this assumption, we screened the wing vein patterns of insects in an encyclopaedia of Japanese insects [20] and the personal collection of Shigeru Kuratani (Riken CDB), comparing differences in venation patterns between left and right wings of the same insect. Orosanga japonicus in particular was found to have a vein pattern similar to the archetype (figure 1c). Although the shape of the wings of O. japonicus is symmetric (figure 1d), the vein patterns are not. As seen in figure 1c, the wing vein pattern on one side is distinct from that of other individuals and even from the other side of the same individual. A map plotting the branch points of 10 wings indicates that fluctuation is high in the centre of the distal region but low in the stem region (figure 1e). Although the positions of the branches seem to be random, the spacing between the veins is almost constant (figure 1c). This suggests that the branch positions are determined by vein spacing, not by absolute position. To test this hypothesis, we collected many O. japonicus individuals from Nagoya and Kagoshima (Japan) and plotted their wing size versus the number of veins (figure 2). The graph shows that the number of veins is roughly parallel to the wing size, indicating spacing is independent of wing size.

Figure 2.

Correlation between the wing size and the number of veins. Scatter plot of distal length versus number of veins. Regression curve, y = 2.6x + 12 (R = 0.65). Insects (Orosanga japonicus) of both sexes were collected in Nagoya and Kagoshima (Japan). The distal length of the wing and the number of veins for each individual were measured.

5. Simulation of reaction–diffusion mechanism precisely reproduced the vein pattern of orosanga japonicus

We simulated the RD mechanism to determine whether it could reproduce characteristics of the venation pattern seen in O. japonicus. When simulations are carried out in a plain square field, a non-directional labyrinth pattern is generated [3,5]. To make the pattern resemble an insect wing, we shaped the field as a tetragon instead, which is structurally similar to the archetype, and introduced diffusion anisotropy that drives the stripes along a specific direction [21] (see methods summary in the electronic supplementary material). Each cell in an insect wing has a planar polarity that provides specific directionality along the radial direction [22]. Such directionality can generate a directional preference for the diffusion.

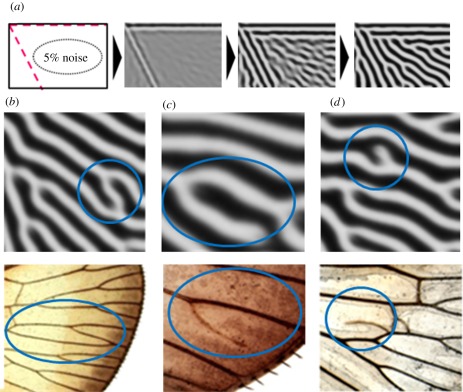
The RD simulation produced a pattern that was very similar to both the archetype and O. japonicus (compare figures 1c with 3a). The stripes ran along the radial direction and were divided so as to keep the spacing constant throughout most of the field. Superimposing branch point data from different runs of the simulation showed that variations in the branching points were small in the stem area and large in the central area of the distal region (figure 4g), which mimics the real venation patterns of O. japonicus (figure 1e). Moreover, some transient local structures occasionally observed in the simulations were also observed in the real venation patterns of O. japonicus (figure 3b,d).

Figure 3.

Similarity between the simulated and natural wing vein pattern of Orosanga japonicus. (a) Time course of the reaction–diffusion simulation (see methods for calculations in the electronic supplementary material). The initial condition for the pattern has an activator with 5% fluctuation (see numerical simulation equations of methods section in the electronic supplementary material). It is difficult to estimate the noise level in vivo. However, in this simulation, we have made sure that the level of noise does not affect the final pattern at least in the range from 2 to 20%. (b–d) Characteristic local patterns during the simulation (top) and corresponding real vein patterns (encircled; bottom). In the simulation, ‘white’ shows the high concentration of activator, which represents the veins (black lines in the real wings).

Figure 4.

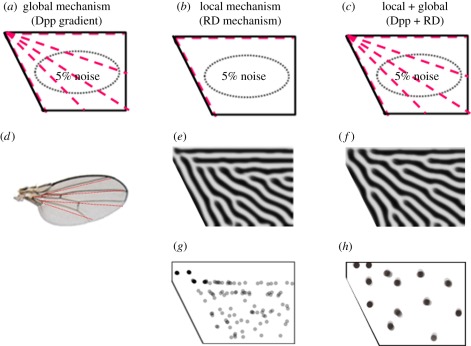
Branching patterns constructed by different models. (a) Four radial lines are given as the pre-pattern. (b,c) Initial conditions of two different simulations. (d) The resulting position of the veins from the radial lines in (a). (e,f) Resulting patterns corresponding to (b) and (c), respectively, with the branches more accurately positioned in (f). (g,h) Branch position corresponding to (b) and (c), respectively, after 10 iterations.

6. Combination of reaction–diffusion model and morphogen gradient model can generate most of the wing vein patterns seen in insects

As shown earlier, the RD model can easily reproduce the bifurcating pattern with constant spacing. However, the positions of the bifurcation are almost random. On the other hand, the morphogen gradient model can specify each position of the veins, but cannot generate the bifurcating pattern. Theoretically, it is not difficult to combine the RD model and morphogen gradient model, because both models are based on diffusion. Because the resulting periodic patterns seen in RD simulations are sensitive to local changes in the field [6,19], one can assume that the local source of the morphogen in the gradient model functions as the boundary condition or initial condition for the RD model [6,19]. Figure 4 shows the effect of combining these two models. The diffusion of Dpp released from the centre line of the wing could establish initial vein positions (vein activator maxima) at the three places, just as it does in Drosophila (figure 4a,d). RD alone would not reliably generate veins at these positions (figure 4b,e) but RD acting on an initial three-vein pre-pattern could elaborate further bifurcation and branching. This combination of two mechanisms does not change the resulting pattern drastically (figure 4c,f), but it does increase the accuracy (figure 4h).

Consequently, the variety of vein patterns here can be explained by a combination of the RD and morphogen gradient mechanisms. When positional information of the morphogen gradient dominates, simple parallel stripes are generated, as in the case of D. melanogaster. When periodic functions dominate, branching stripes with high diversity similar to those seen in O. japonicus are generated. Finally, balancing the mechanisms can generate archetype-like patterns with high accuracy.

7. Molecular basis of the hypothetical reaction–diffusion mechanism

Although simulations presented in this study suggested the involvement of the RD mechanism in the vein formation, compelling molecular evidence is required to conclude the hypothesis. As the original RD model is idealized to meet the needs of mathematical analysis, it is difficult to apply directly to a complex real system. Meinhardt & Gierer [23] showed that a system needs to include only a network that combines ‘a local positive feedback with a long-range negative feedback (LALI)’ in order to generate a Turing pattern. This is now accepted as the basic requirements for Turing pattern formation [4]. As this refinement leaves the types and numbers of reacting factors unspecified, adapting the model to a real system is easier. Especially, the interacting elements need not be limited to molecules, or even to discrete entities; a circuit of cellular signals will do just as well [24]. There is also no need for the stimulus to be provided via diffusion; other modes of transmission can achieve the same result. Other forms of signalling including chemotactic cell migration [25], mechanochemical activity [26] and neuronal interactions [27] have also been shown to be capable of Turing-like pattern formation as far as they retain the local activation and long-range inhibition rule. They all can be called relatives of the RD model. In this study, we used the RD mechanism as the representative of LALI models. Therefore, the result of the simulation does not necessarily suggest the involvement of ‘activator’ and ‘inhibitor’ in the original definition, but suggests that the rule of LALI exists in the system deciding the venation pattern.

8. Conclusion

The random venation pattern we found in O. japonicus strongly suggests the involvement of the RD mechanism, which regulates the constant spacing of wing veins. On the basis of this finding, we performed a computational study to show that a combination of gradient and RD mechanisms can produce the complex and correct wing venation patterns of modern insects. Although this idea does not yet have experimental support, the ability of the combined mechanism to reproduce a variety of wing vein patterns is impressive and suggests wider application of the Turing model than expected.