Towards an integrated experimental–theoretical approach for assessing the mechanistic basis of hair and feather morphogenesis

Abstract

In his seminal 1952 paper, ‘The Chemical Basis of Morphogenesis’, Alan Turing lays down a milestone in the application of theoretical approaches to understand complex biological processes. His deceptively simple demonstration that a system of reacting and diffusing chemicals could, under certain conditions, generate spatial patterning out of homogeneity provided an elegant solution to the problem of how one of nature's most intricate events occurs: the emergence of structure and form in the developing embryo. The molecular revolution that has taken place during the six decades following this landmark publication has now placed this generation of theoreticians and biologists in an excellent position to rigorously test the theory and, encouragingly, a number of systems have emerged that appear to conform to some of Turing's fundamental ideas. In this paper, we describe the history and more recent integration between experiment and theory in one of the key models for understanding pattern formation: the emergence of feathers and hair in the skins of birds and mammals.

1. Introduction

Pattern formation is a repetitive theme in nature, occurring at disparate spatial scales (figure 1a–c). At the scale of landscapes, patchy or striated vegetation can arise in semi-arid climates [1], competition and predation within ecosystems can structure populations into particular niches, while insects, fishes, birds and mammals have an inbuilt capacity to swarm, school, flock or herd [2]. At the scale of cells, colonies of bacteria construct highly intricate patterns in the presence of suitable food sources [3–6] and populations of cellular slime mould, such as Dictyostelium undergo a carefully orchestrated single to multi-cellular transition that ensures their longevity following starvation [7]. A common feature to these examples is that the pattern arises through a process of self-organization: the global order emerges through intrinsic local interactions, rather than some external control.

Figure 1.

Biological pattern formation. (a–c) Self-organization at various spatial scales: (a) aggregation of Dictyostelium discoideum; (b) flocking; (c) patchy vegetation in Nigeria. (d–f) Pigmentation patterns: (d) swallowtail butterfly; (e) zebra; (f) sailfish tang. (g–j) Feathers, hairs and scales: (g) peacock; (h) Vladimir the cat; (i) three-banded armadillo; (j) central bearded dragon. Image information: (d–j) K.J.P.; (a) http://en.wikipedia.org/wiki/File:Dictyostelium_Aggregation.JPG, released into public domain, accessed 21/01/2012; (b) http://en.wikipedia.org/wiki/File:Fugle,_%C3%B8rns%C3%B8_073.jpg, released into public domain by C. Rasmussen, accessed 21 January 2012; (c) http://en.wikipedia.org/wiki/File:Gapped_Bush_Niger_Nicolas_Barbier.jpg, released into public domain by Nicolas Barbier, accessed 21 January 2012.

One of the most astonishing examples of self-organization is the transformation from a single fertilized cell to a complex organism through embryonic development, an event that occurs again and again despite its dependence on the accurately timed coordination of a multitude of events, spanning spatial scales from the molecular to the full embryo. Within the wider sphere of developmental biology, morphogenesis, or the emergence of structure and form, has particularly captured the attention of theoretical scientists, with two fundamental classes of model proposed to explain this phenomenon: pre-patterning mechanisms and symmetry-breaking processes. Simplistically, these two classes can be distinguished according to the initial state of the system. In the former, structure and form are generated through a process of new patterns building on previous patterns, a classic example being the segmentation of the fruitfly Drosophila: here, the striped pattern of gene expression marking the future segments can be traced back to a maternally inherited gradient in the newly fertilized egg [8]. Symmetry breaking mechanisms, on the other hand, require no such specific initial condition: the physical and chemical interactions of the systems conspire to amplify inherent noise into regular structure. Effectively, the symmetry of the uniform steady state is broken to create ordered heterogeneity from homogeneity.

Turing's seminal paper [9] provides an elegant example of a symmetry breaking mechanism. At the heart of the model lies the fundamentally counterintuitive idea that adding diffusion to a system of reacting molecules could break the symmetry of a spatially homogeneous system to generate a regular spatial pattern. In a swoop, Turing provided a mechanism for pattern formation using only a standard biochemical toolkit of chemical reaction and molecular diffusion. Unsurprisingly, this elegant idea has been enthusiastically seized upon in the theoretical models for pattern formation, not only applied to numerous processes of developmental biology, but also scattered to fields including ecology [10] and economics [11]. Turing also coined the term morphogen to describe these elusive chemical drivers of pattern formation, although it should be noted that the concept of morphogens predated Turing, and the term is more generally recognized to denote a graded signalling molecule with the capacity to differentiate a field of cells into patterns based on its multiple threshold concentrations, rather than a specific component in Turing's mechanism.

In development, earlier references to Turing's mechanism were typically confined to a broader discussion of its merit in classic examples of patterning, such as bristle formation in Drosophila [12] and hair follicle patterning [13]. More formal applications of the ideas started appearing in the 1970s, using numerical and mathematical analyses to demonstrate its predictive capacity in patterning processes such as budding hydra [14,15], Drosophila segmentation [16] and pigmentation markings [17,18], and the study of reaction–diffusion patterning rapidly established itself as its own field. Yet, despite this interest, Turing's ideas suffered from a lack of bona fide examples at the molecular level, particularly in the wake of the biotechnology revolution of the 1980s. Furthermore, while reactions such as the Belousov–Zhabotinsky reaction had been found and shown to be capable of generating sustained and complicated oscillatory dynamics (see Maini et al. [19] and references therein), it was not until some 40 years from the publication of Turing's original paper that the theory could even be confirmed within the controlled environment of a purely chemical reaction [19–21]. In the developing embryo, the vast numbers of molecules, together with their countless interactions, implied that nature was far more tortuous than Turing's graceful solution [22] and its importance for biological patterning became somewhat contentious. Despite this, evidence from a number of systems has emerged in recent years in which the underlying molecular interactions could potentially conform to the general underlying principles, including the interactions between lefty and nodal in the determination of left–right asymmetry [23], the morphogenesis of teeth [24], the development of tracheal rings [25] and the formation of skin structures, such as hairs and feathers [26–28]. Notably, it is now more widely recognized that while the simplest formulations of the model can provide useful guidance, their assumptions mask significant underlying complexity.

The skin can be regarded as a textbook system for determining the mechanisms of patterning and integrating experiment and theory: (i) it produces a variety of periodically arranged patterns such as hairs, feathers and scales, sensory bristles, pigmentation markings, etc.; (ii) it is relatively large, accessible and can be successfully cultured, greatly facilitating experimental studies; (iii) it has a relatively simple structure and can, at least initially, be construed as a two-dimensional surface with patterning occurring at the epidermal–dermal interface; and (iv) the genetic basis of skin patterning is well documented, providing a rich tapestry of the components of the signalling pathways and their many interactions. Turing's ideas have frequently recurred in explanations of skin patterning, particularly in the context of pigmentation markings [29–35] and, the subject of the present paper, the periodic arrangement of hairs and feathers.

In this paper, we will provide a brief history of models based on self-organizing principles in morphogenesis, paying particular attention to the reaction–diffusion model of Turing. We do not use this review to cover theories related to gradients and positional information, noting that a number of recent reviews consider this area in detail [8,36–38]. We will proceed to explore the use of these models to explain the patterning of hairs and feathers in developing mammalian and avian skin, illustrating how integrating theory into the experimental cycle can be used to corroborate hypotheses and generate predictions. We will conclude with a brief discussion and argue that, for this system, we are now in a position to move away from the more simplistic modelling that has dominated the field to date, and towards a model founded on the molecular mechanisms that operate at the core of patterning.

2. Models for self-organization in morphogenesis: an overview

A fundamental goal for biological modelling is illuminating and informing our understanding of a given system. While concepts related to gradients and positional information date to Driesch at the end of the nineteenth century [39], relatively few explanations have been made into the origins of ‘pattern’ at the time of Turing's contribution. A notable exception is Wigglesworth's [40] exploration into the factors controlling the size and spacing of bristles in the abdomen of Rhodnius prolixus, proposing a ‘competitive model’ based on the underlying hypothesis that all epidermal cells start off with the same potential to specialize, although when one cell does, the surrounding cells are inhibited from the same course of action.

Pattern formation was therefore an immature field and Turing was alive to the number of liberties he was taking during the model's formulation, stressing early in the introduction that ‘This model will be a simplification and an idealization, and consequently a falsification’: modelling processes where mechanical interactions between cells were considered negligible; concentrating analysis on the relatively simple scenarios of just two or three morphogens; exploring patterning from a quasi-homogeneous initial state rather than a prior pattern; idealizing the tissue to a ‘ring’ of cells, and so on. Despite the huge advance in our biological understanding in the past 60 years, as well as the increased computational power, theoretical modellers still face the same tricky conundrum at the outset: how much detail is necessary? A biological model of some developing process, such as figure 3d, is the accumulated effort of numerous experiments, incorporating multiple components and interactions occurring at scales ranging between the subcellular and the full extent of the developing organism. Yet, these models exclude some unknown fraction of the full system's complexity and any attempt to write down a mathematical model can only ever be viewed as a cartoon of a caricature.

Figure 3.

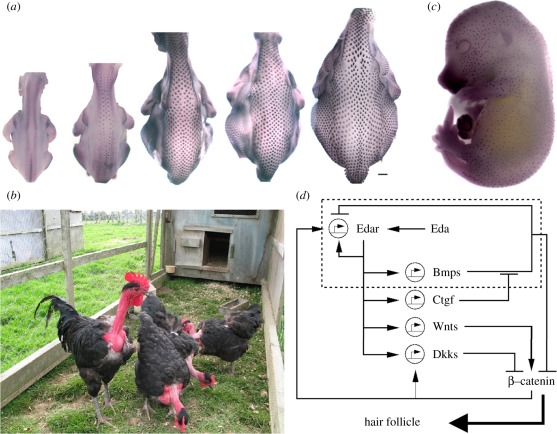
Developmental patterning of hairs and feathers. (a) Spatio-temporal sequence of feather development in the chicken embryo (stages shown range from a third to midway through the incubation period). Feather buds initially develop along two lines either side of the midline and subsequently spread into lateral regions. Note that significant growth occurs during the patterning process. (b) Naked neck chickens, conspicuous by their absence of neck feathering. (c) Mid to late gestation of the mouse embryo, stained for a marker of developing follicles (purple foci). (d) Schematic of the molecular network underpinning mouse follicle formation. The dashed region encloses a specific loop with the features of a pure activator–inhibitor system.

One method would be to apply ‘bottom-up’ thinking: formulate a mechanistic and parametrized mathematical model for the system, complete as far as the biological understanding permits. The validity of a hypothesis can then be examined in rigour, predictions can be made, and failure to reconcile experiment and theory could point the way to missing interactions and components. Against this, there may simply not be enough information to begin with, or the rapid turnover in the molecular level understanding of embryonic patterning raises the risk of a model becoming redundant before completion. Consequently, a critical initial judgement is whether a given system is sufficiently well understood to adopt this tactic. Certain developmental systems, where a substantial portion of the molecular biology is known, are now amenable to this approach. Early morphogenesis of the fruitfly Drosophila would provide one example [34,36], where the existence of a saturated genetic screening ensures that a complete set of jigsaw pieces is available and they only require to be pieced together appropriately.

For less well-understood systems, a general approach would be to adopt a ‘top-down’ method: channel Einstein's maxim that ‘a model should be as simple as possible, but no simpler’ and take a reductionist view. This would involve schematizing proposed biological interactions wherever possible and only adding extra components as demanded; for example, to test a specific hypothesis arising from a particular experiment. Classic theoretical ideas for pattern formation, such as Turing's own work and ideas of positional information and pre-patterning [39,41], may not always carry the finesse to generate a pin-sharp prediction in a particular system but can still provide an important conceptual framework within which experimental work can be targeted.

In §1, we briefly touched upon fundamental distinctions between pre-patterning and symmetry-breaking models of morphogenesis. In this section, we will expand our discussion of the latter, paying particular attention to the reaction–diffusion-based model proposed by Turing.

2.1. Turing and other chemical-based models

The pioneering model of Turing [9] functions solely through the molecular processes of reaction and passive diffusion: there is no need to take mechanical forces arising from cell migration, tissue movements, etc., into account, although these processes undoubtedly play a significant role in many processes during embryonic patterning. The experimental confirmation of Turing patterns within controlled chemical reactions, such as chloride–iodide–malonic acid [20,21] and thiourea–iodate–sulphite [42] reactions, proves the sufficiency of these minimal requirements, even though the nature of the chemical components renders such reactions wholly unrealistic within biological tissues.

While more commonly presented as a system composed of just two morphogens (see §3), the standard Turing model [9,34] comprised multiple (m ≥ 2) partial differential equations, describing the diffusion and reaction between m morphogens within some bounded region of space, :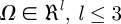

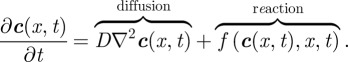2.1

In the above, 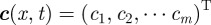is the vector denoting the concentration of each morphogen at position 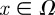and time t, D is the m × m diagonal matrix describing their diffusion coefficients, and 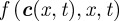describes the reactions–interactions between the morphogens. For applications, the above system is augmented with suitable initial and boundary conditions: for the latter, a typical assumption is to assume no gain/loss (zero-flux) across the boundary of Ω.

Textbook linear stability analysis for equations (2.1) yields a set of diffusion-driven instability conditions: a set of requirements for which a spatially uniform steady-state morphogen distribution, stable in the absence of diffusive terms, is driven unstable through their addition [31,34]. Under these conditions, a non-uniform distribution emerges, which is typically in the form of a stationary and periodic pattern of high- and low-morphogen regions separated by a characteristic spatial wavelength (see figure 2a,b for examples of pattern evolution), although patterns can also undergo continual evolution in time. The implicit assumption in many applications is that this pattern provides the blueprint for cell differentiation and tissue organization, for example, by acting as a positional information cue.

Figure 2.

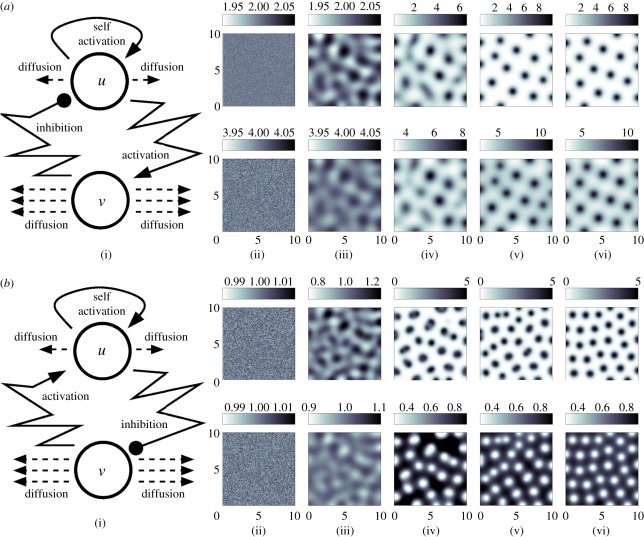
(a(i)) Schematic of the underlying interactions in a pure activator (u)–inhibitor (v) system. (a(ii)–a(vi)) Simulation of a pure AI system showing the spatial pattern for (top) u and (bottom) v at (a(ii)) t = 0, (a(iii)) t = 20, (a(iv)) t = 40 (a(v)) t = 100, at (a(vi)) t = 1000. Peaks of u and v concentration lie in phase. Simulations performed using the Gierer–Meinhardt [15] system, 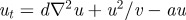and 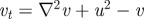with d = 0.025, a = 0.5. (b(i)) Schematic of the underlying interactions in a cross activator–inhibitor system. (b(ii)–b(vi)) Simulation of a cross AI system showing the spatial pattern for (top) u and (bottom) v at (b(ii)) t = 0, (b(iii)) t = 10, (b(iv)) t = 20, (b(v)) t = 50, at (b(vi)) t = 1000. Peaks of u and v concentration lie out of phase. 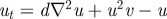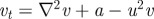Simulations were performed using Schnakenberg [43] kinetics, and , with d = 0.025, a = 1.0. For both sets of simulations, initial conditions were set at a small perturbation of the uniform steady state and zero-flux conditions were employed at the boundaries of a square field of dimensions 10 × 10.

In its most modest and familiar form, and our building block for the present paper, Turing's model requires just two reacting and diffusing components to operate, albeit under a set of precise constraints. A classical and intuitive explanation is the short-range activation, long-range inhibition concept popularized by Gierer and Meinhardt [15,44] (and, independently, by Segel & Jackson [45] in an ecological setting). For example, we suppose that the two reactants adopt the roles of an ‘activator’ and an ‘inhibitor’, respectively, with the activator activating both its own upregulation (self-activation), as well as that of the inhibitor, and the inhibitor downregulating the activator (figure 2a). Crucially, if the activator has a shorter range—it diffuses less rapidly than the inhibitor—then self-activation can dominate locally, while faster inhibitor diffusion leads to a long-range suppression and the emergence of spatial structure.

More generally, two component systems capable of patterning through Turing's mechanism comprise one more slowly diffusing reactant with ‘self-activating’ (such as autocatalysis) properties and inter-component interactions structured into one of two forms—pure or cross activator–inhibitor systems—according to the loop structure [46] (cf. figure 2a,b). The simplicity of these ideas has provided a useful framework for examining whether a given system could form a pattern: in §3, we show how searching for processes of activation and inhibition has shaped experimental research into the mechanisms underlying aspects of skin morphogenesis. At the same time, care should be taken before equating behaviour of the much broader reaction–diffusion model (2.1) with the two-component activator–inhibitor systems. For example, a constraint such as the distinct ranges of diffusion required in the latter relaxes when moving to the greater than two components permitted by the general model (2.1) [47,48].

Nearly, all applications and analyses of Turing's mechanism set up the model as a coupled system of continuous partial differential equations, as in system (2.1). In the context of embryonic development, continuous formulations are an abstraction of the in vivo tissue environment and biochemistry, where distinct elements of a signalling pathway can occur inside, outside or at the cell membrane, and any diffusion-like transport will be contingent on interactions between molecules and the extracellular matrix or the transfer of molecules between cells, etc. In fact, Turing first proposed a discrete cell reaction–diffusion mechanism before proceeding to the ‘continuous’ idealization. Specifically, Turing formulated a system of ordinary differential equations for the dynamical change of each morphogen in each cell in a hypothetical ring, proposing transfer of morphogens between adjacent cells based on their local concentration difference. An extension of Turing's ideas to more generalized discrete cellular networks was undertaken by Othmer & Scriven [49].

Other discrete cell models of pattern formation have also been proposed, relying on more explicit descriptions for the signalling interactions between cells. In juxtacrine signalling, the membrane to membrane binding between a ligand on one cell and its associated receptor on a neighbour triggers an internal signal transduction pathway which could, for example, subsequently feed back to modulate the ligand and/or receptor expression at the cell surface [8]. For appropriate interactions, models of such signalling also show symmetry-breaking phenomena, with a quasi-homogeneous population taking on alternating expression levels [50,51]. Molecular diffusion is not required and the resulting patterns appear to be somewhat distinct, with the alternating salt and pepper pattern that arises typically separated by just a few cells rather than the broader wavelengths that can potentially be generated by Turing's model.

2.2. Mechanical-based models

It is appropriate to note that Turing's proposed model was for the chemical basis of morphogenesis: the mechanism generates only a biochemical template that morphogenesis slavishly follows and the visible manifestation of form would arise through the subsequent differentiation of cells into various subtypes, with their distinct mechanical and growth characteristics. Other models for morphogenesis explicitly incorporate the dynamics of cells, such as their growth, movement and adhesive properties, together with their interactions with the environment. In certain instances, their interplay can also conspire to break the symmetry and create spatial pattern from uniformity, a simple instance being the aggregation of a population through cell–cell adhesion. For multiple populations, this adhesion can generate more complicated spatial patterning through a process of cell-sorting, commonly attributed to a process of differential adhesion [52], in which the distinct adhesive properties of the various populations drive the rearrangement of the populations through energy-minimizing principles akin to the separation of oil and water. Mathematical models for adhesion, both at the level of individual cells and continuous populations, validate the inherent capacity of adhesion to cluster and sort cell populations [53,54].

Chemotaxis, and related forms of directed cell movement, offers another mechanism for self-organization. Insight into chemotaxis-induced pattern formation has primarily resulted from studies into certain bacteria species, such as Escherichia coli and Salmonella tymphirium [3–6] and the cellular slime mould Dictyostelium discoideum [7,55]. Mathematical models [56–58] reveal that at the heart of self-organization lies a powerful feedback mechanism in which the secretion by cells of their own chemoattractant (or degradation of their own chemorepellent) can mobilize a dispersed population into self-supported aggregations. For Dictyostelium, the same chemotaxis mechanism that aggregates the initial population also plays a critical role in the subsequent differentiation and organization of diverse cell subpopulations [7]. A number of lines of enquiry have pointed to chemotaxis playing a role in various processes of embryonic development, including gastrulation [59] and neural crest migration [60].

Moving beyond the relative simplicity of chemotaxis, the mechano-chemical theory of pattern formation pioneered by Oster et al. [61] embraces many of the above concepts (chemical patterning, adhesion and other mechanical interactions) and more (e.g. contractile forces exerted by cells on their surroundings), assuming that the distinct mechanisms that contribute to morphogenetic patterning are not so trivially separated. While, unsurprisingly, mathematical descriptions of the mechano-chemical framework can quickly become complex, they provide enormous scope and have been applied to a wide variety of embryonic processes, including skin patterning, wound healing, skeletal patterning and vasculogenesis (see Murray [31,62] for reviews).

3. Modelling morphogenesis: hair and feather patterning as case studies

The skin of birds and mammals typically carries hair or feathers which first form during embryogenesis. This development is achieved through communication between the two tissue layers of the skin: the dermal layer and the overlying epidermis. At the earliest stages of skin patterning, dermal–epidermal signal exchange results in the formation of localized condensations of epidermal cells, which undergo rapid proliferation to form feather buds or follicle primordia. Subsequent morphogenesis then results in the formation of a mature feather or hair [63,64].

Having explored in more general terms some of the common self-organizing models, in this section, we move on to a key case study: hair and feather patterning in the developing skin of mammals and birds. We tread swiftly through the history of the field, providing a brief account of the salient biology and the contributions of modelling through the decades-long and ongoing process of integrating experiment and theory. This section also acts as the prelude to the more detailed section that follows, where we demonstrate the specific application of reaction–diffusion ideas and its capacity to both recapitulate and predict experiment.

3.1. Biology and modelling of sheep hair follicle patterning

While recent attention has shifted to the de facto developmental model of mice, much of the earlier work on hair development in mammals was performed for sheep, an animal of economic significance in terms of wool production. Hair follicles in sheep first appear approximately 60 days following conception and advance through various stages from initiation to the fully formed fibre [65]. The very first follicles develop at approximately equal distances from their neighbours, with subsequent follicles developing in a series of waves over the following three weeks. Within-pattern patterning occurs, with later generations of follicle initiation producing two further follicles either side of a primary follicle to form a trio group [65].

Early attempts to explain follicle initiation and their equidistant arrangement borrowed heavily from analyses of the spatial distribution of sensory bristles in insects such as Drosophila and R. prolixus. Claxton [13] demonstrated a favourable comparative analysis between follicle-initiation sites and the predictions based on the competitive model of Wigglesworth [40] described earlier. This was expanded upon in a more formal manner by Claxton & Sholl [66], yet the model required additional assumptions and complexity to generate the timing and arrangement of the characteristic trios.

A specific application of Turing's mechanism to explain follicle patterning, again for sheep, was pioneered by Nagorcka and Mooney in a series of papers beginning in the early 1980s [67–72]. Early work explored the cross-sectional pattern within an individual adult hair fibre, proposing that a reaction–diffusion system operated inside each developing hair fibre bulb and generated a pre-pattern that triggers cell differentiation [67]. Despite a lack of information on the precise molecular components, comparative simulations supported the idea that this could pattern the forming fibre. Further papers in the series [68–72] expanded the application of reaction–diffusion models to consider the skin-wide spatial distribution of both primary and secondary wool follicles, as well as the positioning of structures such as sebaceous glands in the bulb. Effectively, previously formed follicles were proposed to create a fixed ‘organizing’ template around which later follicles would form, indicating that a common mechanism could be responsible for many aspects of hair morphogenesis.

Despite this early work, matching the developing wool follicle pattern to Turing-type simulations in terms of their intermediate stages and end result, studies of wool development have declined in recent years owing, in no small part, to the relative impracticality of sheep as an experimental system. Instead, attention has shifted to feather bud formation in birds and hair follicle formation in mice—a direct consequence of their positions as ‘model organisms’. Refer to the study of Rogers [73] for a recent review of sheep hair patterning, and a plea for its rediscovery.

3.2. Biology and modelling of chick feather bud patterning

Formation of the feather bud pattern in the developing chick embryo has been used extensively in theoretical and experimental studies of pattern formation, with the accessibility of the embryo itself granting it a dominant place in studies of development. Feather development begins with the previously undetermined cells in the skin acquiring the cellular fate that leads to the formation of feather buds, which grow rapidly out from the surface of the skin to produce a feather and surrounding follicle. As for sheep, buds develop in a specific spatial and temporal sequence [74]: the first buds to form are arranged in regularly spaced intervals in two anterior–posterior stripes either side of the dorsal midline, with further rows of buds subsequently added in a wave-like fashion that spreads into lateral skin regions (figure 3a). A variety of models, including those based on mechano-chemical [75] and reaction–diffusion [69] principles have been proposed, capable of capturing the spatial and temporal patterning of the feather array. Further extensions have integrated these two modelling approaches [76–78].

At the time of these studies, little was known regarding the genes and molecules responsible for embryonic development. Yet, a seismic shift was taking place, beginning with the ground-breaking screening which revealed the critical genes driving early morphogenesis of the fruitfly Drosophila [79]. Combined with a host of further technical advances, recent decades have unleashed a torrent of information on the genes and molecules that drive pattern formation, not only in Drosophila, but also in the other principal model systems of development, including the chicken and mouse. At this point, we remark that notation varies between species when referring to individual proteins, protein families, genes, etc., and we have preserved this variation to facilitate comparison with cited studies.

In the context of feather bud morphogenesis, this has led to one of the first biological systems in which lines can begin to be drawn between the theoretical concepts of Turing's mechanism and molecular biology, starting in the 1990s. With the underlying principles of activator–inhibitor systems in mind, Jung et al. [80] searched for candidate regulators involved in feather bud formation by focusing on signalling pathways known to operate widely during the development of many organs and in diverse animal species. Based on the gene-expression patterns at the sites of the forming feather buds, sonic hedgehog (SHH) and fibroblast growth factor-4 (FGF-4) were identified as candidate activators and bone morphogenetic protein-2, 4 (BMP-2,4) as possible inhibitors, with their initially widespread production followed by their co-restriction to developing feather primordia as patterning progresses consistent with the operation of a pure activator–inhibitor system (cf. figure 2a). Local application of recombinant proteins from beads on the skin also suggested a greater range of action of the inhibitors over the activators [80–82]. Furthermore, the capacity of disassociated and reconstituted skin to form buds favours a truly self-organizing mechanism acting during skin morphogenesis [81].

With this greater foundation, more recent modelling has been immersed into an integrated experimental/theoretical framework, with mathematical variables in a model more formally linked to specific molecular components. Michon et al. [83] have developed an extended reaction–diffusion framework, with BMP7 and BMP2 fulfilling the roles of activator and inhibitor and augmented by additional equations to describe the proliferative and migratory behaviour of dermal cells, and demonstrated that the model can replicate experimental in vivo data. Lin et al. [84] (see also Baker et al. [85]) have linked experimental data and modelling for the extracellular signal-regulated kinases-dependent chemotaxis of mesenchymal cells in the formation of feather primordia. Results of Mou et al. [86] support a reaction–diffusion-based mechanism underpinning patterning, combining experiment and theory to demonstrate how retinoic acid (RA) can regionally tune parameters in a reaction–diffusion system (see §4).

Moving beyond the formation of a spatially periodic pattern of two-dimensional placodes distributed across the skin, reaction–diffusion ideas have also been proposed to explain the subsequent within-placode patterning which will ultimately lead to a fully formed feather [28,87]. Harris et al. [28] obtained molecular support that SHH and BMP2 operate in an activator–inhibitor type pairing within the feather bud epithelium. Augmented by simulations of a reaction–diffusion model, it is suggested that these interactions form a core component of the mechanism that generates the tubular pattern of `barb ridges’ that determines shape and function of the feather. Beyond the structural formation of the feather itself, reaction–diffusion models have further been proposed as a mechanism for the pigmentation patterning within a feather [87], although identities of potential molecular components are lacking. Similar to sheep wool formation above, this hints that a common set of principles may operate at distinct levels and scales to control multiple aspects of feather patterning.

3.3. Biology and modelling of mouse hair follicle formation

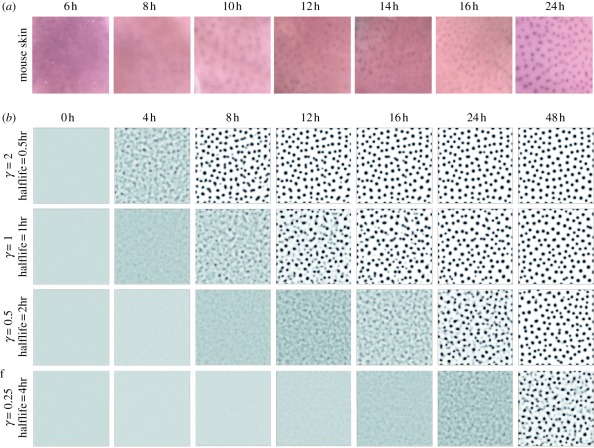
As the dominating mammalian model, understanding morphogenesis in the mouse has enormous significance when it comes to determining our own development. Advantageously, the mouse offers unique genetic tools, such as the ability to create targeted mutations, which have greatly contributed towards piecing together the molecular control of development. As for sheep, mouse hair development proceeds through several rounds of follicle formation, with the primary hair follicles appearing in an approximately equidistant pattern between 13 and 16 days following fertilization and secondary and tertiary follicles forming later in the expanding regions surrounding the primary follicles (figure 3c) [88]. Again, models based on reaction–diffusion ideas are highly adept at replicating experimental observations and features of follicle patterning [27,89]; for example, see figure 5.

Figure 5.

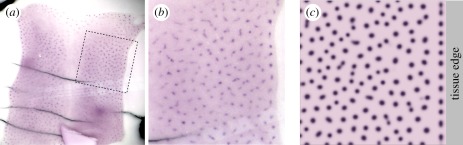
Comparison between experimental and model patterns. (a) Cultured embryonic mouse skin, stained for a marker of developing follicles (purple foci). Note the clear lines of foci aligned parallel to the cut tissue edge. (b) Blow-up of the dashed square in (a). (c) Simulation of equations (4.1) to (4.4). The right-hand side boundary is set to be ‘lossy’, with components of the reaction–diffusion model assumed to flow across the tissue edge boundary, with zero-flux conditions on the remaining three. Simulations were performed using parameters drawn from set 1 of table 1, except 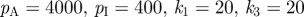and solved on a square field of dimension 3 × 3. For experimental details, see the study of Mou et al. [26].

Having defined possible activatory–inhibitory signalling pathways in the chicken, together with the genetic identification of additional pathways dedicated to skin development in the mouse, the logical next step was to explore whether interactions between these pathways were consistent with the theoretical network topologies of figure 2. Mou et al. [26] paid attention to the signalling pathway composed of the extracellular ligand, Eda, and its receptor, Edar, and its interaction with certain members of the BMP family. Edar expression is critical for primary follicle patterning with Edar signalling resulting in both a rapid positive feedback loop that stimulates both its own expression as well as production of the inhibitors, Bmp4 and Bmp7. Diffusion transports these extracellular signals laterally where they strongly repress Edar transcription and, hence, suppress hair follicle fate. These interactions—a locally operating autocatalytic process coupled to a long-range inhibitory mechanism—appear to conform to the underlying principles of an activator–inhibitor system. Furthermore, this work has also revealed a locally acting BMP-inhibiting process driven by Edar signalling, mediated through the BMP-binding protein connective tissue growth factor (CTGF). Mathematical modelling [48] has demonstrated the sufficiency of the Edar–BMP–CTGF interactions in producing a periodic pattern, at least under certain constraints.

A combination of mathematical modelling and experimental work by Sick et al. [27] has further enhanced our understanding of follicle patterning, uncovering a second potential reaction–diffusion loop that operates both during primary and later stages of follicle patterning. Here, a proposed mechanism counters the activating action of the Wnt/β-catenin pathway against the inhibiting actions of Dkks to localize the developing follicles. Yet, rather than operating in complete independence from the above Edar–BMP–CTGF network, these two loops are proposed to be interlocked, with Edar activating the expression of Wnt10a, Wnt10b and Dkk4, encoding β-catenin pathway ligands and an antagonist, and β-catenin activity subsequently stimulating the expression of Edar itself [90–92].

Overall, these results are inching us towards a detailed knowledge of the molecular processes underpinning hair patterning (figure 3d) and hint at a significantly more complex activator–inhibitor framework than captured in the most simplified realizations of Turing's scheme. It appears that multiple signalling pathways take on the distinct roles of activators and inhibitors, acting together to localize the positions of follicles.

4. Modelling morphogenesis in practice: reaction–diffusion systems applied to skin morphogenesis

The striking qualitative resemblance between the arrangement of feather buds and hair follicles and the patterns produced by reaction–diffusion systems (cf. figures 2 and 3) is compelling. While such prima facie evidence alone is by means sufficient for proof—other plausible mechanisms such as chemotaxis and mechano-chemical models can generate a similar outcome—it has offered a crucial line of enquiry to both biologists and modellers. For biologists, does an underlying network of interactions operate according to the precepts of Turing's theory? For modellers, how well does the theory hold up when confronted with a more rigorous examination?

Regarding the first, we have already summarized some encouraging data that implicate reaction–diffusion networks in the patterning process. In mouse skin, at least two network loops appear to conform to the principles [26,27] while in the chicken, although specific pathways have not been firmly established, the skin's capacity to self-organize and the identification of potential activators (such as Eda, Wnts, FGFs) and inhibitors (e.g. BMPs, Dkks) in mouse or chicken skin provides encouragement. In this section, we aim to highlight the manner in which modelling can both replicate and predict certain features of skin patterning.

4.1. Model formulation

For the purpose of the present review, here we concentrate on the simplest top-down approach founded on Turing's ideas: two principal components (an activator, A and inhibitor, I) both undergoing spatial diffusion and reaction. Following a philosophy of schematic modelling, these components and their interactions need not be strictly considered to represent single molecular entities, rather they can loosely schematize the multiple components and their pathways that generate an overall activatory (or inhibitory) contribution. This framework does, however, still allow us to simulate a specific experimental procedure: for example, application of exogeneous BMP to explanted skin (figure 6) can be recapitulated in silico through a simple additive term to the equation describing the inhibitor component. As we aim to show, this schematic modelling can still provide useful insight. Our simple model is given by:

4.1

and

4.2

In the above, D_A and D_I are the diffusion coefficients of the activator and inhibitor, characterizing their respective spatial range of action: most directly this would be mediated via molecular diffusion in the extracellular space, but it could also be a simplification for other forms of molecular transport, including direct cell to cell passage of signalling molecules through membrane channels such as gap junctions. The kinetic functions f (A, I) and g (A, I) are selected according to the proposed network interactions, and can be modified as appropriate to simulate some experimental perturbation. Taking the interactions between Edar and BMPs in mouse hair follicle specification (cf. boxed region in figure 3d), we observe the hallmarks of a pure-type activator–inhibitor system and choose kinetic terms accordingly, exploiting the well-characterized Gierer–Meinhardt [15] type model:

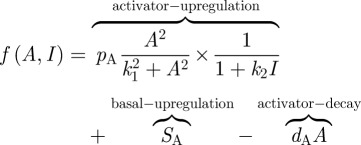4.3

and

4.4

The first term in equation (4.3) incorporates both the autocatalysis of the activator and the inhibition of autocatalysis by the inhibitor. Second and third terms, respectively, represent an independent or basal level of activator upregulation and decay of activity. In the second equation, the first term models the upregulation of inhibitor by the activator while the latter terms again describe basal upregulation and decay. Each of the parameters in the above model holds a biological interpretation (table 1). Equations (4.1) to (4.4) need to be augmented with suitable initial and boundary conditions and our default will be small spatially random perturbations about the uniform steady-state solution for the former, and zero flux (i.e. no loss/gain) for the latter. Of course, specific applications should take into consideration any proposed role for prestructure in pattern initiation, such as the initial appearance of nascent chicken feather buds along the midline.

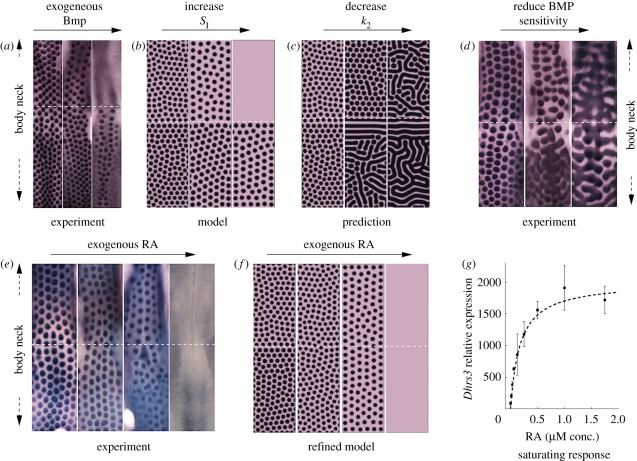
Figure 6.

Figure illustrating the test–predict–refine cycle for modelling. Experimental data are reproduced from the study of Mou et al. [86] and we refer there for full details. Modelling in (b) and (d) is similar to that produced earlier [86], however performed for equations (4.1) to (4.4). Modelling in parts (e–g) is new. (a) Recreation of a ‘naked-neck’ in wild-type skin through application of exogenous BMP12. From left to right: control (no exogenous inhibitor); +20 ng ml^–1; +40 ng ml^–1. (b) In silico hypothesis testing through simulating equations (4.1) to (4.4) with k₂ varying smoothly from neck 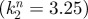to body 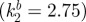to replicate the hypothesized variation in inhibitor sensitivity. Exogenous inhibitor is increased from left to right: control, S_I = 1; S_I = 1.5; S_I = 2. (c) A model prediction showing the impact of uniformly reducing inhibitor sensitivity. From left to right: control, 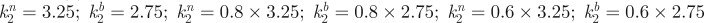. (d) An experimental reproduction shows the same qualitative behaviour. From left to right: control; +8 μM DM, +5 μM SB; +10 μM DM, +5 μM SB. DM, Dorsomorphin; SB, SB203580. (e) RA, which is normally only produced by neck skin, sensitizes the skin to the inhibitor. From left to right: control (no exogenous RA); +0.2 μM RA; +1.0 μM RA; +5.0 μM RA. (f) A refinement of the model in which k₂ saturates according to equation (4.5) and recapitulates the experiment. We set k_max = 4, K = 5 and set varying RA levels for neck (RAⁿ = 20 + RA^e) and body (RA^b = 10 + RA^e) regions. From left to right: control, RA^e = 0 ; RA^e = 20; RA^e = 100; RA^e = 500. (g) Demonstration of saturability of RA signalling in cultured chicken skin. Each data point show the response of the skin to increasing concentrations of RA, measured through the relative expression of the RA response gene Dhrs3. Each point shows the mean expression and error bars, respectively. The RA dose–response curve was generated by quantitative PCR method using FastStart Universal SYBR Green Master Mix (Roche). The primer sequences used were: for Dhrs3, 5′-CTCTGCTGCCACCCAAAC-3′ and 5′-TGGTCTCCTTCAGGCATTTC-3; and for Gapdh, 5′-ATCTTTAACCACTGCTCCTTG-3′ and 5′-CATGCTGAGCCTATTCACTG-3′. The dashed line plots the saturating form of the function given by equation (4.5), with k_max = 2000, K = 0.175.

Table 1.

Parameters, definitions and values employed for simulations. (For set 1, we do not assume any specific dimensional units. Set 2 is a representative dimensional set used solely for illustration and not based on specific data (concentration units remain unspecified, denoted by X). Each parameter marked with an asterisk (*) is scaled by γ for the simulations in figure 7.)

parameter	definition	set 1	set 2
DA	activator diffusion coefficient	0.00025	5 × 10−7 mm2 s−1	*
DI	inhibitor diffusion coefficient	0.0125	5 × 10−9 mm2 s−1	*
pA	maximum activator upregulation rate	1000	1X s−1	*
pI	maximum inhibitor upregulation rate	100	0.1X s−1	*
SA	basal activator upregulation rate	0	0	*
SI	basal inhibitor upregulation rate	1	0	*
dA	activator degradation rate	1	(In 2) h−1	*
dI	inhibitor degradation rate	1	(In 2) h−1	*
k1	activator auto-upregulation coefficient	10	20X
k2	sensitivity of activator to inhibitor	3	2.5X−1
k3	inhibitor upregulation coefficient	10	20X

4.2. Parametrization

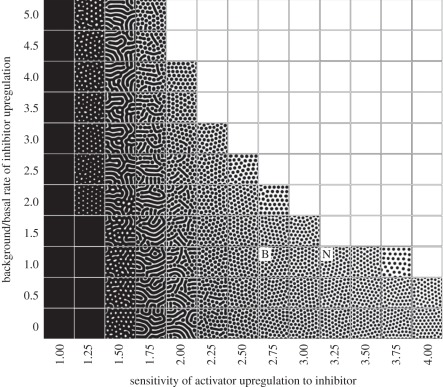
Linear stability analysis (e.g. see [31]) can be applied to establish that diffusion-driven instability will occur for equations (4.1) to (4.4), provided that parameter values lie in a suitable region of parameter space. Such analyses therefore provide a useful checkpoint for determining if a given mechanism has the potential to generate pattern. To illustrate this, in figure 4 we demonstrate the patterns formed when varying two of the parameters and holding the remainder fixed. Notably, patterning is confined to certain regions of the parameter space, with regions outside this generating spatially uniform patterns of either high or low expression (relative to some normalized level). Furthermore, the pattern generated varies over a range, including ‘spots’, ‘stripes’ (or ‘labyrinthine’) and ‘holes’. The question as to whether spotted or striped patterns form has been subject to some more rigorous investigation, with the dominating nonlinearity in the reaction believed to be a major determinant [93–95].

Figure 4.

Turing patterns for the reaction–diffusion system (4.1) to (4.4). Parameters fixed according to set 1 in table 1 except S_I and k₂ (varied as indicated). For each plot, equations (4.1) to (4.4) were solved until a fixed time and activator concentration was plotted using a black (high > 3) to white (low = 0) scale. Patterns develop along a central band, with regions left and right generating ubiquitously high and low activator levels, respectively. Notably, we observe a broad spectrum of patterning, ranging between spots, fusions, stripes and holes. Points marked B and N refer to prospective body and neck parameter sets (see text for details). For all simulations, initial conditions were set at a small perturbation of the uniform steady-state and zero-flux conditions were employed at the boundaries of a square field of dimension 2 × 2.

The above clearly reveals the criticality of model parameter values in the generation of Turing-type spatial patterns: while qualitatively similar patterns to those observed experimentally can be obtained, this will require parameters to be appropriately tuned. Furthermore, in vivo patterning has clear quantitative features, occurring at the spatial and temporal scales relevant to developmental processes: the initially homogeneous mouse skin becomes patterned with the early indicators of the primary hair follicle array over approximately half a day.

Ideally, given a working model of the underlying molecular network for follicle/bud patterning, dimensional model parameters would be determined through targeted experiments in the developing skin and corroboration of a hypothesis could be achieved by exploring whether a mathematical model of the network populated with these numbers could quantitatively recapitulate the observed pattern. As remarked earlier, such approaches are now possible in more established systems such as the formation of morphogen gradients during early Drosophila development. However, for hair and feather patterning, the detail is lacking and, while diffusion coefficients [96–98] and half lives [98,99] have been estimated for other molecular components in other biological systems, their relevance, say, to mouse skin patterning would be highly debatable.

For the purposes of the simulations presented in this section, we will generally confine ourselves to specifying arbitrary and dimensionless sets, concentrating instead on how the framework can still provide useful qualitative information in terms of corroborating hypotheses and generating testable predictions. We will subsequently proceed to consider briefly the implications of a specified quantitative set, demonstrating how a tuned set of parameter values would be necessary to produce a pattern within developmentally relevant spatial scales and time frames.

4.3. Qualitative modelling: demonstration of the modelling workflow

As described earlier, a substantial literature has grown in the decades following Turing's paper, specifically applying the ideas to skin patterning. In recent years, this work has morphed into one more integrated with experiment, targeting the modelling to test specific hypotheses. Given a model capable of capturing basic features of a process, most studies proceed through a test–predict–refine cycle, in which a hypothesis is tested according to the existing data and then used to generate experimental predictions and model refinement. We use this section to illustrate this process; we generally take for granted the capacity for reaction-diffusion based models to capture basic features of skin patterning, such as the spatio-temporal sequence of patterning and refer to the literature outlined in the previous sections.

4.3.1. Replicating core features

Figure 5a shows a fragment of cultured embryonic mouse skin, stained to reveal the foci of presumptive follicles. Notably, we observe activated foci (see expanded region in figure 5b) forming in lines running close to and in parallel to the boundary edge, with those further from the edge showing no such global alignment. Under the default assumption of zero-flux boundary conditions, equations (4.1) to (4.4) do not typically generate such a precise alignment, yet intuitively, the experimental set-up would impose a specific boundary condition along the line of cut: for example, we could hypothesize that extracellular molecules would flow over the edge and out of the patterning field. We can test this assumption by modifying the boundary conditions in equations (4.1) to (4.4) to incorporate a ‘lossy’ edge, where components are assumed to flow across the edge at a rate proportional to their boundary concentration. Simulations (figure 5c) demonstrate that this recreates the experimentally observed pattern, with the edge following follicles in both simulations and experiments lying closer to the edge than interior follicles.

4.3.2. Test–predict–refine

To illustrate the test–predict–refine cycle, we review previous work in our group exploring the across-body pattern variation. We note that while the experimental data reproduced in this paper comes from the set originally published earlier [86], modelling results are newly generated for the specific formulation given by equations (4.1) to (4.4), rather than that employed by Mou et al. [86].

Regional variation is a common feature in patterning: in figure 1, we note the distinct spatial scales of whiskers and fur on the cat and the regionally varying pigmentation on the sailfish tang; our own bodies show (often unwanted) large variations in hair density from one skin region to the next. Reaction–diffusion systems containing spatially varying parameters [100–102] or specific boundary conditions [46] can give rise to different patterns in distinct portions of a field, suggesting a potential origin. In the study of Mou et al. [86], we tackled this problem experimentally and theoretically through a study of the naked neck chicken (figure 3b). Unsurprisingly, naked necks take their name from a lack of neck feathering (a feature that improves tolerance to hotter climates) and resulting from an increase in BMP signalling (which inhibits feather formation) during development.

Surprisingly, wild-type chicken skin treated with the right dose of exogeneous inhibitor (BMP) recreated the naked neck phenotype (figure 6a), rather than completely obliterating feathering. This suggests that normal neck skin is more sensitive to the inhibitor than the body, with this ‘cryptic’ pattern only being revealed by targeted experiments: the feather density of normal chickens varies only slightly between neck and body in embryonic skin, with differential growth further masking any variation in the adult.

To test whether this hypothesis is supported by our model (4.1) to (4.4), we reappraise figure 4. According to our hypothesis, neck and body should occupy two distinct points in parameter space: specifically, we expect the neck to occupy a location to the right of the body, in the direction of increasing sensitivity to the inhibitor (for example, positions ‘B’ and ‘N’). Unperturbed, both locations would reveal a similar arrangement of activated foci, yet treatment with increasing levels of exogenous inhibitor would shift each point upwards (increasing the background level of inhibitor, S_I) and an expected loss of neck patterning at a lower concentration than the body. Performing this process through simulations of equations (4.1) to (4.4) (see also Mou et al. [86]) on a two-dimensional field in which k₂ steps smoothly between simulated body and neck regions shows exactly this phenomenon, reproducing the experimental observations and validating the hypothesis (figure 6b).

Determining the impact of parameter variation (sensitivity analysis) as in figure 4 therefore allows us to intuitively understand experimental perturbations, yet it can also generate testable predictions: our proposed locations for the body/neck also suggests that decreasing sensitivity to inhibitor across the entire patterning field would correspond to a shift left in figure 4, and the intuitive expectation of fused/labyrinthine foci appearing first on the body and later on the neck; see figure 6c for a simulation in which this in silico prediction is performed. An experimental test (figure 6d) confirms this phenomenon, demonstrating the capacity of equations (4.1) to (4.4) to both validate and predict.

Further work by Mou et al. [86] revealed that higher neck sensitivity is mediated through RA signalling, which inhibits feather formation through sensitizing the skin to the inhibitor. Effectively, RA acts as a tuner that locally modulates the feather pattern and parameter k₂ can be reinterpreted as a function of RA. Exogenous RA increases the sensitivity of the skin to inhibitor, with eventual loss of feather patterning (figure 6e) and, with respect to figure 4, we shift to the right. Yet, while in silico experiments (assuming a linear relationship between k₂ and the regionally varying RA level) do capture feather loss when the exogenous level of RA is increased, the observed convergence between neck and body is not captured. This failure to recapitulate a new experimental result requires a model refinement: inevitably, any direct/linear correspondence between a single parameter (k₂) and a specific molecular entity (RA) is overly simplistic and the response would be (highly) nonlinear, with factors such as saturation coming into operation. To test this, we considered simple saturation in dependence on RA for k₂ on neck–body regions:

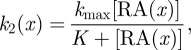4.5

where [RA (x)] is the varying RA level as we move from body to neck, and k_max, K constants. Simulations (figure 6f) show that the above can account for the convergence in the neck–body regions and further experiments to determine the functional response of skin to RA reveals a similar saturation (figure 6g).

4.4. Quantitative modelling: patterning in biological timescales

Above, we have shown how a broad-brush modelling approach—lumping together multiple components, schematizing pathways into simple interactions, ignoring biological scales, etc.—can provide a useful testing ground for guiding experimental studies. The schematic model (4.1) to (4.4) is clearly capable of replicating and predicting pattern formation, yet we should remain mindful of its inherent simplifications and the consequences of moving towards a more rigorous and quantitative test. For example, by ignoring the spatial and temporal scales of pattern formation, we lose a crucial source of information for assessing the predictive capacity of the model.

Tissues form at the spatial and temporal scales relevant to development: for example, the molecular pattern marking locations of primary hair follicles for mouse skin appear within about 12 h from an (assumed) unpatterned state, see figure 7a and [26]. While it would be misleading to suggest that in vivo mouse and feather bud patterning develop completely de novo (i.e. from a completely homogeneous field)—mammary glands appear to act as an organizing centre about which primary hair follicles first form in the mouse, while chicken feather placodes develop initially along the midline before becoming added laterally—dermal condensations in disassociated and reconstituted embryonic chicken skin synchronously appear some 24 h later, suggesting that completely de novo patterning can still take place within a day [81,103].

Figure 7.

(a) Experimental timecourse of Edar expression on a portion of treated mouse skin of field dimension 1 × 1 mm; data originally published in Mou et al. [26]. Note that each time point has been drawn from a distinct experimental dataset. (b) Simulations of equations (4.1) to (4.4) on a square field of dimension 1 × 1 mm showing pattern evolution over 48 h and based on the dimensional parameters drawn from set 2 in table 1. Each frame plots the activator expression, using a white (low)–blue (medium)–black (high) colour scale. Parameters are illustrative and chosen to yield a comparable density to the primary hair follicle pattern shown in (a). For each row, the parameters marked with an asterisk (*) as in table 1 have been scaled by the same constant γ, to produce the same spot density at each parameter set. We also label the corresponding molecular half lives for each value of γ. Initial conditions were set as a small (1%) random perturbation of the uniform steady state, with zero-flux conditions imposed at the domain boundaries.

The speed at which a reaction–diffusion model forms a pattern is a relatively unexplored area. Page et al. [104] have performed a general analysis, casting doubt on their ability to explain a completely de novo mode of patterning for certain embryonic events and suggesting that some accelerating factor (e.g. previous patterning via imposed initial conditions or spatially varying parameters) would be required. Furthermore, incorporating further biological details, such as the delays imposed by gene expression, can further slow down the speed of patterning [105,106].

Intuitively, it would seem unlikely that components operating in some reaction–diffusion system with half-lives of around 10 h could form a sufficiently robust pattern within the same time frame: sufficient turnover of the core components would be expected. In fact, this can be illustrated more clearly by plotting the results of dimensional reaction–diffusion systems as shown in figure 7b. We solve equations (4.2) to (4.5) on a square field of 1 × 1 mm over a timescale of 48 h and, for each simulation, scale certain parameters by the same constant, γ, such that a follicle-like pattern is generated with a foci density comparable with the mouse primary hair follicle pattern. Using the half-lives as guiding parameters (noting that other system parameters are scaled similarly), we observe that for a pattern to be generated within approximately 12 h, many parameters must be suitably bounded. While mindful that the modelling here is confined to the schematic model, this illustrates that moving from a qualitative to a quantitative assessment of a model allows us to more rigorously explore the constraints under which particular processes may be forced to operate.

5. Discussion

Turing's model for morphogenesis has proved to be a rich and powerful tool, providing a mechanism in which pattern can be conjured from uniformity using only simple molecular processes. The original paper is possibly rather obtuse to many experimental scientists: written in an age before visually striking solutions from computer simulations could be produced in minutes, biological reality was sacrificed for analytical tractability. As remarked on earlier, Turing was not blind to these limitations, even noting the core feature of symmetry breaking—seized upon by future generations of theoretical scientists—should be taken with care: ‘Most of an organism, most of the time, is developing from one pattern into another, rather than from homogeneity into a pattern’ (pp. 71–72).

In this review, we have concentrated on its application to a classic case of embryonic pattern formation, and one ideally suited for integrating theory and experiment: the emergence of feathers and hairs in developing skin. To date, the majority of modelling in skin morphogenesis has occurred at a top-down level: the well-established capacity of a model to generate an underlying pattern has been exploited, with a subsequent adaptation to generate specific features of patterning in a given situation. This was highlighted through a selection of examples, demonstrating that such analyses provide a reasonable basis for corroborating hypotheses and formulating predictions. Indeed, various studies have emerged [27,83,84,86] that have linked modelling and experimental investigations of hair and feather patterning more concretely.

An assumption of many modelling studies has been to simplify the field within which pattern is formed to a two-dimensional surface fixed in time. In certain scenarios, such as a tissue explanted and cultured in a controlled in vitro environment, these assumptions may provide a reasonable approximation of the system, yet in vivo embryonic tissues tend to be three-dimensional, heterogeneous and evolving structures: for example, the developing chicken skin in figure 3a is a multi-layered (epithelial, mesenchymal) tissue that undergoes significant expansion and deformation over the course of patterning. The impact of field growth, shape, curvature and specific boundary conditions on patterning in reaction–diffusion systems has been the subject of considerable investigation [31,46,105,107–115], revealing their potential to determine the robust arrangement and sequence of patterning. For example, simulations of reaction–diffusion equations on growing fields predict the insertion of new patterning elements as the field grows in size, a feature recapitulated in certain examples of biological patterning, including the intercalation of new hair follicles in mammals, pigmentation markings in fishes and additional digits during limb development [26,29,107,111,116].

While studies certainly suggest that a reaction–diffusion model could underpin patterning, we cannot take this as ‘proof’: other models, including those based solely on chemotaxis, epidermal–dermal interactions, adhesion, etc., are also highly adept at recapitulating the observed patterning. With a reasonably well-populated schematic for the molecular-level network that underpins mouse hair follicle morphogenesis now in place (figure 3d), we may therefore ask whether the time is ripe for moving towards a ‘bottom-up’ framework: develop a model based on the underlying molecular network topology and determining whether this is capable of producing the desired pattern. Indeed, that the topology of the network, based on current knowledge, is capable of producing some pattern is not in question: a more detailed investigation of a model consisting solely of the topological loop composed from Edar, BMP and Ctgf interactions alone suggests that pattern formation is possible, at least under certain constraints [48]. Less clear cut is whether a model, when populated with parameters determined from experimental data, is capable of giving the right pattern in the right spatial and temporal scales. While this is likely to be both theoretically and experimentally exhausting, it will only be through such approaches that we can truly start to rule whether a particular network alone is sufficient for generating pattern, or whether additional pathways, components and mechanisms must be uncovered.