Abstract
We quantify the variability in diffuse optical tomography (DOT) sensitivity over the cortical surface in eight young adult subjects. We use the 10/5 electroencephalography system as a basis for our whole-head optical high-density probe design. The contrast-to-noise ratio (CNR) is calculated along with the percentage of the cortex that is above a CNR=0 dB threshold. We also quantify the effect of including vasculature on the forward model and list our assumptions that allow us to estimate light penetration depth in the head. We show that using the 10/5 system for optical probe design allows for measurement of 37% of the cortical surface on average, with a mean CNR in the visible region of 5.5 dB. Certain anatomical regions, such as the lateral occipital cortex, had a very high percentage above the CNR threshold, while other regions such as the cingulate cortex were not measurable. Vasculature blocked optical sensitivity over 1% of the cortex. Cortical coverage was positively correlated with intracranial volume and relative cerebrospinal fluid volume, and negatively correlated with relative scalp volume and skull volume. These contributions allow experimenters to understand how anatomical variation in a subject population may impact DOT or functional near-infrared spectroscopy measurements.
Keywords: medical physics, biological physics
1. Introduction
Functional near-infrared spectroscopy (NIRS) is a noninvasive method for measuring changes in oxyhemoglobin and deoxyhemoglobin concentration in the brain with high temporal resolution (Villringer et al. 1993, Gibson et al. 2005). NIRS is a portable and relatively inexpensive technology that can be used when a subject is walking (Suzuki et al. 2008, Miyai et al. 2001), during rehabilitation from brain injuries (Strangman et al. 2006), or concurrently with other brain imaging technologies (Ou et al. 2009, Moosmann et al. 2003). The portability and low cost of NIRS make it an attractive option for development of clinical applications, however the sensitivity of NIRS is limited to superficial regions of the brain because photons only penetrate a few centimeters into the head.
In diffuse optical tomography (DOT), the interpretation of the cortical origin of NIRS measurements is typically achieved by generating a forward model based on simulated photon propagation in the head. An image inversion is then used to recover the location of hemoglobin concentration changes. Subject-specific head geometries may be used for creating forward models, although some work has also been done using an atlas head geometry (Custo et al. 2010). Photon propagation may be calculated with analytical methods based on the diffusion approximation for simple geometries (Boas et al. 2002). For more complex geometries such as a human head, techniques include finite element methods (Dehghani et al. 2009), or Monte Carlo methods (Boas et al. 2002, Okada & Delpy 2003b, Fang 2010). In this work we use a mesh-based Monte Carlo method as described in Fang (2010) to create forward models for a set of eight MRI-derived head geometries. These eight optical forward models demonstrate the anatomical variability that may be seen in an experimental population.
DOT requires the placement of source and detector optodes on the scalp. The arrangement of these optode locations is often called the head probe design. The optical probe design impacts the sensitivity to the cortex, so the probe used in this analysis is an important consideration. Currently, many investigators design DOT head probes with a fixed source-detector spacing of 2 to 3 cm, and these probes are then placed on the scalp over a region of interest such as the frontal, sensorimotor, visual, or auditory cortex (e.g. Ayaz et al. 2012, Huppert et al. 2006, Plichta et al. 2007, Kennan et al. 2002). Another approach is to use high-density probes that have many overlapping source-detector pairs with a range of source-detector spacings (Boas et al. 2004, Zeff et al. 2007, White et al. 2009). The probe design involves not only the spacing of sources and detectors but also how they are positioned on the scalp. It has been proposed to standardize optode locations on the scalp using derivatives of the 10/20 scalp positioning system developed for eletroencephalography (EEG) (Jurcak et al. 2007), such as the high-density 10/5 system (Oostenveld & Praamstra 2001). The 10/20 and 10/5 systems use anatomical landmarks on the scalp to determine the subject-specific placement of sensors. The four landmarks identified on each subject are the nasion, inion, and left and right pre-auricular points. The distance along the scalp between these points is subdivided to determine sensor placement. In the case of the 10/20 system, the distances are divided into 10% and 20% of the total arc length between landmarks for a set of 21 sensor locations (Oostenveld & Praamstra 2001). The high-density 10/5 system upsamples the 10/20 system and has subdivisions of 10% and 5% of the total arc length between landmarks, for a total of up to 329 sensor locations (Jurcak et al. 2007). Using EEG 10/5 locations for optodes would allow for standardization of probe placement across subjects in a study or between laboratories. However, the EEG locations are based on anatomical landmarks on an individual basis, and this causes variation in source-detector distances between different individuals. Recent work has characterized the variability in placement of 10/5 locations (Jurcak et al. 2007), and the nearest brain locations to the 10/20 EEG locations (Okamoto & Dan 2005), but has not explored the effect that using these standardized optode locations would have on optical sensitivity to the cortex. A quantitative evaluation of the anatomical regions of the cortex that would be measurable using the 10/5 locations for optodes is also needed.
Prior work characterizing the sensitivity of DOT to the cortex has relied on a slab representation of head geometry (Okada & Delpy 2003b), or a single representative three-dimensional head geometry (Boas & Dale 2005). Variations in skull and scalp thickness over the head have been quantified, (Okamoto et al. 2004), but the information was strictly geometrically based on anatomy and photon propagation in this complex geometry was not investigated. Prior work can therefore provide guidelines about optical sensitivity on the cortex but it does not inform an experimental investigator if a particular cortical region of interest is likely to be measurable with DOT in a population of subjects. A quantitative study is needed to understand the variability in optical sensitivity over the cortex due to anatomical variation in features such as skull and scalp thickness, sulcal and gyral geometry, and vessel position and size. In addition, blood in vessels is highly light absorbing and many large veins are located between the cortical surface and the outside of the scalp. Some work has been done modeling the effect of vessels on signal reconstruction (Dehaes et al. 2011), but this work was limited to the occipital region of the brain and did not explore population variability in vasculature.
Our approach is to use a full head probe design based on the 10/5 system. Light propagation is simulated using these optode locations, and the optical sensitivity is calculated in terms of a contrast-to-noise ratio (CNR) for the head geometries with and without vasculature. The percentage of the cortex that is above a detection threshold for each head model is reported. Light penetration depth is quantified, as are assumptions about the optical instrument used that allow us to quantify the CNR over the cortex. Differences in sensitivity between subjects are explored in terms of their anatomical features such as skull and scalp thickness. The percentage of cortex visible and CNR are reported for anatomical regions. Correlations between the cortical coverage and anatomical metrics are also reported.
The main contributions of this work are estimating variability in DOT sensitivity over the cortex due to anatomical variations, quantifying which regions of the cortex are most amenable to measurement with DOT, and assessing the forward model variations due to the presence of large pial blood vessels. These contributions allow experimenters to understand how anatomical variation in a subject population may influence DOT or functional NIRS measurements.
2. Methods
2.1. Head models for photon propagation simulation
Eight realistic head models were generated from the probabilistically segmented head models in the BrainWeb Database (Aubert-Broche et al. 2006). These head models are voxel-based and have a probability assigned for each tissue type in each voxel. Subjects were chosen that spanned the range of total head volume available in the database. The mean age of the subjects in the BrainWeb Database was reported as 29.6 years with a range from 24–37 years, and the participants were half female and half male (Aubert-Broche et al. 2006). We expect that the subjects in the subset used in this study have similar demographics. The tissue types included in the head geometries used for optical forward modeling were scalp, skull, cerebrospinal fluid (CSF), gray matter, white matter, and vessels. Models of the same eight heads without vessels were created by replacing the vessel voxels with the next most probable tissue type and recreating the mesh. The BrainWeb head model segmentations contain more tissue types than we require for this study, so the “fat,” “around fat,” “muscle,” and “muscle/skin” tissues were mapped to the scalp class, and the “dura” and “bone marrow” classes were mapped to the skull class. Tetrahedral volume meshes were created from the voxel-based head models using the iso2mesh MATLAB toolbox (Fang & Boas 2009) using the CGAL mesher (CGAL n.d.) with a maximum element volume size of 3 mm3 and a maximum radius of the Delaunay sphere of 2 mm. An example volume mesh is shown in Figure 1. Optical properties for each tissue type are shown in Table 1. Scalp, skull, and cerebrospinal fluid (CSF) optical properties are from Strangman (2003), gray matter and white matter optical properties are from Yaroslavesky (2002) and vessel optical properties are from Roggan (1999) which were derived from circulating blood. There is disagreement in the literature about the values of the optical properties for in vivo head tissues. The sources we used for optical properties are near the middle of their reported range and have been used in other simulation studies (e.g. Custo et al. 2010, Fang 2010).
Figure 1.
Left: Example sagittal slice through volumetric head mesh. Color indicates tissue type. Middle: Vessel-only mesh, sagittal view. Right: Vessel-only mesh, occipital view. Vessel-only mesh shows the spatial extent of the vasculature in the total head mesh.
Table 1.
Tissue optical properties, references in section 2.1.
| Tissue class | μa (mm−1) | μs(mm−1) | g | n |
|---|---|---|---|---|
| skull | 0.0101 | 100 | 0.99 | 1.37 |
| scalp | 0.0101 | 80 | 0.99 | 1.37 |
| CSF | 0.0004 | 1 | 0.99 | 1.37 |
| gray matter | 0.02 | 8.4 | 0.90 | 1.37 |
| white matter | 0.07 | 40.1 | 0.85 | 1.37 |
| vessel | 0.7 | 80 | 0.98 | 1.37 |
2.2. Virtual optode placement
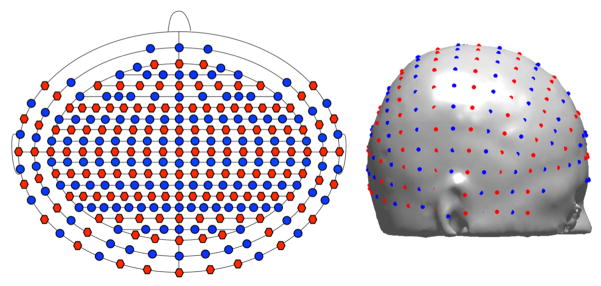
A virtual 10/5 system was placed on the scalp using a three step process. First, the NFRI MATLAB toolbox (Jurcak et al. 2007) was used to find the 10/10 optode positions on the head model scalp based on manual selection of nasion, inion, left preauricular and right preauricular fiducial landmarks. A linear transformation matrix was calculated from the 10/10 coordinate locations in MNI space (Oostenveld & Praamstra 2001) to the 10/10 coordinates on the scalp of the segmented head model. This transform was applied to the MNI 10/5 coordinate locations (Oostenveld & Praamstra 2001) to find the remaining 10/5 locations on the model. Finally, the optode positions were registered and projected to the mesh surface using the Metch MATLAB toolbox (Fang 2011) to align them with the head volume mesh and find the volume element enclosing each optode location. A subset of the 10/5 locations were used that had an inter-optode spacing of at least 1 cm. Sources and detectors were arranged in alternating coronal rows. While some investigators suggest that using a hexagonal layout is better for limiting the dynamic range needed at the detector (Boas et al. 2004), alternating rows of sources and detectors allows for more source-detector separations in the desired length range from 10 mm to 45 mm. The outer bound of 45 mm was used as that was approximately at the noise floor for our setup and assumptions. The total number of modeled optode locations was 286, which included all 10/10 locations and a subset of the 10/5 only locations. Ten of these locations (TTP9, TTP9h, TTP7, TTP10, TTP10h, TTP8, TP9, TP9h, TP10, TP10h) were excluded from further analysis because they usually were located on the ears. The optode positions are shown in schematic and realistic locations in Figure 2.
Figure 2.
Laser sources are red, detectors are blue. A schematic of optode locations is on the left. The front of the head corresponds to the top of the schematic. Optode locations on the scalp are shown on the right.
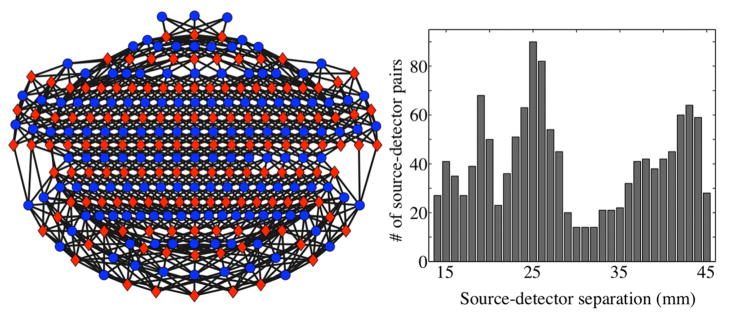
An example of the source-detector pairs for one subject and a histogram of the source-detector pair separations is shown in Figure 3. All source-detector pairs with separations from 10 mm to 45 mm were included in the probe design. Subjects head size varies so the number of source-detector pairs varies with subject. The number of source-detector pairs per subject was 1288 on average with a range from 1236 to 1332. The mean source-detector separation over all subjects and source-detector pairs was 29.3 mm.
Figure 3.
Source-detector pairs are shown for an example subject (Subject 2) in the schematic on the left. Red diamonds indicate source locations, and blue circles indicate detector locations. The front of the head corresponds to the top of the schematic. Black lines denote the selected source-detector pairs. The diagram is a flat projection of a three-dimensional geometry and therefore the actual source-detector distances are not to scale. A histogram of the corresponding source-detector separations is shown on the right, with the number of source-detector pairs in each bin on the y-axis.
2.3. Cortical surface models
Cortical surfaces for each head model were reconstructed using Freesurfer (Dale et al. 1999). These cortical surfaces were created using the standard Freesurfer version 4.5.0 processing stream on the synthetic T1 images generated from the probabilistic tissue segmentations in the BrainWeb Database (Aubert-Broche et al. 2006). Both gray matter (pial) and white matter surfaces were reconstructed. The gray matter surfaces from the reconstruction are used for display. A group average cortical surface was created for display of group averaged results.
2.4. Sensitivity map on the cortical surface
Optical sensitivity (A) represents the change in optical density (OD) for a given source-detector pair (sd) that results from a change in the absorption coefficient (μa) in a mesh volume element (v)
| (1) |
For small changes in μa, sensitivity can be related to the mean partial path length (PPL) the detected light travels within each volume element (Okada & Delpy 2003a)
| (2) |
Monte Carlo simulation was used to estimate the fluence Φ at the nodes (r) from the source (s) or detector (d). Establishing the equivalence of Equations 1 and 2 with Monte Carlo fluence simulation required the use of a sensitivity scaling factor (Zhang et al. 2007). The spatial sensitivity was initially calculated at r using the Rytov approximation
| (3) |
The spatial sensitivity was then computed for each volume element A(sd, v) by averaging the sensitivity at the constituent nodes. The mean optical pathlength (L) for each source-detector pair was calculated from the mean transit time (MTT) of photons estimated from the Monte Carlo simulation by
| (4) |
where ct is the speed of light in the tissue. The volumetric spatial sensitivity A(sd, v) was then rescaled to establish Equation 2 by requiring that
| (5) |
and the same rescaling factors were applied to A(sd, r).
To consider the smooth and complex tissue boundaries, we used the Mesh-based Monte Carlo (MMC) solver (Fang 2010) to calculate the optical forward model. At each optode location, 10 million photons were launched toward the center of the head. Measurements of intensity are converted to absorbance (OD) by
| (6) |
Note that in practice, the relative fluence is replaced by relative light intensity but the ratios are equivalent. All source detector pairs with spacing between 10 mm and 45 mm were included in the calculation weighted by the inverse of its estimated noise. Noise in the detected light intensity was calculated assuming incident power of 5 mW, an optical coupling loss factor of 50%, instrument noise of (Joseph et al. 2006), and a sampling rate of 50 Hz. Sampling was assumed to be time multiplexed over all 136 sources for an overall sampling rate of 6.8 kHz. The wavelength of light was 690 nm. Shot noise equivalent fluence ns was calculated from the square root of the number of photons from a given source location that pass through an infinitesimal spherical surface per unit time at a given detector location. The standard deviation of measurement noise equivalent fluence nm was calculated as
| (7) |
where ni is the instrument noise fluence. The change in OD due to noise in the detected fluence is
| (8) |
which simplifies to
| (9) |
Since Equation 9 is nonlinear, we estimated the noise propagation to ∂OD using a first order Taylor series expansion
| (10) |
Contrast in the volume was calculated using the activation assumptions ∂μa = 0.0001 mm−1 and an activation volume va = 5×5×5 mm3
The contrast to noise ratio (CNR) in absorbance at each element is therefore defined as
| (11) |
We define the total sensitivity for each volume element as the sum of the sensitivity of each source-detector pair. The sensitivity was interpolated from the tetrahedral mesh to a volume with 1 mm3 voxels and sampled at the cortical surface using Freesurfer (Dale et al. 1999). The reported values for CNR on the cortical surface are averages over the gray matter thickness.
2.5. Quantifying intersubject variability in cortical CNR
A sensitivity threshold of CNR=0 dB was chosen and applied across all subjects. The percentage of the cortical surface that was above the threshold was calculated for each hemisphere of each subject. The mean CNR on the cortical surface that was above threshold was also calculated.
Individual subject cortical sensitivity maps were mapped to the averaged cortical surface for intersubject comparison using Freesurfer (Dale et al. 1999). In addition, a mask was made of the cortical areas that were above threshold. These masks were summed to create a map of the number of subjects with sensitivity on the averaged cortical surface.
The average light penetration depth was calculated for each subject by finding the mean distance to the scalp from each node on a CNR=0 dB surface. The CNR=0 dB surface was truncated by the AFpz-T7h-T8h plane and only nodes superior to this plane were used in the calculation to confine the light penetration depth calculation to regions near optodes. To find the average light penetration depth for each subject, we average the shortest nodal distance between the CNR=0 dB surface and the scalp surface weighted by the surface area associated with each node.
2.6. Quantifying cortical region variability in CNR
Freesurfer was used to parcellate each subject’s cortical surface into 36 gyral-based anatomical regions. For details about the parcellation rules, naming conventions, and images of the regions, please see Desikan (2006). The percentage of each anatomical region where CNR was above threshold was calculated for each subject using the head models that contained vasculature. The mean CNR in the visible portion of the regions was also calculated. The group mean coverage and mean CNR for each region was calculated.
2.7. Quantifying vasculature driven variability in cortical CNR
The CNR on the cortical surface was calculated for head models with and without vasculature. Differences in CNR will contain contributions from both including vasculature in the head model and variability due to the statistical noise in the Monte Carlo simulation. To quantify changes due to the Monte Carlo simulation, the simulation was run twice on one head geometry using a different mesh and different random number generator seeds. The CNR on the cortical surface was calculated for both Monte Carlo runs, and the standard deviation of the difference was calculated for nodes where the CNR in the either model was above zero. This standard deviation quantifies the CNR difference contribution from statistical noise in the Monte Carlo simulation, and was used to convert the difference between subject models with vessel or no vessels CNR to a z-score. Nodes on the cortex where the z-score of the difference between the vessels and no vessel models were evaluated for statistical significance (p < 0.05, Bonferroni corrected).
The nodes that were significantly different between the two models were registered to the group average surface and masks were made of these areas. The masks were summed to determine how many subjects showed an effect of vasculature for a particular cortical area. The mean loss of CNR in those regions is also reported.
2.8. Head model anatomical metrics
Anatomical metrics were calculated for comparison with the optical sensitivity metrics, in order to determine which anatomical features drive changes in sensitivity. The relative volume of each tissue type compared to the total head volume was calculated. The ratio of intracranial volume (ICV) to total head volume was also calculated. ICV was defined as the sum of all tissue types that were not scalp or skull. Correlations between the head metrics and cortical sensitivity percent coverage measures are reported. Correlations are also reported between the number of source-detector pairs in each subject’s head probe and cortical CNR.
3. Results
3.1. Volumetric sensitivity
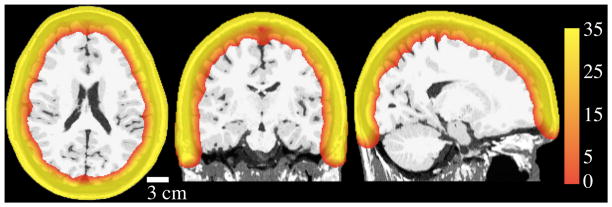
Modeled optical sensitivity in the head is shown for an example subject (Subject 1) in Figure 4. The color scale of the figure is CNR in dB and the threshold is set at 0 dB. The light penetration depth was on average 24.6 mm (std 0.6 mm) for head models with vasculature, and 25.3 mm (std 0.5 mm) for models without vasculature.
Figure 4.
Sample CNR cross-sectional plots for Subject 1. Color shows sensitivity in the volume, displayed on simulated T1. Scale is CNR in dB. Views are horizontal, coronal, and sagittal from left to right. This model included vasculature.
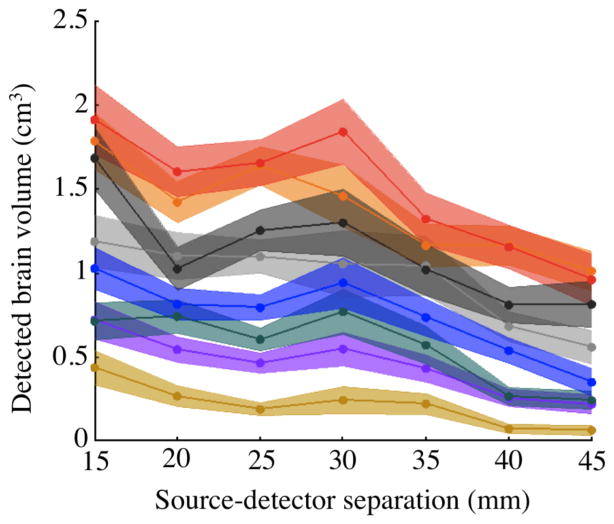
The volume of brain visible for each subject for source-detector pairs with different separations is shown in Figure 5. On average across source-detector pairs and subjects, a source-detector pair measured 0.9 cm3 of brain tissue.
Figure 5.
Mean brain volume detected by individual source-detector pairs above CNR=0 dB threshold vs. source-detector separation. Color indicates subject. All source-detector pairs between 10 mm and 45 mm are included. Source-detector pairs were binned in 5 mm spacing increments and plotted on the x-axis at bin centers. Shaded area shows 95% confidence intervals for each subject.
3.2. Sensitivity variability across subjects
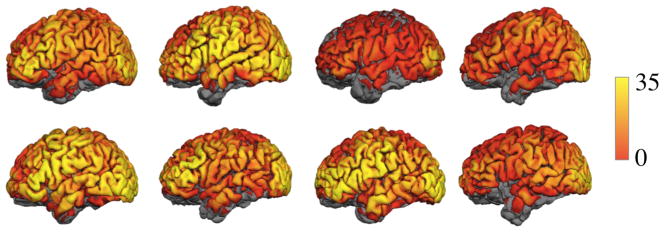
Optical sensitivity varies spatially over the cortex and between subjects. The CNR on the cortex for all subjects is shown in Figure 6 for head models that include vasculature.
Figure 6.
CNR displayed on the cortical surface of 8 subjects, left lateral view. Yellow indicates the highest CNR.
On average the probe is sensitive to 37% of the cortical surface. Sensitivity coverage for a hemisphere varied between 19% and 48% in the population of 8 subjects. The mean CNR in the regions of the cortex that were above threshold varies from 1.7 dB to 8.5 dB with a mean of 5.5 dB. See Table 2 for subject values reported by hemisphere. Cortical coverage percent is strongly correlated with mean CNR (R2 = 0.98, p < 0.01, F = 286). Cortical surface coverage was higher on the left hemisphere as compared to the right (p <0.01, paired two-tailed t-test). Mean CNR was also higher on the left hemisphere as compared to the right (p <0.01, paired two-tailed t-test).
Table 2.
Cortical coverage and mean CNR (dB) for models with vasculature
| Subject | L % | R % | L CNR | R CNR |
|---|---|---|---|---|
| 1 | 38 | 32 | 6.0 | 4.2 |
| 2 | 48 | 44 | 8.5 | 7.3 |
| 3 | 24 | 19 | 2.5 | 1.7 |
| 4 | 33 | 31 | 4.3 | 3.8 |
| 5 | 46 | 43 | 8.4 | 7.3 |
| 6 | 39 | 39 | 6.1 | 5.5 |
| 7 | 35 | 33 | 4.8 | 4.1 |
| 8 | 44 | 39 | 7.5 | 5.7 |
| mean | 38 | 35 | 6.0 | 5.0 |
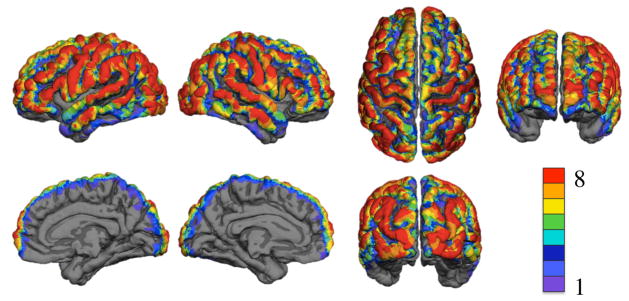
Figure 7 shows the spatial distribution of the number of subjects with CNR above the threshold on the cortex. The number of subjects with cortical CNR above the threshold is represented by a color scale with red indicating that all 8 subjects had sensitivity on that part of the cortex and purple indicating that only one subject had sensitivity on that part of the cortex. The results are displayed on the group averaged surface. All brain views are shown.
Figure 7.
Optical sensitivity displayed on the group averaged surface. Color indicates number of subjects with cortical CNR above the 0 dB threshold. The top row has left lateral, right lateral, superior, and frontal views. The bottom row has right medial, left medial, and occipital views.
3.3. Sensitivity variability across cortical regions
Table 3 reports the mean coverage and CNR of the visible area in the Freesurfer-defined cortical regions across the 8 subjects. Overall coverage of each lobe of the brain is also reported. The parietal lobe had the highest coverage, followed by the frontal, occipital, and temporal lobes. The region with the highest coverage is the lateral occipital cortex. The cingulate cortex is not measurable with this probe design, along with the entorhinal cortex, parahippocampal cortex, and temporal pole regions.
Table 3.
Coverage by region on the left (L) and right (R) hemispheres of the cortex. Percents are cortical surface area with standard deviation in parentheses. CNR is in dB and applies to the visible portion only.
| Region | L% | R% | L CNR | R CNR |
|---|---|---|---|---|
| Parietal lobe | 49 (9) | 46 (10) | 7.7 (2.3) | 6.6 (2.5) |
| inferior parietal cortex | 63 (7) | 59 (10) | 11.0 (2.4) | 9.3 (2.9) |
| postcentral gyrus | 58 (12) | 54 (12) | 9.4 (3.7) | 7.8 (3.4) |
| supramarginal gyrus | 57 (8) | 50 (10) | 9.1 (2.6) | 7.1 (3.0) |
| superior parietal cortex | 53 (13) | 55 (15) | 6.8 (2.5) | 7.1 (3.1) |
| precuneus cortex | 3 (2) | 3 (7) | 0.2 (0.2) | 0.2 (0.5) |
| Frontal lobe | 46 (11) | 40 (11) | 7.0 (2.9) | 5.2 (2.4) |
| frontal pole | 67 (36) | 64 (30) | 9.4 (7.2) | 9.1 (6.0) |
| rostral middle frontal gyrus | 67 (10) | 57 (15) | 10.4 (3.5) | 7.5 (3.3) |
| pars triangularis | 64 (14) | 59 (12) | 12.4 (5.4) | 9.2 (5.0) |
| caudal middle frontal gyrus | 61 (11) | 54 (12) | 9.9 (3.8) | 7.4 (3.4) |
| precentral gyrus | 55 (13) | 50 (14) | 9.0 (3.9) | 7.1 (3.6) |
| pars orbitalis | 54 (18) | 33 (18) | 8.3 (4.9) | 3.5 (2.7) |
| pars opercularis | 48 (15) | 40 (13) | 8.3 (4.5) | 5.4 (2.7) |
| superior frontal gyrus | 45 (12) | 40 (13) | 5.5 (2.8) | 4.1 (2.1) |
| paracentral lobule | 7 (8) | 11 (9) | 0.6 (0.8) | 0.9 (0.9) |
| medial orbitofrontal cortex | 3 (3) | 4 (3) | 0.1 (0.2) | 0.2 (0.2) |
| lateral orbitofrontal cortex | 2 (3) | 0 (0) | 0.1 (0.2) | 0 (0) |
| Occipital lobe | 39 (7) | 39 (7) | 8.1 (2.2) | 7.8 (2.1) |
| lateral occipital cortex | 73 (9) | 73 (6) | 15.4 (3.5) | 15.4 (3.3) |
| cuneus cortex | 15 (14) | 19 (12) | 1.6 (1.6) | 1.9 (1.5) |
| lingual gyrus | 3 (3) | 5 (4) | 0.2 (0.3) | 0.4 (0.4) |
| pericalcarine cortex | 2 (3) | 7 (5) | 0.2 (0.2) | 0.6 (0.5) |
| Temporal lobe | 26 (8) | 23 (7) | 3.7 (1.8) | 3.1 (1.5) |
| middle temporal gyrus | 54 (13) | 48 (9) | 8.0 (3.5) | 6.4 (2.4) |
| superior temporal | 39 (12) | 35 (10) | 5.8 (2.9) | 4.6 (2.4) |
| banks of the superior temporal sulcus | 26 (16) | 15 (11) | 2.7 (2.5) | 1.5 (1.7) |
| inferior temporal gyrus | 20 (10) | 19 (10) | 2.4 (1.5) | 2.5 (1.7) |
| fusiform gyrus | 5 (5) | 3 (3) | 0.6 (0.6) | 0.2 (0.3) |
| transverse temporal gyrus | 2 (2) | 0 (1) | 0.1 (0.1) | 0.0 (0.1) |
| entorhinal cortex | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| parahippocampal cortex | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| temporal pole | 0 (1) | 0 (0) | 0 (0) | 0 (0) |
| Cingulate | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
3.4. Sensitivity variability due to vasculature
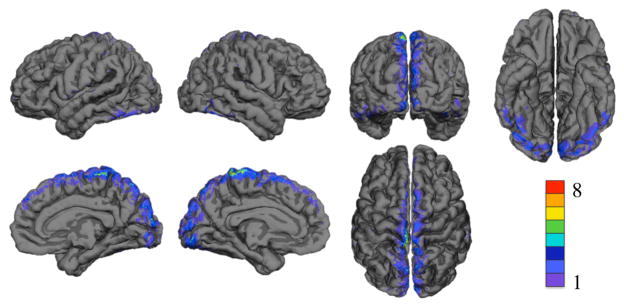
Figure 8 shows the spatial distribution of significant changes in CNR when vasculature was included in the model. Results are displayed on the group averaged cortical surface. Color indicates the number of subjects with reduced sensitivity. On average, including vasculature led to a significant decrease in sensitivity on 1% of the cortex as compared to the forward model that did not include vasculature. The mean difference in CNR in these regions was −0.2 dB. Regions with a significant decrease in sensitivity due to including the vasculature are shown in Table 4. The region with the largest decrease in sensitivity was the cuneus cortex.
Figure 8.
Decrease in optical sensitivity due to including vasculature displayed on the group averaged surface. Color indicates number of subjects with significant decrease in sensitivity. The top row shows left lateral, right lateral, occipital, and inferior views. The bottom row shows right medial, left medial, and superior views.
Table 4.
Difference in coverage percent and mean CNR (dB) from including vasculature, with the standard deviation across subjects in parentheses.
| Region | ΔL % | ΔR % | ΔL CNR | ΔR CNR |
|---|---|---|---|---|
| cuneus cortex | −10 (9)* | −10 (6)* | −1.3 (1.1)* | −1.1 (0.8)* |
| paracentral lobule | −10 (4)* | −8 (4)* | −1.3 (0.8)* | −1.1 (0.6)* |
| lingual gyrus | −4 (3)* | −2 (2)* | −0.8 (0.9)* | −0.3 (.3)* |
| lateral occipital cortex | −4 (4)* | −2 (2)* | −0.6 (0.7) | −0.3 (0.4)* |
| superior parietal cortex | −3 (2)* | −3 (2)* | −0.4 (0.4)* | −0.4 (0.3)* |
| pericalcarine cortex | −2 (2)* | −3 (3) | −0.2 (0.3) | −0.5 (0.8) |
| fusiform gyrus | −2 (3) | −2 (1)* | −0.4 (0.6) | −0.4 (0.4)* |
| precuneus cortex | −2 (1)* | −2 (2)* | −0.3 (0.2)* | −0.4 (0.4)* |
| precentral gyrus | −2 (1)* | −1 (2) | −0.2 (0.1)* | −0.1 (0.2) |
| postcentral gyrus | −2 (1)* | −1 (1)* | −0.2 (0.1)* | −0.1 (0.2) |
| superior frontal gyrus | −1 (1)* | −2 (1)* | −0.2 (0.2)* | −0.2 (0.2)* |
| inferior temporal gyrus | −1 (1)* | −1 (1)* | −0.2 (0.3)* | −0.2 (0.2)* |
Significant differences (p <0.05, two-tailed t-test) are indicated by *.
3.5. Sensitivity variability correlations
Both probe design and individual differences in anatomy impact the sensitivity on the cortex. The probe design we used is flexible and depends on head size so the details of each probe setup are subject-specific. We found that the number of SD pairs is correlated with cortical coverage (R2 = 0.65, p < 0.05, F = 11).
Subject anatomy is also related to the optical cortical sensitivity. Significant positive correlations were found between percent cortical coverage and relative CSF volume (R2 = 0.80, p < 0.01, F = 23) and gray matter volume (R2 = 0.77, p < 0.01, F = 20). Relative intracranial volume was also positively correlated with cortical coverage (R2 = 0.96, p < 0.01, F = 163). Significant negative correlations were found between percent cortical coverage and relative scalp volume (R2 = 0.88, p < 0.01, F = 52) and skull volume (R2 = 0.63, p < 0.05, F = 10). Relative vessel volume, white matter volume, and total head volume were not significantly correlated with coverage percent.
4. Discussion
We propose the 10/5 system with DOT sources and detector arranged in alternating coronal rows as a candidate for standardizing the design of DOT whole-head probes. This probe design has a high number of source-detector pairs in the 1–4.5 cm separation range and relatively uniform sensitivity to superficial cortex compared to other probe layouts we evaluated in designing this study. DOT sensitivity over the cortex using this probe is variable with subject, over cortical regions, and to a lesser extent with inclusion of vasculature in the forward model. DOT is sensitive to 37% of the cortex on average, however the activation assumptions are fairly conservative in this analysis so more of the cortex may be visible for some tasks.
We found slightly higher coverage and sensitivity on the left hemisphere as compared to the right, as shown in Table 2. On average, there were 18 more source-detector pairs above the noise floor on the left side than the right side, out of a total mean of 1288 source-detector pairs per subject. The head is known to be asymmetric with a slightly larger right side (Homan et al. 1987) when sides are defined using the 10/20 landmarks. The larger size of the right side of the head leads to a decrease in source-detector pairs and a subsequent decrease in sensitivity on the right cortical hemisphere as opposed to the left. The brain is also known to be asymmetric, which could potentially contribute to this observation (Toga & Thompson 2003).
Changes in CNR that occur spatially over the cortex match well with known variability in skull thickness (Moreira-Gonzalez et al. 2006), and total skull and scalp thickness (Okamoto et al. 2004). Skull and scalp thickness is not uniform over the head, which is a significant factor in the resulting variability in DOT sensitivity between subjects (Figure 5, Table 2) and between different cortical regions (Figures 6 and 7, Table 3). Brain regions with high CNR in our simulations should correspond to regions with high experimentally measured spatial resolution. Experimental confirmation of high DOT sensitivity to the lateral occipital cortex has been shown with a high-density probe similar to the one presented here (Zeff et al. 2007).
Including vasculature in the forward model caused a significant decrease in visibility in 1% of the cortex, although some cortical regions lost up to 10% coverage. The results from comparing models with and without vasculature agree with Dehaes (2011) in that changes in sensitivity due to vasculature are small for a high density probe. We report that changes in sensitivity due to including vasculature are smaller than changes in sensitivity due to individual anatomy. This result suggests that including vasculature in optical forward models is not necessary, as changes in optical sensitivity due to inclusion of vasculature are small compared to intersubject variability in optical sensitivity arising from skull thickness, scalp thickness, and head size differences.
We show a positive correlation between relative ICV and CSF volume and cortical percent coverage. As intracranial CSF volume is known to increase with age (Grant et al. 1987), this suggests that older individuals would be good subjects for DOT studies. We show a negative correlation between relative skull and scalp volume and cortical percent coverage. Unfortunately, these anatomical metrics do not provide a way to a priori determine if a subject will have good cortical coverage from DOT without an MRI. The BrainWeb Database also does not reveal demographic information such as age or gender of the subjects used to create the head models, so it is not possible to determine if those demographic factors impact DOT sensitivity from our study.
The DOT optode density with whole-head coverage we present is technically achievable with current DOT instrumentation but requires more sources and detectors than are available in the standard commercial configurations. Experimental investigators may choose a subset of these optode locations that are near their region of interest to form a probe. We expect that using this whole-head probe design may become feasible with advances in hardware technology.
One limitation of this study is that our vasculature models are limited to large vessels, including mostly draining veins. Smaller vessels may also affect optical sensitivity, although we would expect the changes would be small given the limited impact on the forward model of the large vessels. We also used a relatively small number of photons for our optical simulations. Many studies use at least 10 times as many photons (Dehaes et al. 2011, Fang 2010). However, for our study, using that many photons would have been prohibitively computationally expensive due to the large number of source and detector locations in our head probe.
One other limitation of the study is the results are for a standardized probe design, which we have described in detail to aid experimenters in reproducing our results, but may not be applicable to a particular experimental setup unless our design is reproduced. The modeled head anatomy is from young adults only and due to computational expense we only modeled 8 subjects. We chose optical properties, instrument properties and brain activation properties that we believe to be reasonable but the true values of these properties are not known. Errors in the assumptions we made in our calculations will have both nonlinear and linear effects on our estimated CNR. For example, if the activation volume increased by a factor of 2, the CNR would increase by 6 dB as indicated by Equation 11. Change in activation ∂μa would impact CNR the same way as activation volume. Baseline tissue μa will affect the light penetration depth exponentially which will result in a linear effect on CNR results in dB. We expect that our analysis is relatively insensitive to tissue μs values, as the photons are propagating in the diffusion regime. The qualitative impact of these changes on light penetration depth and the resulting percentage of cortical coverage can be estimated with Figure 4. Future work in this area could provide a careful analysis of the sensitivity of the CNR calculations to the specified parameters and their likely margins of error.
5. Conclusion
Sensitivity of DOT to selected cortical regions is high with 50% or more visible in the inferior parietal cortex, postcentral gyrus, supramarginal gyrus, superior parietal cortex, frontal pole, rostral middle frontal gyrus, pars triangularis, caudal middle frontal gyrus, precentral gyrus, lateral occipital cortex, middle temporal gyrus. This analysis suggests that these regions are potential targets for clinical applications of DOT because they can be reliably measured with a standardized probe design despite variability in individual anatomy.
Cortical hemispheric coverage varied from 19% to 48%, with an average of 37%. Mean CNR on a hemisphere ranged from 1.7 dB to 8.5 dB. Total cortical coverage varied from 22% to 46% for a subject. There is a considerable amount of variability between subjects in the amount of visible cortical area. CNR and percentage of cortical coverage were linearly related. This analysis also shows that selected cortical regions may not be accessible by DOT, namely the cingulate cortex, entorhinal cortex, parahippocampal cortex, and temporal pole.
Our assessment of CNR and percent coverage are applicable to all DOT studies, regardless of the inverse model used. We did not attempt to evaluate the resolution or localization accuracy of DOT and for that an inverse model is required. Quantifying variability in resolution or localization accuracy would be a useful topic for further study.
Acknowledgments
The authors wish to thank David Boas for his advice on this project. Partial funding was provided by NSF (Graduate Research Fellowship to KLP), NIH (5R01EB006385), a Director’s DISCOVERY grant from the Institute for Quantitative Biomedical Sciences, the Thayer School of Engineering at Dartmouth, and the Bill & Melinda Gates Foundation (#OPP1035992).
References
- Aubert-Broche B, Griffin M, Pike B, Evans A, Collins L. Twenty new digital brain phantoms for creation of validation image data bases. IEEE transactions on medical imaging. 2006;25(11):1410–1416. doi: 10.1109/TMI.2006.883453. [DOI] [PubMed] [Google Scholar]
- Ayaz H, Shewokis PA, Bunce S, Izzetoglu K, Willems B, Onaral B. Optical brain monitoring for operator training and mental workload assessment. NeuroImage. 2012;59(1):36–47. doi: 10.1016/j.neuroimage.2011.06.023. [DOI] [PubMed] [Google Scholar]
- Boas DA, Chen K, Grebert D, Franceschini MA. Improving the diffuse optical imaging spatial resolution of the cerebral hemodynamic response to brain activation in humans. Optics letters. 2004;29(13):1506–1508. doi: 10.1364/ol.29.001506. [DOI] [PubMed] [Google Scholar]
- Boas DA, Culver J, Stott J, Dunn A. Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head. Optics express. 2002;10(3):159–170. doi: 10.1364/oe.10.000159. [DOI] [PubMed] [Google Scholar]
- Boas DA, Dale A. Simulation study of magnetic resonance imaging-guided cortically constrained diffuse optical tomography of human brain function. Applied optics. 2005;44(10):1957–1968. doi: 10.1364/ao.44.001957. [DOI] [PubMed] [Google Scholar]
- CGAL. Computational Geometry Algorithms Library. n.d http://www.cgal.org.
- Custo A, Boas DA, Tsuzuki D, Dan I, Mesquita R, Fischl B, Grimson WEL, Wells W., III Anatomical atlas-guided diffuse optical tomography of brain activation. NeuroImage. 2010;49(1):561–567. doi: 10.1016/j.neuroimage.2009.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale A, Fischl B, Sereno M. Cortical surface-based analysis. I. Segmentation and surface reconstruction. NeuroImage. 1999;9(2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dehaes M, Gagnon L, Lesage F, Pélégrini-Issac M, Vignaud A, Valabrègue R, Grebe R, Wallois F, Benali H. Quantitative investigation of the effect of the extra-cerebral vasculature in diffuse optical imaging: a simulation study. Biomedical optics express. 2011;2(3):680–695. doi: 10.1364/BOE.2.000680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehghani H, Eames ME, Yalavarthy PK, Davis SC, Srinivasan S, Carpenter CM, Pogue BW, Paulsen KD. Near infrared optical tomography using NIRFAST: Algorithm for numerical model and image reconstruction. Communications in Numerical Methods in Engineering. 2009;25(6):711–732. doi: 10.1002/cnm.1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan R, Ségonne F, Fischl B, Quinn B, Dickerson B, Blacker D, Buckner R, Dale A, Maguire P, Hyman B, Albert M, Killiany R. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage. 2006;31(3):968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Fang Q. Mesh-based Monte Carlo method using fast ray-tracing in Plücker coordinates. Biomedical optics express. 2010;1(1):165–175. doi: 10.1364/BOE.1.000165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Q. Metch: a mesh/volume registration toolbox. 2011 http://iso2mesh.sourceforge.net/cgi-bin/index.cgi?metch.
- Fang Q, Boas DA. Tetrahedral mesh generation from volumetric binary and grayscale images. Proceedings of IEEE International Symposium on Biomedical Imaging; 2009; 2009. pp. 1142–1145. [Google Scholar]
- Gibson A, Hebden J, Arridge S. Recent advances in diffuse optical imaging. Physics in Medicine and Biology. 2005;50(4):R1–R43. doi: 10.1088/0031-9155/50/4/r01. [DOI] [PubMed] [Google Scholar]
- Grant R, Condon B, Lawrence A, Hadley DM, Patterson J, Bone I, Teasdale GM. Human cranial CSF volumes measured by MRI: Sex and age influences. Magnetic Resonance Imaging. 1987;5(6):465–468. doi: 10.1016/0730-725x(87)90380-8. [DOI] [PubMed] [Google Scholar]
- Homan R, Herman J, Purdy P. Cerebral location of international 10–20 system electrode placement. Electroencephalography and Clinical Neurophysiology. 1987;66(4):376–382. doi: 10.1016/0013-4694(87)90206-9. [DOI] [PubMed] [Google Scholar]
- Huppert TJ, Hoge RD, Diamond SG, Franceschini MA, Boas DA. A temporal comparison of BOLD, ASL, and NIRS hemodynamic responses to motor stimuli in adult humans. NeuroImage. 2006;29(2):368–382. doi: 10.1016/j.neuroimage.2005.08.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph DK, Huppert TJ, Franceschini MA, Boas DA. Diffuse optical tomography system to image brain activation with improved spatial resolution and validation with functional magnetic resonance imaging. Applied optics. 2006;45(31):8142–10. doi: 10.1364/ao.45.008142. [DOI] [PubMed] [Google Scholar]
- Jurcak V, Tsuzuki D, Dan I. 10/20, 10/10, and 10/5 systems revisited: Their validity as relative head-surface-based positioning systems. NeuroImage. 2007;34(4):1600–1611. doi: 10.1016/j.neuroimage.2006.09.024. [DOI] [PubMed] [Google Scholar]
- Kennan RP, Horovitz SG, Maki A, Yamashita Y, Koizumi H, Gore JC. Simultaneous Recording of Event-Related Auditory Oddball Response Using Transcranial Near Infrared Optical Topography and Surface EEG. NeuroImage. 2002;16(3):587–592. doi: 10.1006/nimg.2002.1060. [DOI] [PubMed] [Google Scholar]
- Miyai I, Tanabe HC, Sase I, Eda H, Oda I, Konishi I, Tsunazawa Y, Suzuki T, Yanagida T, Kubota K. Cortical Mapping of Gait in Humans: A Near-Infrared Spectroscopic Topography Study. NeuroImage. 2001;14(5):1186–1192. doi: 10.1006/nimg.2001.0905. [DOI] [PubMed] [Google Scholar]
- Moosmann M, Ritter P, Krastel I, Brink A, Thees S, Blankenburg F, Taskin B, Obrig H, Villringer A. Correlates of alpha rhythm in functional magnetic resonance imaging and near infrared spectroscopy. NeuroImage. 2003;20(1):145–158. doi: 10.1016/s1053-8119(03)00344-6. [DOI] [PubMed] [Google Scholar]
- Moreira-Gonzalez A, Papay F, Zins J. Calvarial thickness and its relation to cranial bone harvest. Plastic and reconstructive surgery. 2006;117(6):1964–1971. doi: 10.1097/01.prs.0000209933.78532.a7. [DOI] [PubMed] [Google Scholar]
- Okada E, Delpy D. ‘Near-Infrared Light Propagation in an Adult Head Model. I. Modeling of Low-Level Scattering in the Cerebrospinal Fluid Layer. Applied optics. 2003a;42(16):2906–2914. doi: 10.1364/ao.42.002906. [DOI] [PubMed] [Google Scholar]
- Okada E, Delpy D. ‘Near-Infrared Light Propagation in an Adult Head Model. II. Effect of Superficial Tissue Thickness on the Sensitivity of the Near-Infrared Spectroscopy Signal. Applied optics. 2003b;42(16):2915–2922. doi: 10.1364/ao.42.002915. [DOI] [PubMed] [Google Scholar]
- Okamoto M, Dan H, Sakamoto K, Takeo K, Shimizu K, Kohno S, Oda I, Isobe S, Suzuki T, Kohyama K. Three-dimensional probabilistic anatomical cranio-cerebral correlation via the international 10–20 system oriented for transcranial functional brain mapping. NeuroImage. 2004;21(1):99–111. doi: 10.1016/j.neuroimage.2003.08.026. [DOI] [PubMed] [Google Scholar]
- Okamoto M, Dan I. Automated cortical projection of head-surface locations for transcranial functional brain mapping. NeuroImage. 2005;26(1):18–28. doi: 10.1016/j.neuroimage.2005.01.018. [DOI] [PubMed] [Google Scholar]
- Oostenveld R, Praamstra P. The five percent electrode system for high-resolution EEG and ERP measurements. Clinical neurophysiology : official journal of the International Federation of Clinical Neurophysiology. 2001;112(4):713–719. doi: 10.1016/s1388-2457(00)00527-7. [DOI] [PubMed] [Google Scholar]
- Ou W, Nissilä I, Radhakrishnan H, Boas DA, Hamalainen MS, Franceschini MA. Study of neurovascular coupling in humans via simultaneous magnetoencephalography and diffuse optical imaging acquisition. NeuroImage. 2009;46(3):624–632. doi: 10.1016/j.neuroimage.2009.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plichta MM, Heinzel S, Ehlis AC, Pauli P, Fallgatter AJ. Model-based analysis of rapid event-related functional near-infrared spectroscopy (NIRS) data: A parametric validation study. NeuroImage. 2007;35(2):625–634. doi: 10.1016/j.neuroimage.2006.11.028. [DOI] [PubMed] [Google Scholar]
- Roggan A, Friebel M, Doerschel K, Hahn A, Mueller G. Optical properties of circulating human blood in the wavelength range 400–2500 nm. Journal of Biomedical Optics. 1999;4(1):36–46. doi: 10.1117/1.429919. [DOI] [PubMed] [Google Scholar]
- Strangman G, Franceschini M, Boas DA. Factors affecting the accuracy of near-infrared spectroscopy concentration calculations for focal changes in oxygenation parameters. NeuroImage. 2003;18(4):865–879. doi: 10.1016/s1053-8119(03)00021-1. [DOI] [PubMed] [Google Scholar]
- Strangman G, Goldstein R, Rauch SL, Stein J. Near-Infrared Spectroscopy and Imaging for Investigating Stroke Rehabilitation: Test-Retest Reliability and Review of the Literature. Archives of Physical Medicine and Rehabilitation. 2006;87(12):12–19. doi: 10.1016/j.apmr.2006.07.269. [DOI] [PubMed] [Google Scholar]
- Suzuki M, Miyai I, Ono T, Kubota K. Activities in the frontal cortex and gait performance are modulated by preparation. An fNIRS study. NeuroImage. 2008;39(2):600–607. doi: 10.1016/j.neuroimage.2007.08.044. [DOI] [PubMed] [Google Scholar]
- Toga A, Thompson P. Mapping brain asymmetry. Nature reviews. Neuroscience. 2003;4(1):37–48. doi: 10.1038/nrn1009. [DOI] [PubMed] [Google Scholar]
- Villringer A, Planck J, Hock C, Schleinkofer L, Dirnagl U. Near infrared spectroscopy (NIRS): A new tool to study hemodynamic changes during activation of brain function in human adults. Neuroscience Letters. 1993;154(1–2):101–104. doi: 10.1016/0304-3940(93)90181-j. [DOI] [PubMed] [Google Scholar]
- White BR, Snyder AZ, Cohen AL, Petersen SE, Raichle ME, Schlaggar BL, Culver JP. Resting-state functional connectivity in the human brain revealed with diffuse optical tomography. NeuroImage. 2009;47(1):148–156. doi: 10.1016/j.neuroimage.2009.03.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaroslavsky A, Schulze P, Yaroslavsky I, Schober R, Ulrich F, Schwarzmaier H. Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near infrared spectral range. Physics in Medicine and Biology. 2002;47(12):2059–2073. doi: 10.1088/0031-9155/47/12/305. [DOI] [PubMed] [Google Scholar]
- Zeff BW, White BR, Dehghani H, Schlaggar BL, Culver JP. Retinotopic mapping of adult human visual cortex with high-density diffuse optical tomography. PNAS. 2007;104(29):12169–12174. doi: 10.1073/pnas.0611266104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, Brown E, Strangman G. Adaptive filtering for global interference cancellation and real-time recovery of evoked brain activity: a Monte Carlo simulation study. Journal of Biomedical Optics. 2007;12(4):044014. doi: 10.1117/1.2754714. [DOI] [PubMed] [Google Scholar]